Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
1
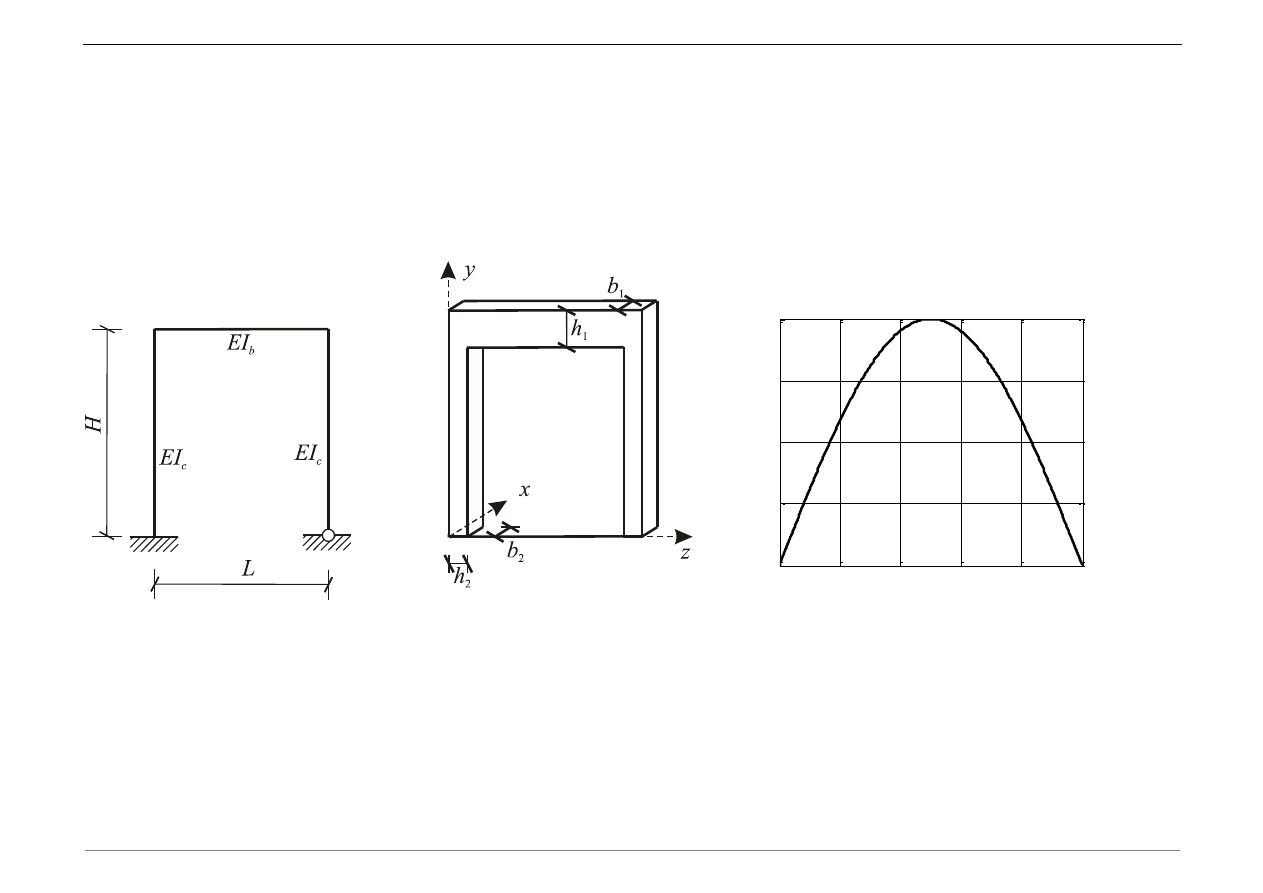
Wyznaczyć częstości i postacie drgań własnych ramy portalowej. Wykreślić postacie
drgań odpowiadające trzem pierwszym częstościom drgań własnych. Obliczyć
przemieszczenie u(t) wywołane obciążeniem p(t) korzystając z metody różnic centralnych.
Zastosować macierzową metodę przemieszczeń (dyskretyzacja na 9 elementów
belkowych). Dane: L, H, b
1
, h
1
, b
2
, h
2
, E,
,
,
0
0.02
0.04
0.06
0.08
0.1
0
500
1000
1500
2000
p
[
N
]
Rozwiązanie:
Napisać program realizujący zadanie w środowisku MATLAB. Jako bazy użyć gotowy
skrypt o nazwie cwiczenie_5_szablon.m. Program ten wykorzystuje następujące funkcje:
ke_beam, m_beam, agreg_k_beam, agreg_m_beam, mrc (funkcje należy skopiować do
katalogu roboczego).
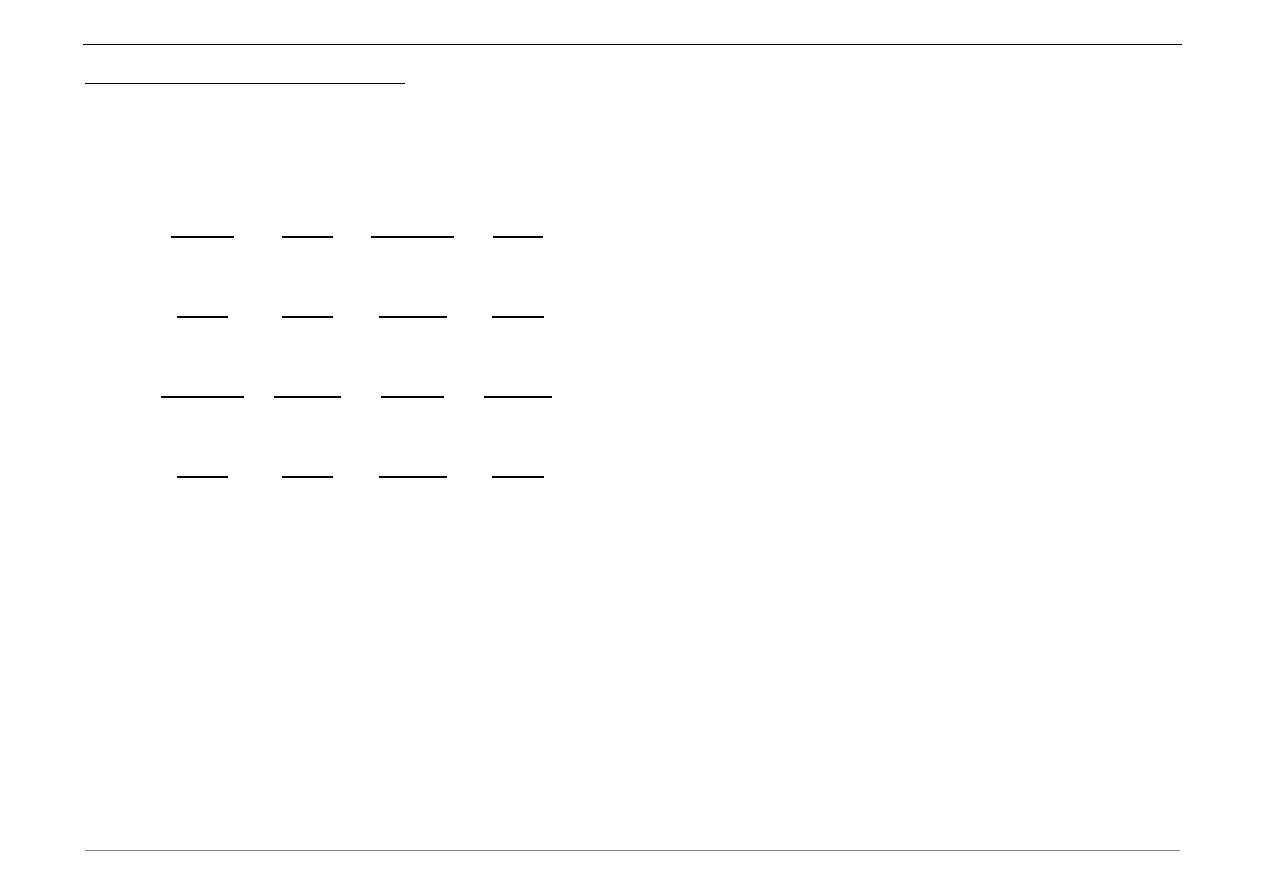
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
2
Opis stosowanych funkcji:
[Ke]=ke_beam(EJ,L)
Funkcja generuje lokalną macierz sztywności elementu belkowego:
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
6
4
6
2
12
6
12
6
6
2
6
4
e
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
EI
EI
EI
EI
L
L
L
L
k
%---------------------------------------------------------------
% WEJSCIE:
% EJ = sztywność giętna EJ
% L = długość elementu
%----------------------------------------------------------------
% WYJSCIE:
% Ke = macierz sztywności 4x4 względem przemieszczeń:
% v_a,fi_a,v_b,fi_b
%----------------------------------------------------------------
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
3
[Me]=me_beam(mi,L)
Funkcja generuje lokalną macierz mas elementu belkowego:
2
2
2
2
156
22
54
13
22
4
13
3
54
13
156
22
420
13
3
22
4
e
L
L
L
L
L
L
L
L
L
L
L
L
L
m
%---------------------------------------------------------------
% WEJSCIE:
% mi = rozkład masy na długości elementu
% L = długość elementu
%----------------------------------------------------------------
% WYJSCIE:
% Me = macierz mas 4x4 względem przemieszczeń:
% v_a,fi_a,v_b,fi_b
%----------------------------------------------------------------
Uwaga: funkcje ke_beam oraz me_beam nie są używane bezpośrednio w skrypcie
cwiczenie_5_przyklad.m. Do funkcji ke_beam oraz me_beam odwołują się funkcje
agreg_k_beam oraz agreg_m_beam.
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
4
[KG]=agreg_k_beam(Neq,Ne,CE,ALOK)
Funkcja agregacji globalnej macierzy sztywności dla płaskiego elementu belkowego
1
el
n
i
e
i
K
k
% WEJSCIE:
% Neq - liczba niewiadomych uogólnionych przemieszczeń
% Ne - liczba elementów
% CE - tablica cech elementów
% ALOK - tablica wektorów alokacji
%----------------------------------------------------------------
% WYJSCIE:
% KG - globalna macierz sztywności
[MG]=agreg_m_beam(Neq,Ne,CE,ALOK)
Funkcja agregacji globalnej macierzy mas dla płaskiego elementu belkowego
1
el
n
i
e
i
M
m
% WEJSCIE:
% Neq - liczba niewiadomych uogólnionych przemieszczeń
% Ne - liczba elementów
% CE - tablica cech elementów
% ALOK - tablica wektorów alokacji
%----------------------------------------------------------------
% WYJSCIE:
% MG - globalna macierz mas
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
5
[u,v,a]=mrc(M,C,K,P,t,u0,v0)
Funkcja całkowania równań ruchu metodą różnic centralnych.
%---------------------------------------------------------
% WEJSCIE:
% M - macierz mas (n x n)
% C - macierz tłumienia (n x n)
% K - macierz sztywności (n x n)
% P - wektor obciążeń zewnętrznych (n x nt)
% t - wektor czasu (1 x nt)
% u0 - wektor przemieszczeń początkowych (1 x n)
% v0 - wektor prędkości początkowych (1 x n)
%----------------------------------------------------------
% WYJSCIE:
% u - wektor przemieszczeń (n x nt)
% v - wektor prędkości (n x nt)
% a - wektor przyspieszeń (n x nt)
%----------------------------------------------------------
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
6
Kolejność obliczeń:
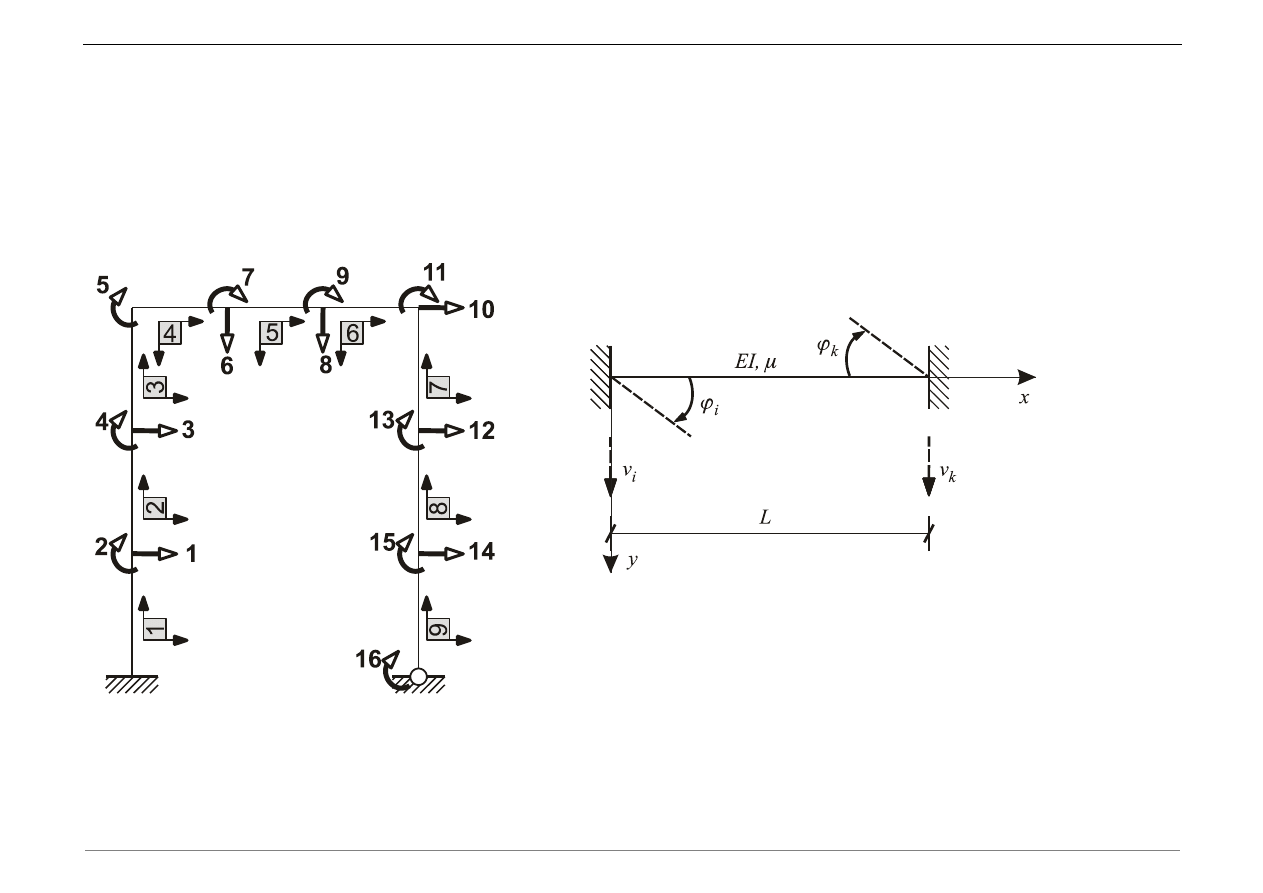
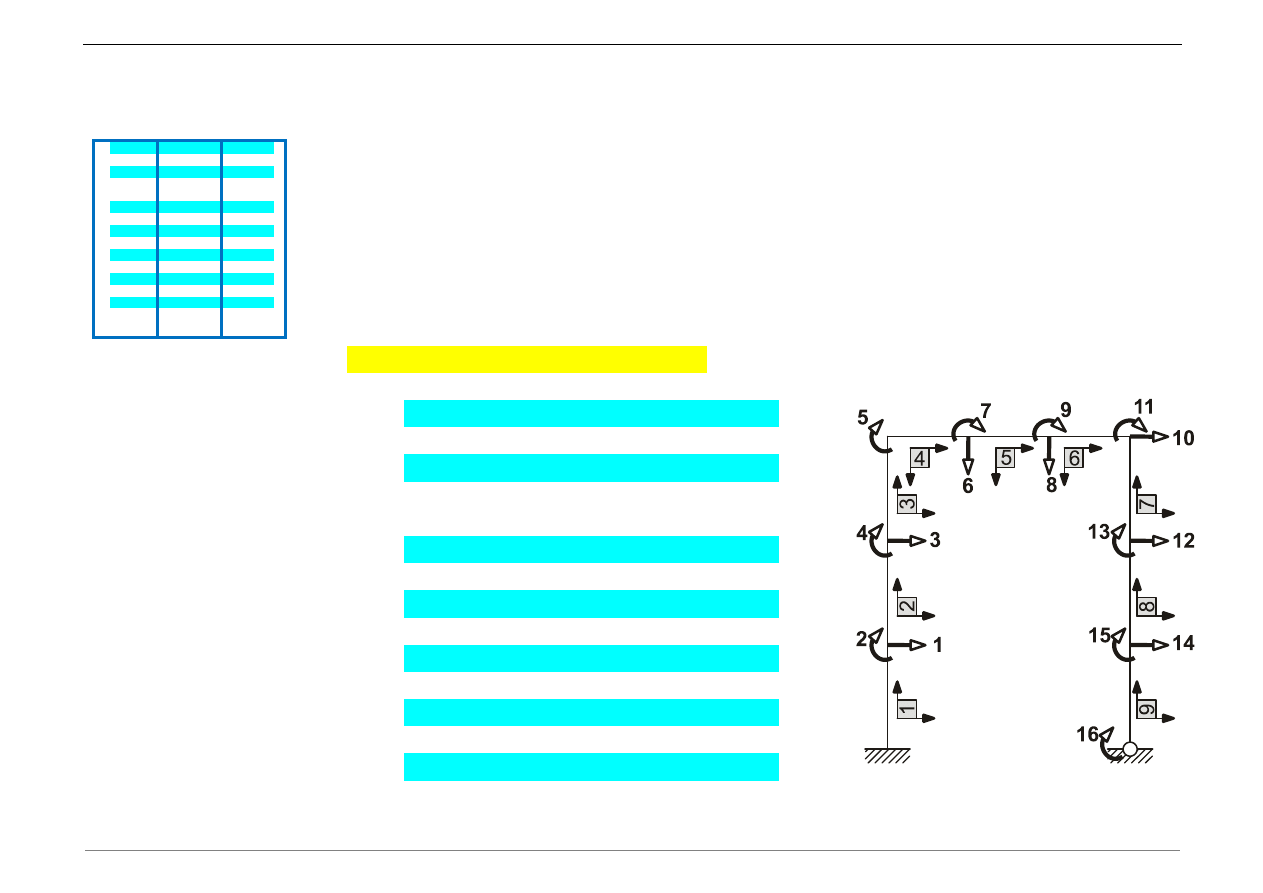
a) Dokonać dyskretyzacji układu stosując element belkowy (z pełnym kompletem
więzów).
Wektor przemieszczeń węzłowych elementu belkowego:
T
e
i
i
k
k
v
v
q
.
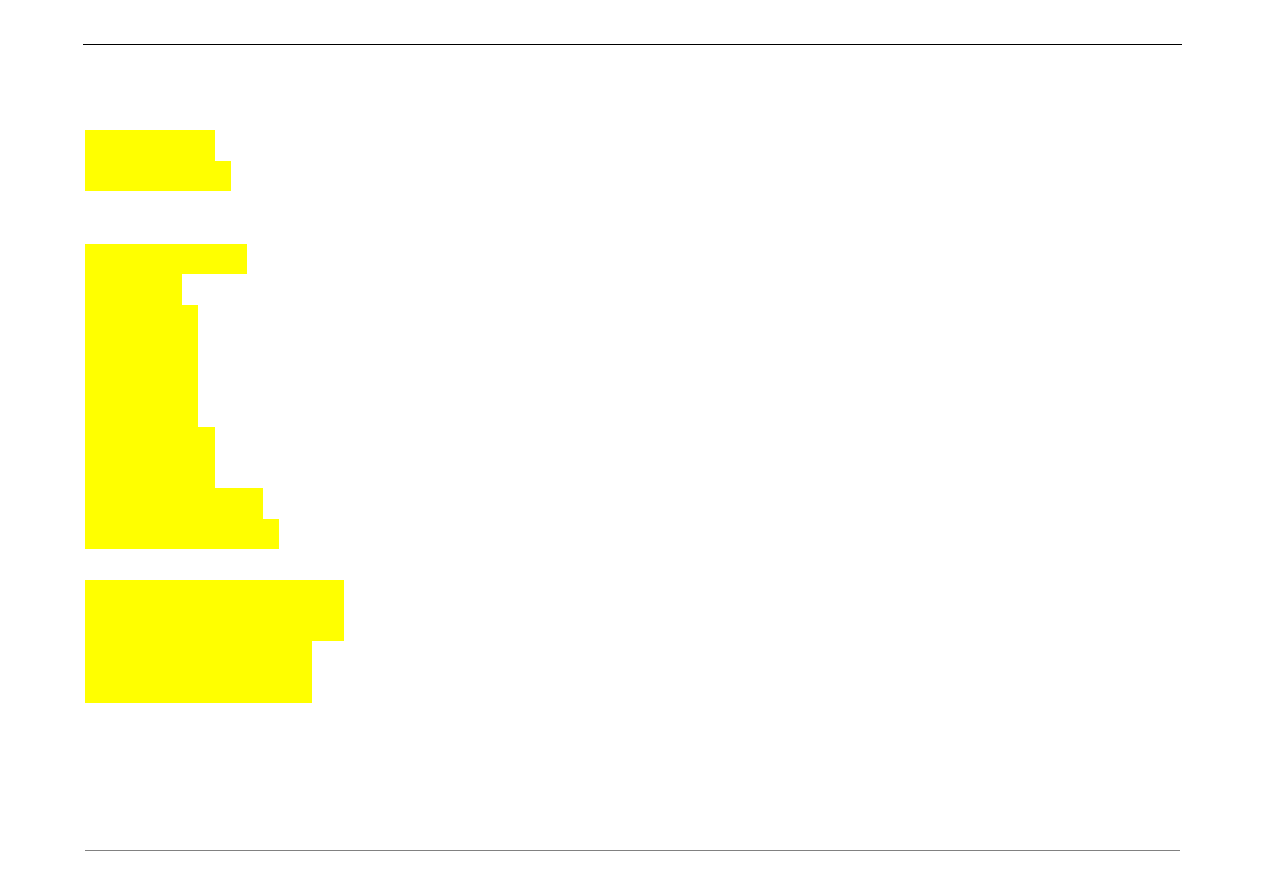
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
7
b) W programie MATLAB zadeklarować liczbę elementów i liczbę niewiadomych
uogólnionych przemieszczeń:
Ne = 9;
% liczba elementow
Neq = 16;
% liczba niewiadomych uogolnionych przemieszczen
c) Zadeklarować zmienne dotyczące danych geometrycznych i materiałowych:
E=15*10^9;
% modul sprezystosci [N/m2]
H=6.2;
% wysokosc ramy [m]
L=4.8 ;
% rozpietosc ramy [m]
b1=0.1;
% szerokosc przekroju belki [m]
h1=0.2;
% wysokosc przekroju belki [m]
b2=0.1;
% szerokosc przekroju slupa [m]
h2=0.12;
% wysokosc przekroju slupa [m]
ro=2300;
% gestosc [kg/m3]
ksi_1=3/100;
% liczba tlumienia ksi 1
ksi_2=5/100;
% liczba tlumienia ksi 2
Ib=(b1*h1^3)/12;
% moment bezwladnosci belki [m4]
Ic=(b2*h2^3)/12;
% moment bezwladnosci slupa [m4]
mi_b=ro*b1*h1;
% masa rozlozona belki [kg/m]
mi_c=ro*b2*h2;
% masa rozlozona slupa [kg/m]
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
8
d) Uzupełnić tablicę cech elementów (tablica CE).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% TABLICA CECH ELEMENTOW
%-------------------------------------------
% Ne EI L ro
%-------------------------------------------
CE = [ 1 E*Ic H/3 mi_c
2 E*Ic H/3 mi_c
3 E*Ic H/3 mi_c
4 E*Ib L/3 mi_b
5 E*Ib L/3 mi_b
6 E*Ib L/3 mi_b
7 E*Ic H/3 mi_c
8 E*Ic H/3 mi_c
9 E*Ic H/3 mi_c];
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
9
e) Uzupełnić tablicę wektorów alokacji (tablica ALOK).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% TABLICA WEKTOROW ALOKACJI
%-------------------------------------------
% Ne | Vi | Fi | Vk | Fk
%-------------------------------------------
ALOK=[ 1 0 0 1 2
2 1 2 3 4
3 3 4 10 5
4 0 5 6 7
5 6 7 8 9
6 8 9 0 11
7 12 13 10 11
8 14 15 12 13
9 0 16 14 15];
f) Dokonać agregacji globalnych macierzy sztywności K i mas M :
[K]=agreg_k_beam(Neq,Ne,CE,ALOK)
[M]=agreg_m_beam(Neq,Ne,CE,ALOK)
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
10
g) Rozwiązać problem własny:
[mode,vale] = eig(K,M)
mode
– macierz modalna
11
12
1
21
22
2
1
2
N
N
jn
N
N
NN
Φ
vale
– macierz widmowa
2
1
2
2
2
2
0
0
0
0
0
0
N
Ω
omega=sqrt(diag(vale));
– częstości kołowe drgań własnych (ekstrakcja diagonali
macierzy widmowej)
f = omega/2/pi;
– częstotliwości drgań własnych
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
11
h) Sortowanie i normalizacja częstości i postaci drgań własnych.
[mode,f]=sort_norm(mode,f)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% funkcja sortujaca i normalizujaca czestosci
% i postaci drgan wlasnych
%----------------------------------------------------------
% WEJSCIE:
% mode - macierz modalna
% f - wektor czestotliwosci
%----------------------------------------------------------
% WYJSCIE:
% mode_s - posortowana macierz modalna
% f_s - posortowany wektor czestotliwosci
%----------------------------------------------------------
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
12
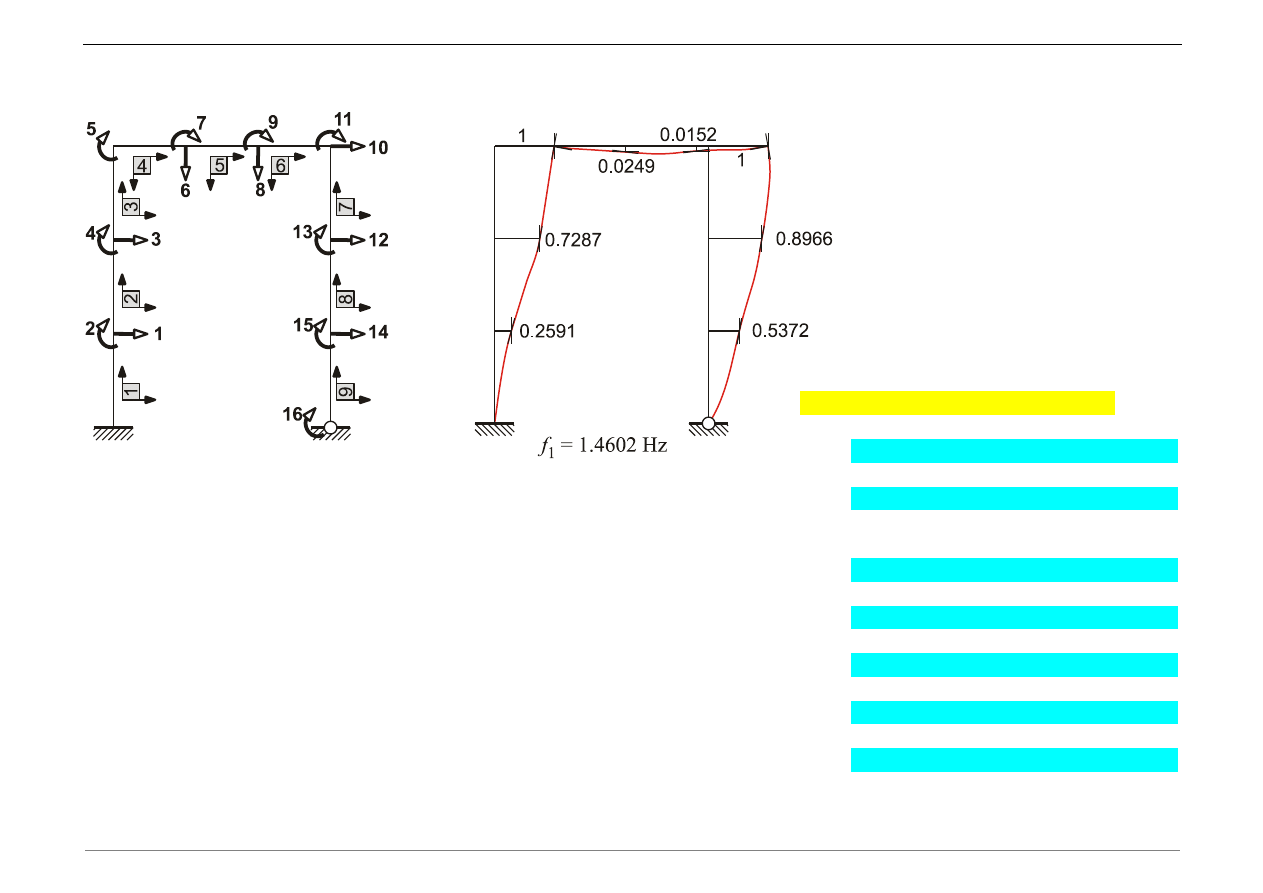
i) Wykreślić postacie drgań odpowiadające trzem pierwszym częstościom drgań
własnych.
mode =
0.2591 -0.4811 -1.0000 -0.8532 0.3807 0.9551 -0.0377 -0.1408 -0.0942 0.0296 0.1079 0.1159 -0.0019 0.0267 -0.0337 0.0118
0.2128 -0.3061 -0.4350 -0.2603 -0.0710 -0.5533 0.1031 0.5251 1.0000 0.4361 0.9081 0.8072 -0.0106 0.1337 -0.1564 0.0516
0.7287 -0.7810 -0.5941 -0.1618 -0.3382 -1.0000 0.0391 0.0382 -0.1825 -0.1109 -0.1555 -0.0683 -0.0004 0.0394 -0.0688 0.0333
0.2079 0.0639 0.7837 0.7205 -0.2885 -0.0034 -0.0996 -0.6169 -0.8840 0.0536 0.7161 1.0000 -0.0206 0.3664 -0.5136 0.2014
0.0323 0.1869 0.3825 -0.6099 -0.1325 0.2758 0.7307 0.3748 0.0556 -0.2315 -0.6771 0.1770 0.0804 1.0000 -0.9958 0.8635
0.0249 0.2311 0.3956 -0.9640 -0.2587 0.0218 0.5723 0.1678 -0.1058 -0.0107 0.0401 0.0369 -0.0106 -0.2067 0.1199 0.0123
0.0018 0.0878 0.0966 -0.4183 -0.0995 -0.1657 -0.3562 -0.2306 -0.0106 0.2031 0.5860 -0.3402 -0.0951 -0.4932 -0.6805 0.9988
0.0152 0.2481 0.3188 -1.0000 -0.1896 -0.2034 -0.5111 -0.2524 0.0678 0.0420 -0.0403 -0.0086 0.0258 0.2034 0.1213 -0.0120
-0.0108 -0.0719 -0.1678 0.3851 0.1611 -0.0287 -0.4537 -0.0672 0.1123 -0.1908 -0.5799 0.3561 0.0524 -0.5169 0.6717 1.0000
1.0000 -0.3908 0.9954 0.3535 -0.3599 0.7718 0.3627 -0.0834 0.2207 0.1204 -0.1861 -0.0976 0.0516 0.1980 -0.0013 0.2037
-0.0052 -0.2343 -0.1725 0.7064 -0.0379 0.2341 0.8612 0.1372 -0.1387 0.2970 0.4880 -0.3175 0.0786 0.9844 1.0000 0.8664
0.8966 0.5858 0.2416 -0.1157 0.8791 -0.3112 -0.1854 0.2943 -0.1603 0.0824 0.0706 -0.0155 0.0711 0.0275 0.0638 0.0324
0.1123 -0.5023 0.7629 -0.1443 -0.1391 0.4316 -0.8617 0.6940 -0.0066 -0.9462 0.9330 -0.0789 -0.4217 0.4118 0.5447 0.2077
0.5372 1.0000 -0.9283 0.2921 -0.5475 0.1826 0.0979 -0.1553 0.1139 -0.2488 0.1945 -0.0169 0.0424 0.0109 0.0225 0.0089
0.2287 0.1796 0.0939 -0.0832 0.7717 -0.5302 0.9664 -0.9158 0.3331 -0.1693 -0.1823 0.0471 -0.8429 0.2785 0.2438 0.0708
0.2760 0.6509 -0.7657 0.2798 -1.0000 0.5780 -1.0000 1.0000 -0.4654 1.0000 -1.0000 0.1145 -1.0000 0.2397 0.1661 0.0409
f =
1.4602
5.7043
9.4556
12.2021
20.1370
25.5384
41.3254
45.5184
56.9852
82.4466
100.4504
114.2185
148.3424
187.8369
257.4507
424.6326
postac_1_2_3=mode(:,1:3);
postac_1_2_3=
0.2591 -0.4811 -1.0000
0.2128 -0.3061 -0.4350
0.7287 -0.7810 -0.5941
0.2079 0.0639 0.7837
0.0323 0.1869 0.3825
0.0249 0.2311 0.3956
0.0018 0.0878 0.0966
0.0152 0.2481 0.3188
-0.0108 -0.0719 -0.1678
1.0000 -0.3908 0.9954
-0.0052 -0.2343 -0.1725
0.8966 0.5858 0.2416
0.1123 -0.5023 0.7629
0.5372 1.0000 -0.9283
0.2287 0.1796 0.0939
0.2760 0.6509 -0.7657
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
13
Rysunek pierwszej postaci drgań własnych:
postac_1_2_3=mode(:,1:3);
postac_1_2_3=
0.2591 -0.4811 -1.0000
0.2128 -0.3061 -0.4350
0.7287 -0.7810 -0.5941
0.2079 0.0639 0.7837
0.0323 0.1869 0.3825
0.0249 0.2311 0.3956
0.0018 0.0878 0.0966
0.0152 0.2481 0.3188
-0.0108 -0.0719 -0.1678
1.0000 -0.3908 0.9954
-0.0052 -0.2343 -0.1725
0.8966 0.5858 0.2416
0.1123 -0.5023 0.7629
0.5372 1.0000 -0.9283
0.2287 0.1796 0.0939
0.2760 0.6509 -0.7657
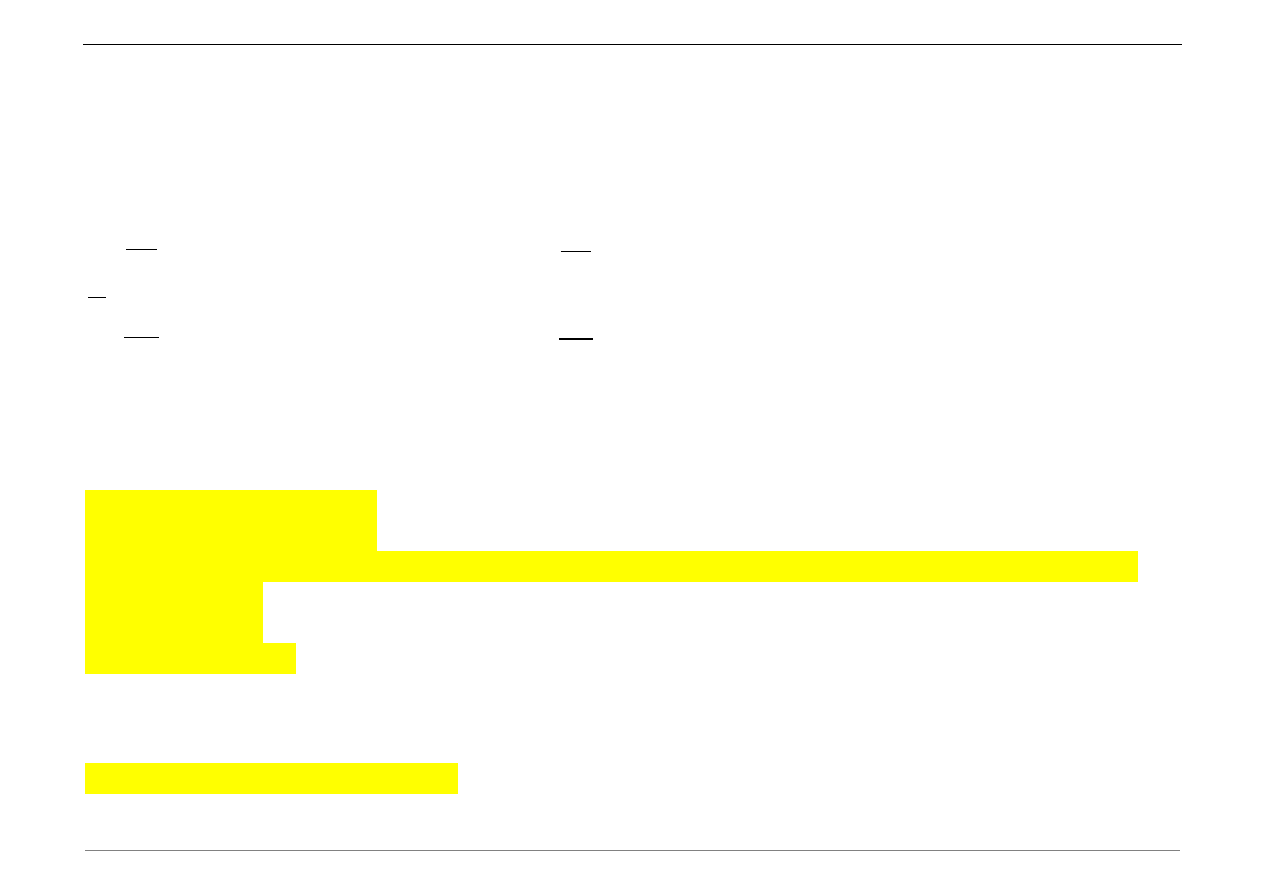
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
14
j) Utworzyć macierz tłumienia C
Macierz tłumienia C wyznaczamy jako macierz tłumienia proporcjonalnego (macierz
Rayleigha):
0
1
a
a
C
M
K .
Współczynniki a
0
i a
1
macierzy tłumienia wyznaczamy z równania:
0
1
1
1
1
2
i
i
i
j
j
j
a
a
,
1
1
1
0
1
1
2
2
2
1
2
1
a
a
.
jeżeli znane są dwie wartości liczby tłumienia
i
i
j
, odpowiadające częstościom drgań
i
oraz
j
.
omega_1=f(1)*2*pi;
omega_2=f(2)*2*pi;
wspl=2*inv([1/omega_1 omega_1; 1/omega_2 omega_2])*[ksi_1;ksi_2];
a0=wspl(1);
a1=wspl(2);
C=a0*M + a1*K;
k) Wyznaczyć krytyczny krok całkowania dt z warunku stabilności metody różnic
centralnych:
dt_mrc=2/(f(end)*2*pi);
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
15
l) Przyjąć
kr
dt
dt
, zdefiniować wektor czasu:
t = [ 0:dt:tk];
Czas końcowy
tk
dobrać tak, by zaobserwować przejście układu w stan spoczynku.
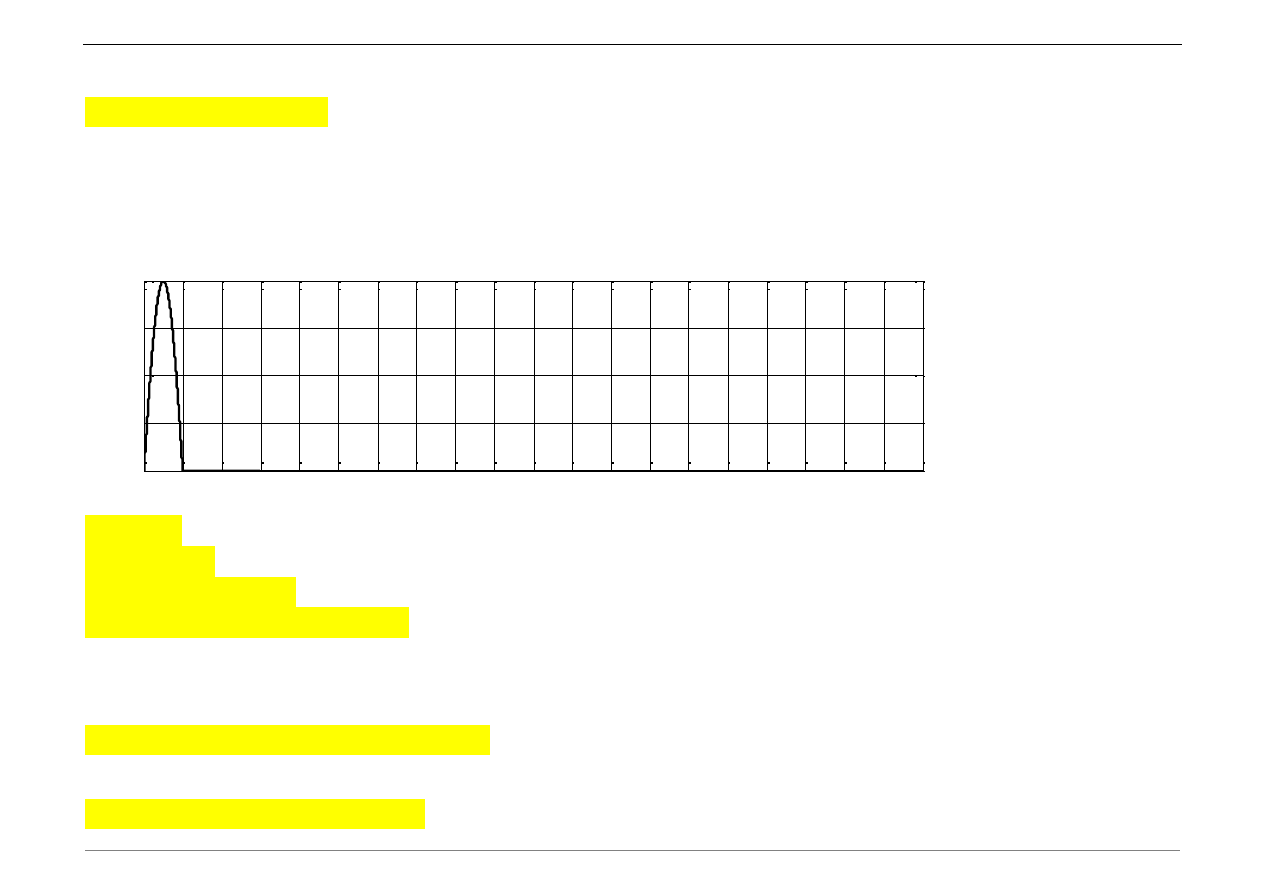
m) Zdefiniować wektor obciążenia p(t), przyłożyć go wzdłuż wybranego stopnia
swobody.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2
0
500
1000
1500
2000
tc=0.1
% czas trwania impulsu [s]
po=2000;
% amplituda impulsu [N]
t1=[0:dt:tc];
p= po*sin(pi/tc*t1);
n) Utworzyć macierz P zawierającą obciążenia zewnętrzne wzdłuż wszystkich stopni
swobody:
P = zeros(Neq,length(t));
Na zadanym stopniu swobody (np. nr 5) w macierzy P umieścić wektor p
P(5,1:(length(p)))=p;
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
16
o) Zdefiniować wektory przemieszczeń i prędkości początkowych u
0
oraz v
0
.
u0=zeros(1,Neq);
% wektor przemieszczenia poczatkowego
v0=zeros(1,Neq);
% wektor predkosci poczatkowej
p) Dokonać całkowania równań ruchu
( )
t
Mu Cu Ku
p
metodą różnic centralnych:
[u,v,a]=mrc(M,C,K,P,t,u0,v0);
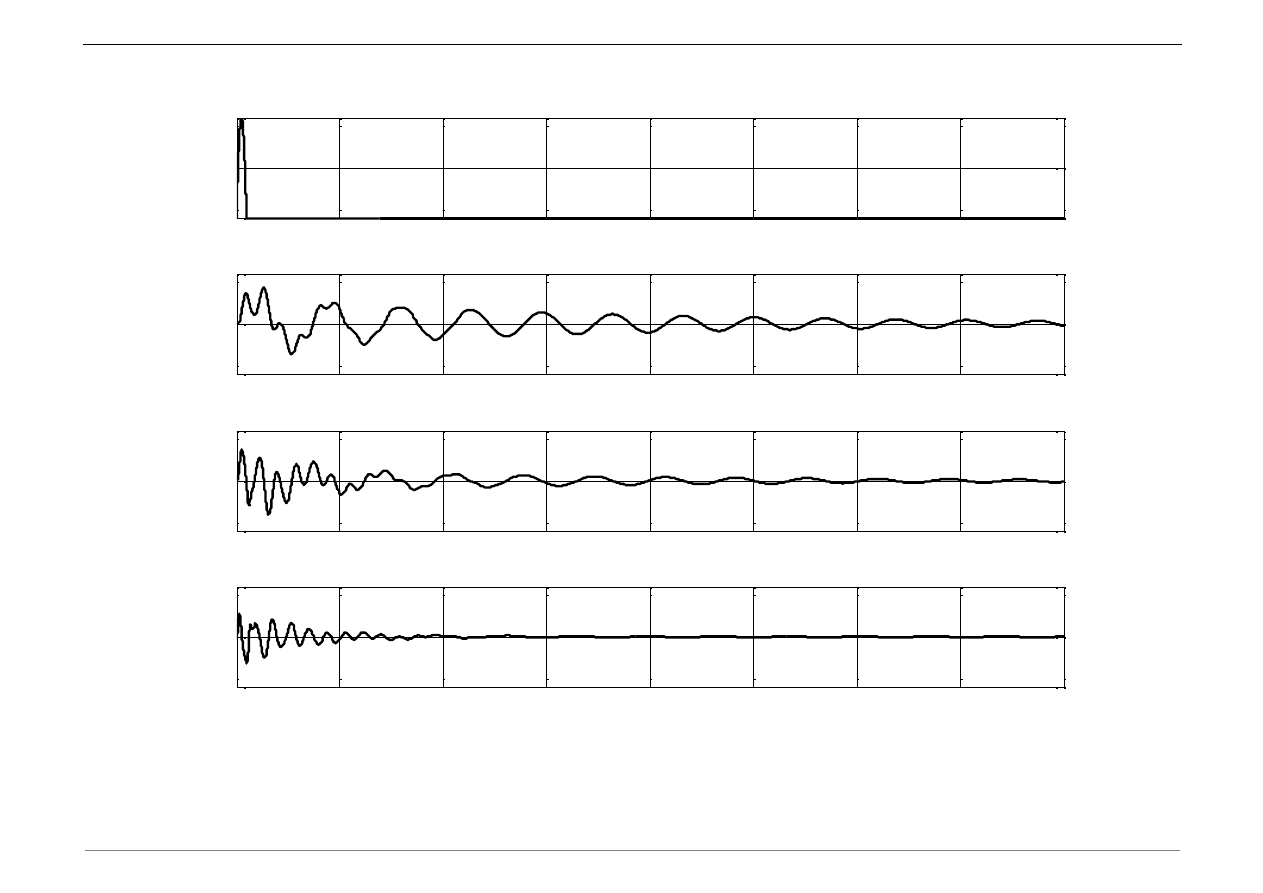
q) Wykreślić odpowiedź układu w czasie wzdłuż wybranych stopni swobody (np. nr 10).
figure(1)
plot(t,u(12,:),
'k'
);grid
on
;ylabel(
'u_1_0 [m]'
);xlabel(
't [s]'
)
figure(2)
plot(t,v(12,:),
'k'
);grid
on
;ylabel(
'v_1_0 [m/s]'
);xlabel(
't [s]'
)
figure(3)
plot(t,a(12,:),
'k'
);grid
on
;ylabel(
'a_1_0 [m/s^2]'
);xlabel(
't [s]'
)
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
17
0
1
2
3
4
5
6
7
8
0
1000
2000
p
5
[
N
]
0
1
2
3
4
5
6
7
8
-5
0
5
x 10
-3
u
1
2
[
m
]
0
1
2
3
4
5
6
7
8
-0.1
0
0.1
v
1
2
[
m
/s
]
0
1
2
3
4
5
6
7
8
-5
0
5
a
1
2
[
m
/s
2
]
t [s]
Dynamika Budowli
– laboratorium
Ćwiczenie 5
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
18
Zadanie do samodzielnego rozwiązania: