
19
Dla warunków podparcia tarczy pokazanych kolejno na rys.4, rys.5 i rys.6 macierz sztywności całej tarczy i wyrazy wolne układu równań
przyjmą postać:
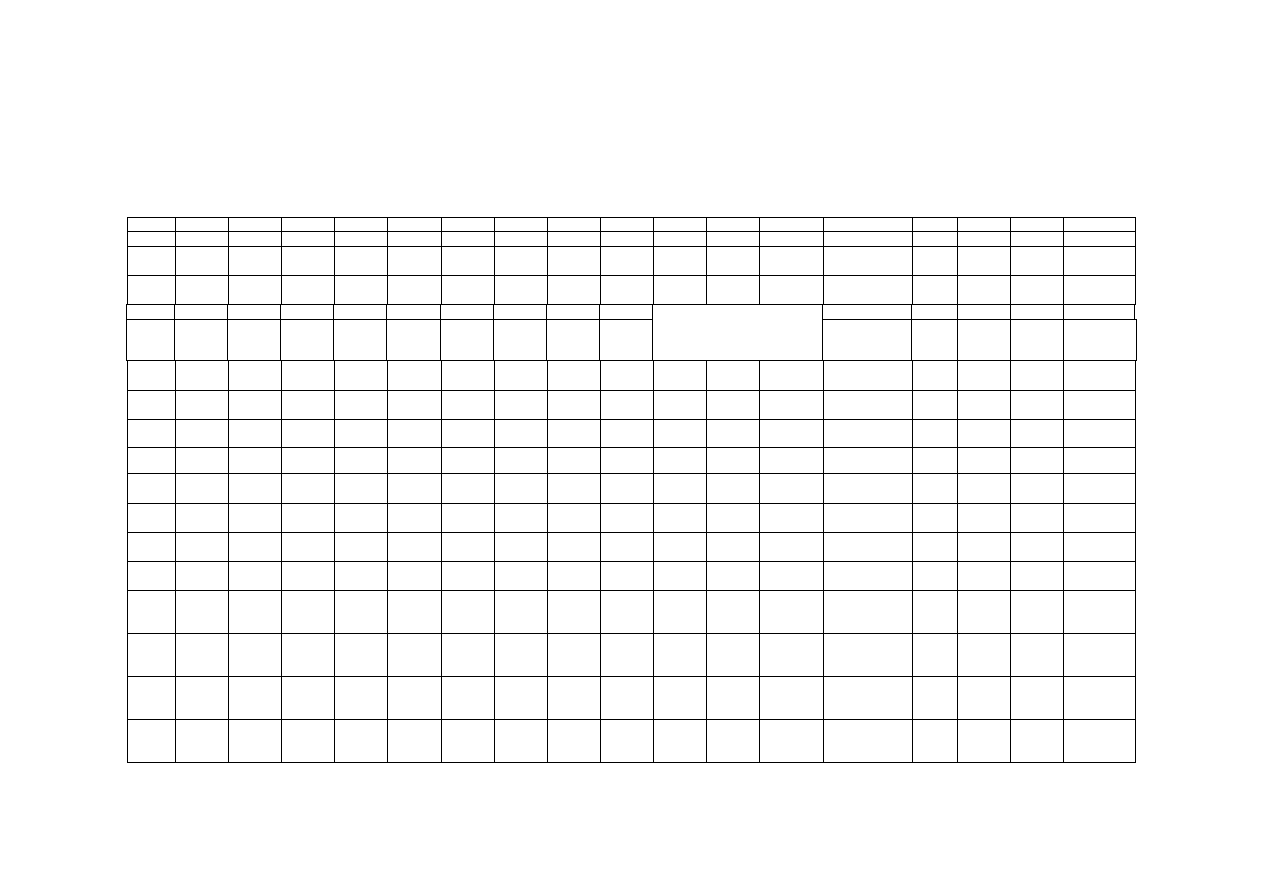
Globalna macierz sztywności układu [K] po wprowadzeniu warunków brzegowych z rys. 4.
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0
0 0 0 0 0
0 0 0 0 0 1 0 0 0 0
SYMETRIA
0 0 0 0 0
0 0 0 0 0 0
7
,
7
k
0 0 0 0 0 0
7
,
8
k
8
,
8
k
0 0 0 0 0 0
7
,
9
k
8
,
9
k
9
,
9
k
0 0 0 0 0 0
7
,
10
k
8
,
10
k
9
,
10
k
10
,
10
k
0 0 0 0 0 0
0 0
9
,
11
k
10
,
11
k
11
,
11
k
0 0 0 0 0 0
0 0
9
,
12
k
10
,
12
k
11
,
12
k
12
,
12
k
0 0 0 0 0 0
0 0
9
,
13
k
10
,
13
k
11
,
13
k
12
,
13
k
13
,
13
k
0 0 0 0 0 0
0 0
9
,
14
k
10
,
14
k
11
,
14
k
12
,
14
k
13
,
14
k
14
,
14
k
0 0 0 0 0 0
7
,
15
k
8
,
15
k
9
,
15
k
10
,
15
k
11
,
15
k
12
,
15
k
13
,
15
k
14
,
15
k
15
,
15
k
0 0 0 0 0 0
7
,
16
k
8
,
16
k
9
,
16
k
10
,
16
k
11
,
16
k
12
,
16
k
13
,
16
k
14
,
16
k
15
,
16
k
16
,
16
k
0 0 0 0 0 0
7
,
17
k
8
,
17
k
9
,
17
k
10
,
17
k
0 0 0 0
15
,
17
k
16
,
17
k
17
,
17
k
0 0 0 0 0 0
7
,
18
k
8
,
18
k
9
,
18
k
10
,
18
k
0 0 0 0
15
,
18
k
16
,
18
k
17
,
18
k
18
,
18
k
20
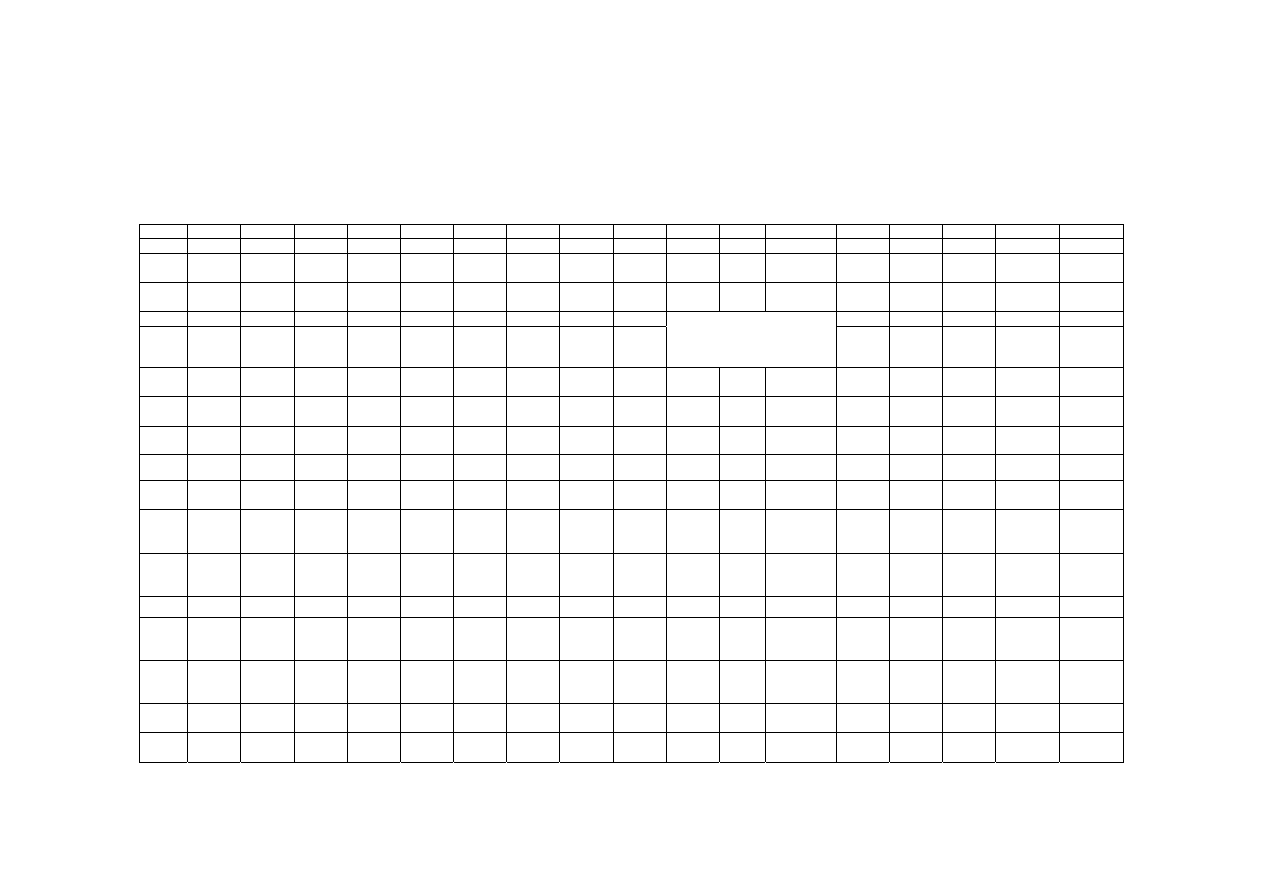
Globalna macierz sztywności układu [K] po wprowadzeniu warunków brzegowych z rys. 5.
1 0 0 0 0 0 0 0 0 0 0 0 0
0
0 0 0 0
0 1 0 0 0 0 0 0 0 0 0 0 0
0
0 0 0 0
0 0
3
,
3
k
0 0
3
,
4
k
4
,
4
k
0 0 0 0 1 0 0 0 0 0
0
0 0 0 0
0 0 0 0 0 1 0 0 0 0
SYMETRIA
0 0
0
0 0
0 0
3
,
7
k
4
,
7
k
0 0
7
,
7
k
0 0
3
,
8
k
4
,
8
k
0 0
7
,
8
k
8
,
8
k
0 0
3
,
9
k
4
,
9
k
0 0
7
,
9
k
8
,
9
k
9
,
9
k
0 0
3
,
10
k
4
,
10
k
0 0
7
,
10
k
8
,
10
k
9
,
10
k
10
,
10
k
0 0
3
,
11
k
4
,
11
k
0 0
0 0
9
,
11
k
10
,
11
k
11
,
11
k
0 0
3
,
12
k
4
,
12
k
0 0
0 0
9
,
12
k
10
,
12
k
11
,
12
k
12
,
12
k
0 0
0 0
0 0
0 0
9
,
13
k
10
,
13
k
11
,
13
k
12
,
13
k
13
,
13
k
0 0
0 0
0 0
0 0
9
,
14
k
10
,
14
k
11
,
14
k
12
,
14
k
13
,
14
k
k
14,14
+k
0 0
0 0
0 0
7
,
15
k
8
,
15
k
9
,
15
k
10
,
15
k
11
,
15
k
12
,
15
k
13
,
15
k
14
,
15
k
15
,
15
k
0 0
0 0
0 0
7
,
16
k
8
,
16
k
9
,
16
k
10
,
16
k
11
,
16
k
12
,
16
k
13
,
16
k
14
,
16
k
15
,
16
k
16
,
16
k
0 0
0 0
0 0
7
,
17
k
8
,
17
k
9
,
17
k
10
,
17
k
0 0 0
0
15
,
17
k
16
,
17
k
17
,
17
k
0 0
0 0
0 0
7
,
18
k
8
,
18
k
9
,
18
k
10
,
18
k
0 0 0
0
15
,
18
k
16
,
18
k
17
,
18
k
18
,
18
k
21
Globalna macierz sztywności układu [K] po wprowadzeniu warunków brzegowych z rys. 6.
1 0 0 0 0 0 0 0 0 0 0 0 0
0
0 0 0 0
0 1 0 0 0 0 0 0 0 0 0 0 0
0
0 0 0 0
0 0
3
,
3
k
0
0 0
3
,
4
k
4
,
4
k
0
0 0 0 0 1 0 0 0 0 0
0
0 0 0 0
0 0 0 0 0 1 0 0 0 0
SYMETRIA
0
0 0 0 0
0 0
3
,
7
k
4
,
7
k
0 0
7
,
7
k
0
0 0
3
,
8
k
4
,
8
k
0 0
7
,
8
k
8
,
8
k
0
0 0
3
,
9
k
4
,
9
k
0 0
7
,
9
k
8
,
9
k
9
,
9
k
0
0 0
3
,
10
k
4
,
10
k
0 0
7
,
10
k
8
,
10
k
9
,
10
k
10
,
10
k
0
0 0
3
,
11
k
4
,
11
k
0 0
0 0
9
,
11
k
10
,
11
k
11
,
11
k
0
0 0
3
,
12
k
4
,
12
k
0 0
0 0
9
,
12
k
10
,
12
k
11
,
12
k
12
,
12
k
0
0 0
0 0
0 0
0 0
9
,
13
k
10
,
13
k
11
,
13
k
12
,
13
k
13
,
13
k
0
0 0 0 0 0 0 0 0 0 0 0 0 0
1
0 0 0 0
0 0
0 0
0 0
7
,
15
k
8
,
15
k
9
,
15
k
10
,
15
k
11
,
15
k
12
,
15
k
13
,
15
k
0
15
,
15
k
0 0
0 0
0 0
7
,
16
k
8
,
16
k
9
,
16
k
10
,
16
k
11
,
16
k
12
,
16
k
13
,
16
k
0
15
,
16
k
16
,
16
k
0 0
0 0
0 0
7
,
17
k
8
,
17
k
9
,
17
k
10
,
17
k
0 0 0
0
15
,
17
k
16
,
17
k
17
,
17
k
0 0
0 0
0 0
7
,
18
k
8
,
18
k
9
,
18
k
10
,
18
k
0 0 0
0
15
,
18
k
16
,
18
k
17
,
18
k
18
,
18
k

22
Globalny wektor obciążeń układu {F} po wprowadzeniu warunków brzegowych z rys. 4.
{ }
{
}
T
9
y
9
x
8
y
8
x
7
y
7
x
6
y
6
x
5
y
5
x
4
y
4
x
F
F
F
F
F
F
F
F
F
F
F
F
0
0
0
0
0
0
F
=
Globalny wektor obciążeń układu {F} po wprowadzeniu warunków brzegowych z rys. 5.
{ }
{
}
T
9
y
9
x
8
y
8
x
7
y
7
x
6
y
6
x
5
y
5
x
4
y
4
x
2
y
2
x
F
F
F
F
F
F
F
F
F
F
F
F
0
0
F
F
0
0
F
=
Globalny wektor obciążeń układu {F} po wprowadzeniu warunków brzegowych z rys. 6.
{ }
{
}
T
9
y
9
x
16,14
8
y
15,14
8
x
13,14
7
x
12,14
6
y
11,14
6
x
10,14
5
y
9,14
5
x
4
y
4
x
2
y
2
x
F
F
k
δ
F
k
δ
F
δ
k
δ
F
k
δ
F
k
δ
F
k
δ
F
k
δ
F
F
F
0
0
F
F
0
0
F
⋅
−
⋅
−
⋅
−
⋅
−
⋅
−
⋅
−
⋅
−
=

23
Wyszukiwarka
Podobne podstrony:
Wykład 16 (19.12.07), toxycologia
przeciwienstwa 04 str 16 19 gawlik
KPC - Wykład (16), 19.02.2013
mes tarcza 13 15
1,7,16,19,22,25
16 (19)
mes tarcza 12
KPC Wykład (16) 19 02 2013
ei 07 2002 s 16 19
16 3 19 3
16 19
16 19
mes tarcza 1 11
Midnight Sun 16 - 19
Rozdział 16 - 19, Dni Mroku 4 - Nadejście chaosu
Wykład 16 (19.12.07), toxycologia
więcej podobnych podstron