1
i
j
r
k
x
y
a
b
a/2
b/2
e
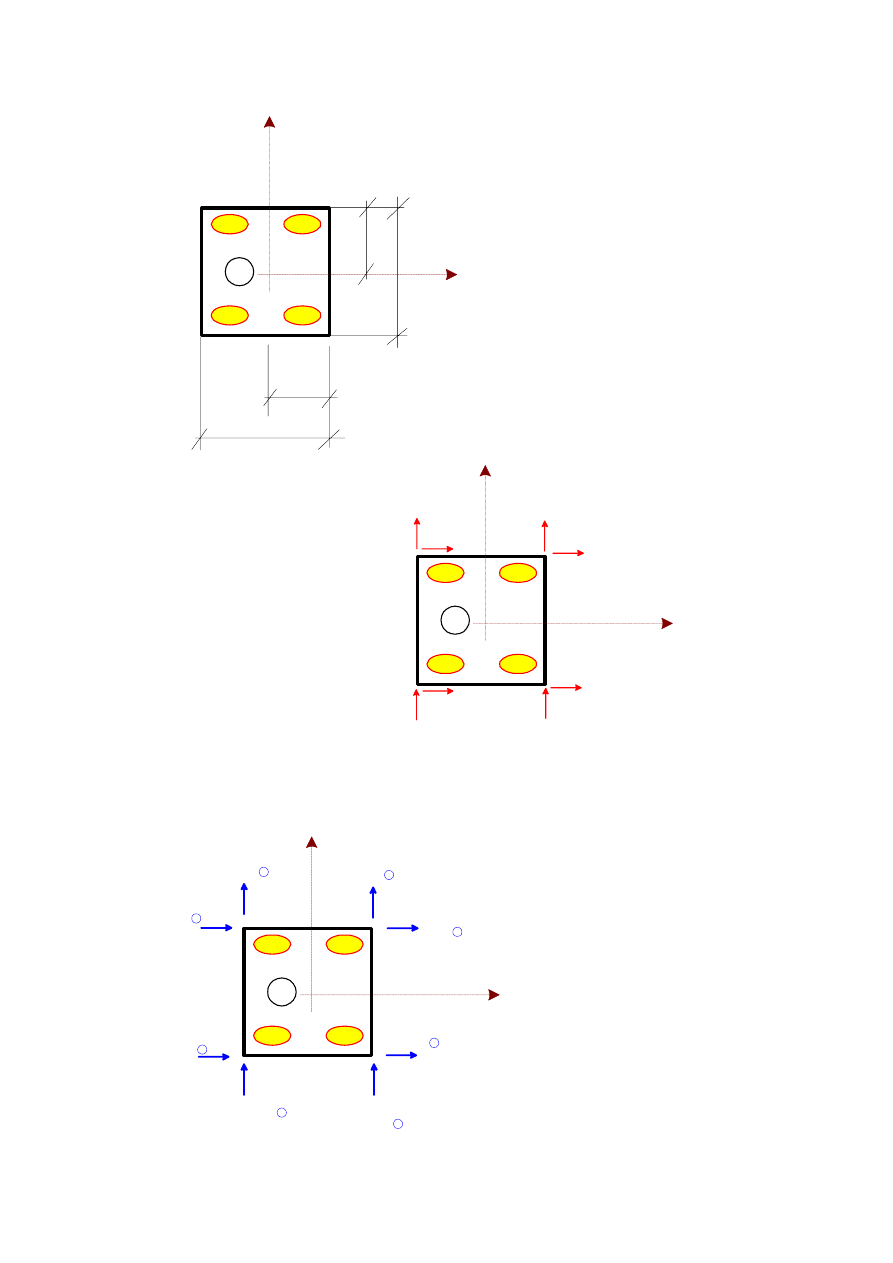
geometria elemenu w układzie
lokalnym
i
j
r
k
x
y
e
v
i
v
r
v
k
v
j
u
i
u
r
u
k
u
j
dodatnie zwroty przemieszczeń
węzłów elementu "e"
v
j
,
r
i
(e)
v
k
,
r
i
(e)
v
r
,
r
i
(e)
u
j
,
r
i
(e)
u
k
,
r
i
(e)
u
r
,
r
i
(e)
u
i
,
r
i
(e)
v
i
,
r
i
(e)
i
j
r
k
x
y
e
dodatnie zwroty sił węzłowych w
elemencie "e"
Rys.1.

2
Przyjmujemy przybliżenie funkcji przemieszczeń w obszarze całego elementu w postaci:
y
x
y
x
y
x
u
⋅
⋅
+
⋅
+
⋅
+
=
4
3
2
1
)
,
(
α
α
α
α
y
x
y
x
y
x
v
⋅
⋅
+
⋅
+
⋅
+
=
4
3
2
1
)
,
(
β
β
β
β
Powyższe równania można zapisać
[ ]
(a)
[
]
{ }
α
y)
A(x,
U
⋅
=
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
⋅
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⋅
=
⎭
⎬
⎫
⎩
⎨
⎧
=
4
3
2
1
4
3
2
1
1
0
0
0
0
0
0
0
0
1
β
β
β
β
α
α
α
α
y
x
y
x
y
x
y
x
)
y
,
x
(
v
)
y
,
x
(
u
Współczynniki
i
α
oraz
i
β
dobieramy tak aby w węzłach elementu wartości funkcji [U] były
równe przemieszczeniom tych węzłów
{ }
{
}
T
r
r
k
k
j
j
i
i
v
u
v
u
v
u
v
u
u
=
podstawiając współrzędne węzłów elementu w odpowiednim układzie współrzędnych
otrzymamy:
{ }
[ ]
{ }
α
β
β
β
β
α
α
α
α
⋅
Φ
=
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
⋅
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
4
3
2
1
4
3
2
1
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
r
r
r
r
r
r
r
r
k
k
k
k
k
k
k
k
j
j
j
j
j
j
j
j
i
i
i
i
i
i
i
i
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
u
Rozwiązując powyższy układ równań otrzymamy:
{ }
[ ]
{ }
u
⋅
Φ
=
−1
α
Podstawiając otrzymane rozwiązanie do (a) otrzymamy:
[ ]
[
] [ ]
{ }
[ ]
{ }
u
N
u
y
x
A
y
x
v
y
x
u
U
⋅
=
⋅
Φ
⋅
=
⎭
⎬
⎫
⎩
⎨
⎧
=
−1
)
,
(
)
,
(
)
,
(

3
Macierz
[N]
można zapisać w postaci:
[ ]
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
=
r
k
j
i
r
k
j
i
r
r
k
k
j
j
i
i
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
N
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
gdzie funkcje typu
nazywane funkcjami kształtu
można przedstawić w postaci:
l
n
)
2
1
(
)
2
1
(
4
1
b
y
a
x
n
i
⋅
−
⋅
⋅
−
⋅
=
,
)
2
1
(
)
2
1
(
4
1
b
y
a
x
n
j
⋅
−
⋅
⋅
+
⋅
=
,
)
2
1
(
)
2
1
(
4
1
b
y
a
x
n
k
⋅
+
⋅
⋅
−
⋅
=
,
)
2
1
(
)
2
1
(
4
1
b
y
a
x
n
r
⋅
+
⋅
⋅
+
⋅
=
,
Dla płaskiego zadania równania geometryczne można zapisać:
{ }
[ ]
[ ] [ ]
{ }
u
B
N
x
y
y
x
y
x
v
y
x
u
x
y
y
x
U
x
y
y
x
x
v
y
u
y
v
x
u
y
x
⋅
=
⋅
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
∂
∂
∂
∂
∂
∂
∂
∂
=
⎭
⎬
⎫
⎩
⎨
⎧
⋅
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
∂
∂
∂
∂
∂
∂
∂
∂
=
⋅
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
∂
∂
∂
∂
∂
∂
∂
∂
=
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
∂
∂
+
∂
∂
∂
∂
∂
∂
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
=
0
0
)
,
(
)
,
(
0
0
0
0
γ
ε
ε
ε
(1)
gdzie:
[ ]
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
x
n
y
n
x
n
y
n
x
n
y
n
x
n
y
n
y
n
y
n
y
n
y
n
x
n
x
n
x
n
x
n
B
r
r
k
k
j
j
i
i
r
k
j
i
r
k
j
i
0
0
0
0
0
0
0
0
Wykonując różniczkowanie oraz przyjmując dodatkowo oznaczenia:
)
2
1
(
2
1
b
y
a
a
⋅
−
⋅
⋅
=
)
2
1
(
2
1
a
x
b
b
⋅
−
⋅
⋅
=
)
2
1
(
2
1
a
x
b
c
⋅
+
⋅
⋅
=
)
2
1
(
2
1
b
y
a
d
⋅
+
⋅
⋅
=
macierz [B] możemy zapisać w postaci:
[ ]
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
−
−
−
=
d
c
d
b
a
c
a
b
c
b
c
b
d
d
a
a
B
0
0
0
0
0
0
0
0

4
W płaskim stanie naprężenia macierz sprężystości ma postać:
[ ]
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
⋅
−
=
2
1
0
0
0
1
0
1
)
1
(
2
ν
ν
ν
ν
E
D
a prawo Hooke’a:
{ }
[ ]
{ }
[ ] [ ]
{ }
u
B
D
D
⋅
⋅
=
⋅
=
ε
σ
(3)
Zgodnie z zasadą prac przygotowanych przy przygotowanych (wirtualnych) przemieszczeniach mamy:
PRACA SIŁ WEWNĘTRZNYCH NA WIRTUALNYCH PRZEMIESZCZENIACH = PRACY SIŁ ZEWNĘTRZNYCH NA TYCH
PRZEMIESZCZENIACH
czyli
z
w
L
L
=
Dowolne lecz zgodne z warunkami kinematycznymi układu przemieszczenie przygotowane (wirtualne)
{ }
Uˆ
wywołuje w ustroju:
1) przemieszczenie dowolnego punktu elementu równe:
{ } [ ]
{ }
U
N
U
ˆ
~
⋅
=
(4)
2) odkształcenie w dowolnym punkcie elementu równe:
{ }
[ ]
{ }
U
B
ˆ
~
⋅
=
ε
(5)
Przyjmując teraz oznaczenia w postaci:
a) wektor sił masowych w elemencie w postaci
{ }
{
}
T
y
x
M
f
ρ
ρ
=
b) wektor obciążeń powierzchniowych rozłożonych na powierzchni o długości od punktu
α do punktu β i
szerokości równej grubości elementu t w postaci
{ }
{
}
T
y
x
S
p
p
f
β
α
β
α
−
−
=
c) wektor obciążeń skupionych przyłożonych w węzłach elementu w postaci:
{ }
{
}
T
r
y
r
x
k
y
k
x
j
y
j
x
i
y
i
x
P
P
P
P
P
P
P
P
P
f
=
Praca sił wewnętrznych na przygotowanych przemieszczeniach wynosi:
{ } { }
(
)
{ }
{ }
(
)
=
⋅
−
⋅
=
∫
∫
V
M
T
V
T
w
dV
f
U
dV
L
~
~
σ
ε
Pracę sił zewnętrznych na odpowiadających im przemieszczeniach wirtualnych obliczymy:
{ } { }
{ }
{ }
[
]
∑ ∫
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
+
⋅
=
λ
ω 1
~
ˆ
S
S
T
P
T
z
dS
f
U
f
U
L
Zatem mamy:
{ } { }
(
)
{ }
{ }
(
)
{ } { }
{ }
{ }
[
]
∑ ∫
∫
∫
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
+
⋅
=
⋅
−
⋅
λ
ω
σ
ε
1
~
ˆ
~
~
S
S
T
P
T
V
M
T
V
T
dS
f
U
f
U
dV
f
U
dV

5
równanie to można zapisać w postaci:
{ } { }
(
)
{ }
{ }
(
)
{ } { }
{ }
{ }
[
]
0
~
ˆ
~
~
1
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
⋅
−
⋅
−
⋅
∑ ∫
∫
∫
=
λ
ω
σ
ε
S
S
T
P
T
V
M
T
V
T
dS
f
U
f
U
dV
f
U
dV
(6)
podstawiając do równania (6) wyrażenia (5) (4) (2) (1) oraz uwzględniając, że wektor
przemieszczeń
wirtualnych jest niezależny od współrzędnych (można wynieść przed znak całki) otrzymamy:
{ }
Uˆ
{ }
[ ] [ ] [ ]
(
)
{ }
[ ]
{ }
(
)
{ }
[ ]
{ }
[
]
0
ˆ
1
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
−
⋅
−
⋅
⋅
⋅
⋅
∑ ∫
∫
∫
=
λ
ω
S
S
T
P
V
M
T
V
T
T
dS
f
N
f
dV
f
N
u
dV
B
D
B
U
Ponieważ równanie to jest spełnione dla każdego dowolnego (dopuszczalnego) wektora
{
przemieszczeń
wirtualnych prawdziwe jest również dla wektora jednostkowego, a więc i dla
}
Uˆ
{ }
Uˆ
=1
[ ] [ ] [ ]
(
)
{ }
[ ]
{ }
(
)
{ }
[ ]
{ }
[
]
0
1
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
−
⋅
−
⋅
⋅
⋅
∑ ∫
∫
∫
=
λ
ω
S
S
T
P
V
M
T
V
T
dS
f
N
f
dV
f
N
u
dV
B
D
B
Oznaczając teraz przez:
[
- macierz sztywności elementu
] [ ] [ ] [ ]
(
dV
B
D
B
K
V
T
∫
⋅
⋅
=
)
{ }
[ ]
{ }
(
dV
f
N
F
V
M
T
M
∫
⋅
=
)
- wektor sił węzłowych wywołanych obciążeniem masowym
{ }
- wektor sił węzłowych wywołanych obciążeniem powierzchniowym elementu
[ ]
{ }
[
]
∑ ∫
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
=
λ
ω 1 S
S
T
S
dS
f
N
F
{ } { }
P
P
f
F
=
- wektor sił węzłowych wynikających z obciążenia skupionego przyłożonego
w węzłach elementu,
gdzie:
1) wektor
sił węzłowych dla obciążeń masowych ma postać:
{ }
{
}
T
M
r
y
M
r
x
M
k
y
M
k
x
M
j
y
M
j
x
M
i
y
M
i
x
M
F
F
F
F
F
F
F
F
F
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
=
2) wektor
sił węzłowych dla obciążeń powierzchniowych ma postać:
{ }
{
}
T
S
r
y
S
r
x
S
k
y
S
k
x
S
j
y
S
j
x
S
i
y
S
i
x
S
F
F
F
F
F
F
F
F
F
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
=
3) wektor
sił węzłowych dla obciążeń skupionych w węzłach ma postać:
{ }
{
}
T
P
r
y
P
r
x
P
k
y
P
k
x
P
j
y
P
j
x
P
i
y
P
i
x
P
F
F
F
F
F
F
F
F
F
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
=
równanie (--)zapiszemy w postaci
[ ]
{ }
{ } { } { }
0
=
−
−
−
⋅
P
S
M
F
F
F
u
K
lub w postaci prostszej
[ ]
{ } { }
0
=
−
⋅
F
u
K
gdzie
{ }
{ } { } { }
P
S
M
F
F
F
F
+
+
=
jest wektorem sumarycznych sił węzłowych dla wszystkich obciążeń elementu o postaci:
{ }
{
}
T
r
y
r
x
k
y
k
x
j
y
j
x
i
y
i
x
F
F
F
F
F
F
F
F
F
=
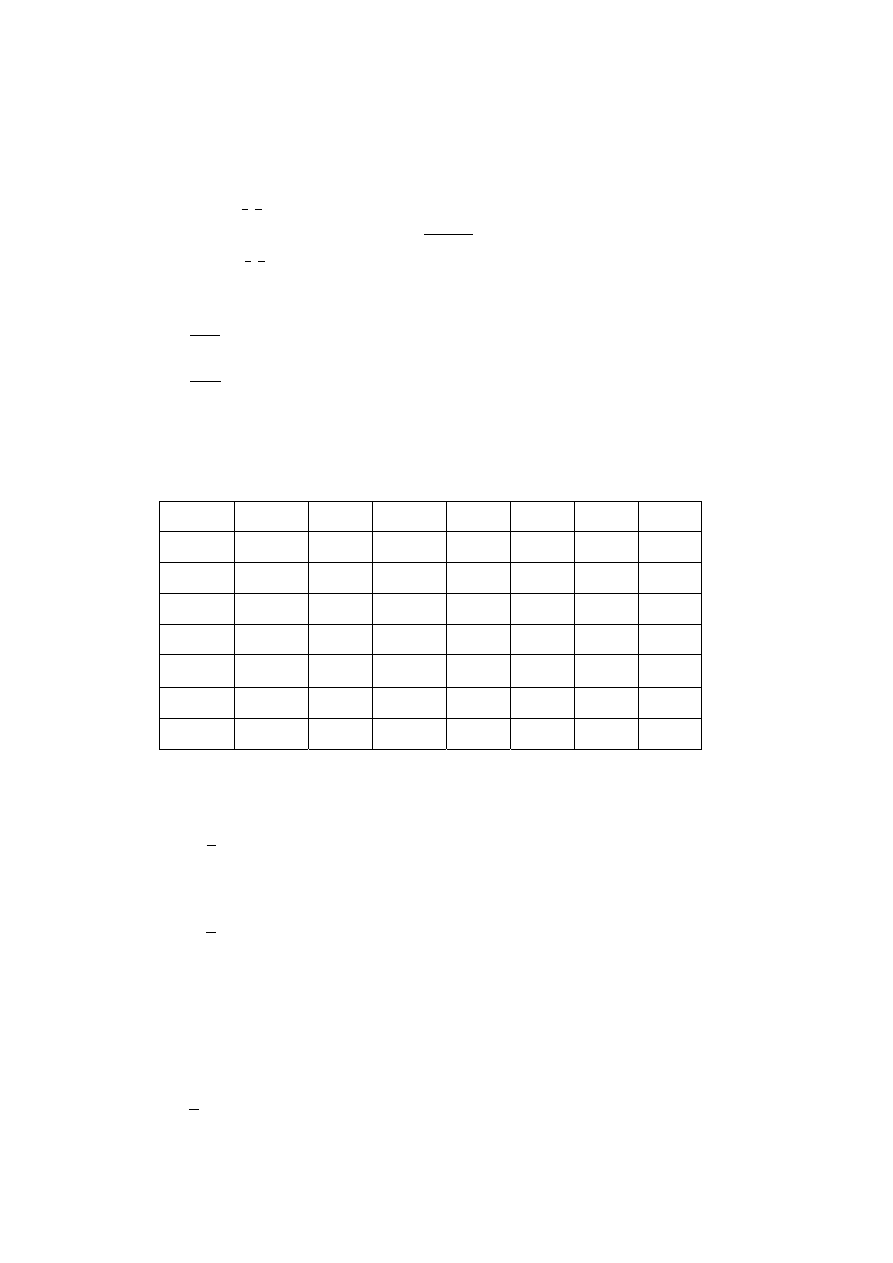
6
Przyjmując teraz wymiary elementu według rysunku otrzymamy macierz sztywności elementu w postaci:
[ ]
[ ] [ ] [ ]
(
)
[ ] [ ] [ ]
(
)
∫ ∫
∫ ∫
− −
− −
⋅
⋅
⋅
⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
=
1
1
1
1
2
2
2
2
)
(
4
η
ξ
d
d
B
D
B
h
b
a
dxdy
B
D
B
h
K
T
b
b
a
a
T
e
gdzie:
a
x
⋅
=
2
ξ
b
y
⋅
=
2
η
Po wykonaniu całkowania otrzymamy macierz sztywności elementu „e” w postaci:
Macierz sztywności
[k]
(e)
elementu prostokątnego nr
„e”
ma postać:
)
(
,
1
1
e
u
u
r
)
(
,
1
1
e
v
u
r
)
(
,
2
1
e
u
u
r
)
(
,
2
1
e
v
u
r
)
(
,
3
1
e
u
u
r
)
(
,
3
1
e
v
u
r
)
(
,
4
1
e
u
u
r
)
(
,
4
1
e
v
u
r
)
(
,
1
1
e
u
v
r
)
(
,
1
1
e
v
v
r
)
(
,
2
1
e
u
v
r
)
(
,
2
1
e
v
v
r
)
(
,
3
1
e
u
v
r
)
(
,
3
1
e
v
v
r
)
(
,
4
1
e
u
v
r
)
(
,
4
1
e
v
v
r
)
(
,
1
2
e
u
u
r
)
(
,
1
2
e
v
u
r
)
(
,
2
2
e
u
u
r
)
(
,
2
2
e
v
u
r
)
(
,
3
2
e
u
u
r
)
(
,
3
2
e
v
u
r
)
(
,
4
2
e
u
u
r
)
(
,
4
2
e
v
u
r
)
(
,
1
2
e
u
v
r
)
(
,
1
2
e
v
v
r
)
(
,
2
2
e
u
v
r
)
(
,
2
2
e
v
v
r
)
(
,
3
2
e
u
v
r
)
(
,
3
2
e
v
v
r
)
(
,
4
2
e
u
v
r
)
(
,
4
2
e
v
v
r
)
(
,
1
3
e
u
u
r
)
(
,
1
3
e
v
u
r
)
(
,
2
3
e
u
u
r
)
(
,
2
3
e
v
u
r
)
(
,
3
3
e
u
u
r
)
(
,
3
3
e
v
u
r
)
(
,
4
3
e
u
u
r
)
(
,
4
3
e
v
u
r
)
(
,
1
3
e
u
v
r
)
(
,
1
3
e
v
v
r
)
(
,
2
3
e
u
v
r
)
(
,
2
3
e
v
v
r
)
(
,
3
3
e
u
v
r
)
(
,
3
3
e
v
v
r
)
(
,
4
3
e
u
v
r
)
(
,
4
3
e
v
v
r
)
(
,
1
4
e
u
u
r
)
(
,
1
4
e
v
u
r
)
(
,
2
4
e
u
u
r
)
(
,
2
4
e
v
u
r
)
(
,
3
4
e
u
u
r
)
(
,
3
4
e
v
u
r
)
(
,
4
4
e
u
u
r
)
(
,
4
4
e
v
u
r
)
(
,
1
4
e
u
v
r
)
(
,
1
4
e
v
v
r
)
(
,
2
4
e
u
v
r
)
(
,
2
4
e
v
v
r
)
(
,
3
4
e
u
v
r
)
(
,
3
4
e
v
v
r
)
(
,
4
4
e
u
v
r
)
(
,
4
4
e
v
v
r
a przy oznaczeniach:
[
]
1
1
)
1
(
2
4
−
⋅
−
⋅
+
⋅
⋅
=
β
ν
β
α
a
)
1
(
2
3
1
ν
α
+
⋅
⋅
=
b
[
]
β
ν
β
α
⋅
−
⋅
+
⋅
⋅
=
−
)
1
(
2
4
1
1
c
[
]
1
1
)
1
(
4
−
⋅
−
+
⋅
−
⋅
=
β
ν
β
α
d
)
3
1
(
2
3
1
ν
α
⋅
−
⋅
⋅
=
e
[
]
β
ν
β
α
⋅
−
⋅
−
⋅
⋅
=
−
)
1
(
2
2
1
1
f
[
]
1
1
)
1
(
2
2
−
⋅
−
⋅
−
⋅
⋅
=
β
ν
β
α
g
[
]
1
1
)
1
(
2
−
⋅
−
−
⋅
−
⋅
=
β
ν
β
α
h
[
]
β
ν
β
α
⋅
−
+
⋅
−
⋅
=
−
)
1
(
4
1
1
i
[
]
−1
β
ν
β
α
⋅
−
−
⋅
−
⋅
=
)
1
(
2
1
j
gdzie:
a
b
=
β
7
)
1
(
12
2
ν
α
−
⋅
⋅
=
h
E
Macierz sztywności
[k]
(e)
elementu prostokątnego nr
„e”
można zapisać w postaci:
a
1
b
1
c
1
d
1
e
1
a
1
symetria
-e
1
f
1
-b
1
c
1
g
1
-e
1
h
1
b
1
a
1
e
1
i
1
b
1
j
1
-b
1
c
1
h
1
-b
1
g
1
e
1
d
1
-e
1
a
1
-b
1
j
1
-e
1
i
1
e
1
f
1
b
1
c
1
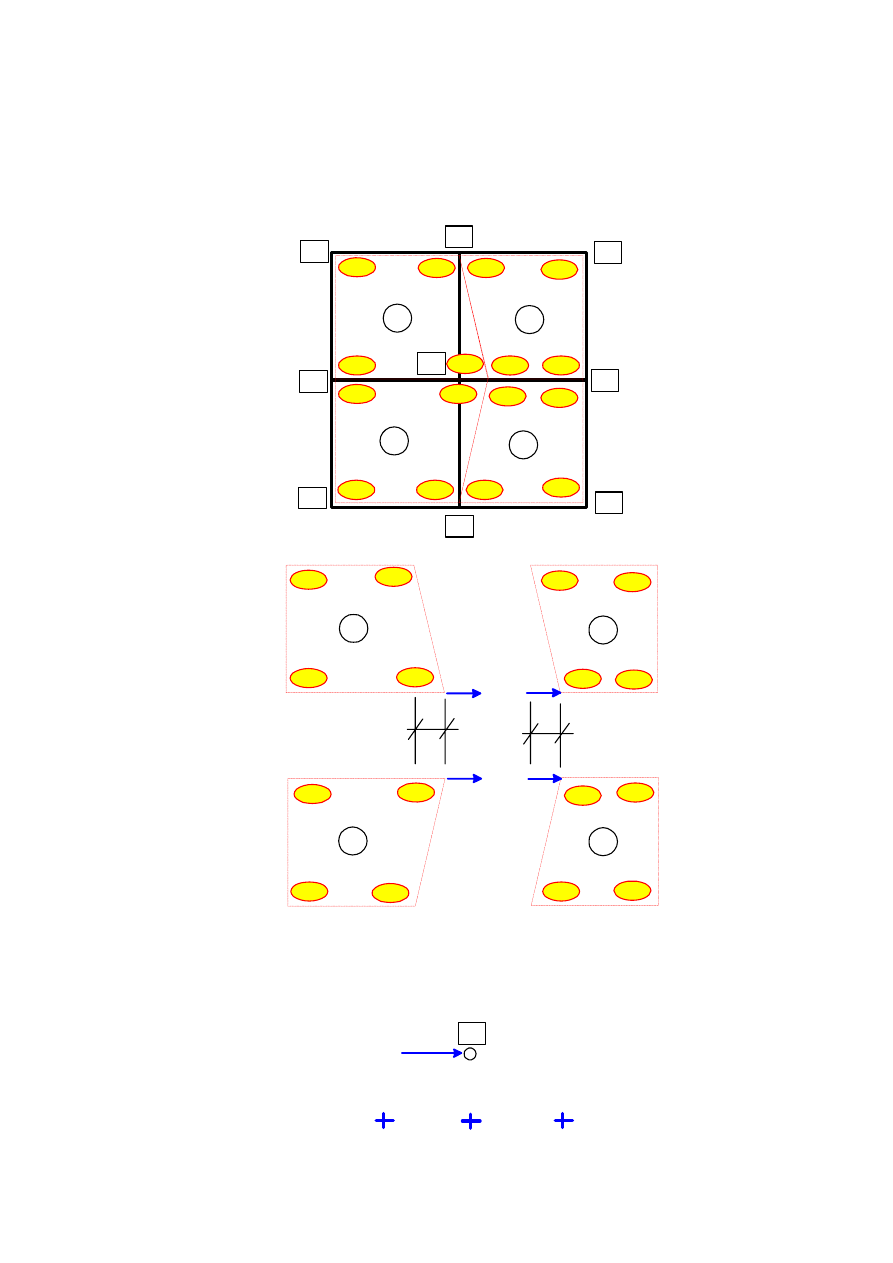
Przyjmując podział tarczy na cztery elementy i numerując węzły i elementy jak na rys.2.
wartości elementów ,macierzy globalnej otrzymamy stosując składanie macierzy
poszczególnych elementów skończonych według schematu pokazanego na rys.3
podział tarczy i numeracja
elementów i węzłów w układzie
globalnym
x
-
4
3
9
4
2
3
1
8
5
6
7
1
2
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
y
-
Rys.2.

8
9
k
9,9
=
r
u
u
,
2
2
(
)
4
r
u
u
,
4
4
(
)
1
r
u
u
,
3
3
(
)
3
r
u
u
,
1
1
(
)
2
5
k
9,9
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
3
4
2
1
u
5
=1
u
5
=1
r
u
u
,
2
2
(
)
4
r
u
u
,
1
1
(
)
2
r
u
u
,
3
3
(
)
3
r
u
u
,
4
4
(
)
1
4
3
9
4
2
5
3
1
8
6
7
1
2
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
obliczenie sumarycznej siły działającej na węzeł 5
czyli wartości ekementu k
9,9
macierzy sztywności
całego układu [K]
fragment ustroju z węzłem nr 5 po
jednostkowym jego przemieszczeniu w kierunku
poziomym
Rys.3.

10
=
1
,
1
k
)
1
(
,
1
1
u
u
r
=
1
,
2
k
)
1
(
,
1
1
u
v
r
=
2
,
2
k
)
1
(
,
1
1
v
v
r
)
1
(
,
1
,
3
1
3
u
u
r
k
=
)
1
(
,
2
,
3
1
3
v
u
r
k
=
)
4
(
,
)
1
(
,
3
,
3
1
1
3
3
u
u
u
u
r
r
k
+
=
)
1
(
,
1
,
4
1
3
u
v
r
k
=
)
1
(
,
2
,
4
1
3
v
v
r
k
=
)
4
(
,
)
1
(
,
3
,
4
1
1
3
3
u
v
u
v
r
r
k
+
=
)
4
(
,
)
1
(
,
4
,
4
1
1
3
3
v
v
v
v
r
r
k
+
=
)
4
(
,
3
,
5
1
3
u
u
r
k
=
)
4
(
,
4
,
5
1
3
v
u
r
k
=
)
4
(
,
5
,
5
3
3
u
u
r
k
=
)
4
(
,
3
,
6
1
3
u
v
r
k
=
)
4
(
,
4
,
6
1
3
v
v
r
k
=
)
4
(
,
5
,
6
3
3
u
v
r
k
=
)
4
(
,
6
,
6
3
3
v
v
r
k
=
)
4
(
,
3
,
7
1
4
u
u
r
k
=
)
4
(
,
4
,
7
1
4
v
u
r
k
=
)
4
(
,
5
,
7
3
4
u
u
r
k
=
)
4
(
,
6
,
7
3
4
v
u
r
k
=
)
2
(
,
7
,
7
3
3
u
u
r
k
=
)
4
(
,
3
,
8
1
4
u
v
r
k
=
)
4
(
,
4
,
8
1
4
v
v
r
k
=
)
4
(
,
5
,
8
3
4
u
v
r
k
=
)
4
(
,
6
,
8
3
4
v
v
r
k
=
)
2
(
,
7
,
8
3
3
u
v
r
k
=
)
2
(
,
8
,
8
3
3
v
v
r
k
=
)
1
(
,
1
,
9
1
4
u
u
r
k
=
)
1
(
,
2
,
9
1
4
v
u
r
k
=
)
4
(
,
)
1
(
,
3
,
9
1
2
3
4
u
u
u
u
r
r
k
+
=
)
4
(
,
)
1
(
,
4
,
9
1
2
3
4
v
u
v
u
r
r
k
+
=
)
4
(
,
5
,
9
3
2
u
u
r
k
=
)
4
(
,
6
,
9
3
2
v
u
r
k
=
)
4
(
,
)
2
(
,
7
,
9
4
2
3
1
u
u
u
u
r
r
k
+
=
)
4
(
,
)
2
(
,
8
,
9
4
2
3
1
v
u
v
u
r
r
k
+
=
)
4
(
,
)
3
(
,
)
2
(
,
)
1
(
,
9
,
9
2
2
3
3
1
1
4
4
u
u
u
u
u
u
u
u
r
r
r
r
k
+
+
+
=
)
1
(
,
1
,
10
1
4
u
v
r
k
=
)
1
(
,
2
,
10
1
4
v
v
r
k
=
)
4
(
,
)
1
(
,
3
,
10
1
2
3
4
u
v
u
v
r
r
k
+
=
)
4
(
,
)
1
(
,
4
,
10
1
2
3
4
v
v
v
v
r
r
k
+
=
)
4
(
,
5
,
10
3
2
u
v
r
k
=
)
4
(
,
6
,
10
3
2
v
v
r
k
=
)
4
(
,
)
2
(
,
7
,
10
4
2
3
1
u
v
u
v
r
r
k
+
=
)
4
(
,
)
2
(
,
8
.
10
4
2
3
1
v
v
v
v
r
r
k
+
=
)
4
(
,
)
3
(
,
)
2
(
,
)
1
(
,
9
,
10
2
2
3
3
1
1
4
4
u
v
u
v
u
v
u
v
r
r
r
r
k
+
+
+
=
)
4
(
,
)
3
(
,
)
2
(
,
)
1
(
,
10
,
10
2
2
3
3
1
1
4
4
v
v
v
v
v
v
v
v
r
r
r
r
k
+
+
+
=
)
1
(
,
1
,
11
1
2
u
u
r
k
=
)
1
(
,
2
,
11
1
2
v
u
r
k
=
)
1
(
,
3
,
11
3
2
u
u
r
k
=
)
1
(
,
4
,
11
3
2
v
u
r
k
=
)
3
(
,
)
1
(
,
9
,
11
3
1
4
2
u
u
u
u
r
r
k
+
=
)
3
(
,
)
1
(
,
10
,
11
3
1
4
2
v
u
v
u
r
r
k
+
=
)
3
(
,
)
1
(
,
11
,
11
1
1
2
2
u
u
u
u
r
r
k
+
=
)
1
(
,
1
,
12
1
2
u
v
r
k
=
)
1
(
,
2
,
12
1
2
v
v
r
k
=
)
1
(
,
3
,
12
3
2
u
v
r
k
=
)
1
(
,
4
,
12
3
2
v
v
r
k
=
)
3
(
,
)
1
(
,
9
,
12
3
1
4
2
u
v
u
v
r
r
k
+
=
)
3
(
,
)
1
(
,
10
,
12
3
1
4
2
v
v
v
v
r
r
k
+
=
)
3
(
,
)
1
(
,
11
,
12
1
1
2
2
u
v
u
v
r
r
k
+
=
)
3
(
,
)
1
(
,
12
,
12
1
1
2
2
v
v
v
v
r
r
k
+
=
)
3
(
,
9
,
13
3
2
u
u
r
k
=
)
3
(
,
10
,
13
3
2
v
u
r
k
=
)
3
(
,
11
,
13
1
2
u
u
r
k
=
)
3
(
,
12
,
13
1
2
v
u
r
k
=
)
3
(
,
13
,
13
2
2
u
u
r
k
=
)
3
(
,
9
,
14
3
2
u
v
r
k
=
)
3
(
,
10
,
14
3
2
v
v
r
k
=
)
3
(
,
11
,
14
1
2
u
v
r
k
=
)
3
(
,
12
,
14
1
2
v
v
r
k
=
)
3
(
,
13
,
14
2
2
u
v
r
k
=
)
3
(
,
14
,
14
2
2
v
v
r
k
=
)
2
(
,
7
,
15
3
2
u
u
r
k
=
)
2
(
,
8
,
15
3
2
v
u
r
k
=
)
3
(
,
)
2
(
,
9
,
15
3
4
1
2
u
u
u
u
r
r
k
+
=
)
3
(
,
)
2
(
,
10
,
15
3
4
1
2
v
u
v
u
r
r
k
+
=
)
3
(
,
11
,
15
1
4
u
u
r
k
=
)
3
(
,
12
,
15
1
4
v
u
r
k
=
)
3
(
,
13
,
15
2
4
u
u
r
k
=
)
3
(
,
14
,
15
2
4
v
u
r
k
=
)
3
(
,
)
2
(
,
15
,
15
4
4
2
2
u
u
u
u
r
r
k
+
=
)
2
(
,
7
,
16
3
2
u
v
r
k
=
)
2
(
,
8
,
16
3
2
v
v
r
k
=
)
3
(
,
)
2
(
,
9
,
16
3
4
1
2
u
v
u
v
r
r
k
+
=
)
3
(
,
)
2
(
,
10
,
16
3
4
1
2
v
v
v
v
r
r
k
+
=
)
3
(
,
11
,
16
1
4
u
v
r
k
=
)
3
(
,
12
,
16
1
4
v
v
r
k
=
)
3
(
,
13
,
16
2
4
u
v
r
k
=

11
)
3
(
,
14
,
16
2
4
v
v
r
k
=
)
2
(
,
10
,
17
1
4
v
u
r
k
=
)
2
(
,
10
,
18
1
4
v
v
r
k
=
)
3
(
,
)
2
(
,
15
,
16
4
4
2
2
u
v
u
v
r
r
k
+
=
)
2
(
,
15
,
17
2
4
u
u
r
k
=
)
2
(
,
15
,
18
2
4
u
v
r
k
=
)
3
(
,
)
2
(
,
16
,
16
4
4
2
2
v
v
v
v
r
r
k
+
=
)
2
(
,
16
,
17
2
4
v
u
r
k
=
)
2
(
,
16
,
18
2
4
v
v
r
k
=
)
2
(
,
17
,
17
4
4
u
u
r
k
=
)
2
(
,
17
,
18
4
4
u
v
r
k
=
)
2
(
,
18
,
18
4
4
v
v
r
k
=
)
2
(
,
7
,
17
3
4
u
u
r
k
=
)
2
(
,
7
,
18
3
4
u
v
r
k
=
)
2
(
,
8
,
17
3
4
v
u
r
k
=
)
2
(
,
8
,
18
3
4
v
v
r
k
=
)
2
(
,
9
,
17
1
4
u
u
r
k
=
)
2
(
,
9
,
18
1
4
u
v
r
k
=
Wyszukiwarka
Podobne podstrony:
mes tarcza 13 15
mes tarcza 12
mes tarcza 16 19
mes tarcza calosc
2005 11 elektroniczna tarcza strzelecka
Zarz[1] finan przeds 11 analiza wskaz
11 Siłowniki
11 BIOCHEMIA horyzontalny transfer genów
PKM NOWY W T II 11
wyklad 11
R1 11
CALC1 L 11 12 Differenial Equations
Prezentacje, Spostrzeganie ludzi 27 11
więcej podobnych podstron