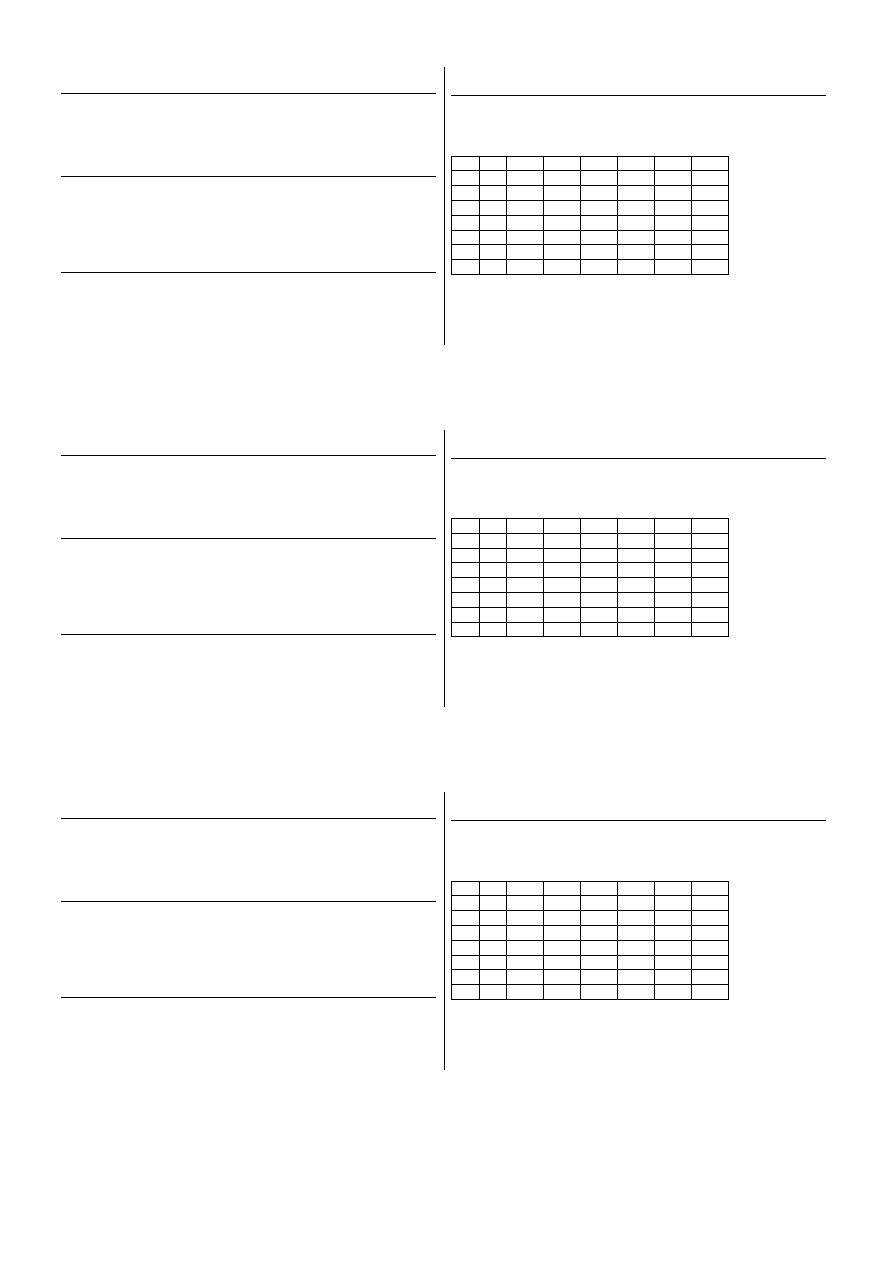
ZESTAW 1.

1. Udowodnij przez indukcję matematyczną, że dla każdego n > 5
prawdziwa jest nierównośc

n

n

> 3n!

2. Narysuj graf nieskierowany, którego macierz sąsiedztwa jest na-

stępująca A =





2

1

1

1

1

2

0

2

1

0

0

2

1

2

2

0





. Ile w tym grafie jest wszystkich

dróg długości 3 z punktu 2 do punktu 1?

3. Narysuj graf nieskierowany, którego macierz sąsiedztwa jest na-

stępująca A =





1

1

0

0

1

0

0

1

0

0

0

1

0

1

1

1





. Do grafu tego zastosuj algorytm

drzewo spinające i algorytm test drzewa.

4. Gmina skladająca się z miejscowości A, B, C, D, E, F , G planuje
budowę sieci wodociągowej. Ze względu na różne ukształtowania te-
renu koszty (w tys. zł) budowy pomiędzy poszczególnymi wioskami
podane są tabeli:

A

B

C

D

E

F

G

A

-

620

520

630

360

360

230

B

-

360

220

260

360

220

C

-

320

660

230

260

D

-

630

260

520

E

-

530

220

F

-

290

G

-

a) Stosując algorytm Kruskala i Prima wyznacz sposób najtańszej
realizacji tego projektu.

ZESTAW 2.

1. Udowodnij przez indukcję matematyczną, że dla każdego n > 5
prawdziwa jest nierównośc

n

n

> 7n!

2. Narysuj graf nieskierowany, którego macierz sąsiedztwa jest na-

stępująca A =





3

3

1

1

3

2

0

0

1

0

1

3

1

0

3

0





. Ile w tym grafie jest wszystkich

dróg długości 3 z punktu 3 do punktu 3?

3. Narysuj graf nieskierowany, którego macierz sąsiedztwa jest na-

stępująca A =





1

0

1

1

0

0

1

0

1

1

1

1

1

0

1

1





. Do grafu tego zastosuj algorytm

drzewo spinające i algorytm test drzewa.

4. Gmina skladająca się z miejscowości A, B, C, D, E, F , G planuje
budowę sieci wodociągowej. Ze względu na różne ukształtowania te-
renu koszty (w tys. zł) budowy pomiędzy poszczególnymi wioskami
podane są tabeli:

A

B

C

D

E

F

G

A

-

270

430

360

360

620

330

B

-

630

530

320

630

530

C

-

670

320

560

360

D

-

230

760

470

E

-

460

570

F

-

790

G

-

a) Stosując algorytm Kruskala i Prima wyznacz sposób najtańszej
realizacji tego projektu.

ZESTAW 3.

1. Udowodnij przez indukcję matematyczną, że dla każdego n > 5
prawdziwa jest nierównośc

n

n

> 7n!

2. Narysuj graf nieskierowany, którego macierz sąsiedztwa jest na-

stępująca A =





2

1

2

1

1

2

0

1

2

0

1

2

1

1

2

0





. Ile w tym grafie jest wszystkich

dróg długości 3 z punktu 2 do punktu 1?

3. Narysuj graf nieskierowany, którego macierz sąsiedztwa jest na-

stępująca A =





0

0

0

1

0

0

0

0

0

0

1

0

1

0

0

0





. Do grafu tego zastosuj algorytm

drzewo spinające i algorytm test drzewa.

4. Gmina skladająca się z miejscowości A, B, C, D, E, F , G planuje
budowę sieci wodociągowej. Ze względu na różne ukształtowania te-
renu koszty (w tys. zł) budowy pomiędzy poszczególnymi wioskami
podane są tabeli:

A

B

C

D

E

F

G

A

-

740

230

460

620

670

360

B

-

640

230

370

640

230

C

-

640

470

260

320

D

-

760

420

240

E

-

260

240

F

-

490

G

-

a) Stosując algorytm Kruskala i Prima wyznacz sposób najtańszej
realizacji tego projektu.

1

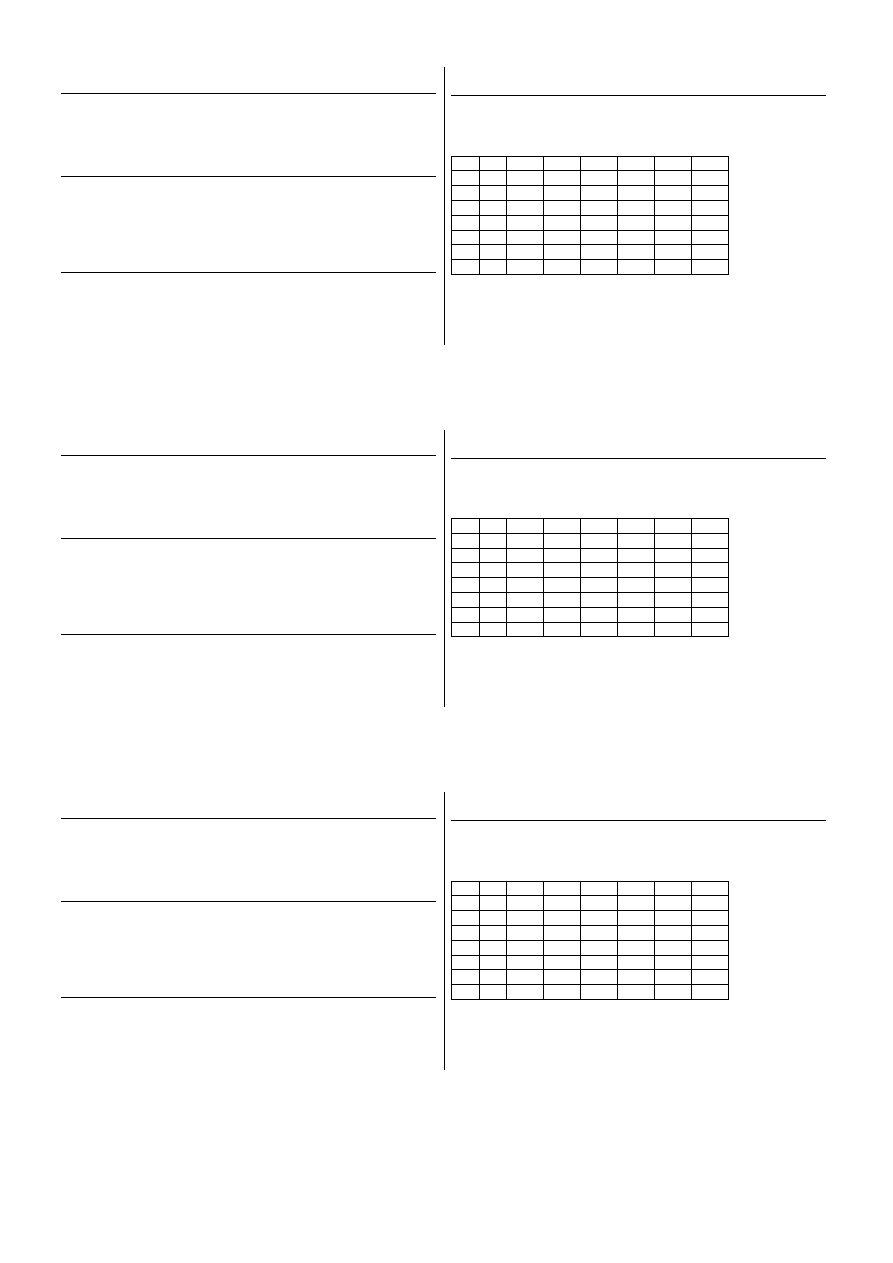
ZESTAW 4.

1. Udowodnij przez indukcję matematyczną, że dla każdego n > 5
prawdziwa jest nierównośc

n

n

> 6n!

2. Narysuj graf nieskierowany, którego macierz sąsiedztwa jest na-

stępująca A =





1

2

2

2

2

2

0

1

2

0

1

1

2

1

1

0





. Ile w tym grafie jest wszystkich

dróg długości 3 z punktu 1 do punktu 2?

3. Narysuj graf nieskierowany, którego macierz sąsiedztwa jest na-

stępująca A =





0

1

1

0

1

0

1

1

1

1

0

0

0

1

0

0





. Do grafu tego zastosuj algorytm

drzewo spinające i algorytm test drzewa.

4. Gmina skladająca się z miejscowości A, B, C, D, E, F , G planuje
budowę sieci wodociągowej. Ze względu na różne ukształtowania te-
renu koszty (w tys. zł) budowy pomiędzy poszczególnymi wioskami
podane są tabeli:

A

B

C

D

E

F

G

A

-

730

350

340

370

470

530

B

-

430

550

570

430

550

C

-

430

370

540

570

D

-

730

370

330

E

-

340

530

F

-

390

G

-

a) Stosując algorytm Kruskala i Prima wyznacz sposób najtańszej
realizacji tego projektu.

ZESTAW 5.

1. Udowodnij przez indukcję matematyczną, że dla każdego n > 5
prawdziwa jest nierównośc

n

n

> 3n!

2. Narysuj graf nieskierowany, którego macierz sąsiedztwa jest na-

stępująca A =





1

2

1

1

2

1

1

2

1

1

0

1

1

2

1

1





. Ile w tym grafie jest wszystkich

dróg długości 3 z punktu 1 do punktu 2?

3. Narysuj graf nieskierowany, którego macierz sąsiedztwa jest na-

stępująca A =





1

0

0

0

0

0

0

0

0

0

0

1

0

0

1

1





. Do grafu tego zastosuj algorytm

drzewo spinające i algorytm test drzewa.

4. Gmina skladająca się z miejscowości A, B, C, D, E, F , G planuje
budowę sieci wodociągowej. Ze względu na różne ukształtowania te-
renu koszty (w tys. zł) budowy pomiędzy poszczególnymi wioskami
podane są tabeli:

A

B

C

D

E

F

G

A

-

730

250

640

430

470

540

B

-

460

450

570

460

450

C

-

430

670

440

530

D

-

740

330

230

E

-

240

430

F

-

390

G

-

a) Stosując algorytm Kruskala i Prima wyznacz sposób najtańszej
realizacji tego projektu.

ZESTAW 6.

1. Udowodnij przez indukcję matematyczną, że dla każdego n > 5
prawdziwa jest nierównośc

n

n

> 3n!

2. Narysuj graf nieskierowany, którego macierz sąsiedztwa jest na-

stępująca A =





1

2

0

1

2

1

1

1

0

1

0

1

1

1

1

1





. Ile w tym grafie jest wszystkich

dróg długości 3 z punktu 1 do punktu 2?

3. Narysuj graf nieskierowany, którego macierz sąsiedztwa jest na-

stępująca A =





0

0

1

0

0

1

0

0

1

0

1

0

0

0

0

1





. Do grafu tego zastosuj algorytm

drzewo spinające i algorytm test drzewa.

4. Gmina skladająca się z miejscowości A, B, C, D, E, F , G planuje
budowę sieci wodociągowej. Ze względu na różne ukształtowania te-
renu koszty (w tys. zł) budowy pomiędzy poszczególnymi wioskami
podane są tabeli:

A

B

C

D

E

F

G

A

-

630

530

420

430

260

340

B

-

240

330

360

240

330

C

-

230

460

320

330

D

-

640

330

530

E

-

520

330

F

-

390

G

-

a) Stosując algorytm Kruskala i Prima wyznacz sposób najtańszej
realizacji tego projektu.

2