
1
Ćw 3
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE CZŁONÓW
AUTOMATYKI
Cel ćwiczenia
Celem ćwiczenia jest zapoznanie się z pojęciem charakterystyki częstotliwościowej, prak-
tycznym sposobem jej rejestracji oraz wykorzystaniem do identyfikacji własności dynamicznych
badanego elementu. Dodatkowym celem jest zapoznanie się z metodami symulacji działania ele-
mentów automatyki, w tym przypadku poprzez graficzne przedstawianie charakterystyk częstotli-
wościowych wykorzystując programy Matlab lub SciLab.
Program ćwiczenia
Cześć doświadczalna
Zarejestrować charakterystykę amplitudowo-fazową zadanego czwórnika.
Opracowanie wyników
1.
Wykonać potrzebne obliczenia. Narysować ręcznie charakterystykę amplitudowo-fazą oraz
charakterystyki logarytmiczne: amplitudową i fazową.
2.
Przeprowadzić identyfikację badanego czwórnika. Porównać wartość stałej czasowej T
wyznaczonej z charakterystyki amplitudowo-fazowej z wartością wynikającą ze struktury czwórni-
ka i wartości R i C.
Narysować wykresy charakterystyk częstotliwościowych czwórnika o wyznaczonej trans-
formacie korzystając z dostępnego oprogramowania. Przeanalizować wpływ parametrów na prze-
bieg charakterystyk częstotliwościowych.
Podstawy teoretyczne
Charakterystyki częstotliwościowe zawierają pełną informację o dynamice układów regulacji,
dlatego też zajmują bardzo ważne miejsce zarówno w teorii jak i praktyce sterowania automatycznego.
Są one określane w zasadzie dla układów liniowych, choć mogą być również z powodzeniem stosowa-
ne dla pewnych klas układów zlinearyzowanych.
Zasada wyznaczania charakterystyk częstotliwościowych oparta jest na następującym rozumo-
waniu:
Na wejście badanego obiektu, układu lub elementu podawane jest wymuszenie harmoniczne o
postaci
t
x
=
)
(t
x
0
sin
(3.1)
Jeżeli badany obiekt jest liniowy i nie działają na niego żadne dodatkowe wymuszenia i zakłócenia,
wówczas na wyjściu obiektu w stanie ustalonym pojawia się sygnał wyjściowy y(t) opisany zależno-
ścią
)
sin(
)
(
0
t
y
t
y
(3.2)
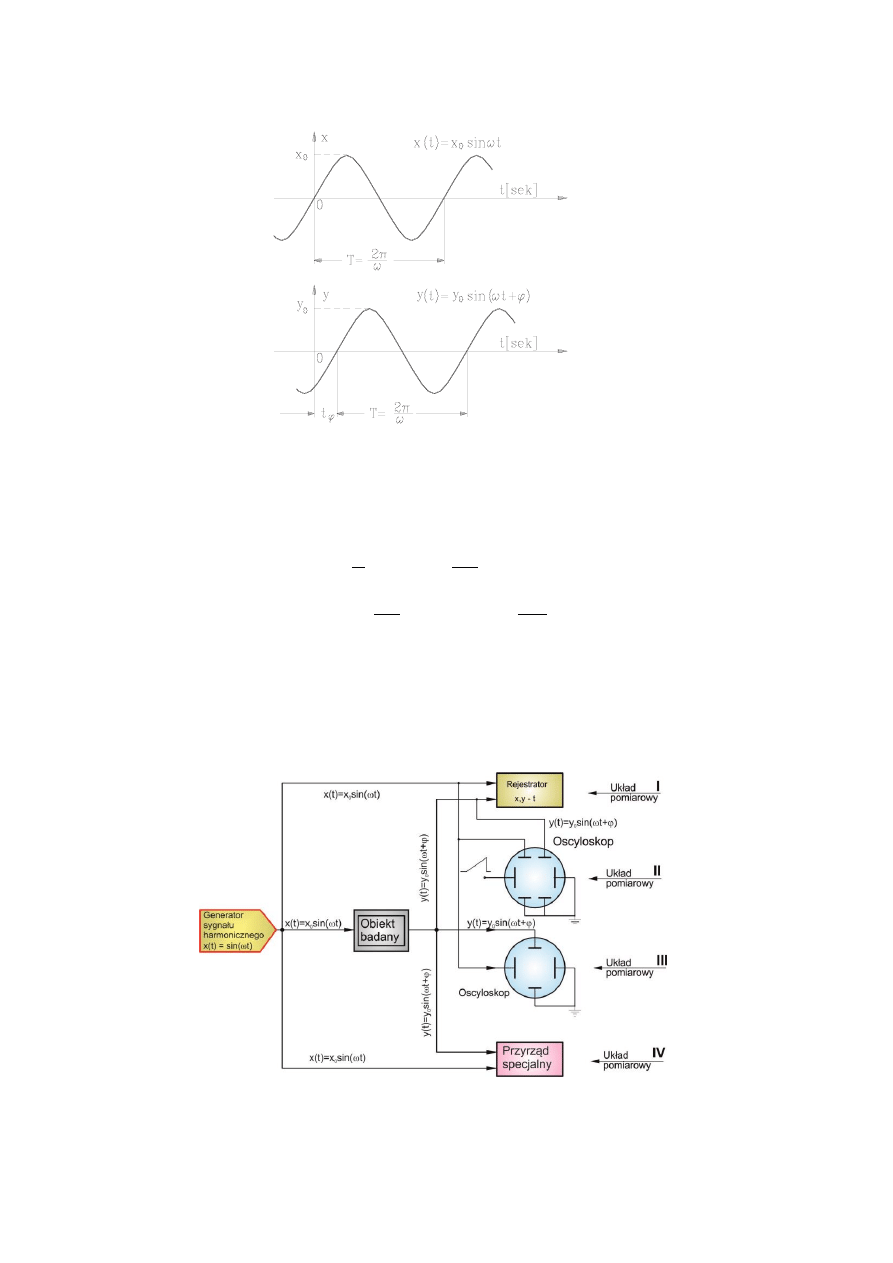
Przebiegi czasowe harmonicznej funkcji wymuszającej x(t) i wyjściowej y(t) dla pewnego obiek-
tu liniowego przy ustalonej pulsacji ω są pokazane na rys. 3.1.
2
Rys. 3.1. Przechodzenie sygnału sinusoidalnego przez człon liniowy
Wprost z przebiegów czasowych, które można otrzymać z wejścia i wyjścia badanego obiektu, zapisu-
jąc je za pomocą rejestratora wielokanałowego, można określić następujące parametry przebiegów
]
s
[rad
T
2
=
;
]
s
[
T
1
=
f
1
-
1
-
(3.3)
[stopni]
T
360
t
=
;
[rad]
T
2
t
=
(3.4)
Rejestrator rejestrujący przebiegi z rys. 3.1 musi spełniać następujący warunek: w paśmie pulsa-
cji badania obiektu od ω
min
do ω
max
nie może wnosić przesunięcia fazowego
r
. Ponadto musi być
znane wzmocnienie kanałów rejestratora, co pozwala wprost z przebiegów czasowych x(t) i y(t), w
sposób podany na rys. 3.1 wyznaczyć x
0
i y
0
.
Charakterystyki częstotliwościowe wyznacza się korzystając z jednego z wariantów układu ba-
dawczo-pomiarowego, przedstawionego na rys. 3.2.
Rys. 3.2. Układ badawczo-pomiarowy do wyznaczania charakterystyk częstotliwościowych
czterema sposobami
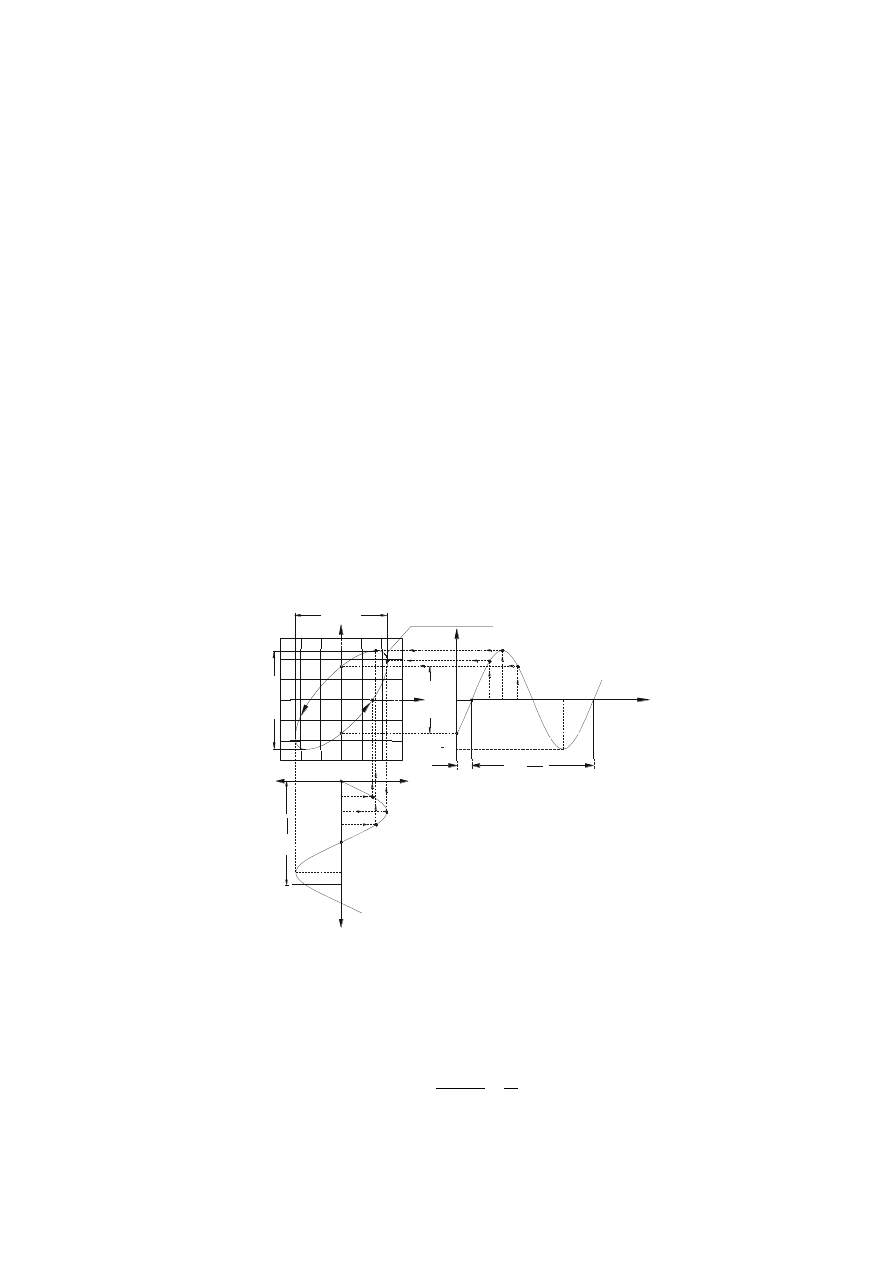
3
Układ pomiarowy I składa się z rejestratora przebiegów czasowych i generatora sygnału harmo-
nicznego oraz obiektu badań. Za pomocą rejestratora zapisuje się przebiegi x(t) i y(t), z których określa
się wzmocnienie k = y
0
(ω ) / x
0
(ω ) oraz kąt przesunięcia fazowego n(ω) w sposób pokazany na rys.
3.1. W celu wyznaczenia charakterystyki częstotliwościowej ustala się poszczególne wartości ω
1
, ω
2
,
..., ω
n
w paśmie częstotliwości pracy układu i wyznacza dla każdego ω
i
, i = 1, 2, ..., n odpowiednio
k(ω
i
) oraz n (ω
i
), zapisując je w tabelce. Dokładność otrzymanych wyników badań zależy przede
wszystkim od dokładności zapisu przebiegów x(t) i y(t) oraz od opracowania graficznego oscylogra-
mów. Zazwyczaj dokładność tej metody jest nie mniejsza niż 5 %. Mankamentem natomiast jest duża
pracochłonność obejmująca skalowanie oscylogramów i ich zapisywanie.
Układ pomiarowy II jest oparty na takiej samej zasadzie wyznaczania charakterystyki częstotli-
wościowej jak układ I. Różni się natomiast przyrządem pomiarowym, za pomocą którego odczytuje
się wartości punktów charakterystyki częstotliwościowej k(ω
i
) i n (ω
i
). Na ekranie dwustrumieniowe-
go oscyloskopu z długim czasem poświaty i podstawą czasu zsynchronizowaną z pulsacją ω
i
otrzymuje
się dwa przebiegi, jak na rys. 3.1. Wprost z ekranu można odczytać wartości k(ω
i
) i
(ω
i
). Zatem
szybciej można uzyskać poszczególne punkty charakterystyki częstotliwościowej. Dokładność tej me-
tody jest co najwyżej rzędu 10 %.
Przy bezpośrednim odczycie wartości k(ω
i
) i n (ω
i
) nie otrzymuje się utrwalonego w postaci
przebiegów dokumentu pomiarowego. W celu ewentualnego utrwalenia przebiegów x(t) i y(t) można
je sfotografować wprost z ekranu oscyloskopu.
Układ pomiarowy III ( rys. 3.2 ) jest oparty na innej zasadzie niż pierwsze dwa układy. Przyrzą-
dem pomiarowym jest tu oscyloskop jednostrumieniowy z długim czasem poświaty, na którego płytki
odchylania poziomego jest doprowadzony sygnał x(t) a na płytki odchylania pionowego y(t). W ten
sposób na ekranie oscyloskopu powstają figury Lissajous. Konstrukcja graficzna figur Lissajous dla
pewnego obiektu, na którego wejście jest doprowadzone wymuszenie harmoniczne x(t) = x
0
sin ω t,
natomiast na wyjściu pojawia się przebieg y(t) = y
0
sin(ω t + n) podana jest na rys. 3.3.
T=
0
0
y
y
0
t[sek]
x
x
-x
0
T
=
t[sek]
y
A
C
[m m ]
[m
m
]
B
0
1
2
3
4
5
[m
m
]
x
0.25T
0.75T
y
0
0.25T
0.75T
1
2
3
4
5
Figura Lissajous
y(t)=y sin( t+ )
0
t
t
x(t)=x sin( t)
0
2
2
Rys. 3.3. Interpretacja figur Lissajous
W układzie współrzędnych X-Y, naniesionym na ekran oscyloskopu, pojawia się charakterystyczna
krzywa Lissajous o kształcie elipsy. Mierząc długość trzech odcinków: A, B, C i korzystając z zależno-
ści podanych niżej wyznaczamy dla danej pulsacji ω dwa parametry charakterystyki częstotliwościo-
wej:
Wzmocnienie
A
B
=
)
(
x
)
(
y
=
)
k(
0
0
(3.5)
przesunięcie fazowe

4
B
C
=
)
(
sin
arc
(3.6)
Zaletą stosowania oscyloskopu jest szerokie pasmo przenoszenia sygnałów, które dla potrzeb
automatyki powinno być w zakresie od 0 do 1 kHz. Zamiast oscyloskopu, dla bardzo niskich i niskich
częstotliwości, może być stosowany rejestrator typu X-Y, którego pasmo zazwyczaj jest zawarte w
zakresie od 0 do kilku Hz. Wprost na papierze rejestratora otrzymuje się wykresy figur Lissajous a
następnie z tych wykresów oblicza się k(ω ) i
(ω) dla każdej częstotliwości, korzystając z oznaczeń
na rys. 3.3 i wzorów (3.5) i (3.6). Jednocześnie wykres z rejestratora X-Y jest dokumentem z przepro-
wadzonych badań obiektu.
Układ pomiarowy IV jest przyrządem specjalizowanym, przeznaczonym wyłącznie dla potrzeb
automatyki. Składa się on z dwóch części: generatora przebiegów harmonicznych z bardzo dokładnie
nastawianą częstotliwością ω , zwykle do 3 – 4 znaków po przecinku, oraz mierników wzmocnienia
k(ω
) i
)
(
.Wiele firm specjalizuje się w produkcji tego rodzaju przyrządów. Generator jest bezpo-
średnio połączony z miernikiem w celu uzyskania sygnału odniesienia x(t) dla pomiaru wzmocnienia
k(ω
) i przesunięcia fazowego
)
(
. Do miernika jednocześnie jest dołączony sygnał wyjściowy y(t)
z badanego obiektu, jak to pokazano na rys. 3.3. Odczyt wartości k(ω) i
)
(
może być cyfrowy lub
analogowy. W przypadku wyjścia cyfrowego do miernika może być dołączona drukarka, która pozwa-
la na udokumentowanie danych charakterystyki częstotliwościowej. Dokładność pomiarów tego rodza-
ju jest rzędu 1%.
W tej samej grupie układów pomiarowych mieszczą się urządzenia do pomiaru charakterystyk
częstotliwościowych oparte na nieco innej zasadzie. Polega ona na wyznaczaniu części rzeczywistej
ReG(jω) = P(ω) i części urojonej ImG(jω) = Q(ω) charakterystyki częstotliwościowej amplitudowo-
fazowej badanego obiektu opisanego transmitancją widmową G(jω) . Tego typu przyrząd zostanie
wykorzystany w czasie praktycznej realizacji ćwiczenia.
Teoretyczną podstawę charakterystyk częstotliwościowych stanowi pojęcie transmitancji wid-
mowej, którą definiujemy
G(s)
=
)
G(j
j
=
s
(3.7)
lub, co jest równoznaczne
x
y
=
)
G(j
(3.8)
gdzie:
y
- jest wartością zespoloną składowej ustalonej odpowiedzi układu wywołanej wymuszeniem
sinusoidalnym, a
x
- wartością zespoloną tego wymuszenia. Podstawiając za
x
i
y
parę odpowia-
dających im funkcji harmonicznych zapisanych w postaci wykładniczej
e
)
(
y
=
y
,
e
)
(
x
=
x
)]
_(
+
t
j[
0
t
j
0
(3.9)
otrzymamy
e
)
M(
=
e
)
(
x
e
e
)
(
y
=
)
G(j
)
(
j
t
j
0
)
(
j
t
j
0
(3.10)
gdzie M(ω) = y
0
(ω)/x
0
(ω) jest modułem charakterystyki częstotliwościowej (stosunkiem amplitud od-
powiedzi do wymuszenia).
Wykres G(jω) nazywa się charakterystyką amplitudowo-fazową lub zespoloną charakterystyką
częstotliwościową. Czasem używa się też nazwy: wykres transmitancji widmowej. Wykres ten jest
miejscem geometrycznym końców wektorów, których długość reprezentuje stosunek amplitud odpo-
wiedzi do wymuszenia, a kąt - przesunięcie fazowe między odpowiedzią a wymuszeniem. Zamiast
wykresu G(jω) można podać oddzielnie wykresy jego współrzędnych biegunowych M(ω) i
)
(
.
Nazywają się one:
)
(
)
(
j
G
M
- amplitudowa charakterystyka częstotliwościowa (wykres modułu charak-

5
terystyki częstotliwościowej)
)
(
= arg G(jω ) fazowa charakterystyka częstotliwościowa (wykres argumentu charakte-
rystyki częstotliwościowej).
Ponieważ G(jω) jest funkcją zespoloną, można rozłożyć ją na część rzeczywistą i część urojoną
[współrzędne prostokątne G(jω)]
)
(
)
(
)
(
jQ
P
j
G
(3.11)
gdzie:
P(ω ) = Re[G(jω)] - część rzeczywista G(jω),
Q(ω ) = Im[G(jω)] - część urojona G(jω).
Przedmiotem badań jest obiekt liniowy, opisany równaniami różniczkowymi zwyczajnymi o sta-
łych współczynnikach, lub transmitancją operatorową o postaci
a
+
s
a
+
+
s
a
+
s
a
b
+
s
b
+
+
s
b
+
s
b
=
N(s)
M(s
=
X(s)
Y(s)
=
G(s)
0
1
1
-
n
1
-
n
n
n
0
1
1
-
m
1
-
m
m
m
)
przy czym transmitancja G(s) jest funkcją wymierną zmiennej s, tzn. M(s) i N(s) są wielomianami z
zastrzeżeniem, że stopień M nie jest większy od stopnia N i jest badany wymuszeniem harmonicznym,
wobec czego można się posłużyć transmitancją widmową obiektu (3.11) o następującej postaci:
e
)
M(
=
)
G(j
Im
j
+
)
G(j
Re
=
=
)
Q(
j
+
)
P(
=
)
d(
j
+
)
c(
)
b(
j
+
)
a(
=
=
a
+
)
(j
a
+
+
)
(j
a
+
)
(j
a
b
+
)
(j
b
+
+
)
(j
b
+
)
(j
b
=
)
G(j
)
j_(
0
1
1
-
n
1
-
n
n
n
0
1
1
-
m
1
-
m
m
m
(3.12)
przy czym
)
G(j
Re
=
]
)
[d(
+
]
)
[c(
)
d(
)
b(
-
)
c(
)
a(
=
)
P(
2
2
(3.13)
jest charakterystyką częstotliwościową rzeczywistą obiektu oraz
)
G(j
Im
=
]
)
[d(
+
]
)
[c(
)
d(
)
a(
-
)
c(
)
b(
=
)
Q(
2
2
(3.14)
jest charakterystyką częstotliwościową urojoną obiektu.
Pomiędzy charakterystykami rzeczywistą i urojoną a charakterystykami amplitudową M(ω ) i fa-
zową
)
(
istnieją następujące zależności:
|
)
G(j
|
=
]
)
[Q(
+
]
)
[P(
=
)
M(
2
2
(3.15)
oraz
)
G(j
=
)
P(
)
Q(
=
)
(
tan
arc
tan
arc
(3.16)
Charakterystykę amplitudowo-fazową (a-f) można zdefiniować jako wykres na płaszczyźnie ze-
spolonej modułu M(ω) i argumentu
)
(
transmitancji widmowej G(jω) w funkcji pulsacji ω, zmie-
niającej się teoretycznie od -
do +
.Wykres charakterystyki a-f dla pulsacji w zakresie od -
do 0
jest lustrzanym odbiciem wykresu otrzymywanego dla pulsacji zmieniającej się od 0 do +
. Wystar-
czy zatem rozpatrywać zakres dodatnich ω .
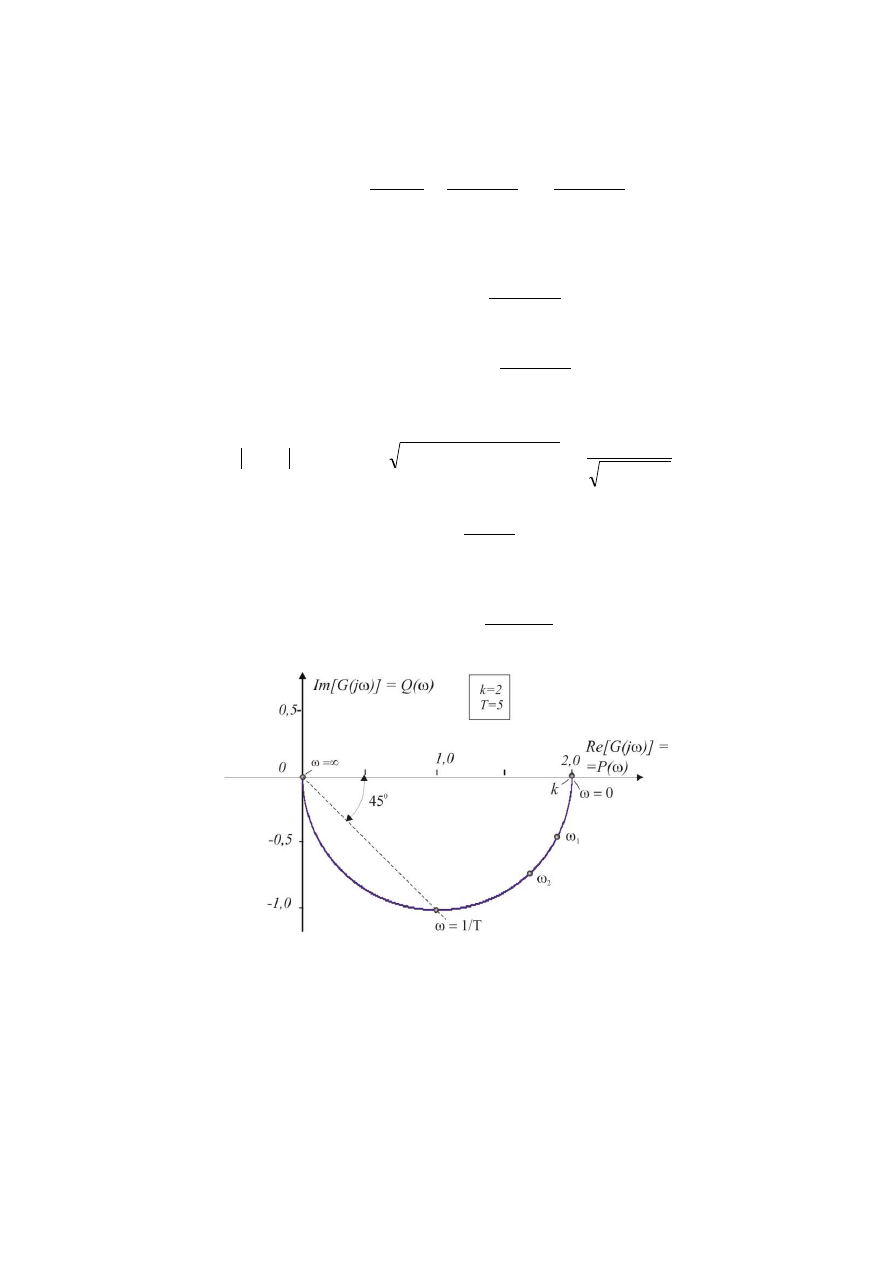
Dla ilustracji na rys. 3.4 przedstawiono wykres charakterystyki amplitudowo-fazowej obiektu
inercyjnego I-go rzędu o transmitancji operatorowej
1)
+
s
(T
k
=
G(s)
(3.17)
6
Podstawiając w (3.17) za s= jω oraz mnożąc licznik i mianownik przez zespoloną liczbę sprzężoną
do liczby zespolonej w mianowniku otrzymamy wzór na transmitancję widmową w postaci ogólnej i
po rozbiciu na część rzeczywistą i urojoną
1
+
)
(T
kT
j
-
1
+
)
(T
k
=
1
+
Tj
k
=
)
(j
G
2
2
(3.18)
Korzystając z równań (3.12) - (3.16) można wyznaczyć analitycznie poszczególne charaktery-
styki:
1. charakterystyka częstotliwościowa rzeczywista
1
+
)
(T
k
=
)
P(
=
)
G(j
Re
2
(3.19)
2. charakterystyka częstotliwościowa urojona
1
+
)
(T
kT
-
=
)
Q(
=
)
G(j
Im
2
(3.20)
3. charakterystyka częstotliwościowa amplitudowa
1
+
)
(T
k
=
]
)
[Q(
+
]
)
P(
[
=
)
M(
=
)
G(j
2
2
2
(3.21)
4. charakterystyka częstotliwościowa fazowa
T
arctg
-
=
)
(
P
)
(
Q
arctg
=
)
(
=
)
(j
G
arg
(3.22)
Ostatecznie więc transmitancję widmową można zapisać w postaci
T
arctg
j
j
e
T
k
e
M
j
G
1
)
(
)
(
2
)
(
(3.23)
Rys. 3.4. Charakterystyka amplitudowo-fazowa członu inercyjnego
Można więc mierzyć dla danej częstotliwości ω wartości Re G(jω) oraz Im G(jω), aby następnie
wykreślić wprost punkt charakterystyki amplitudowo-fazowej, lub mając Re i Im obliczyć na podsta-
wie (3.21) i (3.22) wzmocnienie M i przesunięcie fazowe
dla konkretnej wartości ω.
Istotną sprawą przy wyznaczaniu charakterystyk częstotliwościowych jest wykreślanie ich
kształtu w odpowiednim układzie współrzędnych. Wybór rodzaju układu współrzędnych charaktery-
styk częstotliwościowych zależy od celu, jakiemu mają służyć otrzymane charakterystyki częstotliwo-
ściowe. W teorii sterowania i w praktyce najbardziej znane są trzy układy współrzędnych, w których są
wykreślane charakterystyki częstotliwościowe.
Badanie stabilności najłatwiej może być przeprowadzone na charakterystykach częstotliwościo-
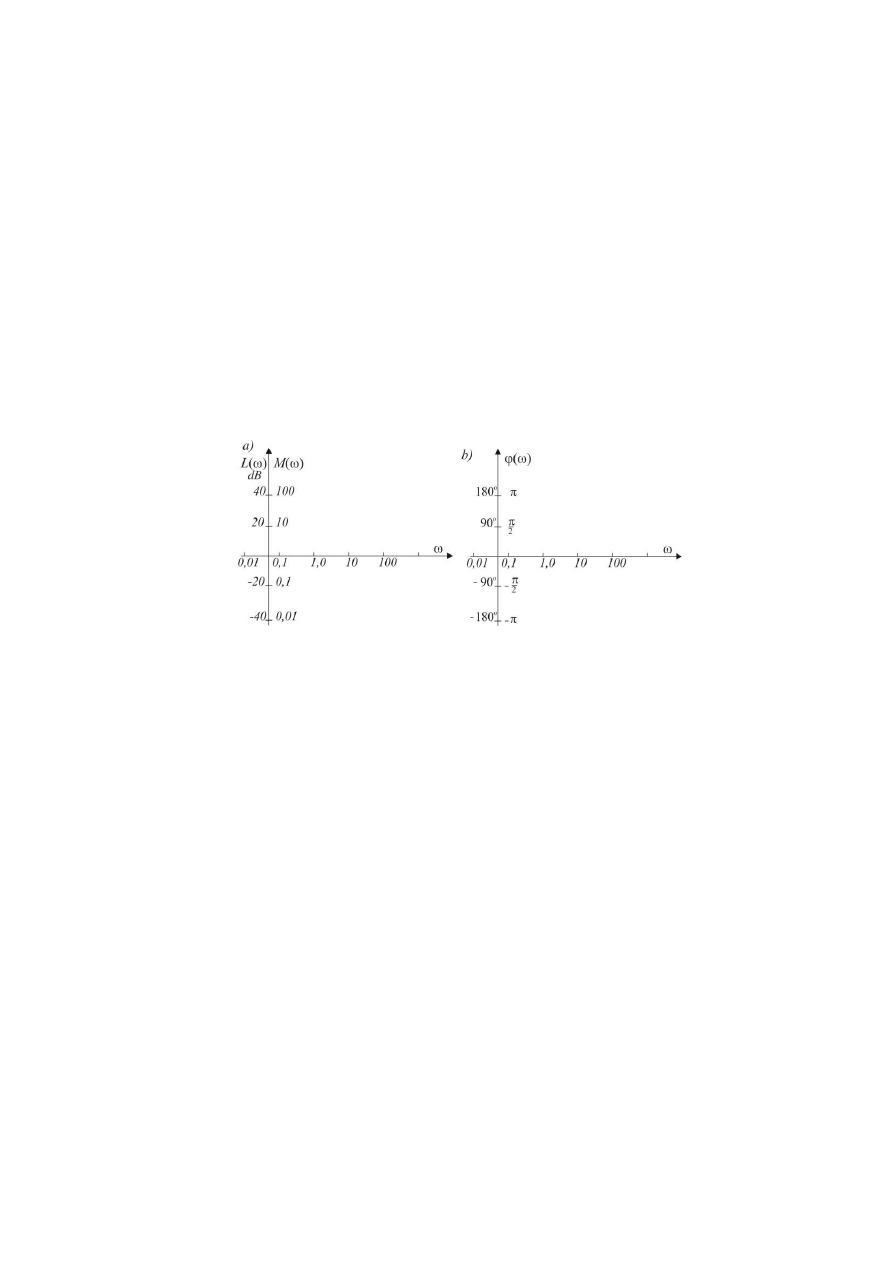
7
wych amplitudowo-fazowych, na płaszczyźnie zmiennej zespolonej. Wówczas charakterystykę często-
tliwościową wykreśla się, jak na rys. 3.4, badając, czy obejmuje punkt (-1, j0). Ogólnie znajduje tu
zastosowanie kryterium stabilności Nyquista, szeroko omówione w licznych pracach z teorii układów
liniowych.
Drugi sposób polega na oddzielnym wykreślaniu dwóch krzywych: charakterystyki amplitudo-
wej (modułu) M(ω) we współrzędnych logarytmicznych, oraz charakterystyki fazowej
w stopniach
[
] w skali liniowej - w funkcji częstotliwości w skali logarytmicznej lg ω. Charakterystyki te nazywają
się wówczas:
L(ω) = 20 log M (ω) - logarytmiczna charakterystyka amplitudowa,
(ω) - logarytmiczna charakterystyka fazowa.
Współrzędne tych charakterystyk przedstawiono na rys. 3.5. Podziałka osi ω jest logarytmiczna, deka-
dowa, tzn. każdej dekadzie ω przyporządkowany jest odcinek o jednakowej długości na osi ω. Po-
działka osi L(ω) jest liniowa, skalowana w decybelach (dB). Często na tej osi odkłada się bezpośrednio
stosunek amplitud M.(ω). Podziałka osi M(ω) jest wówczas logarytmiczna.
Rys. 3.5. Współrzędne logarytmicznych charakterystyk: a) amplitudowej L(
) b) fazowej
)
Przyjęcie takiego układu współrzędnych pozwala, z przybliżeniem wystarczającym do wielu
obliczeń, zastępować niektóre charakterystyki krzywoliniowe charakterystykami złożonymi z odcin-
ków prostych. Ponadto, użycie podziałki logarytmicznej osi M (ω) oraz podziałki liniowej osi
(ω)
umożliwia łatwe wyznaczanie charakterystyk szeregowego połączenia elementów, przez sumowanie
charakterystyk składowych.
Logarytmiczne charakterystyki częstotliwościowe znalazły bardzo duże znaczenie praktyczne.
Służą do badania stabilności, korekcji układu oraz określania właściwości dynamicznych i czasowych
badanego i projektowanego układu regulacji.
Rozpatrzmy zatem najistotniejsze aspekty wykreślania charakterystyk amplitudowych i fazo-
wych w logarytmicznej skali częstotliwości ze względu na potrzebę uzyskania poprawnych wykresów i
podstawowe interpretacje.
Wartości L(ω) obliczamy według wzoru
)
(
lg
20
)
(
M
L
(3.24)
i wynik tego obliczenia otrzymuje miano dB. Mnożnik 20 jest umowny - został wprowadzony, aby
operować najczęściej wartościami L(ω) rzędu od kilku do kilkudziesięciu dB, wygodnymi do obliczeń
pamięciowych, np.:
dla M(ω) = 2 mamy L(ω) = 20 log 2 . 20A0,3 = 6 dB,
dla M(ω) = 10 mamy L(ω) = 20 log 2 = 20A1 = 20 dB.
Podziałka osi
(ω) jest liniowa, przesunięcie fazowe odmierzamy w stopniach lub radianach.
W praktyce przeliczanie skali liniowej modułu na skalę logarytmiczną w decybelach według
wzorów (3.24) jest czasem uciążliwe, dlatego wygodniej jest posługiwać się podanym na rys. 3.6

8
nomogramem. Pozwala on odczytać natychmiast wartość wzmocnienia L(ω) w [dB], gdy dany jest
współczynnik wzmocnienia, czyli moduł M. Sposób korzystania z nomogramu z rys. 3.6 można poka-
zać na prostych przykładach. Jeżeli przy wyznaczaniu charakterystyki częstotliwościowej dla pewnej
częstotliwości ω
i
otrzymuje się M(ω
i
) = 3, wówczas z nomogramu odczytujemy, że wartość L(ω) jest
dodatnia i wynosi 10 dB. Gdy natomiast w pewnym układzie podano, że L(ω) = - 40 dB, to z nomo-
gramu odczytać można, że stosunek amplitud wynosi 10
-2
, co oznacza iż sygnał wyjściowy jest sto-
krotnie mniejszy od sygnału wejściowego.
Wzmocnienie L(ω) [dB] lub moduł M [dB] są zależne od częstotliwości ω, którą na charaktery-
stykach logarytmicznych podaje się również w skali logarytmicznej.
0.1
1.0
10
100
1
2
3
4
5 6 7 8 9 10
0
6
10 1214
17
18
19
20
-10
0
20
40
100
40
20
26
40
32
70
37
L(
)
M(
)
[dB]
Rys. 3.6. Zamiana skali liniowej charakterystyki amplitudowej M(
) na decybele
Drugą charakterystyką częstotliwościową jest przesunięcie kątowe ω w stopniach [
] oznaczane
na osi rzędnych w skali liniowej. Jest ono również zależne od częstotliwości ω, którą podaje się w
identyczny sposób jak dla wzmocnienia L(ω) [dB], to jest w skali logarytmicznej.
Ponieważ skala częstotliwości jest taka sama, więc logarytmiczne charakterystyki częstotliwo-
ściowe mogą być narysowane dwoma sposobami. Pierwszy, w którym oddzielnie są podane wykresy
amplitudy i fazy (wygodnie jest umieszczać je jeden nad drugim) lub drugi sposób - w tej samej skali
częstotliwości i dwóch osiach rzędnych: L(ω) [dB} i
[
] są rysowane razem dwie charakterystyki
częstotliwościowe. Najczęściej wykorzystywany jest pierwszy sposób.
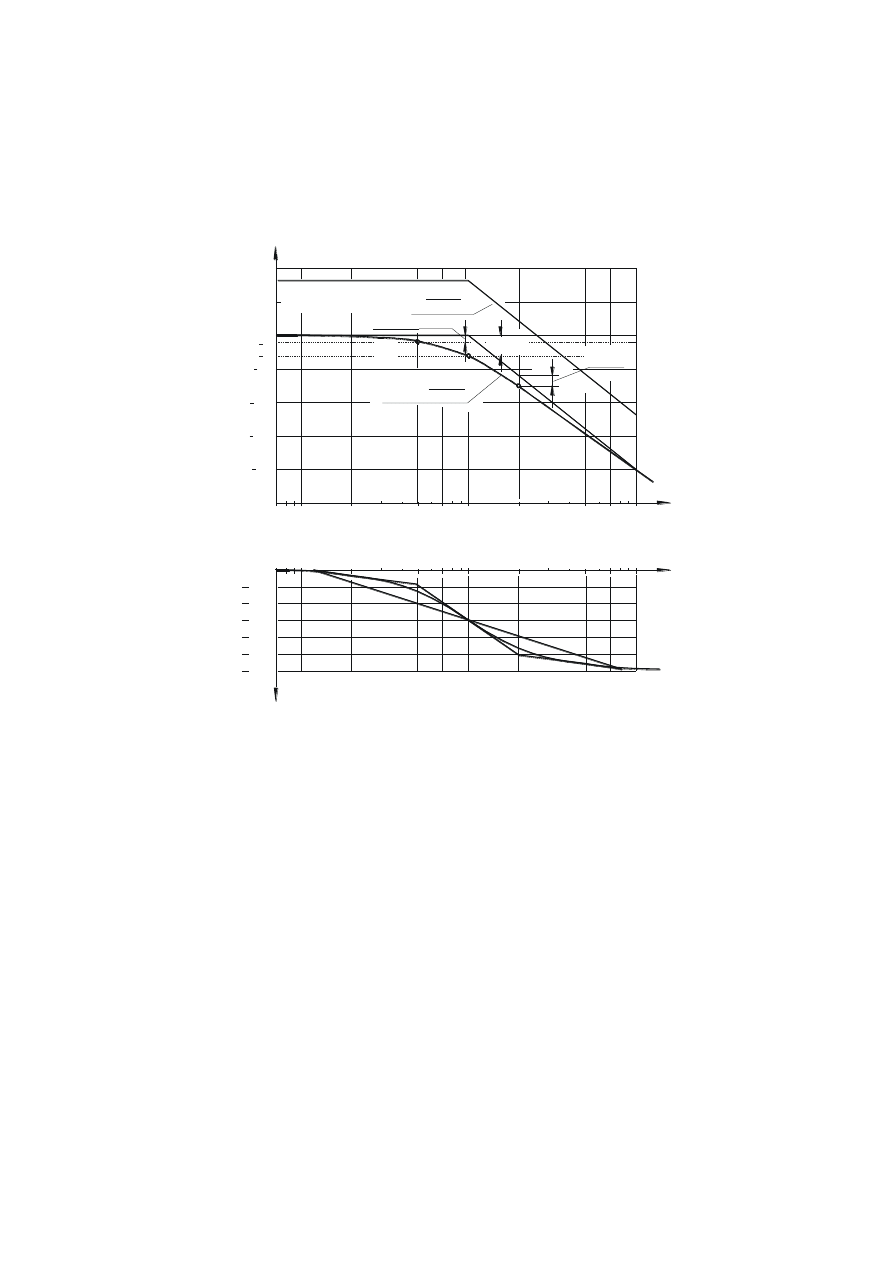
Dla ilustracji na rys. 3.7 przedstawione są częstotliwościowe charakterystyki logarytmiczne
obiektu o transmitancji
1
1
)
(
Ts
s
G
i
1
Ts
k
. Interesujące jest porównanie charakterystyk często-
tliwościowych tego samego obiektu, raz wykreślonych w skali liniowej na płaszczyźnie zespolonej
(rys. 3.4), oraz po raz drugi w skali logarytmicznej na (rys. 3.7).
Łatwo można zauważyć, że charakterystyki częstotliwościowe mogą być wykreślone według
jeszcze innego sposobu, a mianowicie we współrzędnych: moduł M i argument
, przy czym często-
tliwość ω w takim układzie współrzędnych staje się parametrem. Ten sposób wykreślania charaktery-
styk częstotliwościowych znajduje zastosowanie przede wszystkim przy identyfikacji obiektów oraz
przy korekcji projektowanych układów regulacji. Jako rzędne przyjmuje się moduł M w skali logaryt-
micznej czyli L(ω) a jako odcięte - argument
w skali liniowej. Przykład wykreślania charakterystyk
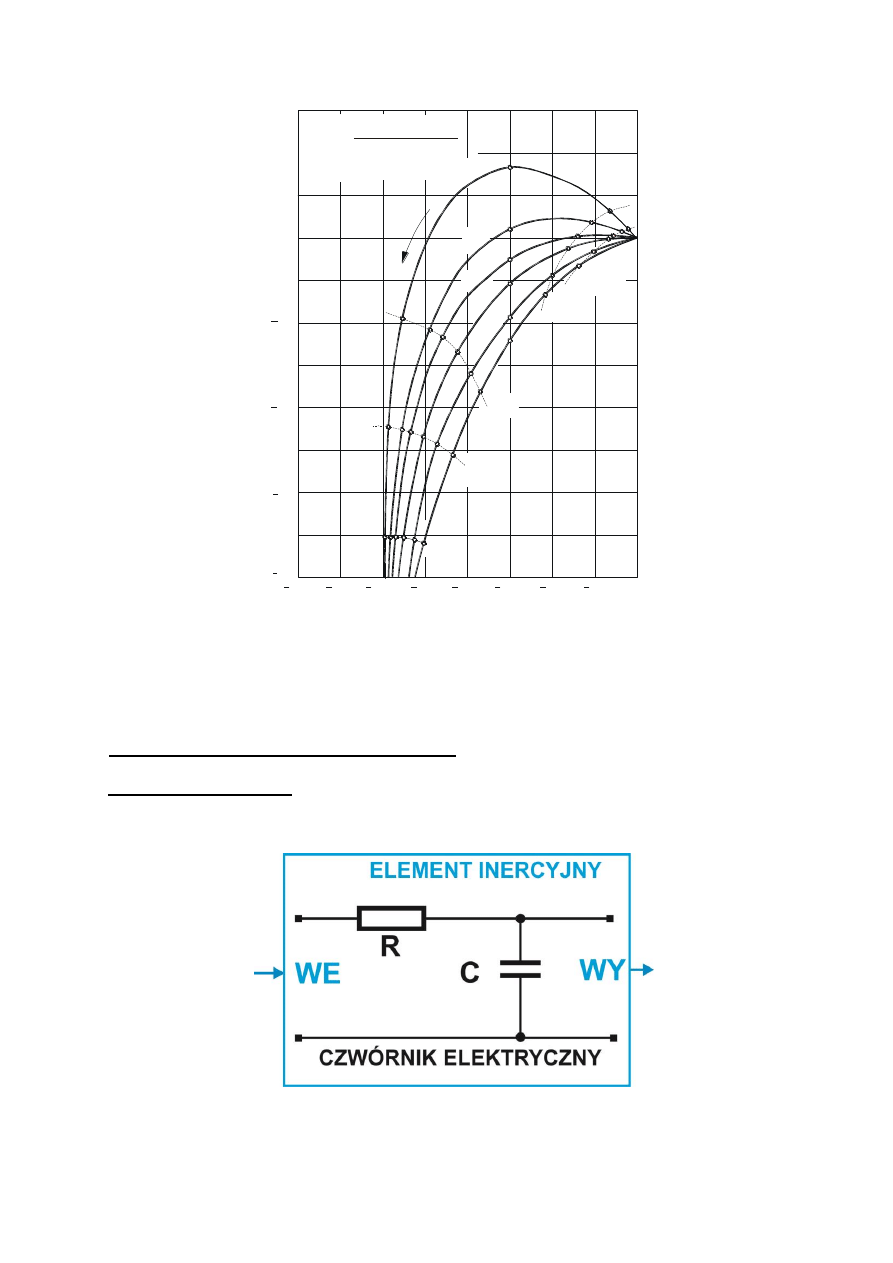
częstotliwościowych we współrzędnych moduł - argument, dla obiektu drugiego rzędu, jest podany na
rys. 3.8.
Charakterystyczną wielkością jest tu wartość przesunięcia fazowego
, która wynosi -90
dla
wszystkich ζ przy ω/ω
o
= 1.
Większość obliczeń związanych z analizą i syntezą układów automatycznej regulacji wykonuje
się obecnie przy pomocy odpowiednich programów komputerowych. Dają one w większości przypad-
ków możliwość prezentowania wyników obliczeń w postaci graficznej. Charakterystyki częstotliwo-
ściowe w programach symulacyjnych mają swoje nazwy, związane zazwyczaj z nazwiskami ich twór-
ców. Nazwy te funkcjonują również w angielskojęzycznej literaturze i są następujące:
nyquist -
charakterystyka amplitudowo-fazowa na płaszczyźnie zespolonej (jak na rys.
3.4)
bode -
logarytmiczne charakterystyki: amplitudowa L(ω) i fazowa n(ω) (jak na rys.
9
3.7)
nicholsa-
charakterystyka częstotliwościowa w układzie współrzędnych moduł-argument
(L,
).
Prezentowane w dalszej części materiału wykresy charakterystyk częstotliwościowych uzyskane
zostały przy pomocy oprogramowania SciLab.
[dB]
1
3
1
2
5
0.7
0.5
0.2
0.1
10
5
0
5
10
15
20
7
10
0.5
0.1
0.2
0.7
1
2
7
5
10
-1dB
-3dB
-1dB
G(s)=
1
Ts+ 1
G(s)=
k
Ts+ 1
Asym ptoty dla
0
15
30
45
60
75
90
o
o
o
o
o
o
o
k
L(
)
[s ]
-1
[s ]
-1
Rys. 3.7. Najczęściej stosowany sposób rysowania logarytmicznych charakterystyk częstotliwo-
ściowych
10
0
30
60
90
120
150
180
210
240
o
o
o
o
o
o
o
o
o
40
30
20
10
0
z =
0.2
=
0.
5
=
0.
70
7
=
1
=
1
.5
=
2
= 1/4
= 1/2
= 1
= 2
= 4
= 8
2
o
L
dB
G(j
)=
(j
2
+j2z
Rys. 3.8. Rodzina charakterystyk częstotliwościowych członu oscylacyjnego w układzie
współrzędnych moduł-argument (L,
)
WYKONANIE ĆWICZENIA
Część doświadczalna
W ramach praktycznej realizacji ćwiczenia należy wykonać pomiary charakterystyki amplitudo-
wo-fazowej zadanego czwórnika elektrycznego RC. Jego schemat przedstawia rys. 3.9.
Rys. 3.9. Schemat badanego czwórnika
11
Elementy czwórnika R i C są wymienne. Należy poznać wartość zastosowanego rezystora i kon-
densatora, albowiem dane te będą przydatne podczas sporządzania sprawozdania.
Pomiary wykonywane będą według metody IV z rys. 3.2. Rolę specjalizowanego przyrządu
spełnia analizator transmitancji Typ 272A firmy UNIPAN. Przyrząd ten zawiera w jednej obudowie
trzy oddzielne układy funkcjonalne:
- generator fali sinusoidalnej, trójkątnej lub kwadratowej,
- miliwoltomierz fazo-czuły mierzący składową rzeczywistą,
- miliwoltomierz fazo-czuły mierzący składową urojoną.
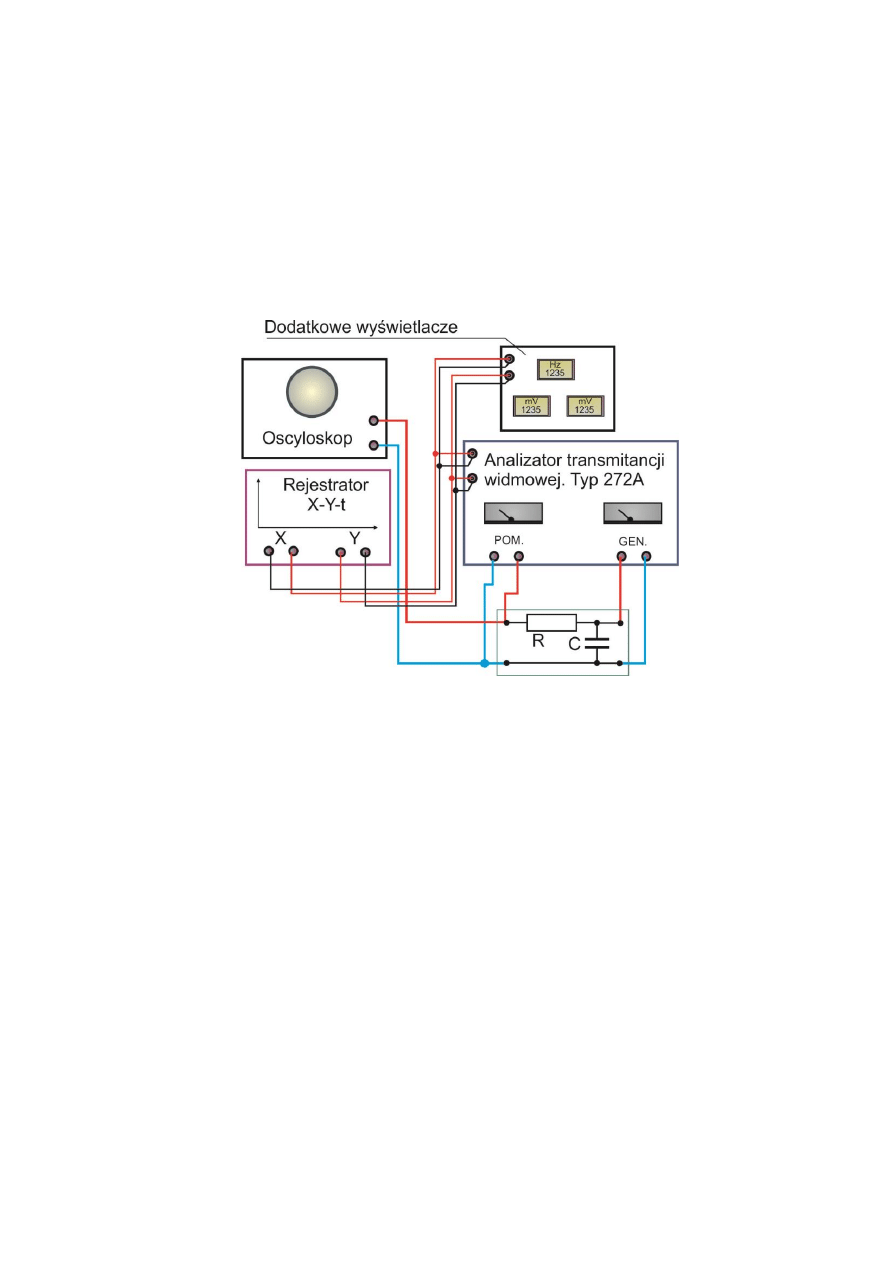
Schemat blokowy układu pomiarowego przedstawiony jest na rys. 3.10 natomiast na foto 3.1
przedstawiony jest rzeczywisty wygląd stanowiska badawczego.
Rys. 3.10. Schemat blokowy układu do pomiaru charakterystyki a-f
Do dodatkowych wyjść analizatora podłączone są dwa woltomierze cyfrowe i rejestrator X-Y.
Woltomierze cyfrowe pozwalają na łatwiejszy i dokładniejszy odczyt mierzonych składowych charak-
terystyki. W szczególności pozwalają odczytywać bezpośrednio znak mierzonych wielkości, czego nie
zapewniają oryginalne wychyłowe mierniki. Rejestrator X-Y spełnia w tym układzie pomocniczą rolę.
Ma ułatwić dobór częstotliwości ω w taki sposób, aby rozmieścić w miarę równomiernie punkty po-
miarowe na wykresie.
Przed rozpoczęciem pomiarów należy analizator przygotować do pracy zgodnie z instrukcją.
Następnie przygotowujemy rejestrator. Zwierając wejścia obydwu kanałów rysujemy ręcznie układ
współrzędnych prostokątnych (płaszczyznę fazową) i zerujemy rejestrator (ustawiamy pisak rejestrato-
ra w zerze narysowanego układu współrzędnych). Do ręcznego rysowania układu wykorzystujemy
pokrętła rejestratora przeznaczone do wstępnego ustawiania zera. Po wykonaniu tych czynności dobie-
ramy czułość poszczególnych kanałów pomiarowych, pamiętając, że maksymalna amplituda sygnału
na wyjściach analizatora wynosi 100 mV.
Pomiar rozpoczynamy od najmniejszej częstotliwości, dla której jest jeszcze możliwy pomiar.
Przy zbyt małej częstotliwości wskazówki wskaźników wychyłowych zaczynają oscylować wokół
średniej wartości. Dla czwórników badanych w laboratorium ω
min
wynosi około 3 Hz. Dla ustawionej
częstotliwości ω
i
odczytujemy wartość P(ω
i
) i Q(ω
i
). Wartości te zapisujemy w tabeli (wzór: Tabela
3.1). Ponadto opuszczając pisak rejestratora nanosimy punkt charakterystyki w uprzednio naniesionym
układzie współrzędnych, odpowiadający częstotliwości ω
i
. Następnie zwiększamy ω do wartości,
przy której pisak rejestratora przemieści się od poprzedniego punktu o około 20 ) 25mm. Dokonuje-
my odczytu wartości P(ω) i Q(ω) i zapisujemy w tabeli. Powtarzając wyżej wymienione czynności

12
odczytujemy około 20 punktów charakterystyki amplitudowo-fazowej badanego elementu.
Foto. 3.1. Fotografia stanowiska do rejestrowania charakterystyki amplitudowo-fazowej
Tabela 3.1. (wzór)
Lp.
ω
[Hz]
P(ω)
[mV]
Q(ω)
[mV]
P(ω)/
66.6
Q(ω)/
66.6
M(ω)
L(ω)
φ(ω)
1.
2.
pomiary
obliczenia
.
.
Dzielenie odczytywanych wyników przez 66.6 wynika z następującego rozumowania:
Mierniki cyfrowe, z których odczytujemy P(ω) i Q(ω) podłączone są do dodatkowych wyjść
analizatora transmitancji widmowej. Sygnał na tych wyjściach unormowany jest do poziomu
±100mV przy maksymalnej amplitudzie na głównych zaciskach, czyli przy 15V.
Wstępnie ustawiliśmy napięcie sinusoidy wymuszającej równe 10V czyli 2/3 maksymalnego
zakresu.
Stąd wynika, że na dodatkowych zaciskach maksymalne napięcie osiągnie poziom:
100mV◦2/3=66,6.. mV.
Wartości P(ω) i Q(ω) definiowane są jako stosunek amplitudy sygnału wyjściowego do ampli-
tudy sygnału wejściowego. Przy ustawieniu 10V amplitudy wymuszenia i korzystaniu z dodat-
kowych wyjść przyrządu należy przyjąć, że amplituda wymuszenia wynosi 66,6mV.
Część obliczeniowa
W tej części ćwiczenia należy wykonać następujące czynności:
1. Wykonać obliczenia przewidziane w pozostałych kolumnach tabeli 3.1. W tym celu należy

13
w pierwszej kolejności pomierzone wartości P(ω) i Q(ω) podzielić przez 66.6. Wyniki
dzielenia będą stanowiły bazę dalszych obliczeń.
2. Obliczyć M(ω) dla poszczególnych wartości ω. W tym celu należy posłużyć się wzorem
(3.15).
3. Obliczyć L(ω) korzystając ze wzoru (3.24).
4. Obliczyć φ(ω) korzystając ze wzoru (3.16) lub (3.22)
5. Narysować na płaszczyźnie fazowej wykres charakterystyki amplitudowo-fazowej łącząc
ręcznie naniesione uprzednio poprawnie punkty P(ω) i Q(ω).
6. Dokonać identyfikacji badanego czwórnika jako członu automatyki. Analogia otrzymanego
wykresu do wykresu z rys.3.4 sugeruje, że badany czwórnik będzie elementem inercyjnym
I-go rzędu. Posiłkując się teorią i informacjami zawartymi na rys.3.4 określić parametry
elementu inercyjnego I-go rzędu (k i T).
7. Obliczyć stała czasową czwórnika elektrycznego jako iloczyn oporności (rezystancji elek-
trycznej) i pojemności elektrycznej tego czwórnika. Udokumentować, że taki iloczyn wyra-
ża się w jednostkach czasu.
8. Porównać otrzymane stałe czasowe (z pkt.7 i pkt. 8).
9. Narysować charakterystyki logarytmiczne czwórnika elektrycznego na podstawie wykona-
nych obliczeń L(ω) i φ(ω).
10. Przeprowadzić symulację komputerową badanego czwórnika w zakresie charakterystyk
częstotliwościowych, czyli zrobić model członu inercyjnego I-go rzędu o otrzymanych
parametrach i narysować jego charakterystyki częstotliwościowe.
Uzyskane wyniki zamieścić w starannie wykonanym sprawozdaniu zespołu z ćwiczenia.
Wyszukiwarka
Podobne podstrony:
9 Ch ka zadymienia zadymienie
ch ka skokowa
9 Ch ka zadymienia tabelki
ch-ka ogolna, IV semestr, Silniki
9 Ch ka zadymienia L4
9 Ch ka zadymienia L1
9 Ch ka zadymienia ch ka zadymien (2)
Ch ka mechaniczna
ch-ka szybkościowa regulatorowa ZS opis, SiMR, Laboratorium Silników spalinowych
Ch-ki czestotliwość, Elektrotechnika, SEM4, ARA ćwiczenia
ch ka wyjsciowa
Zaburzenia mowy ch-ka, psychopatologia, logopedia
SIECI O TOPOLOGII SZYNY - OGÓLNA CH-KA, Notatki, Elektronika AGH III rok, Pendrive, dodatkowe, moje
ch-ka ogolna, STUDIA WRZESIEŃ, Silniki sprawka, oD SUBERLAKA, silniki spalinowe, Sprawka
ch-ka szybkościowa regulatorowa ZS, SiMR, Laboratorium Silników spalinowych
9 Ch ka zadymienia L2
CH-ka zewn., silniki spalinowe
ch-ka zewnetrzna silnika, STUDIA WRZESIEŃ, Silniki sprawka, oD SUBERLAKA, silniki spalinowe, Sprawka
ch ka przejsciowa
więcej podobnych podstron