88

Ć w i c z e n i e 10

Wyznaczanie krytycznej liczby Reynoldsa dla przewodów o kołowym

przekroju poprzecznym

1. Wprowadzenie

Celem ćwiczenia jest doświadczalne określenie krytycznej liczby Reynoldsa dla

przepływu wody przez przewody o kołowym przekroju poprzecznym.

Istnienie dwóch różnych form ruchu płynu, które są nazywane dzisiaj powszechnie

przepływem laminarnym i turbulentnym, udowodnione zostało po raz pierwszy w
doświadczeniach O. Reynoldsa, których wyniki opublikowano w latach 1884 – 1896
[1].

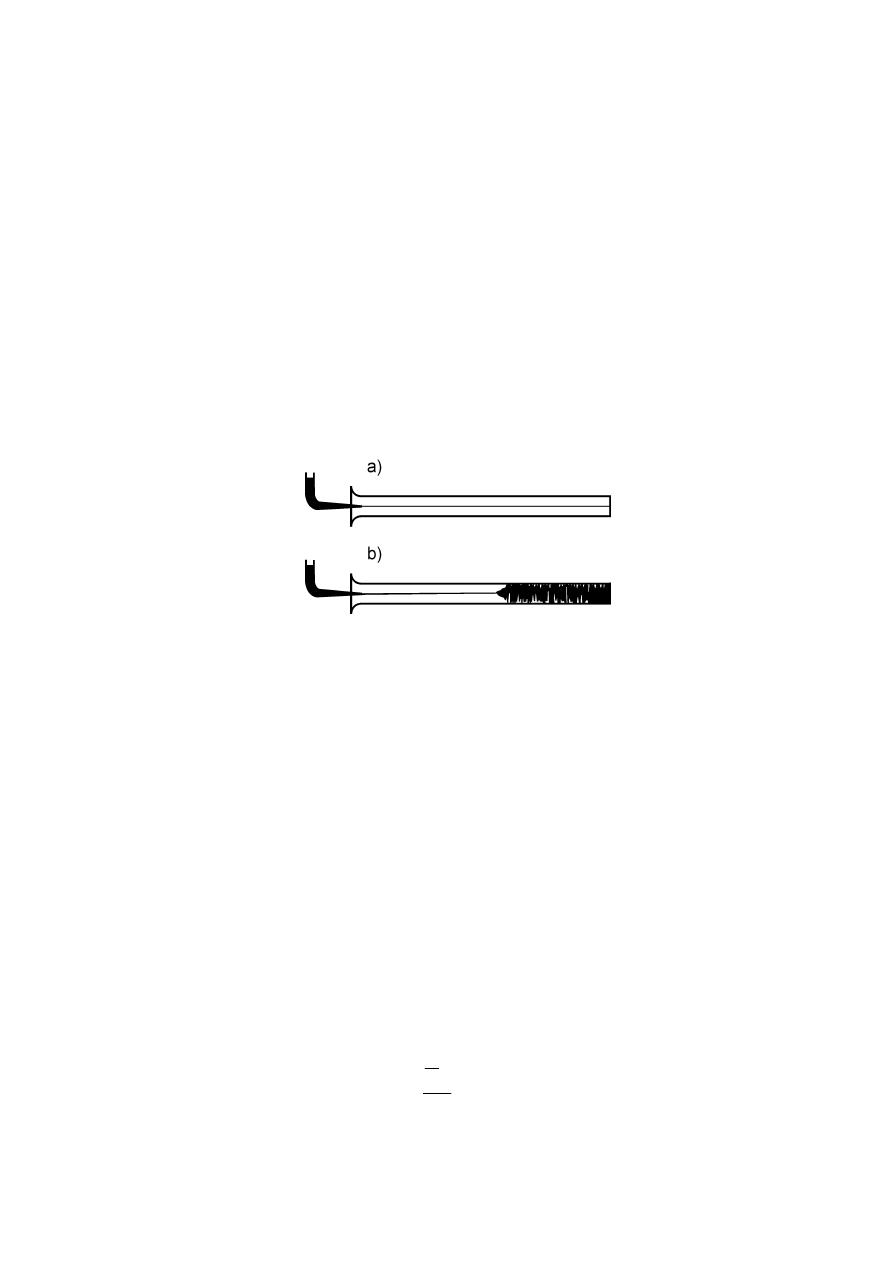
Reynolds badał strukturę przepływu wprowadzając strugę barwnika do kołowej

rury, którą przepływa woda z odpowiednio dobraną prędkością. Na podstawie
obserwacji zachowania barwnej smugi Reynolds wysunął wniosek o istnieniu dwóch
różnych jakościowo form ruchu płynu. Jeżeli bowiem prędkość przepływu wody w
rurze była odpowiednio mała, wówczas struga barwnika poruszała się równolegle do
ścian przewodu nie wykazując śladów dyfuzji w kierunku poprzecznym (rys. 1a).
Przepływ taki nazwany został laminarnym, jako że poszczególne warstwy płynu
poruszają się wówczas w izolacji od siebie i nie występuje między nimi wymiana
elementów płynu. Jeżeli prędkość przepływu w rurze przekroczy pewną wartość
krytyczną, wówczas smuga barwnika ulega gwałtownemu rozmyciu (rys. 1b), co
oznacza, że występują wówczas składowe prędkości prostopadłe do osi przepływu.
Ten rodzaj ruchu, charakteryzujący się występowaniem intensywnej wymiany
elementów płynu w kierunku poprzecznym nazwano przepływem turbulentnym.
Reynolds zauważył również, że przejście od przepływu laminarnego do turbulentnego
zależy nie tylko od prędkości przepływającego płynu, lecz także od jego lepkości i
średnicy rury. Uogólniając wyniki szeregu eksperymentów wykazał on również, że
przejście laminarno-turbulentne w przepływie w rurze zachodzi przy tej samej
wartości bezwymiarowego związku:

2300

ν

d

U

Re

=

=

gdzie:

Rys. 1. Obraz smugi barwnika przy przepływie laminarnym (a) i turbulentnym (b)

89

U - uśredniona w przekroju poprzecznym prędkość płynu, m/s,

d - średnica rury, m,
ν - kinematyczny współczynnik lepkości płynu, m

2

/s.

Kryterium to jest znane powszechnie jako liczba Reynoldsa – Re, a jej wartość

odpowiadającą przejściu laminarno-turbulentnemu nazwano pierwszą krytyczną liczbą
Reynoldsa Re

kr1

. Późniejsze badania wykazały, że na wartość Re

kr1

wywiera wpływ

kształt wlotu do przewodu, gładkość powierzchni rury, drgania przewodu, itp.
Wszystkie te czynniki zewnętrzne powodują zatem, że przejście laminarno-turbulentne
występować może przy różnych wartościach liczby Reynoldsa. W praktyce przyjmuje
się z reguły, że dla Re > Re

kr1

zawsze występuje przepływ turbulentny, przy czym dla

tzw. rur technicznie gładkich zaleca się wartość Re

kr1

= 2320 [2]. Jeżeli aktualna

wartość liczby Reynoldsa zawiera się w zakresie Re < Re

kr1

.wówczas występować

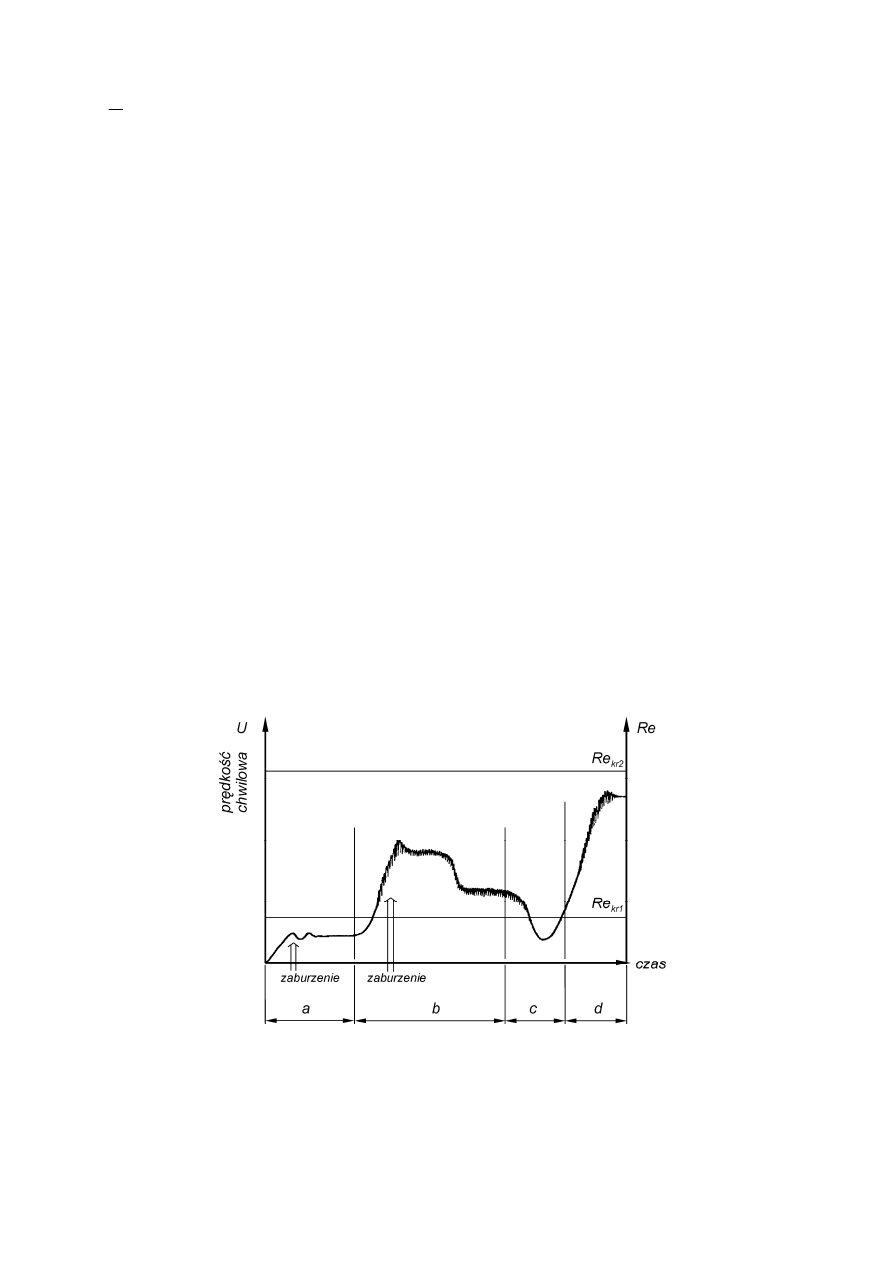
będzie w sposób trwały jedynie przepływ laminarny bez względu na intensywność
zewnętrznych zaburzeń, co zilustrowano na rys. 2 – zakres a.

Jak wykazał to Eckman [3], przy zachowaniu szczególnych środków ostrożności

przepływ laminarny w przewodach kołowych może występować aż do Re = 50000 i tę
wartość przyjmuje się jako tzw. drugą krytyczną liczbę Reynoldsa Re

kr2

, powyżej

której nie udało się dotychczas zaobserwować istnienia przepływu laminarnego. W
przypadku Re > Re

kr2

występować będzie zatem zawsze przepływ turbulentny,

podczas gdy w zakresie Re

kr1

< Re < Re

kr2

obserwować można ruch laminarny lub

turbulentny w zależności od intensywności zewnętrznych zaburzeń (rys. 2 zakresy b i
d). Występujący w tym zakresie przepływ laminarny jest jednak niestateczny co
oznacza, że jeżeli wskutek wystąpienia jakichkolwiek zaburzeń przejdzie on w ruch
turbulentny, wówczas do poprzedniej postaci (tzn. laminarnej) już nie powróci (rys. 2
zakres b). Przywrócenie przepływu laminarnego jest możliwe tylko wtedy, gdy
prędkość przepływu zmniejszymy na tyle, aby Re < Re

kr1

, co zilustrowano na rysunku

2 – zakres c.

Jak wspomniano wcześniej, przepływ laminarny i turbulentny to dwie jakościowo

różne formy ruchu płynu. W przepływie laminarnym dowolna funkcja
hydrodynamiczna H jest równa funkcji uśrednionej:

Rys. 2. Przebieg zmian prędkości w rurze dla przepływu laminarnego i turbulentnego

90

(

)

(

)

t

x

x

x

H

t

x

x

x

H

lam

,

,

,

,

,

,

3

2

1

3

2

1

=

(1)

podczas gdy w przepływie turbulentnym pojawia się dodatkowa składowa
fluktuacyjna h o charakterze losowym:

(

)

(

)

(

)

t

x

x

x

h

t

x

x

x

H

t

x

x

x

H

turb

,

,

,

,

,

,

,

,

,

3

2

1

3

2

1

3

2

1

+

=

(2)

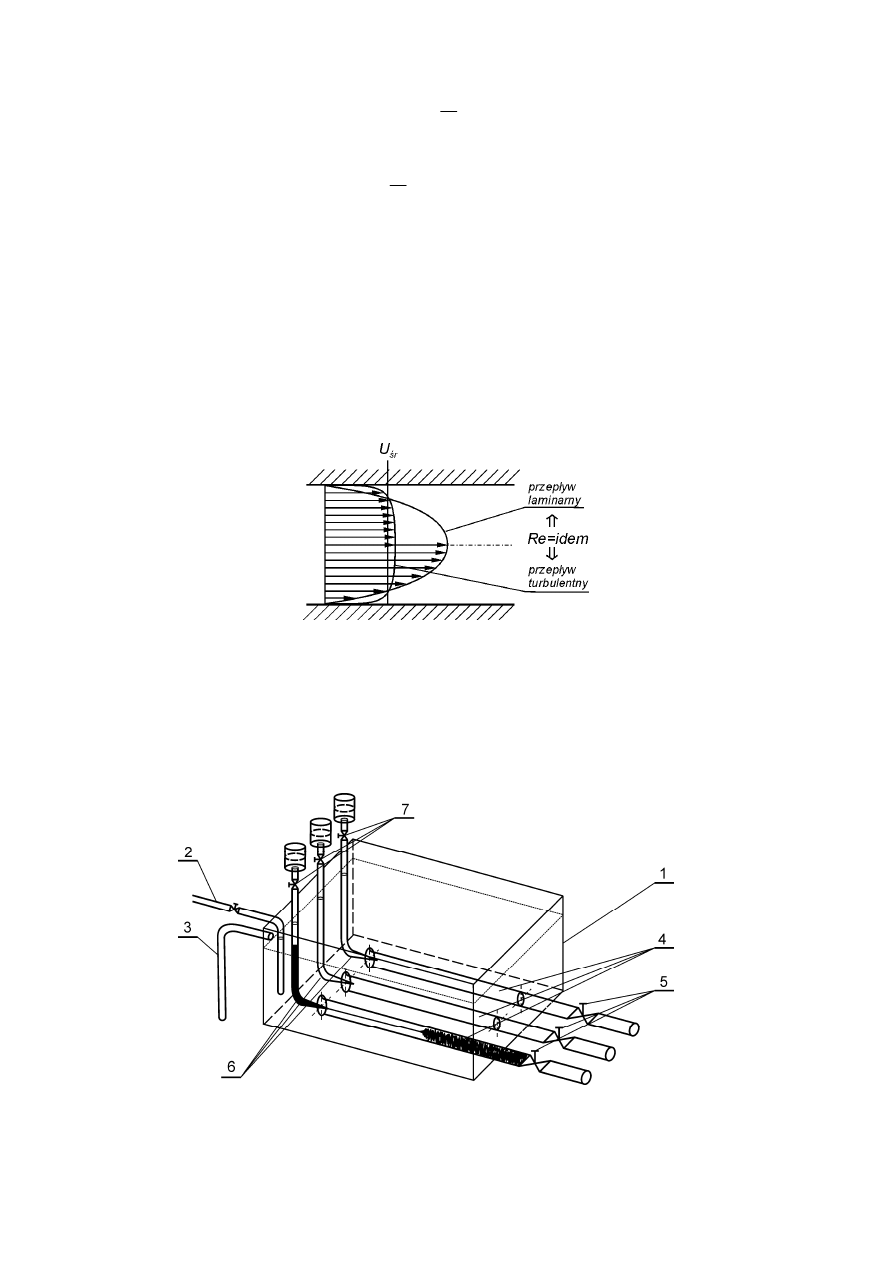
Istnienie fluktuacji prędkości przejawiające się rozmyciem strugi barwnika wywołuje
intensywny transport pędu w kierunku poprzecznym do osi przepływu, co prowadzi do
wyraźnego ujednorodnienia rozkładu prędkości w porównaniu z przepływem
laminarnym. Zmianę tę zilustrowano na rys. 3 przedstawiającym profile prędkości dla
przepływu laminarnego i turbulentnego przy tej samej wartości liczby Reynoldsa.
Intensyfikacja procesów mieszania towarzysząca przejściu przepływu laminarnego w
turbulentny powoduje również wzrost oporów przepływu. O ile bowiem spadek
ciśnienia potrzebny do utrzymania ruchu laminarnego jest proporcjonalny do
pierwszej potęgi prędkości średniej, o tyle w przepływie turbulentnym spadek
ciśnienia jest proporcjonalny do kwadratu prędkości.

2. Stanowisko badawcze

Doświadczenie przeprowadzone jest na stanowisku pomiarowym przedstawionym

schematycznie na rys. 4.

Rys. 4. Schemat stanowiska badawczego

Rys. 3. Zmienność prędkości w poprzecznym przekroju rury

dla przepływu laminarnego i

turbulentnego

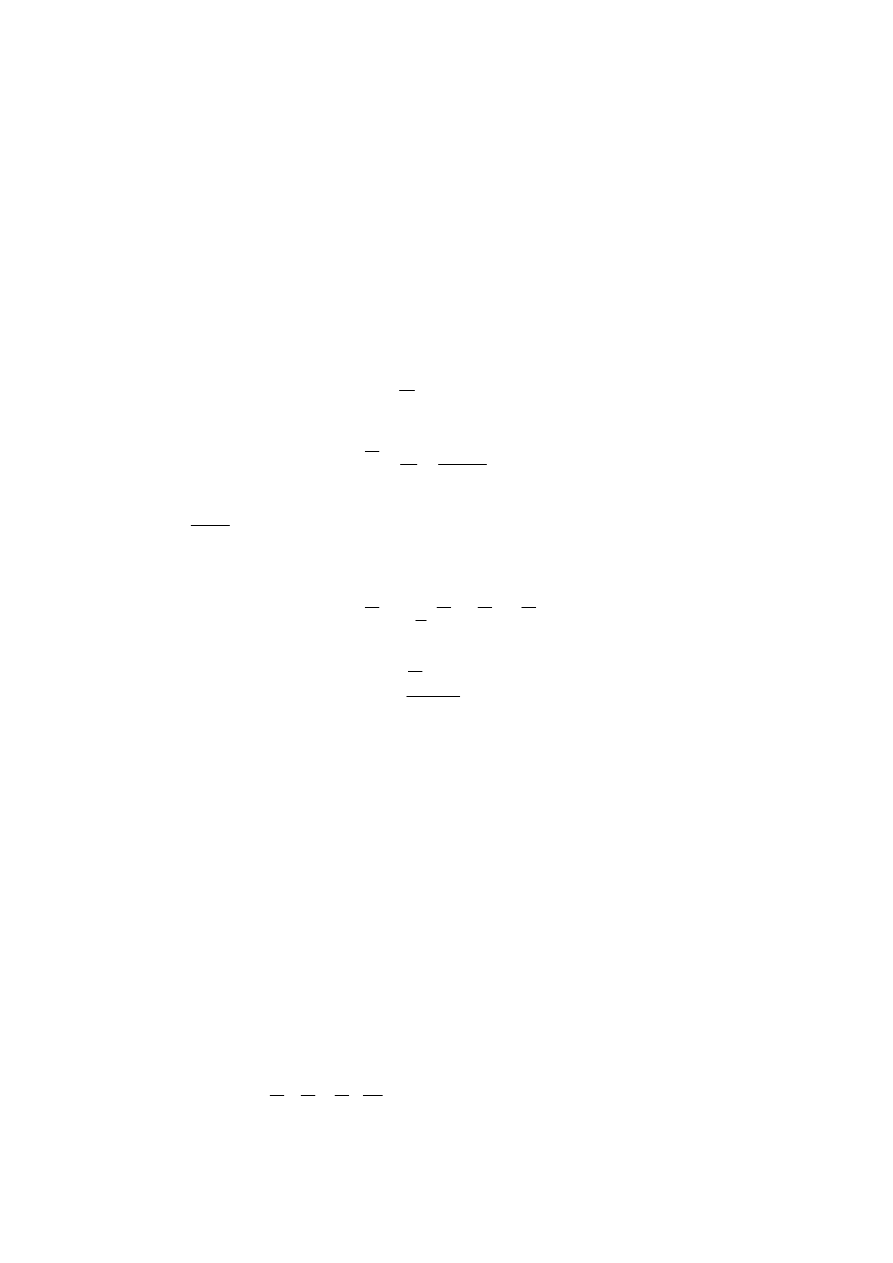
91

Głównym elementem stanowiska jest zbiornik 1, do którego wodę doprowadza

przewód 2, a utrzymanie stałego poziomu jest możliwe dzięki zastosowaniu przewodu
przelewowego 3. Wypływ wody odbywa się przez trzy szklane rury 4 o średnicach
odpowiednio d

1

,

d

2

, d

3

(podaje prowadzący ćwiczenie), a regulację prędkości

przepływu umożliwiają zawory 5.
Barwnik doprowadzony jest do rur 4 przez odpowiednio ukształtowane kapilary 6,
przy czym zawory 7 służą do regulacji natężenia jego wypływu.

3. Metodyka pomiarów i obliczeń

Strumień objętości przepływu wody Q należy określić przez pomiar czasu

napełnienia t miernicy o objętości V, co daje:

/s

m

,

3

t

V

Q =

(3)

wyznaczając następnie prędkość średnią przepływu przez rurę z zależności:

m/s

,

4

2

d

t

V

F

Q

U

π

=

=

(4)

gdzie

4

2

d

F

π

=

- powierzchnia przekroju poprzecznego rury.

Dla poprawy dokładności pomiaru strumienia objętościowego należy wykonać go
trzykrotnie i wyznaczyć następnie średnią wartość prędkości przepływu:

(

)

3

2

1

3

1

U

U

U

U

śr

+

+

=

(5)

i odpowiadającą tej prędkości wartość liczby Reynoldsa:

ν

d

U

Re

śr

⋅

=

(6)

4. Szczegółowy program ćwiczenia

Po napełnieniu zbiornika wodą do wysokości rury przelewowej należy zmierzyć jej

temperaturę t

w

, odczytać z tabel lepkość kinematyczną wody ν

w

i wpisać te wielkości

do tabeli pomiarowej.
Następnie za pomocą zaworu 5 należy ustalić bardzo mały strumień przepływu w
rurze 4 i dobrać zaworem 7 strumień wypływu barwnika w taki sposób, aby utworzyła
się wyraźna jego smuga w całej długości rury.
Następnie trzeba powoli zwiększać strumień przepływu wody zaworem 5 dokonując
jednocześnie niezbędnych korekt ilości podawanego barwnika zaworem 7 do
momentu, gdy barwna smuga zaczyna rozmywać się w sposób pokazany na rysunku
1b. Dla tak ustawionego strumienia przepływu należy wykonać trzykrotnie pomiar
czasu napełniania miernicy notując t i V w rubrykach 3 ÷ 8 tabeli pomiarowej.

Następnym krokiem jest dwukrotne zmniejszenie strumienia przepływu do

uzyskania ruchu laminarnego i powtórne doprowadzenie do momentu przejścia
laminarno-turbulentnego. Potem używając zależności (4) i (5), trzeba wyznaczyć

wartości prędkości

śr

U

U

U

U

,

3

2

1

,

,

(pozycje 9 ÷ 12 tabeli), a następnie wartości

krytycznej liczby Reynoldsa za pomocą związku (6).

92

Cały przebieg doświadczenia powtórzyć należy dla dwóch pozostałych średnic rur

w taki sposób, aby dla każdego d otrzymać trzykrotnie określone wartości liczby
Reynoldsa odpowiadające wystąpieniu przejścia laminarno-turbulentnego.


Literatura

1. Eckam W.: Archiv. für Math. Astr. Phys., 1911, VI, No 12
2. Prosnak W.: Równania mechaniki płynów i ich formy uproszczone, Prace IMP PAN w

Gdańsku, 1981, 111, 1037

3. Reynolds O.: On the Dynamical Theory of Incompressible Viscous Fluids and the

Determination of the Criterion, Phil Trans. Roy. Soc. 1896, vol. 186

4. Wysocki J.: Hydro i Aeromechanika, Politechnika Gdańska, Gdańsk, 1962

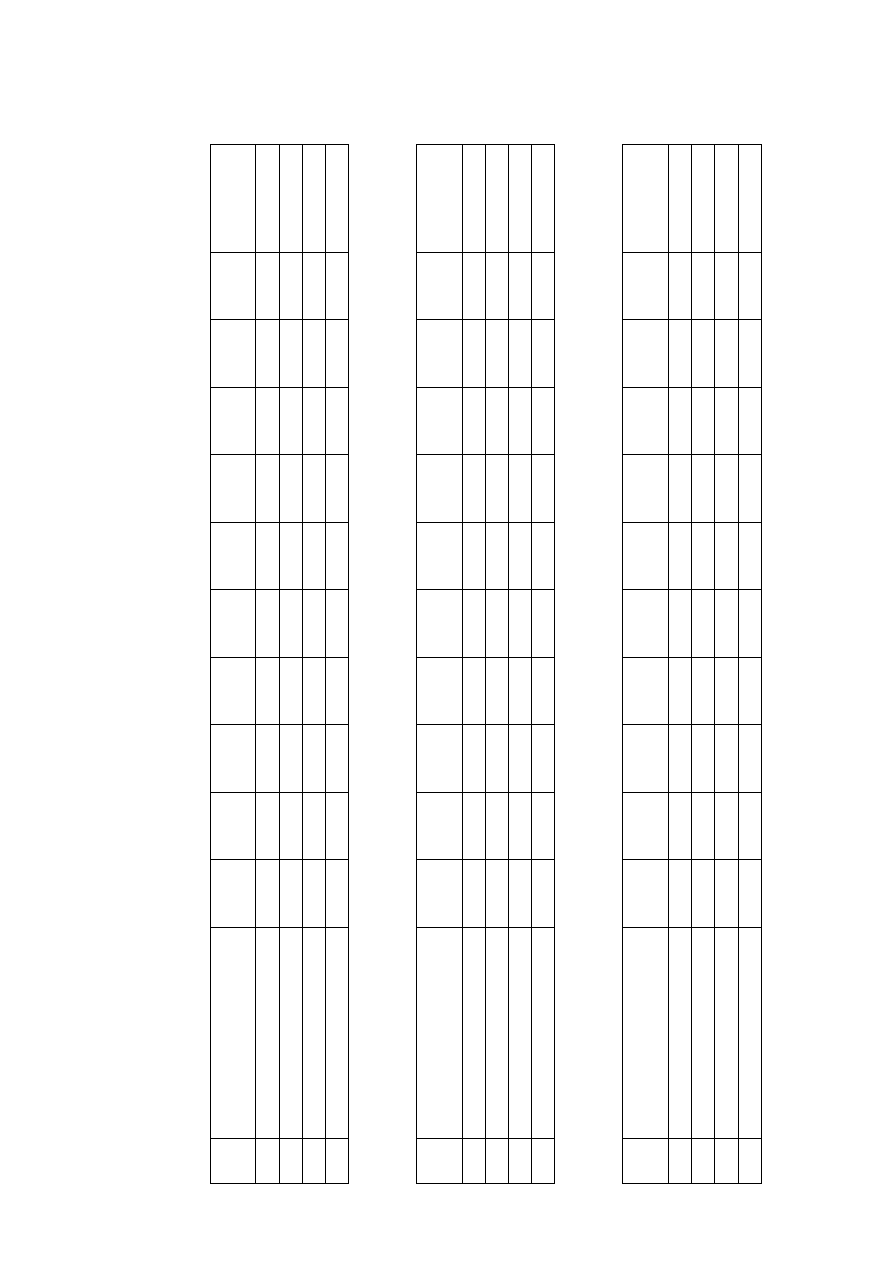
9

3

T

a

b

el

a

p

o

m

ia

ro

w

o

-o

b

li

cz

en

io

w

a

t

w

=

.

..

..

..

..

..

..

.

0

C

,

ν

w

=

.

..

..

..

..

..

..

m

2

/s

.

d

1

=

.

..

..

..

..

..

..

..

.m

L

.p

.

R

y

su

n

ek

b

ar

w

n

ej

s

tr

u

g

i

t

1

s

1

0

6

V

1

m

3

U

1

m

/s

t

2

s

1

0

6

V

2

m

3

U

2

m

/s

t

3

s

1

0

6

V

3

m

3

U

3

m

/s

U

śr

m

/s

R

e

1

2

3

4

5

6

7

8

9

1

0

1

1

1

2

1

3

1

2

3

d

2

=

.

..

..

..

..

..

..

..

.m

L

.p

.

R

y

su

n

ek

b

ar

w

n

ej

s

tr

u

g

i

t

1

s

1

0

6

V

1

m

3

U

1

m

/s

t

2

s

1

0

6

V

2

m

3

U

2

m

/s

t

3

s

1

0

6

V

3

m

3

U

3

m

/s

U

śr

m

/s

R

e

1

2

3

4

5

6

7

8

9

1

0

1

1

1

2

1

3

1

2

3

d

3

=

.

..

..

..

..

..

..

..

.m

L

.p

.

R

y

su

n

ek

b

ar

w

n

ej

s

tr

u

g

i

t

1

s

1

0

6

V

1

m

3

U

1

m

/s

t

2

s

1

0

6

V

2

m

3

U

2

m

/s

t

3

s

1

0

6

V

3

m

3

U

3

m

/s

U

śr

m

/s

R

e

1

2

3

4

5

6

7

8

9

1

0

1

1

1

2

1

3

1

2

3