248

P

ODSTAWY BILANSOWANIA PROCESÓW

Wprowadzenie

Jest wiele praw odkrytych przez badaczy w trakcie rozwoju ludzko ci i jej wysiłków na drodze

zrozumienia przyczyny i natury zjawisk. Zostały one przedstawione w poprzednich rozdziałach.

Niemo liwe jest okre lenie, które z nich s najwa niejsze ani nawet, które s wa niejsze. Jednak e,

niew tpliwie w opisie procesów zachodz cych w rodowisku naturalnym oraz w aparatach

przemysłowych najistotniejsz rol pełni prawa zachowania: prawo zachowania masy oraz prawo

zachowania energii. W rozdziałach 5 oraz 6 po wi cono im wiele miejsca przy okazji przedstawienia

prac Lavoisier’a, dotycz cych wprowadzenia prawa zachowania masy do chemii oraz omówienia I-go

prawa termodynamiki. Umiej tno bilansowania zachodz cych procesów jest praktycznym

zastosowaniem tych praw.

Poj cia i definicje systemu (b d układu) oraz procesu, u ywane w tym rozdziale zostały w

wprowadzone w tak e rozdziale 6, przy rozwa aniu problemów zwi zanych z termodynamicznym
opisem przebiegu zjawisk w przyrodzie oraz procesów zachodz cych w instalacjach przemysłowych

∗

.

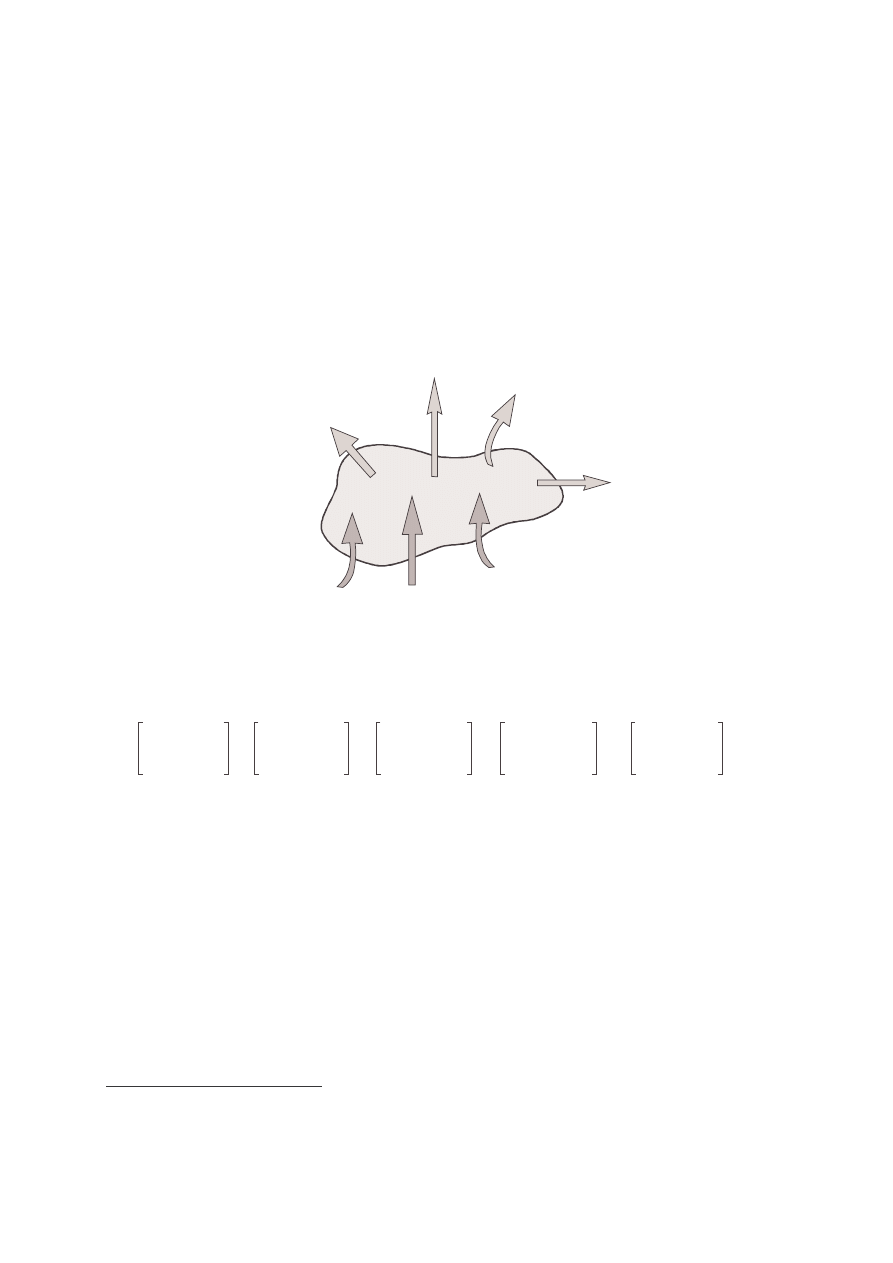
Strumienie

wyj ciowe

Strumienie

wej ciowe

Rysunek 10.1. Schematyczne przedstawienie bilansu dla układu otwartego

Bilans układu otwartego został przedstawiony w ogólny, ideowy sposób na rysunku 10.1,

natomiast ogólne równanie okre laj ce bilans przedstawia zale no 10.1.

Akumulacja

=

-

+

-

Strumienie

wej ciowe

Strumienie

wyj ciowe

ródła

wewn trzne

Strumienie

wyj ciowe

ródła

wewn trzne

(10.1)

Znaczenie poszczególnych członów tworz cych zale no (10.1) jest nast puj ce:

Strumienie wej ciowe oraz wyj ciowe s fizycznymi strumieniami (materii, energii), które

dopływaj z lub odpływaj do otoczenia układu, poprzez jego granice (rzeczywiste lub pomy lane).

Człony oznaczone jako ródła wewn trzne oraz upusty wewn trzny dotycz sytuacji, gdy w

układzie wyst puj strumienie wnosz ce/usuwaj ce do/z układu mas lub energi bez przekraczania

jego wytyczonych, do celu bilansowania, granic. Człony te pojawiaj si przy tworzeniu bilansu dla

składników układu (procesu). Nie mo e na przykład, zaistnie ródło wewn trzne masy ”w ogóle”,

zgodnie z prawem zachowania sformułowanym w najprostszej postaci w postaci stwierdzenia:

„materia nie mo e by stwarzana”. W wyniku reakcji chemicznej mo e jednak wyst pi synteza

(produkcja) jednego lub kilku składników układu z innych składników; mo e tak e by generowane

(lub pobierane) w reakcji ciepło. Reakcja chemiczna mo e by ródłem wewn trznym dla jednego lub

kilku składników. Ta sama reakcja jest jednak wtedy upustem dla składników, które s substratami w

tej reakcji. Wydajno ródła jest zwi zana z szybko ci odno nych reakcji.

Akumulacja oznacza zmian masy lub liczno ci składników tworz cych rozwa any układ lub

bior cych udział w procesie, w okresie czasu, dla którego bilans jest wykonywany. Akumulacja mo e

∗

W rozdziale nie b d rozwa ane układy, w których zachodz przemiany j drowe.

249

pojawi si wył cznie dla procesów nieustalonych. Procesami nieustalonymi nazywane s procesy,

dla których niektóre lub wszystkie funkcje stanu i parametry stanu opisuj ce układ zmieniaj si w

czasie. Je eli proces jest ustalony w czasie, akumulacja równa jest zero z mocy definicji. Nie oznacza

to jednak, e je eli akumulacja równa jest zero to proces jest ustalony.

Przykładem procesu nieustalonego s np. zmiany temperatury wody jeziora w wyniku waha

temperatury. Dotyczy to zarówno waha dobowych jak i zmian w ci gu roku. W ci gu doby

powodowane jest to zmianami temperatury, (ró nicami temperatury) powietrza w ci gu dnia i nocy.

W dłu szych okresach dotyczy to tendencji w zmianach temperatury w ci gu ró nych pór roku.

Niekiedy wielko ci odpowiadaj ce upustom i ródłom zapisywane s w jednym członie opisuj c

go ogólnie jako ródło i przypisuj c mu znak minus, je eli odpowiada upustowi i plus w przypadku

ródła. Wtedy równanie 10.1 przedstawiane jest w prostej postaci:

Akumulacja

=

+

Suma strumieni

wej ciowych i wyj ciowych

Suma

ródeł i upustów

(10.2)

W sposób popularny mo na powiedzie , e bilans, niezale nie od tego czego dotyczy, jest

zliczaniem ilo ci.

Je eli wykonywany jest np. bilans ekonomiczny dowolnego przedsi wzi cia to dotyczy on

zliczania zu ytych rodków oraz osi gni tych efektów wyra onych w kategoriach ekonomicznych.

Innymi słowy, dokonuje si bilansu poniesionych kosztów i uzyskanych wpływów w okre lonym

czasie. Jednostk bilansow jest pieni dz. A ró nica mi dzy stanem pocz tkowym i ko cowym

informuje o zyskach lub stratach. W pierwszym przypadku akumulacja jest dodatnia a w drugim

przypadku akumulacja jest ujemna.

Ogólne zasady formowania bilansu materiałowego

Bilans masowy jest fizycznym zliczaniem materii. Rysunki 10.2 oraz 10.3 przedstawiaj

przykładowe schematy budowania bilansu masowego, odpowiednio dla: sztucznego zbiornika

zalewowego utworzonego na rzece w wyniku postawienia na niej tamy oraz dla silnika z konwertorem

katalitycznym. Granice bilansowanego układu s zaznaczone w obu przypadkach liniami

przerywanymi. Tylko te strumienie, które przekraczaj granice bilansowania musz by uwzgl dnione

przy wykonywaniu oblicze bilansowych. Na rysunku 10.3 przedstawiono dwa mo liwe układy, które

mog by zbilansowane. Linia kropkowana wyznacza bilans ograniczony jedynie do silnika. Linia

przerywana wyznacza granice bilansowania, obejmuj ce układ, składaj cy si zarówno z silnika jak i

konwertera katalitycznego. Mo na zauwa y , e do równa opisuj cych bilanse masowe obu układów

wchodzi b d warto ci innych strumieni.

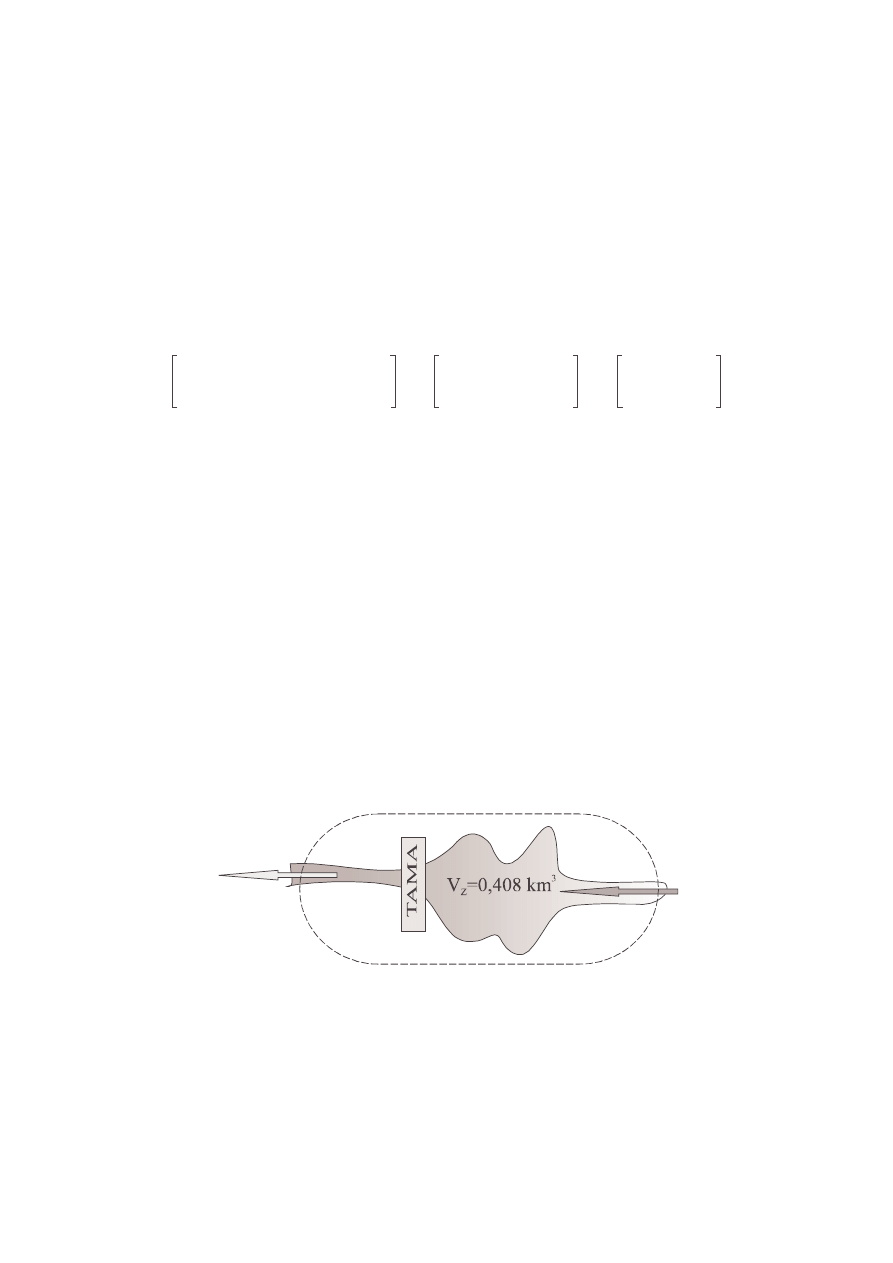
ZALEW

Dopływ

strumienia wej.

Odpływ

strumienia wyj.

Rysunek 10.2. Przykład budowania bilansu masowego w postaci graficznej dla naturalnego zbiornika

wodnego.

250

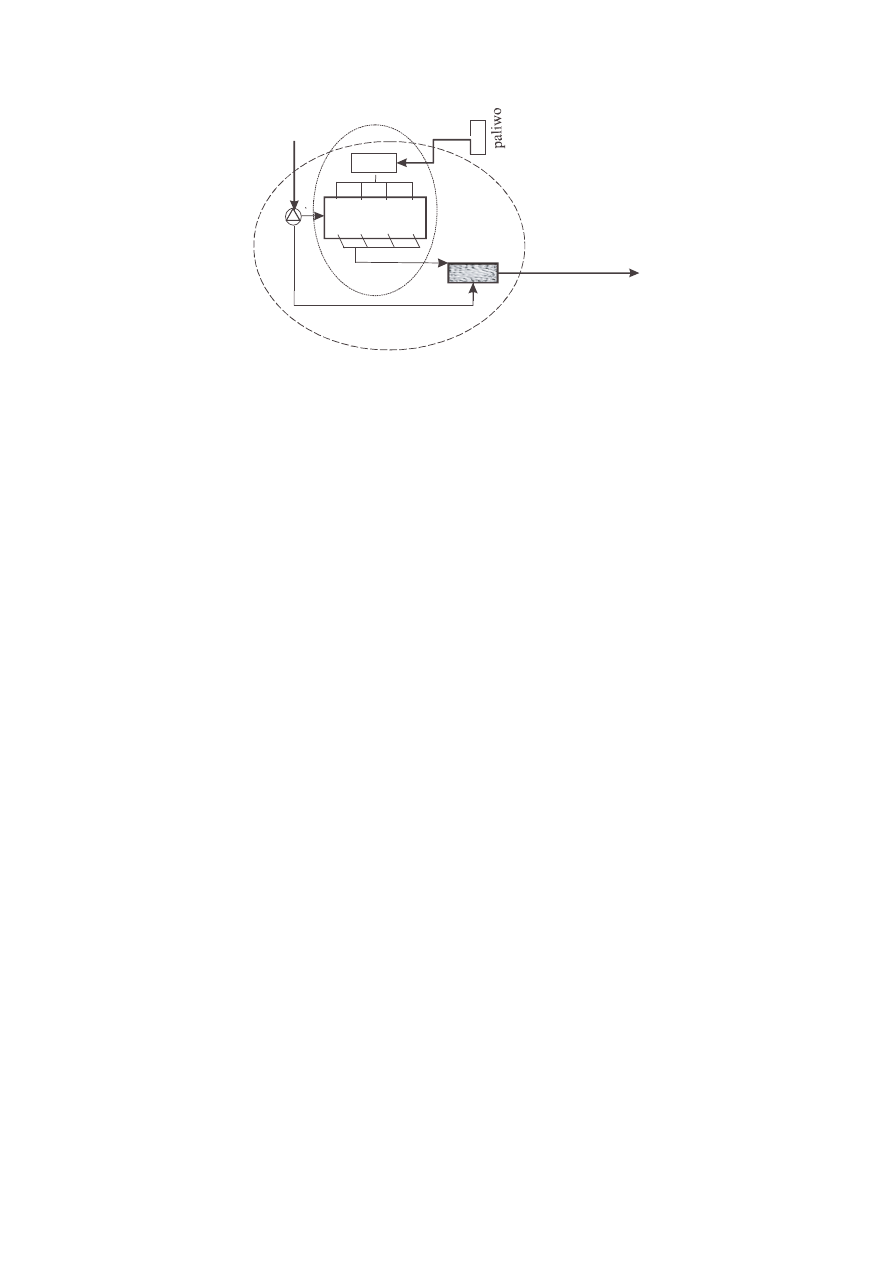
Silnik

po

w

ie

trz

e

Spaliny

Konwerter

katalityczny

Oczyszczone

spaliny

Rysunek 10.3. Przykład budowania bilansu masowego w postaci graficznej dla silnika spalinowego z

konwerterem katalitycznym

Klasyczny bilans masowy wykonywany jest jako bilans masy materii, wyra onej w jej

jednostkach: miligramach, gramach, kilogramach, tonach. Bilans materiałowy mo e by tak e

wykonany dla liczno ci materii wyra onej w jej jednostkach: w milimolach, molach, kilomolach.

Mówi si wtedy o bilansie molowym. Ten sposób wykonania bilansu jest wygodny dla układów, w

których nie zachodz reakcje chemiczne, a bilans molowy pierwiastków jest w wielu przypadkach

najlepszym rozwi zaniem.

Bilansu nie wykonuje si z reguły dla obj to ci, gdy prawo zachowania nie obwi zuje generalnie

dla tego parametru stanu. W wi kszo ci rzeczywistych procesów nast puje, bowiem zmiana obj to ci

składników tworz cych układ w trakcie zachodz cych przemian. W procesach z zachodz cymi

reakcjami chemicznymi g sto ci substratów ró ni si mi dzy sob oraz najcz ciej ró ni si z

g sto ci produktów. Reakcje zachodz ce w fazie gazowej ze zmian ilo ci moli produktów i

substratów powoduj równie , e obj to substratów jest inna ni ł czna obj to produktów.

Przykładem mog by reakcje:

syntezy amoniaku:

3

2

2

2

3

NH

H

N



←→



+

(10.3)

lub spalania propanu:

O

H

CO

O

H

C

2

2

2

8

3

4

3

5

+

→



+

(10.4)

Równie w przemianach fizycznych mo e zachodzi zmiana obj to ci strumienia w trakcie ich

przebiegu. Na przykład, przy rozpuszczaniu gazu w cieczy lub rozpuszczaniu ciała stałego w cieczy

obj to ci składników si nie sumuj . Natomiast procesach fizycznego mieszania ró nych składników

ciekłych w wielu przypadkach dopuszczalny jest bilans obj to ci cieczy, z okre lon dokładno ci .

Mo e jednak w takich przypadkach zachodzi równie zjawisko kontrakcji i suma obj to ci

składników ciekłych nie równa si obj to ci roztworu/mieszaniny (np. obj to mieszaniny powstałej

po zmieszaniu kwasu siarkowego i wody nie jest sum obj to ci czystych składników). Nawet w

przypadku procesu przebiegaj cego z udziałem tylko jednego składnika, obj to takiej samej jego

masy na pocz tku procesu (na wej ciu do aparatu) nie musi by taka sama jak na ko cu procesu (na

wyj ciu z aparatu), je eli proces nie jest izotermiczny. Bilans obj to ci jest dopuszczalny, je eli nie

nast puje zmiana obj to ci w układzie.

Mo na wykonywa zarówno bilans całkowity procesu (układu), bilans jednego ze składników

(zwi zków chemicznych), bilanse wszystkich składników lub bilans pierwiastków (molowy lub

masowy) bior cych udział w procesie. Obowi zuje tu elazna zasada:

Suma bilansów wykonanych dla wszystkich składników (pierwiastków) stanowi

bilans całkowity procesu lub układu.

Bilans masowy (liczno ci materii) mo e by wykonywany praktycznie dla ka dego materiału dla

ka dej substancji chemicznej, dla ka dego pierwiastka i dla układu o dowolnych rozmiarach i

dowolnym stopniu skomplikowania. Dla układów bez przemian chemicznych (w których wła ciwo ci

chemiczne składników chemicznych nie ulegaj zmianie, nie ma znaczenia czy wykonywany jest

bilans masowy czy molowy. Procedura jest zawsze taka sama.

251

Celem ka dego wykonywanego bilansu jest otrzymanie w wyniku jego rozwi zania warto ci

strumieni, st e składników lub innych parametrów, które były nieznane przed wykonaniem bilansu.

Interesuj ce s takie rozwi zania układu równa bilansowych, które maj sens fizyczny oraz które s

jednoznaczne. Nie s interesuj ce z praktycznego punktu widzenia, układy równa bilansowych

posiadaj ce rozwi zania wielokrotne. Zasada, któr nale y stosowa jest zawsze nast puj ca.

Liczba zmiennych wchodz cych w skład równa bilansowych, których warto ci s nieznane

równa jest liczbie niezale nych równa opisuj cych rozwa any bilans.

Mówi si wtedy, e liczba stopni swobody, która jest zdefiniowana jako ró nica mi dzy liczb

zmiennych o nieznanych warto ciach, a liczb równa bilansowych, jest równa zero. Je eli obliczona

liczba stopni swobody po sformułowaniu problemu jest wi ksza od zera nale y poszuka

dodatkowych równa bilansowych lub zrobi dodatkowe zało enia, co do warto ci wybranych

zmiennych o nieznanych warto ciach.. Je eli liczba stopni swobody jest mniejsza od zera oznacza to,

e ilo równa bilansowych jest zbyt du a lub dla zbyt du ej ilo ci zmiennych okre lono ich warto ci

liczbowe. Mo e to te oznacza , e nie wszystkie równania bilansowe s niezale ne. Zwykle (ale nie

zawsze) jest tak, e je eli w układzie nie biegn przemiany chemiczne liczba niezale nych równa

bilansowych jest równa liczbie składników.

Prawidłowo zrobiony bilans materiałowy jest zwi zany z wła ciw metodologi jego wykonania.

Himmelblau w swojej monografii podaje schemat wykonywania bilansu materiałowego, który tutaj

zostanie przytoczony a który jest u yteczny tak e dla bilansów wykonywanych w in ynierii

rodowiska. Strategia rozwi zywania bilansu materiałowego realizowana jest w kolejnych

wymienionych ni ej krokach. Nale y:

1. Zdefiniowa dokładnie problem. Okre li , co jest celem procesu. Okre li , co jest celem

wykonywanego bilansu.

2. Narysowa schemat procesu. Zaznaczy zewn trzne granice bilansowania.

3. Oznaczy symbolami wszystkie zmienne opisuj ce proces (system, układ).

4. Zaznaczy wszystkie zmienne, których warto ci s znane, których warto ci mo na obliczy z

innych danych oraz te, dla których mo na dokona poprawnych zało e .

5. Okre li w sposób jednoznaczny układ jednostek, w którym b d dokonywane obliczenia.

Dokona odpowiednich przelicze warto ci zmiennych, je eli wyst puj niezgodno ci jednostek.

6. Okre li zmienne, których warto ci s nieznane (zarówno dla warto ci strumieni jak i st e

składników).

7. Napisa wszystkie równania, które opisuj układ.

8. Okre li , które z równa s niezale ne (ewentualnie wyznaczy rz d macierzy układu)

Upewni si , e rozwi zanie równa

1

b dzie jednoznaczne. Porówna liczb niezale nych równa i

zmiennych, których warto ci b d obliczane. Je eli nie s one sobie równe (je eli liczba stopni

swobody nie jest równa zero) sprawdzi czy zrobione zało enia s prawidłowe. Ewentualnie poszuka

wi cej informacji lub zrobi inne (nast pne) zało enia.

9. Rozwi za układ.

10. Sprawdzi swoje rozwi zanie (uwaga: łatwiej znale bł d w cudzych obliczeniach ni we

własnych).

10.3. Bilans materiałowy dla procesów ustalonych bez ródeł i upustów wewn trznych

Równanie (10.1 lub 10.2) dla bilansu materiałowego w przypadku procesów ustalonych – bez

upustów oraz ródeł upraszcza si do postaci:

1

W rozwa aniach prowadzonych w tym rozdziale pomini ta s problemy efektywno ci stosowanych metod

matematycznych słu cych rozwi zaniu problemu (zarówno analitycznych jak i numerycznych). Pomini te

zostan s równie problemy niepewno ci okre lania warto ci zmiennych, układów niedookre lonych i

nadokre lonych (ze zbyt mał i zbyt du ilo ci informacji i warunków).

252

0

=

-

Strumie

wej ciowy

Strumie

wyj ciowy

(10.5)

lub

=

Strumie

wej ciowy

Strumie

wyj ciowy

(10.6)

Poni ej zostan zamieszczone przykłady budowania i rozwi zywania układu równa bilansowych

dla procesów ustalonych, bez reakcji chemicznej. W pierwszym przykładzie pokazany jest sposób

budowania bilansu materiałowego dowolnego w zła technologicznego. Kolejno przykładów

odpowiada stopniowi trudno ci w sformułowaniu problemu a nast pnie jego rozwi zaniu.

Przykład 10.2.

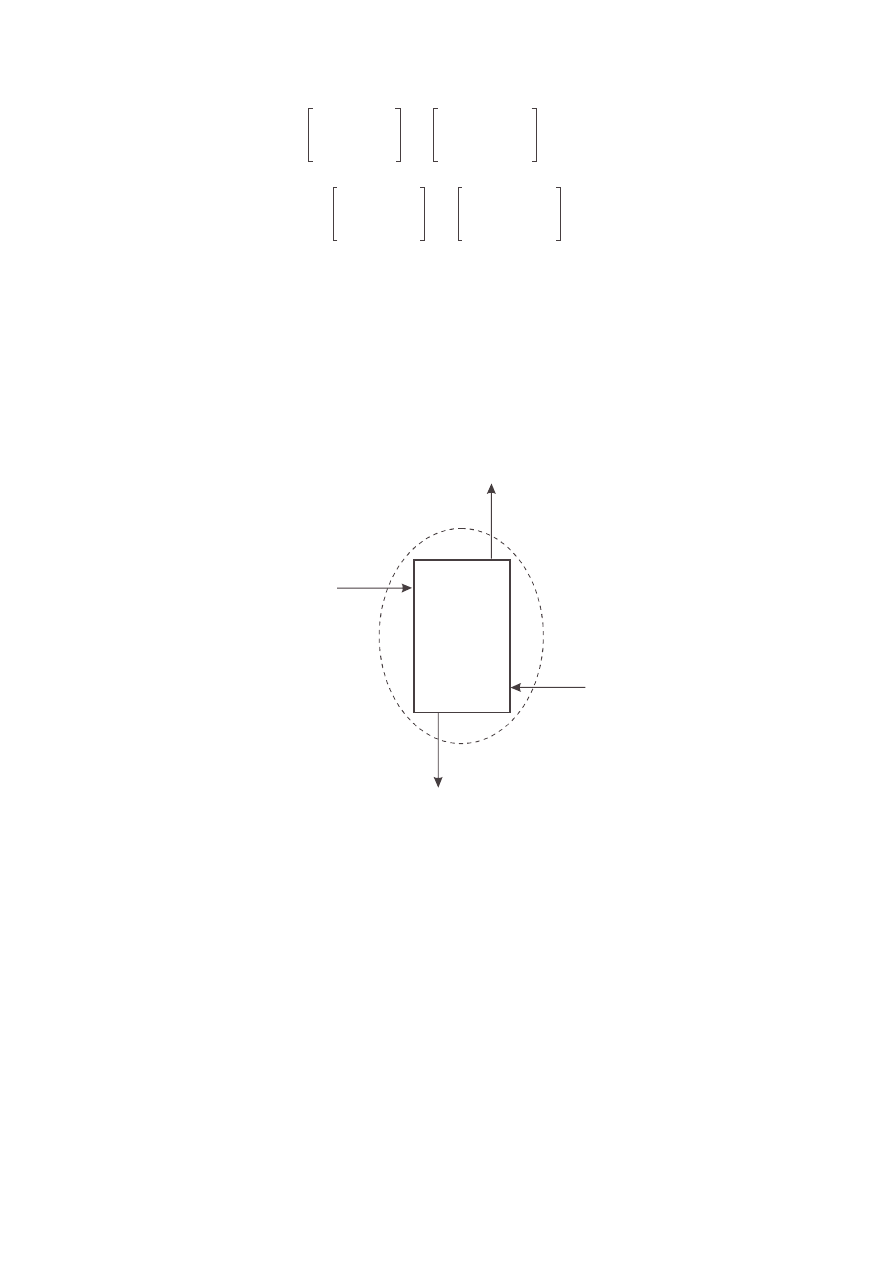
Zamieszczony poni ej rysunek daje graficzny obraz pewnego w zła technologicznego (mo e to

by np. rozdzielacz/separator, lub kolumna absorpcyjna), do którego dopływaj dwa strumienie F i S

oraz dwa E i R odpływaj . Strumienie wyra one s w kmol/s a st enia składników A, B, C w

ułamkach molowych x

A

, x

B

, x

C

. W układzie nie zachodzi reakcja chemiczna – mo na wi c dokona

bilansu liczno ci składników wpływaj cych i wypływaj cych do/z układu.

F

E

x

AE

S

R

x

BE

x

CE

x

AS

x

BS

x

CS

x

AF

x

BF

x

CF

x

AR

x

BR

x

CR

Rysunek 10.4. Przykład bilansowania w zła technologicznego z zadaniem okre lenia liczby stopni

swobody dla układu

Rozwi zanie

W procesie, który zachodzi w rozwa anym aparacie (w le technologicznym) bior udział trzy

składniki (A, B, C) a układ jest opisywany przez 16 zmiennych, po cztery zmienne dla ka dego

molowego strumienia. Nie wszystkie zmienne s jednak niezale ne. Dla ka dego ze strumieni (R, E,

F, S) mo na napisa dodatkowe równanie:

1

1

=

=

C

A

i

x

Oznacza to, e maj c dwa obliczone z bilansu masy składy strumieni, z powy szego równania

mo na obliczy trzeci składnik. W ten sposób liczba zmiennych opisuj ca w sposób wystarczaj cy

układ równa jest 16 – 4 = 12.

Jak podano to wy ej, liczba równa bilansowych opisuj ca układ N-składnikowy równa jest

liczbie składników. W rozwa anym przypadku liczba równa bilansowych wynosi wi c 3. W zwi zku

z tym liczba stopni swobody równa jest 12 – 3 = 9. A eby otrzyma jednoznaczne rozwi zanie nale y

wi c okre li warto ci dziewi ciu zmiennych a wtedy liczba stopni swobody b dzie równa 0, a

253

obliczenia doprowadz do jednego rozwi zania. Zachodzi pytanie, które z warto ci zmiennych

powinny by zało one a które obliczane Z reguły cz

danych wynika z technologii procesu.

Najcz ciej danymi s parametry strumieni dopływaj cych. Je eli oba strumienie F i S s w pełni

okre lone to danych jest 6 zmiennych (po 3 dla ka dego strumienia; warto ci czwartej zmiennej dla

ka dego z nich okre la powy ej zamieszczone równanie okre laj ce, e suma ułamków molowych

wszystkich składników równa jest 1). Dodatkowych brakuj cych warto ci zmiennych nale y szuka w

inny sposób. Mog one wynika z wymaga technologicznych dla st e strumieni wypływaj cych z

w zła. Mo na tak e znale dodatkowe równania, wynikaj ce z zale no ci termodynamicznych

opisuj cych równowag fazow zachodz c w układzie. W opisywanym przypadku zało ono, e ze

wzgl du na wymagan jako produktów niezb dne jest uzyskanie okre lonego st enia składników A

oraz B w strumieniu E oraz, e w strumieniu R nie b dzie składnika B (x

BR

= 0). Zało ono tak e, e

adne zale no ci termodynamiczne nie wi

składów strumieni. W poni szej tablicy 10.1 zestawiono

symbole danych i obliczanych zmiennych:

Tablica 10.1 Zmienne procesowe dane oraz obliczane

Dane s :

Obliczane s .

S, x

AS,

, x

BS

,

F, x

AF,

, x

BF

,

x

BR

x

AE

, x

BE

R, x

AR

E

Razem liczba zmiennych: 9

Razem liczba zmiennych: 3

Trzy równania bilansowe maj posta :

F + S = E + R (bilans ogólny)

F x

AF

+ S x

AS

= E x

AE

+ R x

AR

(bilans składnika A)

F x

BF

+ S x

BS

= E x

BE

+ R x

BR

(bilans składnika B)

Liczba stopni swobody równa jest zero, Układ posiada jedno rozwi zanie. Powy sze zale no ci

pozwalaj na obliczenie, jakie b d warto ci strumieni obu produktów (E oraz R) a tak e ostateczny

skład produktu R.

Bilans materiałowy układów zło onych

Bilansowania układów rzeczywistych nie jest proste z wielu wzgl dów, mi dzy innymi, dlatego,

e z reguły nie s one układami składaj cymi si tylko z jednego obiektu. Instalacje przemysłowe

zawieraj wiele aparatów, w których przebiega równolegle lub szeregowo kilka procesów. Podobnie i

zjawiska przyrodnicze składaj si z wielu biegn cych równie równolegle lub/i szeregowo procesów,

które maj miejsce w ró nych obiektach naturalnych. Bilans całego procesu, je eli chce si pozna

natur zjawiska lub okre li warto ci wszystkich strumieni dopływaj cych i odpływaj cych do/z

aparatów w instalacji przemysłowej, musi wi c składa si z bilansu dla całego

układu/instalacji/procesu oraz bilansów jednostkowych dla poszczególnych jego cz ci składowych.

Problemem wtedy jednak jest okre lenie ilo ci zmiennych niezale nych oraz to, które z bilansów s od

siebie niezale ne.

Zasady bilansowania układów wieloobiektowych s jednak takie same jak dla jednego obiektu.

Najlepsz strategi jest zwykle wykonanie w pierwszym etapie bilansu całego układu (procesu,

instalacji). Przy wykonywaniu tego bilansu ignoruje si wszystkie poł czenia wewn trzne. Nast pnie

nale y bilansowa procesy i układy składowe uwzgl dniaj c zale no ci (niezale no ci) układów

bilansowych. Suma bilansów jednostkowych dla wszystkich obiektów (aparatów, układów) jest

niczym innym jak bilansem całkowitym. W zwi zku z tym nie wszystkie bilanse jednostkowe i bilans

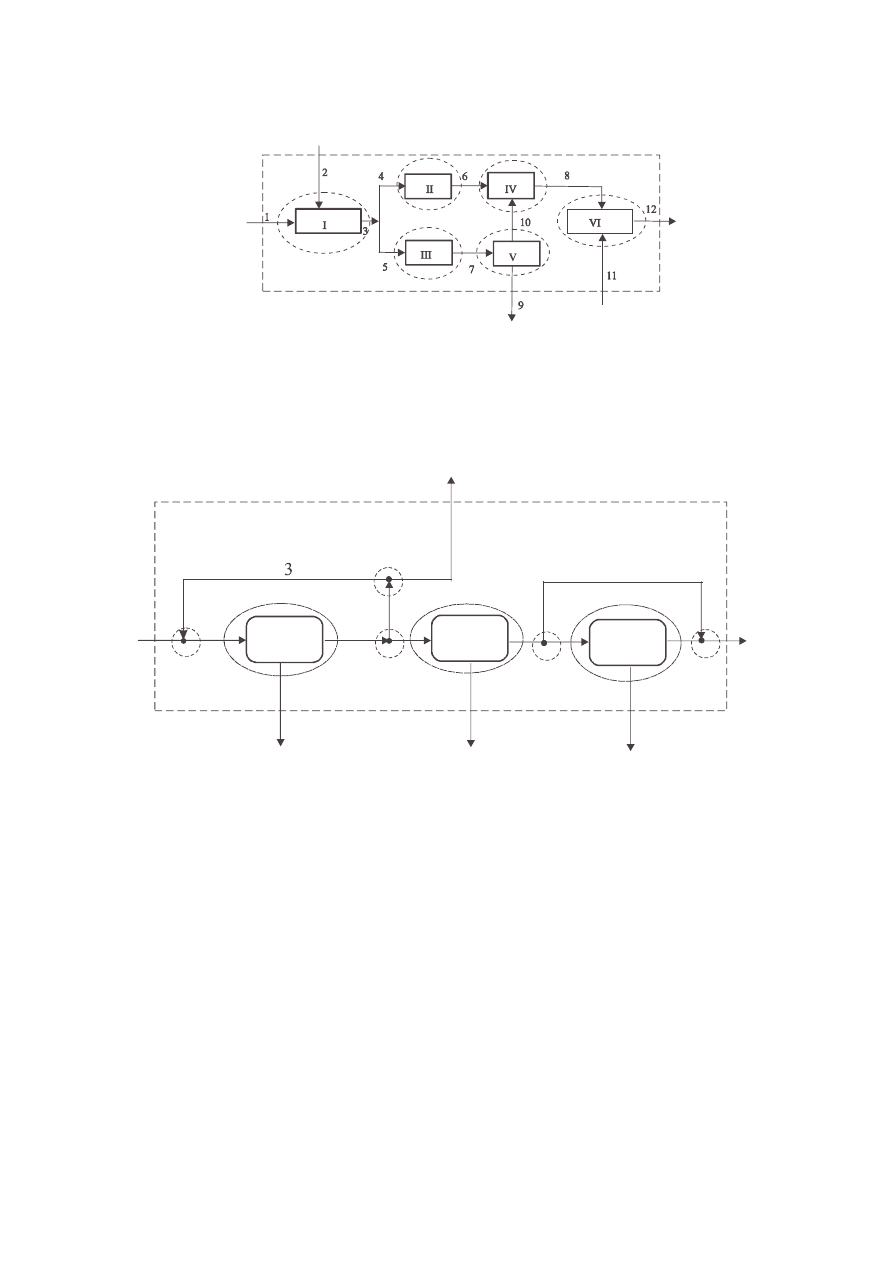
całkowity s niezale ne. Aby to lepiej wyja ni rozwa ony zostanie układ przedstawiony na rysunku

10.10. Liniami przerywanymi zaznaczono granice mo liwych do wykonania bilansów, kształtami

owalnymi zaznaczono bilanse jednostkowe, a prostok tem bilans całkowity.

Rzadziej spotykany sposób post powania wiedzie przez wykonanie najpierw wszystkich bilansów

jednostkowych a nast pnie okre lenie warto ci strumieni bilansu całkowitego. Rozwi zania problemu

bilansowania tego typu układów nie zawsze jest proste. Zale y to od tego, które zmienne s dane lub,

które warto ci mo na zało y a które nale y obliczy . Mo e okaza si , e układy równa

bilansowych dla obiektów daje si obliczy po kolei, ale te mo e te okaza si , e nale y rozwi za

254

wszystkie równania bilansowe dla wszystkich obiektów jednocze nie lub te zastosowa procedury

iteracyjne zakładaj c wst pnie warto ci zmiennych, które nale y oblicza .

Rysunek 10.10. Graficzny przykład bilansowania zło onego układu wielo-obiektowego. Cyframi

arabskimi oznaczono strumienie a rzymskimi bilansowane obiekty

Podobne trudno ci mo na napotka tak e w przypadku instalacji przemysłowych i komunalnych

(rzadziej układów naturalnych), w których wyst puj strumienie zawracane do procesu (ang. recycle),

strumienie z odgał zieniami bocznikuj cymi (ang. bypass) lub strumienie z rozgał zieniami

odprowadzaj cymi cz

produktu lub uzupełniaj cymi układ (ang. purge) o dodatkowe ilo ci

substratów b d wprowadzaj ce inert (rysunek 10.12)

1

A

I

II

III

Recykl

Upust

Bocznikowanie

2

4

5

6

7

B

C

D

E

8

9

10

11

12

13

14

15

Rysunek 10.12. Przykład bilansowania układu zło onego, zawieraj cego strumienie bocznikuj ce,

recyrkuluj ce oraz upusty. Cyframi arabskimi oznaczono strumienie, rzymskim bilansowane obiekty

(aparaty), du ymi literami alfabetu w zły ł cz ce/rozdzielaj ce strumienie

Klasycznymi przykładami takich układów mo e by :

–

zawracanie strumienia w procesie suszenia gazów o wysokiej temperaturze z wylotu

suszarki, a eby odzyska cz

ciepła zawartego w gazach,

–

zawracanie cz ci oczyszczonych cieków – (jako wody u ytkowej) z oczyszczalni

zakładowych do procesów produkcyjnych, które nie wymagaj du ej czysto ci wody (np.

wody ppo ., do zmywania wewn trznych traktów komunikacyjnych i podlewania zieleni),

–

zawracanie zło a adsorbenta (po regeneracji) lub katalizatora w celu zminimalizowania

ich strat oraz maksymalnego wykorzystania ich zdolno ci adsorpcyjnej lub katalitycznej,

–

wprowadzanie inertu do reaktora, a eby uzyska odpowiednie rodowisko reakcyjne,

–

bocznikowanie cz ci strumienia wlotowego lub wylotowego, a eby zmniejszy

obci enia aparatu,

–

bocznikowanie strumienia w celach kontrolnych lub pomiarowych.

Strategia post powania przy bilansowaniu jest dokładnie taka sama jak w przypadku bilansowania

układów wieloobiektowych. W tym przypadku nale y przyj , e w zły rozdzielaj ce strumieniu lub

je ł cz ce nale y traktowa jak oddzielne obiekty (procesy, układy).

255

Bilans energii

Wprowadzenie

Ogólne zasady bilansowanie energii s podobne jak dla bilansu masy a podstawowe równania

bilansu jak dla układu z rysunku 10.1 s analogiczne do równa (10.1) oraz (10.2) i mog by

przedstawione w postaci zale no ci (10.7) lub je eli zostan przypisane odpowiednie znaki

strumieniom energii (10.8):

Strumie

wej ciowy

energii

Strumie

wyj ciowy

energii

ródło

wewn trzne

energii

Upust

wewn trzny

energii

Akumulacja

energii

(10.7)

Suma ródeł i upustów

wewn trznych

energii

Akumulacja

energii

(10.8)

Ponownie nale y przypomnie , e energia mo e wyst powa pod ró n postaci – jako: praca,

ciepło, energia kinetyczna, energia wewn trzna, energia potencjalna, entalpia. Rozwa ane w tym

rozdziale przykłady bilansów energetycznych b d dotyczyły przede wszystkim bilansu ciepła i

entalpii. Przy bilansowaniu układów cieplnych operuje si zwykle poj ciem ciepła lub strumienia

ciepła. Wtedy ciepło jest rozumiane jako cz

energii wymieniana mi dzy układem a otoczeniem

(poprzez granice układu) w wyniku istniej cej ró nicy temperatur mi dzy układem a otoczeniem.

Ciepło mo e by wymieniane na drodze przewodzenia, konwekcji lub promieniowania. Sposoby

obliczania strumieni ciepła omówione były w rozdziale 8.

Zasady przygotowania równa bilansowych dla układów otwartych

Rozwini cie ogólnej formuły podanej zale no ci (10.7) lub (10.8) w równanie matematyczne

wymaga okre lenia wszystkich zmiennych parametrów i funkcji stanu opisuj cych układ. Rozwa any

bilans układu dotyczy pewnego przedziału czasu zawartego w granicach od t

1

do t

2

. Do układu

wpływa masa m

1

a wypływa m

2

. Układ wymienia ciepło z otoczeniem (przyj to konwencj znaków

(+) ciepło wpływa do układu oraz (-) je eli odpływa z układu) i prac (przy tej samej konwencji

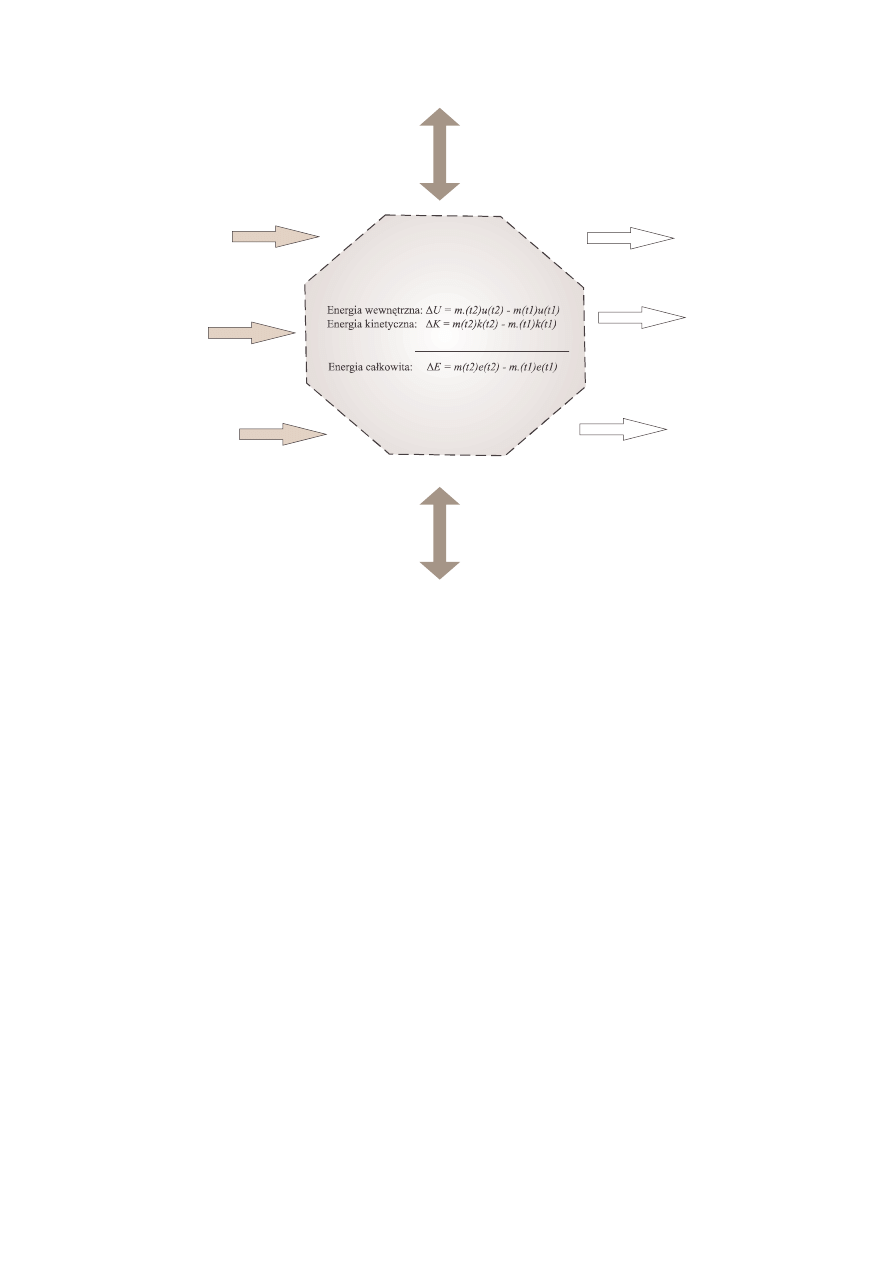
znaków). Problem zilustrowano schematem zamieszczonym na rysunku 10.16

Równanie bilansu energii ma posta :

2

)

2

2

2

(

1

)

1

1

1

(

2

1

m

p

k

u

m

p

k

u

Q

W

E

E

E

t

t

⋅

+

+

−

⋅

+

+

+

+

=

−

=

∆

(10.9)

lub w przypadku opisywania układu wielko ciami molowymi:

)

(

)

2

2

2

(

)

1

1

1

(

2

1

P

K

U

Q

W

P

K

U

P

K

U

Q

W

E

E

t

t

+

+

∆

−

+

=

+

+

−

+

+

+

+

=

−

(10.10)

gdzie:

indeksy t1, t2 – czas okre laj cy bilansowany okres dla rozwa anego układu, s;
E,

∆

E – całkowita energia bilansowanego układu, oraz jej zmiana w czasie

∆

t = t2-t1, J,

W – praca wykonywana nad układem lub przez układ, K;
u, U,

∆

U – energia wewn trzna (wła ciwa, molowa, zmiana energii wewn trznej), J;

k, K,

∆

K – oznaczenia dotycz ce energii kinetycznej, J;

p, P,

∆

P – oznaczenia dotycz ce energii potencjalnej, J;

256

UKŁAD

Akumulacja w układzie

ró nych form energii

Energia potencjalna: P = m.(t2)p(t2) - m(t1)p(t1)

St

ru

m

ie

ni

e

w

ej

ci

ow

e

do

u

kł

ad

u

E

ne

rg

ia

w

pr

ow

ad

za

na

z

z

ew

n

tr

z

do

u

kł

ad

u

(U

1+

K

1+

P1

)m

1

OTOCZENIE

Praca W

H1

K1

P1

H2

K2

P3

(-)

(+)

Strumie ciepła Q

(+)

(-)

E

ne

rg

ia

w

yp

ro

w

ad

za

na

n

a

ze

w

n

tr

z

z

uk

ła

du

(U

1+

K

1+

P1

)m

1

St

ru

m

ie

ni

e

w

yj

ci

ow

e

do

u

kł

ad

u

Rysunek. 10.16. Schemat ilustruj cy bilans energetyczny układu otwartego

Poni ej pokazano niektóre z mo liwych sytuacji pojawiaj cych si przy bilansowaniu energii

zarówno dla układów zamkni tych jak i otwartych, z wyst puj c akumulacj b d bez niej:

1. Układ zamkni ty (bez wymiany masy):

W

Q

E

+

=

∆

(10.11)

2. Układ zamkni ty bez akumulacji energii i wymiany masy;

∆

E = 0:

W

Q

W

Q

−

=

=

+

czyli

0

(10.12)

3. Układ bez akumulacji energii

∆

E=0

, ale z wymian masy

)

(

P

K

H

W

Q

+

+

∆

=

+

(10.13)

gdzie:

∆

H – zmiana entalpii układu (zamiast zamiany energii wewn trznej), J;

4. Układ z akumulacj , wymian masy i wymian ciepła, ale bez zmian w energii kinetycznej,

potencjalnej oraz nie wykonuj cy pracy: K=0, P=0, W=0,

H

Q

E

∆

−

=

∆

(10.14)

5. Układ wymieniaj cy mas , ale bez jej akumulacji oraz bez akumulacji energii a tak e bez

zmian pozostałych form energii –

∆

E = 0, K = 0, P = 0, W = 0:

H

Q

∆

=

(10.15)

6. Układ bez akumulacji masy i energii we wszystkich postaciach oraz bez wymiany ciepła

(poza entalpi niesion przez strumienie masy)

∆

E = 0, K = 0, P = 0, W = 0, Q = 0:

0

=

∆H

(10.16)

Ostatni typ równania bilansowego nazywany jest bilansem entalpii.

Zamieszczone poni ej przykłady s ilustracj dwóch ostatnich typów bilansu energii. Jak

ju napisano w rozdziale 7 uwzgl dnianie w bilansie energetycznym energii kinetycznej

poruszaj cego si układu (obiektu) jest niezb dne, je eli pr dko ci obiektu, poruszaj cego

płynu itd. przekracza 40 m/s a energii potencjalnej, je eli zmiany poziomów s wi ksze ni

100 metrów. Tego typu problemy s stosunkowo rzadko rozwi zywane w in ynierii i

ochronie rodowiska a bilans energetyczny ogranicza si najcz ciej do bilansu entalpii.