Przedmiot:

NAWIGACJA

Jednostka prowadząca kierunek

Akademia Morska w Szczecinie

Wydział Nawigacyjny

Kierunek

NAWIGACJA

Specjalność

TRANSPORT MORSKI

Tryb studiów

Niestacjonarne

Nauczyciel odpowiedzialny za przedmiot

– mgr inż.st.of. Jadwiga Grzeszak

I. Cele kształcenia
Celem kształcenia jest nauczenie metod określania i kontrolowania pozycji statku, prowadzenia bezpiecznej
nawigacji w żegludze oceanicznej, przybrzeżnej i w akwenach ograniczonych, zasad planowania i realizacji
podróży morskiej oraz wdrożenie prawidłowych procedur pełnienia wachty nawigacyjnej i współpracy w
zespole obsady mostka nawigacyjnego.

II. Wymagania wstępne

Zakres szkoły średniej.

III. Znać
Teoretyczne podstawy planowania podróży oraz zasady prowadzenia bezpiecznej i sprawnej nawigacji we
wszystkich fazach realizacji podróży, w różnych warunkach hydrometeorologicznych, z uwzględnieniem
oddziaływania tych warunków (weather routeing), występujących na oceanach, morzach i wodach
śródlądowych, uczęszczanych przez statki morskie; zasady konstrukcji stosowanych w nawigacji map i innych
materiałów kartograficznych oraz zakres i treści szczegółowe morskich pomocy nawigacyjnych; teoretyczne
podstawy prowadzenia zliczenia drogi (graficzne i analityczne) z uwzględnieniem błędów wskazań logów,
kompasów oraz oddziaływania wiatru i prądu; podstawy tworzenia infrastruktury nawigacyjnej akwenów
żeglugowych; podstawy teorii określania pozycji statku za pomocą wszystkich dostępnych technik wraz z oceną
dokładności linii pozycyjnych i pozycji; zasady i procedury pełnienia wachty nawigacyjnej i współpracy w
zespole obsady mostka nawigacyjnego.

IV. Umieć

Definiować i weryfikować wszystkie potencjalne niebezpieczeństwa nawigacyjne; wykorzystywać publikacje
nautyczne; uzyskać ze wszystkich dostępnych źródeł ostrzeżenia nawigacyjne i pogodowe; prowadzić korektę
map i publikacji; wyznaczać pozycję statku metodami terestrycznymi i elektronicznymi oraz określać ich
dokładność; prowadzić bezpieczną nawigację; określać i przewidywać ruch statku w zmiennych warunkach
hydrometeorologicznych; obliczać wartość poprawki kompasów; określać pływy i prądy pływowe; zaplanować
podróż statku; prowadzić obliczenia nawigacyjne dotyczące kursu i drogi statku, wykorzystywać systemy
nawigacji zintegrowanej, w tym ECDIS; przygotować raporty i uczestniczyć w systemach meldunkowych;
stosować procedury wachty nawigacyjnej, zastosować procedury w niebezpieczeństwie; przygotować mostek
nawigacyjny do wyjścia statku w morze.

Materiał do samodzielnej nauki:

G

RUPA TEMATYCZNA

:

PODSTAWY NAWIGACJI

–

AUDYTORIA

–

I ROK

TEMAT: Układy współrzędnych na elipsoidzie. Geodezyjne układy odniesienia współrzędnych-lokalne i
geocentryczne. Transformacja współrzędnych.

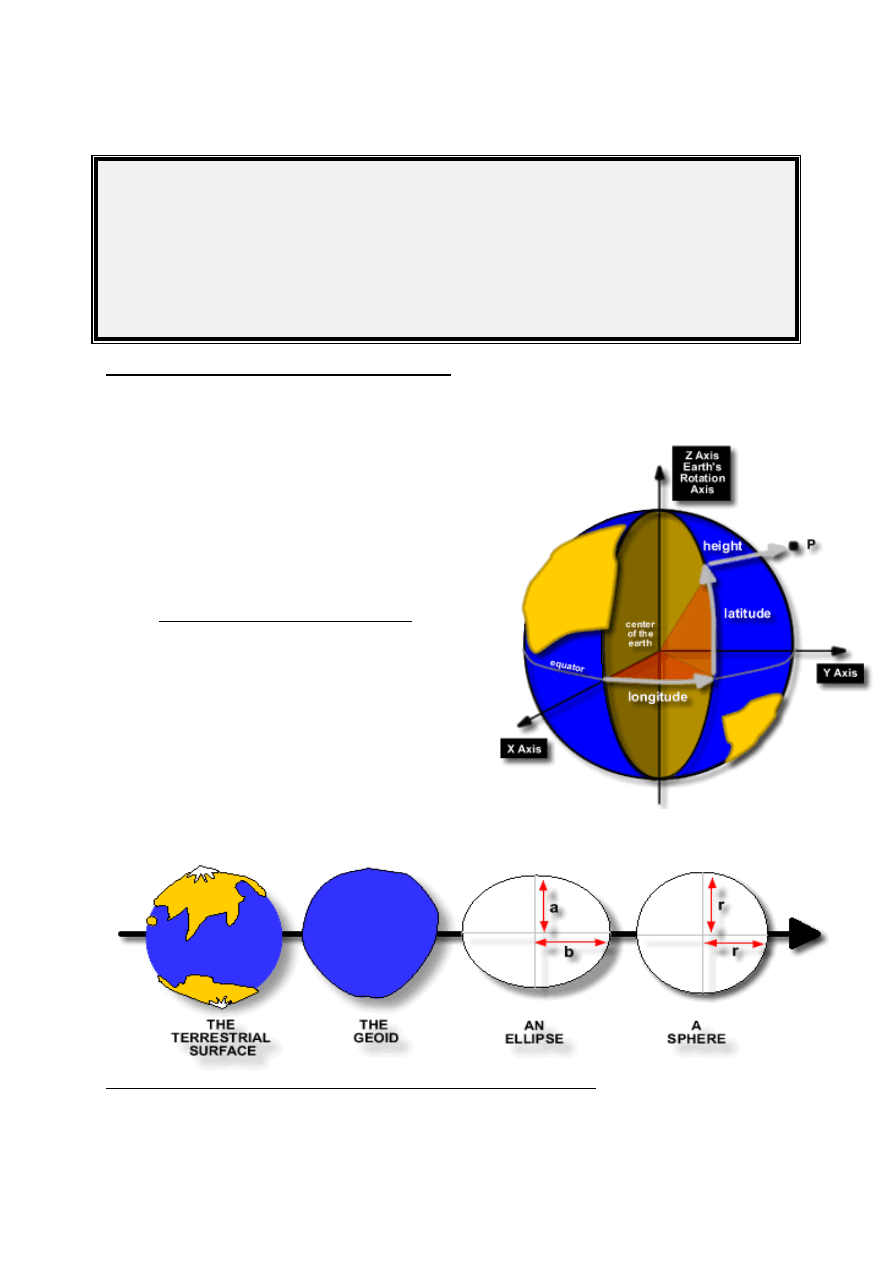
KSZTAŁT ZIEMI

W połowie XVII w. kształt i rozmiary ziemi zostały ściślej określone. Wiek XVIII-XX

to kolejne badania stwierdzające , że nie jest ona idealną kulą .

Kształt Ziemi zbli

ż

ony do elipsoidy obrotowej wpływa na zmian

ę

przyspieszenia ziemskiego oraz zmian

ę

warto

ś

ci promienia.

Ziemia to bryła zwana geoid

ą

, postaci

ą

sw

ą

zbli

ż

ona do elipsoidy obrotowej

czyli do bryły powstałej przy obrocie elipsy dookoła swej małej osi.

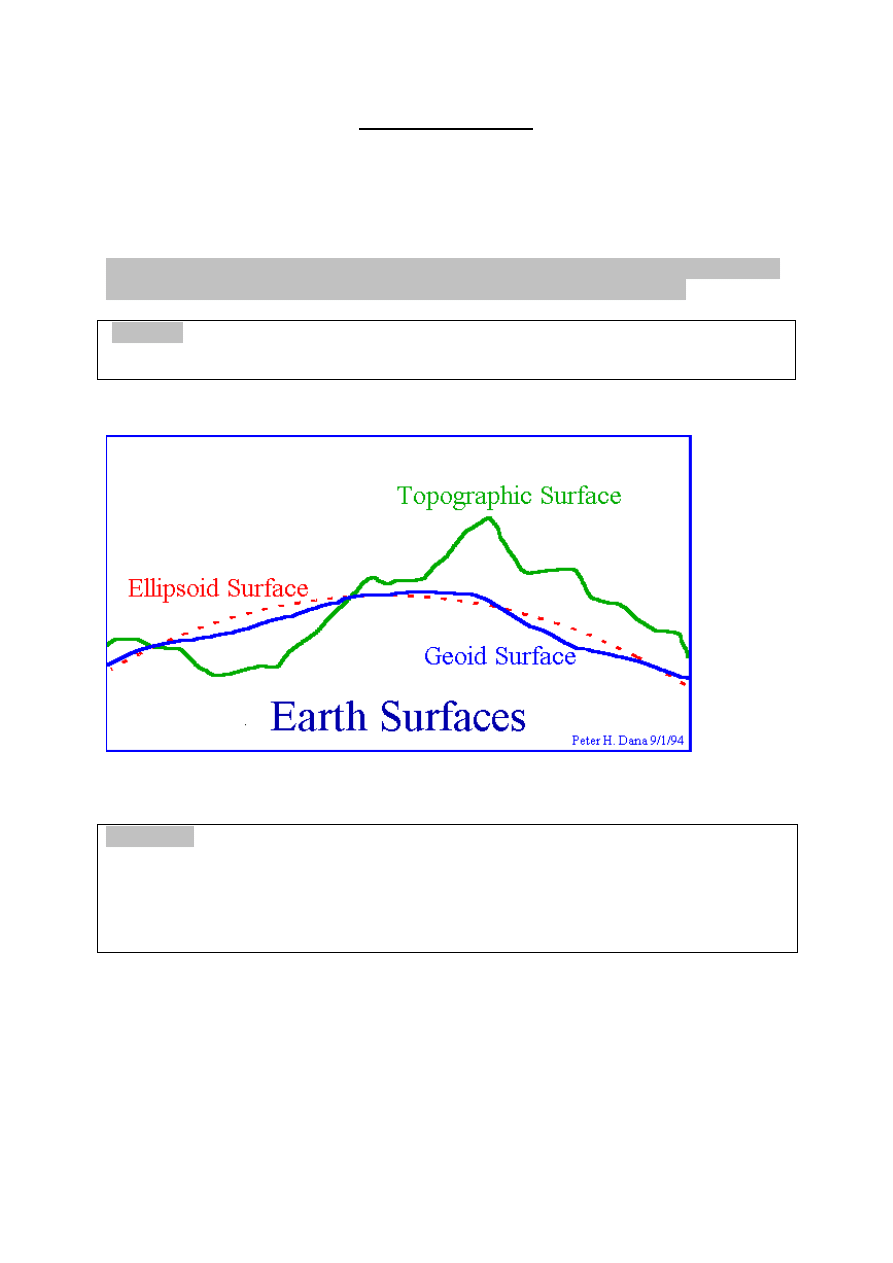
GEOIDA

-jest to bryła ,której powierzchnia przebiega wsz

ę

dzie prostopadle do kierunku siły

ci

ęż

ko

ś

ci z uwzgl

ę

dnieniem zmian tej siły wywołanych ukształtowaniem pionowym

powierzchni ziemskiej.

(Na lądach geoida przebiega nad elipsoidą , a na morzach poniżej elipsoidy.)

http://www.colorado.edu/geography/gcraft/notes/datum/datum_f.html

SFEROIDA –

bryła powstała przy zało

ż

eniu czysto teoretycznym,

ż

e powierzchnia

Ziemi jest płynna .Po ustaleniu równowagi w ka

ż

dym punkcie powierzchni ,sferoida

byłaby prostopadła do kierunku działania siły ci

ęż

ko

ś

ci , który pokrywałby si

ę

z

kierunkiem pionu w danym punkcie.

(Na równiku i biegunach sferoida i elipsoida pokrywałyby się , na φ = 45 ° sferoida
przebiegałaby nad elipsoidą na wysokości 17 m. )

Dla zwykłych potrzeb nawigacyjnych (obliczeń ortodromicznych ) przyjmuje się ,że Ziemia
jest kulą.

Wraz z rozwojem systemów radionawigacyjnych i satelitarnych ,w celu uzyskania większej
dokładności zachodzi potrzeba traktowania Ziemi jako elipsoidę obrotową.

ELIPSOIDA JAKO FIGURA ZIEMI

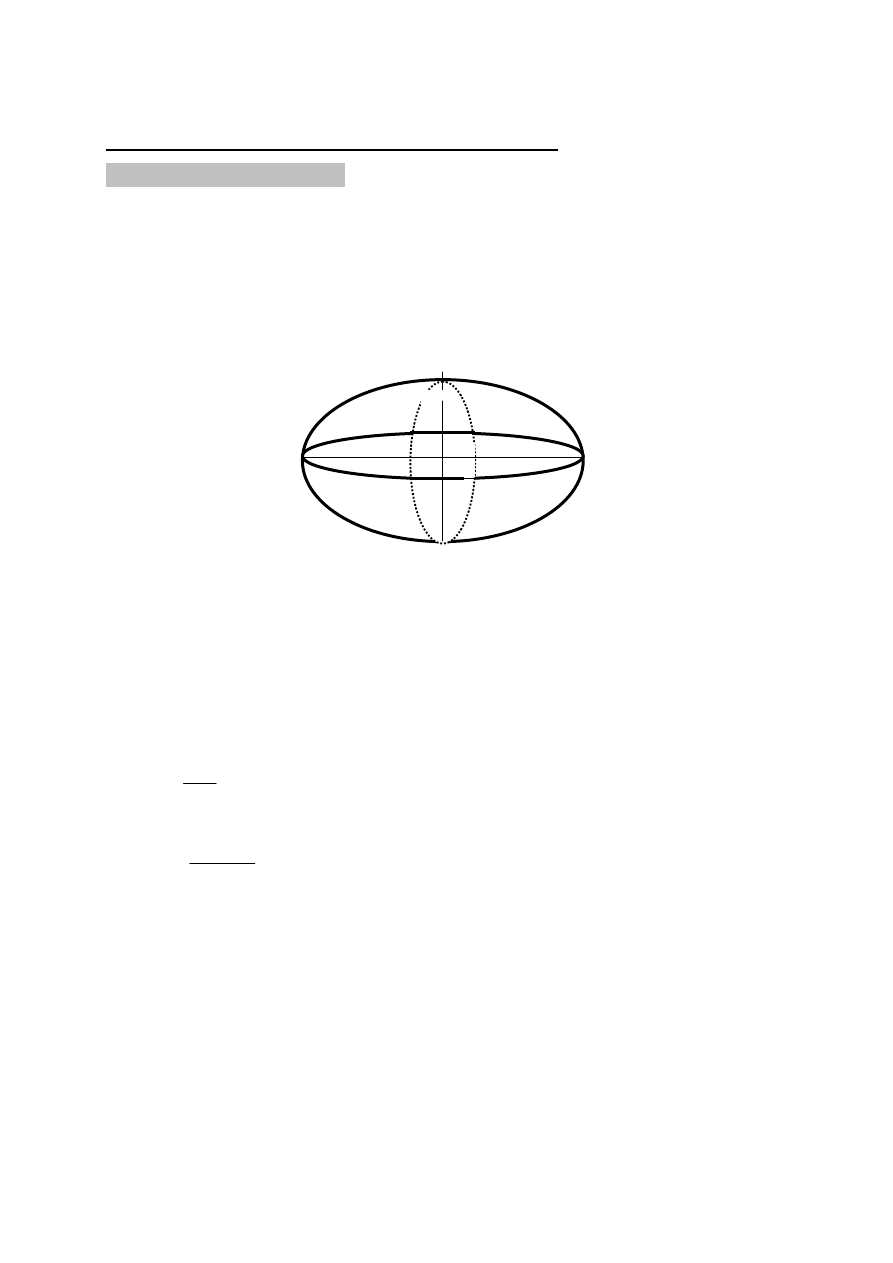
ELIPSOIDA OBROTOWA –bryła powstała w wyniku obrotu elipsy dookoła

mniejszej osi.

(Równik i równoleżniki są okręgami a południki elipsami)Wartość promienia elipsy

zmienia się w zależności od szerokości geograficznej.

W rzeczywistości Ziemia nie jest elipsoidą lecz jest bardzo do niej zbliżona.

B

N

B

S

Równik i równoleżniki to okręgi.
Południki są elipsami

Elementy elipsoidy.

•

a - duża półoś elipsoidy

•

b - mała półoś elipsoidy (dookoła której obraca się Ziemia )

•

f - spłaszczenie elipsoidy :

a - b

f =

a

•

e

2

-mimośród elipsoidy:

a

2

- b

2

e

2

=

a

2

Półoś a - decyduje o rozmiarach elipsoidy .
Mimośród i spłaszczenie – określają kształt elipsoidy.

Pomiarami elementów elipsoidy ziemskiej zajmowali się min. :.Clark , Bessel , Hayford ,
Krassowski.

Wg. Bessel

’

a : wg Krassowskiego : WGS- 84

a= 6377,4 km a = 6378,2 km

a= 6378,173 km

b = 6356,08 km b = 6356,86 km

b=6356,752314 km

f = 1 : 299,2 f = 1 : 298,3

f= 1: 298,257223563

bjjjb

a

.

bbb

a

b

O

W zwykłych zadaniach nawigacyjnych zakłada się, że Ziemia jest kulą równą co do objętości
elipsoidzie ziemskiej stąd :
V

k

= V

E

4 4
п R

3

= п a

2

b => R

3

= a

2

b => R =

3

√a

2

b

3

3

dla elipsoidy Bessel

’

a : R = 6370,3 km

dla elipsoidy WGS-84 : R = 6371,024763 km ,

UKŁADY WSPÓŁRZĘDNYCH NA ELIPSOIDZIE.

Stosując elipsoidę jako powierzchnię odniesienia należy oczekiwać , iż współrzędne

geograficzne odniesione do Ziemi jako kuli nie będą równe współrzędnym wyznaczonym na
Ziemi jako elipsoidzie.

Celem wyznaczenia położenia punktu na elipsoidzie stosuje się następujące układy

współrzędnych:

•

układ współrzędnych geograficznych elipsoidalnych ( geodezyjny )

•

układ współrzędnych geocentrycznych

•

układ współrzędnych astronomicznych

•

układ współrzędnych zredukowanych

•

układ współrzędnych prostokątnych przestrzennych

Rys Szerokość geograficzna, geocentryczna, zredukowana.

Długość geodezyjna

λλλλ

punktu na elipsoidzie , długość geocentryczna, długość

astronomiczna oraz długość zredukowana jest to kąt pomiędzy płaszczyzną południka
zerowego i płaszczyzną południka danego punktu.

ϕϕϕϕ

ψ

ψ

ψ

ψ

A

1

A

a

b

O

Okrąg o promieniu
równym dużej płosi a

Elipsa
południkowa

a

Φ

Φ

Φ

Φ

Szerokość geograficzna (geodezyjna ) punktu na elipsoidzie

ϕϕϕϕ

e

jest kątem w

płaszczyźnie elipsy południkowej pomiędzy płaszczyzną równika i normalną do
powierzchni elipsoidy w danym punkcie.

tg

Ψ

tg

ϕ

e

=

( 1- e

2

)

normalna do elipsoidy

Rys. Szerokość geodezyjna

.

Szerokość geocentryczna

ψ

ψ

ψ

ψ

punktu jest to kąt utworzony przez promień

wodzący (łączący punkt ze środkiem mas Ziemi ) danego punktu ( OP) z
płaszczyzną równika.

b

2

tg

Ψ

= . tg

ϕ

= ( 1- e

2

) tg

ϕ

e

a

2

P Promień wodzący punktu P

Rys. Szerokość geocentryczna

ϕϕϕϕ

e

O

ψ

ψ

ψ

ψ

O

Powierzchnia
geoidy

Środek mas

H – wysokość nad
powierzchnię
elipsoidy

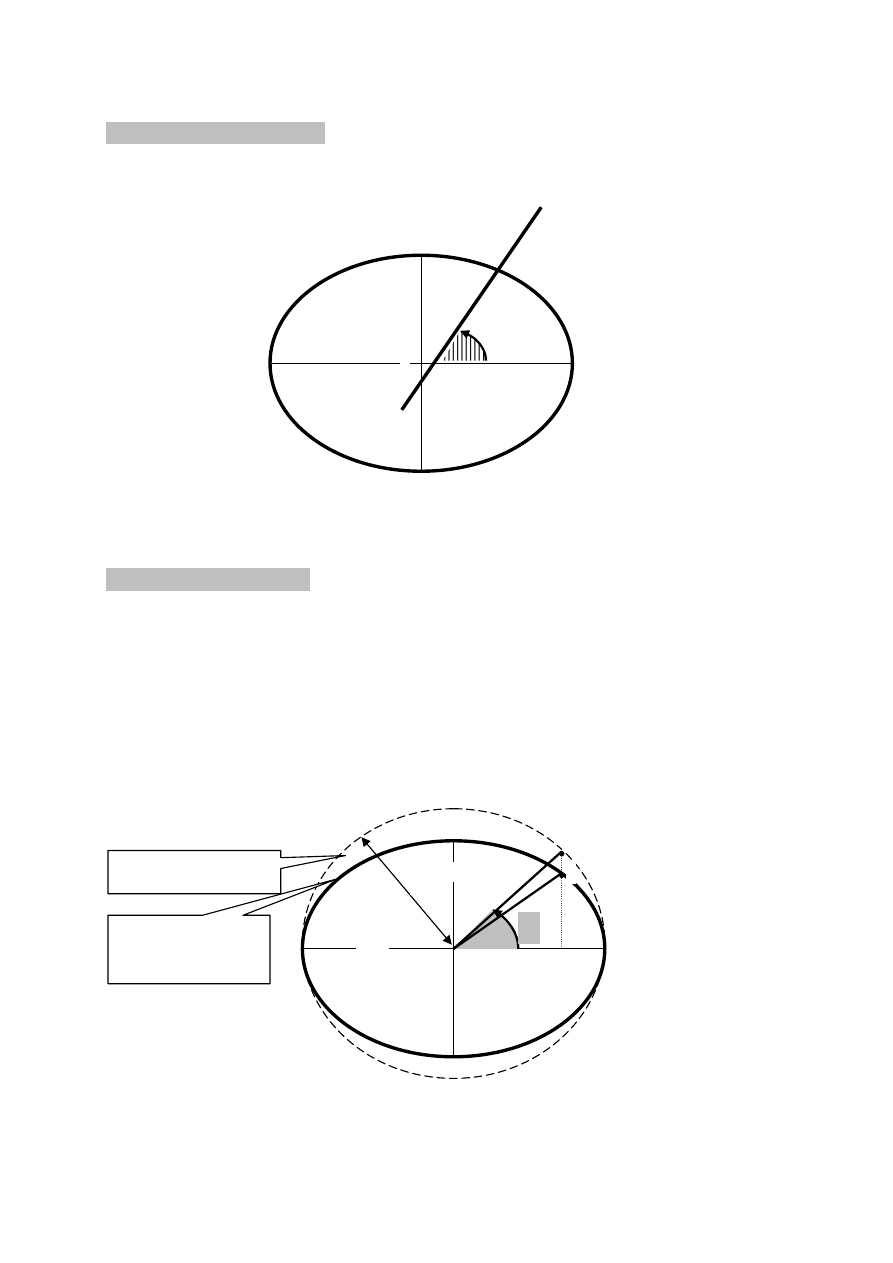
Szerokość astronomiczna φ

A

punktu jest to kąt pomiędzy kierunkiem działania siły

ciężkości a płaszczyzną równika

Linia pionu

.

Szerokość zredukowana

Φ

Φ

Φ

Φ

punktu jest to kąt pomiędzy płaszczyzną równika a prostą (

OA

1

) łączącą środek elipsoidy z rzutem danego punktu (równoległym do małej osi b ) na

okrąg utworzony przez dużą półoś elipsoidy

Celem wyznaczenia szerokości zredukowanej określamy punkt A na elipsie

południkowej. Następnie ze środka elipsy zataczamy okrąg o promieniu równym wielkością
półosi dużej a.
Z punktu A kreślimy prostopadłą do półosi a oraz przedłużamy ją do przecięcia z
wykreślonym okręgiem otrzymując punkt A

1

Rys. Szerokość zredukowana

ϕϕϕϕ

A

O

A

1

A

a

r

O

Okrąg o promieniu
równym dużej płosi a

Elipsa
południkowa

a

Φ

Φ

Φ

Φ

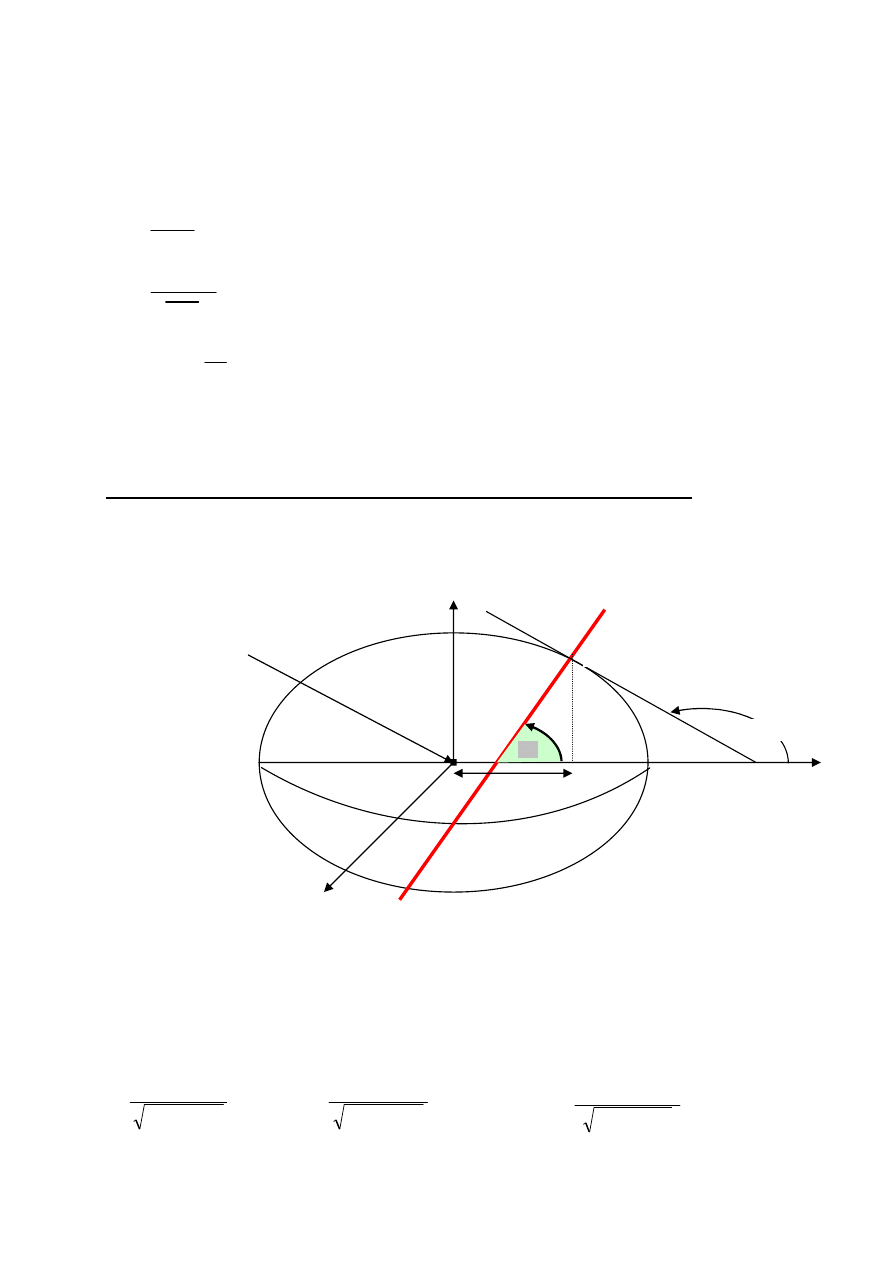
Związki zachodzące pomiędzy szerokością geodezyjną a szerokością geocentryczną i zredukowaną pozwalają
wyliczać jedną z szerokości za pomocą pozostałych.

•

Szerokość zredukowana w funkcji szerokości geograficznej:

tg

Φ

=√ 1- e

2

tg

ϕ

e

;

•

szerokość zredukowana w funkcji szerokości geocentrycznej:
tg

Ψ

tg

Φ

=

√ 1- e

2

•

maksyma różnica między szerokością geograficzną i geocentryczną:

e

2

( φ

e

-ψ )max = sin 2 φ

e

2
gdzie:

Φ

- szerokość zredukowana

ϕ

e

- szerokość geodezyjna (geograficzna )

Ψ

-szerokość geocentryczna

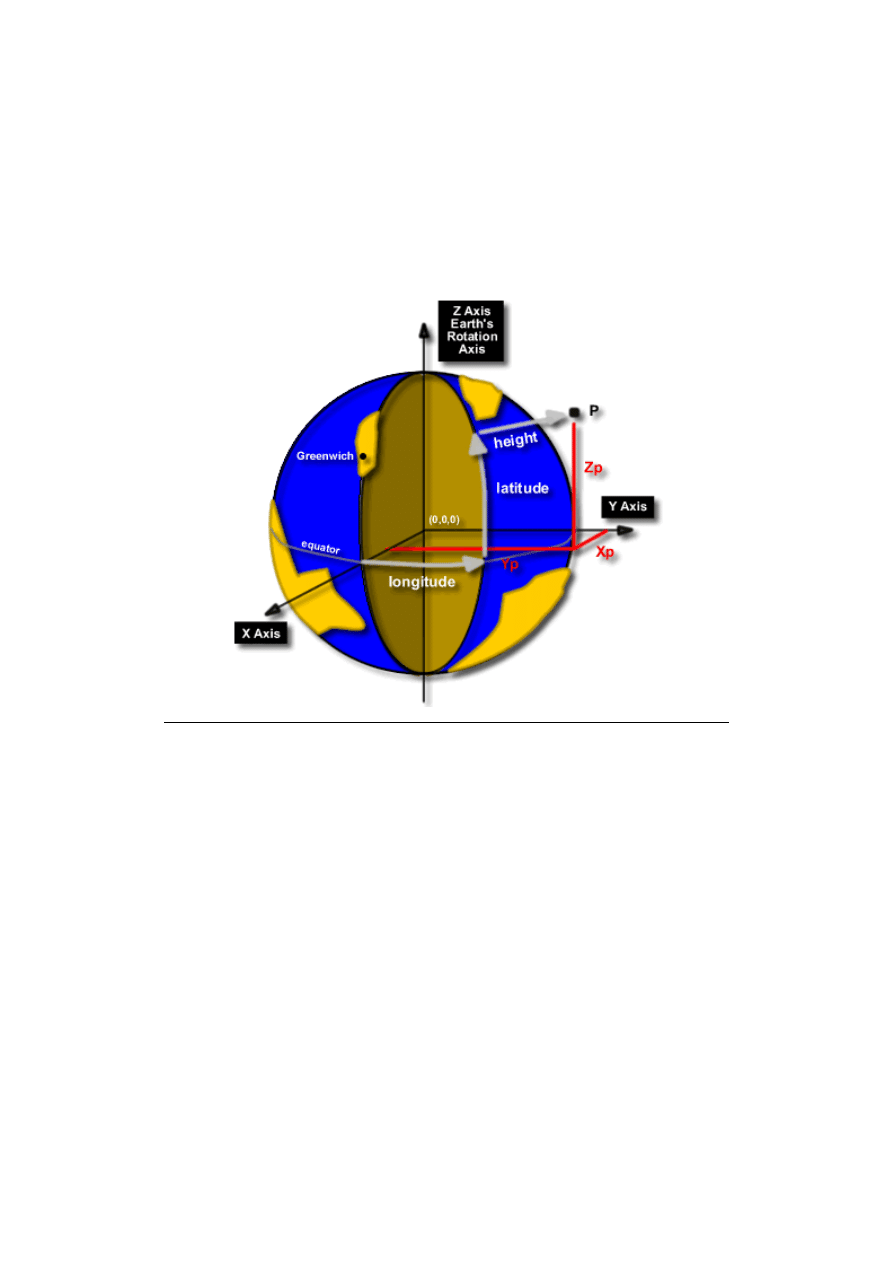
UKŁAD WSPÓŁRZĘDNYCH PROSTOKĄTNYCH PRZESTRZENNYCH

Położenie punktu na elipsoidzie można wyznaczyć za pomocą współrzędnych

prostokątnych przestrzennych: X, Y, Z odniesionych do płaszczyzny równika i dwóch
płaszczyzn południkowych
wzajemnie prostopadłych.

Styczna normalna

Środek geometryczny elipsoidy

Rys .Współrzędne prostokątne przestrzenne.

•

Początek układu pokrywa się ze środkiem geometrycznym elipsoidy

•

Oś Z skierowana jest do bieguna ziemskiego

•

Oś X leży w płaszczyźnie południka zerowego

•

Oś Y dopełnia prawoskrętny ortogonalny układ współrzędnych

Zależności między współrzędnymi prostokątnymi przestrzennymi i współrzędnymi geograficznymi
przedstawiają się następująco:

ϕϕϕϕ

A

z

z

x

y

y

90

0

+

ϕ

φφφφ

λλλλ

ϕϕϕϕ

2

2

sin

e

-

1

sin

cos

a

=

Y

φφφφ

λλλλ

ϕϕϕϕ

2

2

sin

e

-

1

cos

cos

a

=

X

φφφφ

ϕϕϕϕ

2

2

2

sin

e

-

1

)sin

e

-

(1

a

=

Z

UKŁADY ODNIESIENIA WSPÓŁRZĘDNYCH

Układ odniesienia – to konkretny układ współrzędnych
w ścisły sposób związany z ciałem fizycznym lub
układem ciał fizycznych , dla którego określono
powierzchnię odniesienia , położenie początku układu ,
rodzaj współrzędnych.

Układ odniesienia obejmuje:

•

powierzchnię odniesienia ( elipsoidę)

•

zorientowanie elipsoidy tj.:

•

punkt przyłożenia
elipsoidy do geoidy

•

zorientowanie w bryle
geoidy.

Orientowanie elipsoidy polega
na równoległym ułożeniu
małej osi elipsoidy do osi
obrotu Ziemi i jednoczesnej
równoległości pozostałych obu
osi elipsoidy do tych samych
osi geoidy.

http://www.ga.gov.au/earth-monitoring/geodesy/geodetic-datums/about.html

Układy odniesienia stosowane w nawigacji :

1.

Lokalne

(np.: ED 50, PUŁKOWO 42,NAD 1983,

OSGB 1936)

2. Globalne ( geocentryczne ):

WGS 72, WGS 84

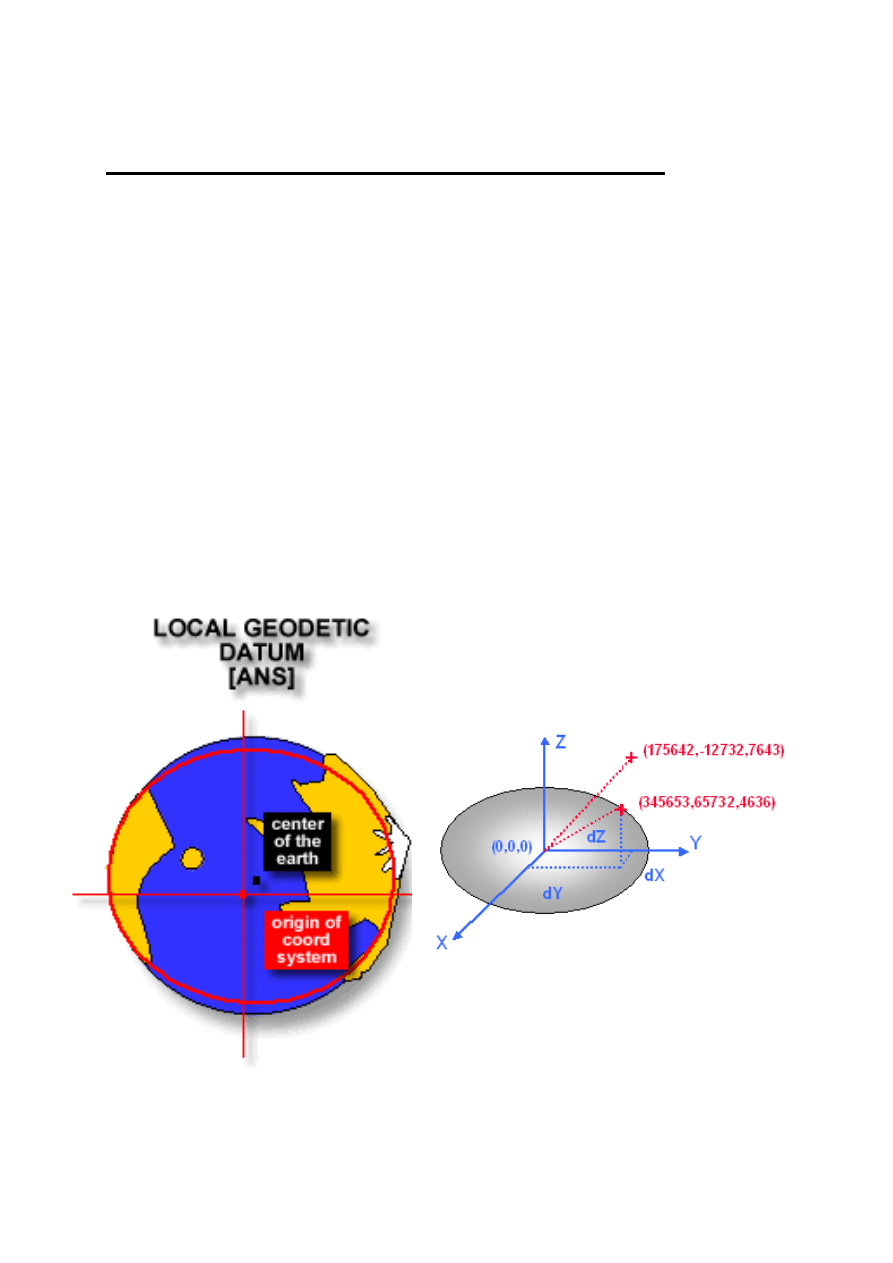
LOKALNE UKŁADY ODNIESIENIA
WSPÓŁRZĘDNYCH

Są to układy współrzędnych oparte na różnych elipsoidach ,których parametry

określono poprzez pomiary głównie naziemne. Zorientowanie elipsoidy polega

na określeniu punktu przyłożenia w taki sposób, aby powierzchnia elipsoidy na

danym obszarze ,była zbliżona do powierzchni geoidy. Początek układu

lokalnego znajduje się w środku geometrycznym elipsoidy odniesienia, który

nie pokrywa się ze środkiem mas ziemi. Lokalne układy służyły do

odwzorowania obszarów znajdujących się w pobliżu punktu przyłożenia, często

więc mają charakter narodowy- lokalny.

Na świecie istnieje kilkaset układów

lokalnych.

http://www.ga.gov.au/earth-monitoring/geodesy/geodetic-datums/about.html

UKŁADY GLOBALNE- GEOCENTRYCZNE

Obecnie podstawową elipsoidą globalną (dla systemów satelitarnych jak i dla nowo
opracowywanych map ) jest elipsoida WGS-84, która najbardziej aproksymuje geoidę w
każdym jej punkcie , a nie tylko w obszarze dopasowania

http://www.ga.gov.au/earth-monitoring/geodesy/geodetic-datums/about.html

Współrz

ę

dne WGS84 odnosz

ą

si

ę

do układu współrz

ę

dnych ziemskich

ortokartezja

ń

skich, realizowanym na bazie zmodyfikowanego układu NSWC 9Z-2

(WGS72 - NNSS TRANSIT).

•

Pocz

ą

tek układu współrz

ę

dnych WGS84 pokrywa si

ę

ze

ś

rodkiem mas Ziemi

,który jest jednocze

ś

nie

ś

rodkiem geometrycznym elipsoidy WGS84

•

o

ś

Z jest skierowana do umownego bieguna ziemskiego (Conventional

Terrestrial Pole - CTP). O

ś

Z jej osi

ą

obrotu.

•

Kierunek osi X jest wyznaczony przez przeci

ę

cie płaszczyzny południka

pocz

ą

tkowego i płaszczyzny równika

•

o

ś

Y uzupełnia prawoskr

ę

tny ortogonalny układ współrz

ę

dnych.

Modyfikacje układu NSWC 9Z-2 s

ą

nast

ę

puj

ą

ce:

- przesuni

ę

cie pocz

ą

tku układu NSWC 9Z-2 o wielko

ść

4.5 m na południe

wzdłu

ż

osi Z,

- obrót południka odniesienia układu NSWC 9Z-2 o k

ą

t 0.814 arc sek (0,554”)

wokół osi Z do kierunku zdefiniowanego przez BIH (na pocz

ą

tek 1984) jako

południk zerowy,

- zmiana skali układu NSWC 9Z-2 o -0.6 ppm.

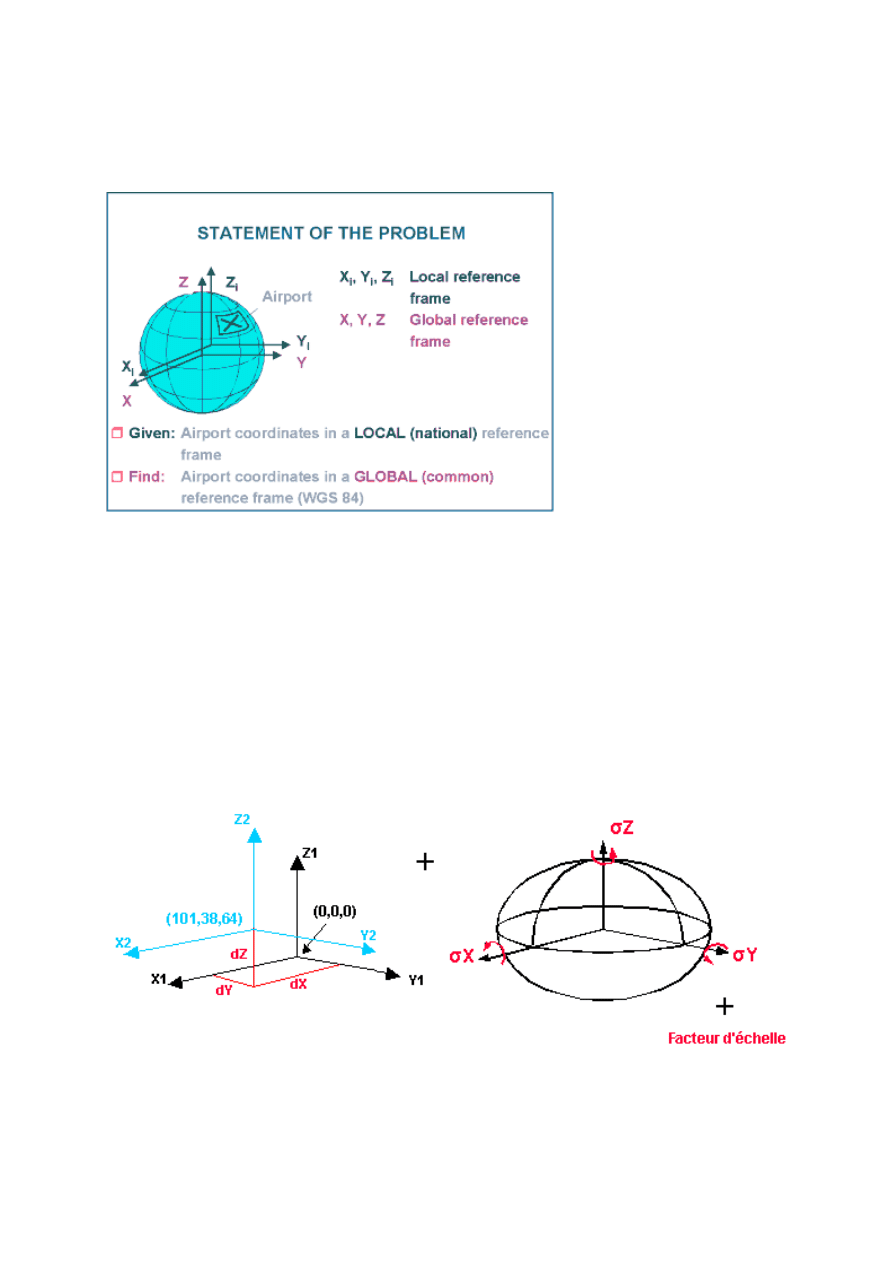
Transformacja współrzędnych stacji dopplerowskich (WGS72) do układu WGS84 nastąpiła przy zastosowaniu
wzorów transformacji Mołodienskiego z użyciem powyższych parametrów.

http://www.dqts.net/wgs84.htm

Podstawowy problem transformacji współrz

ę

dnych to znajomo

ść

parametrów

transformacji i formuł matematycznych.
W zale

ż

no

ś

ci od zdefiniowanych parametrów transformacji rozró

ż

nia si

ę

transformacj

ę

:

•

3-parametrow

ą

- uwzgl

ę

dniaj

ą

ca przesuni

ę

cie

ś

rodków układów o

∆∆∆∆

X,

∆∆∆∆

Y,

∆∆∆∆

Z

•

7-parametrow

ą

- uwzgl

ę

dniaj

ą

ca przesuni

ę

cie

ś

rodków układów o

∆∆∆∆

X,

∆∆∆∆

Y,

∆∆∆∆

Z,

oraz

Z

Y

X

ε

ε

ε

,

,

- k

ą

ty obrotów wokół kolejnych osi układów pierwotnych

m – parametr zmiany skali układu

http://www.dqts.net/wgs84.htm

TRANSFORMACJA 3 PARAMETROWA- METODA BEZPOŚREDNIA

Założenia:

•

Jeden z układów jest układem geocentryczny

•

Ś

rodek układu to środek geometryczny elipsoidy

•

Oś Z pokrywa się z osią obrotu elipsoidy

•

Oś X leży w płaszczyźnie południka początkowego

•

Płaszczyzna XY pokrywa się z płaszczyzną Równika

•

Znane są parametry transformacji

∆∆∆∆

X,

∆∆∆∆

Y,

∆∆∆∆

Z

Z

WGS

Z

L

Y

L

Y

WGS

Y

WGS

X

L

X

WGS

1. Przeliczanie

2.Transformacja

3.Przeliczanie

y

loka

uklad

y

loka

uklad

WGS

WGS

H

Z

Y

X

Z

Y

X

Z

Y

X

H

ln

ln

84

84





















⇒





















=





















∆

∆

∆

−





















⇒





















λλλλ

ϕϕϕϕ

λλλλ

ϕϕϕϕ

r

Ś

rodek mas

Elipsoida
lokalna

Elipsoida
geocentryczna

geoida

Obszar dopasowania
elipsoidy do geoidy

∆

Z

∆

Y

∆

X

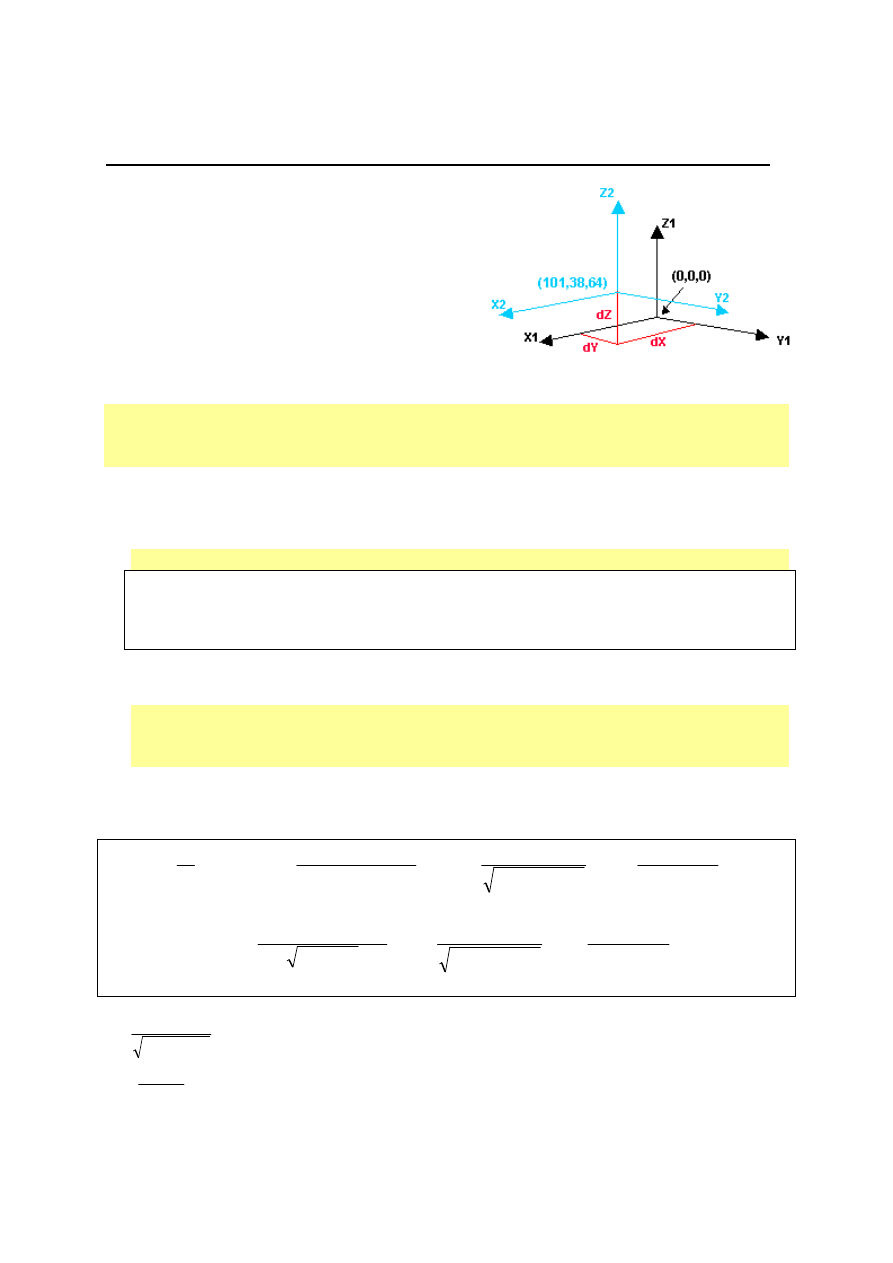
TRANSFORMACJA 3 PARAMETROWA- METODA BEZPOŚREDNIA

Założenia:

•

Jeden z układów jest geocentryczny

•

Środek układu to środek geometryczny
elipsoidy

•

Oś Z pokrywa się z osią obrotu elipsoidy

•

Oś X leży w płaszczyźnie południka
początkowego

•

Płaszczyzna XY pokrywa się z płaszczyzną
Równika

•

Znane są parametry transformacji

∆∆∆∆

X,

∆∆∆∆

Y,

∆∆∆∆

Z

1.

Przeliczanie współrzędnych geograficznych na prostokątne przestrzenne

w

układzie wyjściowym ( WGS 84)

X = ( N + H ) cos φ cos λ

Y = ( N + H ) cos φ sin λ
Z = [ N ( 1 – e

2

) + H ] sin φ

2.

TRANSFORMACJA 3 parametrowa

y

loka

uklad

WGS

Z

Y

X

Z

Y

X

Z

Y

X

ln

84





















=





















∆

∆

∆

−





















Do układu lokalnego dodajemy wartości poprawek

Od układu geocentrycznego odejmujemy wartości poprawek

3.

Przeliczanie współrzędnych prostokątnych przestrzennych na geograficzne

w

układzie lokalnym

metodą kolejnych przybliżeń

λ = arc tg

Y

X

; φ

1

=

arctg

Z

X

Y

(

cos

sin

)

λ

λ

+

; N

1

=

a

e

1

2

2

1

−

sin

ϕ

; H

1

=

X

N

cos

sin

ϕ

λ

1

1

−

obliczenie kolejnych przybliżeń φ i H

φ

i

=

arctg

Z

N e

X

Y

i

i

(

sin

+

+

−

−

1

2

1

2

2

ϕ

); N

i

=

a

e

i

1

2

2

−

sin

ϕ

; H

i

=

X

N

i

i

cos

cos

ϕ

λ

−

aż :



φ

i

– φ

i-1



<<<<

ε;



H

i

– H

i-1



<<<<

ε . a ( gdzie ε – założona dokładność np. ε= 10

–7

radiana, a – duża półoś elipsoidy

Gdzie :

N =

a

e

1

2

−

sin

ϕ

- promień przekroju pierwszego wertykału ;

e

2

=

a

b

a

2

2

2

−

kwadrat pierwszego mimośrodu ;

a – duża półoś elipsoidy ; b – mała półoś elipsoidy

X,Y,Z – współrzędne prostokątne przestrzenne ; φ,λ, H - współrzędne geograficzne ( geodezyjne)

84

84

WGS

WGS

Z

Y

X

H





















⇒





















λλλλ

ϕϕϕϕ

y

loka

uklad

y

loka

uklad

H

Z

Y

X

ln

ln





















⇒





















λλλλ

ϕϕϕϕ

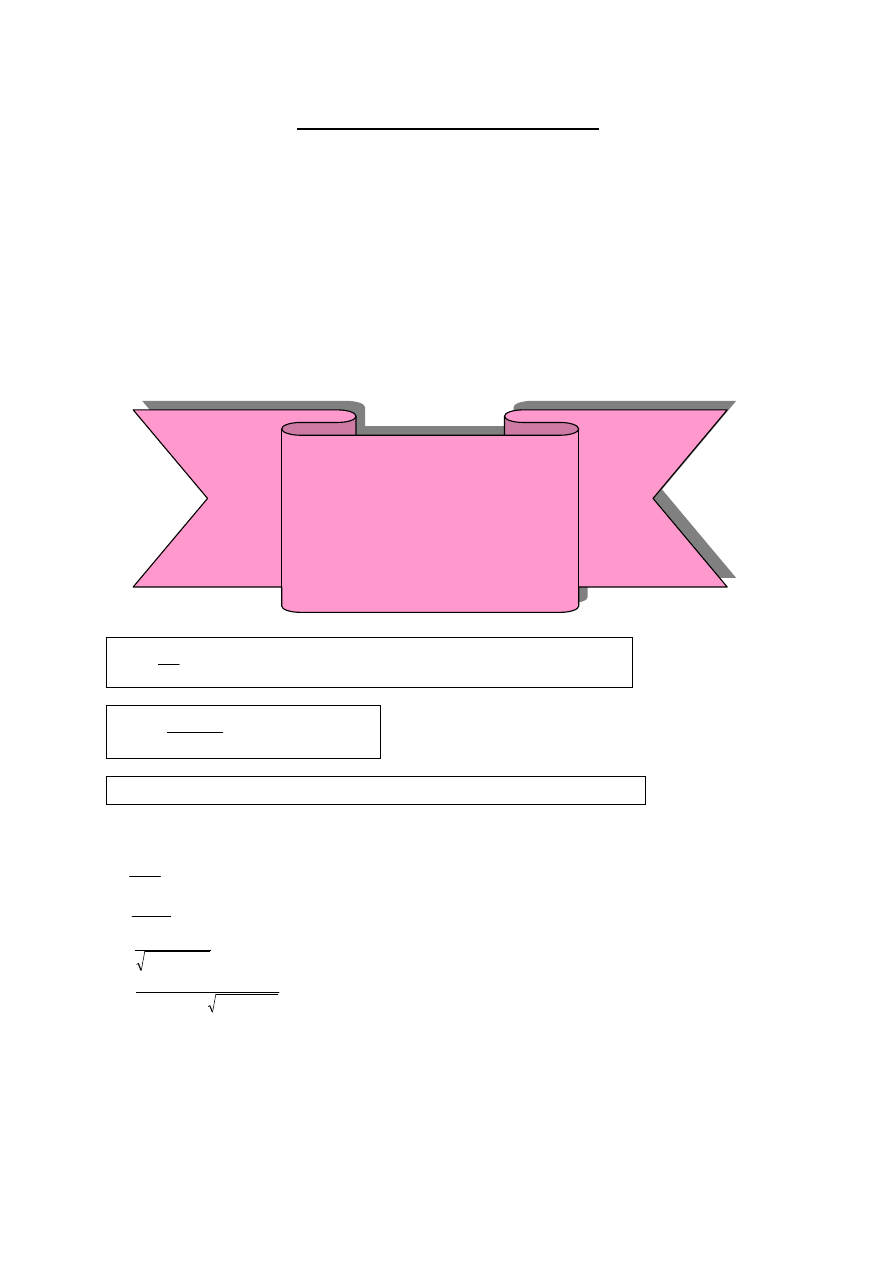
METODA MOŁODIEŃSKIEGO

Metoda polega na obliczeniu poprawek do współrzędnych

∆∆∆∆ϕϕϕϕ

”,

∆∆∆∆λλλλ

”,

∆∆∆∆

H[m] z

uwzględnieniem 3 parametrów transformacji

∆∆∆∆

X,

∆∆∆∆

Y,

∆∆∆∆

H.

Metoda była zalecana przez IHO przy transformacji z WGS 72 do WGS 84

Założenia transformacji :

•

Układy odniesienia są wzajemnie równoległe

•

Środki układów przesunięte o wektor r

•

Jeden z układów jest układem geocentrycznym

∆

∆

∆

∆

∆

∆

ϕ

ρ

ϕ

λ

ϕ

λ

ϕ

ϕ

"

"

[

sin cos

sin sin

cos

sin

=

−

−

+

+

+

M

X

Y

Z

a f

f

a

2

∆

∆

∆

λ

ρ

ϕ

λ

λ

"

"

cos

(

sin

cos )

= −

−

N

X

Y

∆

∆

∆

∆

∆

∆

∆

H

X

Y

Z

a f

f a

a

m

=

+

+

+

+

−

cos cos

cos sin

sin

(

) sin

ϕ

λ

ϕ

λ

ϕ

ϕ

2

gdzie:
ρ

”

= 206264,806246– wartość radiana wyrażona w sekundach

a-

duża półoś elipsoidy lokalnej, b- mała półoś elipsoidy lokalnej

f = a

b

a

−

- spłaszczenie elipsoidy lokalnej

e

a

b

a

2

2

2

2

=

−

e – pierwszy mimośród elipsy południkowej

N

a

e

=

−

1

2

2

sin

ϕ

- N – promień krzywizny pierwszego wertykału

M

a

e

e

e

=

−

−

−

(

)

(

sin

)

sin

1

1

1

2

2

2

2

2

ϕ

ϕ

- M – promień krzywizny południka

∆f – różnica spłaszczeń elipsoid; ∆a- różnica wartości dużych półosi elipsoid,
∆a = a

WGS

–a

L ,

∆f = f

WGS

– f

L

( przeliczając z układu lokalnego do geocentrycznego)

∆a =a

L

- a

WGS ,

∆f = f

L

- f

WGS

( przeliczając z układu geocentrycznego do lokalnego)

∆X, ∆Y, ∆Z –poprawki współrzędnych prostokątnych przestrzennych ; φ,λ,H- współrzędne geograficzne punktu

2.

TRANSFORMACJA

y

loka

uklad

WGS

H

H

H

ln

84





















=





















∆

∆

∆

+





















λλλλ

ϕϕϕϕ

λλλλ

ϕϕϕϕ

λλλλ

ϕϕϕϕ

ϕϕϕϕ

λλλλ

H

przeliczenie

X
Y

Z

WGS-84

Parametry
transformacji

m

Z

Y

X

Z

Y

X

,

,

,

,

,

εεεε

εεεε

εεεε

∆

∆

∆

X
Y

Z

ϕϕϕϕ

λλλλ

H

przeliczenie

=

układ
lokalny

układ
lokalny

TRANSFORMACJA 7-PARAMETROWA.

Polega na uwzględnieniu siedmiu parametrów transformacyjnych, a mianowicie:

-

∆X, ∆Y,∆Z – wartości przesunięć środków układu

-

Z

Y

X

ε

ε

ε

,

,

- kąty obrotów wokół kolejnych osi układów pierwotnych

-

m – parametr zmiany skali układu

Wzory na transformację z układu WGS 84 do Pułkowo 42:

X

K

=

∆

X + (1 + 0.8407728

⋅

10

-6

)

⋅

X

G

+

ε

z

⋅

Y

G

+ ( -

ε

y

⋅

Z

G

)

Y

K

=

∆

Y -

ε

z

⋅

X

G

+ (1 + 0.8407728

⋅

10

-6

)

⋅

Y

G

+

ε

x

⋅

Z

G

Z

K

=

∆

Z +

ε

y

⋅

X

G

+ ( -

ε

x

⋅

Y

G

) + (1 + 0.8407728

⋅

10

-6

)

⋅

Z

G

∆

X =

−−−−

33.4297 m,

∆

Y = +146.5746 m,

∆

Z = +76.2865 m,

m = 1 + 0.8407728

⋅⋅⋅⋅

10

-6

εεεε

x

=

−−−−

1.7388854

⋅⋅⋅⋅

10

-6

[rad] =

−−−−

0.35867 ”

εεεε

y

=

−−−−

0.2561460

⋅⋅⋅⋅

10

-6

[rad] =

−−−−

0.05283 ”

εεεε

z

= + 4.0896031

⋅⋅⋅⋅

10

-6

[rad] = +0.84354 ”

εεεε

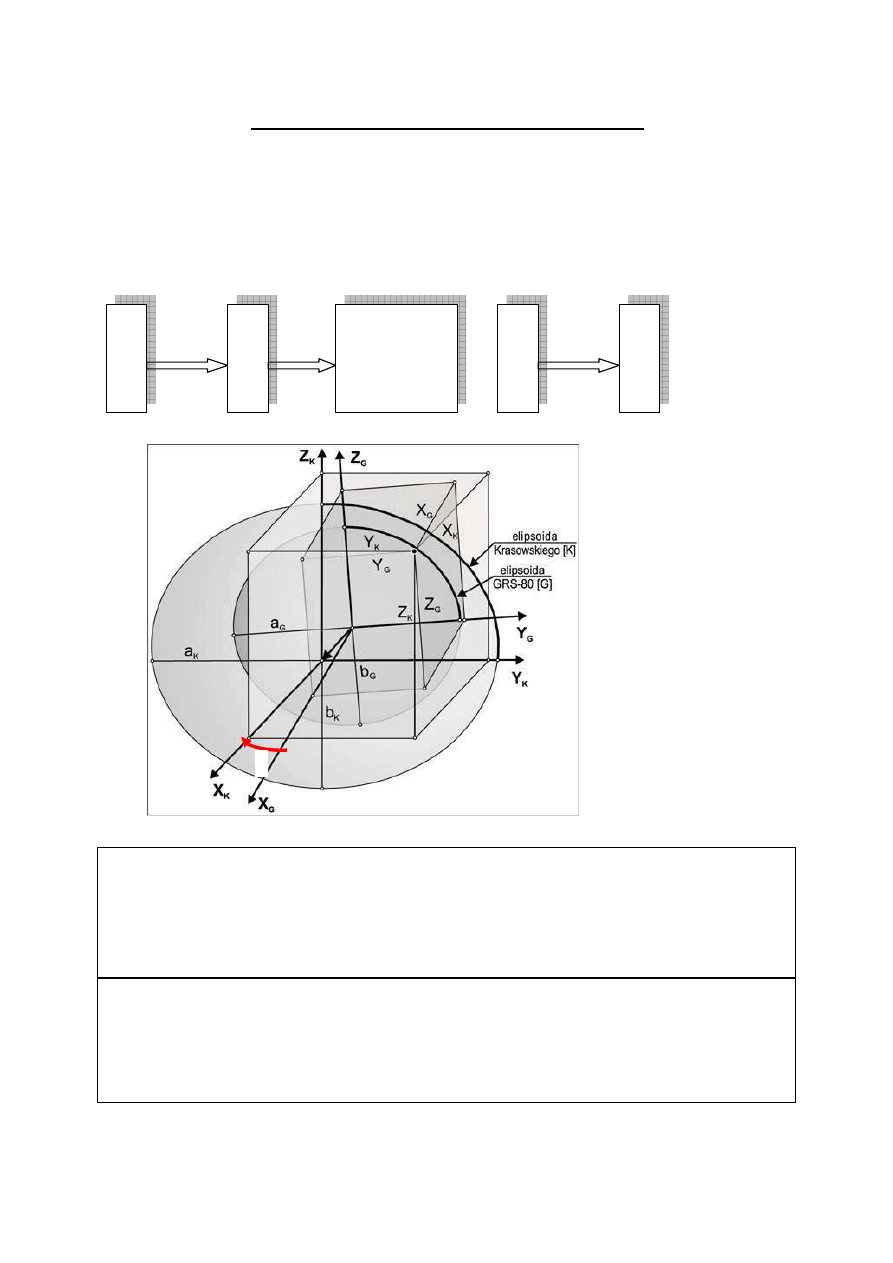
Współrz

ę

dne geodezyjne

φ

,

λ

na elipsoidzie Krassowskiego w

stosunku do współrz

ę

dnych WGS 84 s

ą

:

•

wi

ę

ksze o

ś

rednio ok. 1” w szeroko

ś

ci

φ

zmiana szeroko

ś

ci geodezyjnej

φ

o 1” odpowiada przyrostowi łuku

południka o ok. 30 m,

•

wi

ę

ksze ok. 6.5” w długo

ś

ci

λ

, zmiana długo

ś

ci

λ

o 1” daje

przyrost długo

ś

ci łuku równole

ż

nika ok. 20m

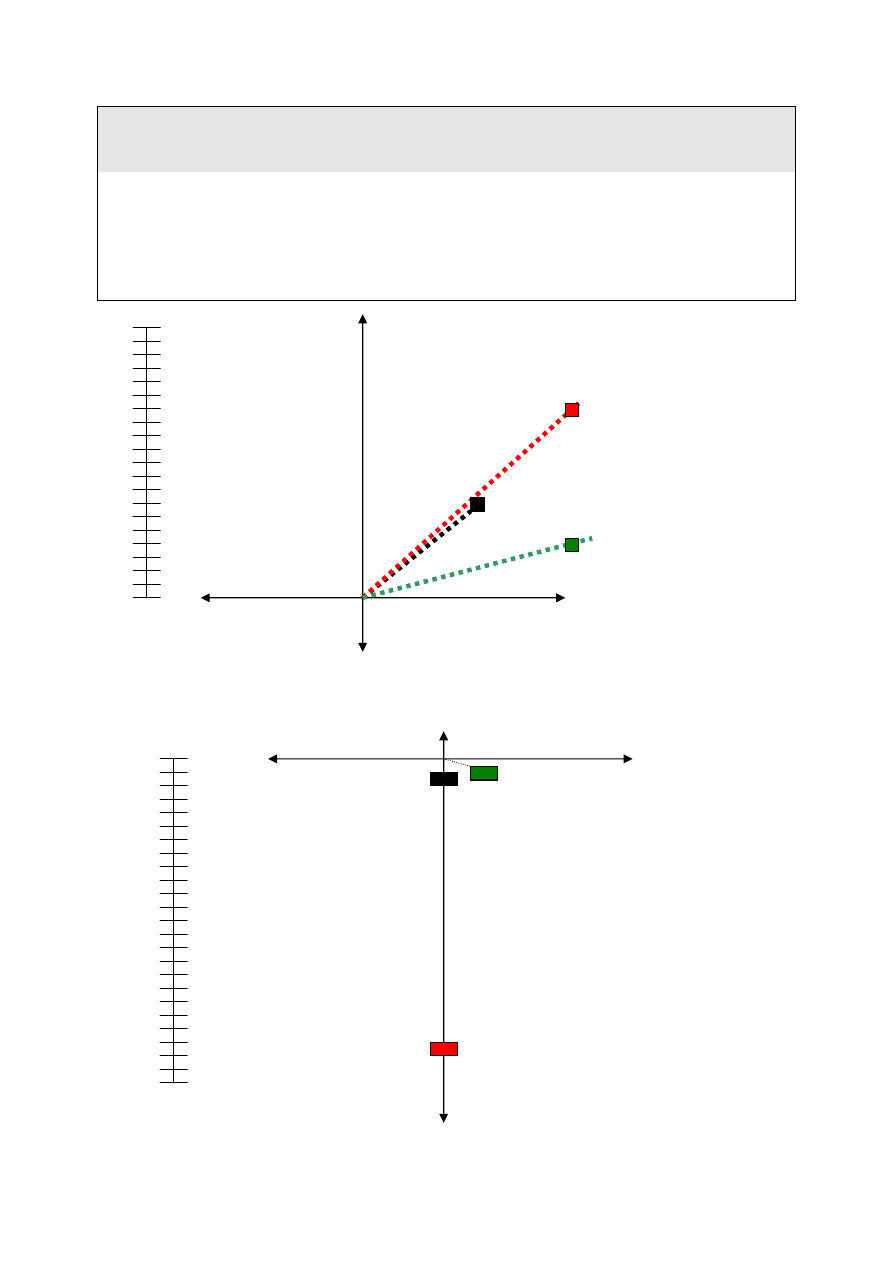
Rys.5.4. Latarnia Razewie w układzie Pułkowo ’42 w stosunku do układu WGS-84

Rys. 5.6. Latarnia Rozewie w układzie WGS-72 w stosunku do układu WGS-84

0

160

140

120

100

80

60

40

20

200

180

Pułkowo’42 met. bezpośrednia
D=189,7245m kąt=40,82596˚

Pułkowo’42 met. Mołodieńskiego
D=89,519m kąt=45,161˚

Pułkowo’42 met. 7-parametrowa
D=129,7330122m kąt=74,647729˚

S

N

W

E

WGS-84

metry

90

10

20

30

40

50

60

70

80

110

0

WGS-72 met. Mołodieńskiego

D=2,793m kąt=180˚

WGS-72 met. bezpośredenia
D=107,95703m kąt=180˚

WGS-72 met. 7-parametrowa
D=10,300975m kąt=101,5116˚

S

W

E

WGS - 84

metry

120

100

N

W

S

E

100m

100m

100m

100m

WGS-84

150m

50m

50m

150m

50m

150m

50m

150m

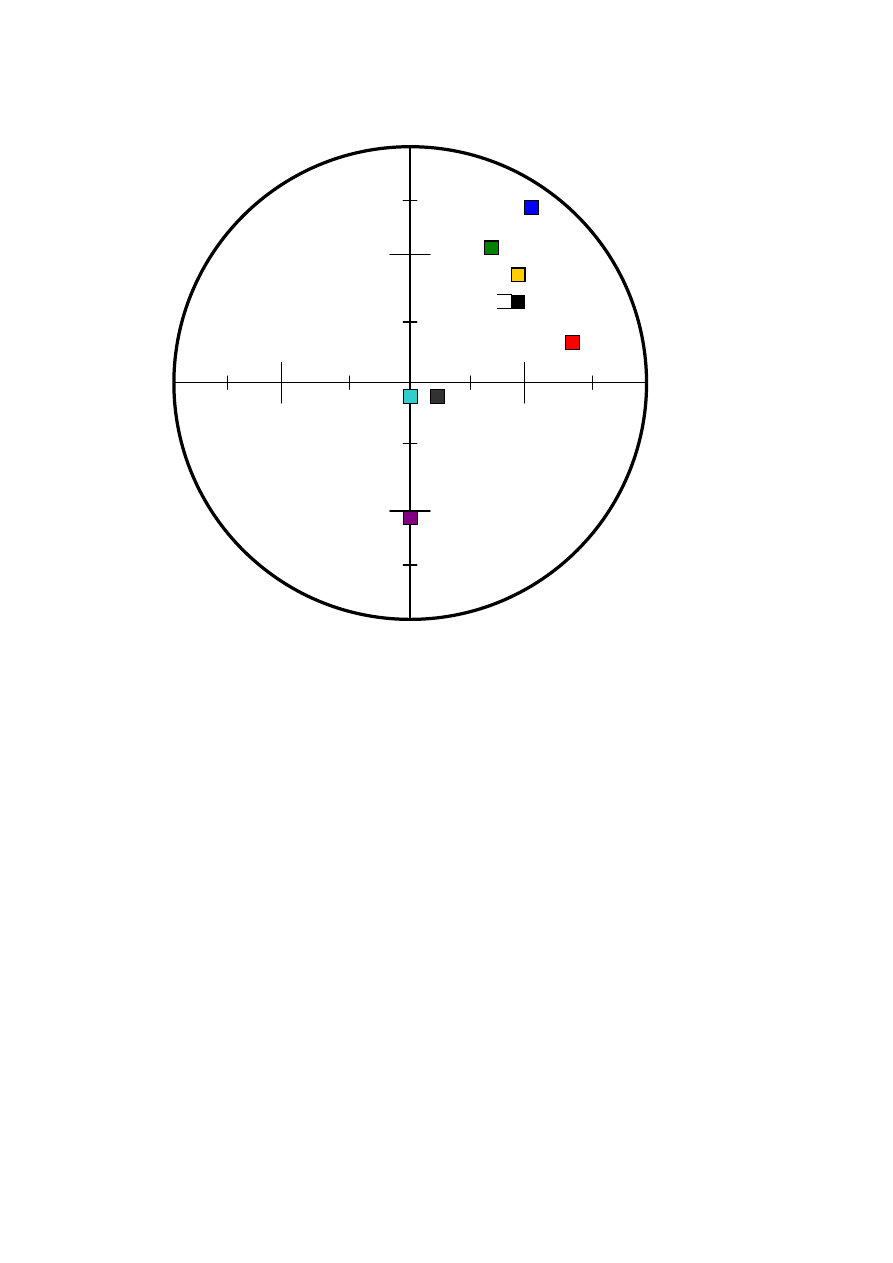
Rys Położenie latarni Rozewie w różnych układach

LEGENDA do rysunku

1942 met..7-parametrowa

54°50,055651’N 18°20,113823’E

1942 met. Mołodieńskiego

54°50,071’N 18°20,056’E

1942 met. bezpośrednia

54°49,95959’N 18°19,88025’E

ED50 met. 7-parametrowa

54°50,071’N 18°20,058’E

ED50 met. Mołodieńskiego

54°50,071’N 18°20,057’E

ED-50 met. bezpośrednia

54°49,98982’N 18°19,93719’E

WGS-72 met. 7-parametrowa

54°50,036’N 18°20,006’E

WGS-72 met. Mołodieńskiego 54°50,036’N 18°19,997’E

WGS-72 met. bezpośrednia

54°49,978813’N 18°19,996537’E

WGS-84

54°50,037’N 18°20’E – punkt odniesienia

http://www.colorado.edu/geography/gcraft/notes/datum/datum_f.html

•

Literatura:

•

Department of Defense World Geodetic System 1984 : Its Definition and Relationships with
Local Geodetic Systems. DMA Technical Report 8350.2, The Defense Mapping Agency,
1991.

•

GAJDEROWICZ I., Problemy transformowania sieci GPS do układu pa

ń

stwowego "1965".

Acta Acad. Agricult. Techn. Olst., 446, Geodaesia et Ruris Regulatio, 23, Olsztyn,

•

GAJDEROWICZ I., Kartografia matematyczna dla geodetów, podr

ę

cznik, Wydawnictwo ART.,

Olsztyn, 1991.

•

HOFMANN - WELLENHOF B., LICHTENEGGER H., COLLINS J., Global Positioning System
: Theory and Practice. Springer - Verlag, Wien - New York, 1994.

•

LAMPARSKI J.,

Ś

WI

Ą

TEK K., Wyznaczanie wysoko

ś

ci punktów z wykorzystaniem pomiarów

GPS, Zeszyty Naukowe Akademii Rolniczej we Wrocławiu, Geodezja i Urz

ą

dzenia Rolne XII,

Nr. 251, 1994.

•

Banachowicz A.: Ocena dokładno

ś

ci pozycji w nawigacji zliczeniowej. Zeszyty Naukowe AMW

nr 2 1988

•

Banachowicz A. Urba

ń

ski J. : Obliczenia nawigacyjne AMW , Gdynia 1987

LINKI:

Navstar GPS Joint Program Office
The Ministry of Defence of the Russian Federation Coordination Scientific Information Center
(KNITs)
Global Positioning System Data & Information maintained by the United States Naval Observatory
US Coast Guard Navigation Center
Peter H. Dana Global Positioning System Overview
Global Positioning System (GPS) Resources ...
GPS Related Internet Sites
Jenny's GPS Links
Lotnicze systemy nawigacyjne
Macropol Sp.z o.o.