Rachunek kwantyfikatorów

W rachunku zdań tworzyliśmy formuły zdaniowe, które mogły oznaczać różne zdania w zależności od
interpretacji zmiennych zdaniowych wchodzących w ich skład. W rachunku kwantyfikatorów przy
pomocy symboli oznaczających funkcje zdaniowe, symbolu równości

, kwantyfikatorów, spójników

logicznych, zmiennych i nawiasów tworzymy wyrażenia oznaczające nowe funkcje zdaniowe lub zdania
(w zależności od tego, czy wszystkie zmienne w tych wyrażeniach są związane, czy nie). Wyrażenia takie
nazywamy formułami rachunku kwantyfikatorów, lub krótko formułami. Przykładowo rozważmy formułę

W formule tej symbole i odczytujemy jako ``dla każdego'' i ``istnieje''. Symbole

i

mogą być tu interpretowane jako konkretne funkcje zdaniowe na wiele sposobów. Wyjątek czynimy dla
symbolu równości

, który zawsze interpretujemy jak prawdziwą równość. Gdy

oznaczają

konkretne funkcje zdaniowe, gdzie wspólnym zakresem zmiennych

jest jakaś przestrzeń

, formuła

również oznacza funkcję zdaniową zmiennej o zakresie

. Jeśli na przykład poprzedzimy ją

kwantyfikatorem

(wiążącym zmienną ), stanie się ona zdaniem. Dlatego formuły, w których

wszystkie zmienne są związane przez kwantyfikatory, nazywamy formułami domkniętymi lub (niezbyt
poprawnie) zdaniami.

W formule

kwantyfikator

odnosi się do formuły

nie zaś tylko do jej części

. Podobnie kwantyfikator

odnosi się do formuły

nie zaś do jej części

. Dlatego w obu przypadkach formuły te dodatkowo ograniczyliśmy

nawiasami. Gdyby tych nawiasów nie było, formułę

domyślnie należałoby odczytywać jako

Wtedy obie zmienne w

pozostałyby niezwiązane (inaczej: wolne).

Gdy w formule

za symbole i podstawimy konkretne funkcje zdaniowe, stanie się ona sama

(złożoną) funkcją zdaniową. Na przykład, niech

oznacza funkcję zdaniową

(tzn: ``

dzieli ''), zaś

oznacza funkcję zdaniową

. Wówczas

staje się funkcją

zdaniową:

którą dla uproszczenia będziemy teraz oznaczali przez

, gdyż w tej funkcji zdaniowej występuje

jako zmienna wolna. To wolne wystąpienie zmiennej w formule

zaznaczyliśmy kropką, pozostałe

wystąpienia zmiennej w tej formule sa związane przez kwantyfikatory. Zakres zmienności zmiennej w

tej funkcji zdaniowej to

. Sprawdźmy dla przykładu, czy formuła

jest prawdziwa dla

, tzn.

czy

jest zdaniem prawdziwym. Jest to zdanie następujące:

(Powstało ono z

przez podstawienie liczby za każde wolne wystąpienie zmiennej .) Zdanie to

mówi, że

dla każdej liczby naturalnej , jeśli dzieli , to

.

Nie jest to prawda, gdyż np. liczba

dzieli oraz dla

formuła

jest

fałszywa.

Można sprawdzić, że dla każdego

, zdanie

jest fałszywe, czyli

.

Definicja 7..1 Formułę domkniętą nazywamy tautologią (rachunku kwantyfikatorów), gdy jest zdaniem
prawdziwym przy dowolnym rozumieniu występujących w niej symboli funkcji zdaniowych.

Przykładem tautologii jest formuła

Ogólniej, jeśli

jest tautologią rachunku zdań, to formuła

jest tautologią rachunku kwantyfikatorów, gdzie symbole

oznaczają teraz funkcje zdaniowe zmiennej .

Podobnie jak w rachunku zdań, wiele tautologii rachunku kwantyfikatorów ma postać równoważności.
Pozwalają one przekształcać w sposób równoważny zdania tak, by uzyskać jak najprostszą formę.

Definicja 7..2 (1) Mówimy, że dwie funkcje zdaniowe

i

(o wspólnym zakresie zmiennej ) są

równoważne, gdy mają ten sam wykres. Innymi słowy, gdy

oznacza wspólny zakres zmiennej w tych

funkcjach, znaczy to, że

(2) Mówimy, że dwie formuły domknięte i są równoważne, gdy formuła

jest tautologią.

Podobnie definiujemy równoważność funkcji zdaniowych większej liczby zmiennych.

Uwaga 7..3 Dwie funkcje zdaniowe

i

są równoważne wtedy i tylko wtedy, gdy zdanie

jest prawdziwe.

Dowód. Niech oznacza zdanie

i

są równoważne.

zaś zdanie

Zdanie

jest prawdziwe.

By udowodnić równoważność obu zdań korzystamy z faktu, że zdanie

jest równoważne koniunkcji

dwóch implikacji

i

. Wystarczy więc udowodnić każdą z tych implikacji.

. Wystarczy udowodnić zdanie zakładając, że jest prawdziwe. Załóżmy, że jest prawdziwe,

to znaczy funkcje zdaniowe

i

są równoważne. Znaczy to, że

. Oznaczmy przez

ten zbiór. Dlatego dla każdego

mamy, że

zdania

i

mają tę samą wartość logiczną (a mianowicie są oba fałszywe, gdy

i oba

prawdziwe, gdy

). Dlatego dla każdego

zdanie

jest prawdziwe. Oznacza to, że

prawdziwe jest zdanie

, czyli .

. Tu dowód pozostawiamy jako ćwiczenie.

Podamy teraz przykłady prostych tautologii rachunku kwantyfikatorów. Wiele z nich ma postać
równoważności.

(prawa de Morgana rachunku kwantyfikatorów)

1.

(przemienność dużych kwantyfikatorów)

2.

(przemienność małych kwantyfikatorów)

3.

4.

(rozdzielność względem )

5.

(rozdzielność względem )

6.

7.

8.

9.

Przed dowodem zauważmy, że intuicyjnie formuły te istotnie zawsze oznaczają zdania prawdziwe.
Dowód. Udowodnimy niektóre punkty. (1) Udowodnimy, że

jest tautologią. W

tym celu rozważmy dowolną konkretną funkcję zdaniową

. Wystarczy pokazać, że zdania

i

są równoważne. Niech

Zatem

i

są rozłączne (prawo sprzeczności) i w sumie dają cały zbiór

(prawo wyłączonego

środka). Korzystając z definicji kwantyfikatorów dostajemy ciąg zdań równoważnych

który świadczy o żądanej równoważności.

(2) Obie strony równoważności mówią, że

, dlatego są

równoważne.

(4) Podobnie jak w punkcie (1) interpretujemy najpierw

jako funkcję zdaniową na jakiejś

(dowolnej) przestrzeni

. Mamy pokazać, że przy tej interpretacji zdanie

jest prawdziwe.

Niech

oznacza wykres funkcji zdaniowej

. Zatem

oznacza dokładnie, że

jeśli pewne cięcie pionowe zbioru

jest całym

, to każde cięcie poziome zbioru

jest

niepuste.

By to udowodnić, załóżmy, że

oraz

. Znaczy to, że każda para postaci

, gdzie

, należy do

. Wobec tego dla każdego

mamy

, gdyż

, więc

.

W tym miejscu zwróćmy uwage, że implikacja odwrotna do (4)

nie jest tautologią. Świadczy o tym przykład o dudku z rozdziału 5. Podobnie implikacje odwrotne do
(7),(8),(9) nie są tautologiami.

(5) Jak wyżej, rozważamy funkcje zdaniowe

i

. Mamy pokazać, że zdania

są równoważne. W tym celu oznaczmy przez

wykres funkcji zdaniowej

, zaś przez

wykres

funkcji zdaniowej

. Wówczas zbiór

jest wykresem funkcji zdaniowej

. Dlatego

mamy następujący ciąg zdań równoważnych.

co kończy dowód.

Dowody pozostałych punktów jedną z powyższych metod pozostawiamy jako ćwiczenie.

Należy tu zaznaczyć, że chociaż dowody, że powyższe formuły są tautologiami, są dość łatwe, ogólnie nie
istnieje algorytm (tzn. przepis) sprawdzania, czy dana formuła jest tautologią. Jak pamiętamy, algorytm
taki istnieje w przypadku tautologii rachunku zdań (tabelka).

Z uwagi na przemienność kwantyfikatorów stosujemy konwencję łączenia sąsiednich dużych i sąsiednich
małych kwantyfikatorów, tzn. zamiast

piszemy

i podobnie dla .

Warto tu wspomnieć o tym, że niekiedy w matematyce traktuje się duży kwantyfikator jako kwantyfikator
domyślny. Jest tak na przykład w zdaniach typu:

W przestrzeni

prawdziwa jest równość

.

Oczywiście równość

nie jest zdaniem, w tym przypadku jednak domyślnie rozumie się, że

chodzi tu o prawdziwość zdania

, duży kwantyfikator jest tu domyślny. W

niniejszym wykładzie ze względów dydaktycznych będziemy jednak unikać tej konwencji.

Aby uzasadnić, że formuła nie jest tautologią, trzeba podać przykład (tzn. interpretację tej formuły jako
konkretnego zdania), w którym jest ona zdaniem fałszywym. W tym celu potrzebujemy dużo przykładów
funkcji zdaniowych. Dostarczają ich nam relacje.

Relacje. Relacja oznacza określony związek między obiektami jakiegoś typu. Przykładowo niech
oznacza zbiór mężczyzn, zaś

zbiór kobiet. Na zbiorach tym rozważamy relację

bycia synem, tzn.

fakt, że mężczyzna

i kobieta

są w relacji

oznacza dokładnie, że

jest synem

. Zwróćmy

uwagę, że relacja

jest w pełni opisana przez zbiór

(podobnie jak spójnik logiczny jest w pełni określony przez tabelkę wartości logicznych). W przypadku
spójników logicznych definiowaliśmy również abstrakcyjne spójniki, nie mające odpowiednika w języku
potocznym, poprzez właśnie zadanie tabelki wartości. Podobnie możemy postąpić w przypadku relacji.

Definicja 7..4 Relacją R na zbiorach

i

nazywamy dowolny podzbiór produktu kartezjańskiego

. W tym przypadku fakt, że elementy

i

są w relacji zapisujemy na dowolny z

poniższych sposobów.

(sposób teoriomnogościowy)

1.

2.

3.

Zwróćmy uwagę, że każdy ze sposobów 1-3 z definicji

7.4

jest symbolicznym sposobem zapisu funkcji

zdaniowej `` i są w relacji

'', gdzie zakres to

, zaś zakres to

. Relacja

, jako podzbiór

produktu

, jest natomiast wykresem tej funkcji zdaniowej. W ten sposób dostajemy mnóstwo

przykładów funkcji zdaniowych.

W definicji

7.4

wprowadziliśmy pojęcie relacji dwuargumentowej (binarnej). Rozważa się również relacje

o innej liczbie argumentów. Mianowicie, dla

relacja -argumentowa na zbiorach

to

dowolny podzbiór

produktu kartezjańskiego

. Dla

relację

nazywamy też

relacją unarną. W przypadku, gdy

mówimy, że jest to relacja -argumentowa na zbiorze

. Funkcję zdaniową ``

są w relacji

''

w przypadku

zapisujemy w sposób 2. z definicji

7.4

, w przypadku

zapisujemy ją w sposób 1.

lub 2. Jeśli nie określamy jawnie liczby argumentów relacji

(tzn. jej arności), to w domyśle zakładamy,

że jest to relacja binarna.

W przypadku relacji binarnej

na zbiorach

i

definiujemy dziedzinę i obraz relacji

jako zbiory

Zauważmy, że wtedy

, czyli

jest też relacją na zbiorach

i

.

Widzimy też, że w istocie

to rzut

na pierwszą oś, a

to rzut

na drugą oś

7.1

.

Definiujemy też relację odwrotną

do relacji

wzorem

Mamy zatem dla wszystkich

.

jest więc relacją na zbiorach

i

.

Gdy

jest relacją na zbiorze

oraz

jest podzbiorem

, to definiujemy ograniczenie (obcięcie)

relacji

do zbioru

wzorem

W przypadku relacji

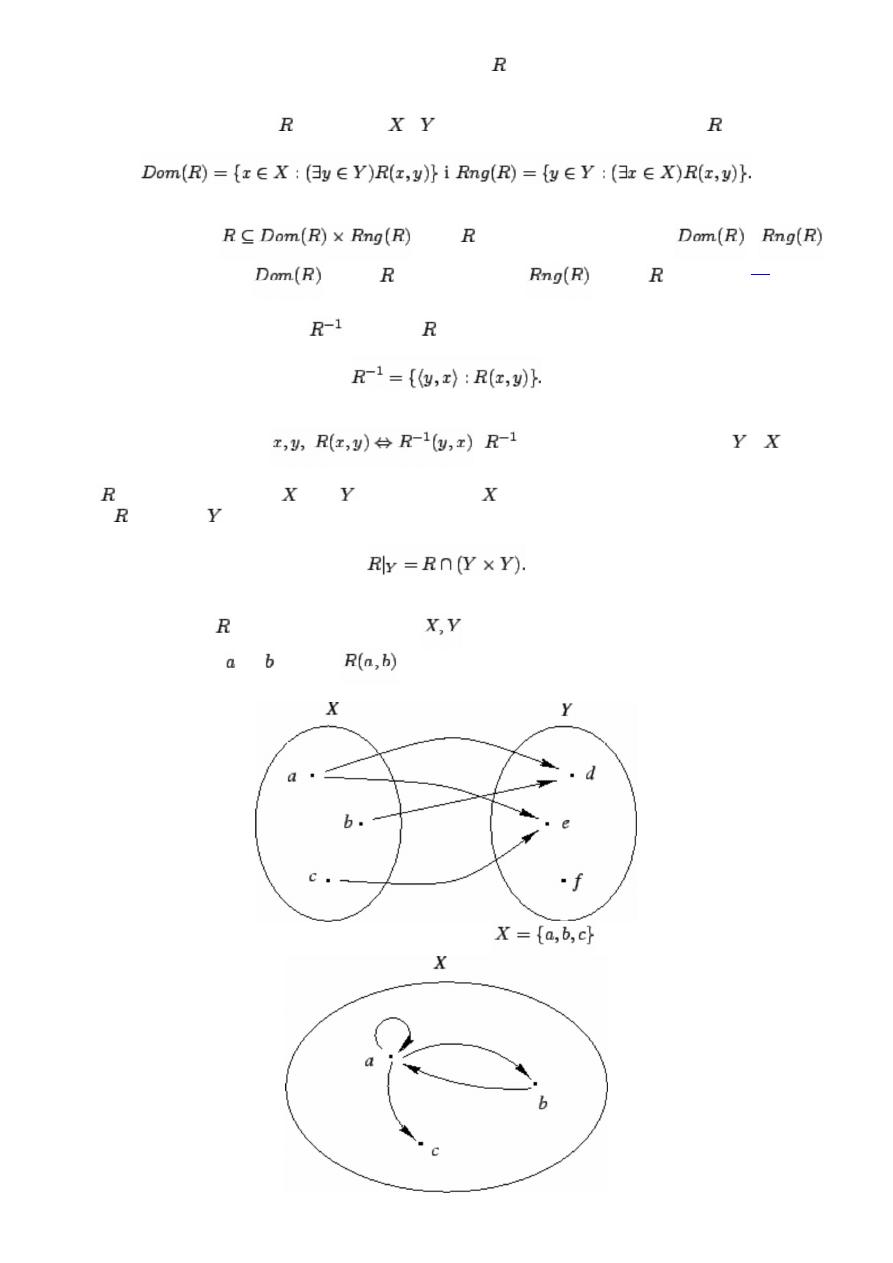
na zbiorach skończonych

wygodnie jest przedstawiać ją graficznie w postaci

diagramu. Strzałka od do oznacza

.

Poniżej zamieszczamy przykład diagramu relacji na zbiorze

.

Przykłady. 1. Relacja pusta

jest -argumentowa dla wszystkich

.

2. Relacja porządku

na zbiorze liczb rzeczywistych.

3. Relacja równoległości

na zbiorze prostych na płaszczyźnie.

4. Relacja podzielności

na zbiorze liczb naturalnych

.

5. Relacja inkluzji

na zbiorze potęgowym

dla ustalonego zbioru

.

Jak już wspomnieliśmy, relacji można używać do definiowania funkcji zdaniowych wskazujących, że
pewne formuły nie są tautologiami. Przykładowo zrobimy to dla formuły

W tym przypadku przyjmujemy

i definiujemy

(sugerujemy narysowanie

diagramu relacji

). Wtedy zdanie

jest prawdziwe, zaś

jest fałszywe. Zatem implikacja

jest fałszywa, co pokazuje, że

nie jest

tautologią rachunku kwantyfikatorów.

Rozważa się różne własności relacji

na zbiorze

.

Definicja 7..5 Załóżmy, że

jest relacją na zbiorze

.

jest zwrotna

.

1.

jest przechodnia (tranzytywna)

.

2.

jest symetryczna

.

3.

jest antysymetryczna

.

4.

jest spójna

.

5.

Jako ćwiczenie pozostawiamy stwierdzenie, jak przy pomocy diagramu relacji

rozpoznać powyższe

własności.

W powyższych przykładach relacji, relacja pusta jest przechodnia, symetryczna, antysymetryczna, lecz

nie jest zwrotna ani spójna (na niepustym zbiorze

).

Relacja

na zbiorze

jest zwrotna, przechodnia, antysymetryczna i spójna.

Relacja równoległości na zbiorze prostych na płaszczyźnie jest zwrotna, symetryczna i przechodnia,

lecz nie jest antysymetryczna ani spójna.

Relacja podzielności na zbiorze

jest zwrotna, przechodnia, antysymetryczna, lecz nie jest symetryczna

ani spójna.

Relacja inkluzji na zbiorze

jest zwrotna, przechodnia, antysymetryczna, lecz nie jest spójna ani

symetryczna (gdy

ma więcej niż jeden element).

W następnych dwóch rozdziałach poznamy najważniejsze rodzaje relacji: relacje porządkujące i relacje
równoważności.