Piotr Łukowski, Wykład dla studentów prawa

1

Logiczne podstawy prawoznawstwa

Piotr Łukowski

Piotr Łukowski, Wykład dla studentów prawa

2

WYKŁAD 8

klasyczny rachunek kwantyfikatorów

Piotr Łukowski, Wykład dla studentów prawa

3

Ludwik Borkowski, Elementy logiki formalnej, PWN, Warszawa 1977, s.154

(cienka książka)

Nie korzystamy z książki Ziembińskiego!

Piotr Łukowski, Wykład dla studentów prawa

4

Kwantyfikatory o ograniczonym zakresie

∀

Q(x)

P(x)

↔

∀

x (Q(x)

→

P(x))

Przykład
Każdy słoń ma trąbę = Każdy x jeśli x jest słoniem, to x ma trąbę.

∃

Q(x)

P(x)

↔

∃

x (Q(x)

∧

P(x))

Przykład
Pewien słoń ma trąbę = Pewien x jest słoniem i x ma trąbę.

Uwaga:
Ograniczenie kwantyfikatora działa jak określenie dziedziny. Wszystkie prawa rachunku
kwantyfikatorów zachowują swą ważność, gdy kwantyfikatory będą miały (konsekwentnie)
ograniczony zakres.

∀

x

∀

y =

∀

x,y

∃

x

∃

y =

∃

x,y

Piotr Łukowski, Wykład dla studentów prawa

5

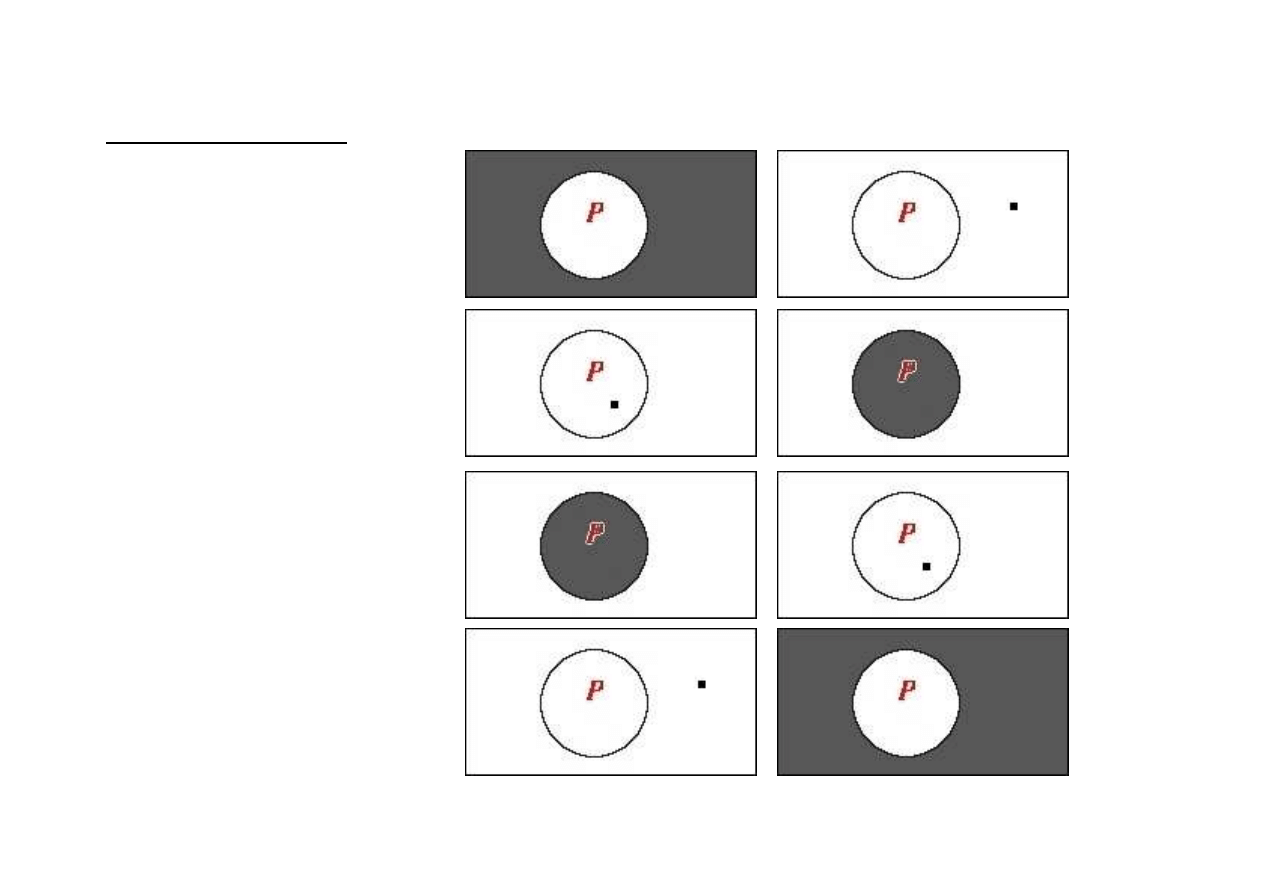
diagramy Venna

zdanie prawdziwe

zdanie fałszywe

∀

x P(x)

∃

x P(x)

∀

x

¬

P(x)

∃

x

¬

P(x)

Piotr Łukowski, Wykład dla studentów prawa

6

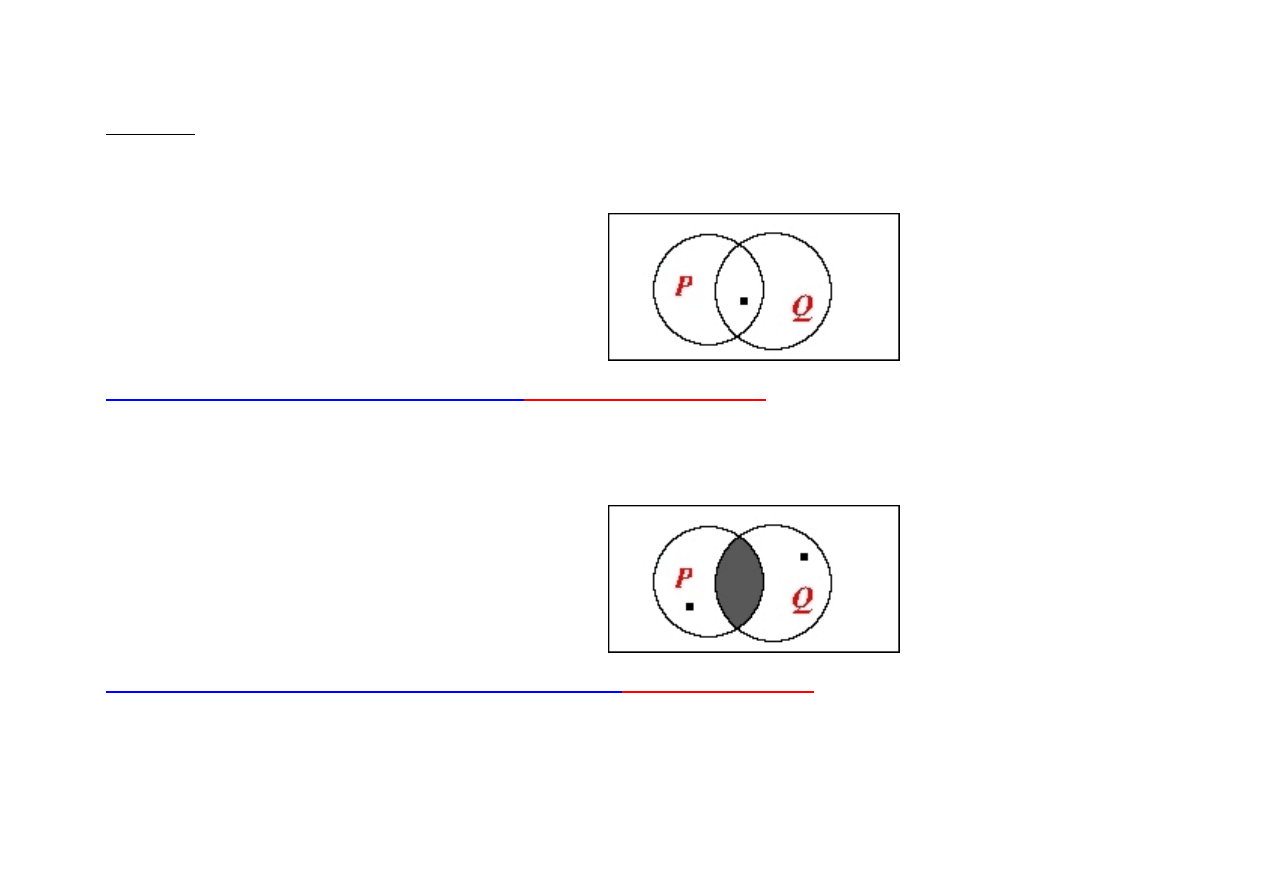
Zadanie Wykazać:

- niezawodność schematu rozkładu kwantyfikatora szczegółowego na koniunkcję

∃

x (P(x)

∧

Q(x))

→

∃

x P(x)

∧

∃

x Q(x)

Przykład potwierdzaj

ą

cy (weryfikuj

ą

cy)

(nie ma mocy dowodu)

: jeśli istnieje [jakaś] koszula w paski z

zielonymi guzikami, to istnieje [jakaś] koszula w paski i istnieje [jakaś] koszula z zielonymi guzikami.

- zawodność schematu

(

∃

x P(x)

∧

∃

x Q(x))

→

∃

x (P(x)

∧

Q(x))

Kontrprzykład (przykład obalaj

ą

cy, falsyfikuj

ą

cy)

(ma moc dowodu)

: jeśli istnieje jakaś matka i istnieje

jakiś ojciec, to nie znaczy że istnieje ktoś, kto jest jednocześnie ojcem i matką.

Piotr Łukowski, Wykład dla studentów prawa

7

Wyjaśnienie:

Pojedynczy przykład potwierdzający dany schemat nie jest dowodem na jego niezawodność,
gdyż poza nim może istnieć inny przykład, który ten schemat obali (przykład obalający, czyli
kontrprzykład). Siłę dowodu ma dopiero sytuacja, w której wszystkie możliwe przykłady byłyby
przykładami potwierdzającymi. Naturalnie, siłę dowodu obalającego niezawodność schematu
(czyli stwierdzającego jego zawodność) ma już jeden przypadek obalający.

Piotr Łukowski, Wykład dla studentów prawa

8

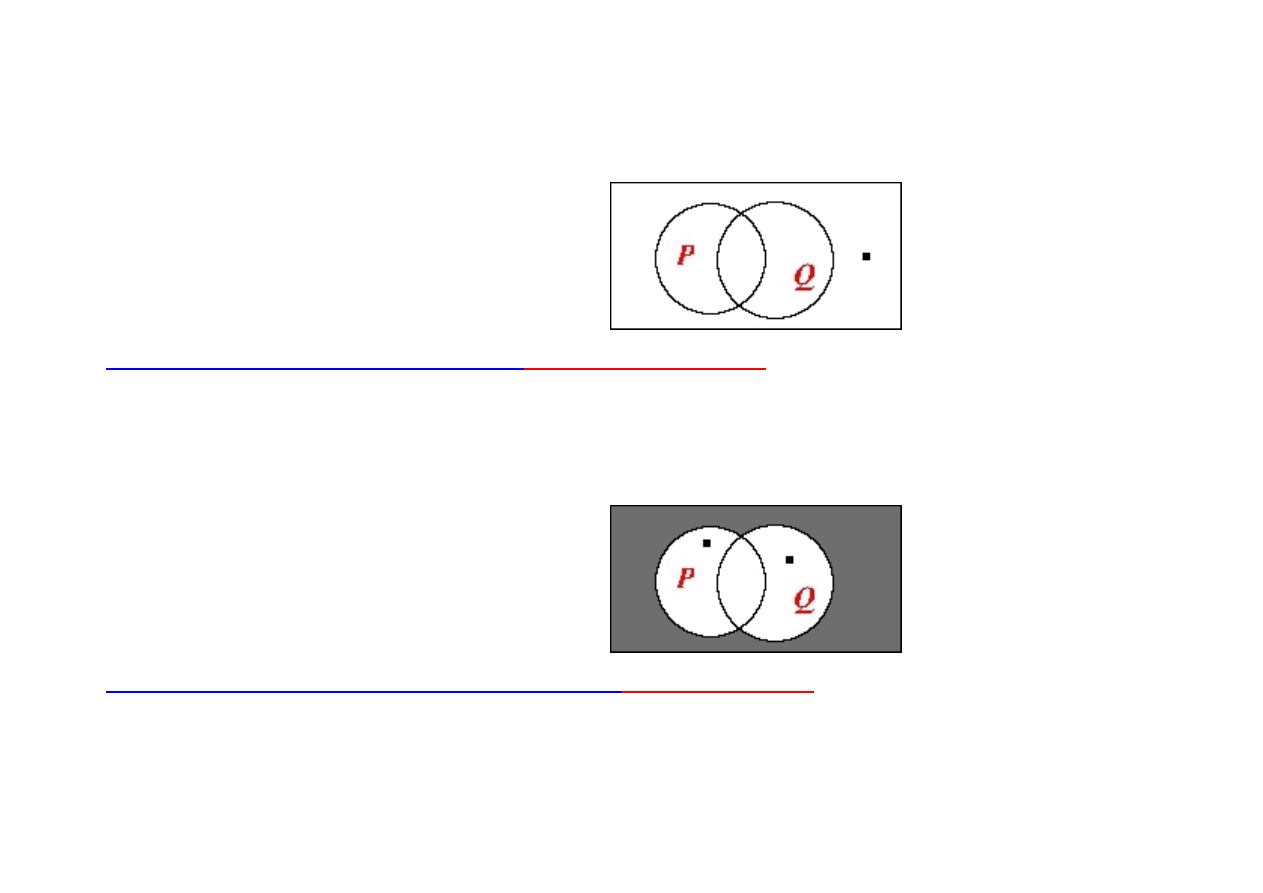
- niezawodność schematu wyciągania kwantyfikatora ogólnego przed alternatywę

(

∀

x P(x)

∨

∀

x Q(x))

→

∀

x (P(x)

∨

Q(x))

(załóżmy fałszywość wniosku)

Przykład potwierdzaj

ą

cy (weryfikuj

ą

cy)

(nie ma mocy dowodu)

: jeśli każda zebra ma paski lub każda

zebra ma cętki, to każda zebra ma paski lub cętki.

- zawodność schematu

∀

x (P(x)

∨

Q(x))

→

(

∀

x P(x)

∨

∀

x Q(x))

Kontrprzykład (przykład obalaj

ą

cy, falsyfikuj

ą

cy)

(ma moc dowodu)

: jeśli każdy dorosły człowiek jest

kobietą lub mężczyzną, to nie znaczy, że każdy dorosły człowiek jest kobietą lub każdy dorosły człowiek jest
mężczyzną (jeśli wszyscy dorośli ludzie są kobietami lub mężczyznami, to nie znaczy, że wszyscy dorośli
ludzie to kobiety lub wszyscy dorośli ludzie to mężczyźni).

Piotr Łukowski, Wykład dla studentów prawa

9

- niezawodność schematu rozkładania kwantyfikatora ogólnego na koniunkcję

∀

x (P(x)

∧

Q(x))

↔

(

∀

x P(x)

∧

∀

x Q(x))

Przykład potwierdzaj

ą

cy (weryfikuj

ą

cy)

(nie ma mocy dowodu)

: powiedzieć, że każda zebra ma paski i

kopyta, to to samo, co powiedzieć, że każda zebra ma paski i każda zebra ma kopyta.

- niezawodność schematu rozkładania kwantyfikatora szczegółowego na alternatywę

∃

x (P(x)

∨

Q(x))

↔

(

∃

x P(x)

∨

∃

x Q(x))

(rozważmy fałszywość jednej strony, potem

fałszywość drugiej strony)

Przykład potwierdzaj

ą

cy (weryfikuj

ą

cy)

(nie ma mocy dowodu)

: powiedzieć, że istnieje słoń co ma

trąbę lub skrzydła, to to samo, co powiedzieć, że istnieje słoń co ma trąbę lub istnieje słoń co ma skrzydła.

Piotr Łukowski, Wykład dla studentów prawa

10

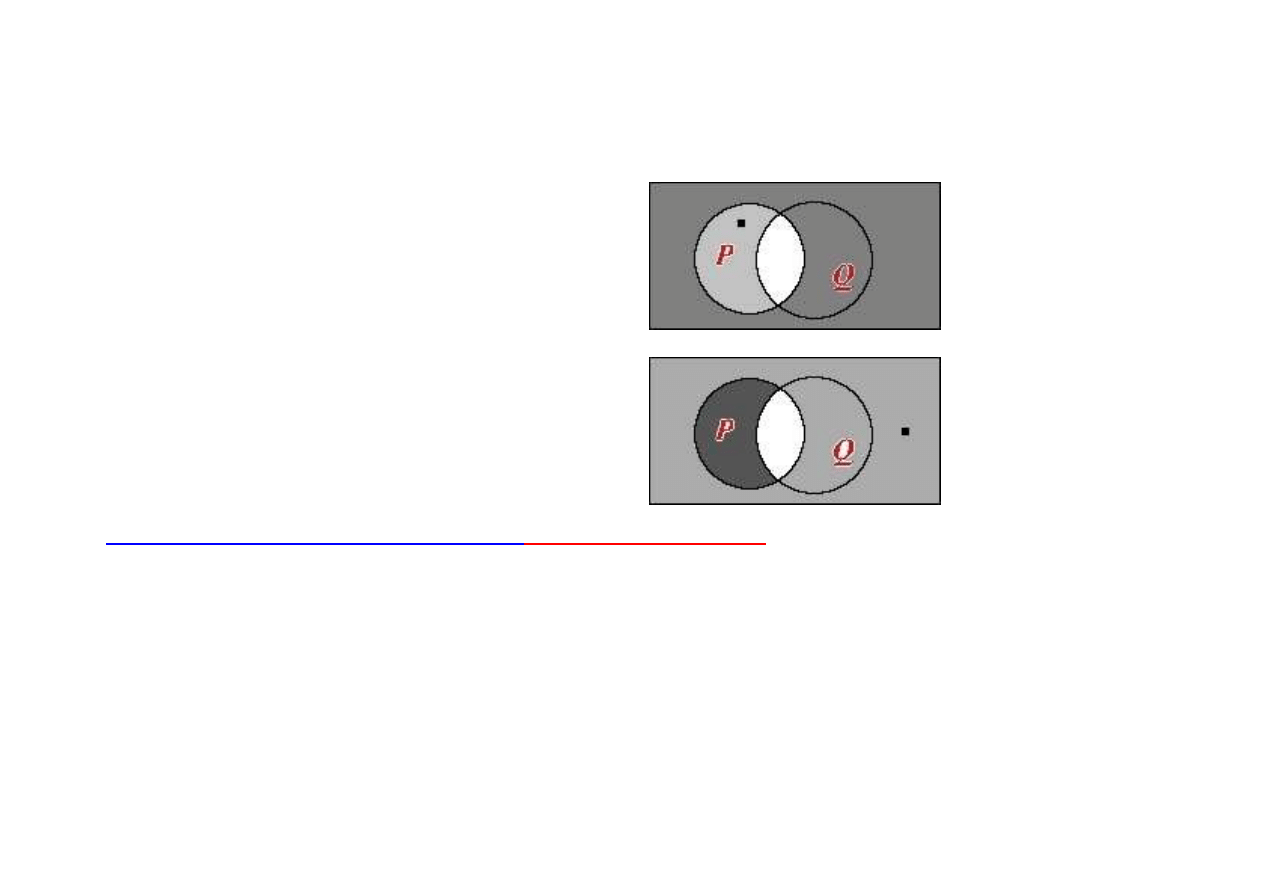
Przypomnienie:
tautologią klasycznego rachunku zdań jest

¬

(p

→

q)

↔

(p

∧

¬

q).

zdanie prawdziwe

zdanie fałszywe

∀

x (P(x)

→

Q(x))

Piotr Łukowski, Wykład dla studentów prawa

11

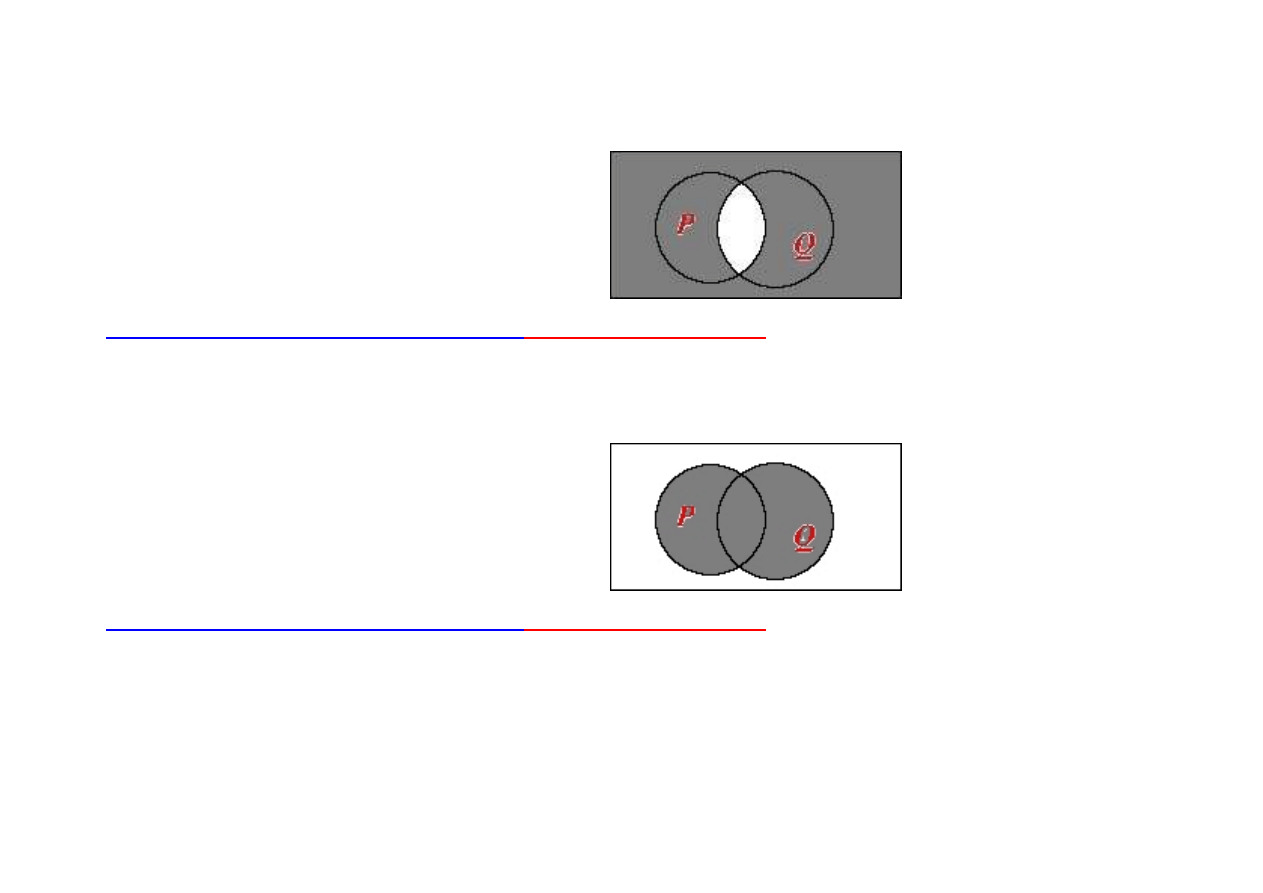
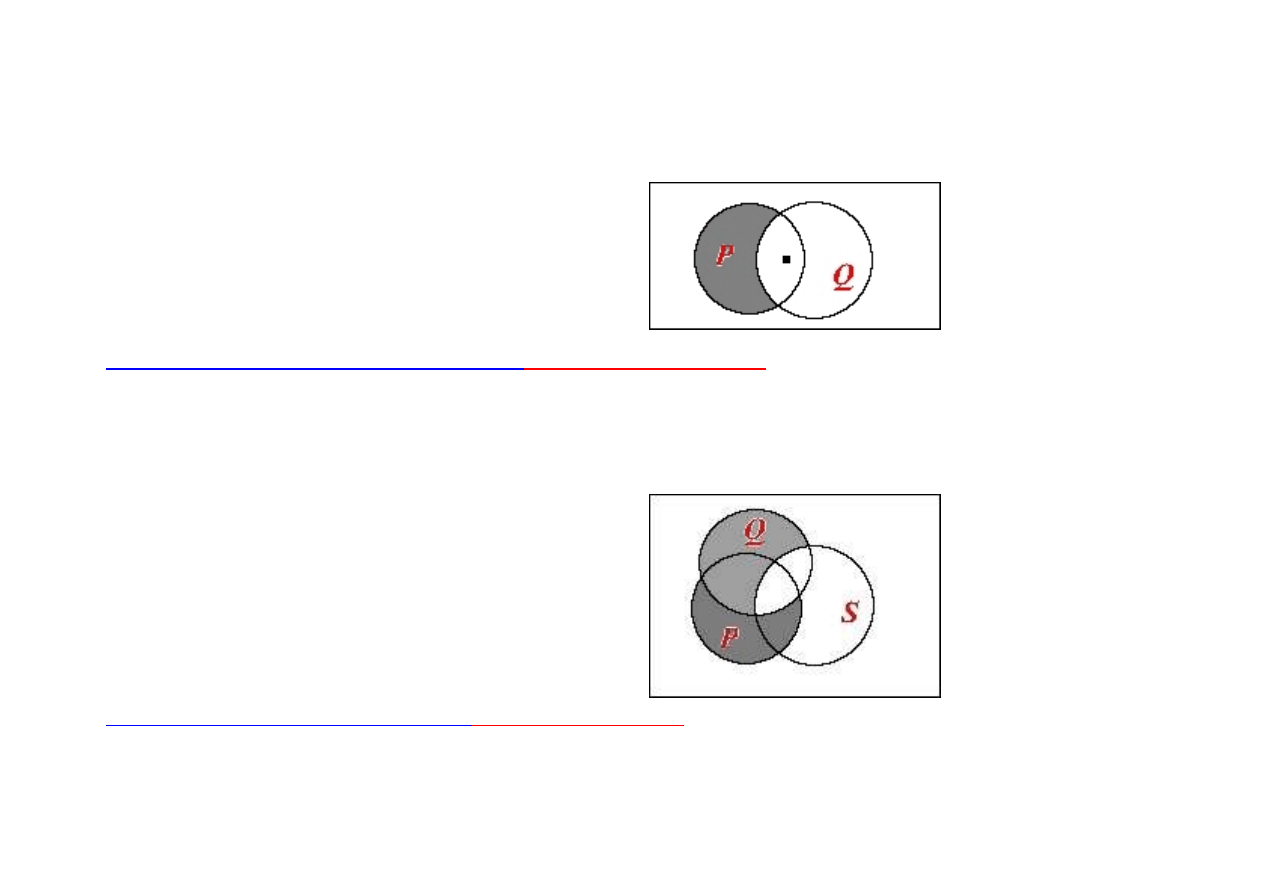
- niezawodność schematu rozkładania kwantyfikatora ogólnego na implikację

∀

x (P(x)

→

Q(x))

→

(

∀

x P(x)

→

∀

x Q(x))

(dowód nie wprost - zakładamy prawdziwość obu

przesłanek:

∀

x (P(x)

→

Q(x)) i

∀

x P(x); oraz fałszywość

wniosku

∀

x Q(x). Mamy wówczas dwa przypadki, tak jak

na rysunkach. W obu dochodzimy do sprzeczności - nie

może bowiem być tak, aby coś należało do zbioru

pustego.)

Przykład potwierdzaj

ą

cy (weryfikuj

ą

cy)

(nie ma mocy dowodu)

: jeśli każdy kto jest zaszczepiony

przeciwko ospie jest odporny na wirusa ospy, to jeśli każdy jest zaszczepiony przeciwko ospie, to każdy jest
odporny na wirusa ospy.

Piotr Łukowski, Wykład dla studentów prawa

12

- niezawodność schematu

∀

x (P(x)

→

Q(x))

→

(

∃

x P(x)

→

∃

x Q(x))

(załóżmy prawdziwość obu przesłanek

∀

x (P(x)

→

Q(x)) oraz

∃

x P(x)

- sylogizm hipotetyczny bezkoniunkcyjny)

Przykład potwierdzaj

ą

cy (weryfikuj

ą

cy)

(nie ma mocy dowodu)

: jeśli każdy kto jest zaszczepiony

przeciwko ospie jest odporny na wirusa ospy, to jeśli ktoś jest zaszczepiony przeciwko ospie, to ktoś jest
odporny na wirusa ospy.

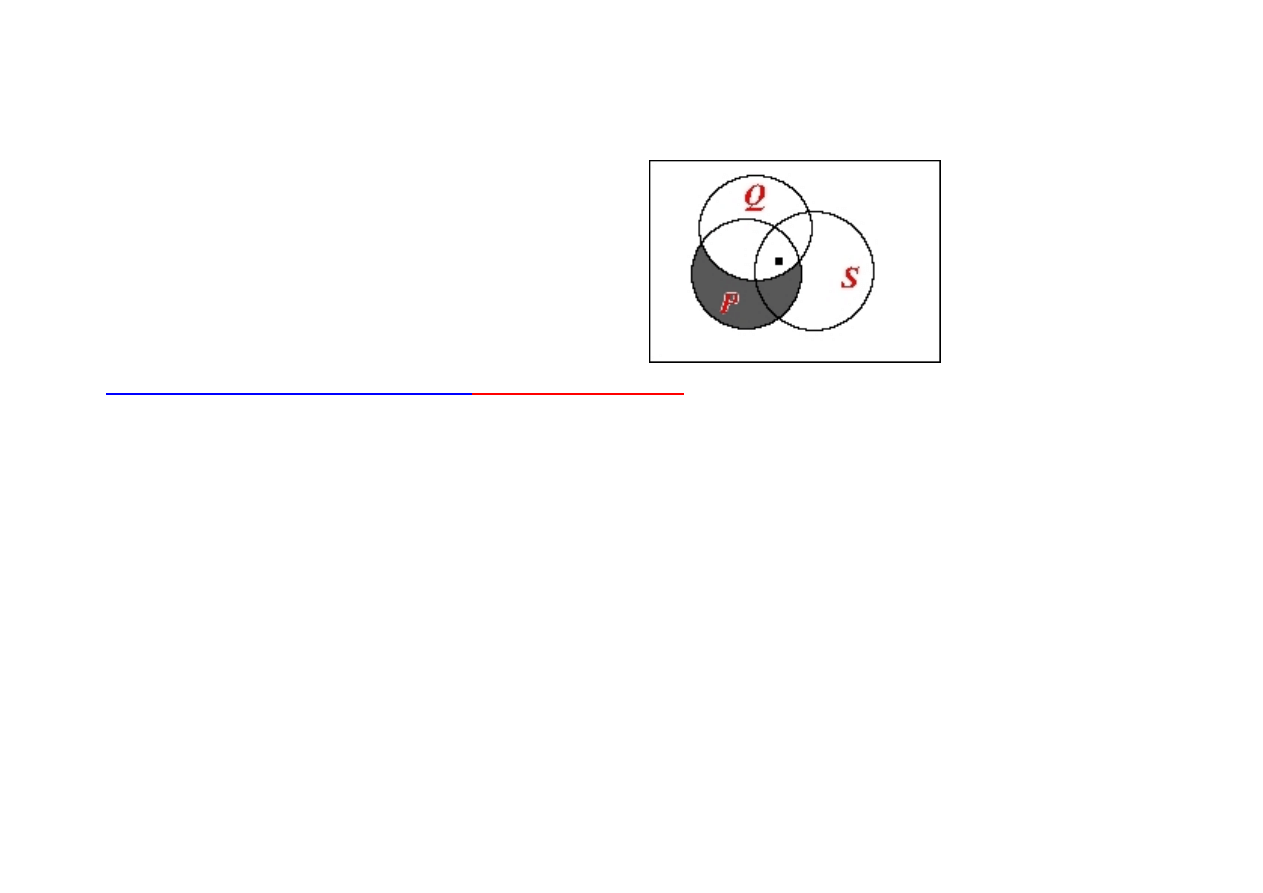
- niezawodność schematu

(

∀

x (P(x)

→

Q(x))

∧

∀

x (Q(x)

→

S(x)))

→

∀

x

(

P(x)

→

S(x))

Przykład potwierdzaj

ą

cy (weryfikuj

ą

cy)

(nie ma mocy dowodu)

: jeśli każdy zaszczepiony przeciwko ospie jest odporny

na wirusa ospy, i każdy odporny na wirusa ospy może bez ryzyka zachorowania kontaktować się z chorymi na ospę, to każdy
zaszczepiony przeciwko ospie może bez ryzyka zachorowania kontaktować się z chorymi na ospę.

Piotr Łukowski, Wykład dla studentów prawa

13

- niezawodność schematu

(

∀

x (P(x)

→

Q(x))

∧

∃

x (P(x)

∧

S(x)))

→

∃

x

(

Q(x)

∧

S(x))

Przykład potwierdzaj

ą

cy (weryfikuj

ą

cy)

(nie ma mocy dowodu)

: jeśli każdy zaszczepiony przeciwko ospie jest odporny

na wirusa ospy, i pewien kominiarz jest zaszczepiony przeciwko ospie, to pewien kominiarz jest odporny na wirusa ospy.

Piotr Łukowski, Wykład dla studentów prawa

14

Zamiana kwantyfikatorów

niezawodne schematy:

∀

x

∀

y P(x,y)

↔

∀

y

∀

x P(x,y)

∃

x

∃

y P(x,y)

↔

∃

y

∃

x P(x,y)

∃

x

∀

y P(x,y)

→

∀

y

∃

x P(x,y)

Przykłady potwierdzaj

ą

ce

:

Każdy każdemu wilkiem = Każdemu każdy wilkiem.
Ktoś kogoś kocha = Ktoś jest kochany przez kogoś.

(P(x,y) możemy tu czytać, albo jako „x kocha y”, albo „y jest kochany przez x”)

Jeśli ktoś jest ojcem każdego człowieka, to każdy człowiek ma ojca.

zawodny schemat:

∀

x

∃

y P(x,y)

→

∃

y

∀

x P(x,y)

Kontrprzykład

:

To że każdy kogoś kocha, nie implikuje tego, że ktoś jest kochany przez każdego.

Piotr Łukowski, Wykład dla studentów prawa

15

Identyczność

zwrotność identyczności

∀

x (x = x)

symetryczność identyczności

∀

x,y (x = y

→

y = x)

przechodniość identyczności

∀

x,y,z ((x = y

∧

y = z)

→

x = z)

zamienialność w każdym kontekście nazw tego samego obiektu
(prawo tożsamości Leibniza)

∀

x,y (P(x)

∧

x = y)

→

P(y))

∀

x,y (P(x)

∧

¬

P(y))

→

x

≠

y)

Uwaga:
Mówienie o dwóch (a więc w domyśle dwóch różnych) identycznych obiektach, to jak mówienie
o mniejszej lub większej połowie. Lepiej jest mówić (myśleć) o tym, że dwie różne nazwy a i b
oznaczają ten sam obiekt: więc zamiast „a i b są sobie równe (są identyczne)” lepiej jest mówić
„a jest tym samym co b”.

Identyczno

ść

jest trywialna!

(zachodzi mi

ę

dzy obiektem a nim samym)

Nietrywialn

ą

relacj

ą

jest podobie

ń

stwo, czyli identyczno

ść

pod jakim

ś

wzgl

ę

dem

(np. ze wzgl

ę

du na jak

ąś

cech

ę

lub przynale

ż

no

ść

do jakiej

ś

wspólnej klasy).

„P” jest tu dowolnym(!) predykatem,

który „gwarantuje” dowolność kontekstu

Piotr Łukowski, Wykład dla studentów prawa

16

Kwantyfikator jednostkowy

∃

!x P(x)

↔

(

∃

x P(x)

∧

(

∀

x,y (P(x)

∧

P(y)

→

x = y)))

Istnieje dokładnie jeden x taki, że P(x) wtedy i tylko wtedy, gdy istnieje x taki, że P(x) oraz dla każdego y,
jeśli P(y), to y jest x-em.

Negacja kwantyfikatora jednostkowego

¬∃

!x P(x)

↔

(

∀

x

¬

P(x)

∨

(

∃

x,y (P(x)

∧

P(y)

∧

x

≠

y)))