POLITECHNIKA BIAŁOSTOCKA

Wydział Budownictwa

i In

ż

ynierii

Ś

rodowiska

Katedra Ciepłownictwa

Instrukcja do zaj

ęć

laboratoryjnych

Temat

ć

wiczenia

:

WSPÓŁCZYNNIK STRAT NA DŁUGO

Ś

CI

Ć

wiczenie nr 5

Laboratorium z przedmiotu

IN

ś

YNIERIA PROCESOWA

Opracował:

dr in

ż

. Piotr Rynkowski

Białystok 2009

Kod:

Politechnika Białostocka

Ć

wiczenie nr 5

Katedra Ciepłownictwa

Współczynnik strat na długości

2/11

1.

Cel ćwiczenia.

Celem ćwiczenia jest zapoznanie się z metodą pomiaru współczynnika strat na długości

λλλλ

oraz wskazanie na zależność tego współczynnika od liczby Reynoldsa Re.

2. Podstawy teoretyczne.

Podczas przepływu cieczy lub gazu, następuje przemiana energii mechanicznej płynu na

energię cieplną, spowodowaną lepkością płynu. Ćwiczenie polega na określeniu spadku energii
mechanicznej dla ustalonego przepływu cieczy, prostoliniowym odcinkiem o stałej średnicy.

W ćwiczeniu energia potencjalna wysokości jest stała. Przyjmujemy, że energia kinetyczna

również jest stała, gdyż zakładamy, że profile prędkości są jednakowe. Spadek energii mechanicznej
przejawiać się będzie wyłącznie jako spadek ciśnienia wzdłuż przewodu.

Wielkość liniowych strat energii - spadku ciśnienia

∆∆∆∆

p przy przepływie zależna jest od

wielu czynników:

1)

parametrów geometrycznych rury:

−

ś

rednicy wewnętrznej d

w

,

−

długości l, na której występuje spadek ciśnienia,

−

chropowatości wewnętrznej powierzchni s,

2)

stałych fizycznych cieczy:

−

lepkości

µ,

−

gęstości

ρ

,

3)

wielkości charakteryzujących ruch płynu - stałej prędkości średniej v

ś

r

.

Zależność tą można zapisać:

p = f ( d

w

, l, s,

µ, ρ,

v

ś

r

)

Dla ustalonego przepływu cieczy rzeczywistej w rurociągach o dowolnym kształcie przekroju

poprzecznego, można wykazać, że zarówno dla przepływów laminarnych, jak i turbulentnych -
wysokość liniowych oporów hydraulicznych wzdłuż rurociągu wyrażana jest wzorem:

h

f

S v

A g

=

2

2

(1)

gdzie: f - bezwymiarowy współczynnik tarcia tarcia hydraulicznego,

S - pole pow. tarcia strumienia o ściany przewodu,
A - pole pow. przekroju poprzecznego,
v- średnia prędkość strumienia w przekroju poprzecznym.

Najczęściej stosowanym wzorem do określenia wysokości strat energii w przewodzie

kołowym o stałej średnicy d i długości L jest formuła (wyprowadzona ze wzoru (1)) Darcy-
Weisbacha:

h

l v

d g

=

λ

2

2

,

(2)

gdzie: l - długość rozważanego rurociągu,

d - średnica wewnętrzna przekroju poprzecznego rury,
g - przyspieszenie ziemskie.

Wzór nazywany jest wzorem Darcy-Weisbacha.

Elementem określającym wielkość strat ciśnienia jest współczynnik oporów liniowych

λ.

λ.

λ.

λ.

Politechnika Białostocka

Ć

wiczenie nr 5

Katedra Ciepłownictwa

Współczynnik strat na długości

3/11

Henry Philibert Gaspard Darcy

Julius Ludwig Weisbach

Henry Philibert Gaspard Darcy (1803-1858) – francuski uczony. Należy dodać, że rurka Prandtla została
opracowana (jako udoskonalenie wcześniejszego wynalazku francuskiego inżyniera Henri Pitota zwanego Rurką
Pitota) przez Ludwiga Prandtla oraz właśnie Henry Darcy’ego.

Julius Ludwig Weisbach (1806 -1871) – niemiecki matematyk i inżynier. Studiował razem z Carl’em
Friedrich’em Gauss’em w Göttingen.

Formułę (wzór 2) określił pierwszy Henry Darcy. Zmodyfikował ją Julius Weisbach, która wkrótce stała się
znana jako formuła Darcy-Weisbacha.

Wzór Darcy-Weisbacha nie jest jedynym, który określa opory na długości, lecz jest

niewątpliwie najczęściej stosowany.

W przypadku, gdy kształt przekroju poprzecznego przewodu jest inny niż kołowy, jako

liniowy wymiar charakteryzujący przekrój stosuje się promień hydrauliczny R

h

definiowany jako:

h

z

F

R

Q

=

(3)

gdzie: F – pole przekroju poprzecznego przewodu,

Q

z

– długość obwodu zwilżonego przewodu.

Podstawowym problemem związanym z zastosowaniem wzoru Darcy-Weisbacha jest

poprawne określenie wartości współczynnika strat na długości (oporów liniowych)

λλλλ

, który

uwzględnia rodzaj ruchu płynu oraz chropowatość materiału.

Z technicznego punktu widzenia każdy materiał wykazuje pewną chropowatość.

Chropowatość jest związana z rodzajem materiału i stopniem jego zużycia (np.: korozja przewodów).
Miarą chropowatość jest średnia wysokość nierówności na powierzchni przewodu, z uwzględnieniem
nierównomierności ich rozmieszczenia. Wielkość ta nazywana jest chropowatością bezwzględną k.
Ze względu na różne średnice przewodów wielkość chropowatości bezwzględnej nie jest miarodajna.
Za miarodajna uznaje się tzw.: chropowatość względną

εεεε

– odniesiona do liniowego wymiaru

charakteryzującego przekrój poprzeczny (wzór 5). Aby określić wpływ chropowatości na wysokość
strat na długości należy uwzględnić relację pomiędzy chropowatością bezwzględna k a grubością
warstwy przyściennej

δδδδ

1111

. Wpływ chropowatości na parametry przepływu uwidacznia się wówczas gdy

nierówności powierzchni przewodu wystają poza obręb warstwy przyściennej ( k >

δ

). Mówi się

wówczas o tzw. hydraulicznie szorstkiej. W przeciwnym wypadku ( k <

δ

) rurę nazywa się

hydraulicznie gładką.

1

„Zaproponowane przez Prandtla (1904) rozróżnienie przepływu płynu na dwa regiony - cienką warstwę tuż

przy ścianie (np. rury) oraz pozostałą część objętości płynu (rdzeń). Uprościło to matematyczne rozważania nad
przepływami oraz ułatwiło prowadzenie obliczeń dla oddziaływań płynu na ciała w nim zanurzone. Charakter
przepływu w tej warstwie może być laminarny lub burzliwy (w tym przypadku rozróżnia się dwie podwarstwy:
burzliwą oraz lepką). Przykładowa grubość warstewki przyściennej może wynosić dla w pełni rozwiniętego
przepływu burzliwego wody w rurze od setnych części do kilku milimetrów. Grubość tej warstwy spada wraz ze
wzrostem liczby Re.”
Ź

ródło: "http://pl.wikipedia.org/wiki/Warstwa_przy%C5%9Bcienna"

Politechnika Białostocka

Ć

wiczenie nr 5

Katedra Ciepłownictwa

Współczynnik strat na długości

4/11

Obszerne badania współczynnika

λ

przypadają na koniec XIX w. R. Mises wykazał, że

współczynnik liniowych oporów hydraulicznych (współczynnik tarcia wewnętrznego płynu)

λ

jest

zależnością funkcyjną :

λ =

f (Re,

ε

)

(4)

przy czym:

vd

4Q

Re

d

k

d

=

=

ν

π ν

ε =

(4)

(5)

gdzie:

ν

- kinematyczny współczynnik lepkości,

k - chropowatość bezwzględna wewnętrznych ścian rurociągu,

ε

- chropowatość względna wewnętrznej ściany rurociągu (tzw. chropowatość względna

rurociągu),

Re - liczba Reynoldsa.

Dla przepływów laminarnych, dla których liczba Reynoldsa zawiera się w przedziale

0

<

Re

≤

2 320, współczynnik strat tarcia

λλλλ

nie zależy od chropowatości przewodu i jest on opisany

zależnością analityczną:

λ =

64

Re

(6)

W zakresie liczb Reynoldsa 2320

≤

Re

≤

4000 przepływy cieczy w przewodach mają bardzo

niestabilny charakter (przejście laminarno-turbulentne), wobec czego jednoznaczne określenie
współczynnika strat tarcia

λλλλ

nie jest możliwe.

W przypadku przepływów turbulentnych Re

>

4 000, dominujących w urządzeniach

technicznych i sieciach hydraulicznych współczynnik strat tarcia

λ

jest złożoną funkcją wielu

czynników i wyznacza się go empirycznie.
W odniesieniu do przewodów o gładkich ściankach dobrym przybliżeniem opisującym wartości
współczynnika strat tarcia

λλλλ

w zakresie liczb Reynoldsa Re

≤

8*10

4

jest formuła Blasiusa [1],[3]:

λ =

0 316

0 25

.

Re

.

(7)

Wobec szczególnej zależności współczynnika strat tarcia

λλλλ

od charakteru przepływu cieczy

w przewodach wyróżnia się umownie szereg stref przepływu, w których jest on opisany zależnościami
analitycznymi (w obszarze przepływu laminarnego) i formułami empirycznymi (w obszarze
przepływu turbulentnego) w pewnych przedziałach liczb Reynoldsa (wykresy 1,2 i 3.):

Politechnika Białostocka

Ć

wiczenie nr 5

Katedra Ciepłownictwa

Współczynnik strat na długości

5/11

Przepływ laminarny

Przepływ laminarny

Strefa przej

ś

ciowa

Strefa przej

ś

cia

Przepływ burzliwy

Rura g

ładka

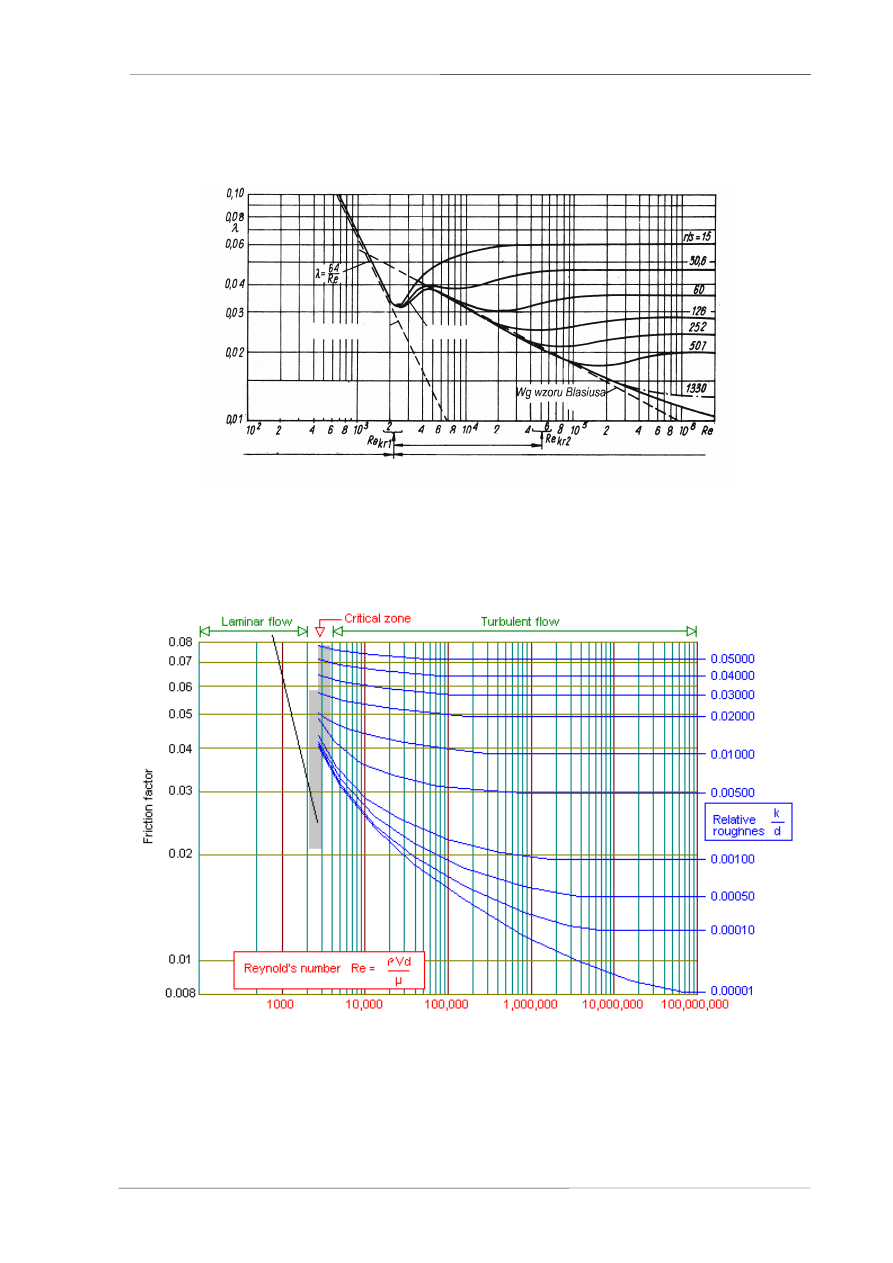
Wykres 1. Zależność współczynnika strat przepływu od chropowatości

względnej i liczby Reynoldsa - wg doświadczenia Nikuradse.

Wykres 2. Zależność współczynnika strat przepływu od chropowatości

względnej i liczby Reynoldsa - wg Moody’ego.

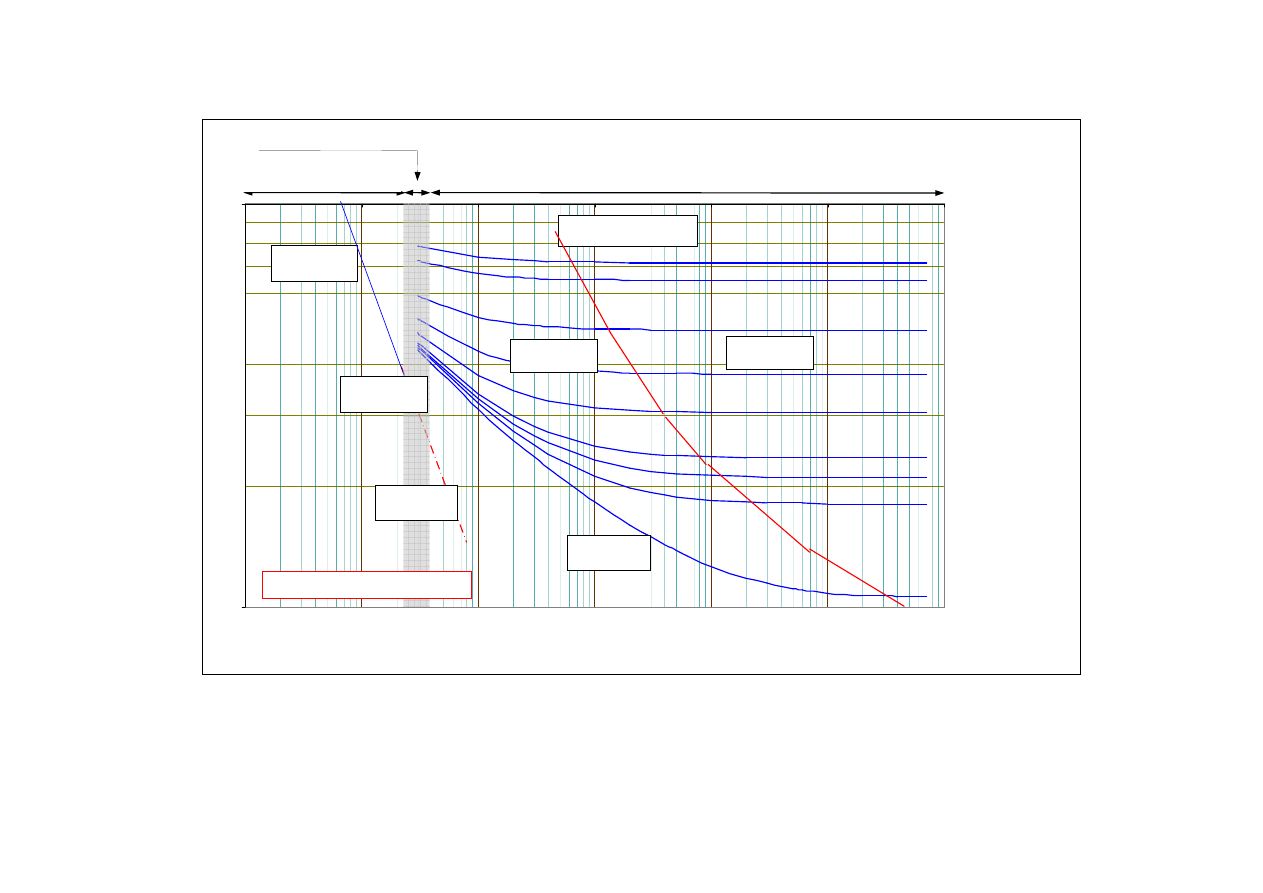
Wykres 3. Zależność współczynnika strat przepływu od chropowatości względnej i liczby Reynoldsa - według wzoru Colebrooka-White’a.

srefa

srefa

Re

e =

Wykres Colebrook'a-White'a

λ

= f(Re,

ε

)

0,01

0,10

1,0E+02

1,0E+03

1,0E+04

1,0E+05

1,0E+06

1,0E+07

1,0E+08

λλλλ

strefa I

strefa III

krzywa graniczna

strefa IV

c

h

ro

p

o

w

a

to

ś

ć

strefa V

w

s

p

ó

łc

z

y

n

n

ik

s

tr

a

t

n

a

d

łu

g

o

ś

c

i

λλλλ

Re

kr

strefa II

Liczba Reynoldsa Re

przepływy laminarne

przepływy turbulentne

przepływy niestabilne

Wykresy można podzielić na 5 stref:

−

strefa I - odpowiada przepływowi laminarnemu, wzór (1) Re

≤

2 320,

−

strefa II - stanowi strefę przepływów niestabilnych, dla 2 320 < Re

<

4 000

,

−

strefa III - przepływów turbulentnych w rurach hydraulicznie gładkich; rurę nazywamy
hydraulicznie gładką wtedy, gdy nierówności jej ścianek pokrywa całkowicie laminarna warstwa
przyścienna,

−

strefa IV - strefa mieszana lub strefa przejściowych przepływów turbulentnych w rurach
chropowatych, w miarę wzrostu liczby Re zmniejsza się coraz bardziej podwarstwa laminarna,
której grubość jest mniejsza od współczynnika chropowatości; w tym zakresie współczynnik
oporów liniowych zależy od liczby Re i współczynnika względnej chropowatości,

−

strefa V - przepływów turbulentnych, zanika zupełnie wpływ podwarstwy laminarnej. Krzywe
stają się prostymi równoległymi do osi odciętych; wynika z tego, że współczynnik

λ

przestaje być

zależny od liczby Re, a zależy wyłącznie od współczynnika chropowatości względnej

λ=

f(

ε).

Spośród przedstawionych na Międzynarodowym Kongresie Zaopatrzenia w Wodę w Paryżu

w 1952 r. najlepiej potwierdzoną zgodnością z wynikami pomiarów dla rur z chropowatością
naturalną charakteryzuje się wzór Colebrooka-White’a. Wzór ten zaproponowano i wprowadzono do
norm jako obowiązujący

w zastosowaniach

technicznych [1].

1

2

2 51

3 71

λ

λ

ε

= −

+













lg

,

Re

,

(8)

Wielkość współczynnika strat na długości określamy zależnością:

w

2
sr

2 p d

l v

∆

λ =

ρ

(6)

gdzie:

ρ

- gęstość wody.

2.

Budowa stanowiska.

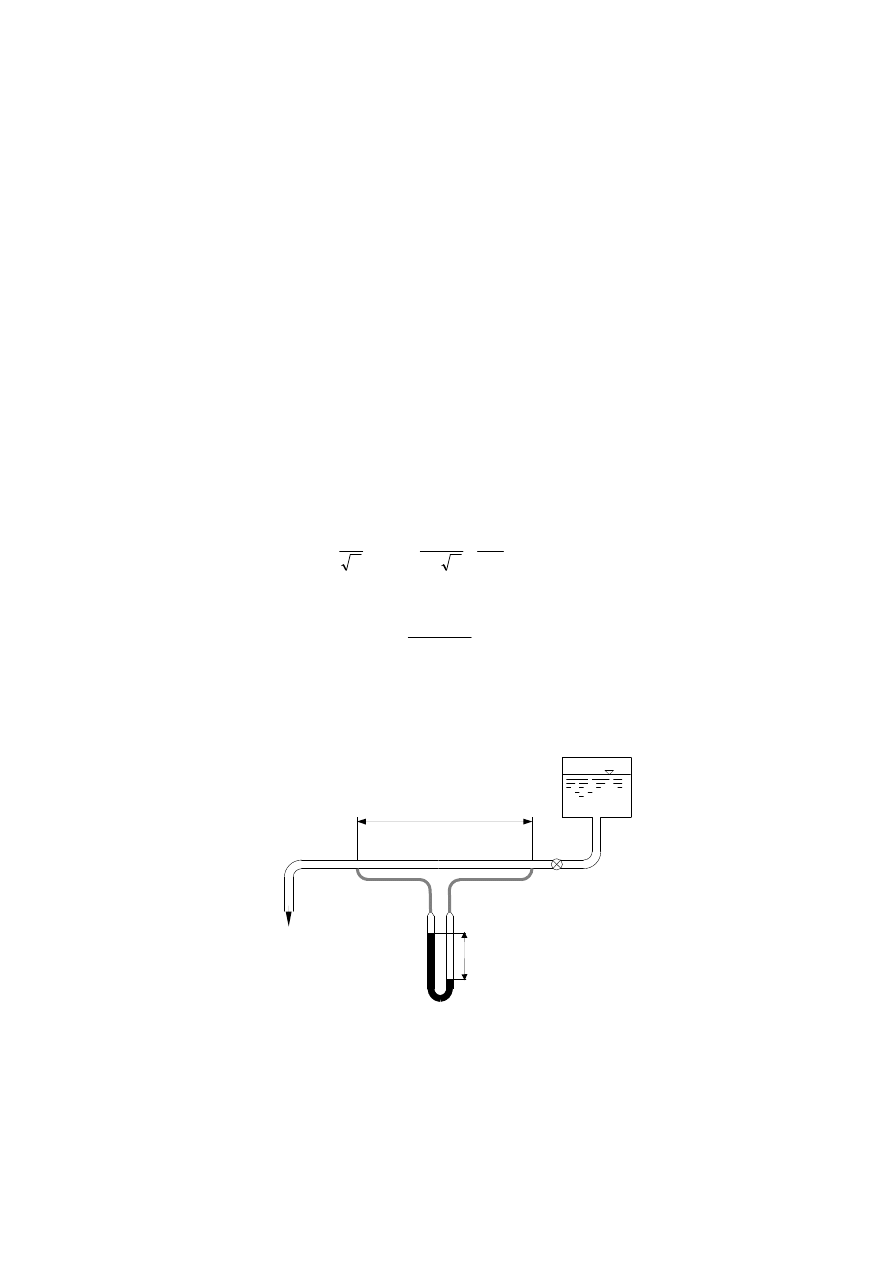
Rysunek 2. Szkic stanowiska.

L

H

rotametr

odpływ

manometr

Politechnika Białostocka

Ć

wiczenie nr 9

Katedra Ciepłownictwa

Współczynnik strat na długości

8/11

4.Wykonanie ćwiczenia.

1)

zmierzyć długość odcinka pomiarowego L rury stalowej i rury z tworzywa,
a)

ś

rednica wewnętrzna rury stalowej d

w

= 11 mm,

b)

ś

rednica wewnętrzna rury z tworzywa d

w

= 10 mm,

2)

po ustabilizowaniu się przepływu odczytać temperaturę wody,

3)

dla podanych przez prowadzącego czterech wielkości natężenia przepływu, odczytać na
manometrze różnicę ciśnień odpowiadającą odpowiednim przepływom w następujący sposób:
a)

nastawić zaworem na rotametrze A żądany pierwszy przepływ,

b)

odczytać różnicę ciśnień,

c)

zmienić wielkość przepływu do drugiej wartości,

d)

ponownie odczytać różnicę ciśnień,

e)

zmieniać natężenie przepływu do czwartej zadanej wielkości, za każdym razem
odczytując różnicę ciśnień

f)

czynności od a) do e) powtórzyć siedmiokrotnie.

g)

wartości skrajne odrzucić, do obliczeń przyjąć pozostałe pięć pomiarów dla każdej
wielkości natężenia przepływów.

4)

pomiar

λ

dla rury tworzywowej przeprowadzić jak w 2) dla rury stalowej.

5. Opracowanie wyników.

a)

obliczyć wielkości współczynników

λ

dla rury stalowej i tworzywowej oraz odpowiadające im

wartości liczb Reynoldsa.

b)

zaznaczyć na wykresie Colebrooka-White’a (wykres 3) punkty odpowiadające obliczonym
wielkościom

λ

i Re wraz z wartością wyznaczonego błędu.

c)

wnioski; dotyczyć mają m.in.: porównania stopnia zgodności wartości współczynników strat na
długości z danymi dostępnymi w literaturze, analiza poprawności wartości współczynników

λ

w poszczególnych strefach przepływów.

Politechnika Białostocka

Ć

wiczenie nr 9

Katedra Ciepłownictwa

Współczynnik strat na długości

9/11

d)

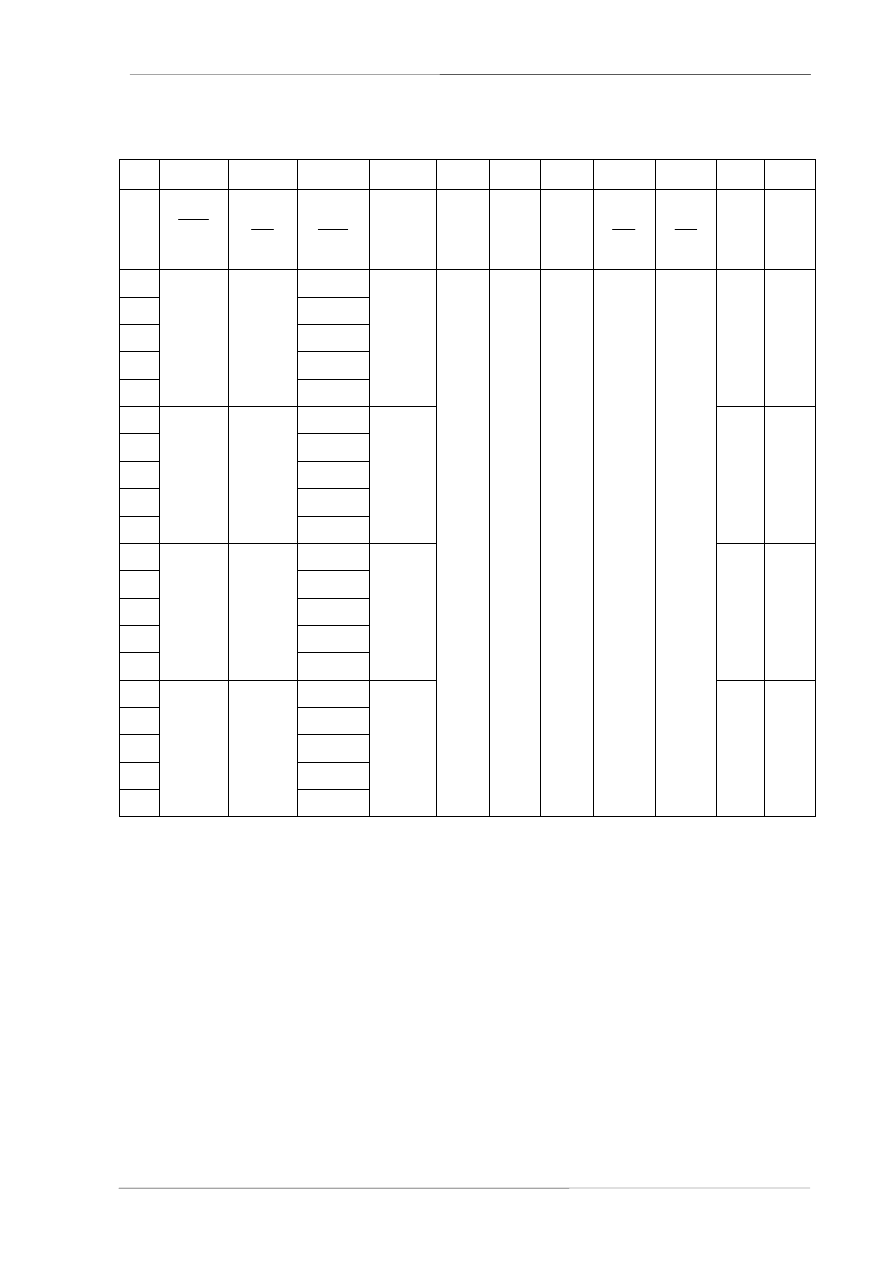
Wyniki pomiarów

Tabela [1]. Rura stalowa

Lp

Q

Q

∆∆∆∆

p

∆∆∆∆

p

sr

L

d

w

T

H2O

νννν

ρρρρ

λλλλ

Re

-

3

dm

h













3

m

s













2

kG

cm













[Pa]

[m]

[m]

[

o

C]

2

m

s













3

kg

m













[ - ]

[ - ]

1

2

3

4

5

1

2

3

4

5

1

2

3

4

5

1

2

3

4

5

0

,0

1

1

Podpis prowadzącego:

Data:

Politechnika Białostocka

Ć

wiczenie nr 9

Katedra Ciepłownictwa

Współczynnik strat na długości

10/11

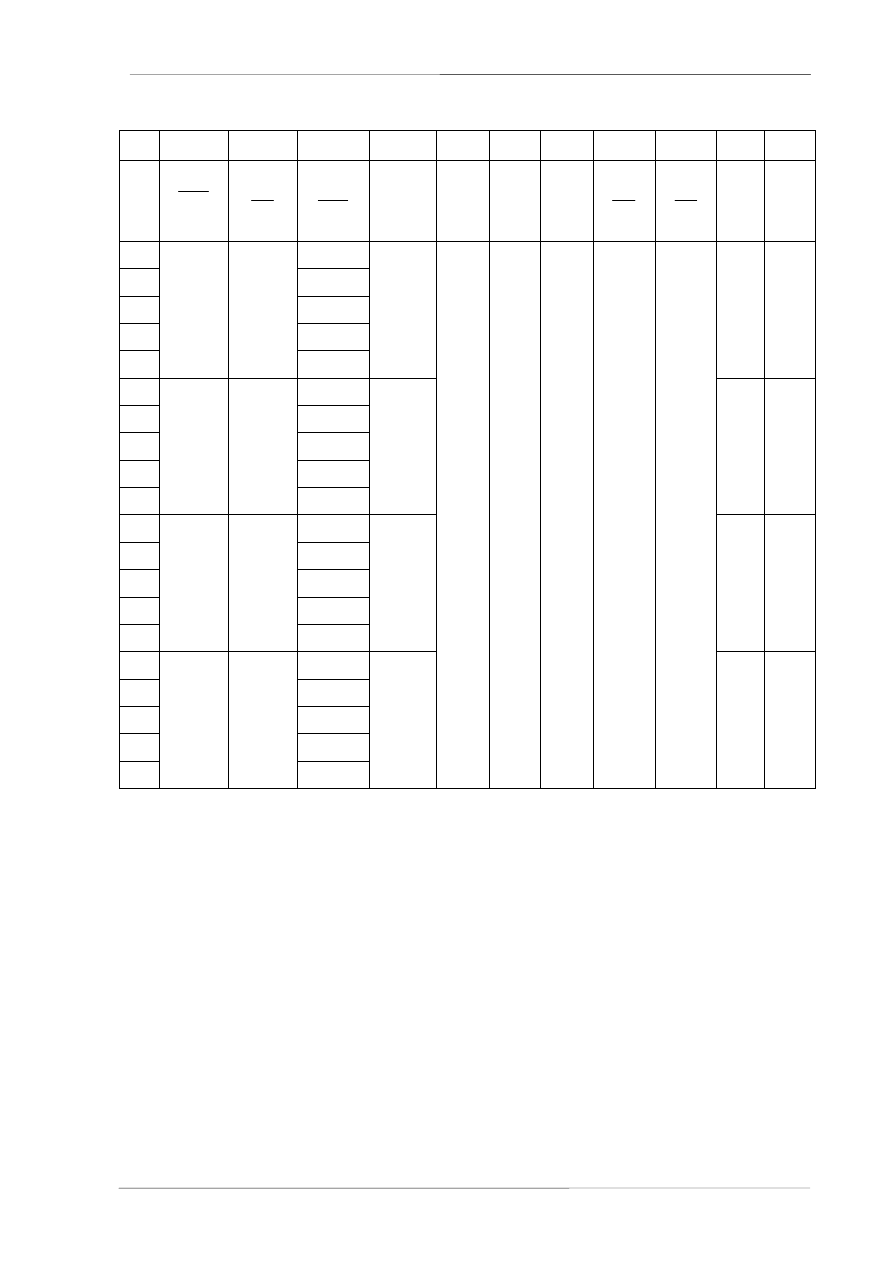
Tabela [2]. Rura z tworzywa

Lp

Q

Q

∆∆∆∆

p

∆∆∆∆

p

sr

L

d

w

T

H2O

νννν

ρρρρ

λλλλ

Re

-

3

dm

h













3

m

s













2

kG

cm













[Pa]

[m]

[m]

[

o

C]

2

m

s













3

kg

m













[ - ]

[ - ]

1

2

3

4

5

1

2

3

4

5

1

2

3

4

5

1

2

3

4

5

0

,0

1

0

Podpis prowadzącego:

Data:

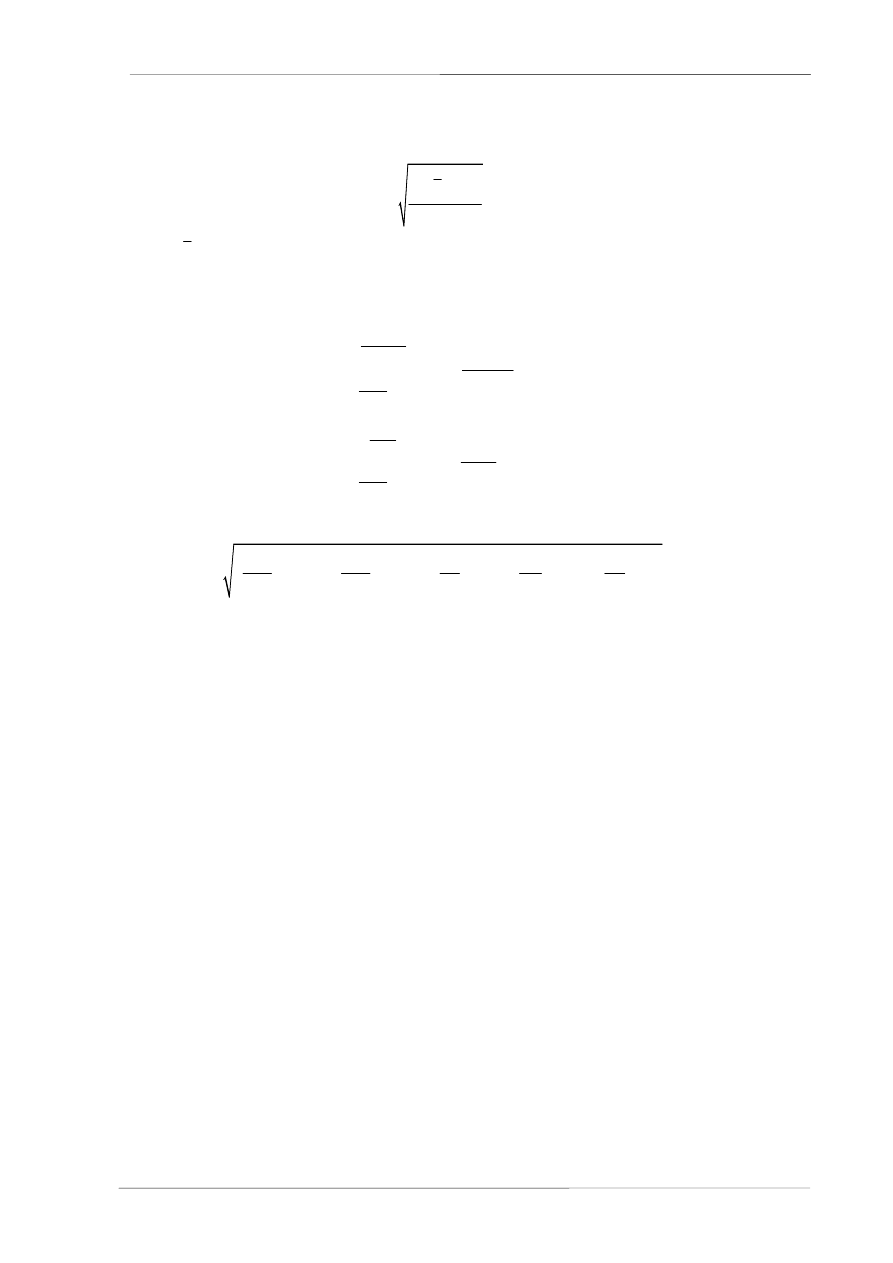
Politechnika Białostocka

Ć

wiczenie nr 9

Katedra Ciepłownictwa

Współczynnik strat na długości

11/11

Przeprowadzić analizę błędów pomiarów.

Odchylenie standardowe pojedynczego wyniku pomiarowego przeprowadzić w oparciu o równanie:

(

)

(

)

n

2

i

i 1

x

x

x

n n 1

=

−

δ =

−

∑

(6)

gdzie:

x

-średnia arytmetyczna z pomiarów danej wielkości,

x

i

- wartość uzyskana z pomiaru danej wielkości,

n – ilość pomiarów o jednakowej dokładności.

Układ równań do opracowania wyników wygląda następująco:

w

2

2

5
w

2

2
w

w

w

2
w

2 pd

c L

pd

4Q

8 Q L

c

d

cd

Re

4Q

Re

4Q

d

c

d

∆



λ =



ρ

π ∆



⇒

λ =



ρ



=



π





=



ν



⇒

=



π ν



=

π



(7)

Błąd wyznaczenia

δλ

wyznaczyć wykorzystując zależność (8):

2

2

2

2

2

w

w

p

d

Q

L

p

d

Q

L













∂λ

∂λ

∂λ

∂λ

∂λ









δλ =

δ∆

+

δ

+

δρ +

δ

+

δ





















∂∆

∂

∂ρ

∂

∂





















(8)

gdzie poszczególne zmienne jak w tabelach [1] i [2].

4. Wymagania BHP

[1.]

Do wykonywania ćwiczeń dopuszczeni są studenci, którzy zostali przeszkoleni (na pierwszych
zajęciach) w zakresie szczegółowych przepisów BHP obowiązujących w laboratorium.

[2.]

W trakcie wykonywania ćwiczeń obowiązuje ścisłe przestrzeganie przepisów porządkowych
i dokładne wykonywanie poleceń prowadzącego.

[3.]

Wszystkie czynności związane z uruchamianiem urządzeń elektrycznych należy wykonywać za
zgodą prowadzącego zajęcia.

[4.]

Zabrania się manipulowania przy urządzeniach i przewodach elektrycznych bez polecenia
prowadzącego.

6. Literatura uzupełniająca.

[1.]

Grabarczyk Cz.: Przepływy w przewodach zamkniętych. Metody obliczeniowe. Envirotech.
Poznań. 1997.

[2.]

Kołodziejczyk L., Mańkowski S., Rubik M., Pomiary w inżynierii sanitarnej, Arkady,
Warszawa 1980.

[3.]

Prosnak W. J.: Mechanika Płynów T1. PWN Warszawa 1970.

[4.]

Walden H. Mechanika Płynów, Wydawnictwa Politechniki Warszawskiej 1978.

[5.]

Johnson R.W.: The Handbook of Fluid Mechanics. CRC Press. Springer Heidelberg 1999.