CEL ĆWICZENIA
Celem ćwiczenia jest wyznaczenie wartości współczynników wnikania ciepła dla konwekcji swobodnej w przestrzeni nieograniczonej i konwekcji wymuszonej. Określa się także wpływ promieniowania cieplnego na wartość współczynnika wnikania ciepła dla konwekcji swobodnej oraz porównuje wartości wyznaczonych doświadczalnie i obliczonych teoretycznie współczynników wnikania ciepła dla konwekcji wymuszonej.
Opracowanie wyników pomiarów
Przykład obliczeń dla trzeciej serii pomiarowej.
I. KONWEKCJA WYMUSZONA
Na podstawie otrzymanych wartości pomiarowych obliczam strumień ciepła ze wzoru:
![]()
gdzie:
Vk - objętość kondensatu w zbiorniczku pomiarowym [m3]
ρk - gęstość kondensatu [kg/m3]
r - ciepło kondensacji pary wodnej pod ciśnieniem atmosferycznym [J/kg]
τ - czas gromadzenia kondensatu równy wartości średniej z trzech oznaczeń [s]
![]()
Obliczam średnią logarytmiczną różnicę temperatur:
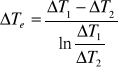
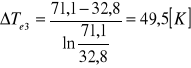
Obliczam doświadczalną wartość współczynnika wnikania ciepła ze wzoru:
![]()
gdzie:
q - strumień ciepła [W]
A - powierzchnia wymiany ciepła [m2] obliczona z wymiarów wymiennika
A = 0,2355 [m2]
![]()
Obliczam wartość liczby Nusselta:
![]()
gdzie:
d - średnica przewodu [m]
λ - przewodnictwo cieplne [W/m2⋅K], odczytane z tablic fizykochemicznych
![]()
ln (Nu3) = 1,615
Obliczam wartość liczby Reynoldsa:
![]()
u - średnia liniowa prędkość przepływu [m/s]
d - średnica przewodu [m]
ρ - gęstość płynu [kg/m3]
η - lepkość płynu [Pa⋅s]
![]()
ln (Re) = 3,847
Tabela wyników pomiarów:
Seria pomiarowa |
Prędkość [m/s] |
Wlot |
Wylot |
Czas średni [s] |
Objętość kondensatu [m3] |
|
|
Temperatura średnia [˚C] |
Temperatura średnia [˚C] |
|
|
I. |
5,36 |
27,2 |
65,2 |
220 |
0,00004 |
II. |
3,97 |
27,6 |
65,7 |
270 |
0,00004 |
III. |
2,82 |
28,9 |
67,2 |
332 |
0,00004 |
IV. |
7,77 |
27 |
64,3 |
175 |
0,00004 |
Tabela wyników obliczeń:
Seria |
q1 |
ΔT1 [K] |
ΔT2 [K] |
ΔTe [K] |
α |
I. |
410,18182 |
72,8 |
34,8 |
51,48363867 |
33,83111105 |
II. |
334,22222 |
72,4 |
34,3 |
50,99985516 |
27,82758182 |
III. |
271,80723 |
71,1 |
32,8 |
49,50502591 |
23,31421512 |
IV. |
515,65714 |
73 |
35,7 |
52,1453147 |
41,99086622 |
Seria |
Nu [-] |
Re [-] |
ln Nu |
ln Re |
I. |
59,7300689 |
13380,1383 |
1,776193 |
4,126460604 |
II. |
49,1306176 |
9910,28903 |
1,691352 |
3,996086321 |
III. |
41,162103 |
7039,5504 |
1,614498 |
3,847544922 |
IV. |
74,1364163 |
19396,208 |
1,870032 |
4,287716833 |
Przedstawienie wyników obliczeń za pomocą wykresu:
Z powyższego wykresu odczytuję współczynniki w równaniu:
![]()
A = 10(-0,6457) = 0,2261
b = 0,5865
II. KONWEKCJA SWOBODNA
I sposób:
Na podstawie otrzymanych wartości pomiarowych obliczam strumień ciepła ze wzoru:
![]()
![]()
Obliczam średnią logarytmiczną różnicę temperatur dla konwekcji swobodnej:
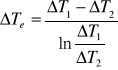
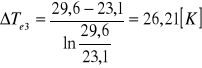
Obliczam doświadczalną wartość współczynnika wnikania ciepła ze wzoru:
![]()
A - powierzchnia wymiany ciepła [m2] dla konwekcji swobodnej
A = 0,9891 [m2]
![]()
Obliczam wartość współczynnika rozszerzalności objętościowej:
![]()
![]()
Obliczam wartość liczby Grashoffa:
![]()
g - przyspieszenie ziemskie [m/s2]
L - długość elementu grzejnego [m]
ν - współczynnik lepkości kinematycznej [m2/s]
![]()
Obliczam wartość liczby Nusselta korzystając z zależności:
![]()
ponieważ wartość iloczynu (Gr⋅Pr) jest z zakresu 2⋅107<(Gr⋅Pr)<1013
![]()
Obliczam teoretyczną wartość współczynnika wnikania:
![]()
![]()
II sposób:
Obliczam wartość temperatury powierzchni osłony izolacji wymiennika:
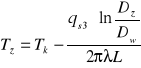
Tk - temperatura kondensacji pary [K]
Dw - średnica wewnętrzna izolacji [m]
Dz - średnica zewnętrzna izolacji [m]
λ - przewodnictwo właściwe cieplne izolacji [W/(mK)]
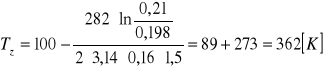
Obliczam strumień ciepła wymieniony na drodze promieniowania:
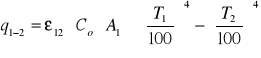
ε12 - zastępczy stopień czarności obu ciał
Co - techniczna stała promieniowania ciała doskonale czarnego [W/m2K4]
A - powierzchnia wymiany ciepła [m2] dla konwekcji swobodnej
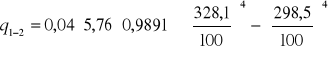
![]()
Obliczam wartość doświadczalnego współczynnika wnikania ciepła z równania bilansu:
![]()
![]()
Obliczam wartość współczynnika rozszerzalności objętościowej:
![]()
![]()
Obliczam wartość liczby Grashoffa:
![]()
g - przyspieszenie ziemskie [m/s2]
L - długość elementu grzejnego [m]
ν - współczynnik lepkości kinematycznej [m2/s]
![]()
Obliczam wartość liczby Nusselta korzystając z zależności:
![]()
ponieważ wartość iloczynu (Gr⋅Pr) jest z zakresu 2⋅107<(Gr⋅Pr)<1013
![]()
Obliczam teoretyczną wartość współczynnika wnikania:
![]()
![]()
Tabela wyników pomiarów:
Seria pomiarowa |
Temp. otoczenia [˚C] |
Temp. izolacji wew. [˚C] |
Temp. izolacji zew. [˚C] |
Czas napełniania kondensatu [s] |
Objętość kondensatu [m3] |
I. |
25,6 |
54,6 |
48,3 |
169 |
0,00002 |
II. |
25,4 |
55,3 |
48,1 |
180 |
0,00002 |
III. |
25,5 |
55,1 |
48,6 |
160 |
0,00002 |
Tabela wyników obliczeń:
Seria pomiarowa |
q
|
Tz [K] |
Gr [-] |
Pr [-] |
q1-2
|
q - q1-2
|
α2 |
I. |
266,9822 |
362,5771 |
10930201129 |
0,722 |
8,1313 |
258,8509 |
2,9215 |
II. |
250,6667 |
363,2141 |
11090514135 |
0,722 |
8,4049 |
242,2618 |
2,7150 |
III. |
282,0000 |
361,9908 |
11121845615 |
0,722 |
8,3162 |
273,6838 |
3,1093 |
Ocena zgodności wartości doświadczalnych i teoretycznych:
Wartość |
α1 |
α2 |
Tz [˚C] |
Doświadczalna |
10,875 |
3,109 |
55,100 |
Teoretyczna |
4,879 |
3,930 |
88,991 |
Zgodność |
- |
+ |
- |
Wnioski:
W wyniku przeprowadzonego doświadczenia otrzymaliśmy wartości współczynnika wnikania ciepła α, który dla konwekcji swobodnej (α2 ) jest zgodny z obliczoną wartością teoretyczną, natomiast dla konwekcji wymuszonej (α1 ) otrzymana wartość doświadczalna odbiega od obliczonej wartości teoretycznej, co może być spowodowane nieszczelną izolacją wymiennika ciepła. Wpływ na otrzymany wynik może mieć także niedokładność w przeprowadzaniu pomiarów. Porównując wartości α dla konwekcji swobodnej i wymuszonej otrzymaliśmy większe dla konwekcji wymuszonej, co jest zgodne z rzeczywistością.
Wynikiem obliczeń dla konwekcji wymuszonej są otrzymane wartości współczynników w równaniu: ![]()
A = 0,2261
b = 0,5865.
2
Wyszukiwarka
Podobne podstrony:
ciąg dalszy 10, SEMESTR 6, INŻYNIERIA PROCESOWA, sprawko 10
10. wyniki - moje, SEMESTR 6, INŻYNIERIA PROCESOWA, sprawko 10
kasia w, SEMESTR 6, INŻYNIERIA PROCESOWA, sprawko 10
SPRAWOZDANIE ĆW 10, Semestr 1, Fizyka
Karta sprawozdania cw 10
Sprawozdanie ćw 10
sprawozdanie ćw 10, PWR, optyka
Sprawozdanie destylacja, SGGW - WNoŻ, Inżynierskie 1st, Semestr 4, Inżynieria Procesowa, Ćwiczenia
sprawko opory, SGGW - WNoŻ, Inżynierskie 1st, Semestr 4, Inżynieria Procesowa, Ćwiczenia
Karta sprawozdania cw 10
Sprawozdanie z ćw 10 Interferencja
sprawozdanie automatyka2, studia, V semestr, Automatyka i robotyka, sprawko automaty stabilność
SPRAWOZDANIE CW 14, Semestr 1, Fizyka
inz-ustny, SGGW TECHNOLOGIA ŻYWNOŚCI I ŻYWIENIE CZŁOWIEKA, V Semestr, Inżynieria procesowa
Sprawozdanie ćw.4, Politechnika Wrocławska, Inżynieria Środowiska, I rok, Biologia i Ekologia, Spraw
Regulamin, Studia, UTP Ochrona środowiska, III rok, Semestr V, Inżynieria procesowa
więcej podobnych podstron