Tomasz Studzioski

Spis treści

1.

Elementarne algorytmy sortowania. Nieelementarne algorytmy sortowania (sortowanie

szybkie, sortowanie przez łączenie, sortowanie pozycyjne). .................................................................. 2

1.1.

Sortowanie przez selekcję(selection sort) ................................................................................... 2

1.2.

Przez wstawianie ......................................................................................................................... 3

1.3.

Sortowanie bąbelkowe ................................................................................................................ 4

1.4.

Sortowanie szybkie ...................................................................................................................... 5

1.5.

Sortowanie przez łączenie(scalanie) ........................................................................................... 7

1.6.

Sortowanie pozycyjne ................................................................................................................. 8

2.

Elementarne metody wyszukiwania................................................................................................ 9

2.1.

Wyszukiwanie liniowe/sekwencyjne ........................................................................................... 9

2.2.

Wyszukiwanie binarne ................................................................................................................ 9

2.3.

Wyszukiwanie max lub min ....................................................................................................... 10

2.4.

Naiwne wyszukiwanie wzorca w tekście ................................................................................... 11

2.5.

Alogorytm Karpa-Rabina ........................................................................................................... 11

3.

Tablice symboli i metody ich realizacji. ......................................................................................... 12

1. Elementarne algorytmy sortowania. Nieelementarne algorytmy

sortowania (sortowanie szybkie, sortowanie przez łączenie,
sortowanie pozycyjne).

Na początek omówię kilka podstawowych pojęd związanych z algorytmami (nit tylko sortowania):



Złożonośd obliczeniowa – liczba elementarnych operacji wykonywanych przez algorytm np.
liczba porównao



Złożonośd pamięciowa – wielkośd pamięci potrzebnej do przechowywania danych,oraz
pośrednich i koocowych i wyników obliczeo



Złożonośd czasowa – czas do wykonania algorytmu



Złożonośd pesymistyczna – przypadek najmniej korzystny



Klasy złożoności algorytmów:

 O(logn) - logarytmiczna
 O(n) - liniowa
 O(nlogn) - liniowo-logarytmiczna
 O(

) - kwadratowa

 O(

) - wielomianowa

 O(

) - wykładnicza

 O(n!) – silnia



Problem sortowania

Dany jest ciąg e(1),...,e(n), którego elementy należą do pewnego liniowo uporządkowanego

zbioru <E,<= >. Znaleźd taką permutację

,...,

liczb 1,...,n by e(

)<=...<=e(

).Algorytmy

rozwiązywania tego problemu będziemy nazywali algorytmami sortowania.



Bez względu na konkretne algorytmy, sortowanie można sklasyfikowad niezależne na
pewne kategorie:

 adaptacyjne (zmienia swoje działanie w zależności od układu elementów

sortowanego zbioru) i

nieadaptacyjne (działa tak samo niezależnie od układu

element

ów sortowanego zbioru),

 wewnętrzne (ma dostęp do całego sortowanego zbioru) i zewnętrzne (ma

dost

ęp do sortowanego zbioru blokami),

 bezpośrednie (stosowane przy małych elementach; operacja wstawiania

odbywa si

ę na elementach) i pośrednie (stosowne przy dużych elementach;

operacja wstawiania odbywa si

ę na wskaźnikach do elementów),

 stabline i niestabilne – dotyczą sortowania elementów o dwóch kluczach.

Sortowanie stabilne, to takie, kt

óre sortuje wg jednego klucza elementy

posortowane wcze

śniej wg drugiego klucza, zachowując względną kolejnośd

wzgl

ędem drugiego klucza.

Przyjęło się mówid że elementarne metody sortowania to te których czas działania jest równy

Zaliczają się do nich następujące algorytmy sortowania :

1.1.

Sortowanie przez selekcję(selection sort)

Jest nieadaptacyjne, wewnętrzne i stabilne oraz nie wymaga dodatkowej pamięci. Jego czas

działania jest określony z góry przez O(

– dokładnie algorytm wykonuje n (

) porównao

i n−1 zamian. Sortowanie to jest najlepsze, spośród innych elementarnych, do sortowania
elementów o małych kluczach i dużych polach, ponieważ wykonuje najmniej wstawieo.
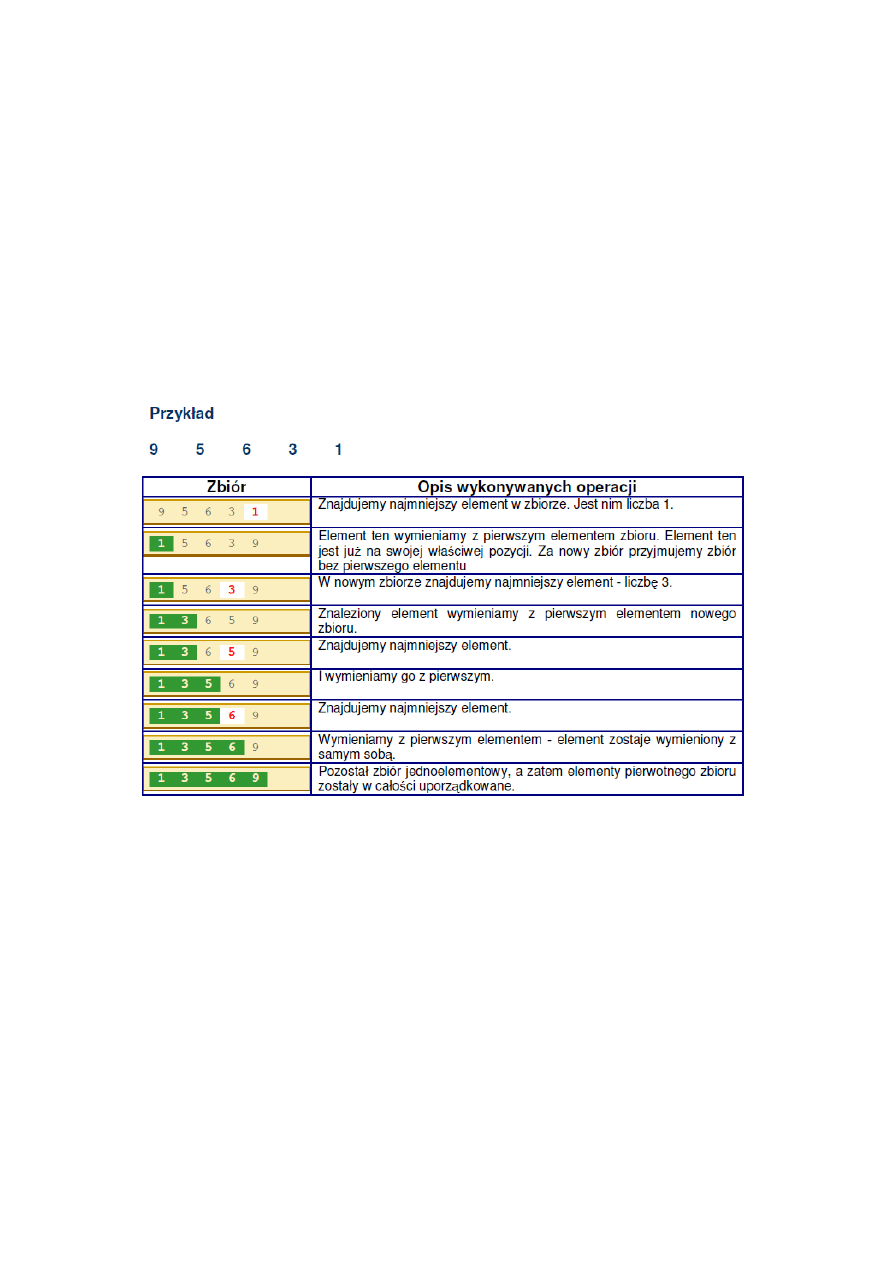
Poniżej sposób działania algorytmu (i – indeks, r – rozmiar tablicy, T – tablica):

1. i := 1;
2. jeśli i <= r, to idź dalej, w przeciwnym wypadku koniec;
3. znajdź najmniejszy element na przedziale T[i..r];
4. zamieo i-ty element z najmniejszym elementem;
5. i := i + 1; przejdź do 2.

W pierwszym przebiegu algorytm znajduje najmniejszy element w tablicy i zamienia go
z pierwszym. W drugim przebiegu algorytm znajduje najmniejszy element w podtablicy [2..r]
i zamienia go z drugim. I tak aż do zamiany r-tego elementu z r-1 elementem.

1.2.

Przez wstawianie

Sortowanie przez wstawienie (insertion sort) to algorytm, którego czas działania wynosi O(

). Jest

on skuteczny dla małej ilości danych. Jest to jeden z prostszych i jeden z bardziej znanych algorytmów
sortowania. Jest on stabilny i nie wymaga dodatkowej pamięci (działa w miejscu). Najważniejszą
operacją w opisywanym algorytmie sortowania jest wstawianie wybranego elementu na listę
uporządkowaną. Zasady są następujące:

1) Na początku sortowania lista uporządkowana zawiera tylko jeden, ostatni element

zbioru.Jednoelementowa lista jest zawsze uporządkowana.

2) Ze zbioru zawsze wybieramy element leżący tuż przed listą uporządkowaną. Element ten

zapamiętujemy w zewnętrznej zmiennej. Miejsce, które zajmował, możemy potraktowad jak
puste.

3) Wybrany element porównujemy z kolejnymi elementami listy uporządkowanej.

4) Jeśli natrafimy na koniec listy, element wybrany wstawiamy na puste miejsce - lista rozrasta

się o nowy element.

5) Jeśli element listy jest większy od wybranego, to element wybrany wstawiamy na puste

miejsce - lista rozrasta się o nowy element.

6) Jeśli element listy nie jest większy od wybranego, to element listy przesuwamy na puste

miejsce. Dzięki tej operacji puste miejsce wędruje na liście przed kolejny element.
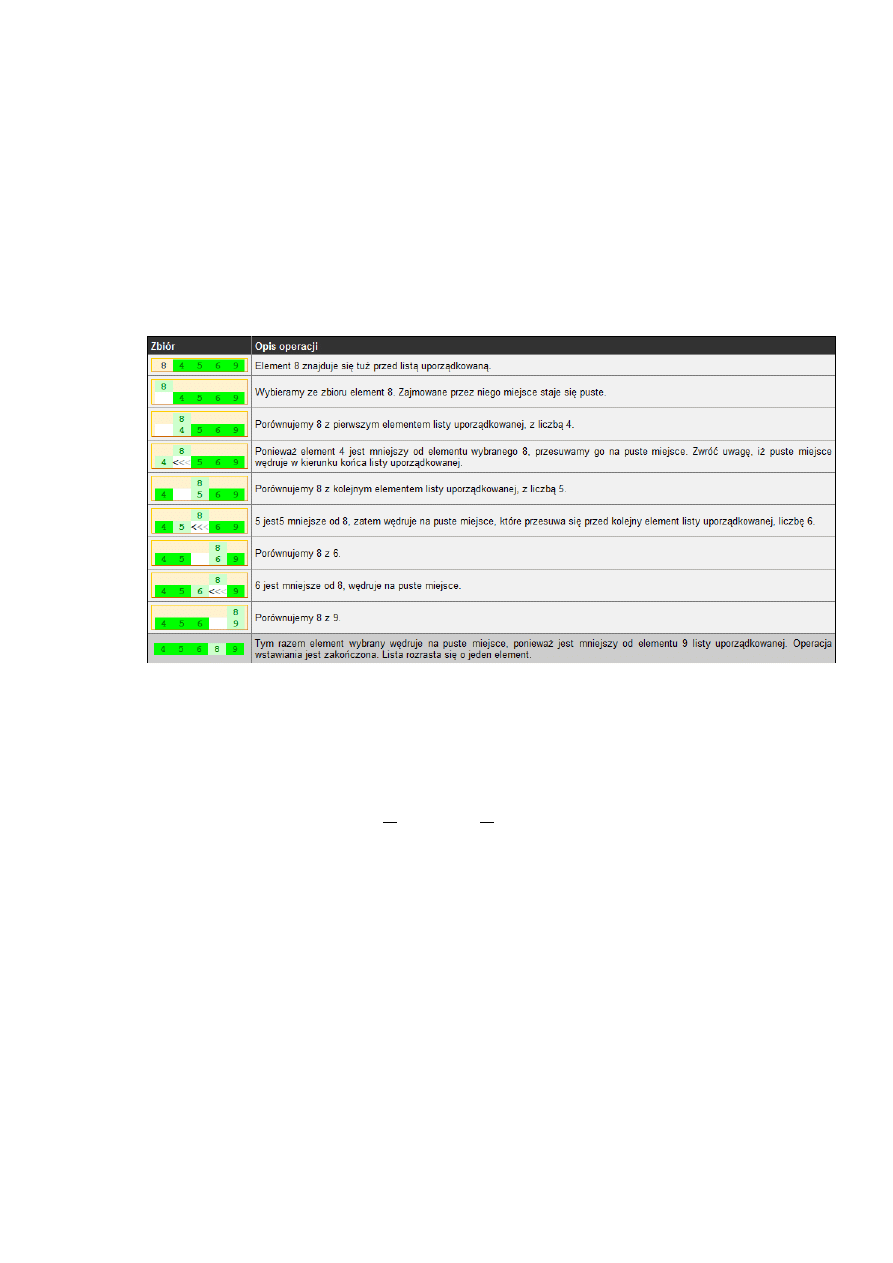
Kontynuujemy porównywanie, aż wystąpi sytuacja z punktu 4 lub 5.

Przykład dla zbioru {8 4 5 6 9}.

1.3.

Sortowanie bąbelkowe

Jest to algorytm nieadaptacyjny, wewnętrzny i stabilny oraz nie wymagający dodatkowej pamięci.
Jego czas działania jest określony z góry przez wynosi O(

– algorytm wykonuje

w najgorszym i średnim przypadku około

porównao i

zamian. Zasada działania opiera się na

cyklicznym porównywaniu par sąsiadujących elementów i zamianie ich kolejności w przypadku
niespełnienia kryterium porządkowego zbioru. Operację tę wykonujemy dotąd, aż cały zbiór zostanie
posortowany.

Lista kroków
1:

Dla j = 1,2,...,n - 1: wykonuj Krok 2

2:

Dla i = 1,2,...,n - 1: jeśli d[i] > d[i + 1], to d[i] ↔ d[i + 1]

3:

Zakoocz

gdzie:
n- liczba elementów w sortowanym zbiorze
d[ ]- zbiór n-elementowy, który będzie sortowany. Elementy zbioru mają indeksy od 1 do n.


Jako przykład działania algorytmu sortowania bąbelkowego posortujemy przy jego pomocy 5-cio
elementowy zbiór liczb ,5 4 3 2 1-

Do „nieelementarnych” algorytmów sortowania zaliczamy :

1.4.

Sortowanie szybkie

Algorytm sortowania szybkiego opiera się na strategii "dziel i zwyciężaj" (ang. divide and conquer),
którą możemy krótko scharakteryzowad w trzech punktach:



DZIEL - problem główny zostaje podzielony na podproblemy



ZWYCIĘŻAJ - znajdujemy rozwiązanie podproblemów



POŁĄCZ - rozwiązania podproblemów zostają połączone w rozwiązanie problemu głównego

Idea sortowania szybkiego jest następująca:



DZIEL:

najpierw sortowany zbiór dzielimy na dwie części w taki sposób, aby wszystkie elementy

leżące w pierwszej części (zwanej lewą partycją) były mniejsze lub równe od wszystkich
elementów drugiej części zbioru (zwanej prawą partycją).



ZWYCIĘŻAJ :

każdą z partycji sortujemy rekurencyjnie tym samym algorytmem.



POŁĄCZ :

połączenie tych dwóch partycji w jeden zbiór daje w wyniku zbiór posortowany.

W przypadku typowym algorytm ten jest najszybszym algorytmem sortującym z klasy złożoności
obliczeniowej O(n log n) - stąd pochodzi jego popularnośd w zastosowaniach. Musimy jednak
pamiętad, iż w pewnych sytuacjach (zależnych od sposobu wyboru piwotu oraz niekorzystnego
ułożenia danych wejściowych) klasa złożoności obliczeniowej tego algorytmu może się degradowad
do O(n2), co więcej, poziom wywołao rekurencyjnych może spowodowad przepełnienie stosu i
zablokowanie komputera. Z tych powodów algorytmu sortowania szybkiego nie można stosowad
bezmyślnie w każdej sytuacji tylko dlatego, iż jest uważany za jeden z najszybszych algorytmów

sortujących - zawsze należy przeprowadzid analizę możliwych danych wejściowych właśnie pod
kątem przypadku niekorzystnego.

Dla przykładu podzielimy na partycje zbiór:, 7 2 4 7 3 1 4 6 5 8 3 9 2 6 7 6 3 -

Po zakooczeniu podziału na partycje wskaźnik j wyznacza pozycję piwotu. Lewa partycja zawiera
elementy mniejsze od piwotu i rozciąga się od początku zbioru do pozycji j - 1. Prawa partycja
zawiera elementy większe lub równe piwotowi i rozciąga się od pozycji j + 1 do kooca zbioru.

1.5.

Sortowanie przez łączenie(scalanie)

Jest nieadaptacyjne, zewnętrzne i stabilne oraz wymaga dodatkowej pamięci

proporcjonalnej do n. Jego czas działania jest określony z góry przez O(n log(n)) . Sortowanie
przez scalanie jest nieadaptacyjne, ale jest za to relatywnie szybkie niezależnie od układu danych.
W związku z tym algorytm ten stosuje się, gdy jednocześnie ważna jest szybkośd algorytmu i nie
akceptowana jest wydajnośd najgorszego przypadku innych sortowao, a do tego możemy jeszcze
pozwolid sobie na poświęcenie trochę pamięci na operację sortownia.

Ideą działania algorytmu jest dzielenie zbioru danych na mniejsze zbiory, aż do uzyskania n

zbiorów jednoelementowych, które same z siebie są posortowane , następnie zbiory te są łączone w
coraz większe zbiory posortowane, aż do uzyskania jednego, posortowanego zbioru n-
elementowego. Etap dzielenia nie jest skomplikowany, dzielenie następuje bez sprawdzania
jakichkolwiek warunków. Dzięki temu, w przeciwieostwie do algorytmu „sortowania szybkiego”,
następuje pełne rozwinięcie wszystkich gałęzi drzewa. Z kolei łączenie zbiorów posortowanych
wymaga odpowiedniego wybierania poszczególnych elementów z łączonych zbiorów z
uwzględnieniem faktu, że wielkośd zbioru nie musi byd równa (parzysta i nieparzysta ilośd
elementów), oraz tego, iż wybieranie elementów z poszczególnych zbiorów nie musi następowad
naprzemiennie, przez co jeden zbiór może osiągad swój koniec wcześniej niż drugi. Robi sie to w
następujący sposób. Kopiujemy zawartośd zbioru głównego do struktury pomocniczej. Następnie,
operując wyłącznie na kopii, ustawiamy wskaźniki na początki kolejnych zbiorów i porównujemy
wskazywane wartości. Mniejszą wartośd wpisujemy do zbioru głównego i przesuwamy odpowiedni
wskaźnik o 1 i czynności powtarzamy, aż do momentu, gdy jeden ze wskaźników osiągnie koniec
zbioru. Wówczas mamy do rozpatrzenia dwa przypadki, gdy zbiór 1 osiągnął koniec i gdy zbiór 2
osiągnął koniec. W przypadku pierwszym nie będzie problemu, elementy w zbiorze głównym są już
posortowane i ułożone na właściwych miejscach. W przypadku drugim trzeba skopiowad pozostałe
elementy zbioru pierwszego po kolei na koniec. Po zakooczeniu wszystkich operacji otrzymujemy
posortowany zbiór główny.

Przykładowy przebieg algorytmu ukazany jest na schemacie poniżej:

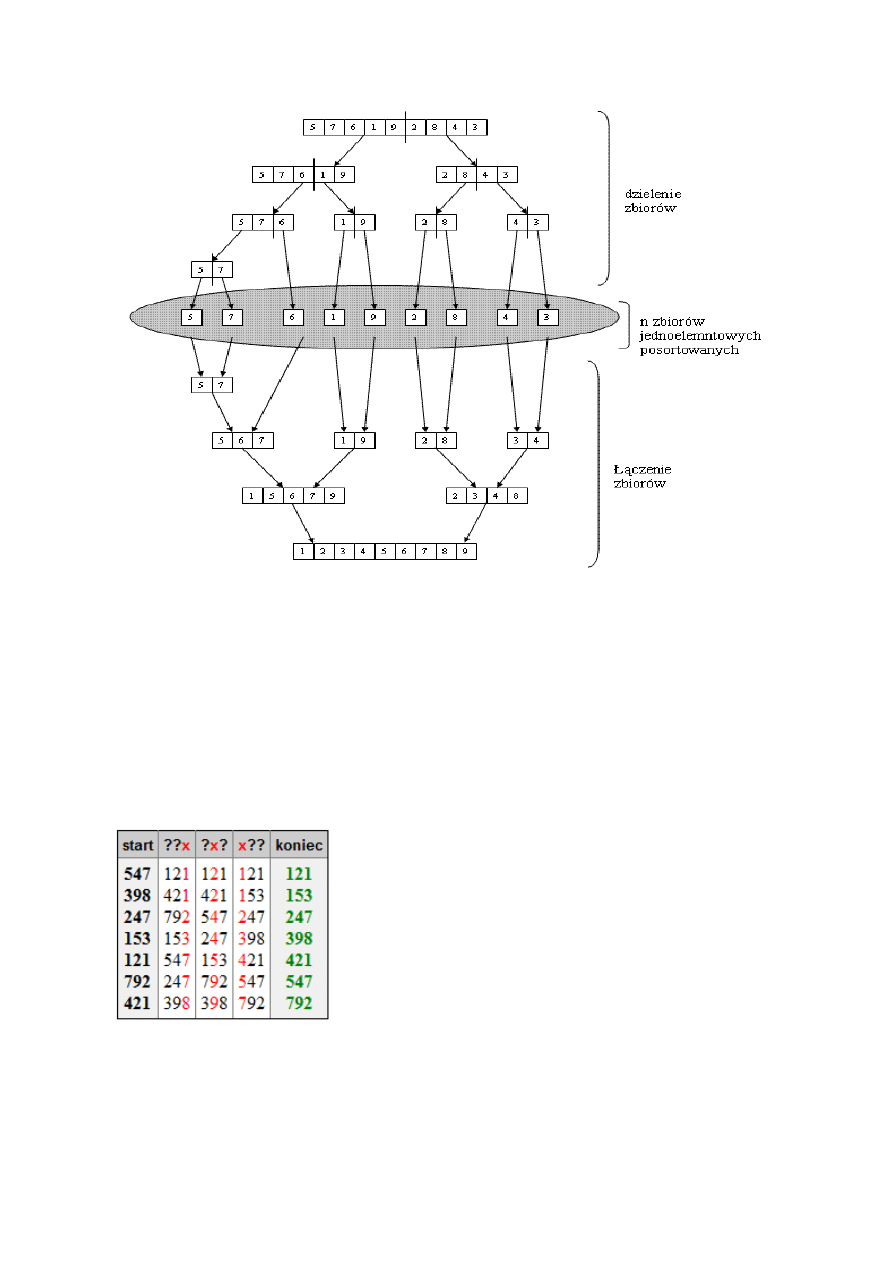
1.6.

Sortowanie pozycyjne

Algorytm sortowania porz

ądkujący stabilnie ciągi wartości (liczb, słów) względem konkretnych

cyfr, znak

ów itp, kolejno od najmniej znaczących do najbardziej znaczących pozycji. Złożonośd

obliczeniowa jest r

ówna O(d(n + k)), gdzie k to liczba różnych cyfr, a d liczba cyfr w kluczach.

Wymaga O(n + k) dodatkowej pami

ęci. Pozycją (ang. radix) nazywamy miejsce cyfry w zapisie

liczby.. Algorytm sortuj

ący musi byd stabilny, tzn. nie może zmieniad kolejności elementów równych,

w przeciwnym razie efekty poprzednich sortowa

o zostaną utracone.

Przykład:
Posortowad algorytmem sortowania pozycyjnego zbiór liczb:, 547 398 247 153 121 792 421 }

Po posortowaniu ostatniej cyfry liczby tworzą ciąg posortowany.

Sortowanie pozycyjne stosuje się nie tylko do sortowania liczb, czy wyrazów. W ten sposób

możemy także sortowad np. daty. Musimy jednak pamiętad, aby sortowad od pozycji najmniej
znaczących. W przypadku dat - najpierw sortujemy je według dni, potem według miesięcy, a na koocu
według lat.

Sortowanie pozycyjne możemy także zastosowad do sortowania rekordów baz danych. Na przykład
chcemy posortowad książkę telefoniczną według nazwisk, a w razie gdyby się one powtarzały to
według imion, a w przypadku identyczności imion i nazwisk według numeru telefonu. Aby otrzymad
taki wynik powinniśmy tą książkę telefoniczną posortowad najpierw według numeru telefonu, potem
według imion, a na koocu według nazwisk. Złożonośd obliczeniowa takiego sortowania pozycyjnego
na pewno nie będzie O(n). Wynika to z tego, że do posortowania np. nazwisk trudno jest użyd
sortowania przez zliczanie.

2. Elementarne metody wyszukiwania

2.1.

Wyszukiwanie liniowe/sekwencyjne

Wyszukiwanie liniowe (ang. linear search), zwane również sekwencyjnym (ang. sequential

search) polega na przeglądaniu kolejnych elementów zbioru Z. Jeśli przeglądany element posiada
odpowiednie własności (np. jest liczbą o poszukiwanej wartości), to zwracamy jego pozycję w zbiorze
i kooczymy. W przeciwnym razie kontynuujemy poszukiwania aż do przejrzenia wszystkich
pozostałych elementów zbioru Z.

W przypadku pesymistycznym, gdy poszukiwanego elementu nie ma w zbiorze lub też znajduje

się on na samym koocu zbioru, algorytm musi wykonad przynajmniej n obiegów pętli sprawdzającej
poszczególne elementy. Wynika z tego, iż pesymistyczna klasa złożoności obliczeniowej jest równa
O(n), czyli jest liniowa - stąd pochodzi nazwa metody wyszukującej.

Często chcemy znaleźd wszystkie wystąpienia w zbiorze poszukiwanej wartości elementu. W

takim przypadku algorytm na wejściu powinien otrzymywad dodatkowo pozycję (indeks) elementu,
od którego ma rozpocząd wyszukiwanie. Pozycję tę przy kolejnym przeszukiwaniu podajemy zawsze o
1 większą od ostatnio znalezionej. Dzięki temu nowe poszukiwanie rozpocznie się tuż za poprzednio
znalezionym elementem.

Schemat algorytmu:

n - liczba elementów w tablicy Z* +, n ∈N
Z[ ]- tablica zawierająca elementy do przeszukania. Indeksy elementów rozpoczynają się od 0, a

kooczą na n-1

p - indeks pierwszego elementu Z* +, od którego rozpoczniemy poszukiwania. p ∈C
k - poszukiwana wartośd, czyli tzw. klucz, wg którego wyszukujemy elementy w Z* +

01: Dla i = p,p+1,...,n-1: wykonuj krok 2

; przeglądamy kolejne elementy w zbiorze

02: Jeśli Z[i] = k, to zakoocz zwracając i ; jeśli napotkamy poszukiwany element, zwracamy

jego pozycję

03: Zakoocz zwracając -1 ; jeśli elementu nie ma w tablicy, zwracamy -1

2.2.

Wyszukiwanie binarne

Wyszukiwanie binarne jest algorytmem opierającym się na metodzie dziel i zwyciężaj, który w

czasie logarytmicznym stwierdza, czy szukany element znajduje się w uporządkowanej tablicy i jeśli
się znajduje, podaje jego indeks. Np. jeśli tablica zawiera milion elementów, wyszukiwanie binarne
musi sprawdzid maksymalnie 20 elementów () w celu znalezienia żądanej wartości. Dla porównania
wyszukiwanie liniowe wymaga w najgorszym przypadku przeglądnięcia wszystkich elementów
tablicy.

Zasada działania : Jeśli zbiór jest pusty, to kooczymy algorytm z wynikiem negatywnym. W

przeciwnym razie wyznaczamy element leżący w środku zbioru. Porównujemy poszukiwany element

z elementem środkowym. Jeśli są sobie równe, to zadanie wyszukania elementu jest wypełnione i
kooczymy algorytm. W przeciwnym razie element środkowy dzieli zbiór na dwie partycje - lewą z
elementami mniejszymi od środkowego oraz prawą z elementami większymi. Jeśli porównywany
element jest mniejszy od środkowego elementu zbioru, to za nowy zbiór poszukiwao przyjmujemy
lewą partycję. W przeciwnym razie za nowy zbiór przyjmujemy prawą partycję. W obu przypadkach
rozpoczynamy poszukiwania od początku, ale w nowo wyznaczonym zbiorze.

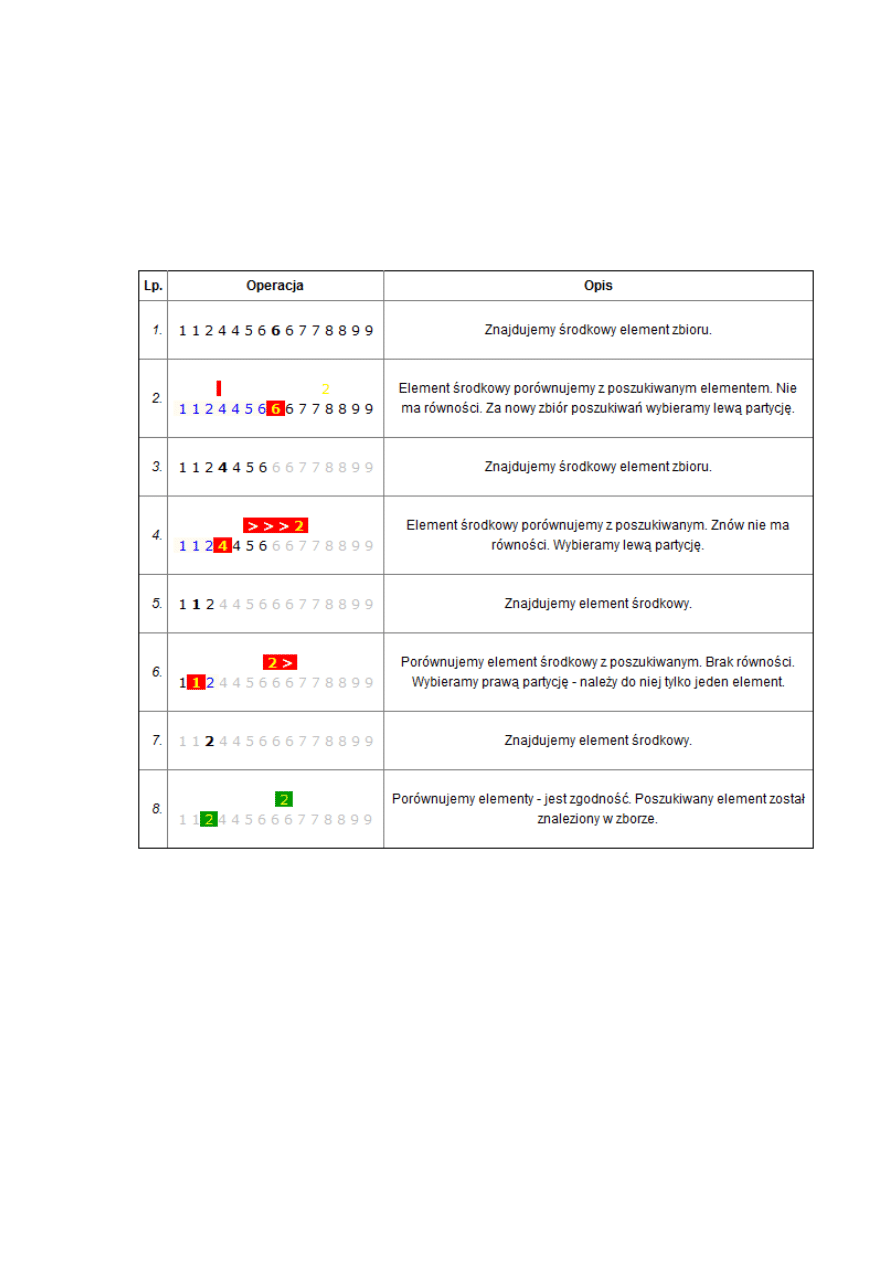
Przykład: Znajdziemy element 2 w zbiorze { 1, 1, 2, 4, 4, 5, 6, 6, 6, 7, 7, 8, 8, 9, 9 }

2.3.

Wyszukiwanie max lub min

Zadanie znajdowania elementu maksymalnego lub minimalnego jest typowym zadaniem

wyszukiwania, które rozwiązujemy przy pomocy algorytmu wyszukiwania liniowego. Za tymczasowy
maksymalny (minimalny) element przyjmujemy pierwszy element zbioru. Następnie element
tymczasowy porównujemy z kolejnymi elementami. Jeśli któryś z porównywanych elementów jest
większy (mniejszy) od elementu tymczasowego, to za nowy tymczasowy element maksymalny
(minimalny) przyjmujemy porównywany element zbioru. Gdy cały zbiór zostanie przeglądnięty, w
elemencie tymczasowym otrzymamy element maksymalny (minimalny) w zbiorze.

Poniżej podajemy algorytm wyszukiwania max. Wyszukiwanie min wykonuje się identycznie,

zmianie ulega tylko warunek porównujący element tymczasowy z elementem zbioru

Schemat algorytmu:

n - liczba elementów w tablicy Z* +, n ∈N
Z[ ] - tablica zawierająca elementy do zliczania. Indeksy elementów rozpoczynają się od 0, a

kooczą na n - 1..

maxZ - tymczasowy element maksymalny

1: maxZ ← Z[0] ; za tymczasowy element maksymalny bierzemy pierwszy element
2: Dla i = 1,2,...,n-1 wykonuj K03 ; przeglądamy następne elementy zbioru
3: Jeśli Z[i] > maxZ, to maxZ ← Z[i]

; jeśli natrafimy na większy od maxZ, to

zapamiętujemy go w maxZ

4: Zakoocz zwracając maxZ

2.4.

Naiwne wyszukiwanie wzorca w tekście

Algorytm N - naiwny - ustawia okno o długości wzorca p na pierwszej pozycji w łaocuchu s.

Następnie sprawdza, czy zawartośd tego okna jest równa wzorcowi p. Jeśli tak, pozycja okna jest
zwracana jako wynik, po czym okno przesuwa się o jedną pozycję w prawo i cała procedura powtarza
się. Algorytm kooczymy, gdy okno wyjdzie poza koniec łaocucha. Klasa pesymistycznej złożoności
obliczeniowej algorytmu N jest równa O(n × m), gdzie n oznacza liczbę znaków tekstu, a m liczbę
znaków wzorca. Jednakże w typowych warunkach algorytm pracuje w czasie O(n), ponieważ zwykle
wystarczy porównanie kilku początkowych znaków okna z wzorcem, aby stwierdzid, iż są one
niezgodne.

2.5.

Alogorytm Karpa-Rabina

Danemu wzorcu możemy przyporządkowad odpowiadającą mu wartośd dziesiętną - klucz. Dla

danego tekstu obliczamy wartości dziesiętne kolejnych podsłów długości wzorca zaczynając od
początku tekstu – uzyskujemy różne klucze. Teraz wystarczy porównad wartośd dziesiętną
odpowiadającą wzorcu z wartościami dziesiętnymi odpowiadającymi kolejnym podsłowom czyli
sprawdzamy czy klucze są identyczne. Jeżeli są one równe możemy podejrzewad, że wzorzec
występuje w tekście. Wystarczy wtedy sprawdzid warunek P*1…m+=T*s+1…s+m+. Na rys 2 pokazany
jest przykład *2+. Wzorzec i tekst jest złożony z cyfr od 0 do 9. Możemy, więc traktowad go jak liczbę.
Bierzemy kolejne ciągi znaków z tekstu, których długośd jest równa długości wzorca, a następnie
obliczamy resztę z dzielenia przez 13. Kolejno otrzymujemy różne wartości. Ponieważ reszta z
dzielenia wzorca (31415) przez 13 jest równa 7, więc szukamy tylko tych wartości, dla których reszta
wynosi też 7. Widzimy, że wartośd 7 odpowiada dwóm podsłowom. Są to potencjalni kandydaci.
Musimy jeszcze sprawdzid czy rzeczywisty wzorzec odpowiada danemu podsłowu.

3. Tablice symboli i metody ich realizacji.

Czym jest tablica symboli?

Najprościej tłumacząc, tablica symboli jest po prostu pewną strukturą danych, która

przechowuje informacje o napotkanych w kodzie symbolach. O tym, co jest symbolem, a co nie,
decydujemy my (np. etykieta może byd symbolem, ale nie musi). Każdy symbol w tablicy
identyfikowany jest przez swój indeks (np. liczbę całkowitą). Tablicę symboli tworzymy po to, żeby
nam ułatwiła generowanie kodu. Dzięki niej możemy operowad tylko na indeksach, mając ten
komfort, że za ich pomocą zawsze możemy się odnieśd do potrzebnych informacji o symbolu. Tablica
symboli ułatwia też ujednolicenie pewnych operacji generowania kodu.
Jedyną odpowiedzią na pytanie "czy moja tablica symboli jest wystarczająco dobra?" jest "to się
okaże". Trudno jest zweryfikowad, czy tablica przechowuje wszystkie potrzebne informacje, dopóki
nie zaczniemy generowad za jej pomocą kodu.

Co przechowywad w tablicy symboli?

Co do samych symboli, to właściwie powinno się przekazywac wszystkie zmienne, stałe liczbowe (np.
kiedy natrafimy na 123.23 to też powinniśmy umieścid tą liczbę w tablicy symboli), nazwy procedur,
funkcji.

Jeśli zaś chodzi o informacje dotyczące symboli, to z dostępnej przykłądowej tablicy symboli można
wywnioskowad, iż powinno się przechowywad:



nazwę symbolu,



typ symbolu (integer, real, procedura, funkcja, tablica, żaden),



informację o tym, czy jest to referencja, czy też nie,



zakres (są na to co najmniej dwa sposoby, o czym później)



dodatkowe informacje zależne od typu symbolu (np. początkowy i koocowy indeks dla
tablicy, typ zwracany i argumenty dla funkcji itd.)



adres w pamięci

Tworzenie tablicy symboli

Tablicę symboli tworzy parser , rozpoznaje deklaracje identyfikatorów, deklaracje
modułów(=unit.)Gdy parser
stwierdzi, że wystąpiła deklaracja wpisuje informację do bieżącego węzła struktury SymTab.
Informacja zawiera
klucz(=key) którym jest identyfikator oraz dodatkowe cechy np. typ zmiennej prostej. Gdy
stwierdzono deklarację
modułu - otwiera się dla niego nowy węzeł w strukturze SymTab. Zaznacza się dla tego węzła - węzeł
ojciec oraz węzeł
klasy z której dziedziczy węzeł biezący. W ten sposób struktura węzłów SymTab rozpatrywana wraz z
atrybutem ojciec
jest strukturą drzewa. Ten sam zbiór węzłów rozpatrywany z atrybutem “dziedziczę z ...” tworzy
strukturę lasu.

Możliwe sposoby realizacji:

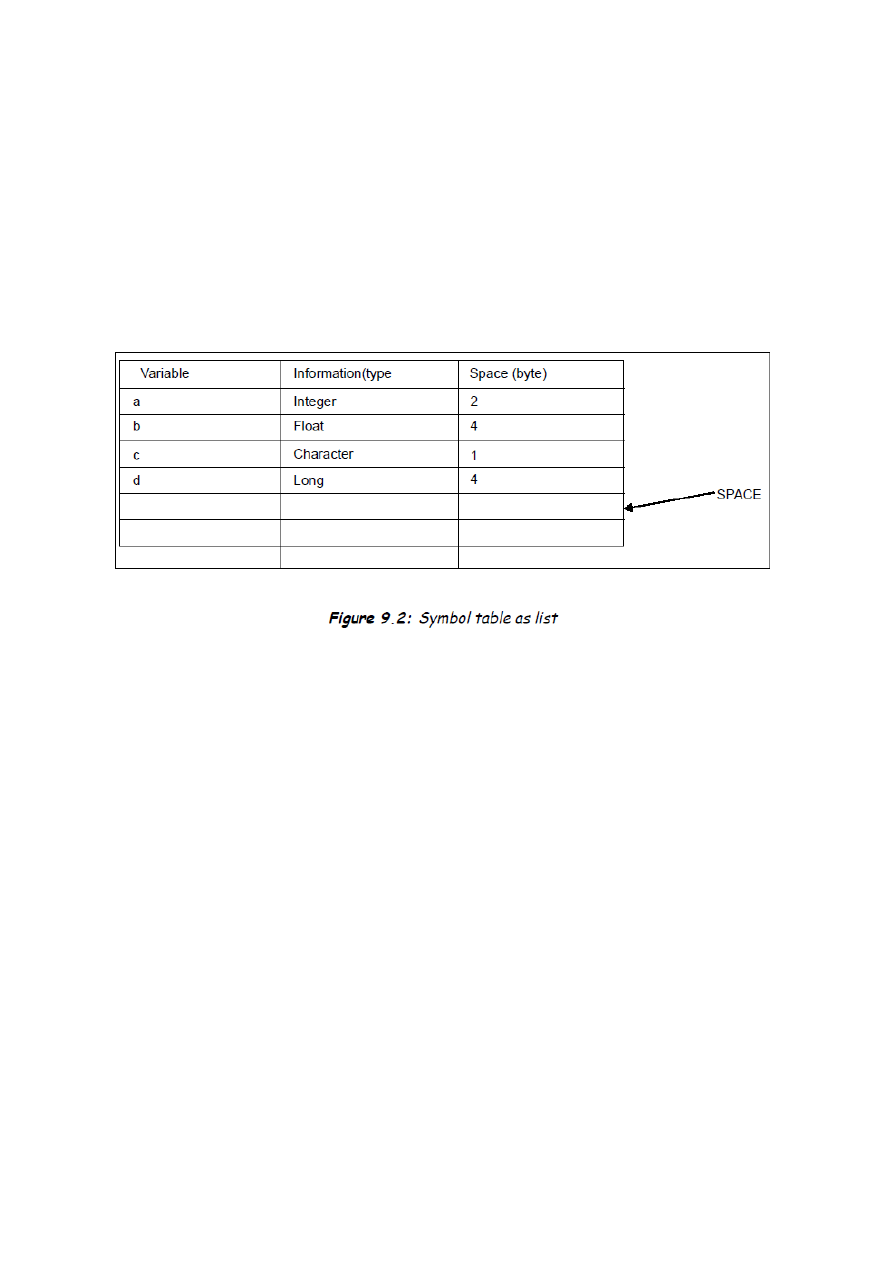
1. Lista

Najprostszym i najłatwiejszym sposobem implementacji struktury tablicy symboli jest liniowa lista
rekordów. Używamy pojedynczej tablicy lub kolekcji tablic w celu przechowywania nazwy i
związanych z nimi informacji. Nazwy są dodawane do kooca tablicy. Koniec tablicy oznaczany jest
jako przestrzeo(space). Kiedy wstawiamy nową nazwę tablica jest przeszukiwana od kooca do
początku. Jeśli tablica ma 'n' symboli i chcemy wstawid kolejny to w najgorszym przypadku musimy
przeszukad n razy - złożonośd O(n). Jeśli wstawiamy n symboli to złożonośd wyniesie do O(

)

Przykład 1

Przykład 2

int a,b,c;
int sum (int x, int y)
{
a = x+y
return (a)
}
main ()
{
int u,
u=sum (5,6);
}

Implementacja powyższego przykładu(2) za pomocą listy

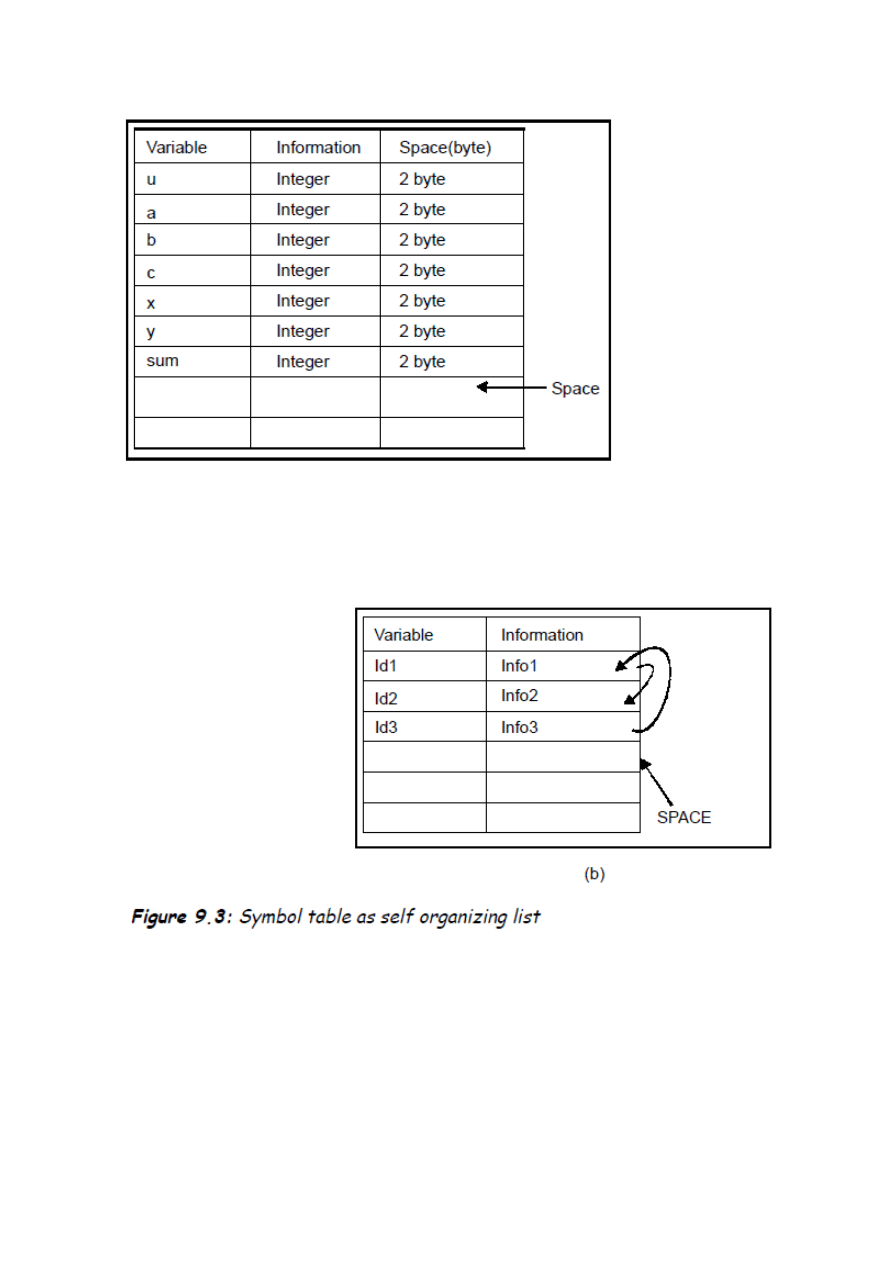
2. Samoorganizująca Lista

w celu zredukowania czasu przeszukiwania można dodad dodatkowe pole „linker” do każdego pola
rekordu lub indeksu tablicy. Przykład samoorganizującej listy w której Id1 jest w relacji z Id2 i Id3 jest
w relacji z Id1

3.

Reprezentacja za pomocą „

hash table” lub „hash map”

Głowną zaletą tego podejścia jest to że możemy usuwad i dodawad dowolną liczbę lub nazwę czasie
O(n)(pesymistyczna opcja).

Przykład 1

class Symbol {
public String key;
public Object binding;
public Symbol next;

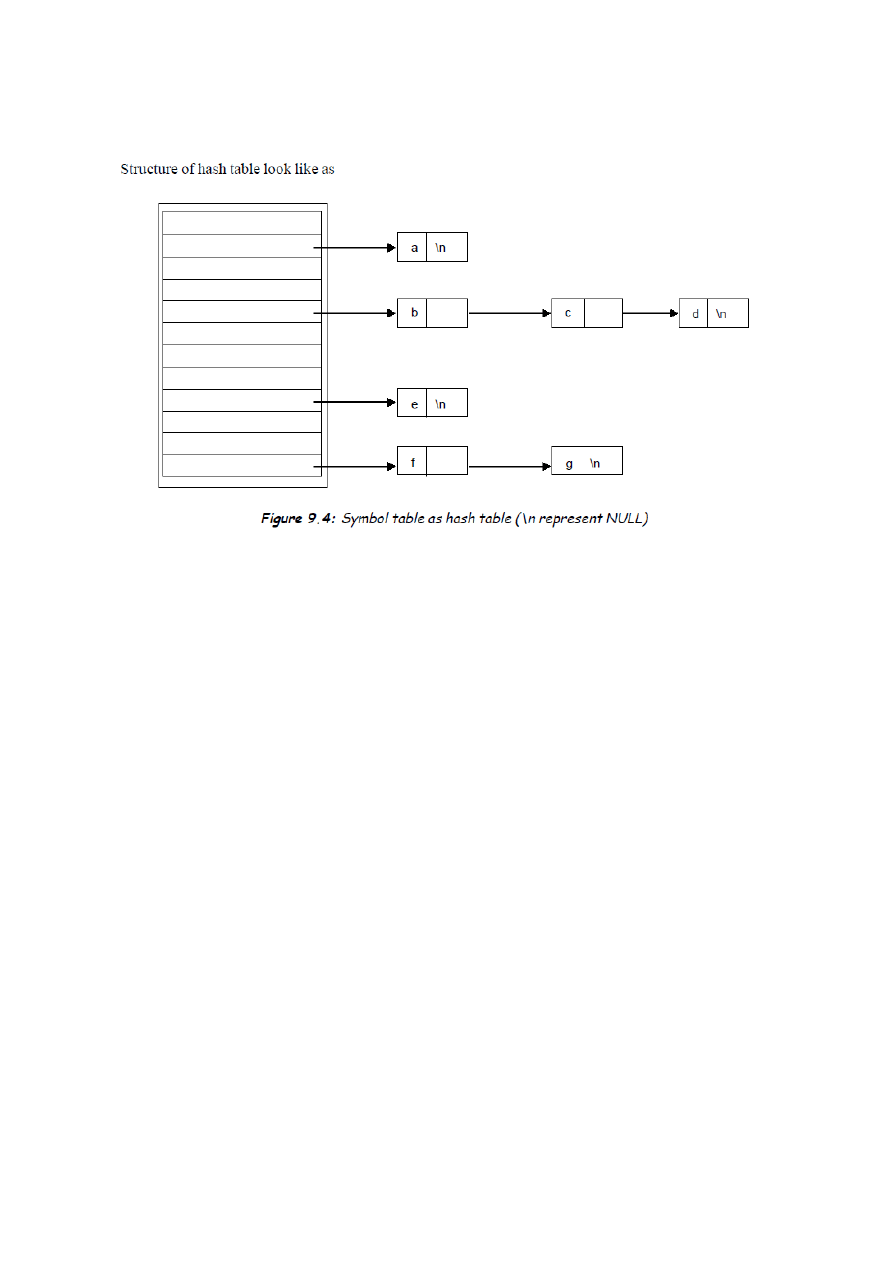
public Symbol ( String k, Object v, Symbol r ) { key=k; binding=v;
next=r; }
}

Przykład 2:

int a,b,c;
int sum (int x, int y)
{
a = x+y
return (a)
}
main ()
{
int u,
u=sum (5,6);
}

Implementacja powyższego przykładu(2) za pomocą HashTable

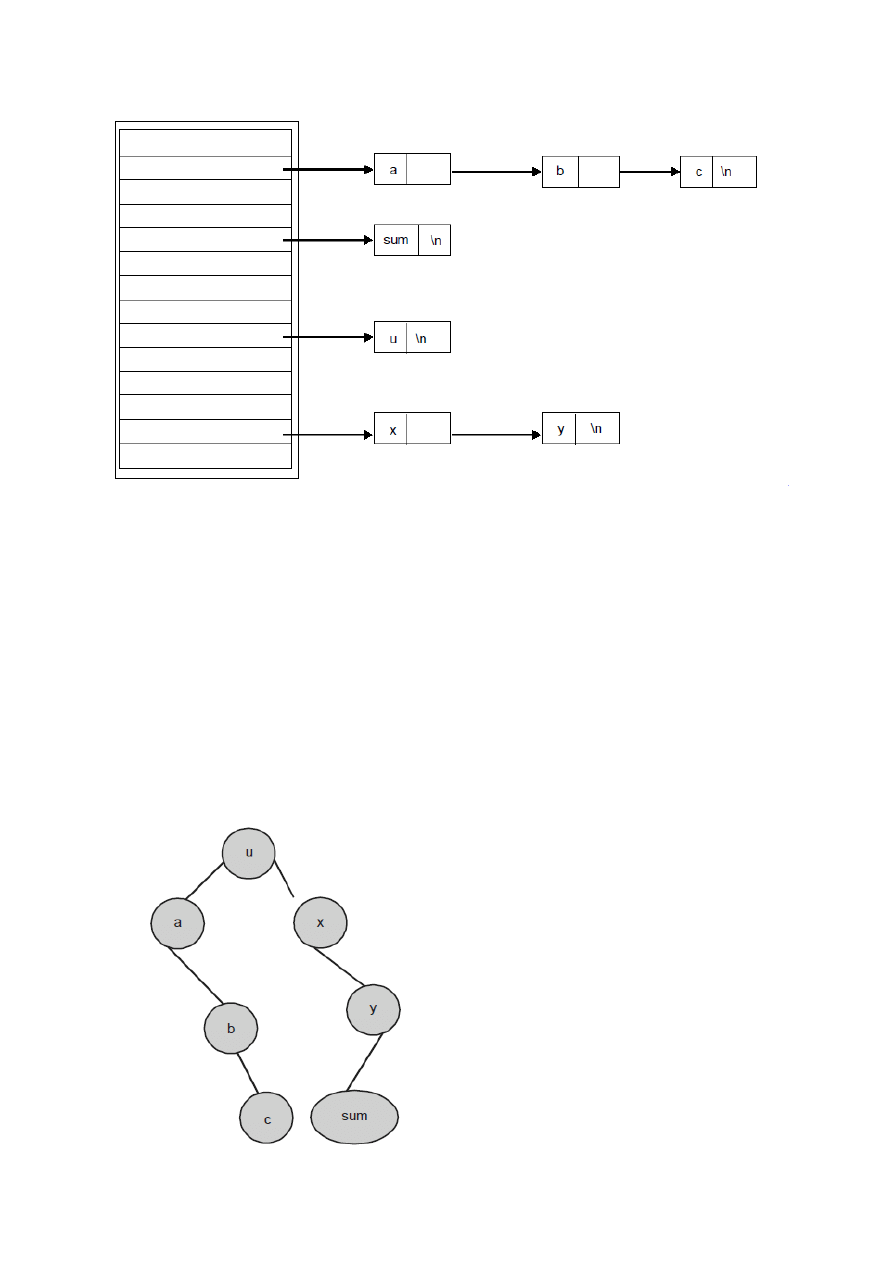
4. Drzewo Poszukiwao(Search Tree)

Przykład 1:
int a,b,c;
int sum (int x, int y)
{
a = x+y
return (a)
}
main ()
{
int u,
u=sum (5,6);
}
Implementacja powyższego przykład(1)u za pomocą drzewa poszukiwao