Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych

Nr 59

Politechniki Wrocławskiej

Nr 59

Studia i Materiały Nr

26

2006

__________

Elektrownia wiatrowa, turbina wiatrowa

oscylacje mocy, model matematyczny

symulacja komputerowa

Piotr Uracz

*

, Bogusław KAROLEWSKI

F

*

F

MODELOWANIE TURBIN WIATROWYCH

Z WYKORZYSTANIEM CHARAKTERYSTYK

WSPÓŁCZYNNIKA MOCY

Przedstawiono sposób modelowania turbin wiatrowych z wykorzystaniem wcześniej określonej

rodziny charakterystyk zależności współczynnika mocy turbiny od współczynnika szybkobieżności.
Uwzględniono oscylacje momentu turbiny wywołane asymetrią koła wiatrowego, wpływem wieży
oraz drgań łopat. Przedstawiono wyniki przykładowych obliczeń przebiegu momentu turbiny, mo-
mentu elektromagnetycznego generatora indukcyjnego oraz prądu oddawanego do sieci.

1. WPROWADZENIE

Elektrownie wiatrowe odgrywają coraz większą rolę w produkcji energii elektrycz-

nej. Ich dynamiczny rozwój na przestrzeni ostatnich dwudziestu lat spowodował wzrost
ich mocy od pojedynczych kilowatów do kilku megawatów. Równie dynamicznie roz-
wija się światowy rynek energetyki wiatrowej. Moc zainstalowana w elektrowniach
wiatrowych w 2005 roku wyniosła prawie 60 GW, zwiększając się o ponad 11 GW
w ciągu roku [5].

W związku z rosnącym udziałem elektrowni wiatrowych w mocy generowanej, coraz

większego znaczenia nabiera określenie wpływu, jaki wywierają one na istniejący sys-
tem. Do problemów z tym związanych można zaliczyć: migotanie napięcia i wolniejsze
jego zmiany, pulsacje mocy, emisję harmonicznych, wpływ na wartości prądów zwar-
ciowych. Problemy te powinny zostać rozpoznane jeszcze w fazie planowania inwesty-
cji. Aby to było możliwe, niezbędne jest opracowanie modelu całego urządzenia. Jed-
nym z najistotniejszych elementów takiego modelu jest sposób opisu turbiny wiatrowej.

*

Politechnika Wrocławska, Instytut Maszyn, Napędów i Pomiarów Elektrycznych, 50-372 Wrocław,

ul Smoluchowskiego 19, [e-mail], [e-mail]

2. MODELOWANIE TURBINY WIATROWEJ W OPARCIU O

CHARAKTERYSTYKĘ WSPÓŁCZYNNIKA MOCY

Elementem napędowym każdej elektrowni wiatrowej jest turbina, nazywana też

silnikiem wiatrowym [3]. Parametrem charakteryzującym turbinę wiatrową jest jej
współczynnik mocy, czyli stosunek mocy turbiny do całkowitej mocy zawartej w wie-
trze. Współczynnik mocy turbiny zależy od parametrów konstrukcyjnych, do których
można zaliczyć liczbę płatów i ich profil. Współczynnik ten zależy także od chwilo-
wych warunków pracy, a konkretnie od prędkości obrotowej wirnika i chwilowej
prędkości wiatru, a w nowoczesnych konstrukcjach również od aktualnego kąta na-
stawienia płatów turbiny.

Istnieje kilka modeli turbiny o różnym stopniu złożoności. Często stosuje się mo-

del oparty o charakterystyki współczynnika mocy danej turbiny [6, 8–10, 12–15].
Współczynnik ten jest definiowany jako stosunek mocy turbiny P

t

do mocy całkowitej

strumienia powietrza przepływającego przez powierzchnię turbiny:

3

2

5

,

0

V

R

P

C

t

p

⋅

⋅

⋅

⋅

=

π

ρ

(1)

gdzie: ρ – gęstość powietrza,

R – promień koła zataczanego przez łopaty turbiny,
V – prędkość wiatru.

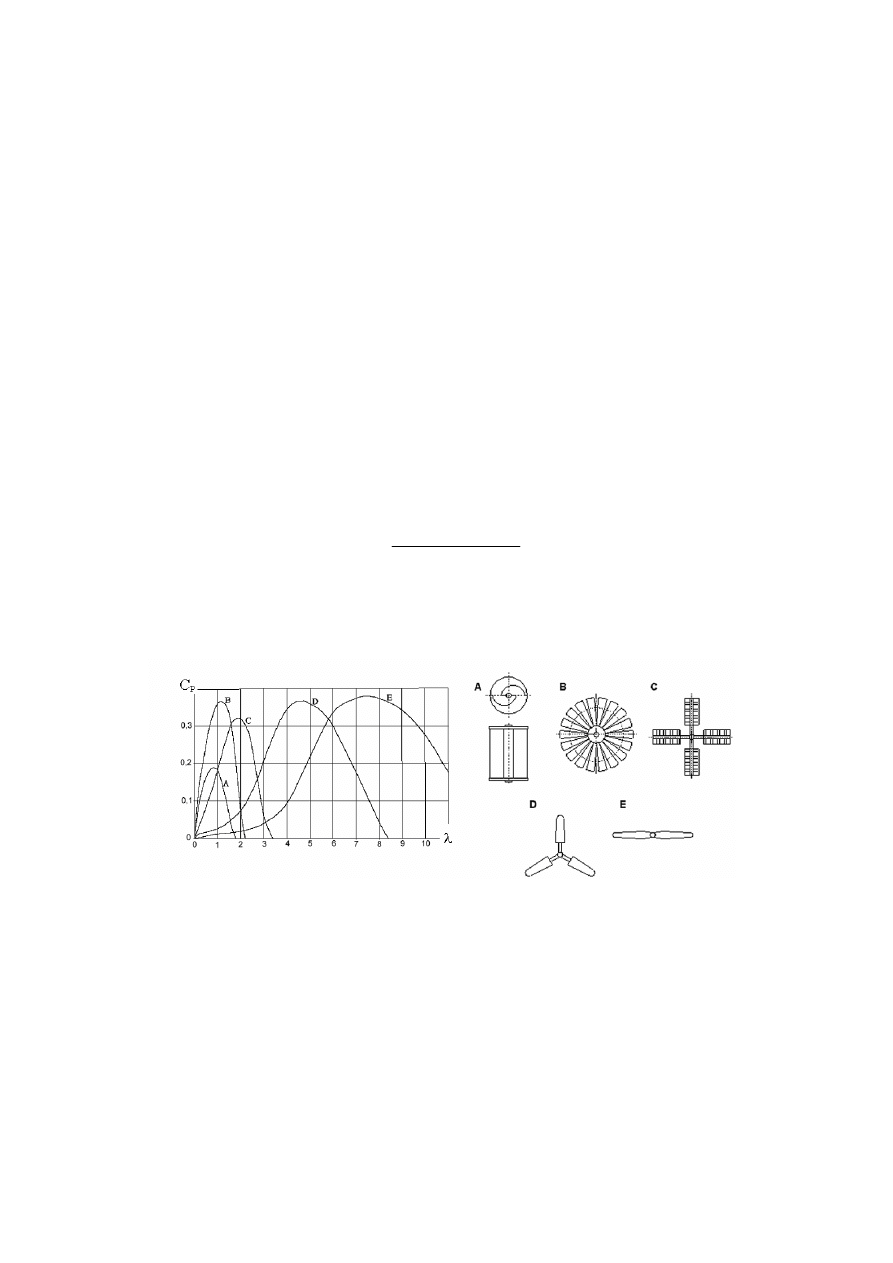
Rys. 1. Charakterystyki współczynnika mocy różnych typów turbin [3]

Fig. 1. Power coefficient of various types of wind turbine

Wspomniane charakterystyki podawane są zazwyczaj w funkcji tzw. współczynni-

ka szybkobieżności (rys. 1). Jest to stosunek prędkości obwodowej końcowego ele-
mentu płata turbiny do prędkości wiatru i definiowany jest następująco:

3

V

R

t

⋅

Ω

=

λ

(2)

gdzie: Ω

t

– prędkość kątowa turbiny.

Powszechnie stosowana w nowoczesnych turbinach regulacja mocy przez sterowa-

nie kątem nachylenia (

β

) łopat turbiny sprawia, że do modelowania konieczna jest

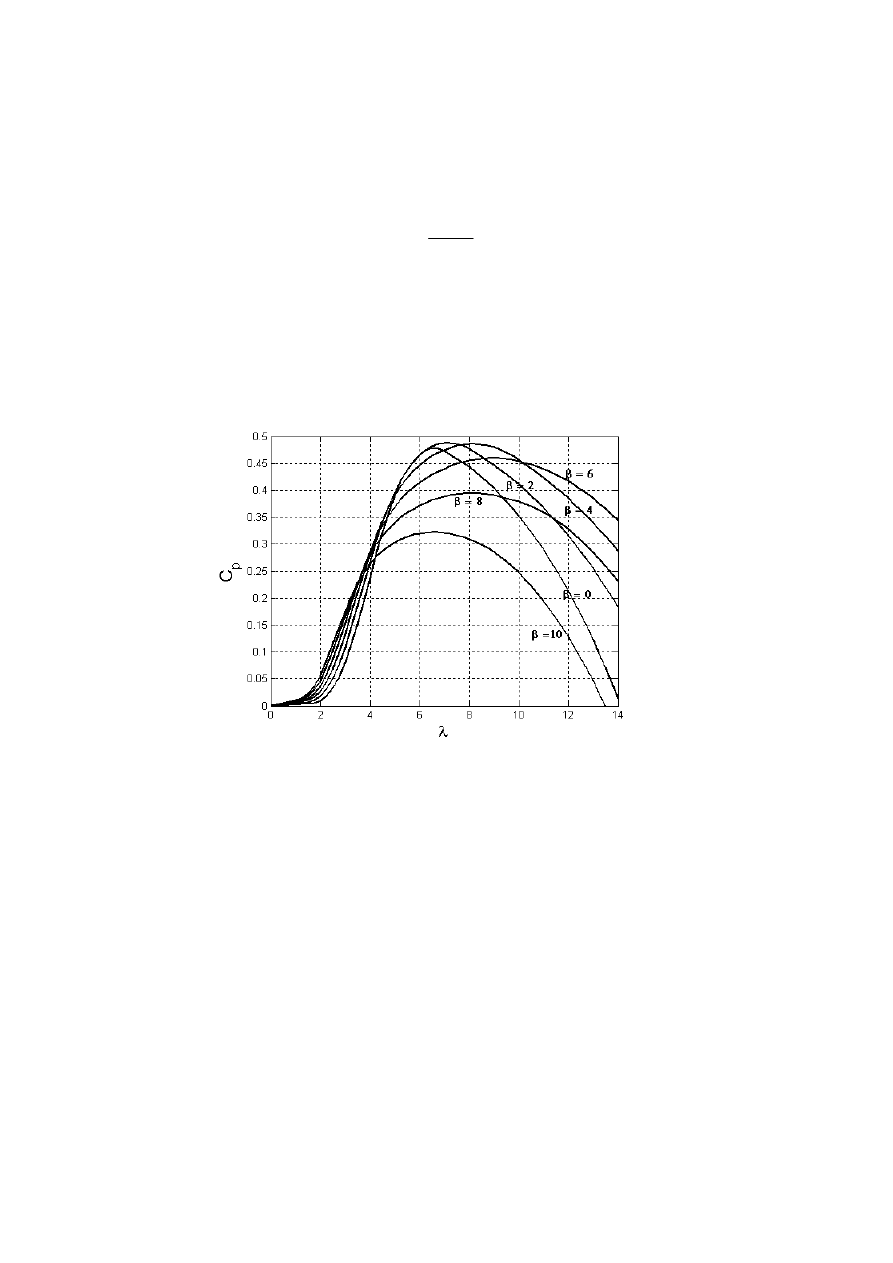
znajomość charakterystyk współczynnika mocy także w funkcji tego kąta. Rodzinę
charakterystyk turbiny trójłopatowej dla różnych kątów ustawienia łopat przedstawio-
no na rys. 2. Charakterystyki te uzyskuje się pomiarowo lub wykorzystując bardziej
zaawansowane modele.

Rys. 2. Charakterystyki współczynnika mocy dla różnych kątów nastawienia płata

Fig. 2. Power coefficient – tip speed and pitch angle performance curve

Model wykorzystujący zależność współczynnika mocy od szybkobieżności pozwa-

la na proste uwzględnienie zachowania turbiny, niezależnie od jej typu. Wykorzystuje
się wtedy stabelaryzowane wartości przebiegów, takich jak przedstawione na rysunku
2. Ze względu na szybkość obliczeń model ten jest często stosowany w badaniach
wpływu elektrowni wiatrowych na system energetyczny. Jest także szczególnie przy-
datny w modelowaniu turbin o pionowej osi obrotu, w których przepływ powietrza
jest bardzo skomplikowany, co nie pozwala na stworzenie innego, względnie prostego
modelu matematycznego.

3. OSCYLACJE MOCY TURBINY WIATROWEJ

Analizując pracę elektrowni wiatrowej w systemie elektroenergetycznym i jej

wpływ na ten system, konieczne jest uwzględnienie zjawisk, które objawiają się pod-
czas pracy wirnika jako oscylacje skrętne. Oscylacje te (zwane mechanicznymi koły-
saniami własnymi) przenoszą się na wał i do generatora, a następnie w postaci harmo-
nicznych prądów i napięć pojawiają się w mocy oddawanej do systemu
elektroenergetycznego [7]. Do najważniejszych wahań mocy wyjściowej elektrowni
wiatrowej, wynikających z drgań momentu mechanicznego, w przypadku najczęściej
wykorzystywanej turbiny 3-łopatowej można zaliczyć:

– zmiany mocy wynikające z asymetrii koła wiatrowego przy typowym

nierównomiernym rozkładzie prędkości wiatru, tj. większych prędkościach wiatru
w górnej części koła wiatrowego - kołysania nazywane 1P, o częstotliwości pro-
porcjonalnej do prędkości kątowej koła wiatrowego,

– zmiany mocy związane z przechodzeniem łopat koła wiatrowego przed wieżą

elektrowni, tj. niejako w cieniu wieży (w rzeczywistości to wieża stanowi „cień”
dla łopat), co powoduje chwilowe zmniejszenie energii uzyskiwanej z wiatru -
kołysania o częstotliwości proporcjonalnej do prędkości kątowej koła wiatrowego
i liczby łopat nazywane 3P,

– zmiany mocy związane z kołysaniami łopat, które zależą od konstrukcji i długości

łopaty.

Powtarzalność powyższych zjawisk umożliwia modelowanie ich w postaci uprosz-

czonej, tj. w postaci sumy sygnałów harmonicznych dodawanych do sygnału mocy P

t

uzyskanej przez turbinę z wiatru. Moc mechaniczną na wale elektrowni wiatrowej
można więc zdefiniować wzorem [1, 7]:

( ) ( )

( )

( )

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

+

=

∫

∑

∑

=

=

t

km

k

km

k

m

km

km

k

k

t

W

d

m

t

g

t

h

t

g

a

A

P

P

0

2

1

3

1

sin

1

ϕ

ς

ς

ω

(3)

gdzie: A

k

- wartość k-tego rodzaju kołysań mocy;

ω

k

- częstotliwość własna k-tego

rodzaju kołysań mocy; h

k

(t) - modulacja k-tego rodzaju kołysań mocy; m - numer

harmonicznej; g

km

- rozkład k-tego rodzaju kołysań mocy m-tej harmonicznej; a

km

-

znormalizowany współczynnik; g

km

,

ϕ

km

- faza k-tego rodzaju kołysań mocy m-tej

harmonicznej; t,

ς

- czas.

Takie podejście do modelowania kołysań mocy mechanicznej jest stosunkowo pro-

ste, lecz wymaga danych pochodzących z eksperymentów lub ze szczegółowych mo-
deli części mechanicznej elektrowni wiatrowej [7].

4. WYNIKI BADAŃ SYMULACYJNYCH

5

Do obliczeń symulacyjnych wykorzystano model obwodowy silnika indukcyjnego,

opisany w [4, 11, 16]. Model przystosowano do badania pracy generatora indukcyjne-
go, połączonego za pośrednictwem linii zasilającej o zadawanej rezystancji i reaktan-
cji z siecią sztywną. Należy w tym celu między innymi zmienić znak momentu obcią-
żenia, który staje się wtedy momentem napędzającym. Model rozbudowano o baterię
kondensatorów do kompensacji mocy biernej.

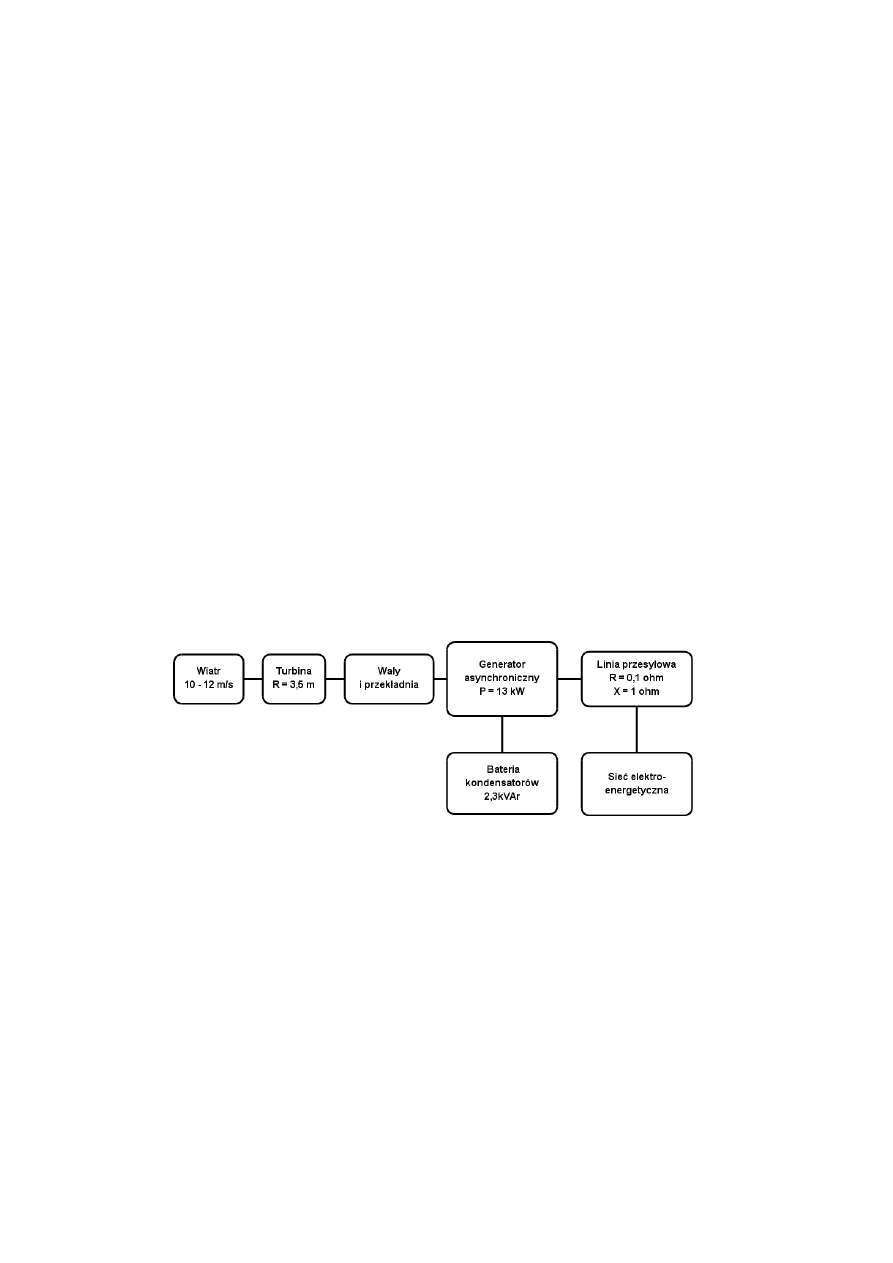
Schemat modelowanej elektrowni wiatrowej przedstawiono na rys. 3. Zadawana

prędkość wiatru narastała podczas symulacji w sposób liniowy od 10 do 12 m/s w
przedziale czasu t = 5–13s, w pozostałej części symulacji pozostawała stała.

W modelu turbiny wykorzystano charakterystykę przedstawioną na rys. 2, dla sta-

łego kąta nastawienia łopat wynoszącego 0 st. Charakterystykę tę obliczono przy wy-
korzystaniu bardziej szczegółowego modelu opartego na teorii elementu płata. Przyję-
to następujące parametry oscylacji mocy turbiny: A

1

= 0,01 A

2

= 0,08 A

3

= 0 a

11

=

0,8 a

12

= 0,2 a

21

= 0,8 a

22

= 0,25. Wartości parametrów dobrano tak, aby przebieg

momentu był zbliżony do typowych przebiegów pomiarowych, przedstawianych w
literaturze [2].

Przyjęto, że połączenia mechaniczne – wały, sprzęgła i przekładnia – są sztywne, a

moment bezwładności jest sumą momentu bezwładności turbiny i generatora. Jako
generator pracowała maszyna o mocy 13kW, napięciu 380V i prędkości synchronicz-
nej 1500 obr/min. Krok całkowania wynosił T

p

= 4

⋅10

-4

s. Obliczenia wykonano w

środowisku MATLAB.

Rys. 3. Schemat ideowy układu elektrowni wiatrowej przyjęty do symulacji

Fig. 3. Simulated wind turbine system

Wyniki badań przedstawiono na rysunkach 4 i 5. Przebieg momentu elektromagne-

tycznego generatora ma charakter oscylacyjny, co jest wynikiem pulsacji momentu
turbiny wiatrowej (rys. 4). Oscylacje momentu generatora mają znacznie mniejszą
amplitudę niż turbiny, co można tłumaczyć wpływem bezwładności układu. Oscylacje
obu momentów są przesunięte w fazie w przybliżeniu o 180 stopni, przy czym drgania
momentu generatora są opóźnione względem momentu turbiny.

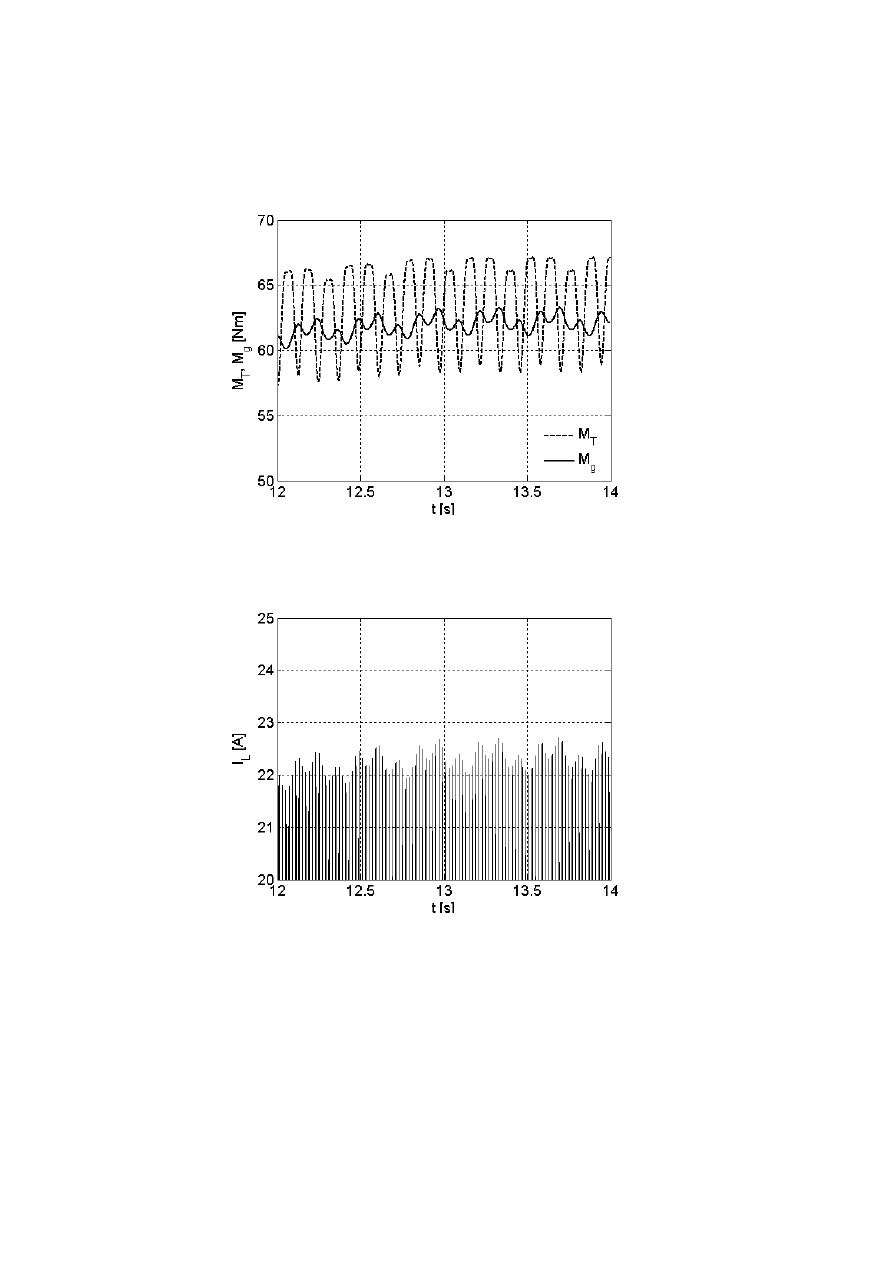
Rys. 4. Przebieg momentu turbiny (przeliczonego na prędkość generatora) i generatora

Fig. 4. Torque of turbine (referred to generator’s speed) and generator

Rys. 5. Przebieg prądu linii

Fig. 5. Line current

7

Oscylacje momentu turbiny mają odzwierciedlenie także w przebiegu prądu odda-

wanego przez generator do linii. Na rysunku 5 przedstawiono w powiększeniu dodat-
nie amplitudy przebiegu wartości chwilowych prądu. Widoczna jest wyraźna modula-
cja amplitudy prądu. Kształt obwiedni prądu przypomina przebieg zmian momentu
elektromagnetycznego.

5. PODSUMOWANIE

Modelowanie elektrowni wiatrowych jest istotnym zagadnieniem, między innymi

ze względu na rosnącą liczbę i moc tych urządzeń, podłączanych do systemu elektro-
energetycznego. Sposób modelowania turbiny ma krytyczny wpływ na uzyskiwane
wyniki, ale trzeba również uwzględniać pozostałe elementy układu. Przedstawione
rezultaty obliczeń pokazują, iż nawet w tak wyidealizowanych warunkach wiatro-
wych, oscylacje momentu turbiny przenoszą się na przebieg mocy przekazywanej do
sieci energetycznej. Pomijanie tych zjawisk w badaniach może prowadzić do błędnych
wyników i wniosków. Istotny wpływ na przebieg generowanej mocy mogą mieć także
właściwości połączenia mechanicznego, dlatego dalszym etapem pracy będzie
uwzględnienie elastyczności wałów napędowych, sprzęgieł i przekładni elektrowni
wiatrowej.

LITERATURA

[1] AKHMATOV V., KNUDSEN H., NIELSEN A.H., Advanced simulation of windmills in the electric

power supply. Electrical Power & Energy Systems, 2000, Vol. 22, s. 421-434

[2]

DOLAN D.S.L., LEHN P. W.: Real-time wind turbine emulator suitable for Power Quality

and Dynamic Control Studies., Int. Conf. on Power System Transients (IPST’05), Mont-
real, Canada, 2005

[3]

JAGODZIŃSKI W. Silniki wiatrowe, Warszawa, PWT, 1959.

[4] KAROLEWSKI B., ŚWIDERSKI P., Modelowanie silników indukcyjnych w naturalnym układzie

współrzędnych, Zeszyty Problemowe Maszyny Elektryczne 2003, nr 66, Wyd. BOBRME KOMEL,
Katowice 2003, s. 129-135.

[5] KROGSGAARD P., MADSEN B.T., International wind energy development world market update

2005. Forecast 2006-2010., BTM Consult ApS, 2005, www.btm.dk

[6] LEI Y., MULLANE A., LIGHTBODY G., YACAMINI R., Modeling of the wind turbine with a

doubly fed induction generator for grid integration studies. IEEE Trans. on Energy Conversion,
2006, Vol. 21, No. 1, s. 257-264

[7] LUBOŚNY Z., Elektrownie wiatrowe w systemie elektroenergetycznym. Warszawa, WNT, 2006
[8] MIHET-POPA L., BLAABJERG F., BOLDEA I., Wind turbine generator modeling and simulation

where rotational speed is the controlled variable. IEEE Trans. on Industry Applications, 2004, Vol.
40, No. 1, s. 3-10

[9] MULJDADI E., BUTTERFIELD C.P., Pitch-controlled variable-speed wind turbine generation.

IEEE Trans. on Industry Applications, 2001, Vol. 37, No. 1, s. 240-246

[10] NUNES M.V.A., PECAS LOPES J.A. et al, Influence of the variable-speed wind generators in

transient stability margin of the conventional generators integrated in electrical grids. IEEE Trans.
on Energy Conversion, 2004, Vol. 19, No. 4, s.692-701

[11] PASZEK W., Dynamika maszyn elektrycznych prądu przemiennego., Gliwice, Helion, 1998
[12] SLOOTWEG J.G., DE HAAN W.H., POLINDER H., KLING W.L., General model for representing

variable speed wind turbines in power system dynamics simulations. IEEE Trans. on Power Systems,
2003, Vol. 18, No. 1, , s. 144-151

[13] SLOOTWEG J.G, POLINDER H., KLING W.L., Dynamic modeling of a wind turbine with doubly

fed induction generator., Vancouver, IEEE Power Engineering Society Meeting, 2001, Vol. 1, s. 644-
649

[14] SUN T. CHEN Z., BLAABJERG F., Flicker study on variable speed wind turbines with doubly fed

induction generators. IEEE Trans. on Energy Conversion, 2005, Vol. 20, No. 4, s.896-905

[15] TAPIA A., TAPIA G. et al, Modeling and Control of a Wind Turbine Driven Doubly Fed Induction

Generator. IEEE Trans. on Energy Conversion, 2003, Vol. 18, No. 2, s. 194-204

[16] URACZ P., Przystosowanie modelu obwodowego silnika do wyznaczania wartości skutecznych

prądów i mocy, Magisterska Praca Dyplomowa, Politechnika Wrocławska, Wrocław, 2004.

MODELING OF WIND TURBINES WITH THE USE OF POWER COEFFICIENT

CURVES

This article describes a procedure of wind turbine modeling with the use of earlier determined curves

of turbine's power coefficient depending on tip speed ratio. Turbine's torque oscillations, caused by
asymmetry, tower influence and blades vibrations, has been taken into account. Exemplary results of
calculated turbine and generator torque as well as current supplying the power grid has been presented.