Politechnika Śląska w Gliwicach

Wydział Automatyki, Elektroniki i Informatyki

KOMPUTEROWE WSPOMAGANIE

PODEJMOWANIA DECYZJI

Laboratorium 05

PROCESY DECYZYJNE W POSTACI EKSTENSYWNEJ

O SUMIE NIEZEROWEJ

AiR gr. TI 1 sekcja 2

Gacki Piotr

Juraszek Michał

Zadanie 1.

Rozwiązanie problemu dla dwóch graczy o liczbie etapów równej 3.

Rozważając problem gier o sumie niezerowej gracze dążą do minimalizacji strat.

Rozwiązanie takiego problemu jest możliwe na dwa sposoby.
Pierwszy z nich to sposób macierzowy, a drugi to sposób z użyciem drzewa decyzyjnego, na
którym w łatwy sposób można dostrzec możliwe do wyboru decyzje.

Rozpatrywany problemie każdy z graczy w danym etapie może podjąć jedną z dwóch

możliwych decyzji. W obrębie jednego etapu gracze nie wiedzą nic o decyzji podjętej przez
przeciwnika. Dopiero w kolejnych etapach gracze mogą się dowiedzieć jaką decyzje podjął
przeciwnik.

Macierze starta dla graczy
D1

3 4

2

-1 2 0

1

1

-2 -3 2

1

0

1

2

3

4

5

2

3

1

-2

D2

2 5

3

2

1 2

0

3

-1 4

0

2

1

2

3

4

2

5

3

-1 1

-3

D1

2 2

3

4

3 2

3

2

0

1

1

3

5

1

7

5

3

1

2

6

3

7

D2

2 1

3

2

1 0

1

2

0

0

5

3

2

3

8

6

4

2

2

3

6

7

D1

2 2

4

4

1 -4 2

1

4

3

3

2

0

-1 1

5

2

5

1

4

D2

1 0

3

0

5 -2 3

1

-1 2

2

-1 -1 3

2

-2 3

6

1

4

W trzecim etapie gry każdy z graczy musi podjąć 16 decyzji.

Gracz 1.

D1\D2

1

2

1

3

4

2

2

-1

Strategia (2,2), wynik(-1,2)

D1\D2

1

2

1

2

0

2

1

1

Strategia (2,1), wynik(1,0)

D1\D2

1

2

1

-2

-3

2

2

1

Strategia (1,1), wynik(-2,-1)

D1\D2

1

2

1

0

1

2

2

3

Strategia (1,1), wynik(0,1)

D1\D2

1

2

1

4

5

2

2

3

Gracz 2.

D1\D2

1

2

1

2

5

2

3

2

D1\D2

1

2

1

1

2

2

0

3

D1\D2

1

2

1

-1

4

2

0

2

D1\D2

1

2

1

1

2

2

3

4

D1\D2

1

2

1

2

5

2

3

-1

Strategia (2,2), wynik(3,-1)

D1\D2

1

2

1

1

-2

2

2

2

Strategia (1,2), wynik(-2,-3)

D1\D2

1

2

1

3

4

2

3

2

Strategia (2,2), wynik(2,0)

D1\D2

1

2

1

3

2

2

0

1

Strategia (2,1), wynik(0,0)

D1\D2

1

2

1

1

3

2

5

1

Strategia (2,2), wynik(1,3)

D1\D2

1

2

1

7

5

2

3

1

Strategia (2,2), wynik(1,2)

D1\D2

1

2

1

2

6

2

3

7

Strategia (1,1), wynik(2,2)

D1\D2

1

2

1

2

2

2

4

4

Strategia (1,2), wynik(2,0)

D1\D2

1

2

1

1

-4

2

2

1

Strategia (1,2), wynik(-4,-2)

D1\D2

1

2

1

4

3

2

3

2

Strategia (2,2), wynik(2,-1)

D1\D2

1

2

1

0

-1

2

1

5

Strategia (1,1), wynik(0,-1)

D1\D2

1

2

1

1

-3

2

2

1

D1\D2

1

2

1

3

2

2

1

0

D1\D2

1

2

1

1

2

2

0

0

D1\D2

1

2

1

5

3

2

2

3

D1\D2

1

2

1

8

6

2

4

2

D1\D2

1

2

1

2

3

2

6

7

D1\D2

1

2

1

1

0

2

3

0

D1\D2

1

2

1

5

-2

2

3

1

D1\D2

1

2

1

-1

2

2

2

-1

D1\D2

1

2

1

-1

3

2

2

-2

D1\D2

1

2

1

2

5

2

1

4

Strategia (2,1), wynik(1,1)

D1\D2

1

2

1

3

6

2

1

4

Na poziomie etapu drugiego każdy z graczy podejmuje 4 decyzje

D1\D2

1

2

1

-1

1

2

-2

0

Strategia (2,1), wynik(-2,-1)

D1\D2

1

2

1

3

-2

2

2

0

Strategia (1,2), wynik(-2,-3)

D1\D2

1

2

1

1

1

2

2

2

Strategia (2,2), wynik(2,0)

D1\D2

1

2

1

-4

2

2

0

1

D1\D2

1

2

1

2

0

2

-1

1

D1\D2

1

2

1

-1

-3

2

0

0

D1\D2

1

2

1

3

2

2

2

0

D1\D2

1

2

1

-2

-1

2

-1

1

Strategia (1,1), wynik(-4,-2)


W pierwszym etapie każdy z graczy podejmuje jedną decyzje

D1\D2

1

2

1

-2

-2

2

2

-4

Strategia (2,2), wynik(-4,-2)


Drzewo decyzyjne naszej gry :

D1\D2

1

2

1

-1

-3

2

0

-2

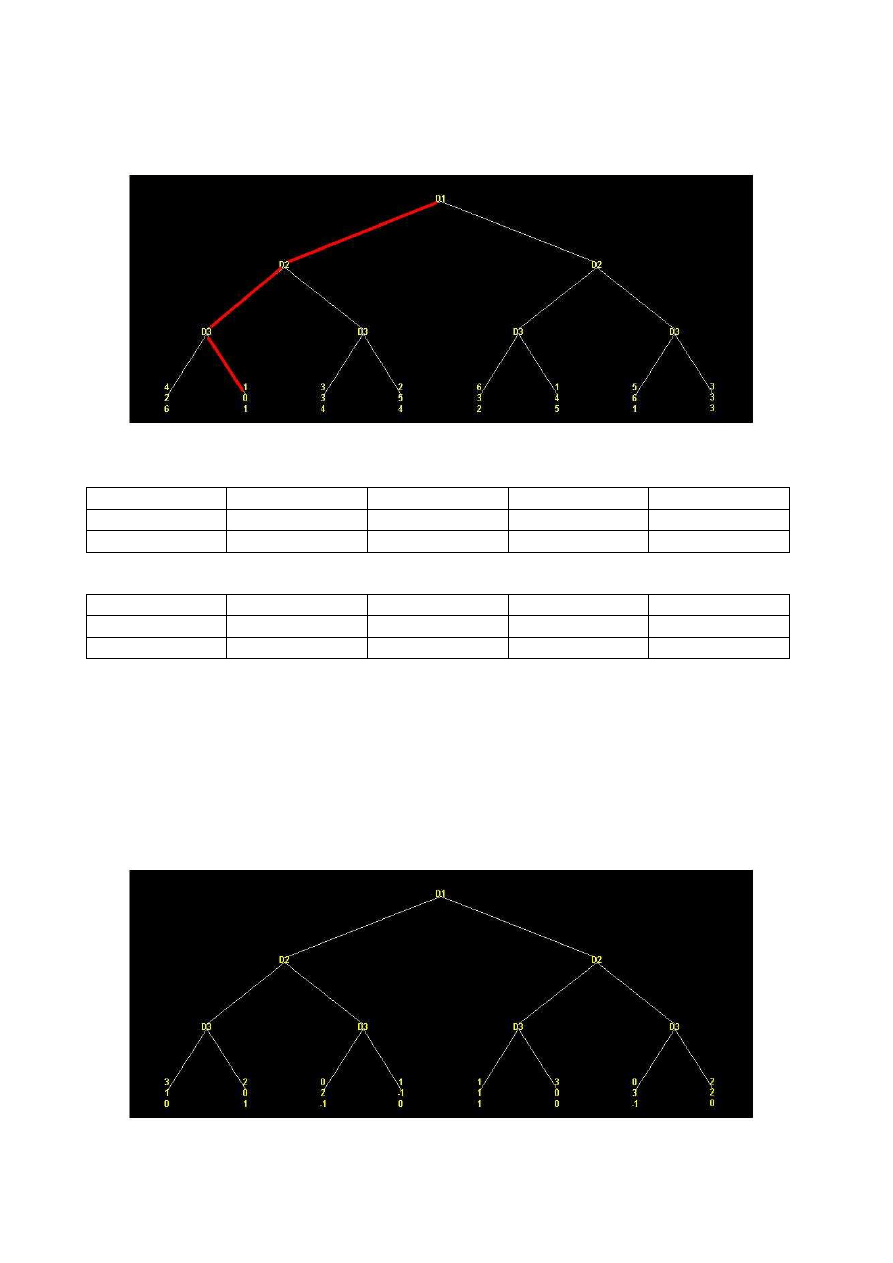
Zadanie 2.

Rozwiązanie problemu jednoetapowego dla trzech graczy.

Problem w postaci drzewa decyzyjnego:

Gra w postaci macierzowej

D1/D2 D3

1,1

1,2

2,1

2,2

1

2

0

3

5

2

6

1

4

4

D1/D2 D3

1,1

1,2

2,1

2,2

1

6

1

5

3

2

2

5

1

3

Strategia (1,1,2), wynik(1,0,1)


Zadanie 3.

Rozwiązanie problemu jednoetapowego dla trzech graczy z hierarchią.

Problem w postaci drzewa decyzyjnego:

Przy decyzji u1=1 otrzymamy macierze

D2/D3

1

2

1

1

0

2

2

-1

Strategia (1,1,1), wynik(3,1,0)


Przy decyzji u1=2 otrzymamy macierze

D2/D3

1

2

1

1

0

2

3

2

Strategia (2,1,2), wynik(2,0,1)

Gracz 1, jako iż wie jakie kroki podejmą pozostali gracze, aby zminimalizować swoje straty,
powinien zagrać w 2. Gra zakończy się wtedy z wynikiem (2,0,1)


Podsumowanie

Dzięki wykorzystaniu metody drzew decyzyjnych można lepiej opisać strukturę gry.
Obejmując wzrokiem wszystkie możliwe opcje gry, jesteśmy w stanie wyznaczyć strategie
odpowiednią dla wszystkich graczy.
Wprowadzenie hierarchii do gier powoduje, że jeden z gracz pełniący funkcje lidera, jest w
stanie przewidzieć zagrania pozostałych graczy i dostosować swoje decyzje do uzyskania jak
najbardziej korzystnego wyniku dla niego.


Listing programu

D2/D3

1

2

1

0

1

2

-1

0

D2/D3

1

2

1

1

0

2

-1

0