
Podstawy Robotyki
Sprawozdanie
Dynamika
Krzysztof Gruba
grupa 23
rok IID
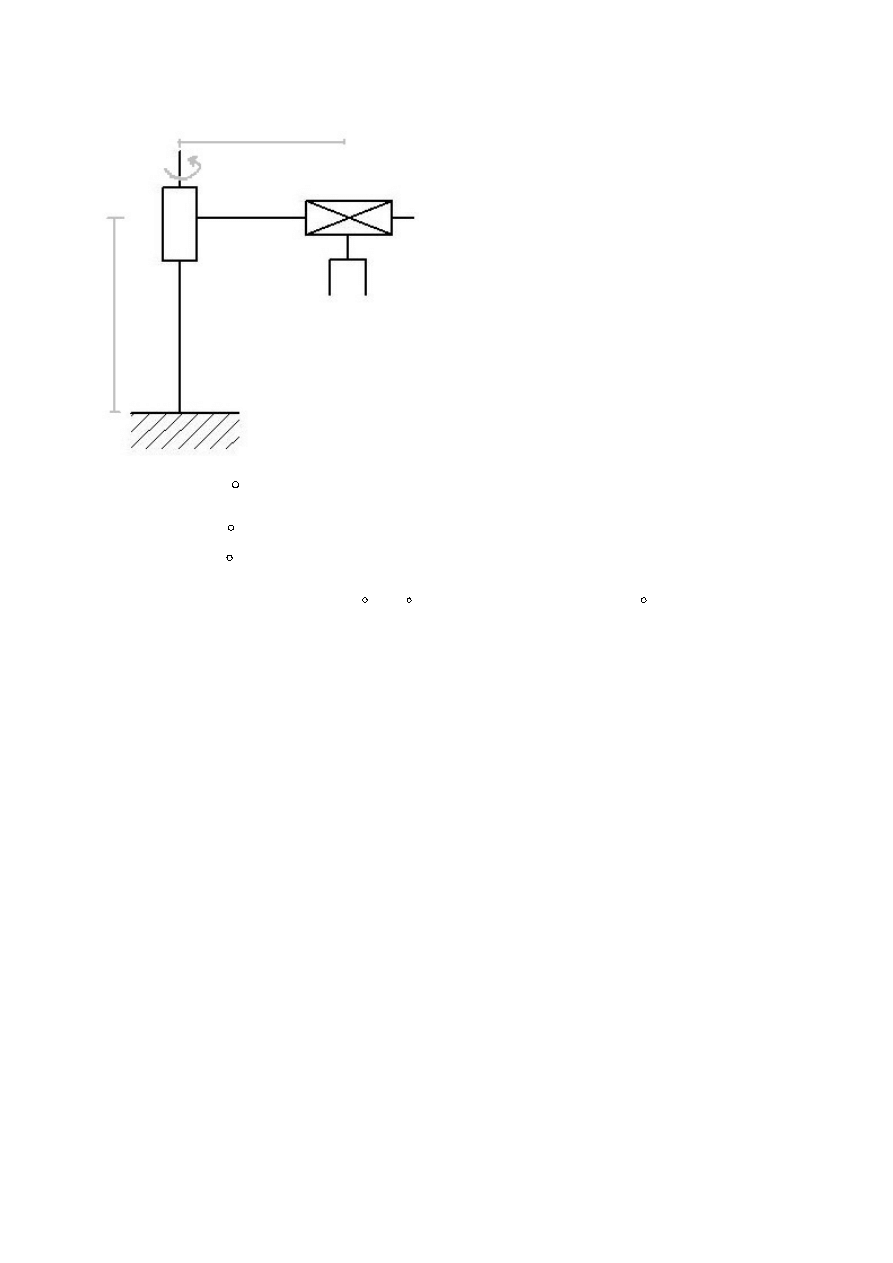
1)
x
2
θ
1
2
1
x
1
Dane:
J
1
, m
1
, m
2
E
1
= ½∙m
1
∙ẋ
1
2
+ ½∙J
1
θ
1
2
E
2
= ½∙m
2
(ẋ
1
2
+ ẋ
2
2
)
E = ½∙m
1
∙ẋ
1
2
+ ½∙J
1
θ
1
2
+ ½∙m
2
(ẋ
1
2
+ ẋ
2
2
)
V
1
= m
1
x
1
g
V
2
= m
2
x
1
g
V = x
1
g(m
1
+ m
2
)
L = ½∙m
1
∙ẋ
1
2
+ ½∙J
1
θ
1
2
+ ½∙m
2
(ẋ
1
2
+ ẋ
2
2
) - x
1
g(m
1
+ m
2
)
δL/δθ
1
= 0
δL/δx
1
= -g(m
1
+ m
2
)
δL/δx
2
= 0
δL/δθ
1
= J
1
θ
1
δL/δẋ
1
= m
1
∙ẋ
1
+ m
2
∙ẋ
2
δL/δẋ
2
= m
2
∙ẋ
2
d/dt (δL/δθ
1
) = J
1
Ӫ
1
d/dt (δL/δx
1
) = m
1
∙ẍ
1
+ m
2
∙ẍ
2
d/dt (δL/δx
2
) = m
2
∙ẍ
2
J
1
Ӫ
1
= τ
1
m
1
∙ẍ
1
+ m
2
∙ẍ
2
+ g(m
1
+ m
2
) = τ
2
m
2
∙ẍ
2
= τ
3
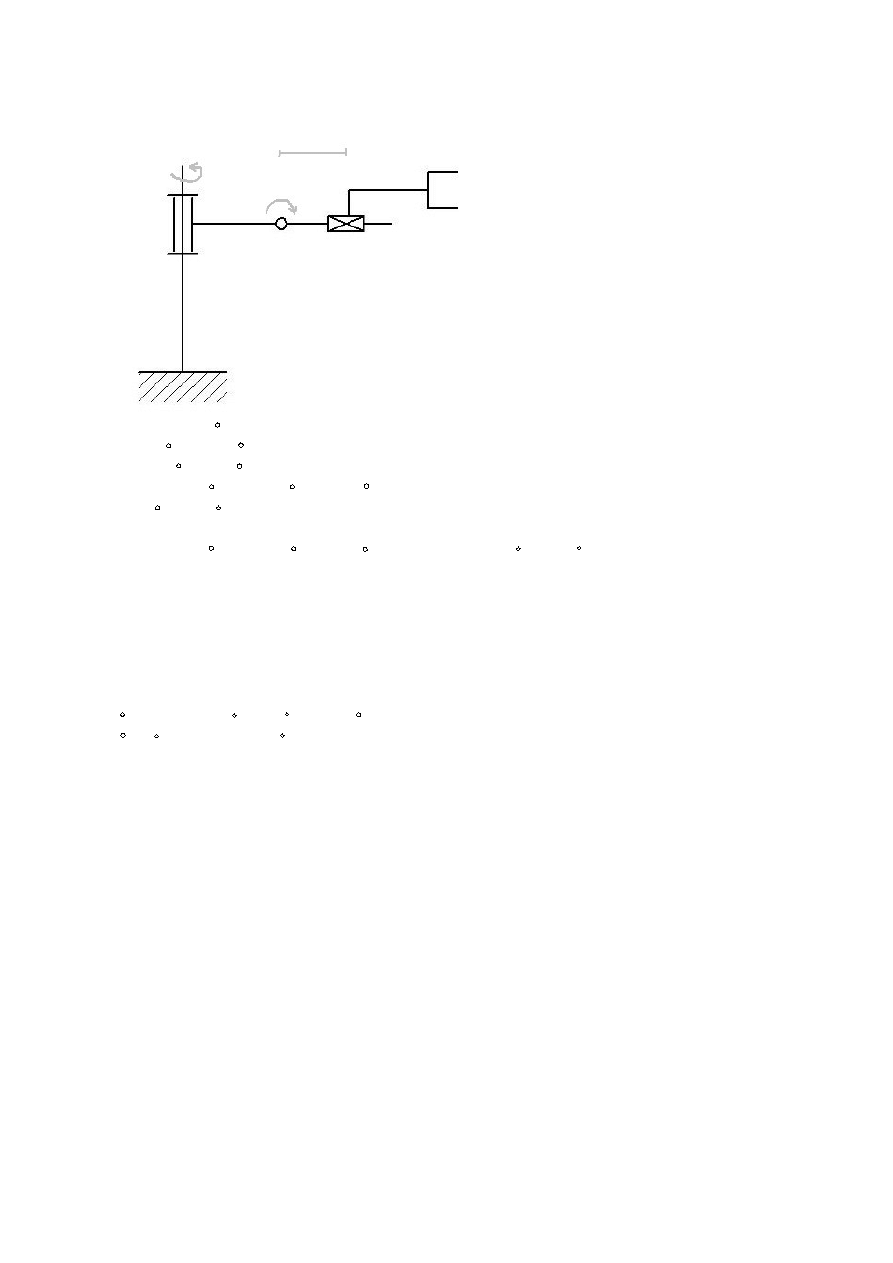
2)
x
3
θ
1
3
θ
2
1
2
Dane:
m
1
, m
2
, m
3
E
1
= ½(1/3∙m
1
l
1
2
)∙θ
1
2
E
2
= ½∙m
2
(θ
1
l
1
)
2
+ ½∙θ
2
(1/3m
2
l
2
2
)
E
3
= ½∙m
3
( (θ
1
l
1
)
2
+ (θ
2
l
2
)
2
+ ẋ
3
2
)
E = ½(1/3∙m
1
l
1
2
)∙θ
1
2
+ ½∙m
2
(θ
1
l
1
)
2
+ ½∙θ
2
(1/3m
2
l
2
2
) +
+ ½∙m
3
( (θ
1
l
1
)
2
+ (θ
2
l
2
)
2
+ ẋ
3
2
)
V
1
= 0
V
2
= m
2
g∙½∙l
2
∙sinθ
2
V
3
= m
3
gx
3
sinθ
2
V = m
2
g∙½∙l
2
∙sinθ
2
+ m
3
gx
3
sinθ
2
L = ½(1/3∙m
1
l
1
2
)∙θ
1
2
+ ½∙m
2
(θ
1
l
1
)
2
+ ½∙θ
2
(1/3m
2
l
2
2
) + ½∙m
3
((θ
1
l
1
)
2
+ (θ
2
l
2
)
2
+ ẋ
3
2
) - m
2
g∙½∙l
2
∙sinθ
2
-
- m
3
gx
3
sinθ
2
δL/δθ
1
= 0
δL/δθ
2
= - m
2
g∙½∙l
2
∙cosθ
2
– m
3
gx
3
cosθ
2
δL/δx
3
= - m
3
gsinθ
2
δL/δθ
1
= (1/3∙m
1
l
1
2
)∙θ
1
+ m
2
θ
1
l
1
2
+ m
3
θ
1
l
1
2
δL/δθ
2
= θ
2
(1/3m
2
l
2
2
) + m
3
θ
2
l
2
2
δL/δẋ
3
= m
3
ẋ
3
d/dt (δL/δθ
1
) = Ӫ
1
(1/3∙m
1
l
1
2
) + m
2
Ӫ
1
l
1
2
+ m
3
Ӫ
1
l
1
2
d/dt (δL/δx
1
) = Ӫ
2
(1/3m
2
l
2
2
) + m
3
Ӫ
2
l
2
2
d/dt (δL/δx
2
) = m
3
ẍ
3
Ӫ
1
(1/3∙m
1
l
1
2
) + m
2
Ӫ
1
l
1
2
+ m
3
Ӫ
1
l
1
2
= τ
1
Ӫ
2
(1/3m
2
l
2
2
) + m
3
Ӫ
2
l
2
2
+ m
2
g∙½∙l
2
∙cosθ
2
+ m
3
gx
3
cosθ
2
= τ
2
m
3
ẍ
3
+ m
3
gsinθ
2
= τ
3
Wyszukiwarka
Podobne podstrony:
podstawy robotyki odpowiedzi
CHRAPEK,podstawy robotyki, Urz dzenia chwytaj ce i g owice technologiczne robotów przemys owych cz 2
Podstawy Robotyki lab3 id 36832 Nieznany
prim sciaga, PG ETI AiR i eletele, Sem4, Podstawy Robotyki
Robotyka-ściąga2, Studia ATH AIR stacjonarne, Rok II, Semestr III, Podstawy robotyki I, Pomoce nauko
notatek pl egzamin podstawy robotyki 2
wzory do wspolrzednosciomierza, PK WM AiR, UCZELNIA, OD SOLTYSA, Podstawy Robotyki
więcej podobnych podstron