Moce w obwodach pr

ą

du

sinusoidalnie zmiennego

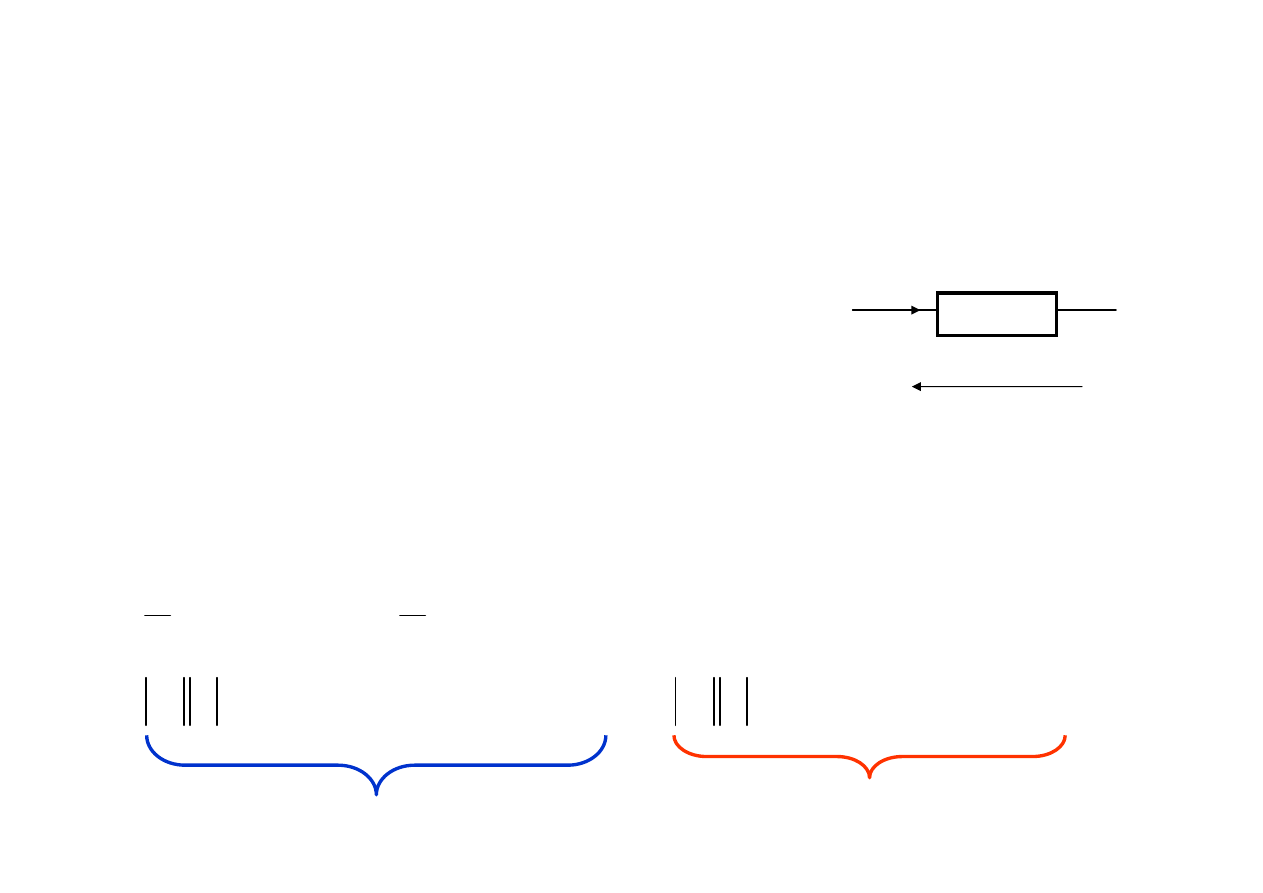
Rozpatrujemy dwójnik, którego napi

ę

cie i pr

ą

d maj

ą

t

ę

sam

ą

pulsacj

ę

u

i

moc chwilowa

)

sin(

)

sin(

)

sin(

i

m

i

m

u

m

t

I

i

t

U

t

U

u

ϕ

ω

ϕ

ϕ

ω

ϕ

ω

+

=

+

+

=

+

=

)

2

2

sin(

sin

))

2

2

cos(

1

(

cos

)

2

2

cos(

2

1

cos

2

1

)

sin(

)

sin(

i

i

i

m

m

m

m

i

m

i

m

t

I

U

t

I

U

t

I

U

I

U

t

I

t

U

ui

p

ϕ

ω

ϕ

ϕ

ω

ϕ

ϕ

ϕ

ω

ϕ

ϕ

ω

ϕ

ϕ

ω

+

+

+

−

=

+

+

−

=

+

+

+

=

=

podstawowe zale

ż

no

ś

ci

Moc chwilowa i moc czynna

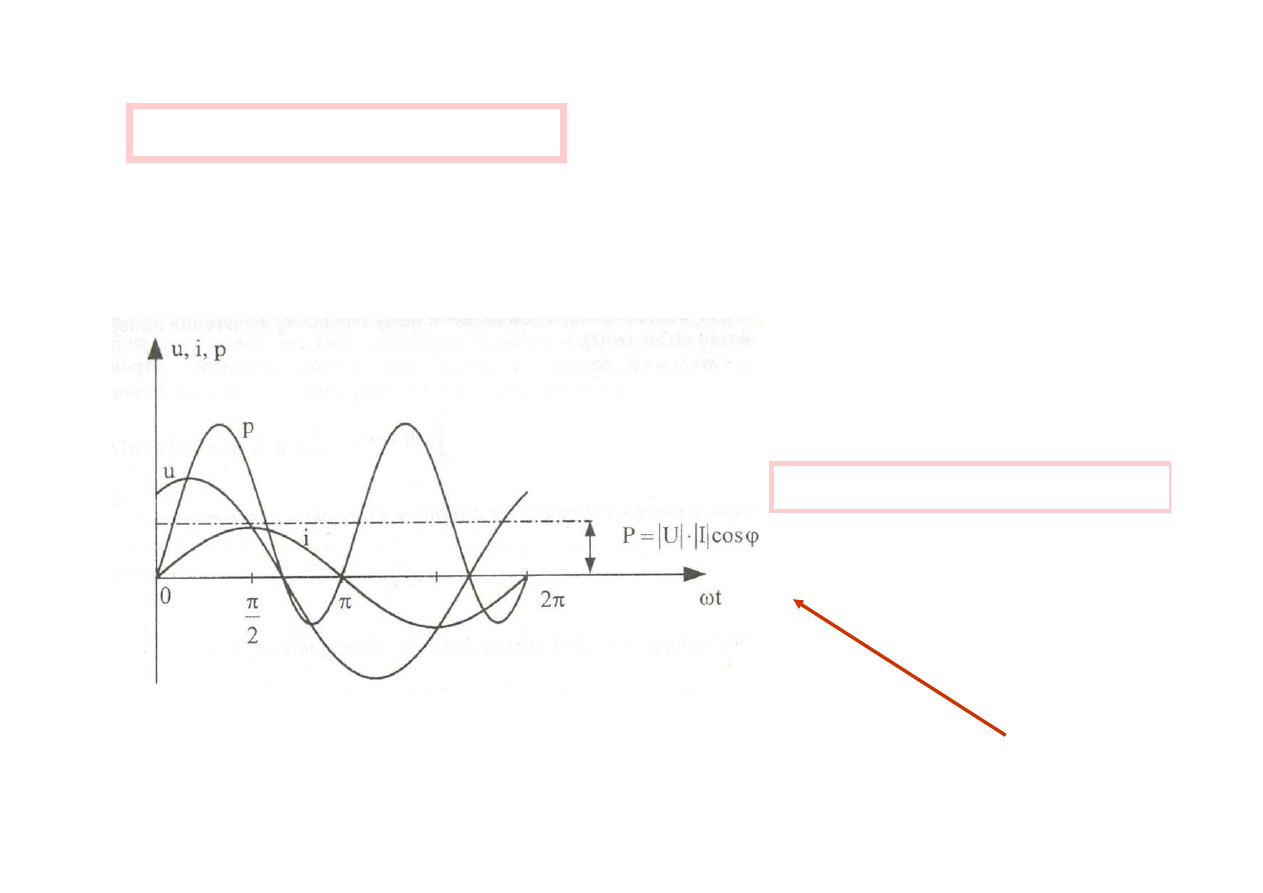
A wi

ę

c

p= p

1

+p

2

p

1

- składowa t

ę

tni

ą

ca mocy

p

2

- składowa przemienna mocy

przykładowe przebiegi u, i, p

moc czynna

moc czynna – czyli warto

ść ś

rednia za

okres mocy chwilowej

ϕ

cos

1

0

I

U

pdt

T

P

T

=

=

∫

Poniewa

ż

∫

=

T

dt

p

0

2

0

wi

ę

c

∫

=

T

dt

p

T

P

0

1

1

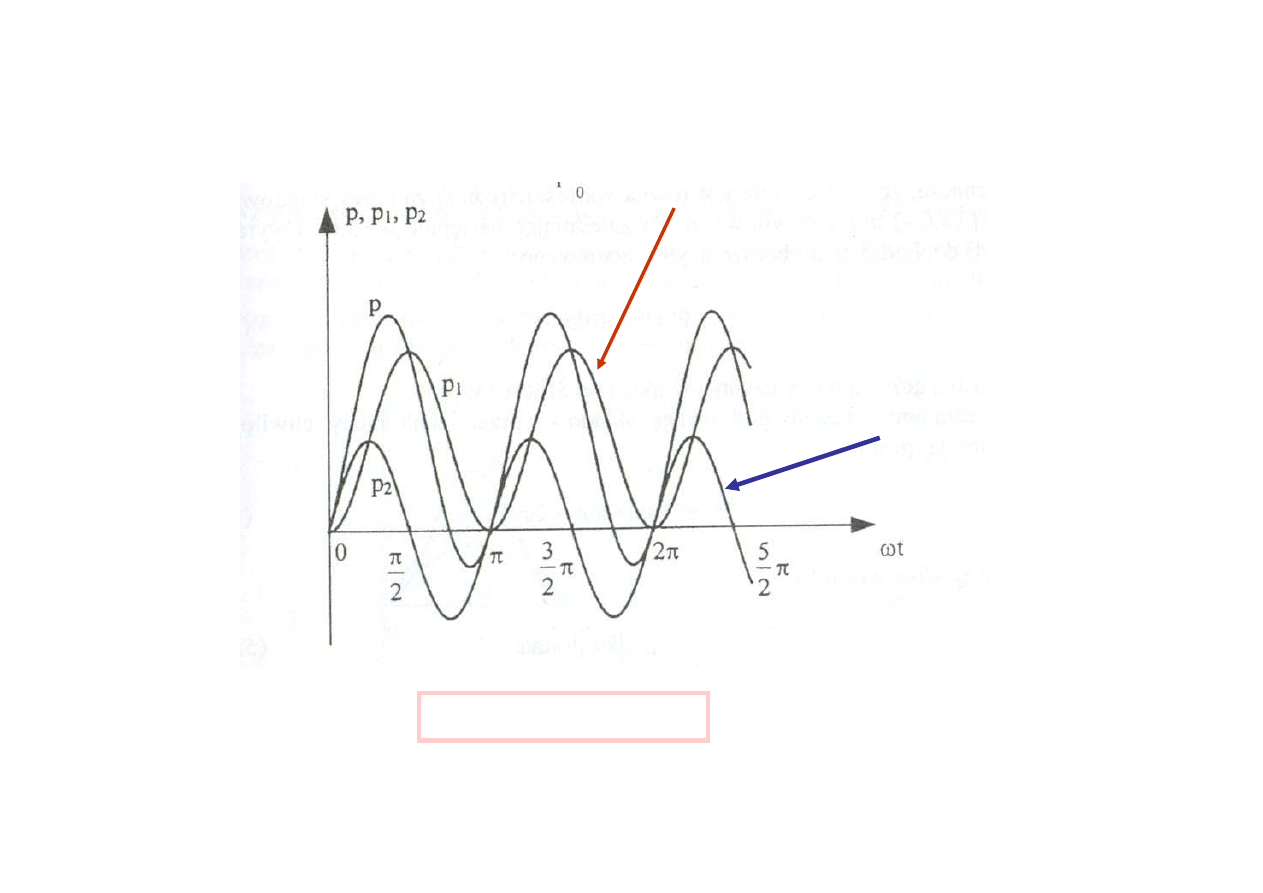
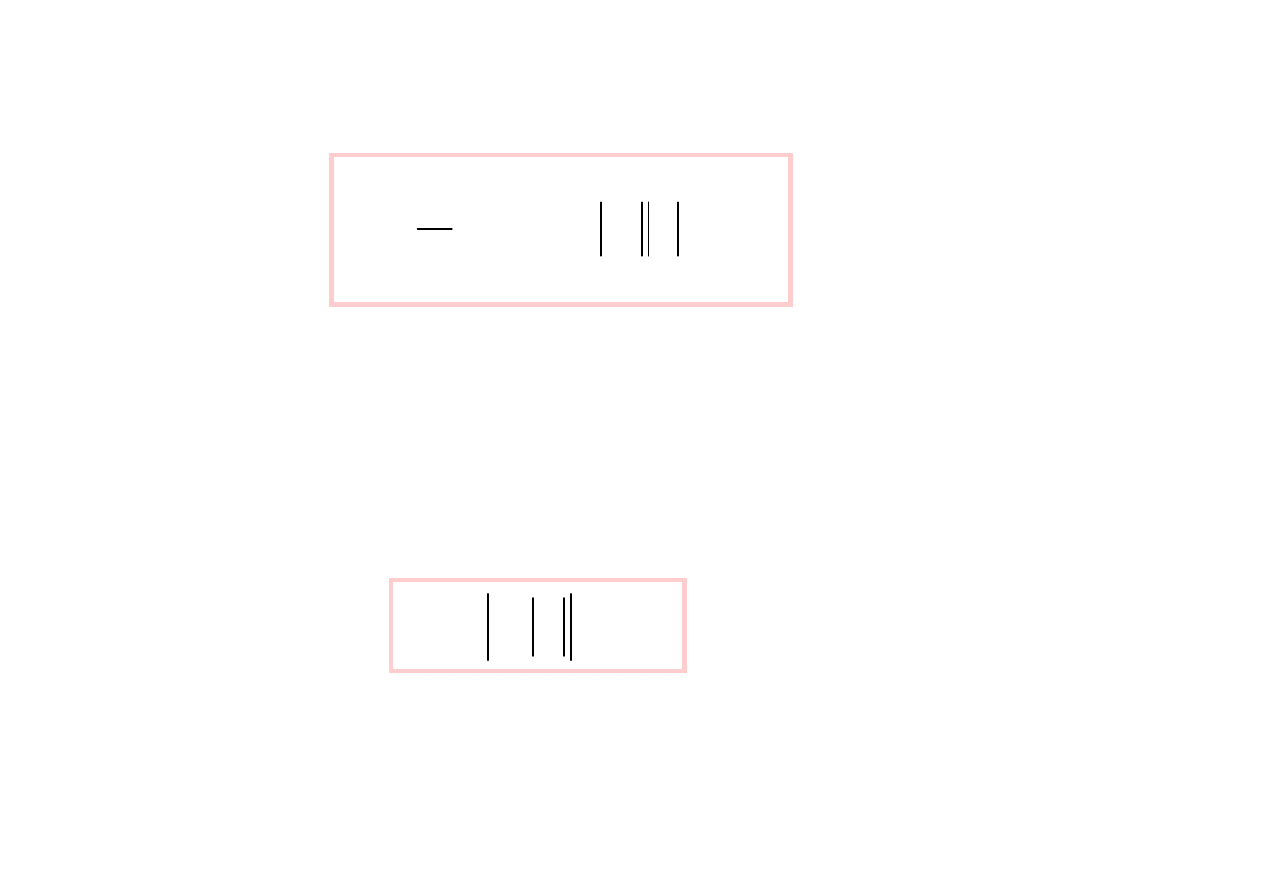
przebiegi p , p

1

i p

2

moc t

ę

tni

ą

ca

moc przemienna

Rozkład mocy chwilowej na moc t

ę

tni

ą

c

ą

i moc przemienn

ą

Wró

ć

my na moment do wzoru opisuj

ą

cego moc czynn

ą

ϕ

cos

1

0

I

U

pdt

T

P

T

=

=

∫

Podali

ś

my wcze

ś

niej ,

ż

e moc czynna równa si

ę

warto

ś

ci

ś

redniej za okres

składowej t

ę

tni

ą

cej mocy chwilowej p

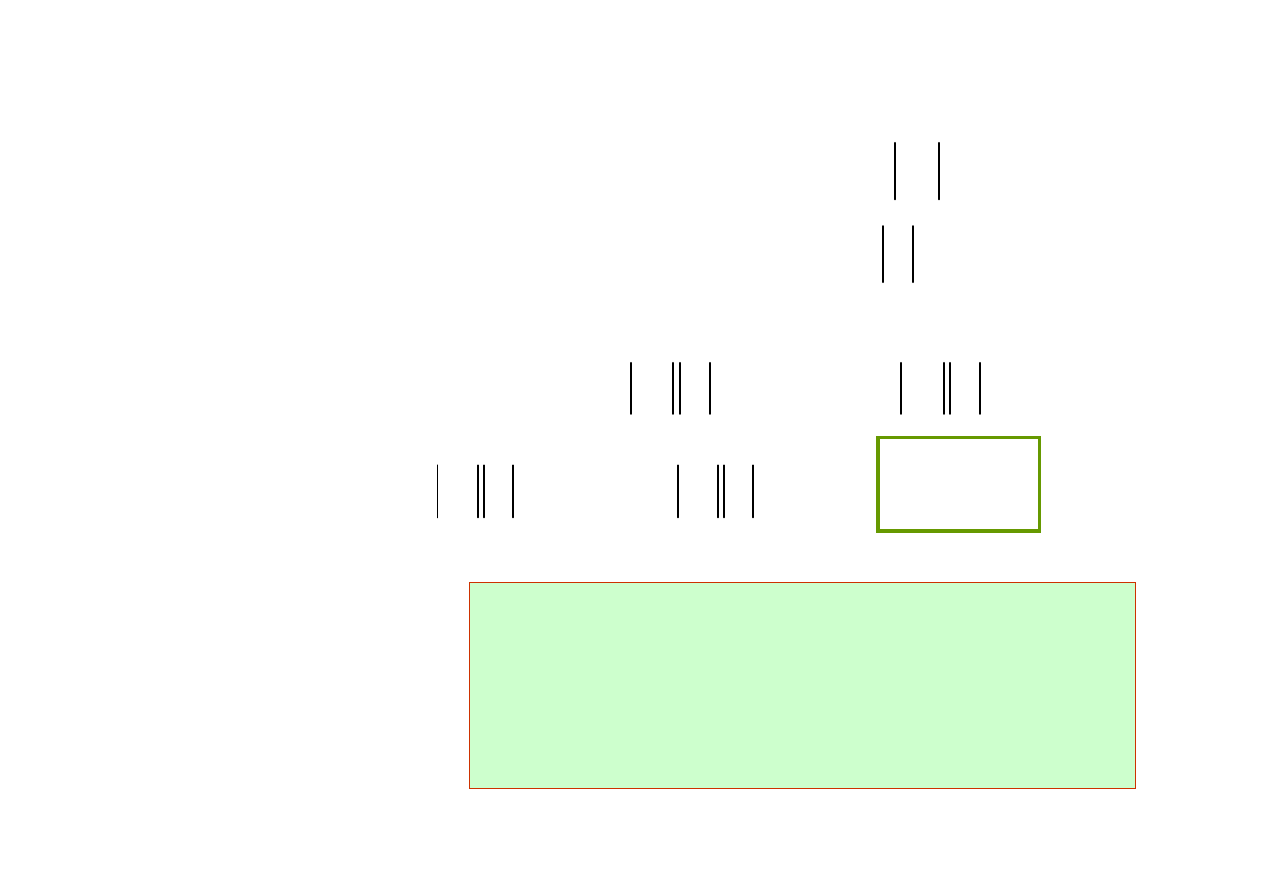
Natomiast moc bierna Q jest zwi

ą

zana ze składow

ą

przemienn

ą

mocy

chwilowej

ϕ

sin

I

U

Q

=

1W

1Var

Posługuj

ą

c si

ę

metod

ą

zespolona otrzymamy

:

je

ż

eli

to

i

u

j

j

e

I

I

e

U

U

ϕ

ϕ

=

=

i

u

i

m

u

m

t

I

i

t

U

u

ϕ

ϕ

ϕ

ϕ

ω

ϕ

ω

−

=

+

=

+

=

)

sin(

)

sin(

rozpatrzmy iloczyn

ϕ

ϕ

ϕ

j

j

e

I

U

e

I

U

UI

i

u

=

=

−

∗

)

(

czyli

jQ

P

I

U

j

I

U

UI

+

=

+

=

∗

ϕ

ϕ

sin

cos

Moc symboliczna

jest

liczb

ą

zespolon

ą

o cz

ęś

ci rzeczywistej równej

mocy czynnej oraz cz

ęś

ci urojonej równej

mocy biernej

S

UI

=

∗

VA

S

1

]

[

=

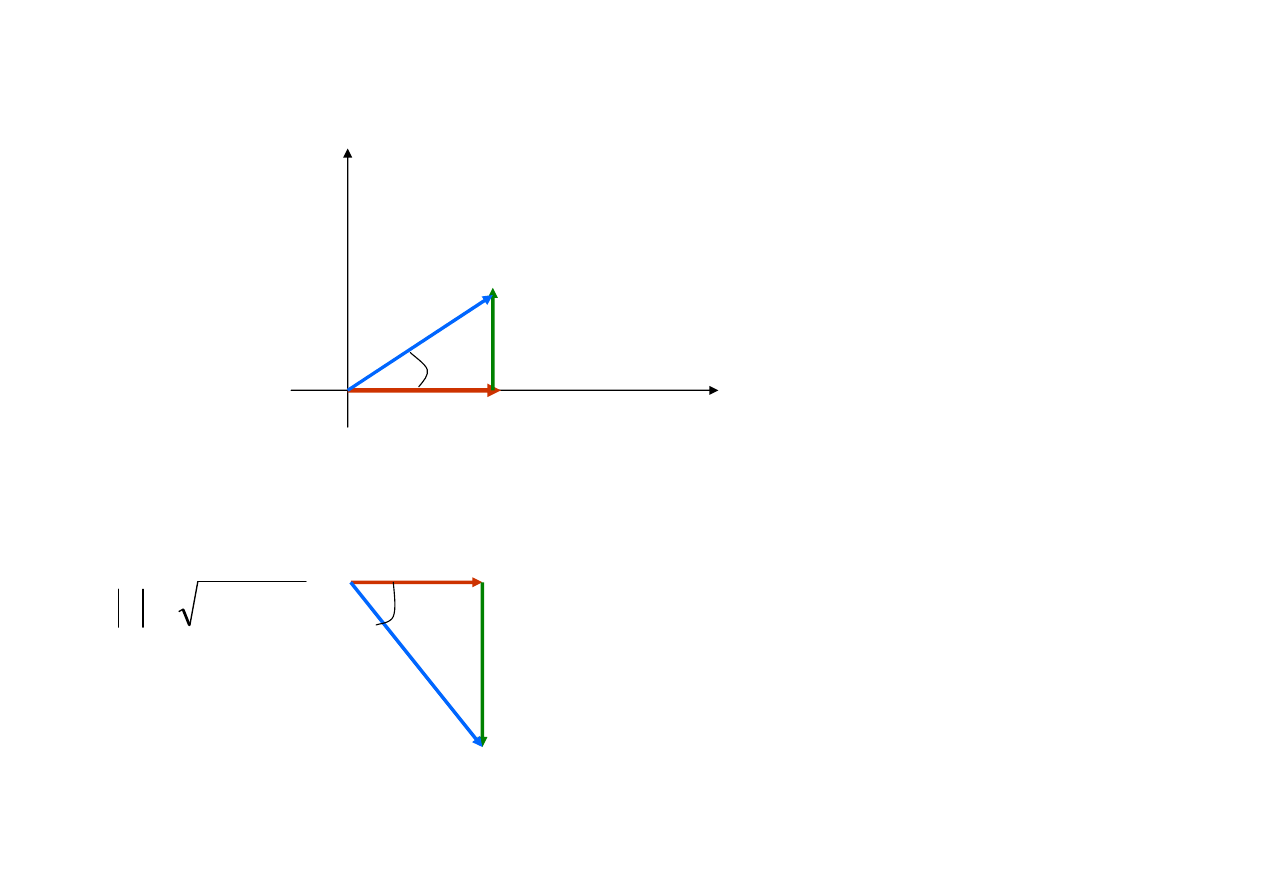
Geometryczn

ą

interpretacj

ą

mocy symbolicznej jest

trójk

ą

t mocy

)

Im( S

)

Re( S

P

jQ

jQ

P

S

+

=

0

Q > 0

P

Q < 0

|S|

Q

2

2

Q

P

S

+

=

u

i

Z

Rozpatrzmy dwójnik o impedancji

Z=R+jX

2

2

)

(

I

jX

I

R

II

jX

R

UI

jQ

P

S

+

=

=

+

=

=

+

=

∗

∗

P

Q

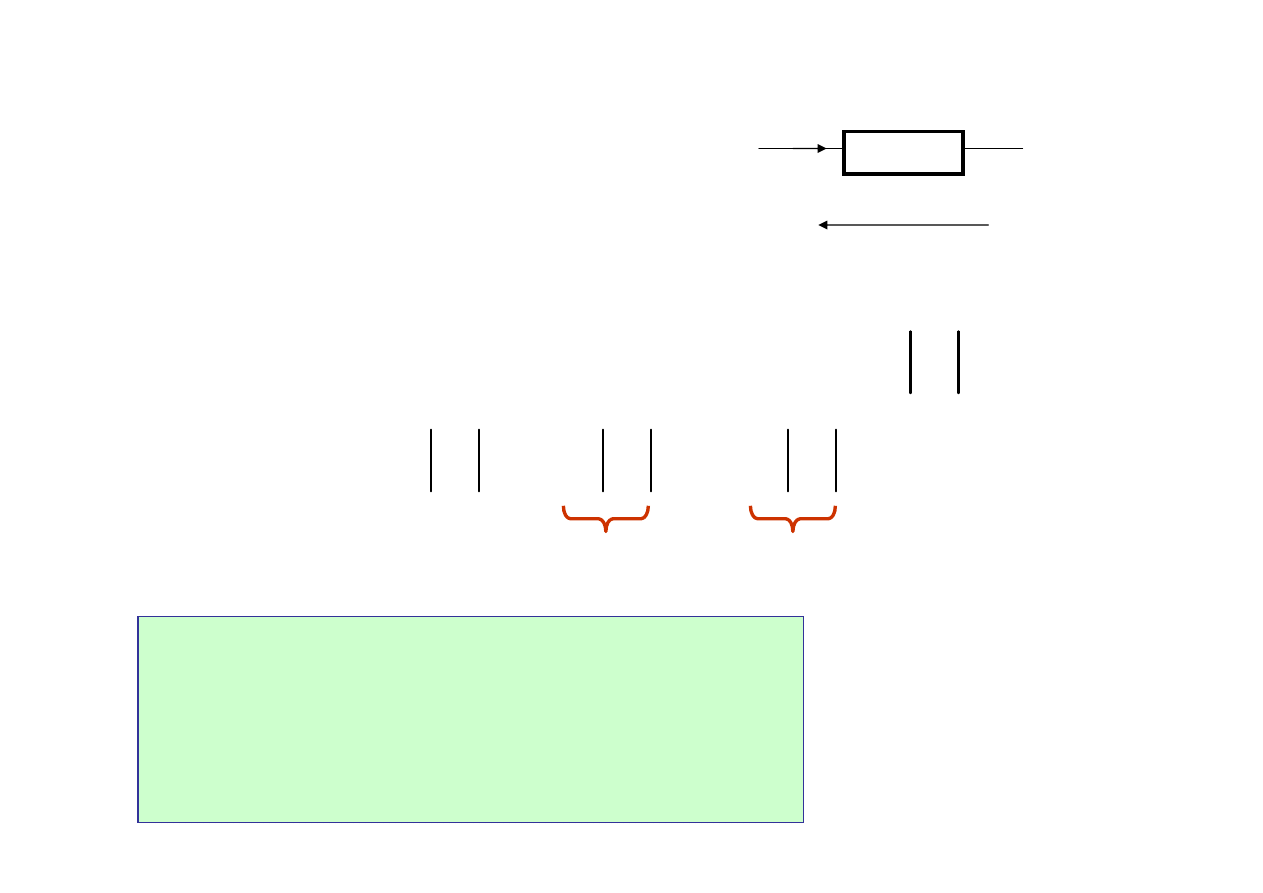
Moc symboliczna

jest

liczb

ą

zespolon

ą

o cz

ęś

ci rzeczywistej równej

mocy czynnej oraz cz

ęś

ci urojonej równej

mocy biernej

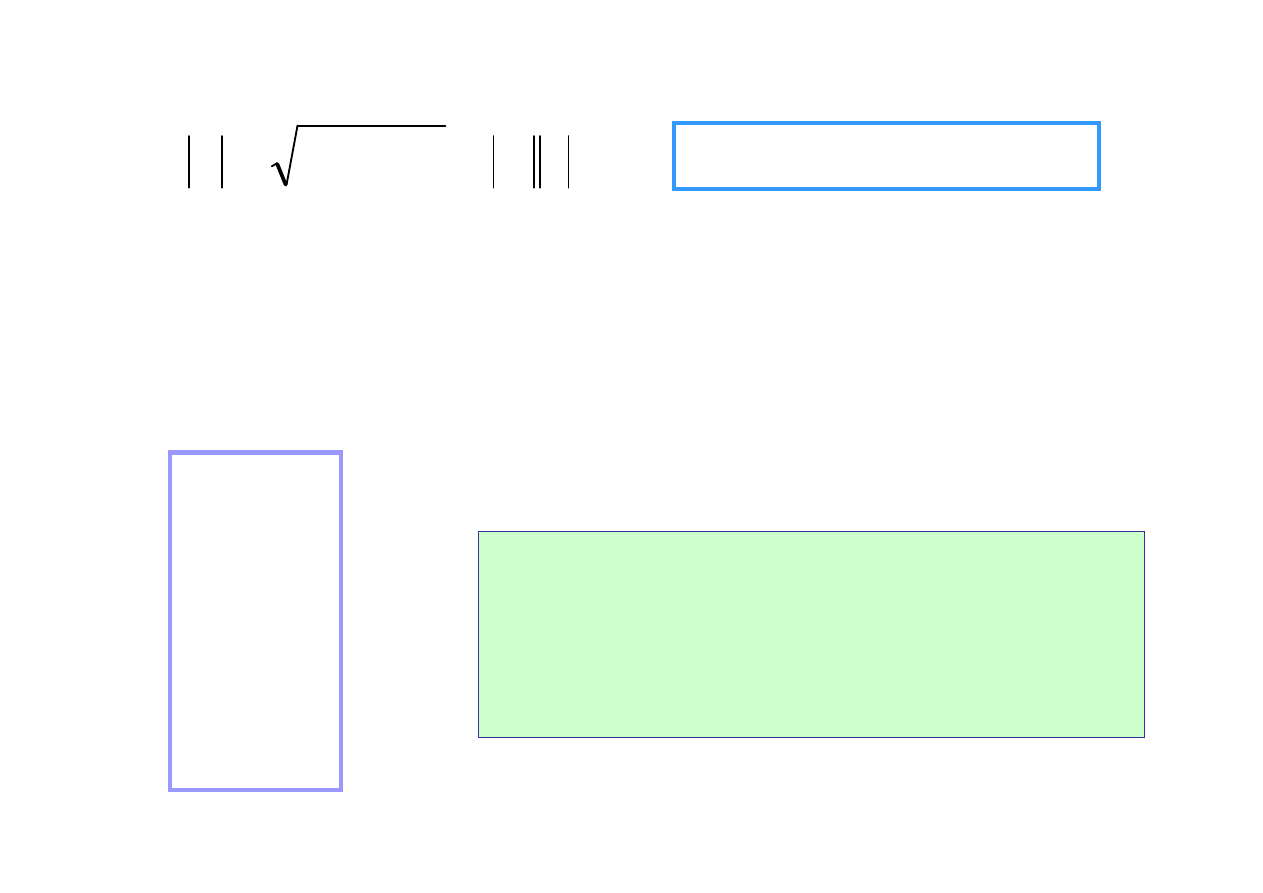
Dla dwójnika o admitancji

Y=G+jB

2

2

2

2

)

(

)

(

U

jB

U

G

U

jB

G

U

Y

YU

U

UI

jQ

P

S

−

=

−

=

=

=

=

=

+

=

∗

∗

∗

Q

P

u

i

Y

Moc symboliczna

jest

liczb

ą

zespolon

ą

o cz

ęś

ci rzeczywistej równej

mocy czynnej oraz cz

ęś

ci urojonej równej

mocy biernej

I

U

Q

P

S

=

+

=

2

2

Jest to moc pozorna

Jednostka jest VA

∑

∑

∑

=

=

=

n

k

n

k

n

k

Q

Q

P

P

S

S

1

1

1

Na podstawie znanego tw Tellegena otrzymujemy nast

ę

puj

ą

ce wzory

Moc symboliczna

jest

liczb

ą

zespolon

ą

o cz

ęś

ci rzeczywistej równej

mocy czynnej oraz cz

ęś

ci urojonej równej

mocy biernej

Dopasowanie odbiornika do źródła
ze względu na moc czynną

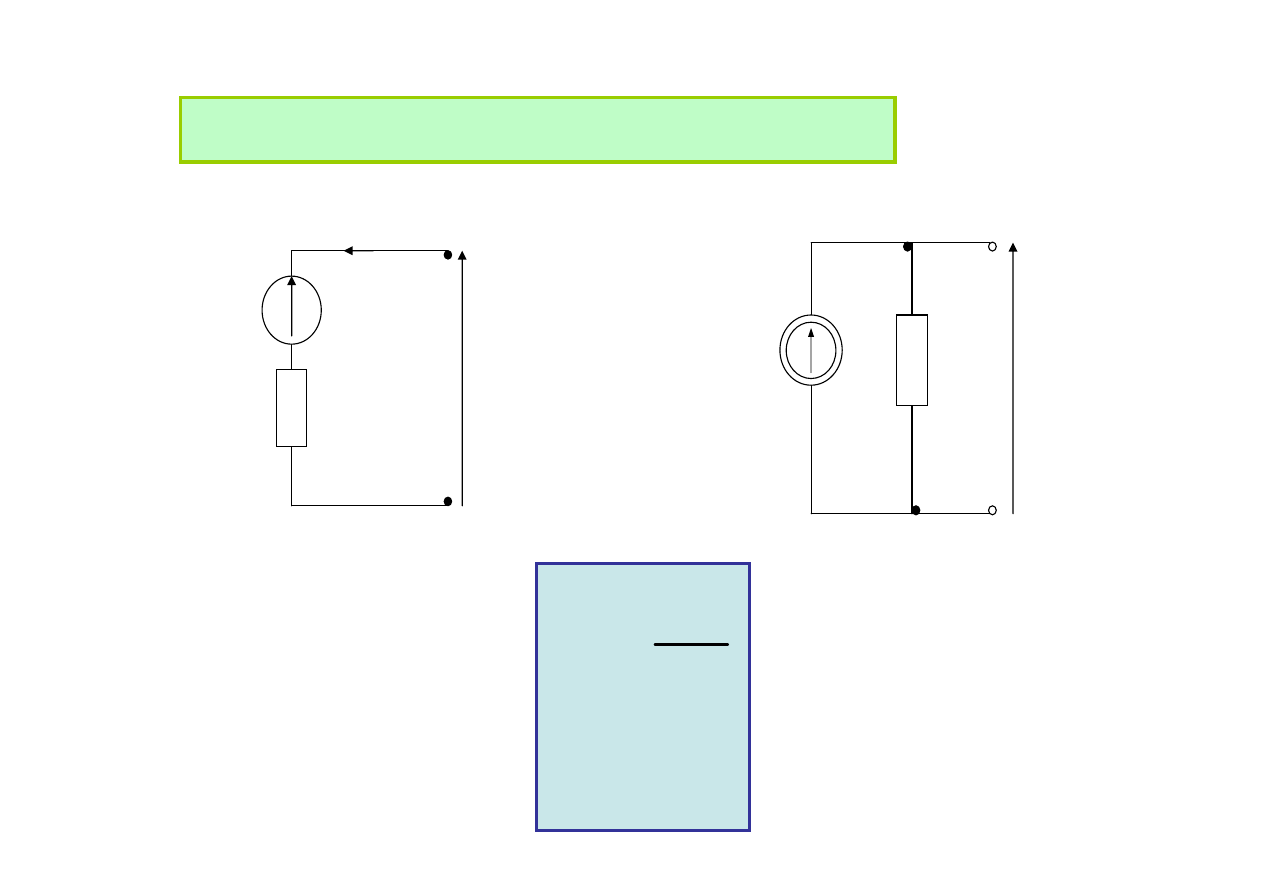
Rozpatrzmy rzeczywiste źródło energii

I

U

z

I

w

w

w

jB

G

Y

+

=

U

w

w

jX

R

Z

+

=

z

U

1

−

=

=

w

w

w

z

z

Z

Y

Z

U

I

( )

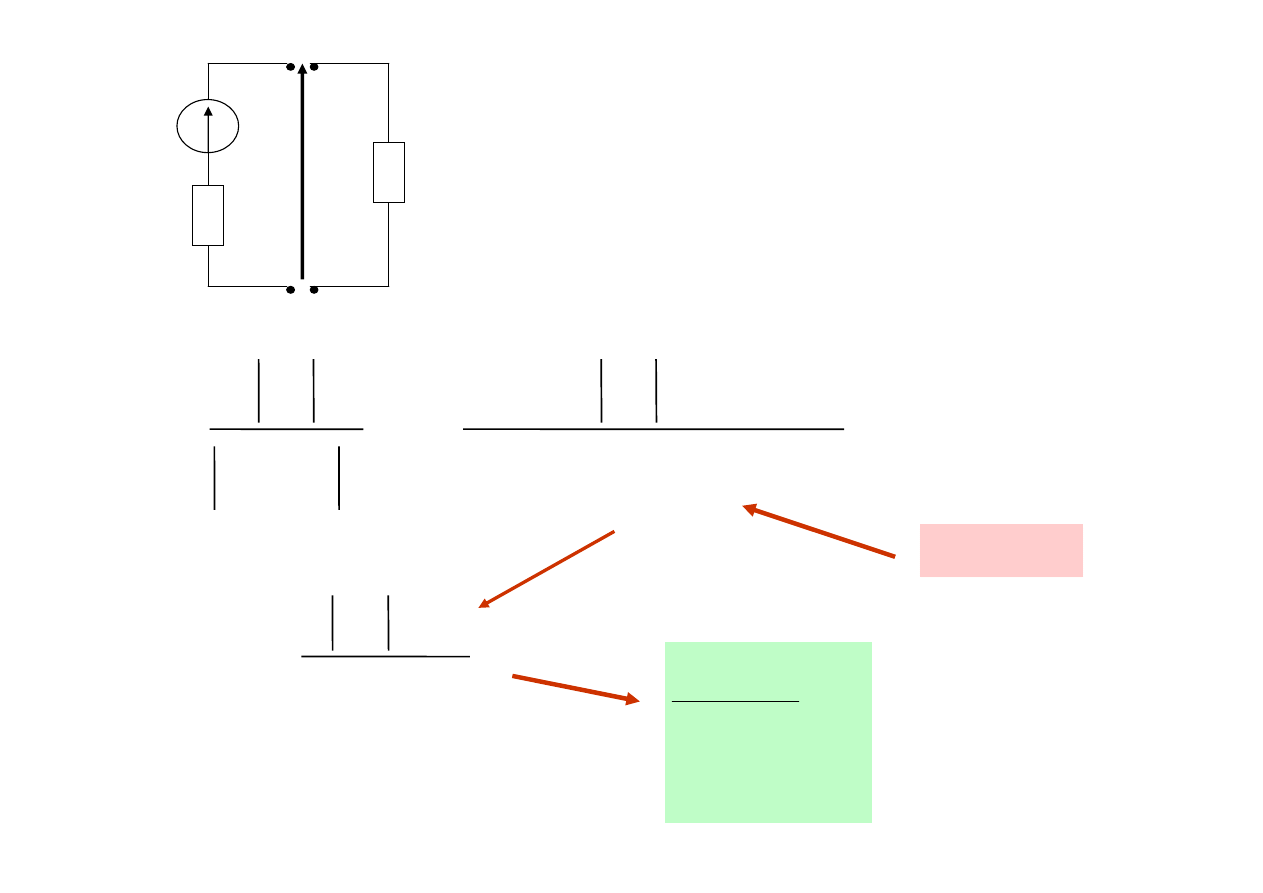
w

m

R

R

dR

R

dP

=

=

0

( )

(

)

2

2

max

w

z

R

R

R

U

R

P

+

=

w

X

X

−

=

(

) (

)

2

2

2

2

2

w

w

z

w

z

X

X

R

R

R

U

R

Z

Z

U

P

+

+

+

=

+

=

U

Z=R+jX

z

U

Dopasowanie odbiornika do źródła ze względu na moc
czynną zachodzi dla :

*

2

max

*

4

w

w

w

w

z

w

w

w

Y

jB

G

Y

R

U

P

Z

jX

R

Z

=

−

=

=

=

−

=

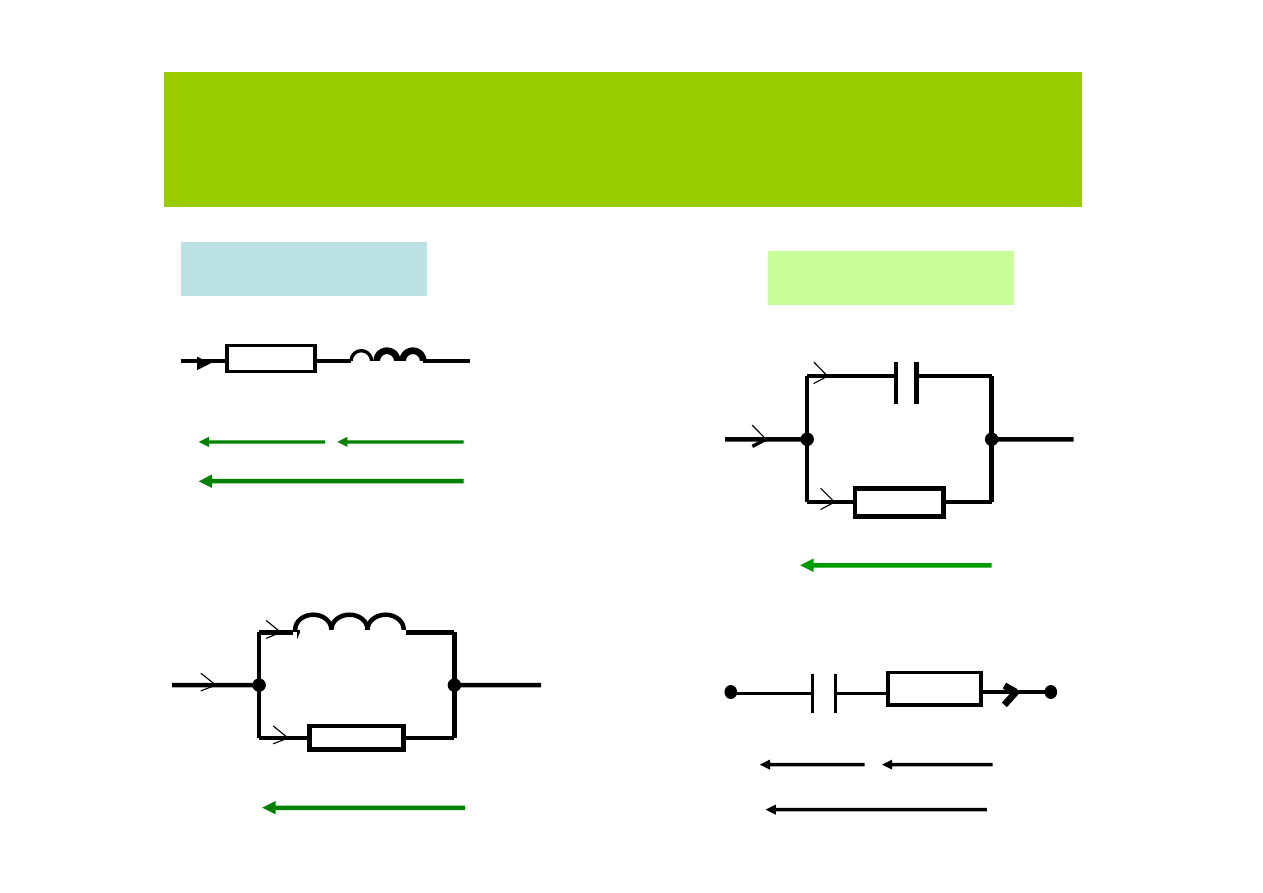
Elementy rzeczywiste

C

R

U

I

I

R

I

C

R

L

u

R

u

L

I

u

R

L

U

I

I

R

I

L

R

C

U

L

U

R

I

U

cewka

kondensator

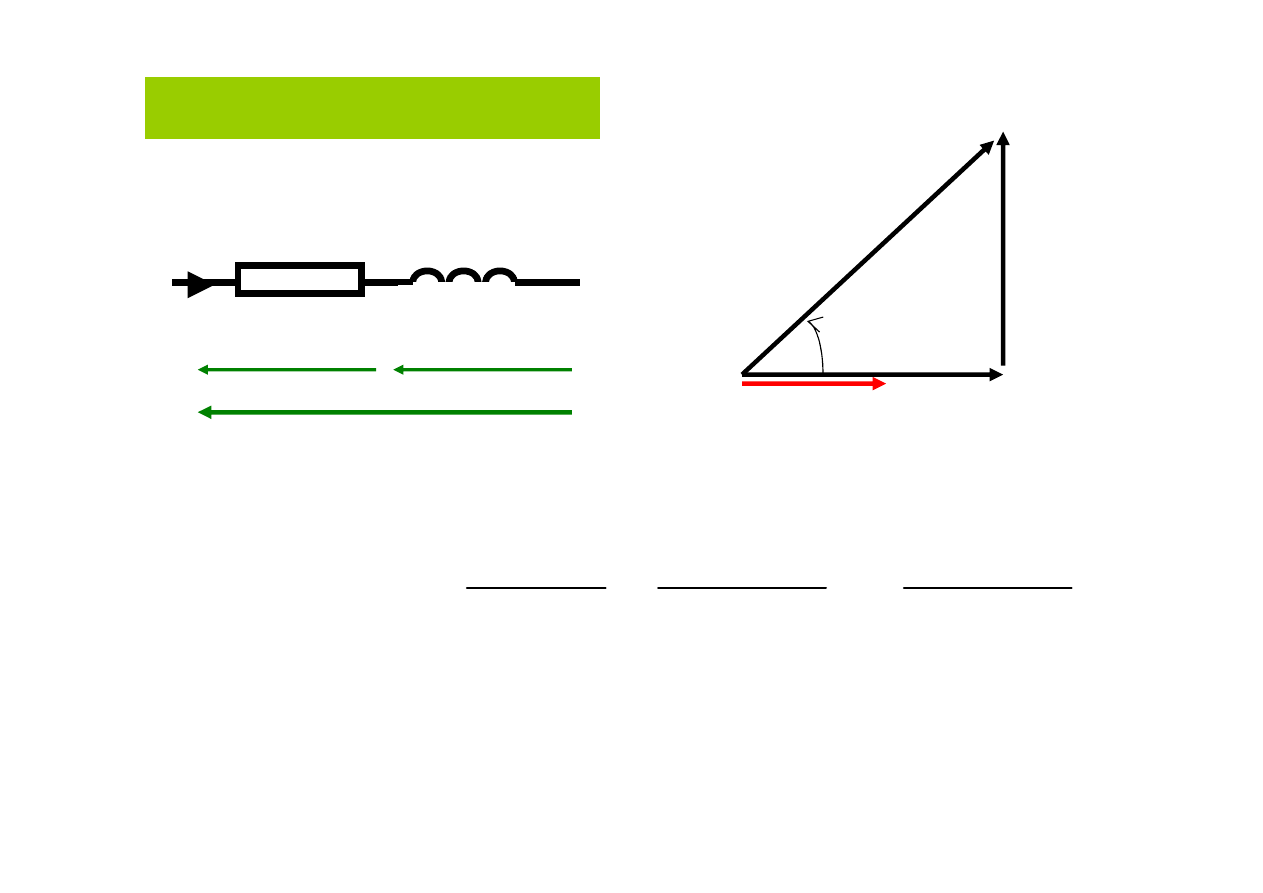
R

L

u

R

u

L

I

u

Połączenie szeregowe RL

I

U

R

U

L

U

ϕ

0

0

1

2

2

2

2

<

>

=

+

−

+

=

+

=

+

=

L

L

B

L

X

B

G

B

j

B

G

G

jB

G

L

j

R

Z

ω

ω

Przypomnienie!!!

(

)

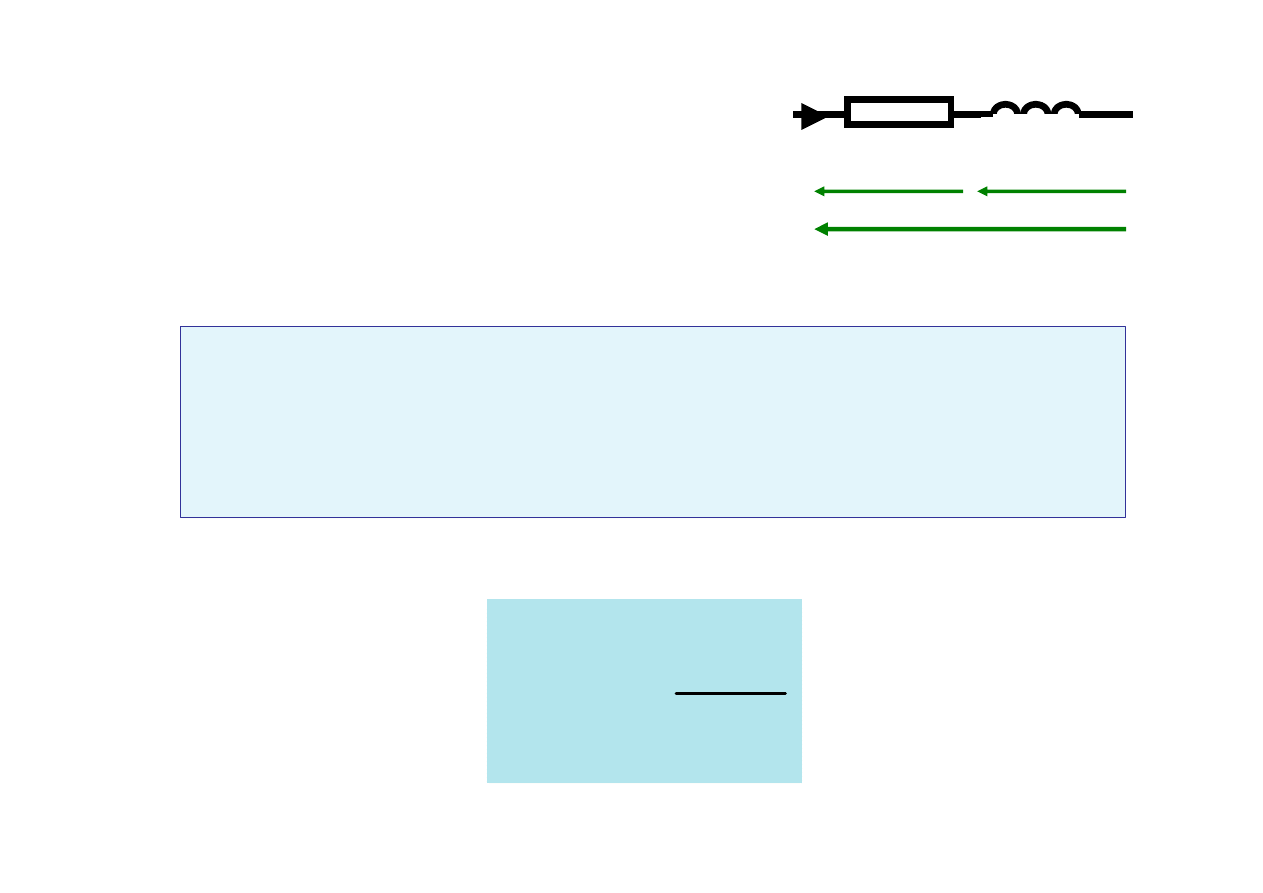
L

R

U

U

L

jI

IR

L

j

R

I

IZ

U

+

=

=

+

=

+

=

=

ω

ω

R

L

ω

ϕ

=

tg

R

L

u

R

u

L

I

u

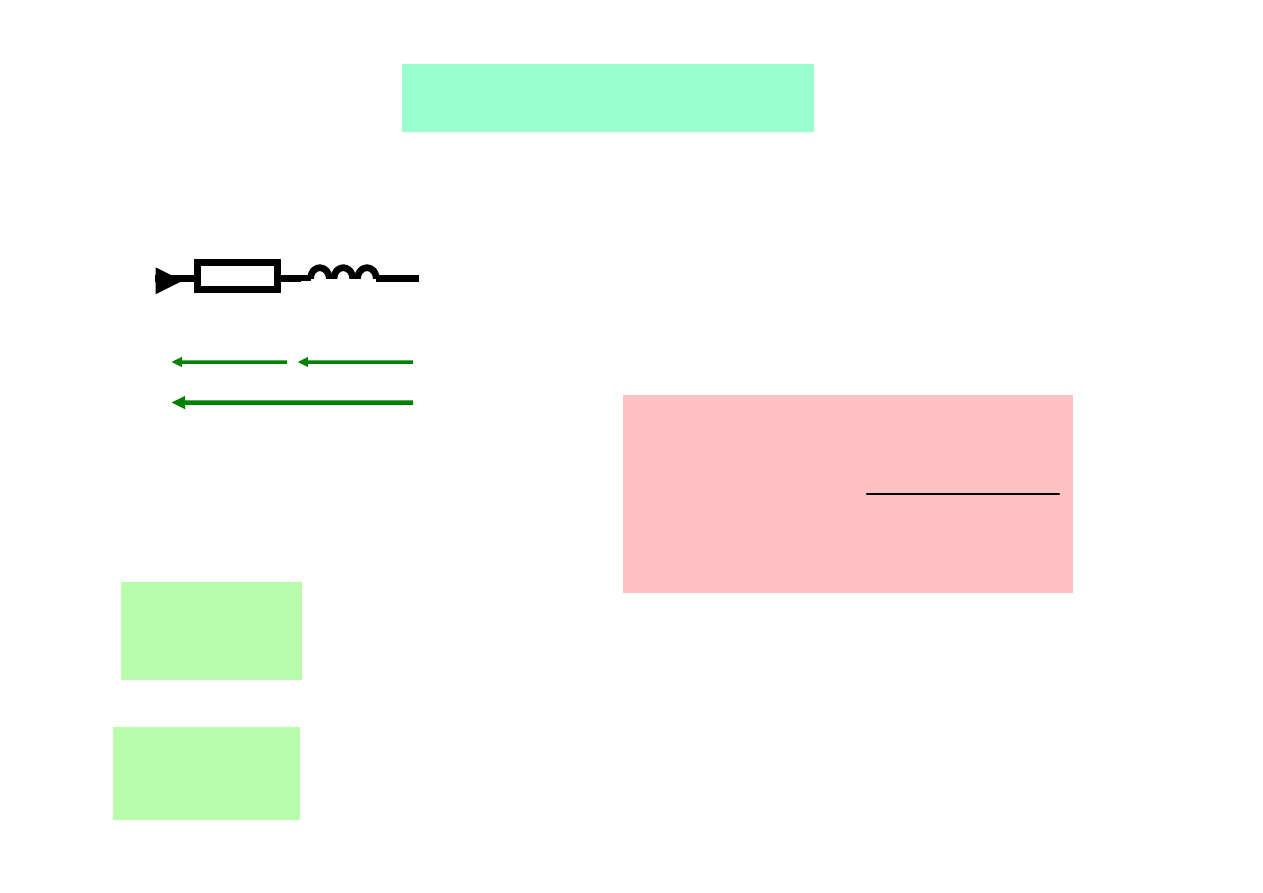
Cewka rzeczywista

Cewkę rzeczywistą charakteryzuje jej dobroć

Definicja
dobroci

( )

T

w

w

Q

R

L

L

max

2

π

=

max

L

w

( )

T

w

R

R

L

u

R

u

L

I

u

- wartość maksymalna energii w polu magnetycznym cewki

- energia rozproszona w rezystancji cewki w ciągu okresu

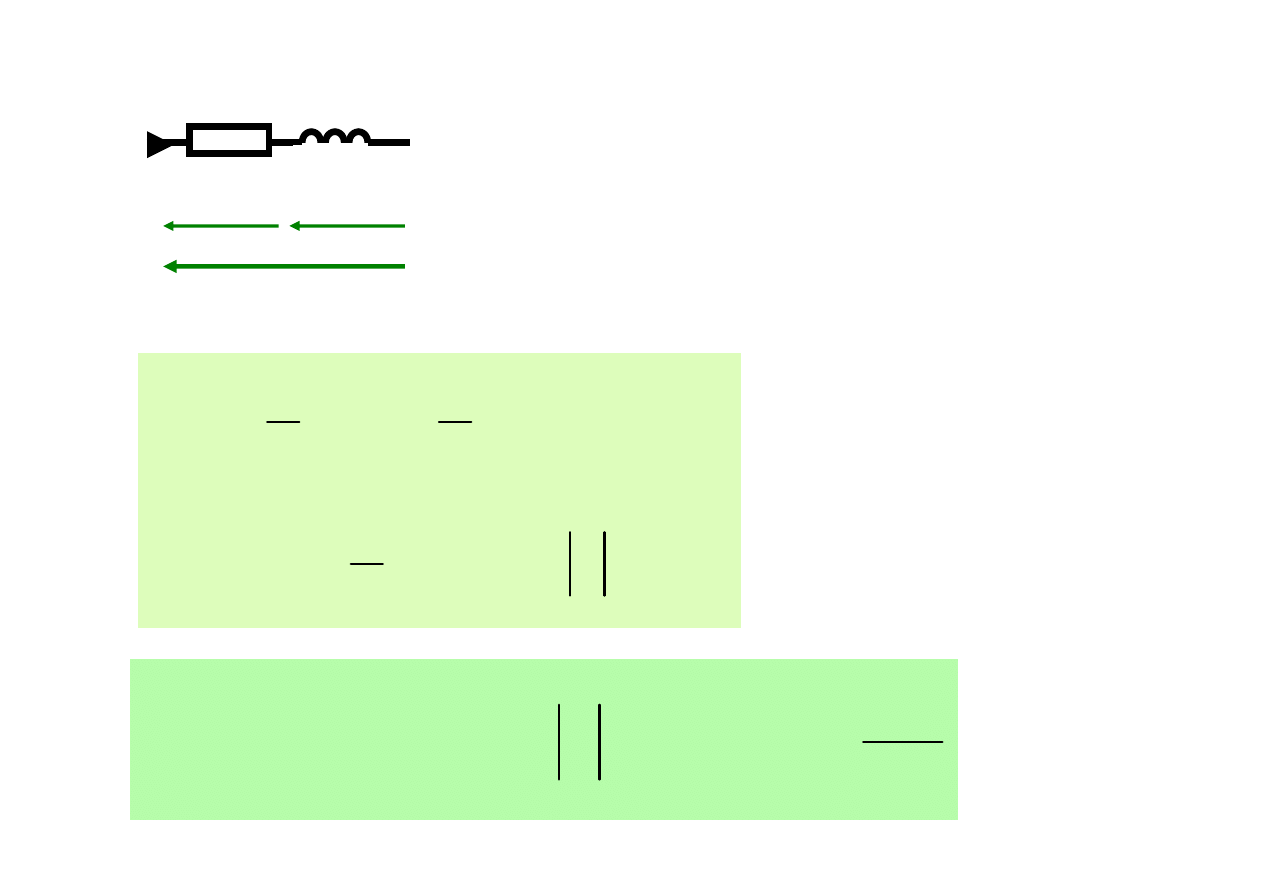
2

2

max

2

2

2

2

1

sin

2

1

2

1

I

L

LI

w

t

LI

Li

w

m

L

m

L

=

=

=

=

ω

( )

ω

π

2

2

=

=

=

T

T

I

R

PT

T

w

R

R

L

u

R

u

L

I

u

t

I

i

m

ω

sin

=

Je

ż

eli

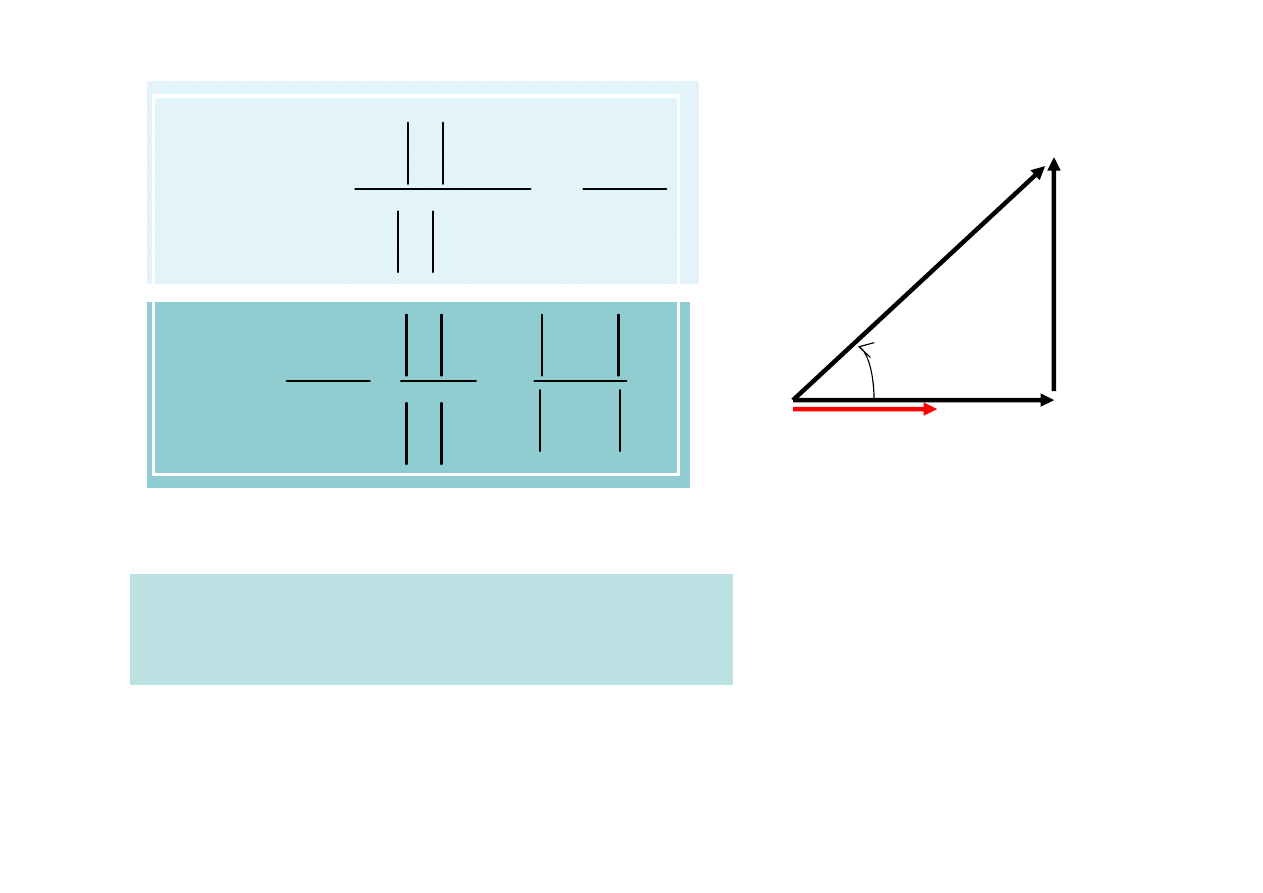
R

L

L

L

U

U

I

I

R

L

Q

R

L

I

R

I

L

Q

=

⋅

=

=

=

2

2

2

2

2

2

ω

ω

π

ω

π

I

U

R

U

L

U

ϕ

Interpretacja fizyczna dobroci
wynika z wykresu wskazowego

ϕ

tg

=

L

Q

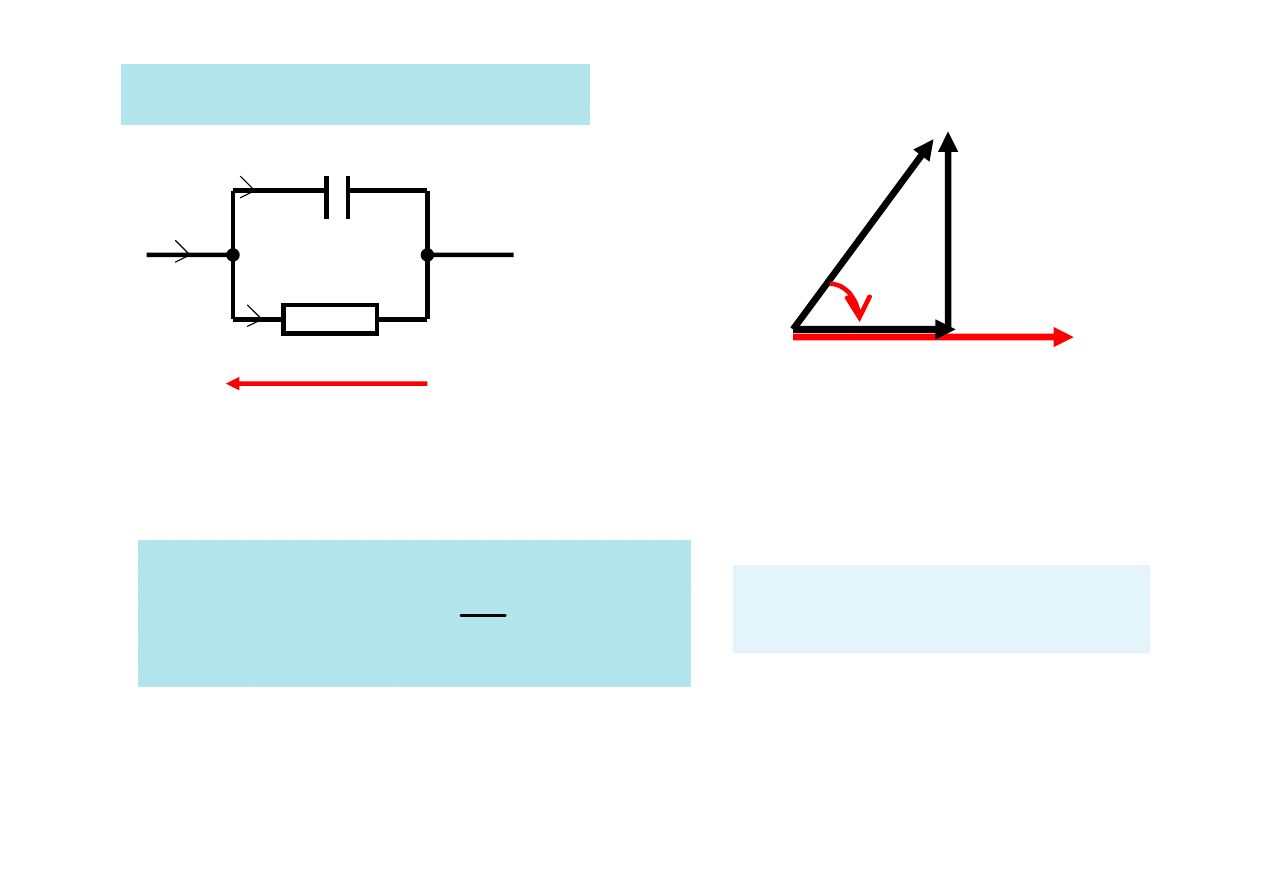
Połączenie równoległe RC

C

R

U

I

I

R

I

C

U

I

R

I

C

I

ϕ

C

j

R

jB

G

Y

ω

+

=

+

=

1

(

)

CR

ω

ϕ

=

−

tg

- kondensator rzeczywisty

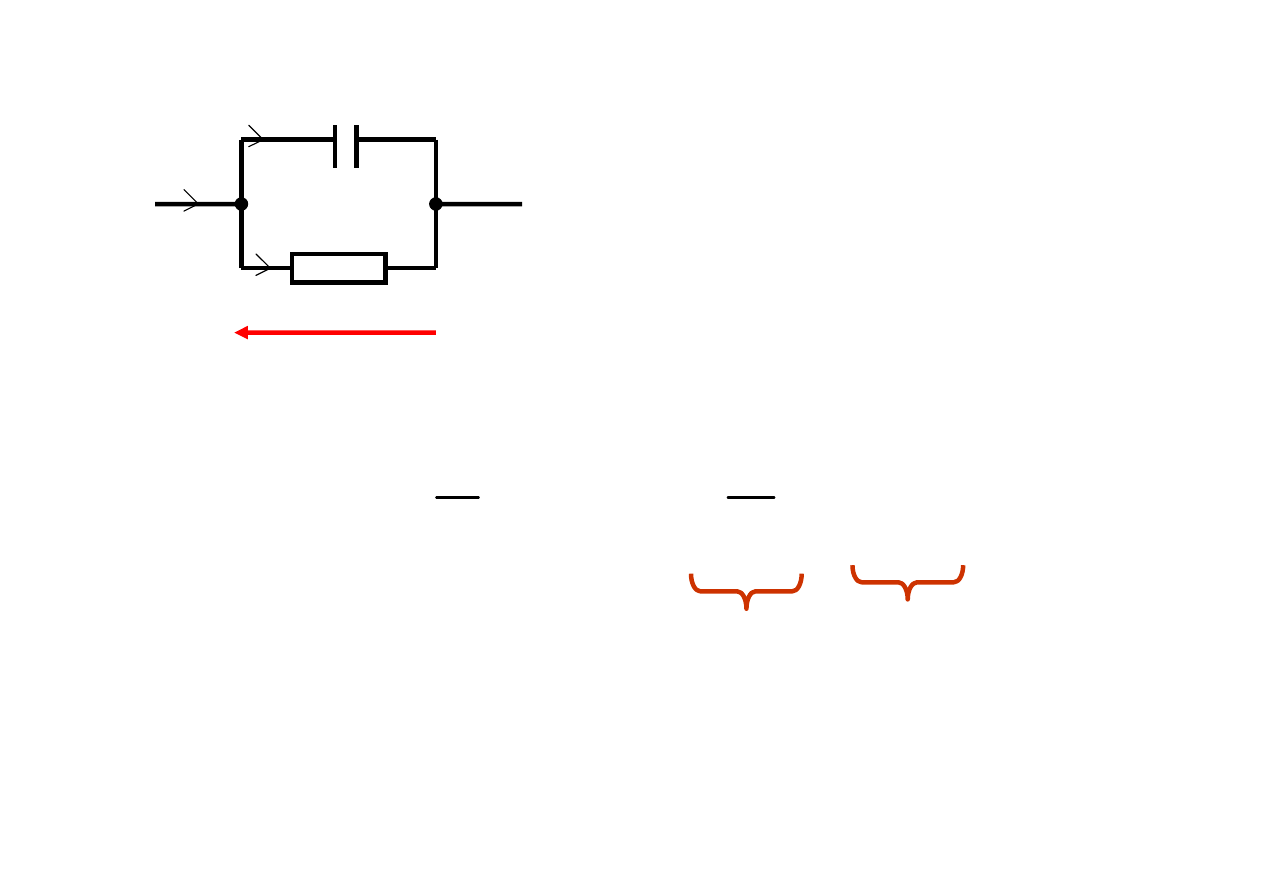
C

jU

R

U

C

j

R

U

UY

I

ω

ω

+

=













+

=

=

1

C

R

I

I

I

+

=

C

R

U

I

I

R

I

C

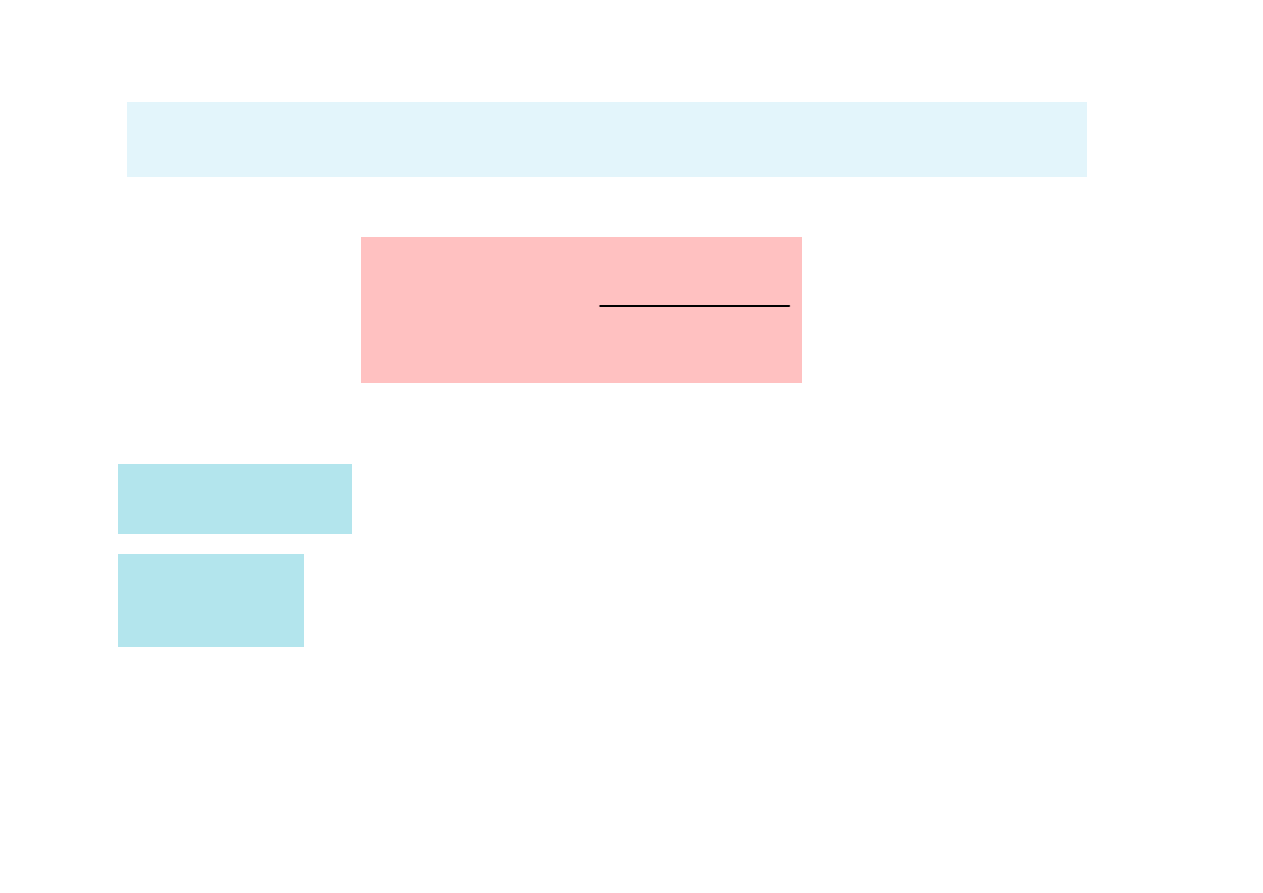
Kondensator rzeczywisty charakteryzuje jego

dobroć

( )

T

w

w

Q

R

C

C

max

2

π

=

max

C

w

( )

T

w

R

- maksimum energii w polu elektrycznym kondensatora

- energia pobrana przez rezystancję kondensatora
w ciągu okresu

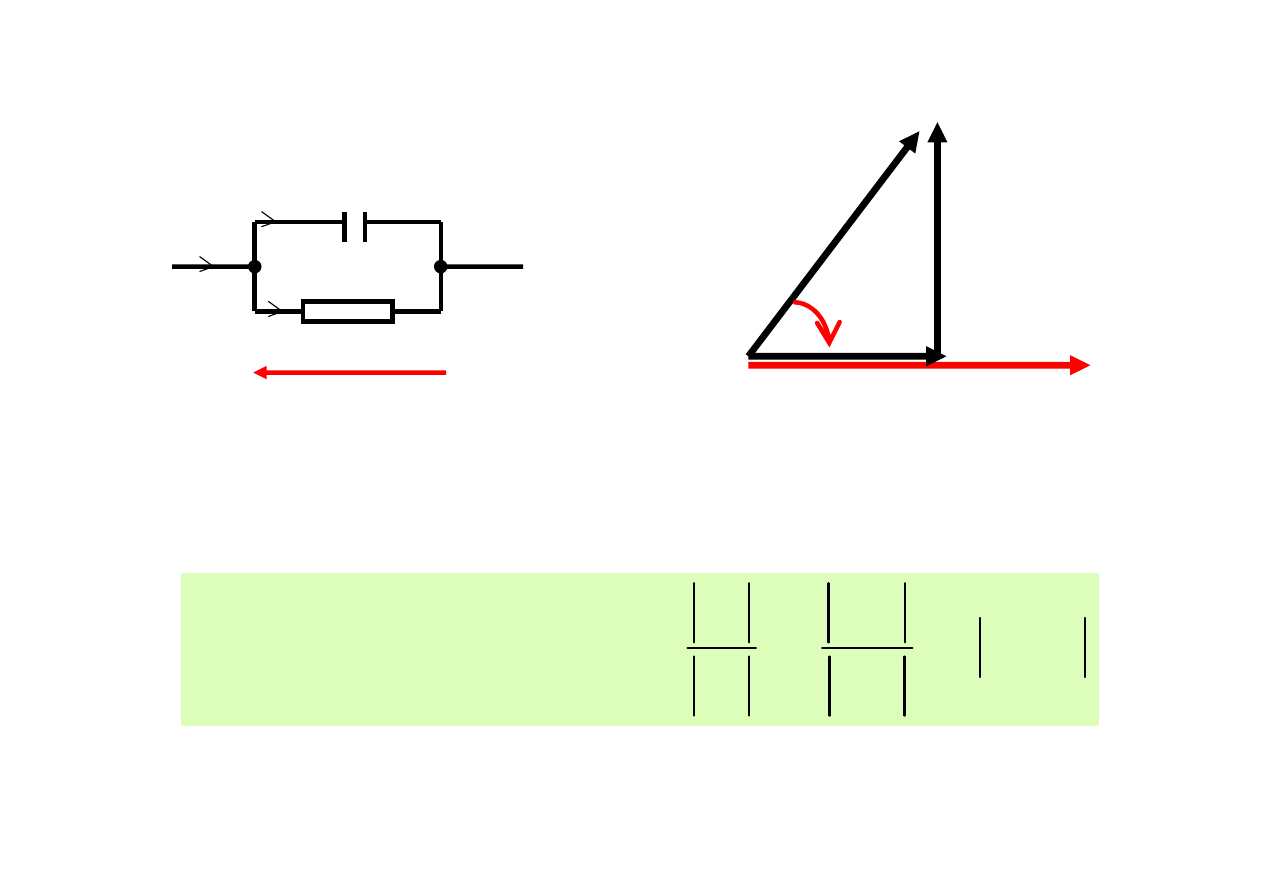
ϕ

ω

ω

tg

=

=

⋅

=

=

R

C

C

I

I

U

U

CR

CR

Q

U

I

R

I

C

I

ϕ

C

R

U

I

I

R

I

C

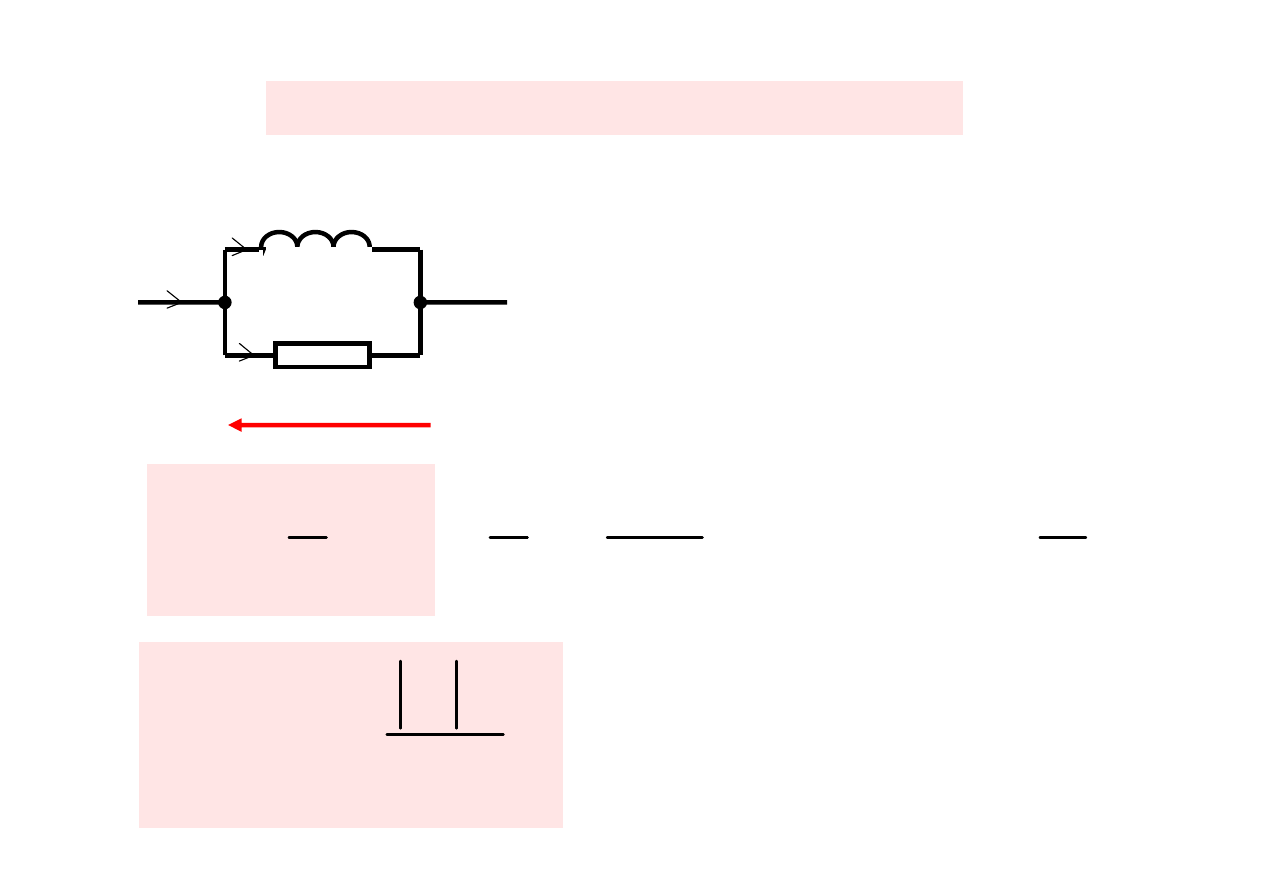
R

L

U

I

I

R

I

L

Model równoległy – cewki rzeczywistej

t

U

u

m

ω

sin

=

Niech

L

U

w

t

L

U

L

Li

w

L

m

L

2

2

max

2

2

2

2

sin

2

1

2

1

ω

π

ω

ω

=













−













=

=

( )

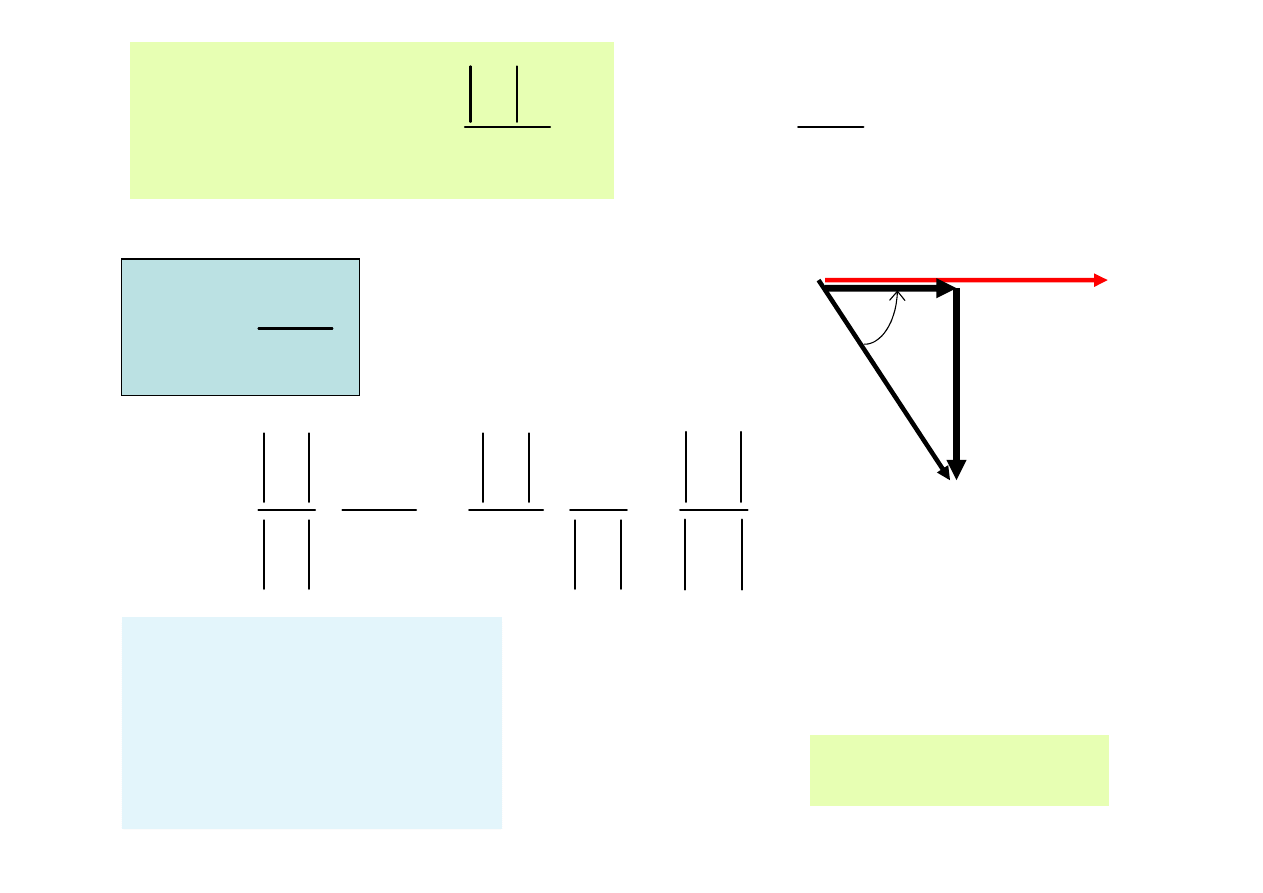
ω

π

2

2

=

=

=

T

T

R

U

PT

T

w

R

R

L

L

L

I

I

U

R

L

U

L

R

U

U

Q

L

R

Q

=

⋅

=

⋅

=

=

ω

ω

ω

ϕ

tg

=

L

Q

Fizyczna
interpretacja dobroci
wynika z wykresu
wskazowego

U

I

L

I

R

I

ϕ

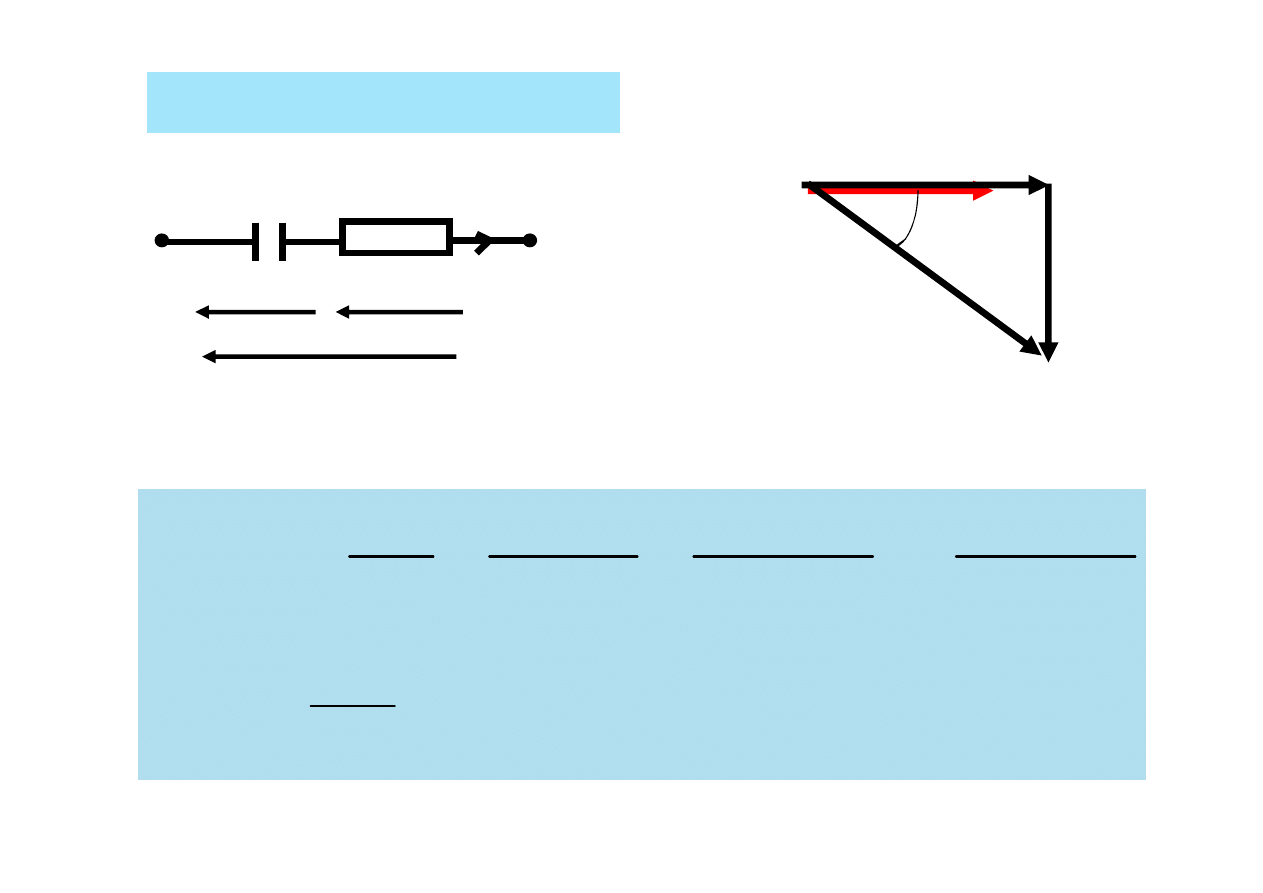
Połączenie szeregowe RC

R

C

U

L

U

R

I

U

U

R

I

U

C

U

ϕ

0

0

1

1

1

2

2

2

2

>

=

<

−

=

+

−

+

=

+

=

−

=

C

B

C

X

B

G

B

j

B

G

G

jB

G

C

j

R

Z

C

C

ω

ω

ω

przypomnienie!!!

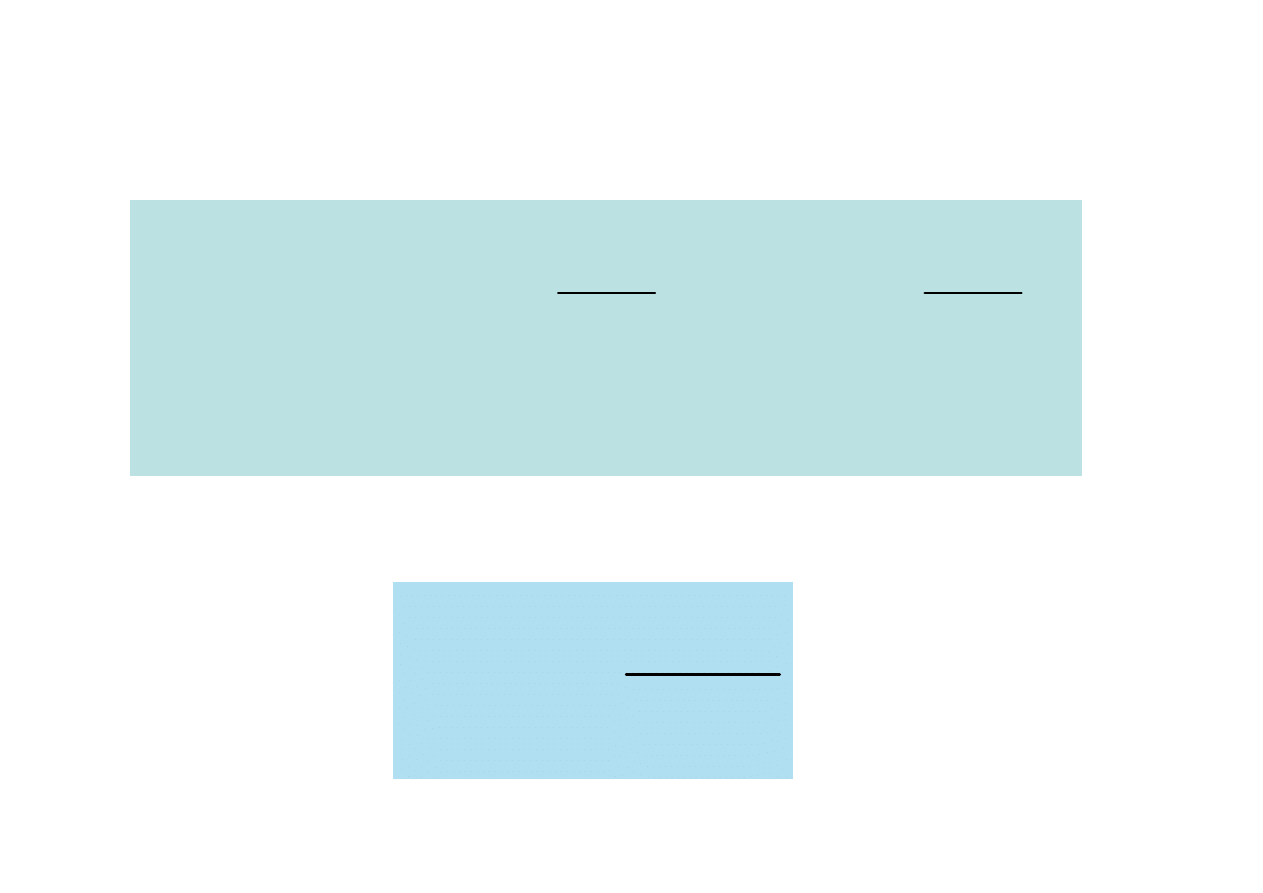
C

R

U

U

C

jI

IR

C

j

R

I

IZ

U

+

=

=

−

=













−

=

=

ω

ω

1

1

CR

ω

ϕ

1

tg

−

=

( )

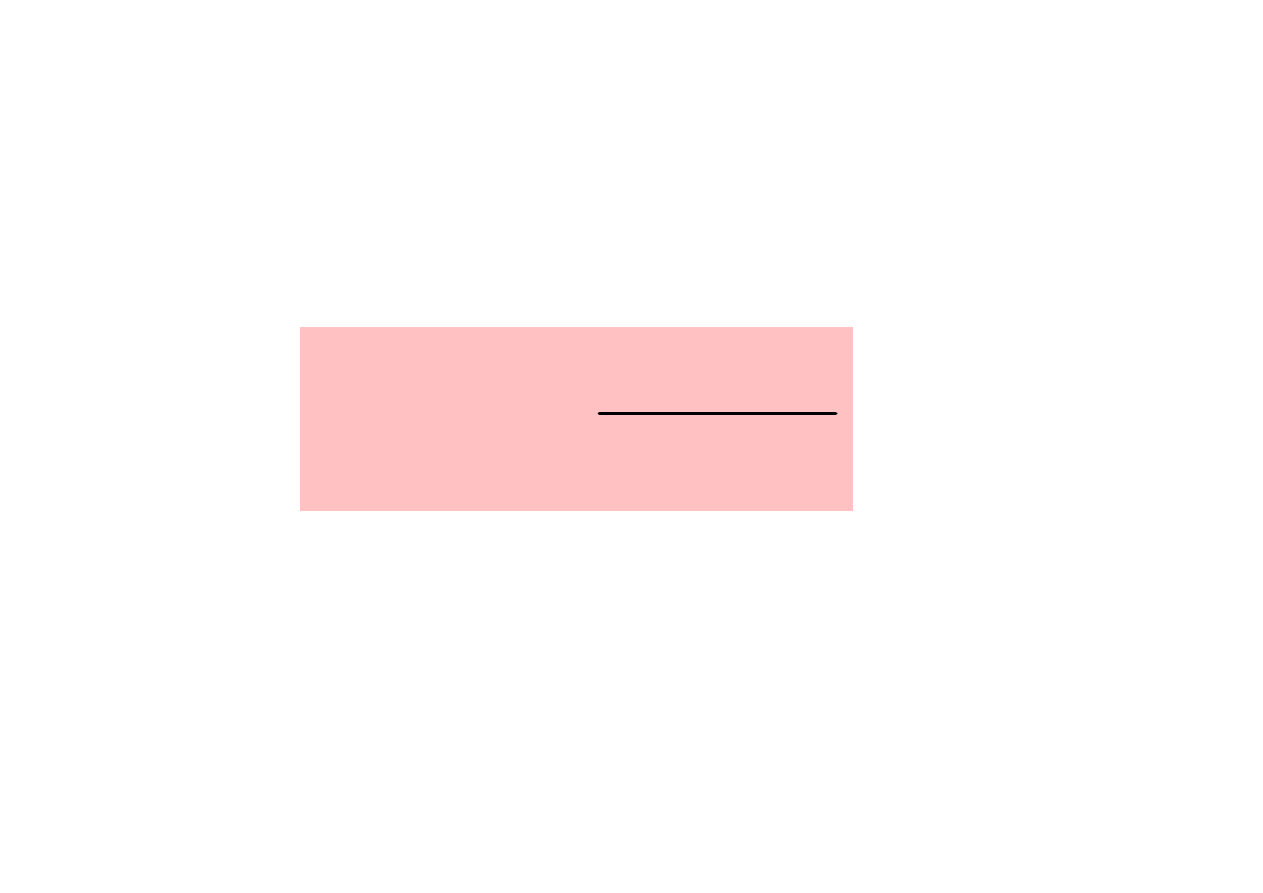
T

w

w

Q

R

C

C

max

2

π

=

Dobro

ć

kondensatora liczymy z wzoru

( )

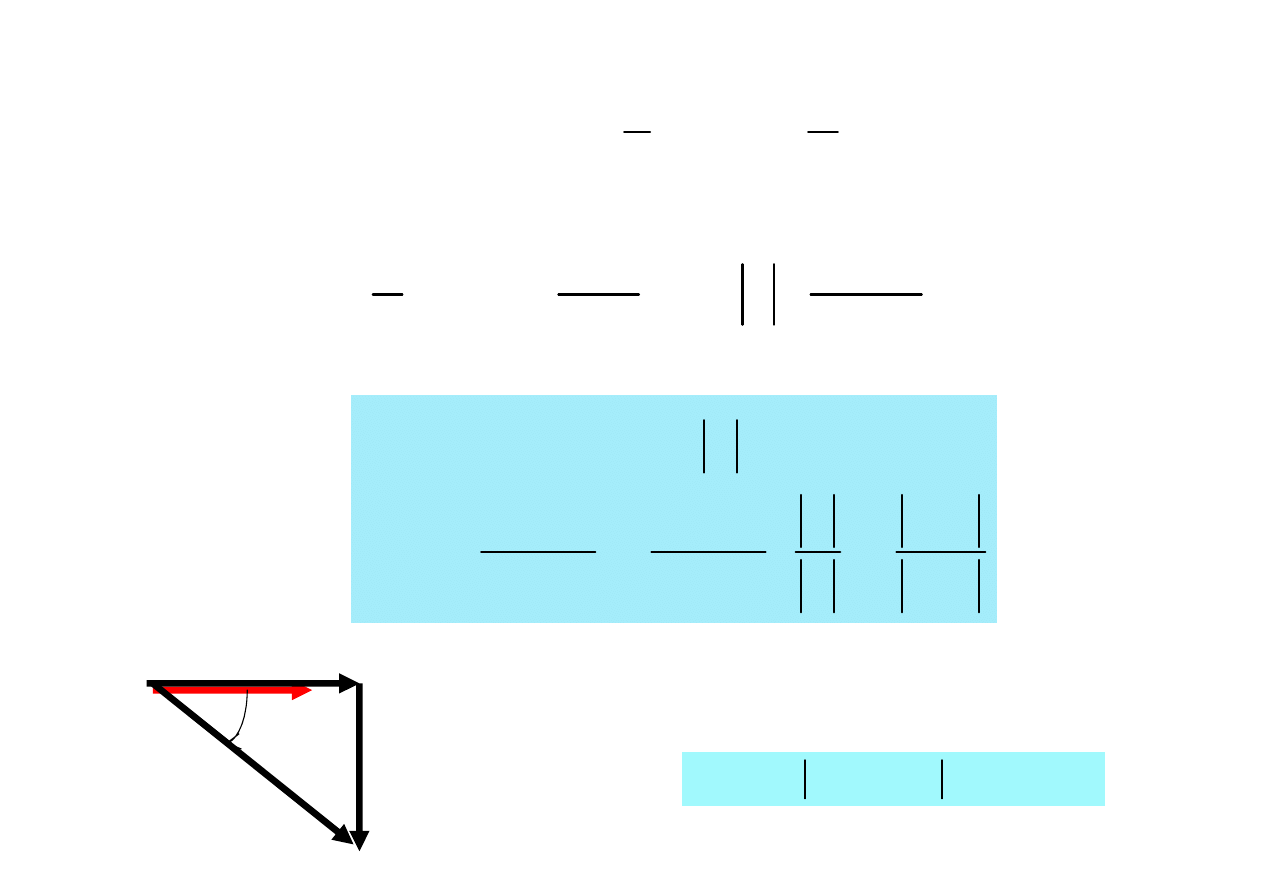
C

I

C

I

C

CU

Cu

w

Cm

Cm

C

C

2

2

2

2

2

2

1

max

1

1

2

1

2

1

max

ω

ω

=













=

=

=

=

( )

R

C

C

R

U

U

I

I

CR

CR

Q

T

I

R

PT

T

w

=

⋅

=

=

=

=

ω

ω

1

1

2

CR

Q

C

ω

ϕ

=

=

tg

U

R

I

U

ϕ

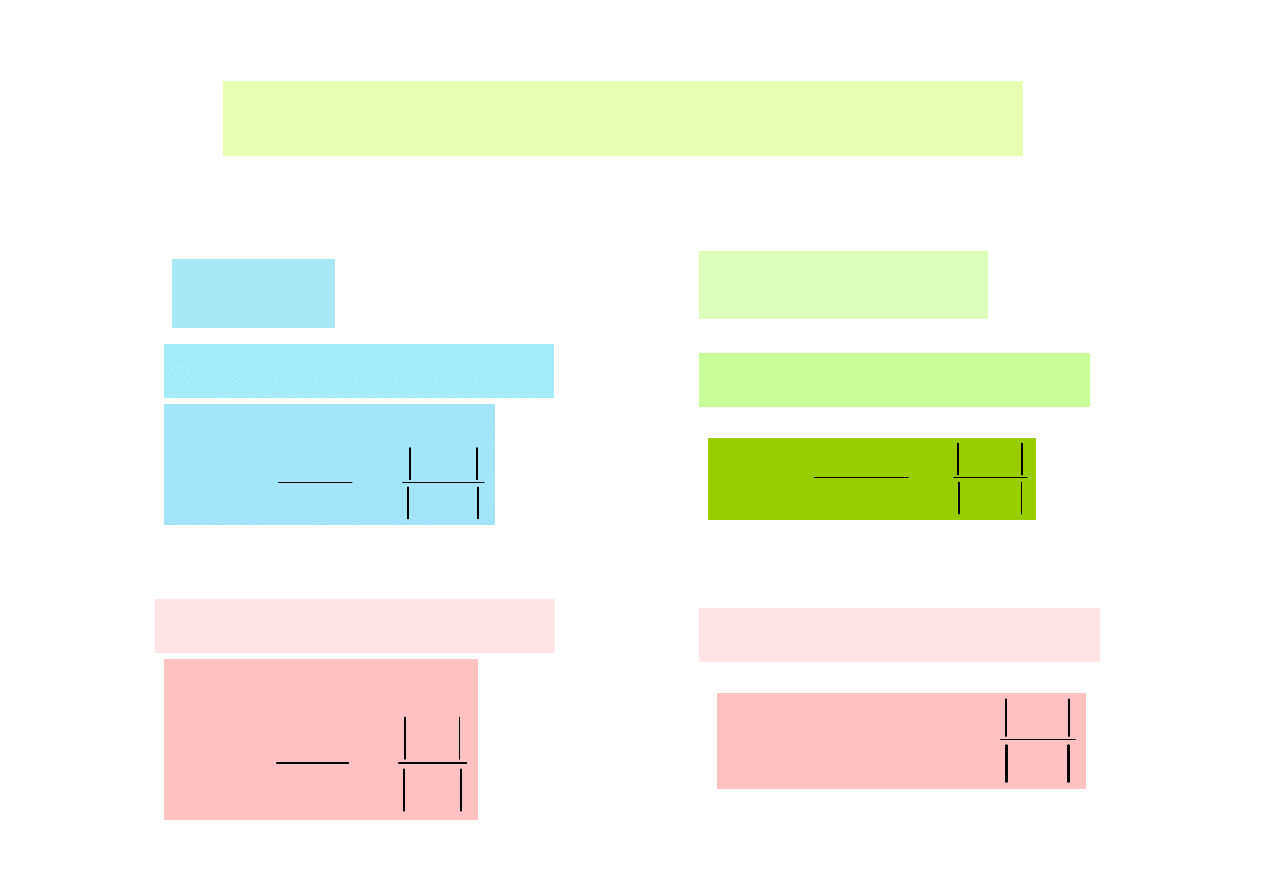
Dobroć

elementów rzeczywistych

R

L

L

I

I

L

R

Q

=

=

ω

B. połączenie równoległe

Cewka

A. połączenie szeregowe

R

L

L

U

U

R

L

Q

=

=

ω

Kondensator

A. połączenie szeregowe

B. połączenie równoległe

R

C

C

U

U

CR

Q

=

=

ω

1

R

C

C

I

I

CR

Q

=

=

ω

PODSUMOWANIE

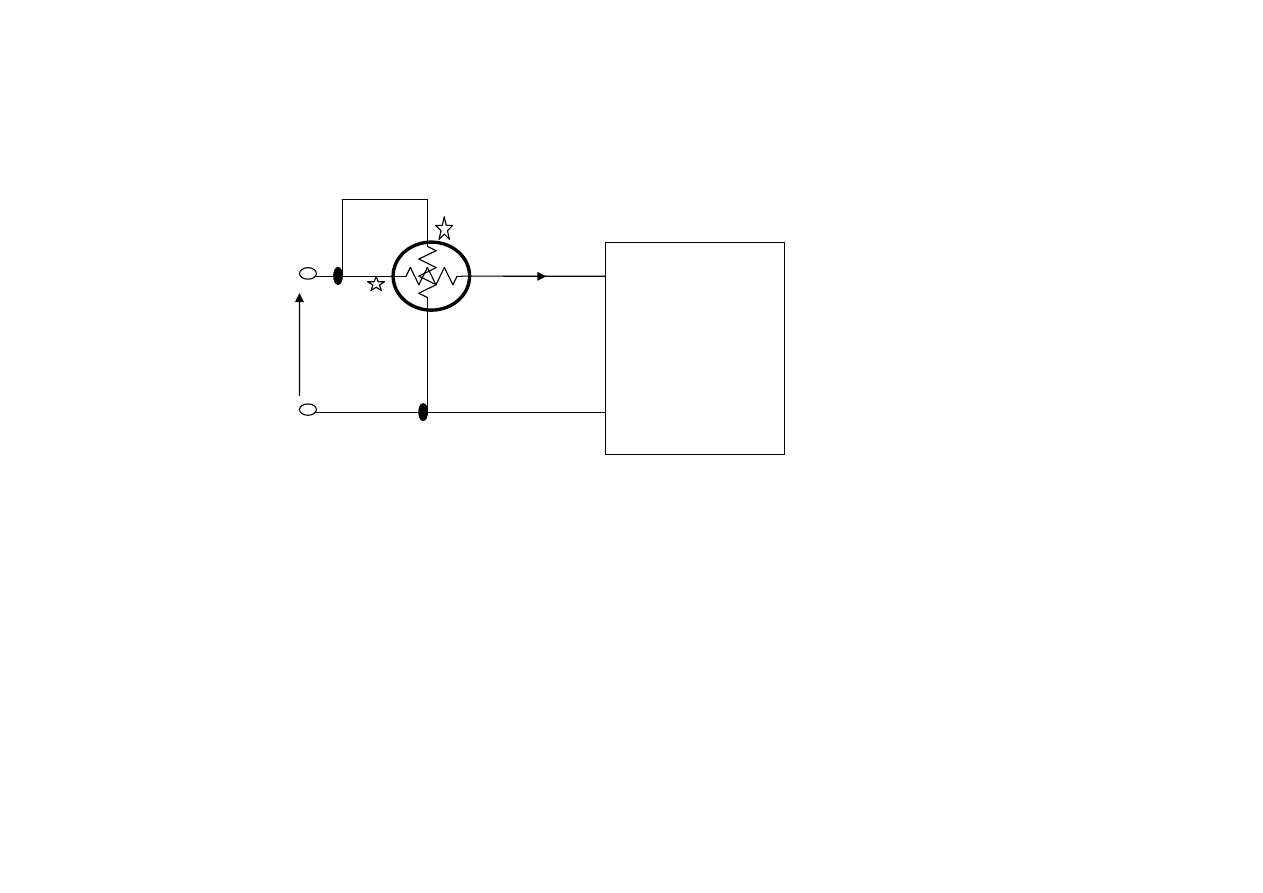
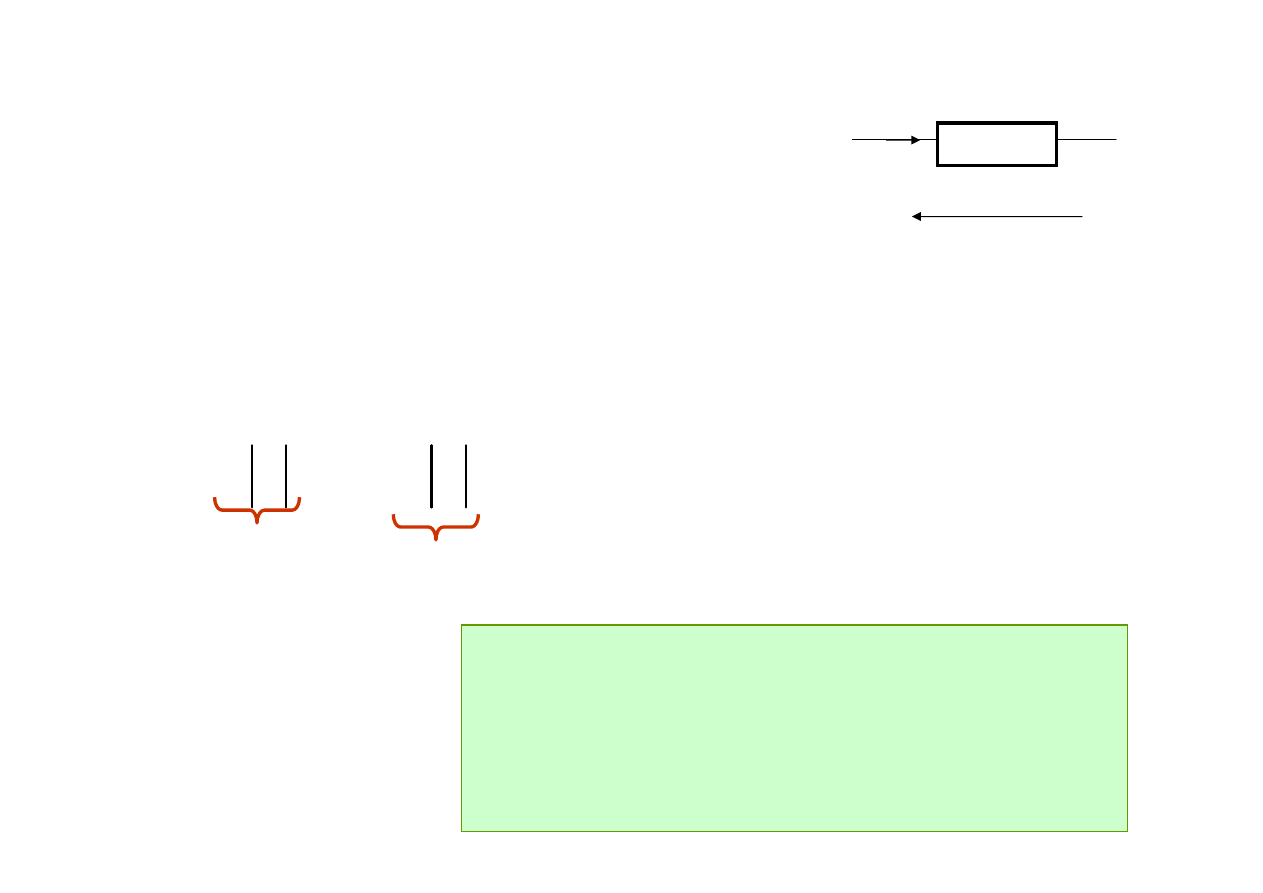
Kilka słów o watomierzu

Watomierz słu

ż

y do pomiaru mocy czynnej , zbudowany jest z

dwóch cewek :

cewki napi

ę

ciowej i cewki pr

ą

dowej podł

ą

czonych odpowiednio

do punktów obwodu wzgl

ę

dem, których chcemy zmierzy

ć

moc.

Gwiazdk

ą

albo kropk

ą

oznaczamy pocz

ą

tki ka

ż

dego z uzwoje

ń

I

U

odbiornik

Wskazania watomierza

:

}

Re{

}

Re{

cos

)

,

cos(

∗

=

=

=

=

UI

S

P

I

U

I

U

I

U

P

W

W

ϕ

Moc symboliczna

jest

liczb

ą

zespolon

ą

o

cz

ęś

ci rzeczywistej równej mocy czynnej

oraz cz

ęś

ci urojonej równej mocy biernej

S = P + j Q

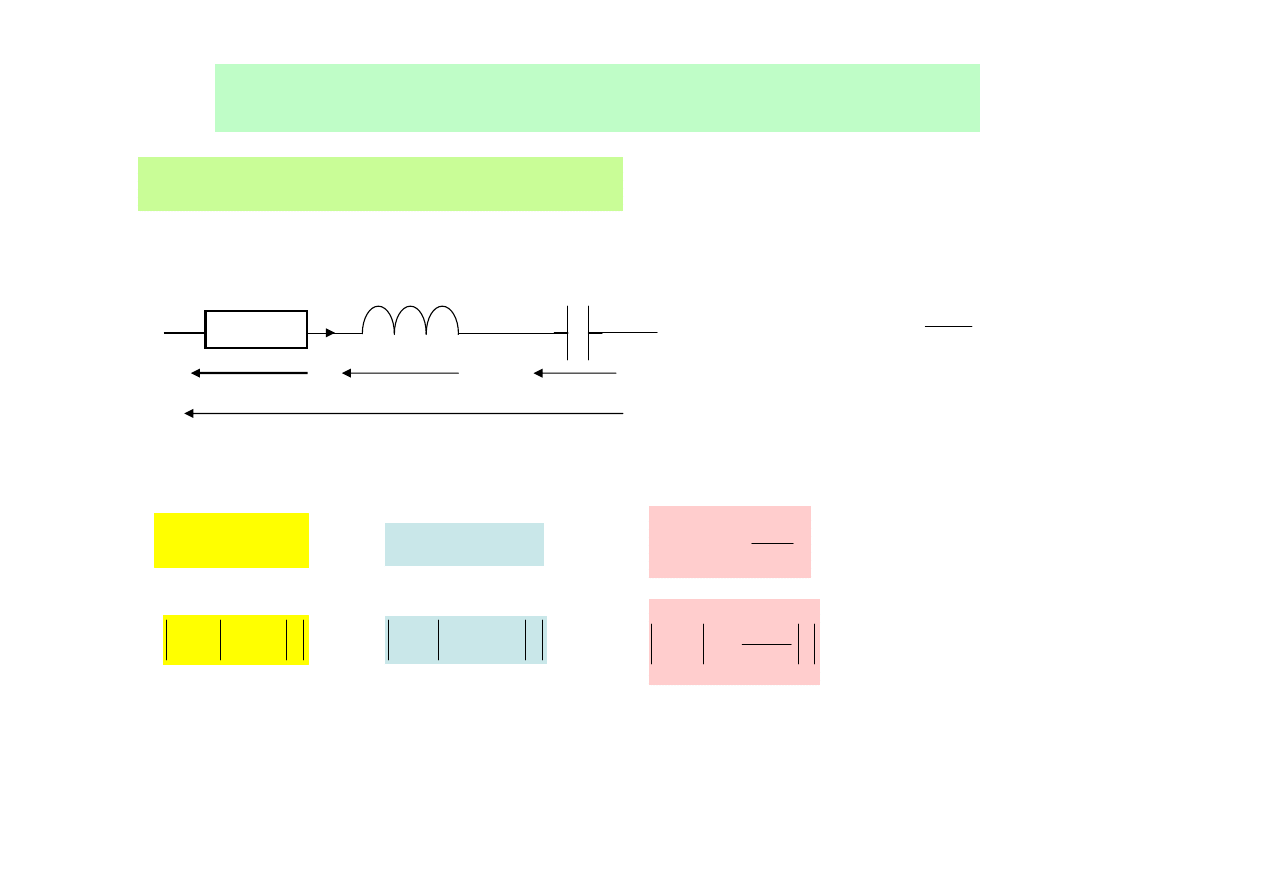
REZONANS w OBWODACH

Rezonans szeregowy -- napięć

R

i

L

C

R

U

L

U

C

U

U

jX

R

C

1

L

j

R

Z

+

=













ω

−

ω

+

=

RI

U

R

=

I

R

U

R

=

LI

j

U

L

ω

=

I

L

U

L

ω

=

I

C

1

j

U

C

ω

−

=

I

C

1

U

C

ω

=

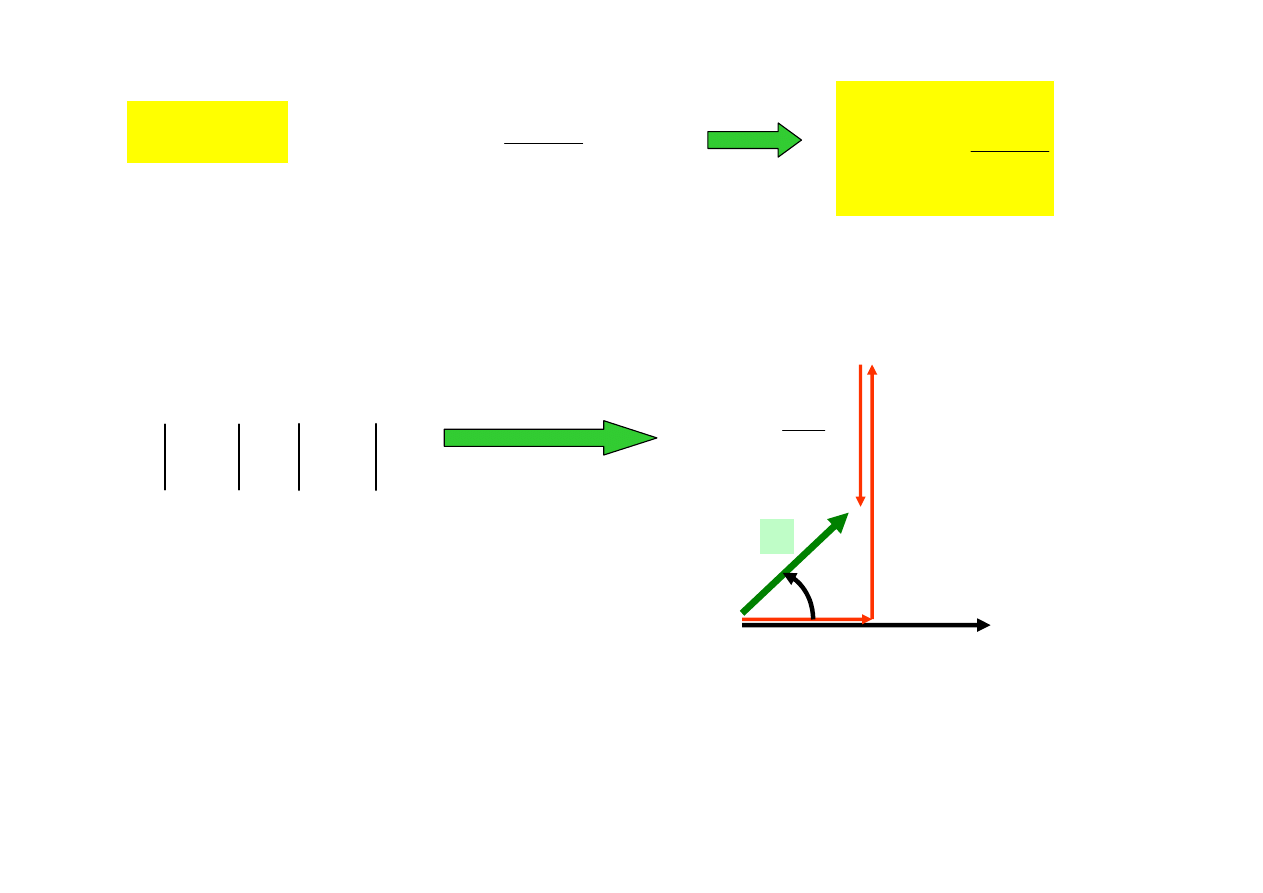
I

RI

LI

j

ω

I

ωC

1

j

−

U

ϕ

0

>

ϕ

0

X

>

0

C

1

L

>

ω

−

ω

C

1

L

ω

>

ω

C

L

U

U

>

OBWÓD MA CHARAKTER INDUKCYJNY

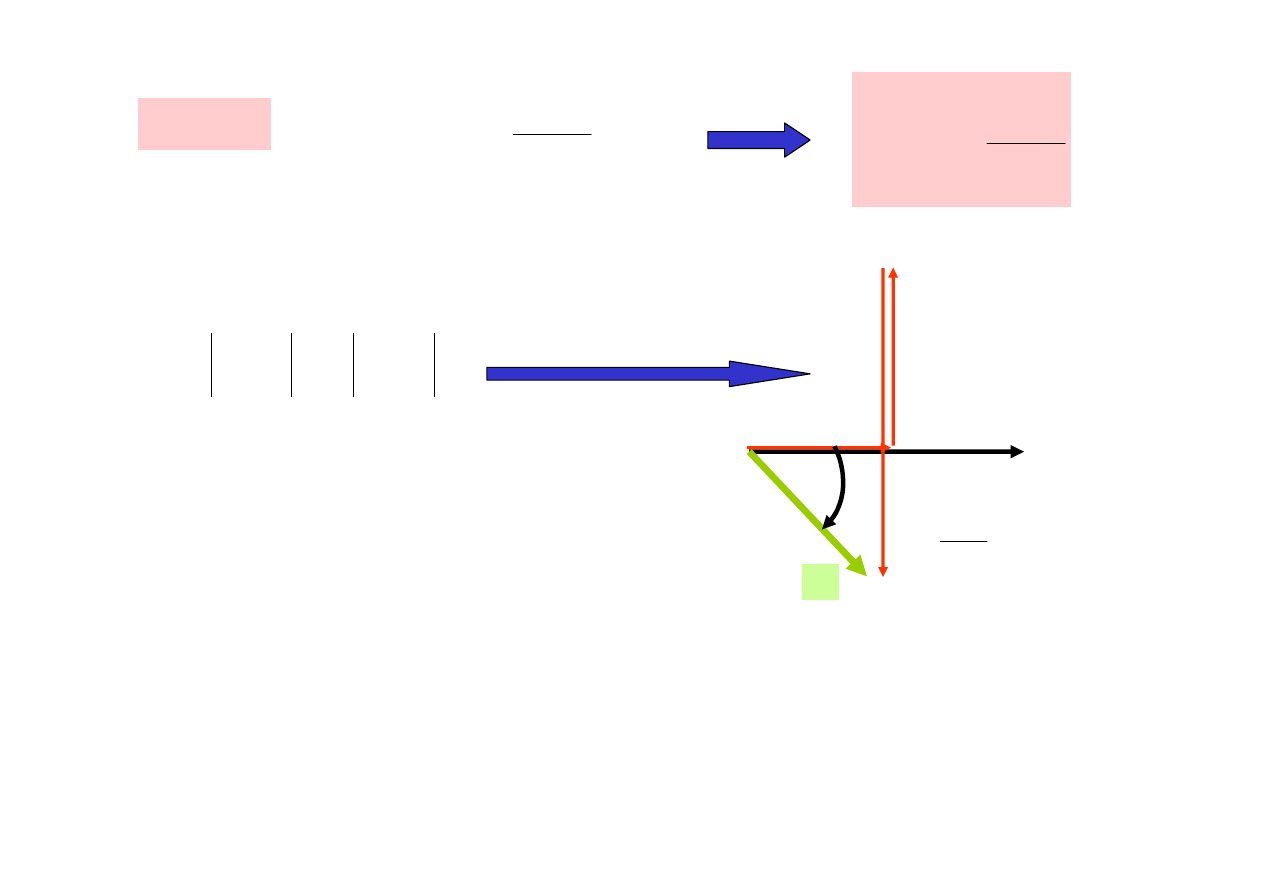
I

RI

LI

j

ω

I

ωC

1

j

−

U

ϕ

0

<

ϕ

0

X

<

0

C

1

L

<

ω

−

ω

C

1

L

ω

<

ω

C

L

U

U

<

OBWÓD MA CHARAKTER POJEMNOŚCIOWY

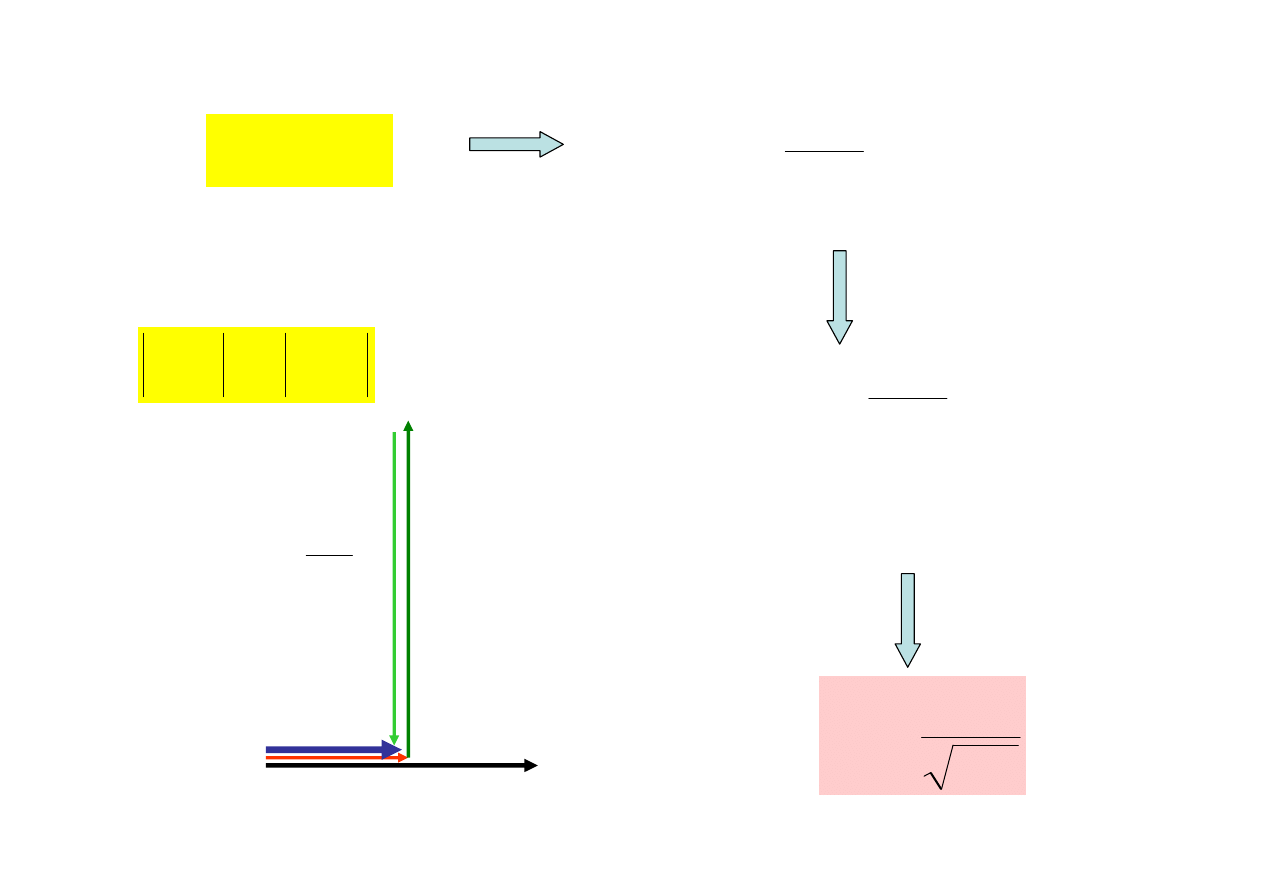
0

X

=

0

C

1

L

=

ω

−

ω

C

1

L

ω

=

ω

C

L

U

U

=

LC

1

r

=

ω

I

RI

I

ωC

1

j

−

U

=

0

=

ϕ

LI

j

ω

Jest to stan rezonansu

Jest to stan rezonansu

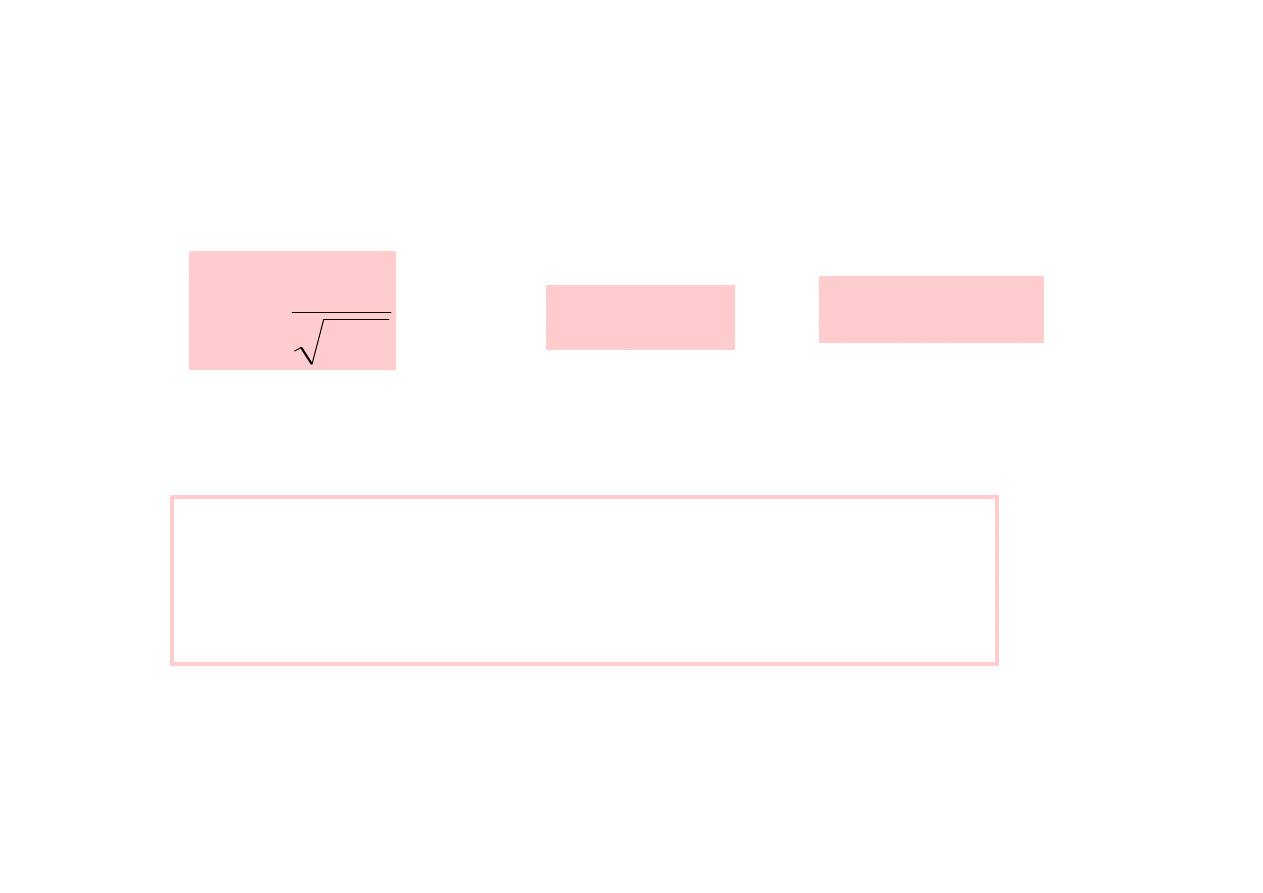
LC

1

r

=

ω

W stanie rezonansu

R

Z

=

0

)

(

X

r

=

ω

Cech

Cech

ą

ą

charakterystyczna rezonansu fizycznego

charakterystyczna rezonansu fizycznego

jest

jest

istnienie dużych odpowiedzi

przy ma

przy ma

ł

ł

ym

ym

pobudzeniu o

pobudzeniu o

ś

ś

ci

ci

ś

ś

le okre

le okre

ś

ś

lonej cz

lonej cz

ę

ę

stotliwo

stotliwo

ś

ś

ci.

ci.

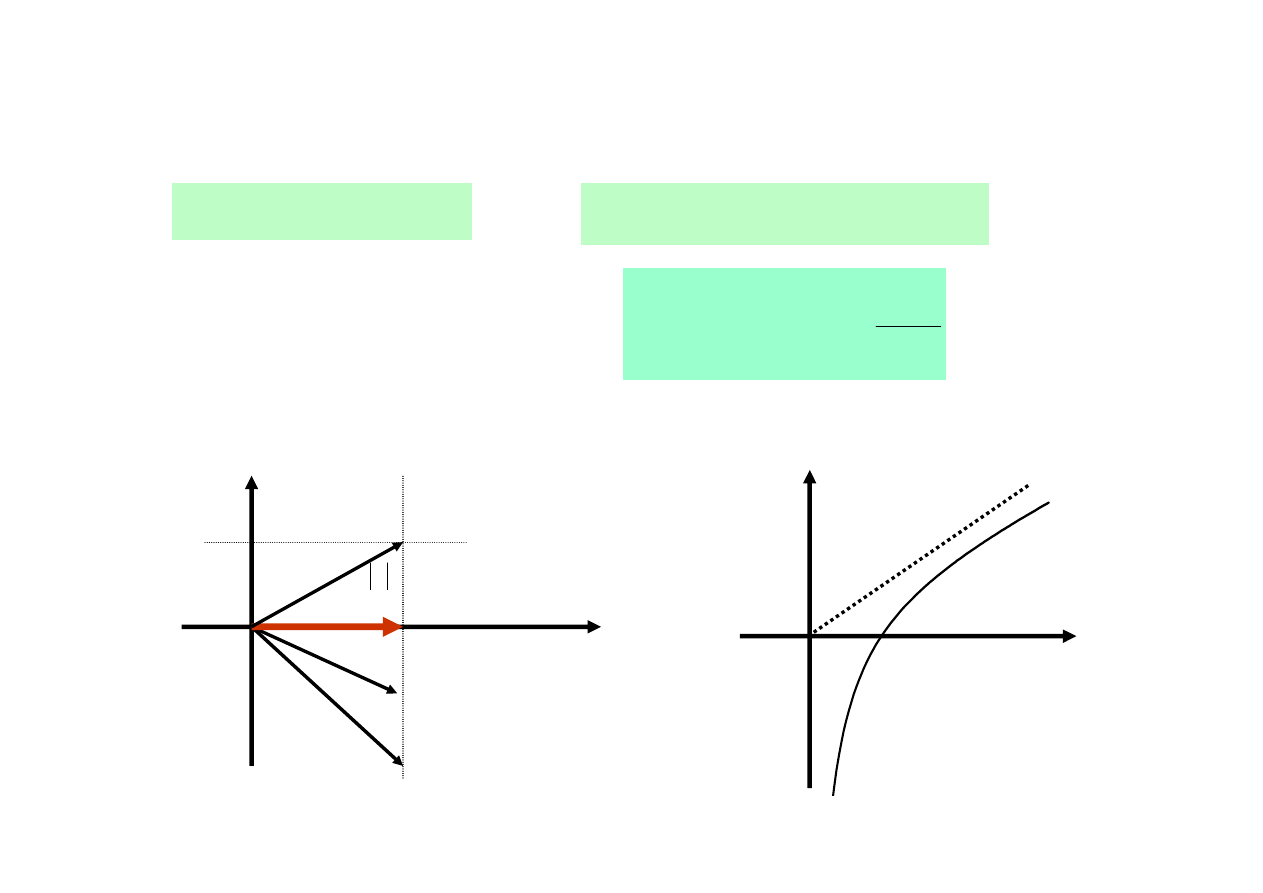
Dla analizy zmian impedancji w funkcji pulsacji rozpatrujemy :

)

(

jX

R

Z

ω

+

=

R

)

(

jX

R

Z

r

=

ω

+

=

C

1

L

)

(

X

ω

−

ω

=

ω

R(

ω

) = R = const

a

)

Z

Re(

)

Z

Im(

Z

R

)

(

X

ω

ω

r

ω

)

(

ω

X

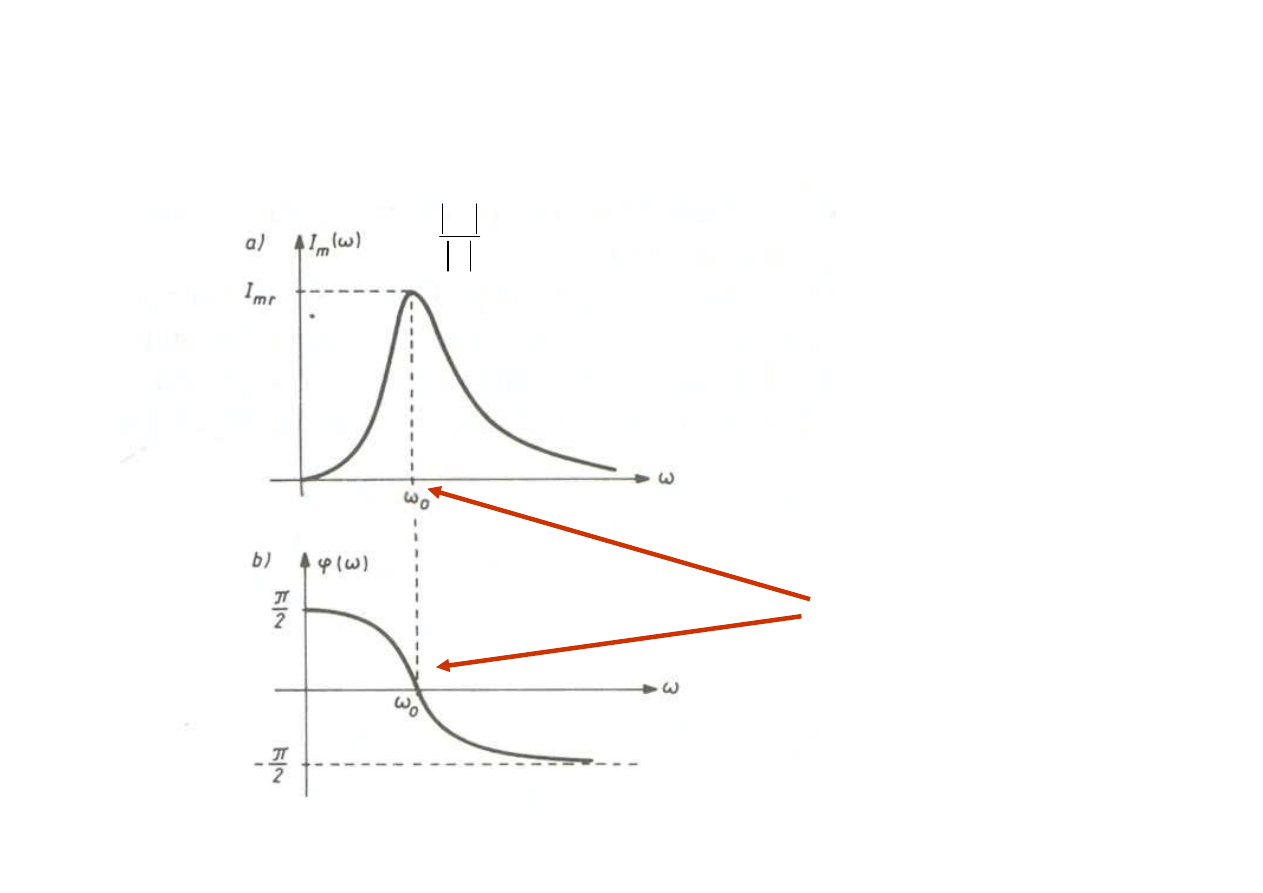
W stanie rezonansu amplituda pr

ą

du i jego faza zmieniaja

si

ę

jak na rysunku

Te wykresy nazywane s

ą

krzywymi

rezonansowymi

amplitudow

ą

i fazow

ą

stan rezonansu

0

ω

ω

<

0

ω

ω

>

0

ω

ω

=

)

(

U

U

R

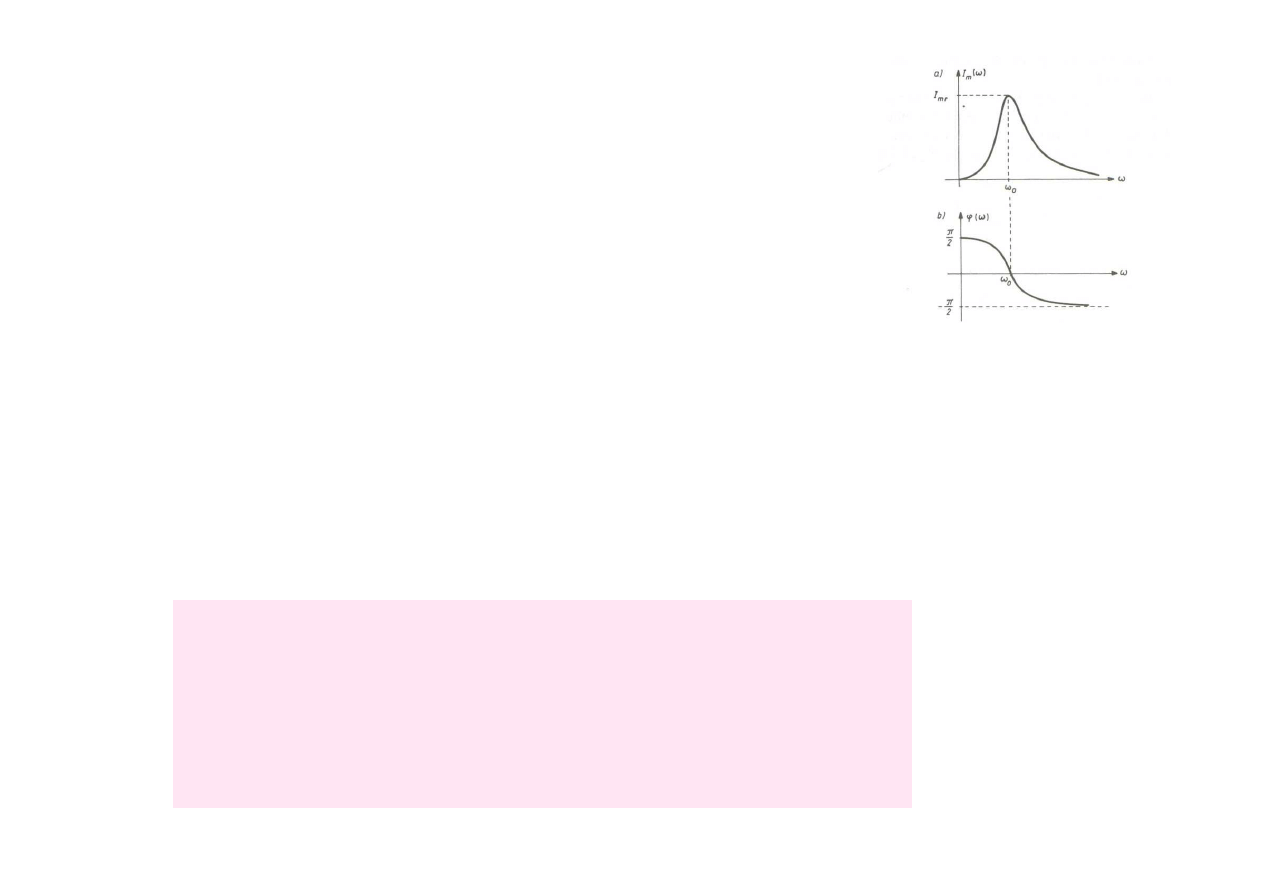
Obwód rezonansowy ma wła

ś

ciwo

ś

ci

selektywne

Sygnały o pulsacjach

bliskich pulsacji

rezonansowej s

ą

przenoszone

przez

obwód ,

A sygnały o pulsacjach

odległych

od

pulsacji rezonansowej s

ą

tłumione

( filtrowane) przez obwód
rezonansowy.

Selektywno

ść

obwodu rezonansowego

jest tym lepsza im zakres pulsacji
przenoszonych przez obwód jest
mniejszy

Zjawiska energetyczne w obwodzie
RLC w stanie rezonansu

(

)

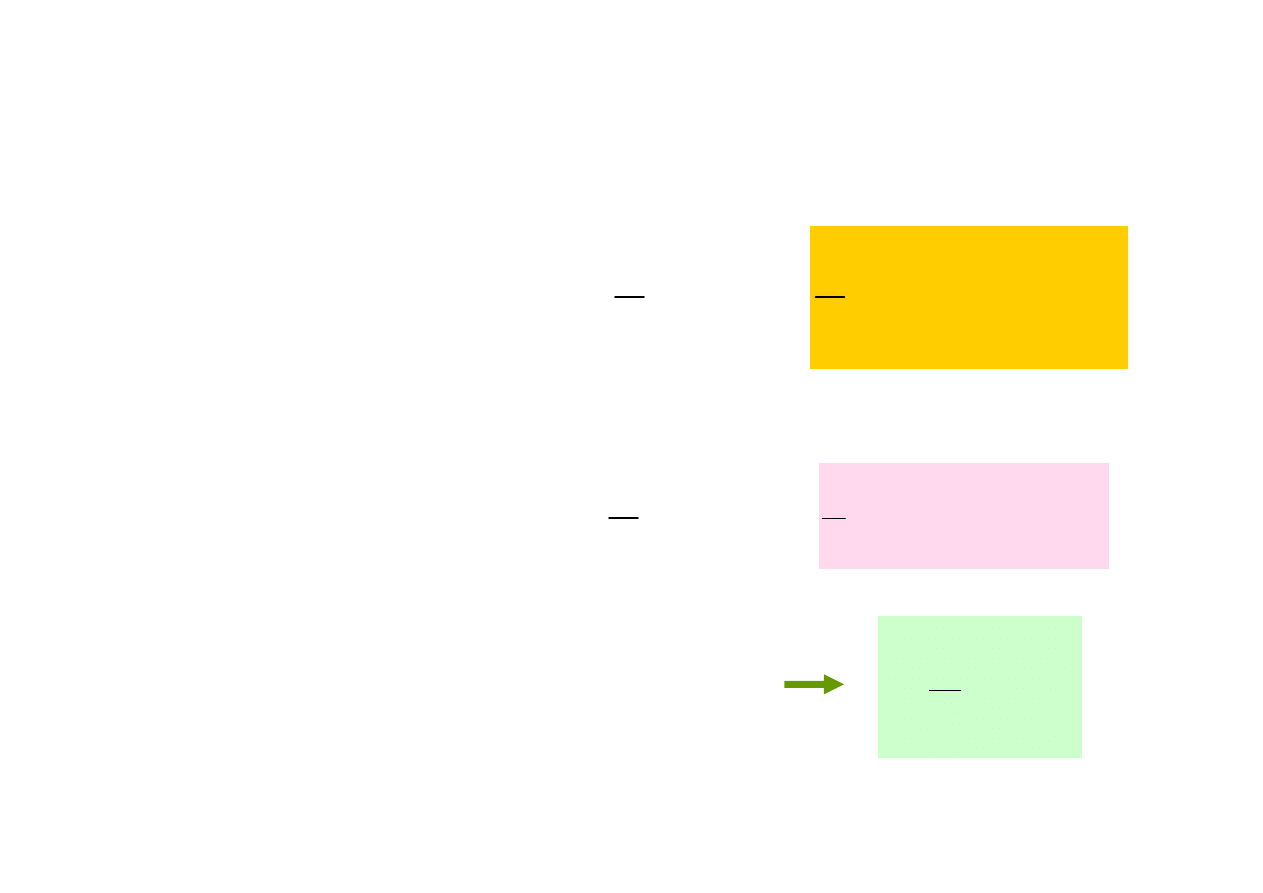
t

I

t

I

t

i

r

m

i

r

m

ω

ϕ

ω

sin

sin

)

(

=

+

=

( )

t

LI

t

Li

w

r

m

L

ω

2

2

2

sin

2

1

)

(

2

1

=

=

( )

t

cos

LI

2

1

r

2

2

m

ω

SUMA

2

m

LI

2

1

=

Je

ż

eli

w

w

ó

ó

wczas

wczas

energia cewki

energia cewki

a

energia kondensatora

energia kondensatora

=

=

)

(

2

1

2

t

Cu

w

C

Suma energii cewki i kondensatora w
stanie rezonansu jest w ka

ż

dej chwili

stała

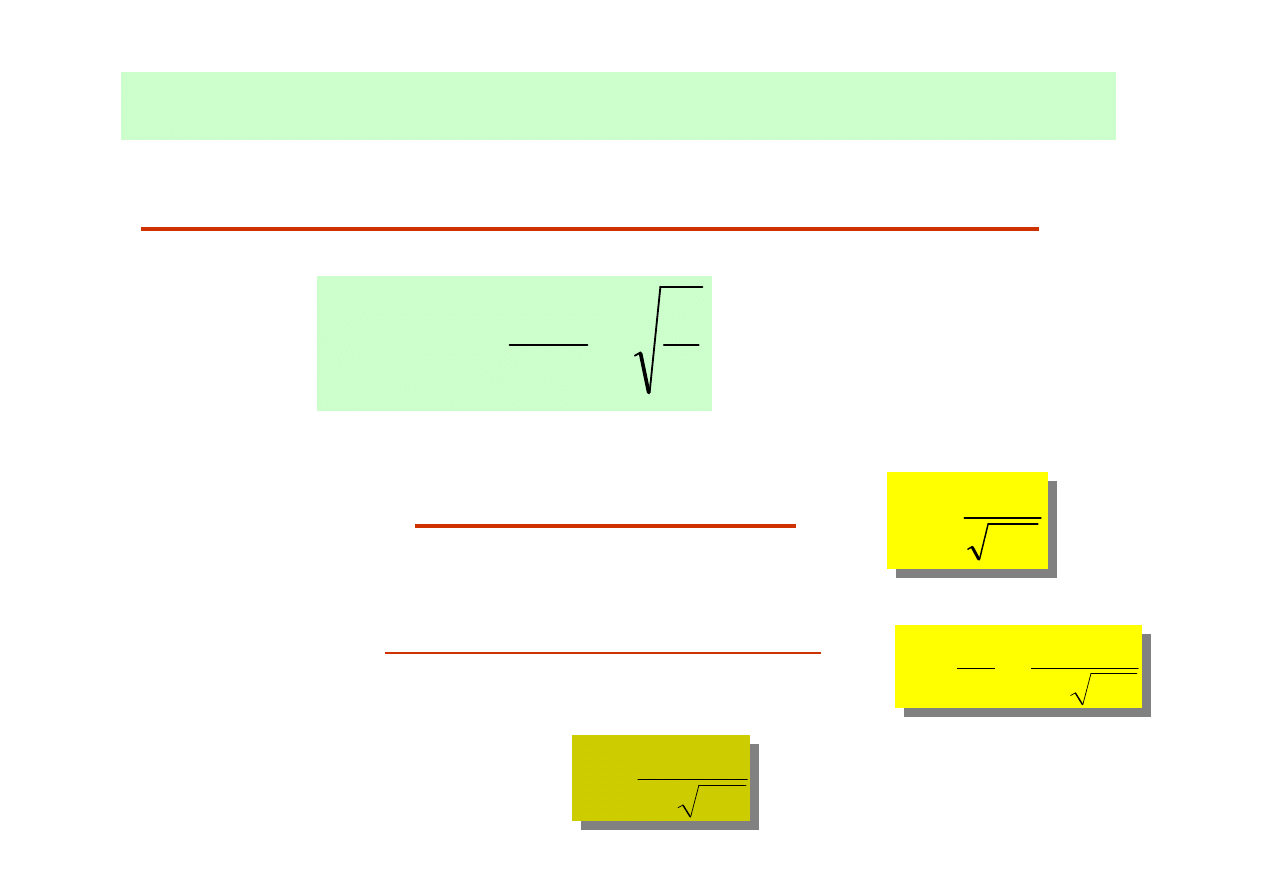
1.

opór charakterystyczny obwodu rezonansowego

:

LC

r

1

=

ω

LC

2

1

2

f

r

r

π

=

π

ω

=

Inne oznaczenie:

Inne oznaczenie:

LC

2

1

f

o

π

=

C

L

C

L

r

r

=

=

=

ω

ω

ρ

1

Wielkości charakteryzujące stan rezonansu

gdzie

r

ω

2. pulsacja rezonansowa

3. cz

ę

stotliwo

ść

rezonansowa

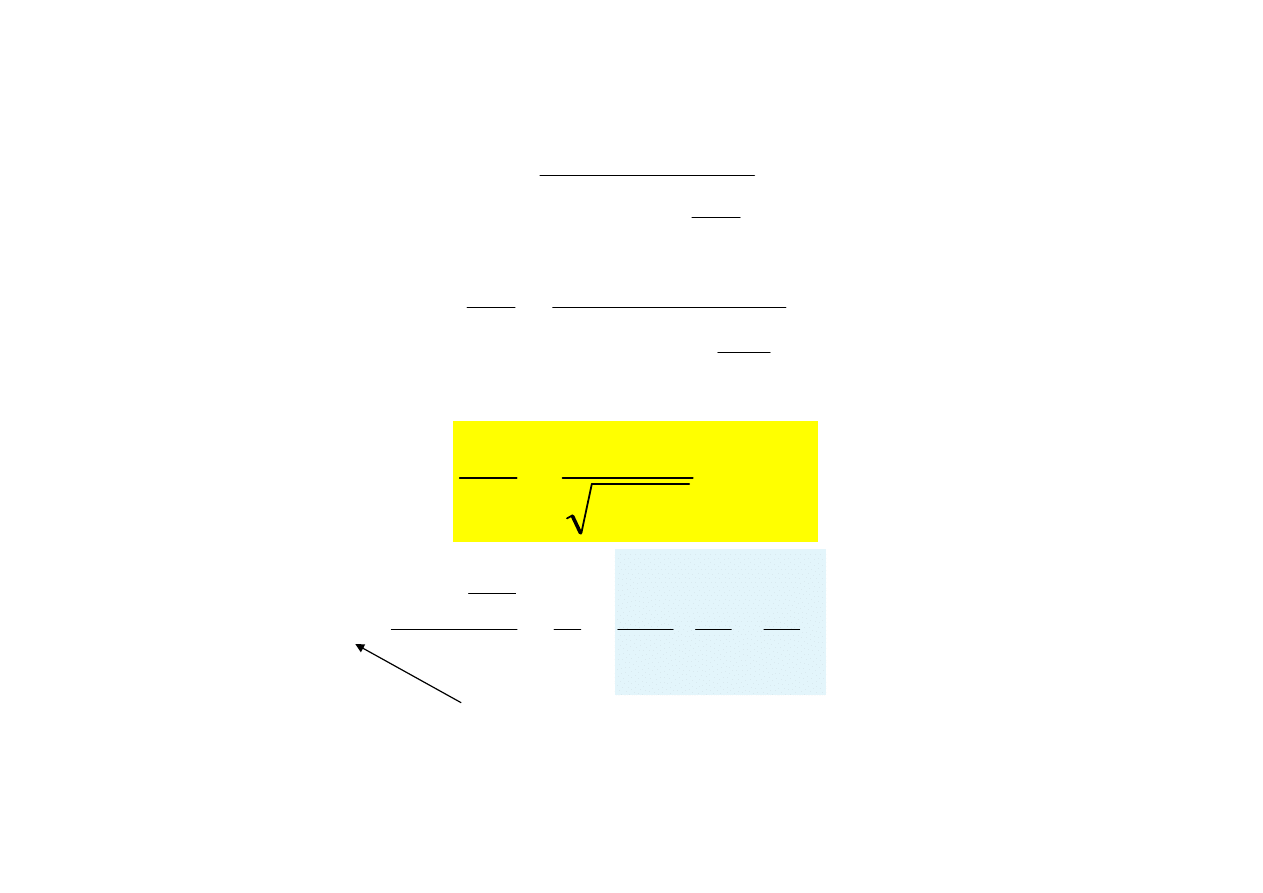
Niech obwód zasilany jest napi

ę

ciem o stałej amplitudzie i zmieniaj

ą

cej si

ę

pulsacji

Dla ustalonej pulsacji

R

C

L

j

R

U

U

R

)

1

(

ω

ω

−

+

=

)

1

(

C

L

j

R

R

U

U

R

ω

ω

−

+

=

jarctgx

R

e

x

U

U

−

+

=

2

1

1

lub inaczej

X przyjmuje warto

ś

ci

)

,

(

+∞

−∞

ale jest równy zero dla rezonansu













ω

ω

−

ω

ω

ω

=

=

ω

−

ω

=

r

r

r

R

L

R

X

R

C

1

L

x

4. rozstrojenie bezwzględne

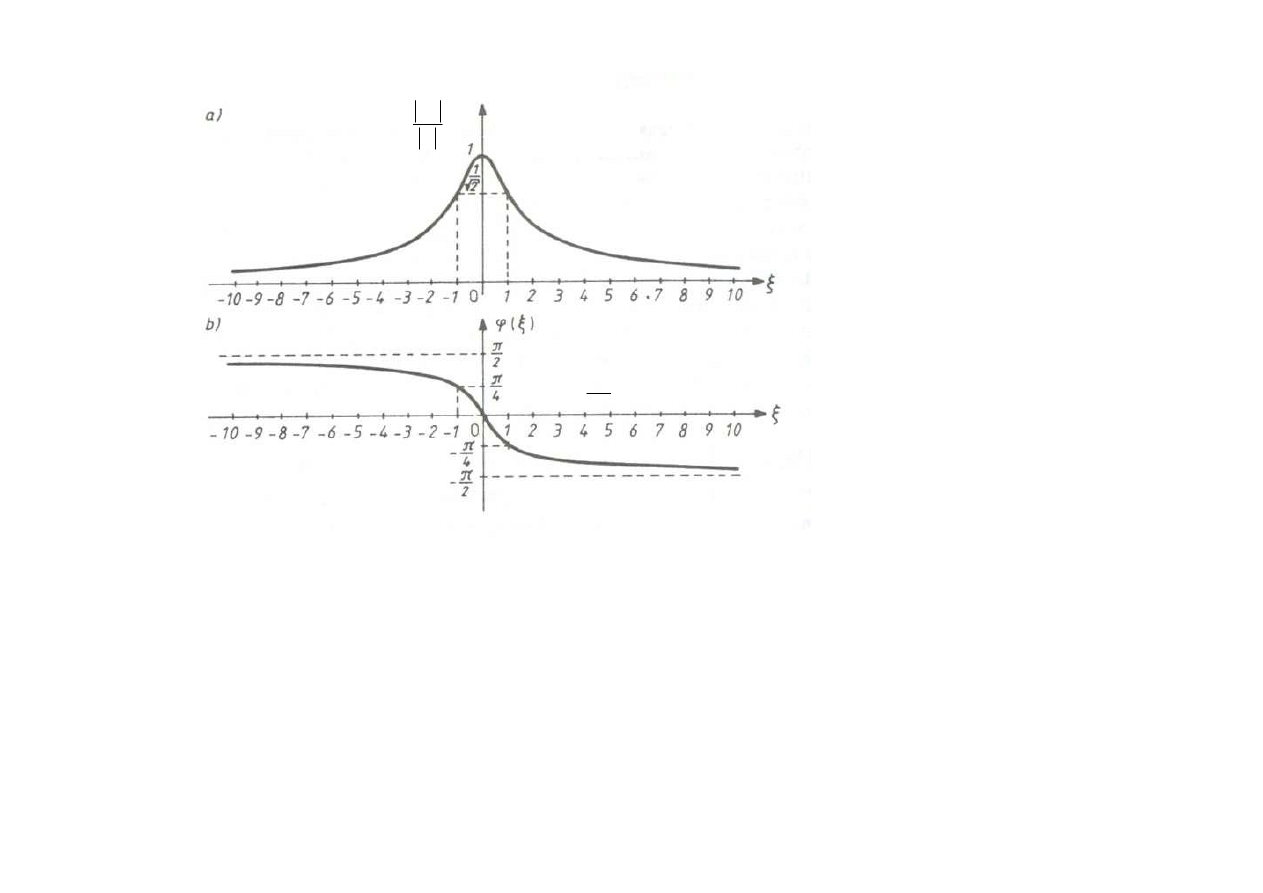
U

U

R

)

arg(

U

U

R

to uniwersalne krzywe rezonansowe

i odnosz

ą

si

ę

do ka

ż

dego szeregowego obwodu

rezonansowego

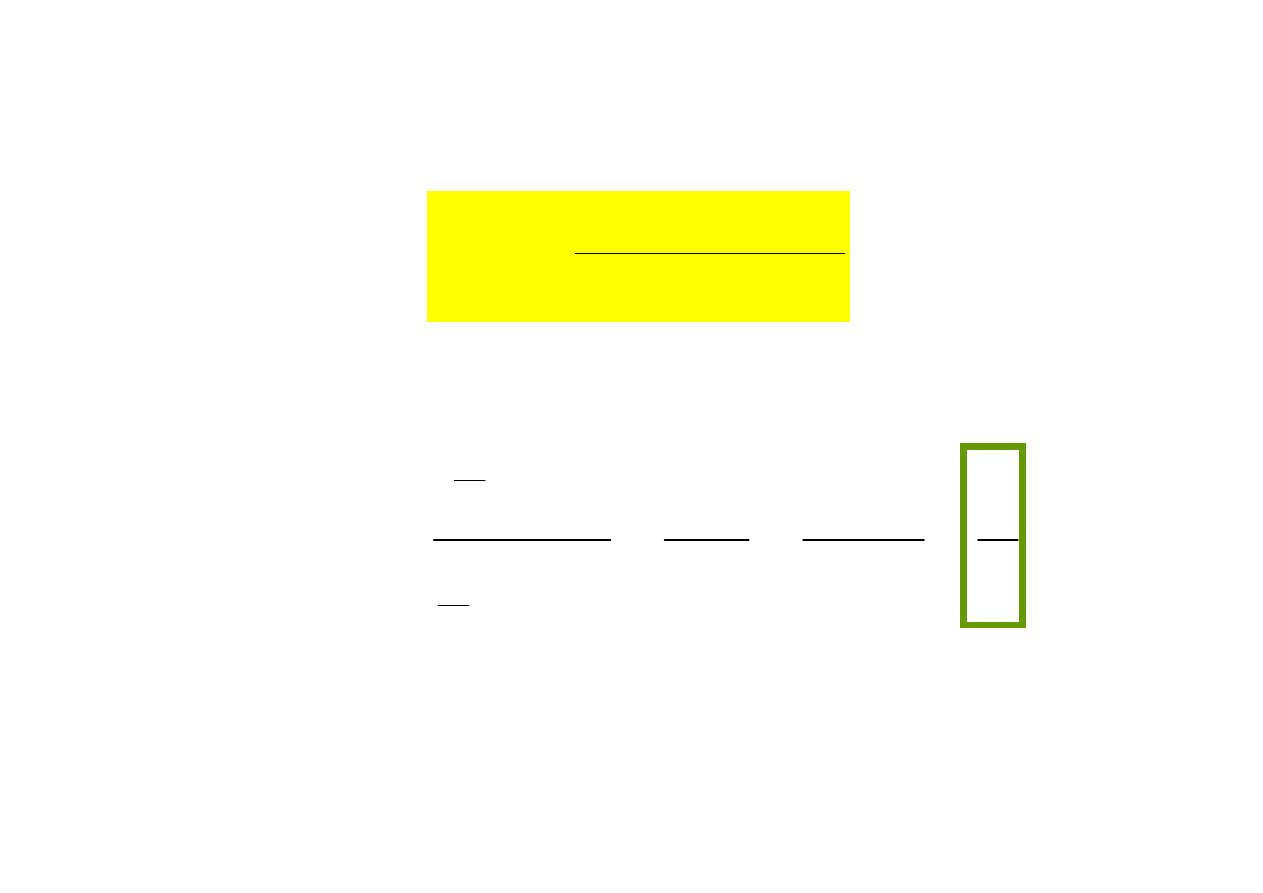
R

CR

L

T

RI

LI

Q

r

m

m

ρ

ω

ω

π

=

=

=

=

1

R

2

1

2

1

2

r

2

2

4.

dobroć obwodu

w stanie rezonansu:

)

T

(

w

)

w

w

(

2

Q

R

max

C

L

+

π

=

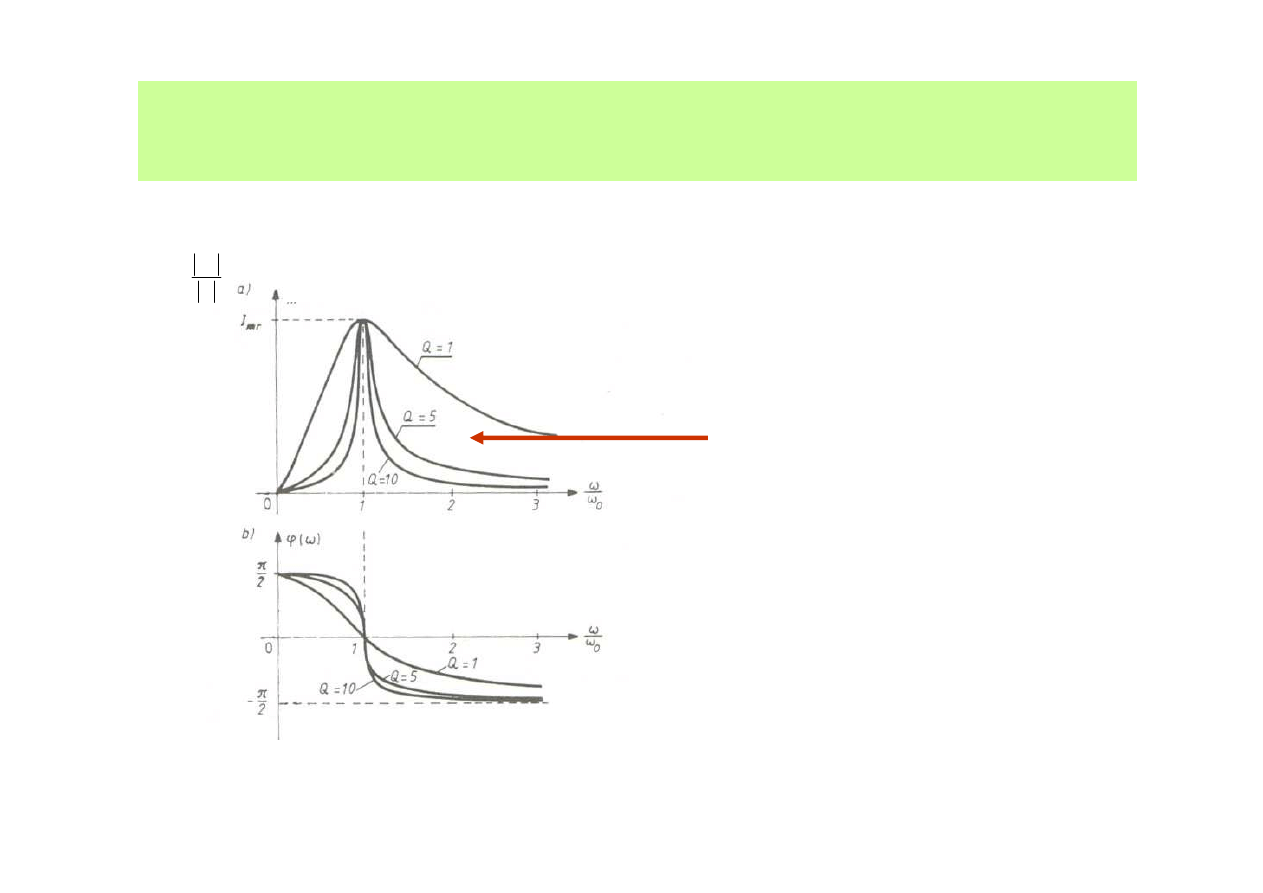
Wpływ dobroci Q na kształt krzywych rezonansowych pokazano

na wykresach

:

Im wi

ę

ksza dobro

ć

,

tym obwód bardziej
selektywny –
w

ęż

sze pasmo

przepuszczania

U

U

R

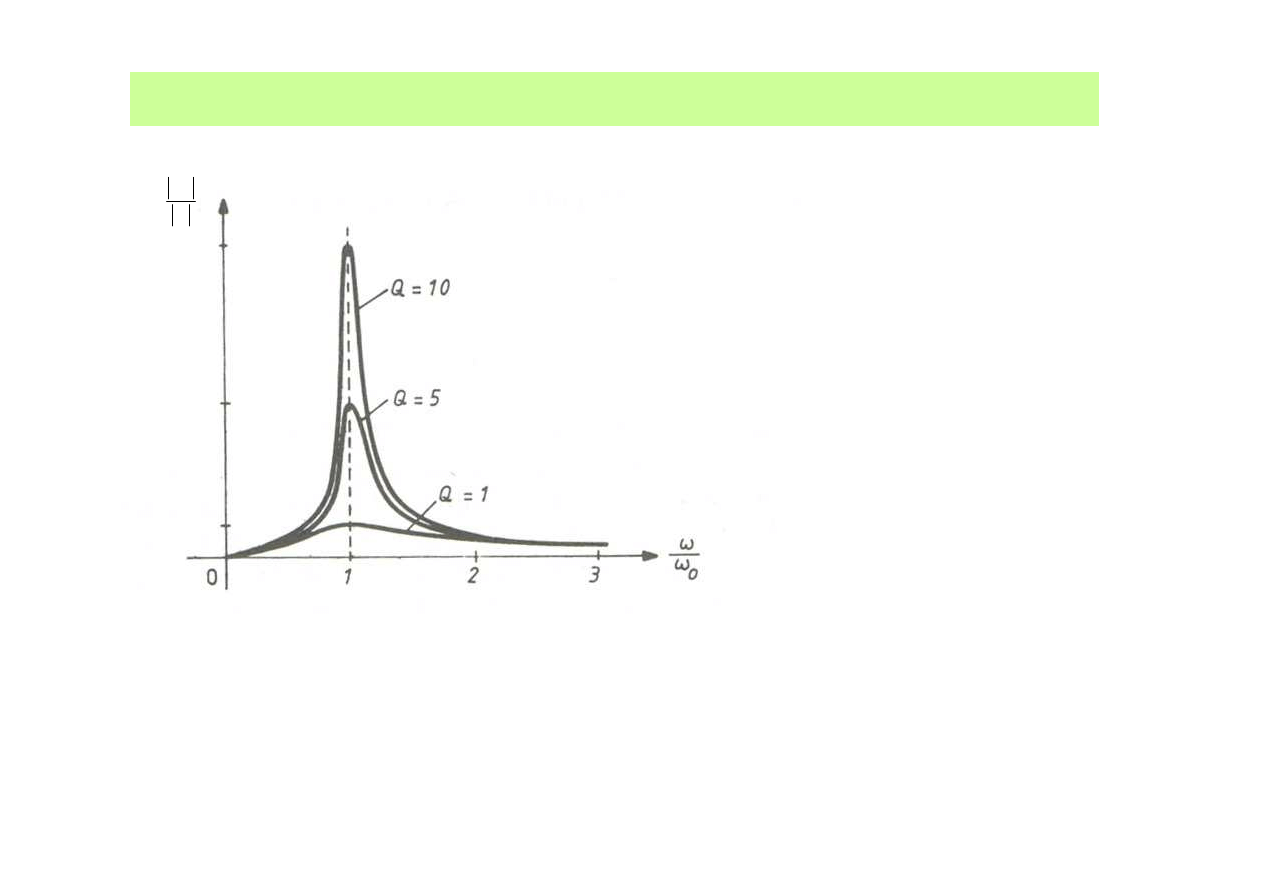
Wpływ dobroci na selektywno

ść

obwodu rezonansowego

Dobro

ć

zmieniana regulacj

ą

R

przy pozostałych elementach
stałych

Dobro

ć

obwodu jest podstawowym parametrem obwodu rezonansowego

decyduj

ą

cym o jego jako

ś

ci jako obwodu selektywnego

U

U

R

5. rozstrojenie wzgl

ę

dne

ω

ω

ω

ω

δ

r

r

−

=

R

Q

x

ρδ

δ

=

=

Przy tym samym rozstrojeniu bezwzgl

ę

dnym x w obwodzie o wi

ę

kszej

dobroci wyst

ę

puje mniejsze rozstrojenie wzgl

ę

dne

W bliskim otoczeniu pulsacji rezonansowej

r

r

Q

Q

x

ω

ω

ω

δ

−

≅

=

2

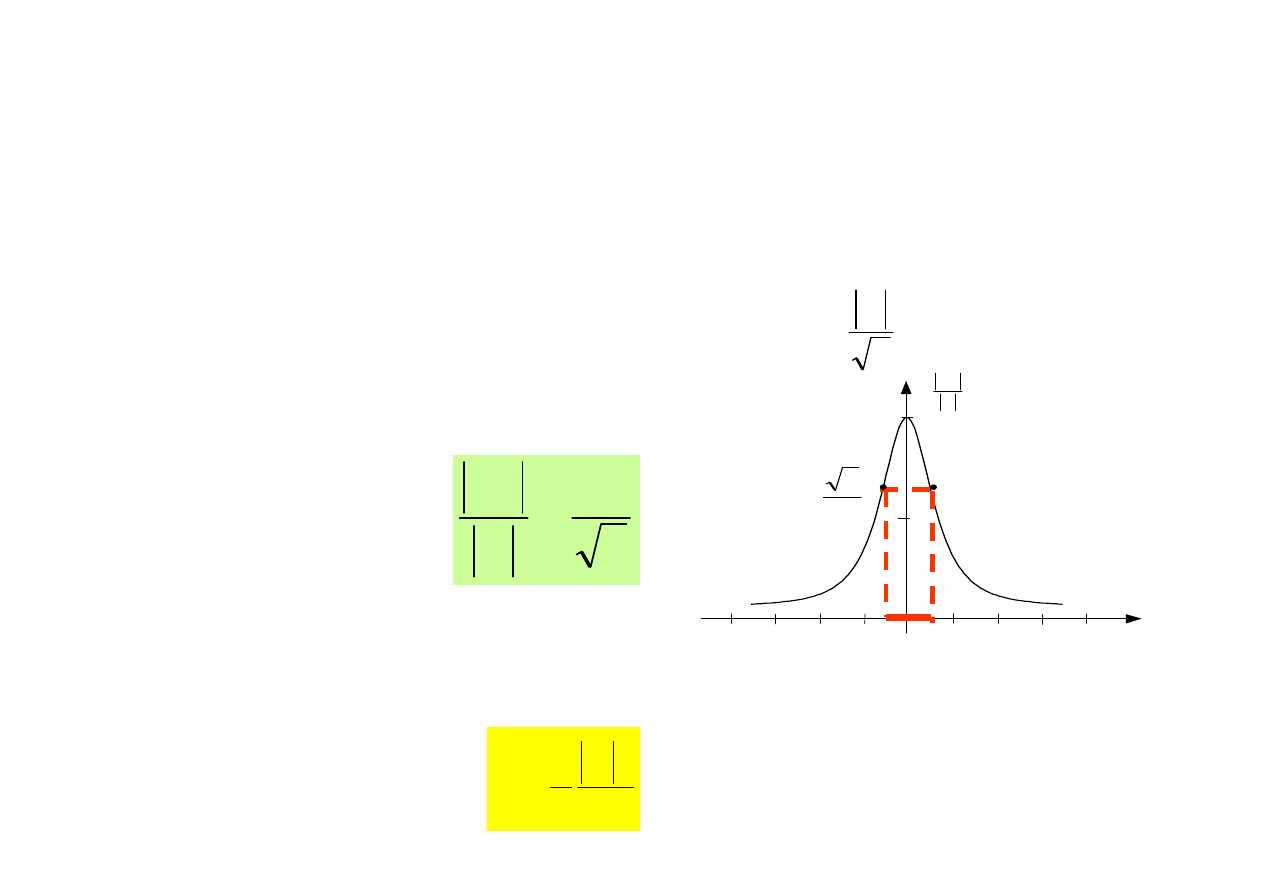
6. Pasmo przepuszczania obwodu rezonansowego

Pasmem przepuszczania obwodu rezonansowego nazywamy przedział
pulsacji

〉

〈

2

1

,

ω

ω

w otoczeniu pulsacji rezonansowej na kra

ń

cach

którego warto

ść

skuteczna napi

ę

cia

R

U

jest równa

2

U

W pa

ś

mie przepuszczania

2

1

≥

U

U

R

Moc czynna obwodu na kra

ń

cach

pasma przepuszczania

R

U

P

2

2

1

=

8

6

4

2

-8

-6

-4

-2

0,5

1

0

x

U

U

R

2

2

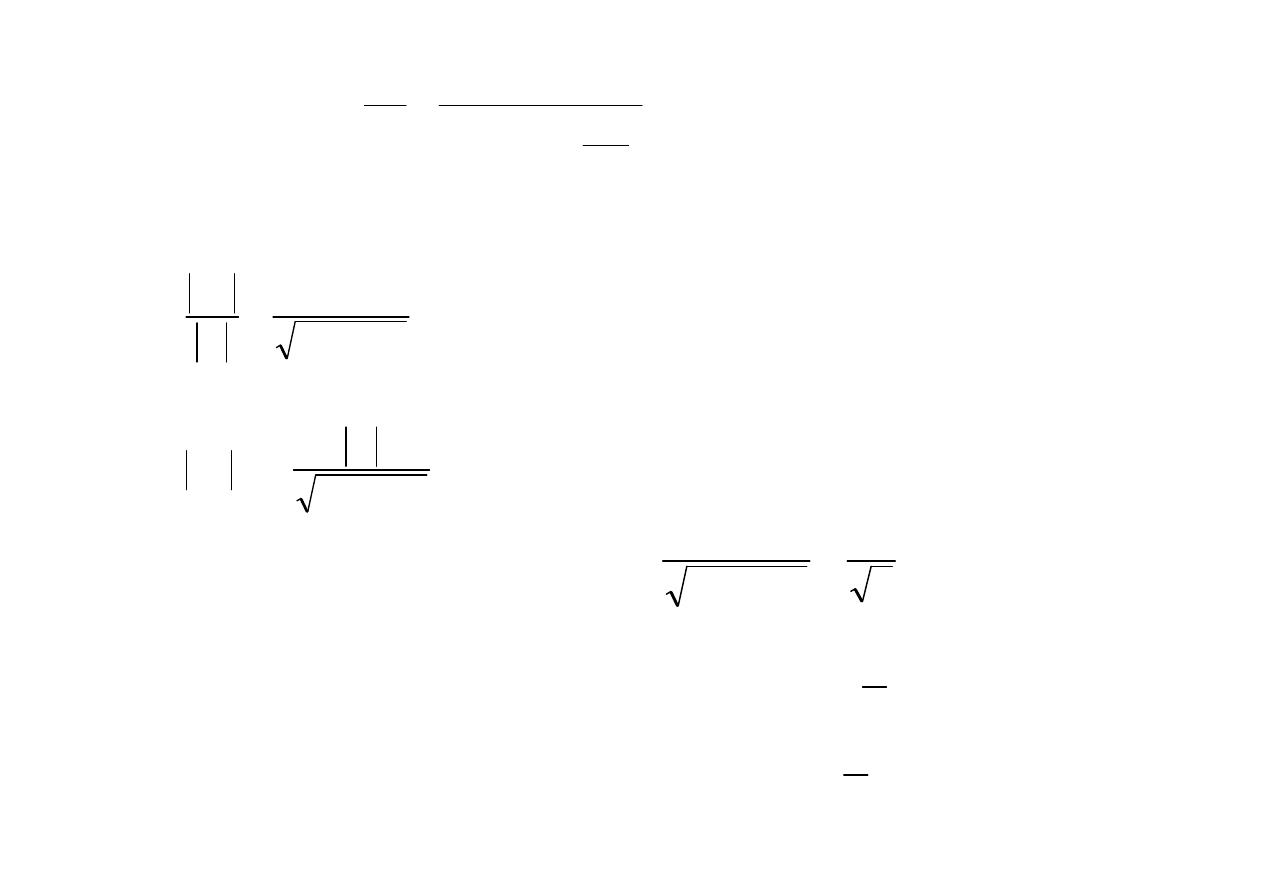
poniewa

ż

to dla wartosci skutecznych

2

2

2

2

X

R

U

R

U

czyli

X

R

R

U

U

R

R

+

=

+

=

)

1

(

C

L

j

R

R

U

U

R

ω

ω

−

+

=

Dla kra

ń

cowych pulsacji

2

1

,

ω

ω

2

1

2

2

=

+

X

R

R

R

X

R

X

=

−

=

)

(

,

)

(

2

1

ω

ω

oraz

4

,

4

2

1

π

ϕ

π

ϕ

=

−

=

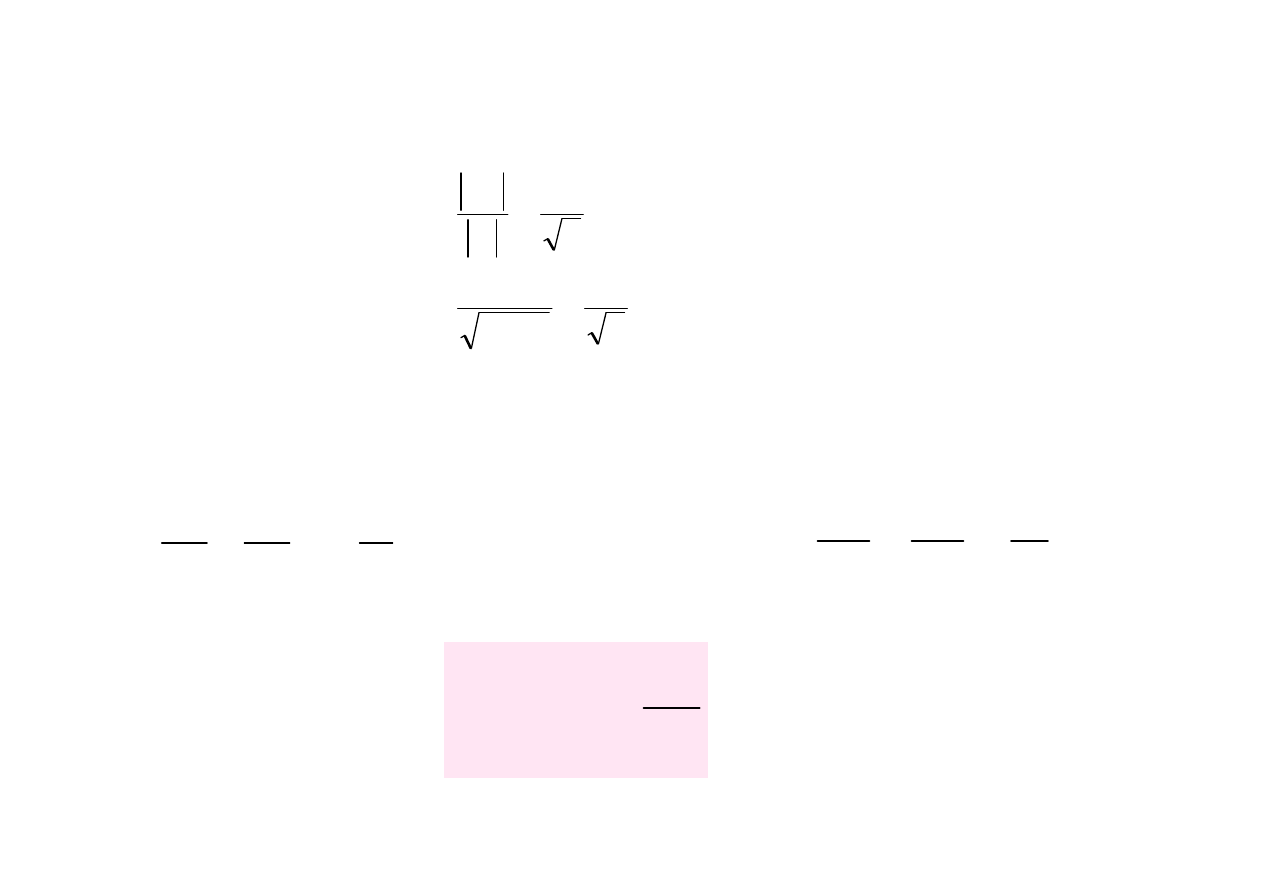
Aby wyprowadzic wzór na

szeroko

ść

pasma przepuszczania

korzystamy z zale

ż

no

ś

ci

2

1

1

1

2

1

2

=

+

=

x

U

U

R

1

±

=

=

δ

Q

x

Q

r

r

1

1

1

−

=

−

ω

ω

ω

ω

Q

r

r

1

2

2

=

−

ω

ω

ω

ω

Q

r

ω

ω

ω

=

−

1

2

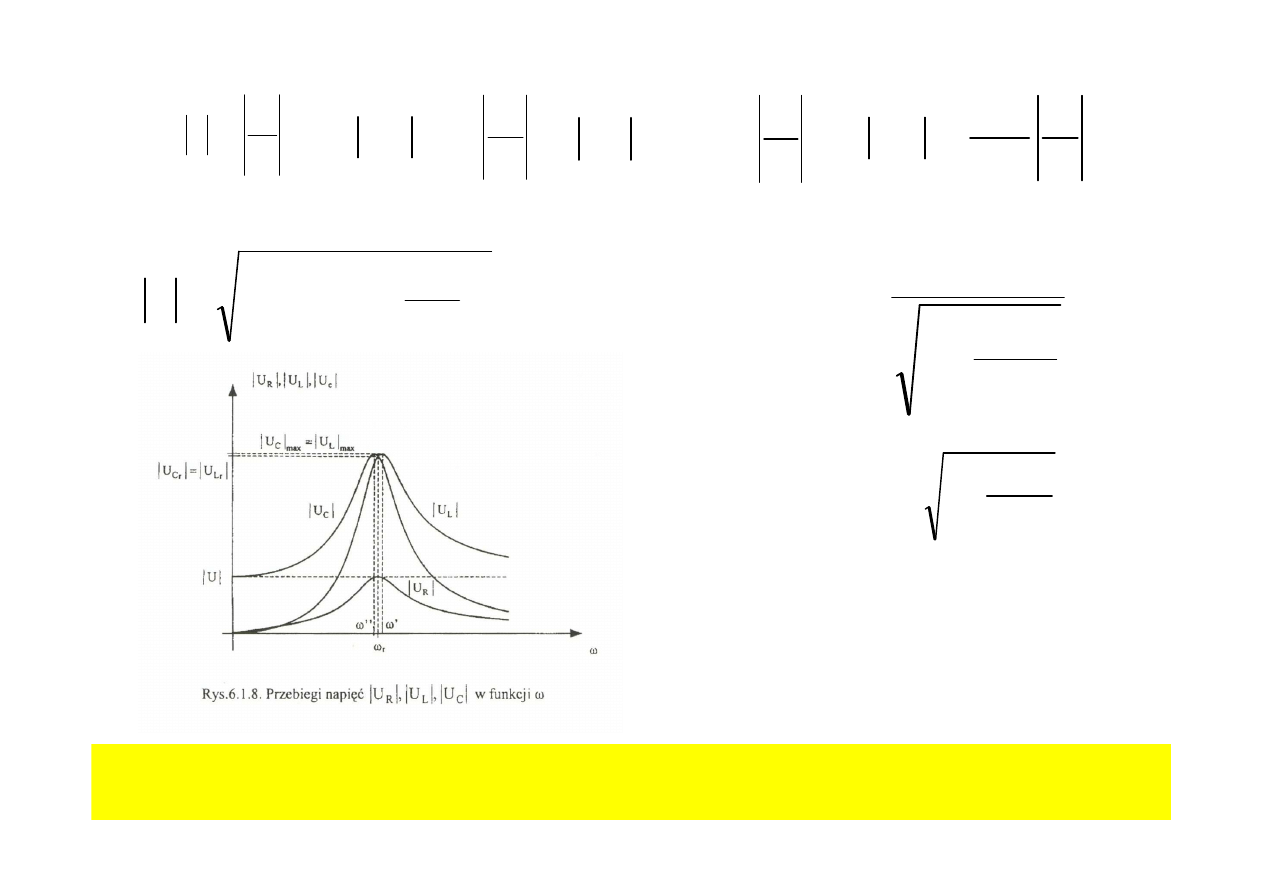
Z

U

I

=

Z

U

R

U

R

=

Z

U

L

U

L

=

=

ω

Z

U

C

U

C

ω

1

=

2

2

)

1

(

C

L

R

Z

ω

ω

−

+

=

2

2

1

1

Q

r

−

ω

=

ω′

2

2

1

1

Q

r

−

ω

=

ω′′

2
r

ω

=

ω′′

ω′

Przy dostatecznie du

ż

ej dobroci Q punkty s

ą

bardzo bliskie pulsacji

rezonansowej

``

`

,

ω

ω

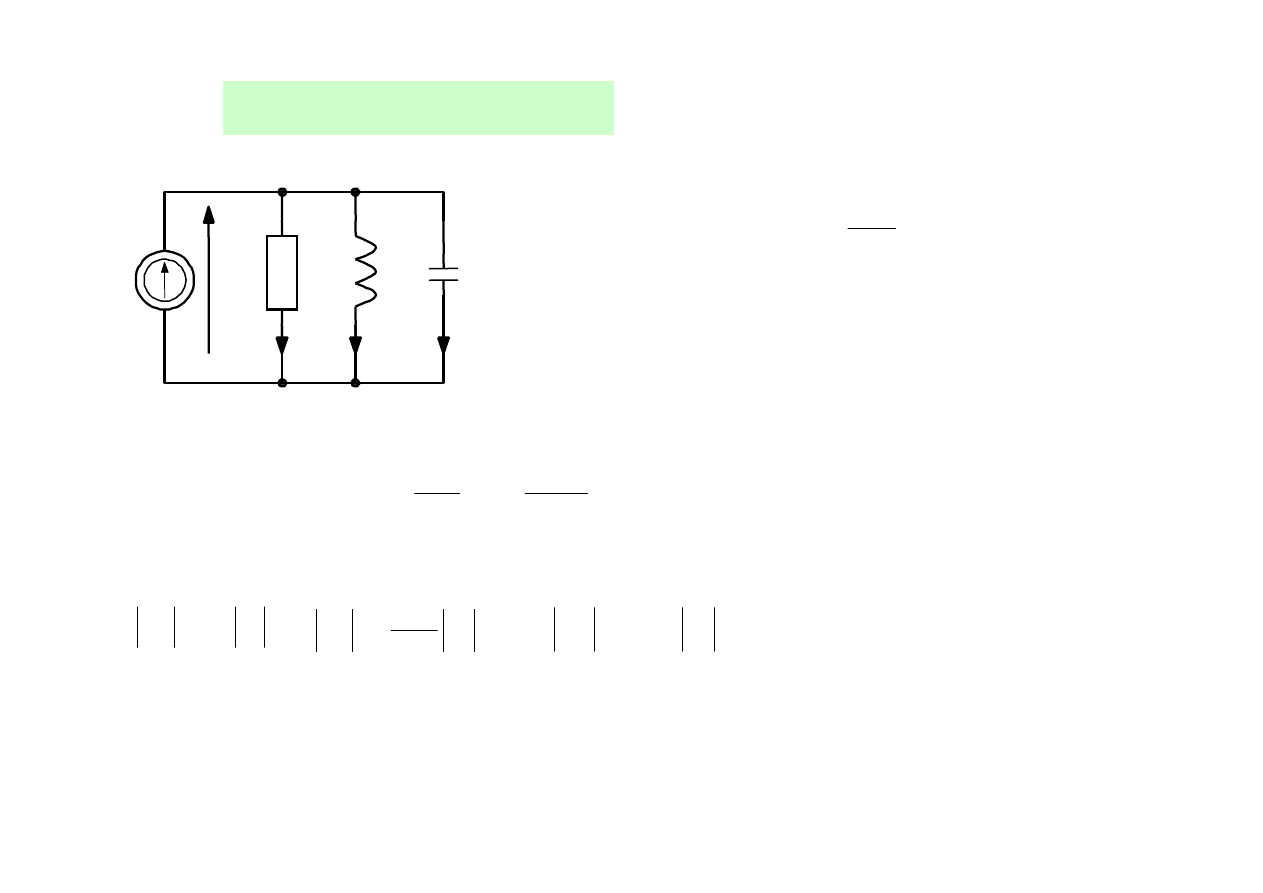
Rezonans równoległy

I

L

I

C

I

R

I

U

G

L

C

jB

G

L

C

j

G

Y

+

=













−

+

=

ω

ω

1

GU

I

R

=

L

j

U

U

L

j

I

L

ω

ω

=

−

=

CU

j

I

C

ω

=

U

G

I

G

=

U

L

I

L

ω

1

=

U

C

I

C

ω

=

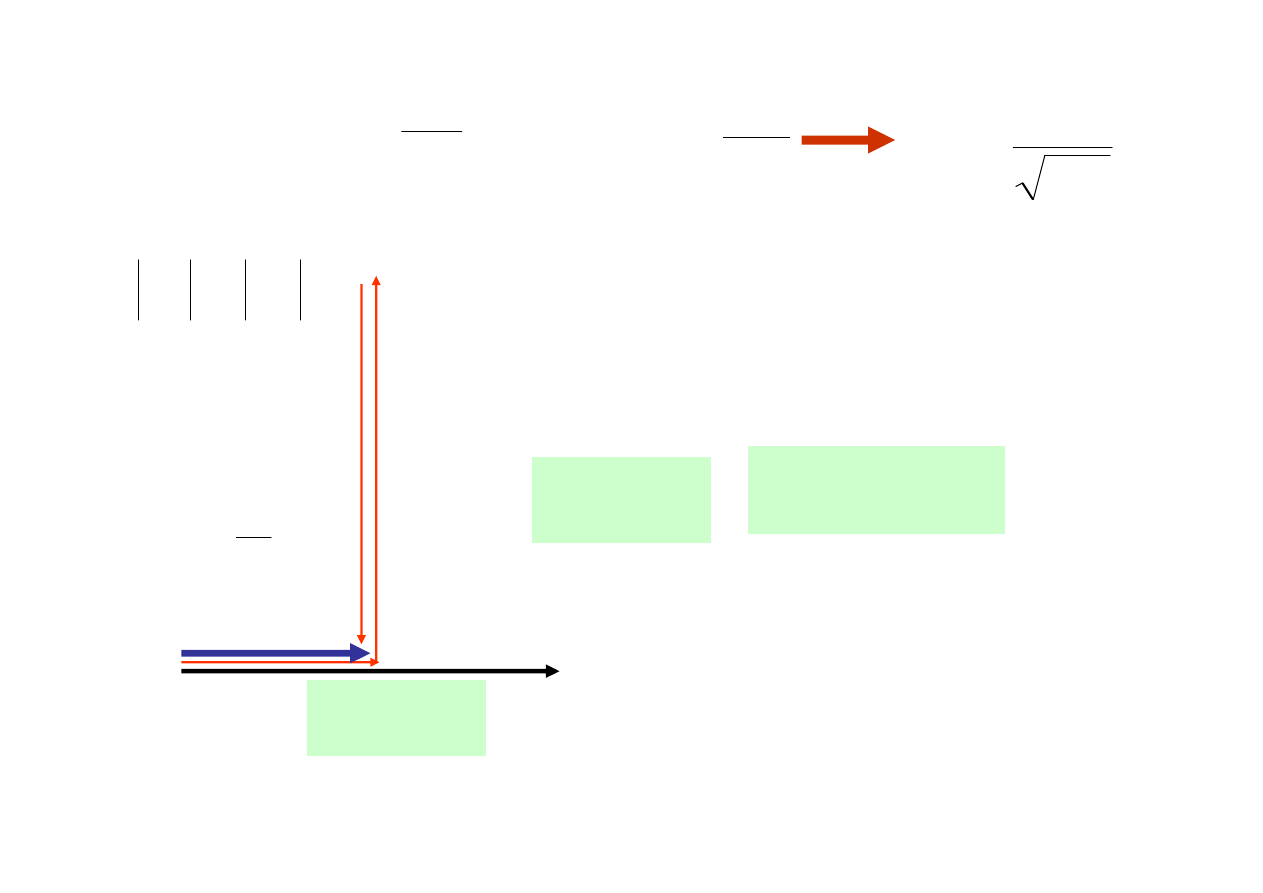
0

=

B

0

1

=

−

L

C

ω

ω

L

C

ω

ω

1

=

C

L

I

I

=

U

GU

C

I

CU

j

=

ω

L

I

U

L

=

−

ω

1

j

R

I

I

=

=

0

=

ϕ

OBWÓD O CHARAKTERZE REZYSTANCYJNYM

LC

1

r

=

ω

G

Y

=

0

=

)

(

B

r

ω

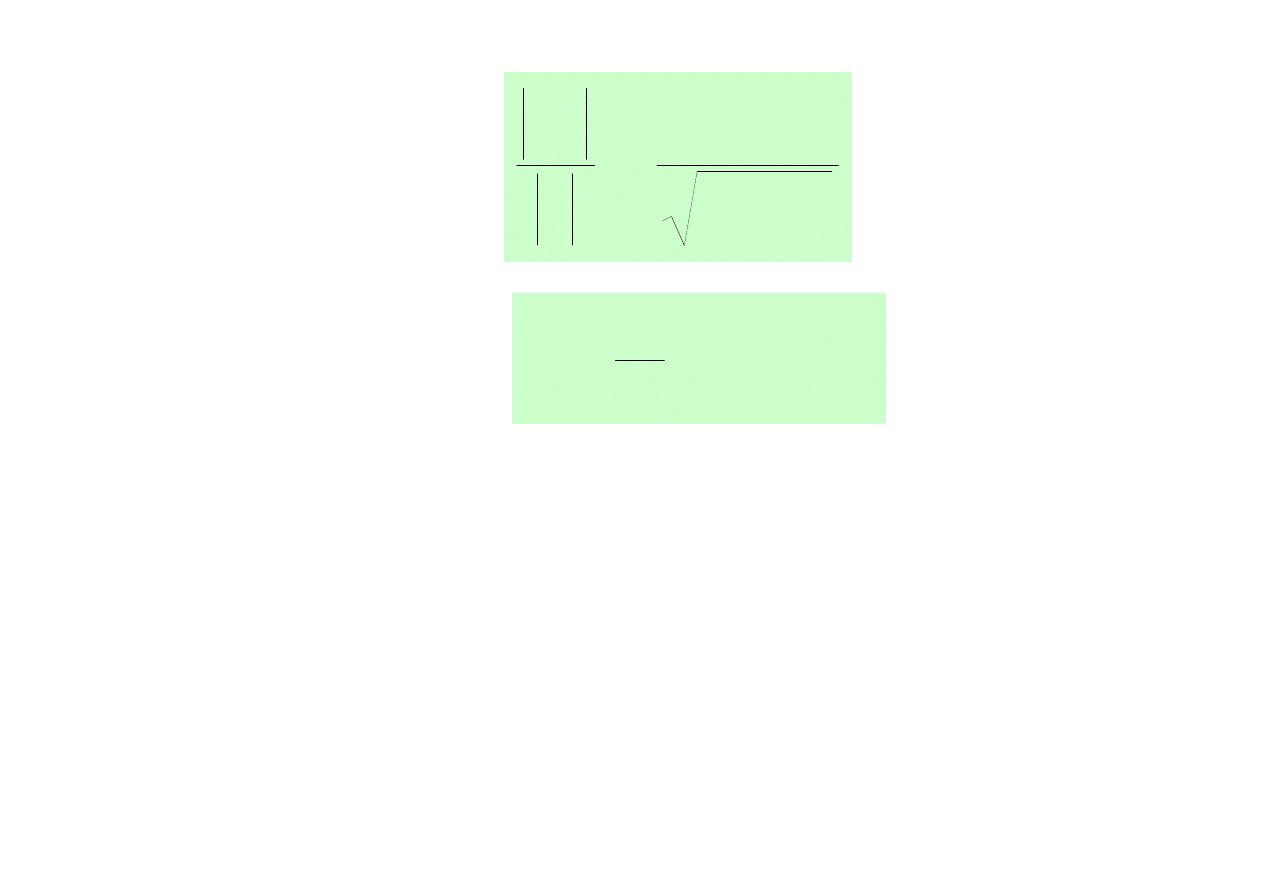
2

1

1

x

I

I

R

+

=

tgx

arc

I

I

arg

R

−

=













Wykresy funkcji:

Noszą nazwę

uniwersalnych krzywych rezonansowych

i odnoszą się do każdego równoległego obwodu
rezonansowego

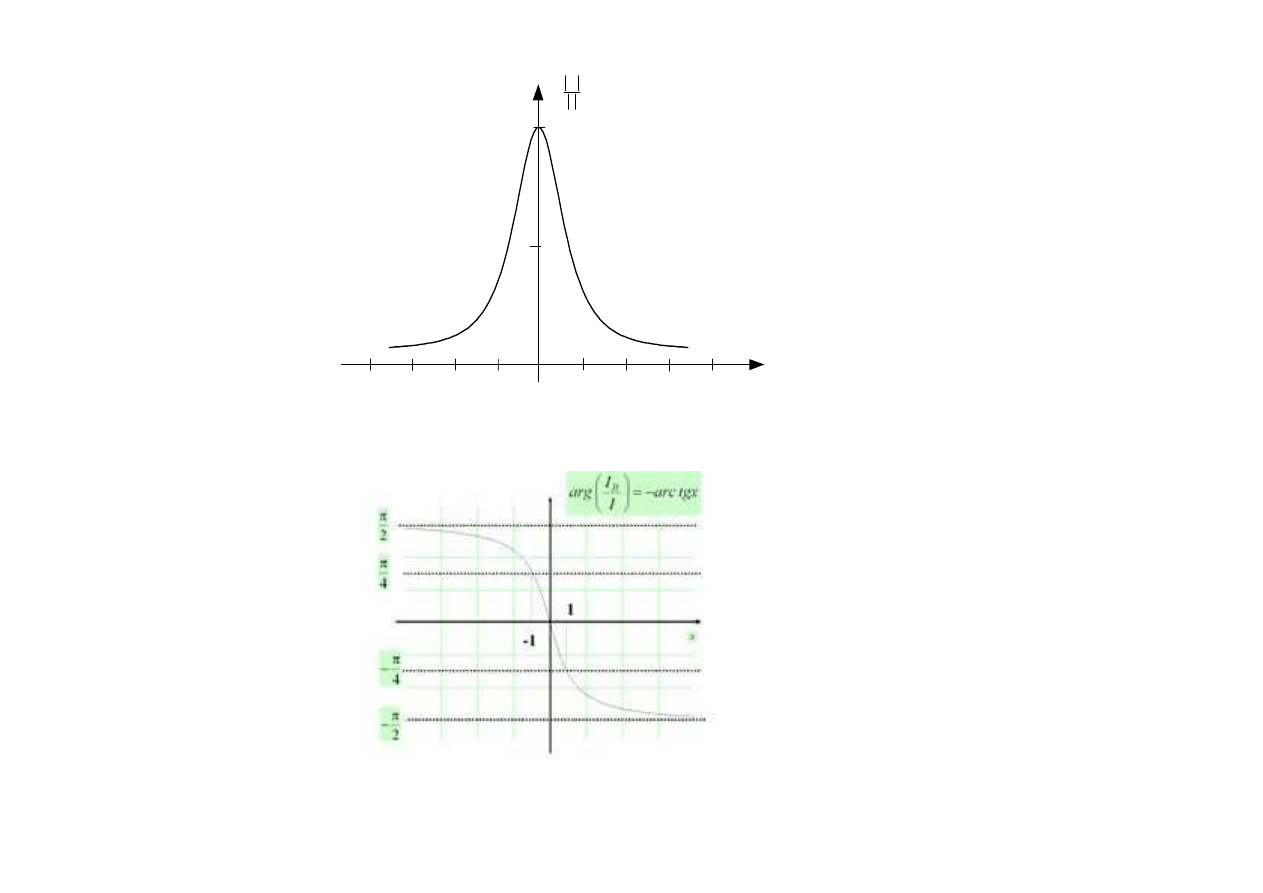
8

6

4

2

-8

-6

-4

-2

0,5

1

0

x

I

I

R

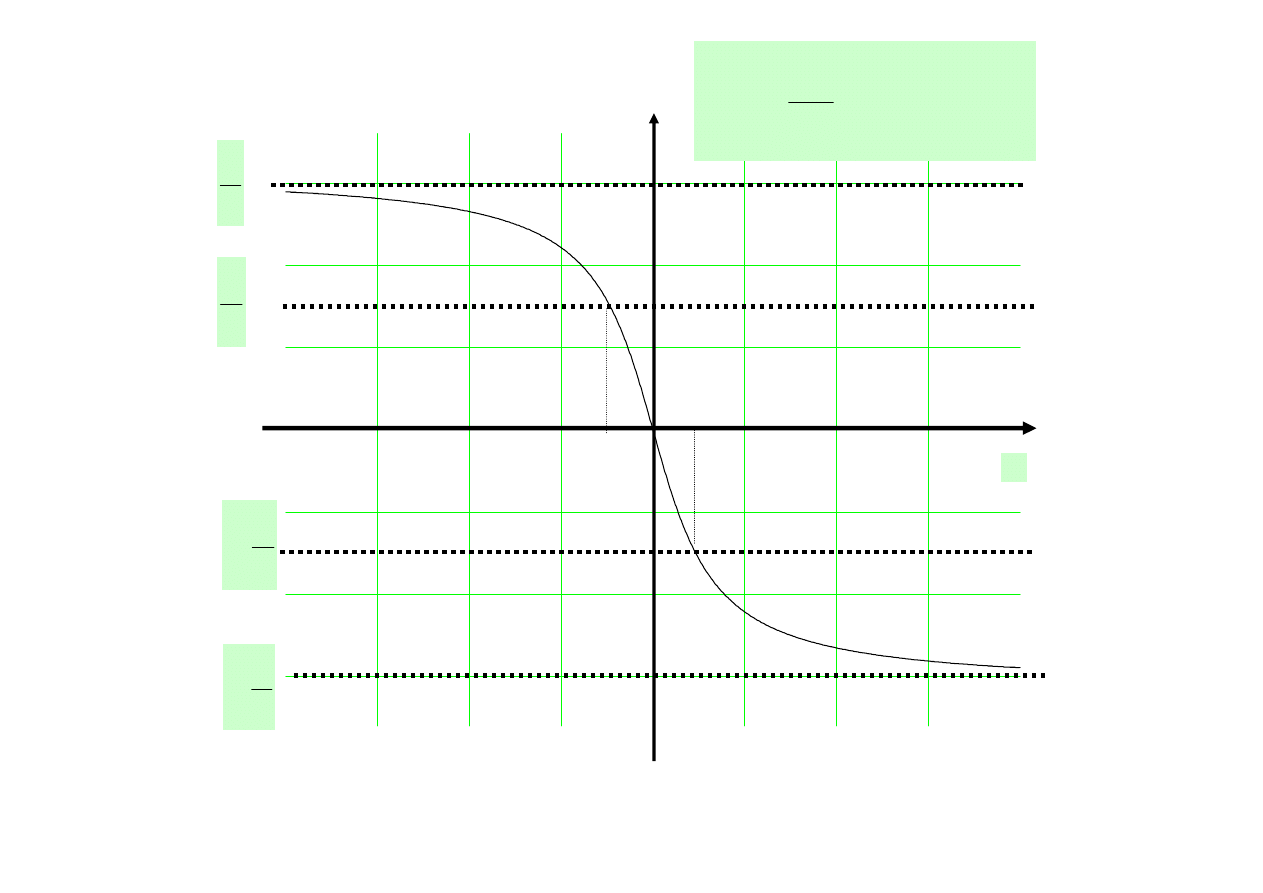
x

tgx

arc

I

I

arg

R

−

=













2

π

4

π

2

π

−

4

π

−

-

-

1

1

1

1

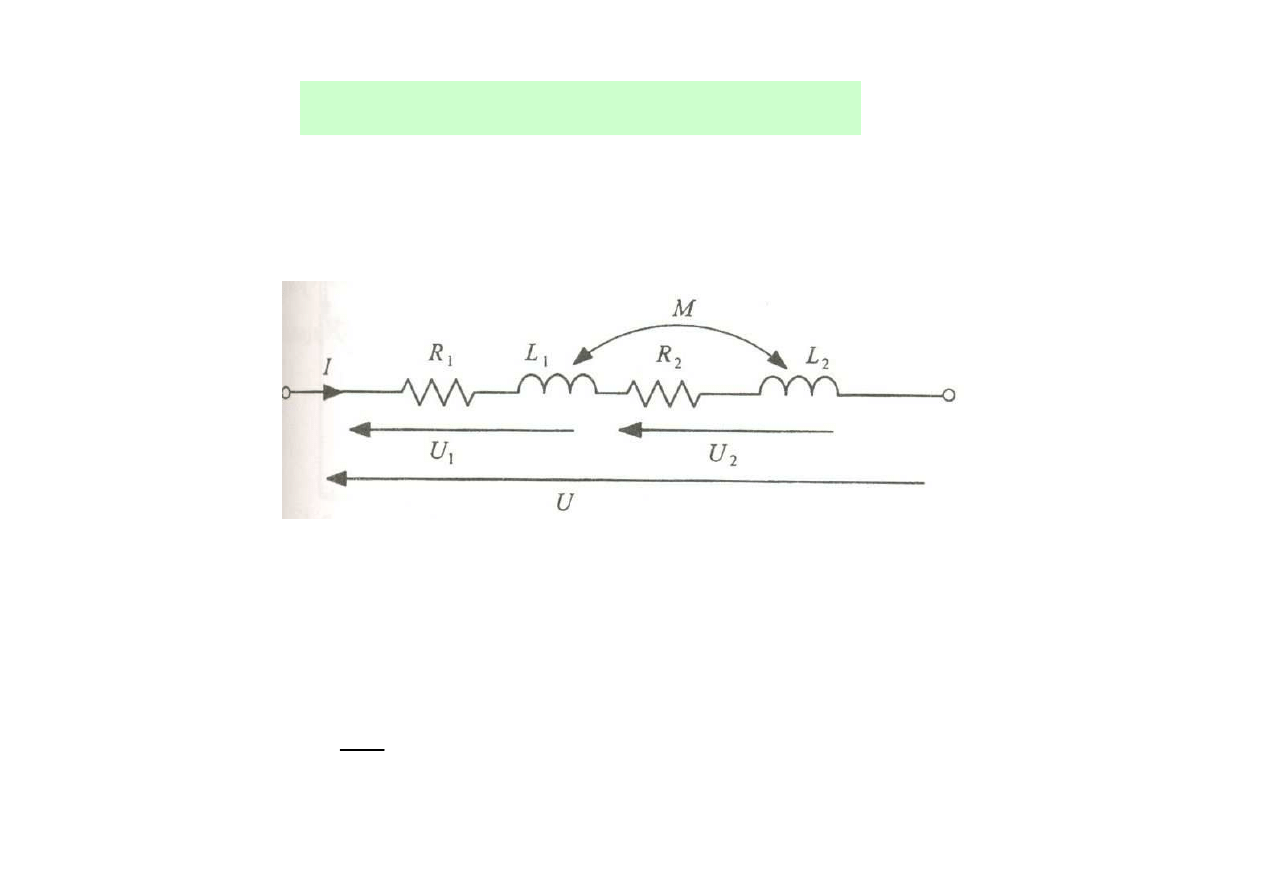
Cewki magnetycznie sprz

ę

zone

Poł

ą

czenie szeregowe

[

]

I

M

L

L

j

R

R

U

2

(

2

1

2

1

+

+

+

+

=

ω

)

2

(

2

1

2

1

M

L

L

j

R

R

I

U

Z

+

+

+

+

=

=

ω

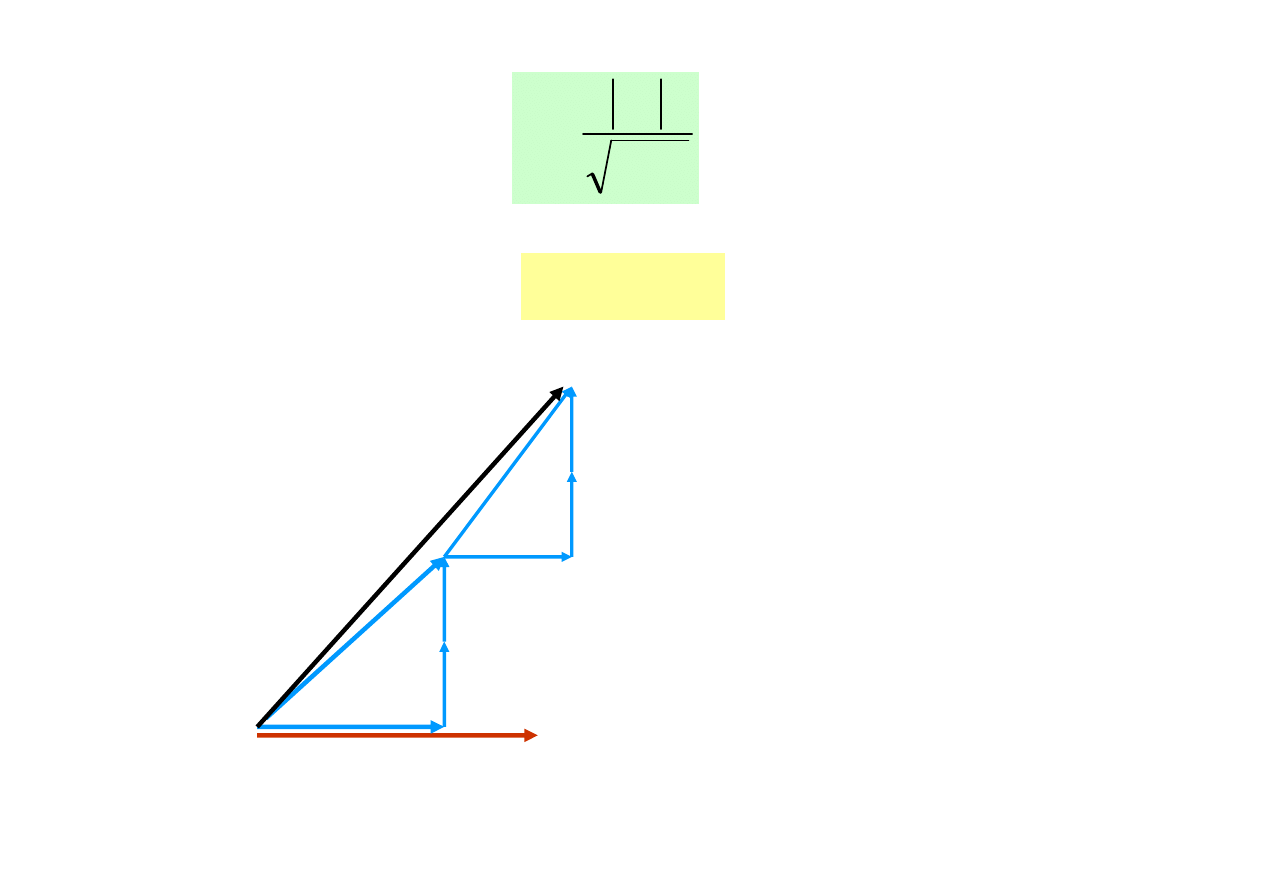
Współczynnik sprz

ęż

enia

2

1

L

L

M

k

=

1

0

≤

≤

k

I

1

IR

I

L

j

1

ω

MI

j

ω

MI

j

ω

I

L

j

2

ω

1

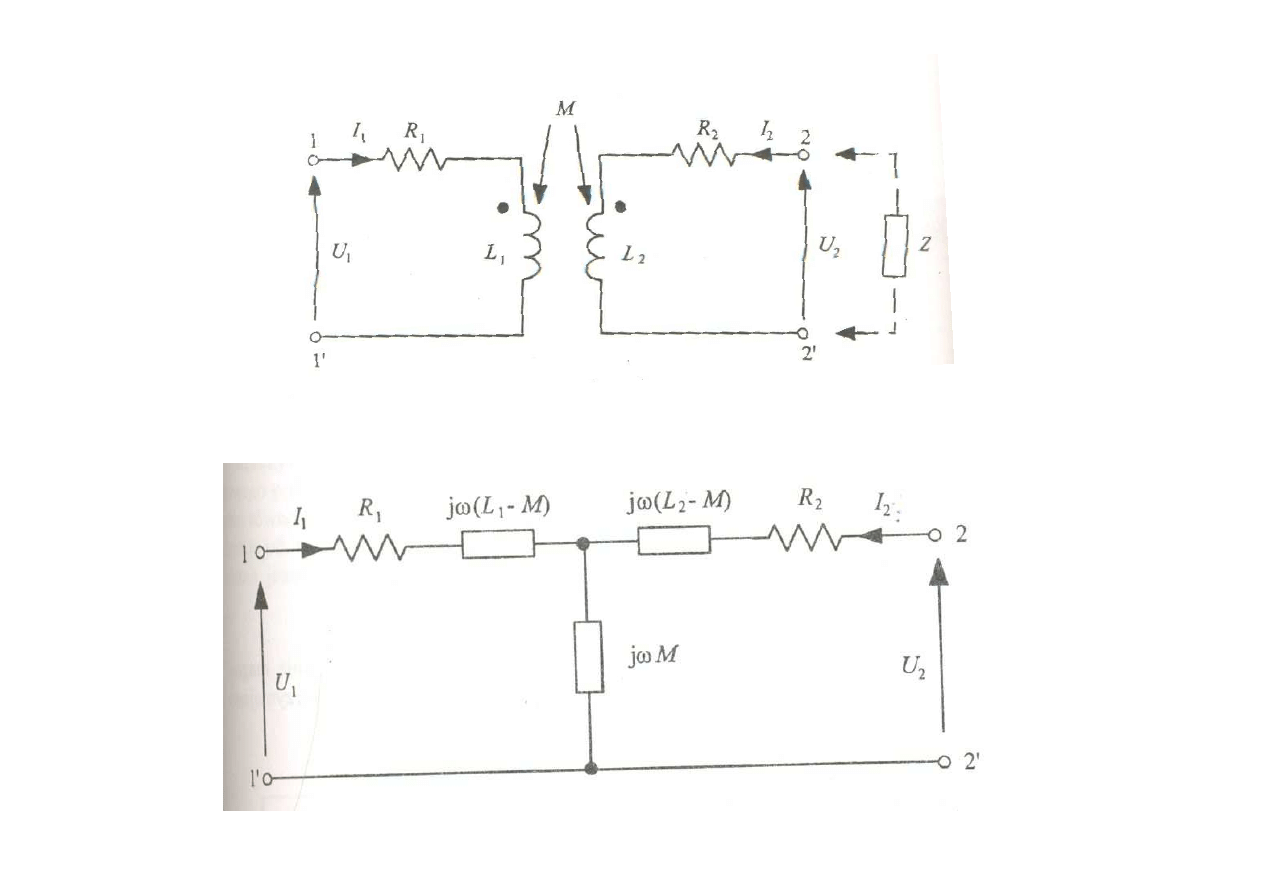
U

2

U

U