Rozpatrujemy dwójnik, którego napi

ę

cie i pr

ą

d maj

ą

t

ę

sam

ą

pulsacj

ę

u

i

moc chwilowa

)

sin(

)

sin(

)

sin(

i

m

i

m

u

m

t

I

i

t

U

t

U

u

ϕ

ω

ϕ

ϕ

ω

ϕ

ω

+

=

+

+

=

+

=

)

2

2

sin(

sin

))

2

2

cos(

1

(

cos

)

2

2

cos(

2

1

cos

2

1

)

sin(

)

sin(

i

i

i

m

m

m

m

i

m

i

m

t

I

U

t

I

U

t

I

U

I

U

t

I

t

U

ui

p

ϕ

ω

ϕ

ϕ

ω

ϕ

ϕ

ϕ

ω

ϕ

ϕ

ω

ϕ

ϕ

ω

+

+

+

−

=

+

+

−

=

+

+

+

=

=

podstawowe zale

ż

no

ś

ci

Moc chwilowa i moc czynna

przypomnienie

1

p

2

p

Moce w obwodach pr

ą

du sinusoidalnie zmiennego

Z

A wi

ę

c

p= p

1

+p

2

p

1

- składowa t

ę

tni

ą

ca mocy

p

2

- składowa przemienna mocy

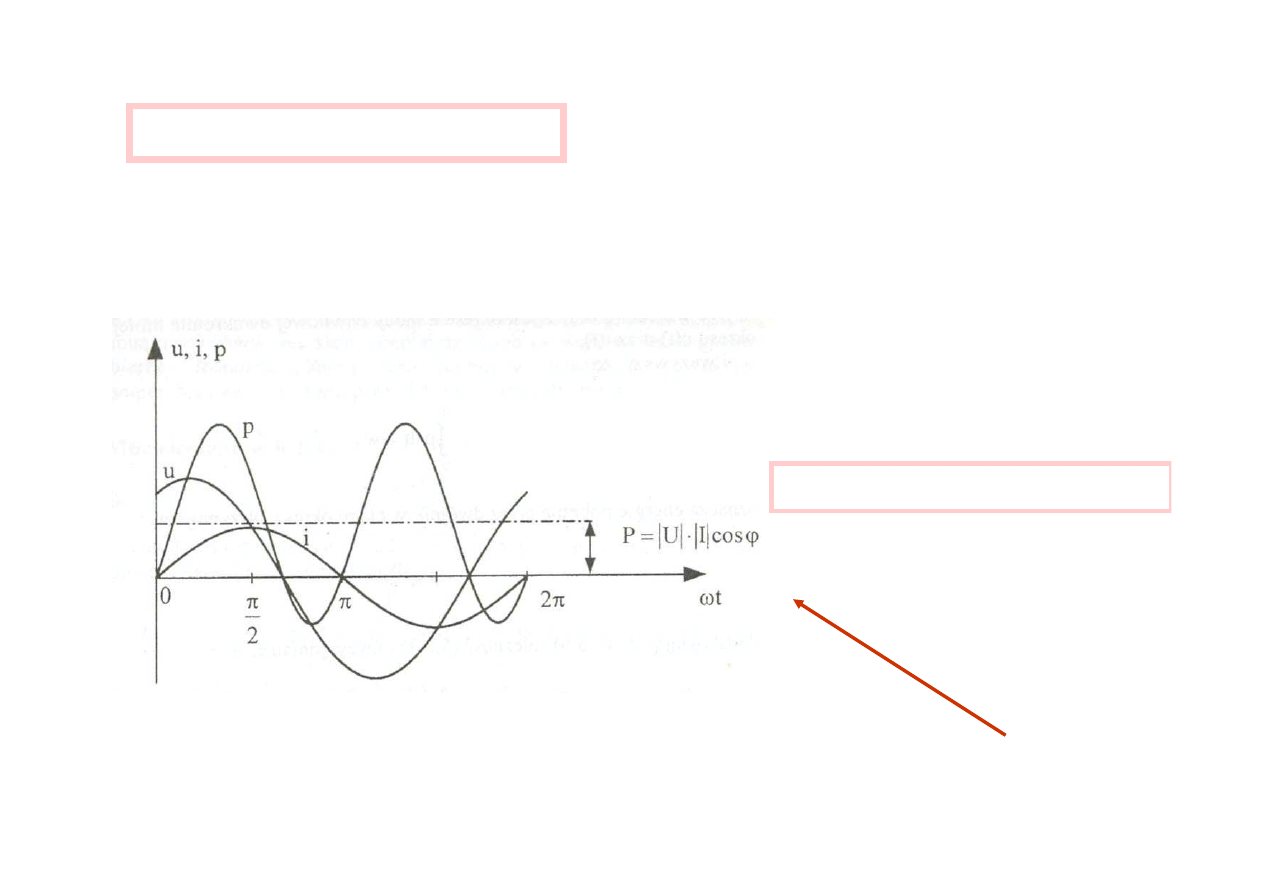
przykładowe przebiegi u, i, p

moc czynna

moc czynna – czyli warto

ść ś

rednia za okres

mocy chwilowej

ϕ

cos

1

0

I

U

pdt

T

P

T

=

=

∫

Poniewa

ż

∫

=

T

dt

p

0

2

0

wi

ę

c

∫

=

T

dt

p

T

P

0

1

1

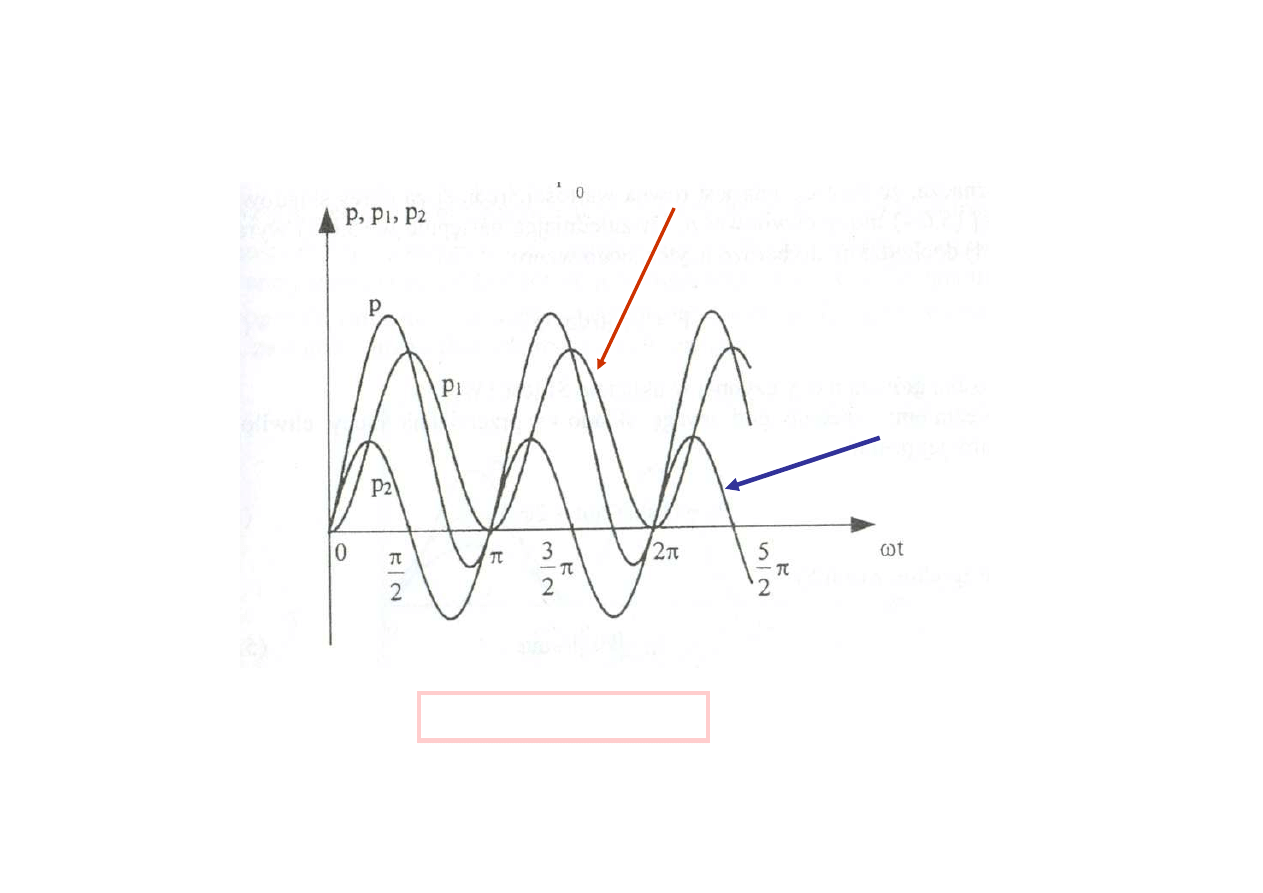
przebiegi p , p

1

i p

2

moc t

ę

tni

ą

ca

moc przemienna

Rozkład mocy chwilowej na moc t

ę

tni

ą

c

ą

i moc przemienn

ą

Wró

ć

my na moment do wzoru opisuj

ą

cego moc czynn

ą

ϕ

cos

1

0

I

U

pdt

T

P

T

=

=

∫

Podali

ś

my wcze

ś

niej ,

ż

e moc czynna równa si

ę

warto

ś

ci

ś

redniej za okres

składowej t

ę

tni

ą

cej mocy chwilowej p

Natomiast moc bierna Q jest zwi

ą

zana ze składow

ą

przemienn

ą

mocy

chwilowej

ϕ

sin

I

U

Q

=

1W

1Var

Posługuj

ą

c si

ę

metod

ą

zespolona otrzymamy

:

je

ż

eli

to

i

u

j

j

e

I

I

e

U

U

ϕ

ϕ

=

=

rozpatrzmy iloczyn

ϕ

ϕ

ϕ

j

j

e

I

U

e

I

U

UI

i

u

=

=

−

∗

)

(

i

u

i

m

u

m

t

I

i

t

U

u

ϕ

ϕ

ϕ

ϕ

ω

ϕ

ω

−

=

+

=

+

=

)

sin(

)

sin(

czyli

jQ

P

I

U

j

I

U

UI

+

=

+

=

∗

ϕ

ϕ

sin

cos

S

UI

=

∗

Sum

ę

mocy czynnej i biernej nazywamy moc

ą

symboliczn

ą

VA

S

1

]

[

=

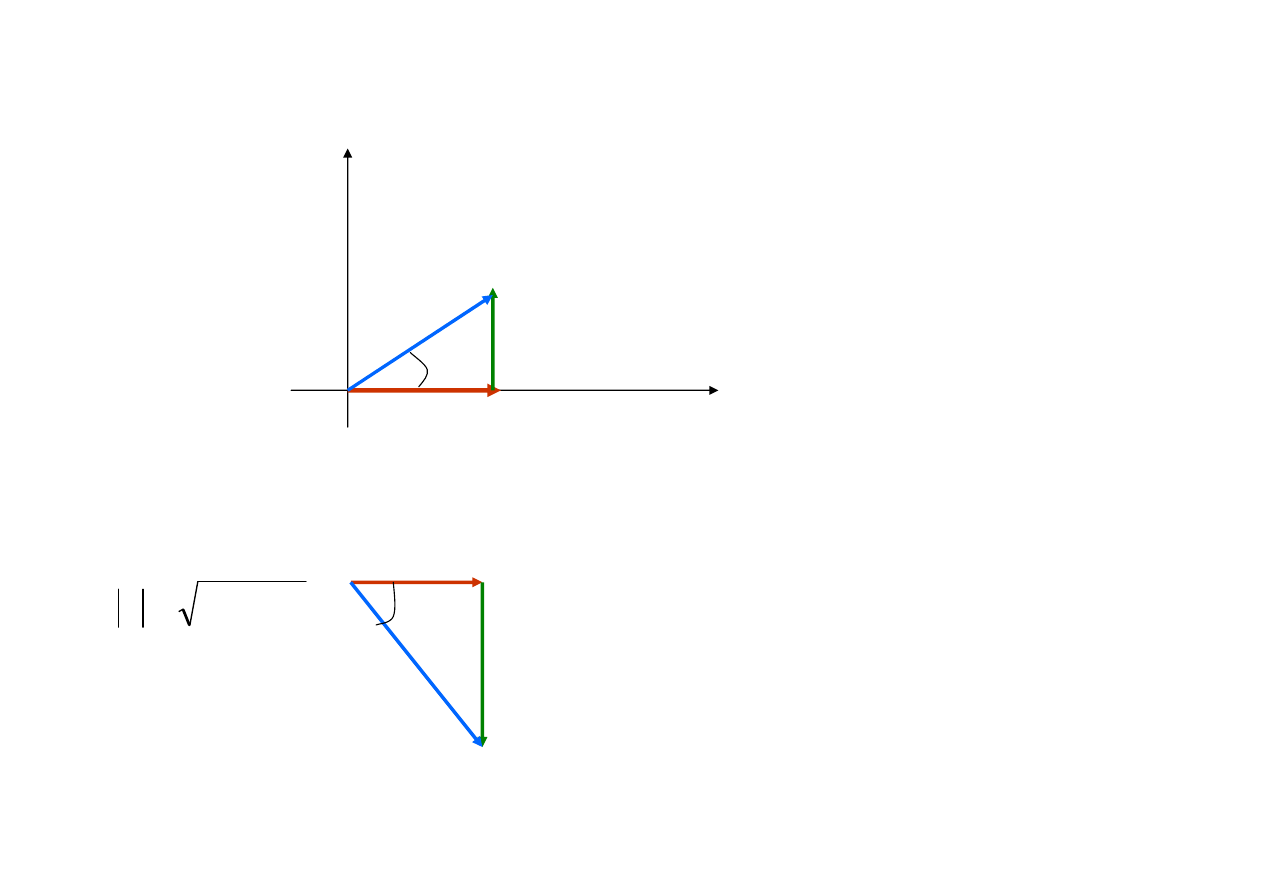
Geometryczn

ą

interpretacj

ą

mocy symbolicznej jest

trójk

ą

t mocy

)

Im( S

)

Re( S

P

jQ

jQ

P

S

+

=

0

Q > 0

P

Q < 0

|S|

Q

2

2

Q

P

S

+

=

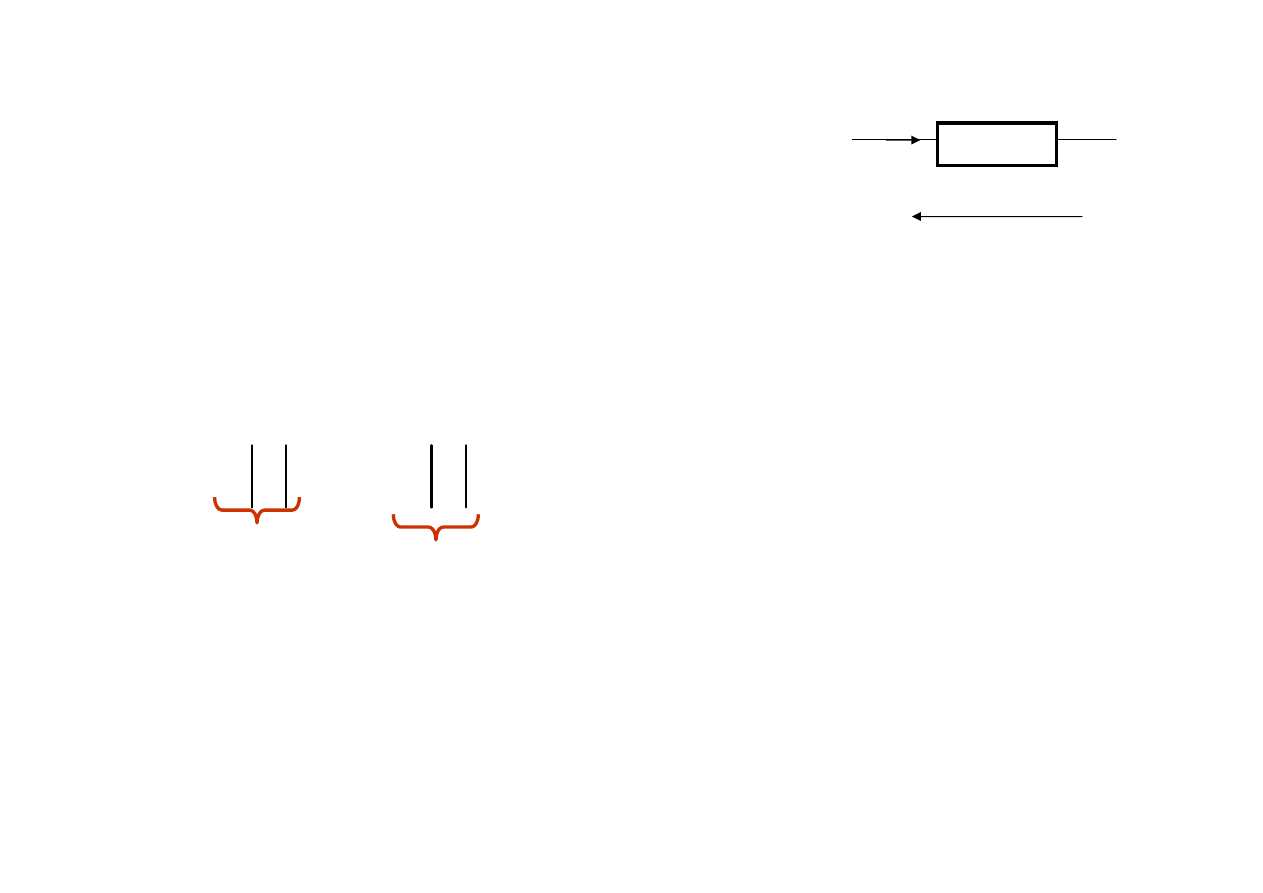
u

i

Z

Rozpatrzmy dwójnik o impedancji

Z=R+jX

2

2

)

(

I

jX

I

R

II

jX

R

UI

jQ

P

S

+

=

=

+

=

=

+

=

∗

∗

P

Q

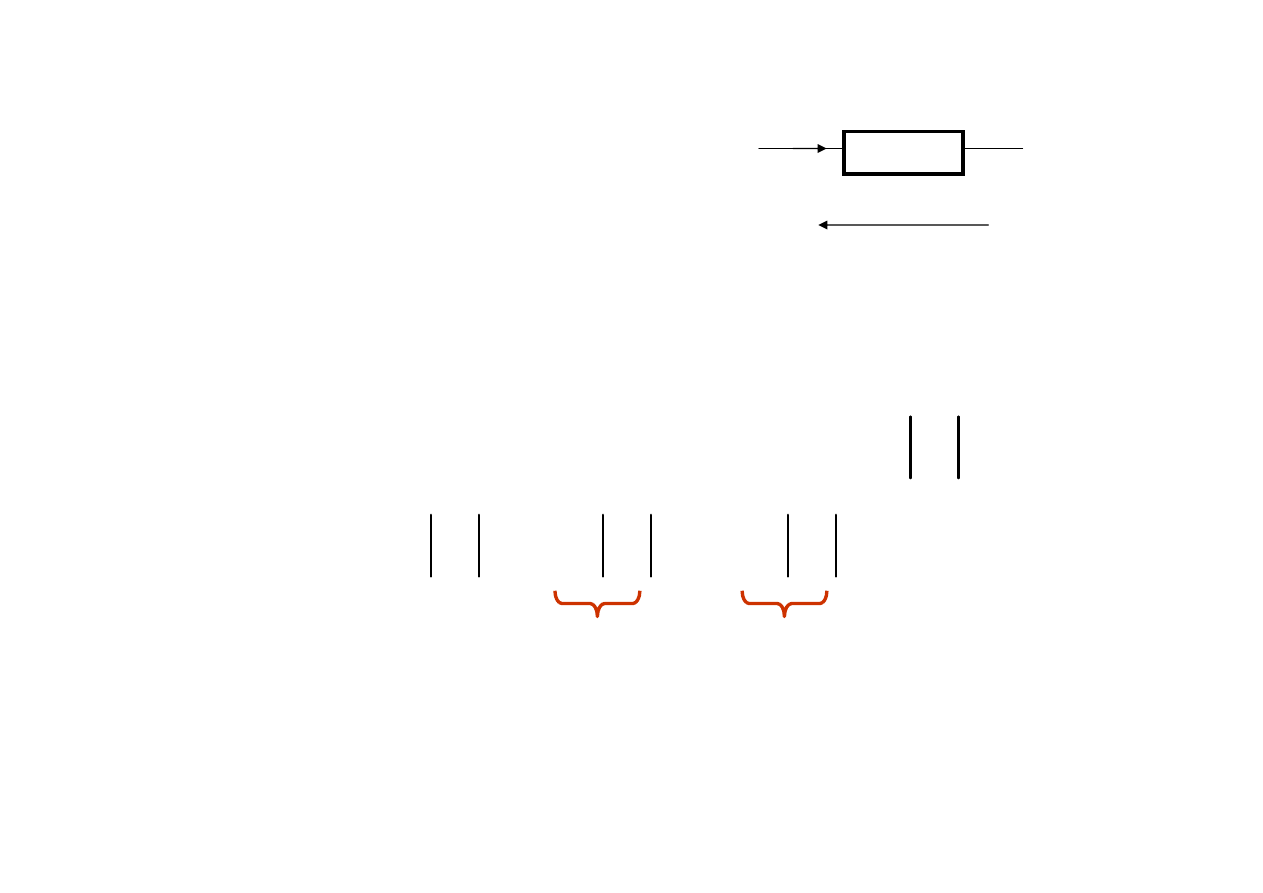
Dla dwójnika o admitancji

Y=G+jB

2

2

2

2

)

(

)

(

U

jB

U

G

U

jB

G

U

Y

YU

U

UI

jQ

P

S

−

=

−

=

=

=

=

=

+

=

∗

∗

∗

Q

P

u

i

Y

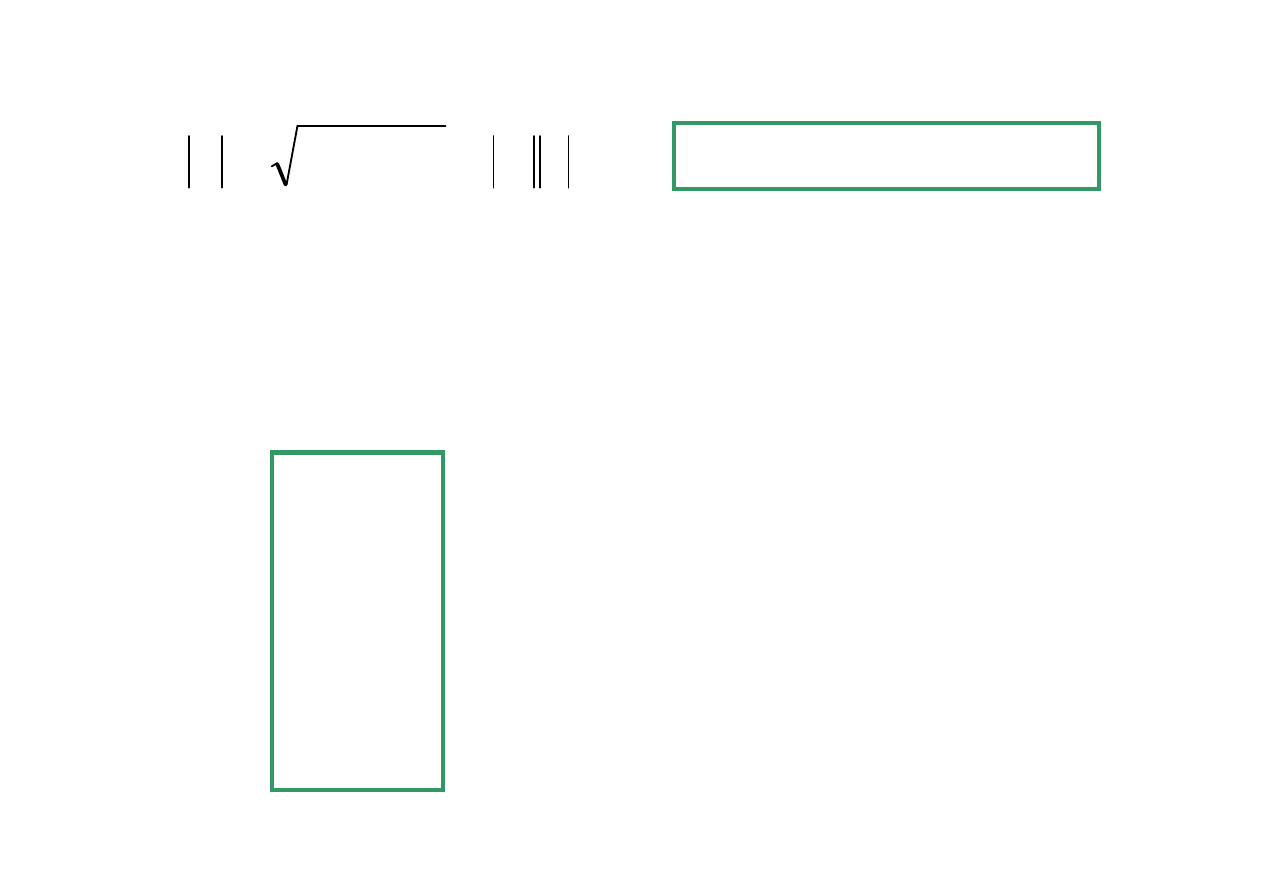
I

U

Q

P

S

=

+

=

2

2

Jest to moc pozorna

Jednostka jest VA

∑

∑

∑

=

=

=

n

k

n

k

n

k

Q

Q

P

P

S

S

1

1

1

Na podstawie znanego tw Tellegena otrzymujemy nast

ę

puj

ą

ce wzory