v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
70
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
METODA PRZEMIESZCZEŃ – część druga
Zad. 6.1
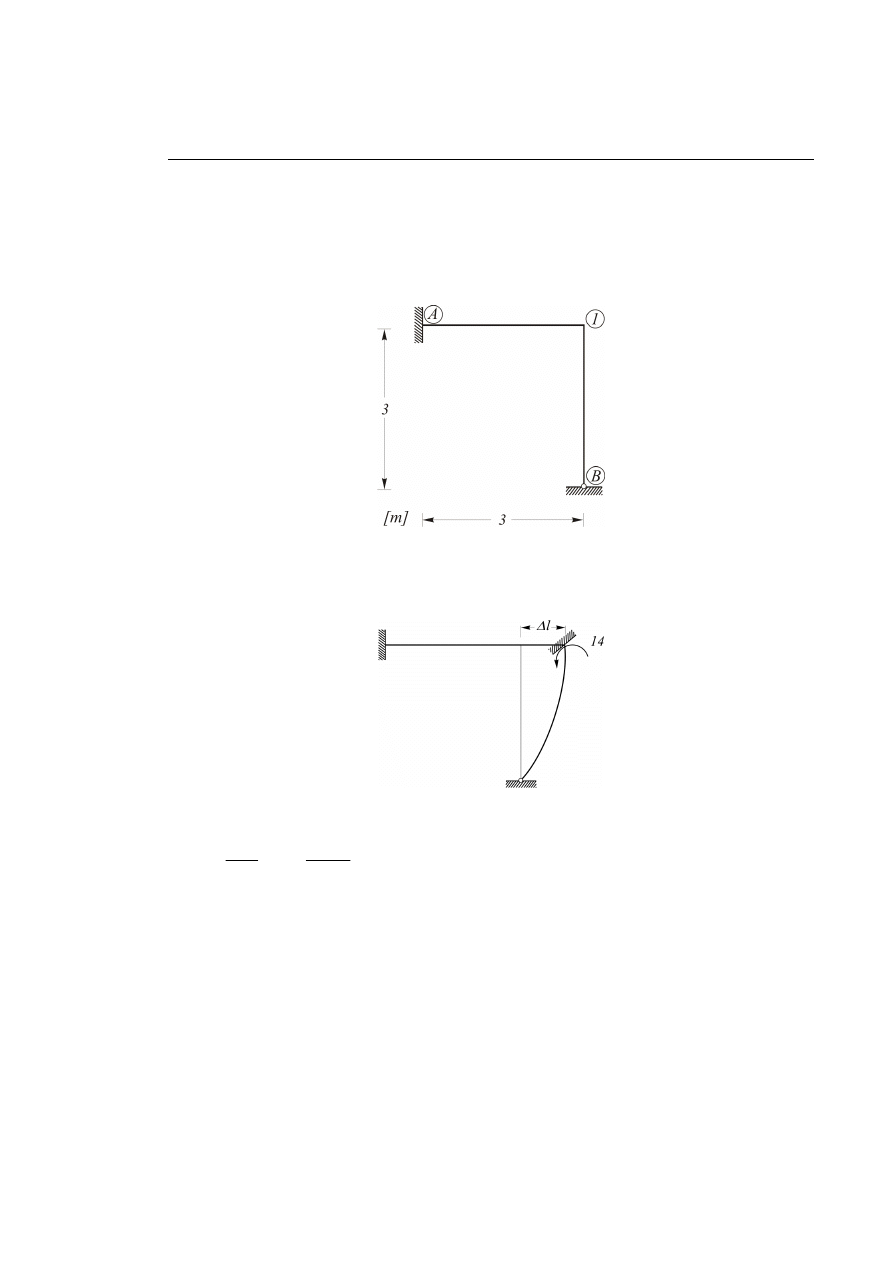
Wyznaczyć siły wewnętrzne powstałe na skutek wmontowania pręta A-1 dłuższego o
3 [
]
l
cm
∆ =
.
Przyjąć
2
1400 [
]
EI
kNm
=
Rys. 6.1.1.
Stopień geometrycznej niewyznaczalności układu
1( )
g
n
ϕ
=
Schemat geometrycznie wyznaczalny:
Rys. 6.1.2.
Momenty wyjściowe:
0
1
2
2
3
3 1400
0, 03
14 [
]
3
3
B
EI
M
l
kNm
⋅
⋅
= −
⋅ ∆ = −
⋅
= −
Momenty przywęzłowe w układzie geometrycznie wyznaczalnym powstałe na skutek wymuszonego kąta
obrotu
1
ϕ
=
:
v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
71
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
Rys. 6.1.3.
Sumaryczne momenty przywęzłowe:
1
1
1
4
2
,
14
,
3
3
A
B
A
M
EI
M
EI
M
EI
ϕ
ϕ
ϕ
=
= − +
=
Równanie równowagi :
1
1
1
0
A
B
M
M
M
Σ
=
+
=
Stąd:
7
6
14
0
3
EI
EI
ϕ
ϕ
− +
=
⇒
=
Wartości momentów przywęzłowych:
1
1
1
4
2
6
8 [
],
14 6
8 [
],
6
4 [
]
3
3
A
B
A
M
kNm
M
kNm
M
kNm
= ⋅ =
= − + = −
= ⋅ =
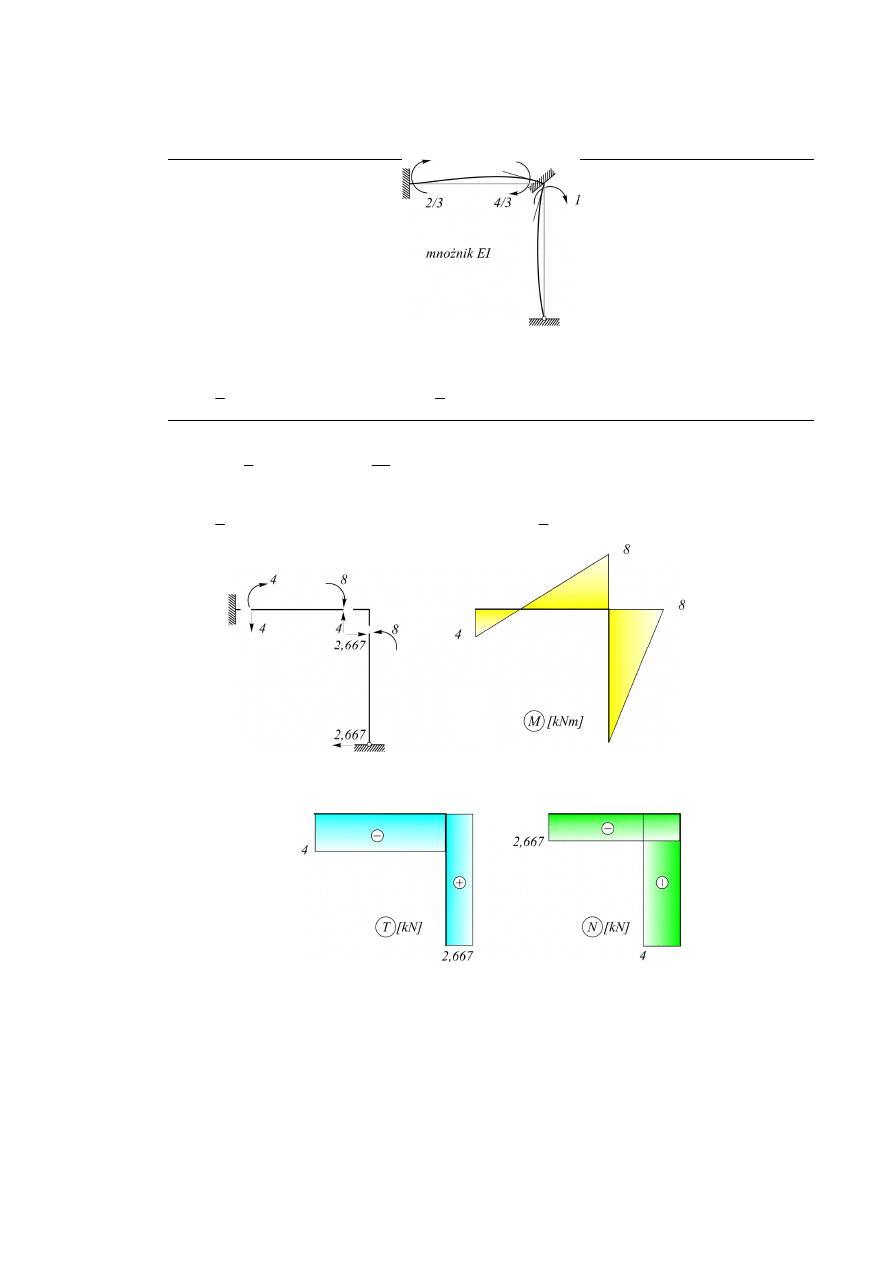
Wykresy:
Rys. 6.1.4.
Rys. 6.1.5.
v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
72
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
Zad. 6.2
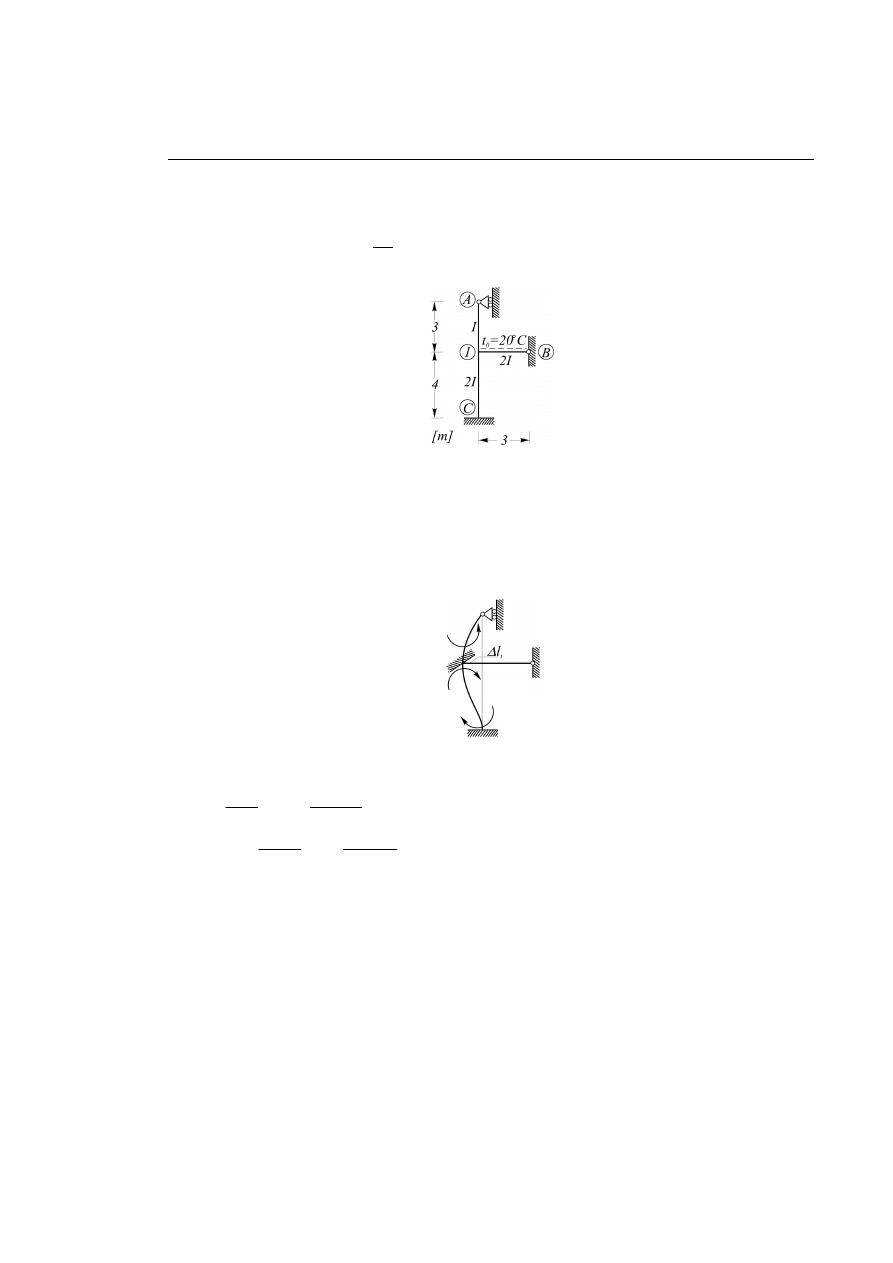
Dany jest układ ramowy przedstawiony na rysunku 6.2.1. Wyznaczyć siły wewnętrzne powstałe na skutek
równomiernego ogrzania jednego z elementów o wielkość
0
t względem temperatury montażu.
2
5
1
10000 [
],
10
t
o
EI
kNm
C
α
−
=
=
Rys. 6.2.1.
Stopień geometrycznej niewyznaczalności układu :
1( )
g
n
ϕ
=
Swobodne wydłużenie termiczne elementu 1-B:
5
4
0
10
20 3
6 10
[ ]
t
t
l
t
l
m
α
−
−
∆ =
⋅ ⋅ =
⋅ ⋅ = ⋅
Schemat geometrycznie wyznaczalny:
Rys. 6.2.2.
Momenty wyjściowe:
0
4
1
2
2
0
0
4
1
1
2
3
3 10000
6 10
2 [
]
3
3
6
2
6 20000
6 10
4,5 [
]
16
4
A
t
C
C
t
EI
M
l
kNm
E
I
M
M
l
kNm
−
−
⋅
⋅
= −
⋅ ∆ = −
⋅ ⋅
= −
⋅
⋅
=
=
⋅ ∆ =
⋅ ⋅
=
Momenty przywęzłowe:
v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
73
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
1
1
1
1
3
2
2
3
3
2
2
3
4
2
4, 5
4,5 2
4
2
2
4, 5
4,5
4
A
B
C
C
EI
M
EI
E
I
M
EI
E
I
M
EI
E
I
M
EI
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
= − +
= − +
⋅
=
=
⋅
=
+
=
+
⋅
=
+
=
+
Równanie równowagi :
1
1
1
1
0
A
B
C
M
M
M
M
Σ
=
+
+
=
Stąd:
1
2,5 5
0
2
EI
EI
ϕ
ϕ
+
=
⇒
= −
Wartości momentów przywęzłowych:
1
1
1
1
2 0, 5
2, 5 [
]
1[
]
4, 5 1
3, 5 [
]
4, 5 0, 5
4 [
]
A
B
C
C
M
kNm
M
kNm
M
kNm
M
kNm
= − −
= −
= −
=
− =
=
−
=
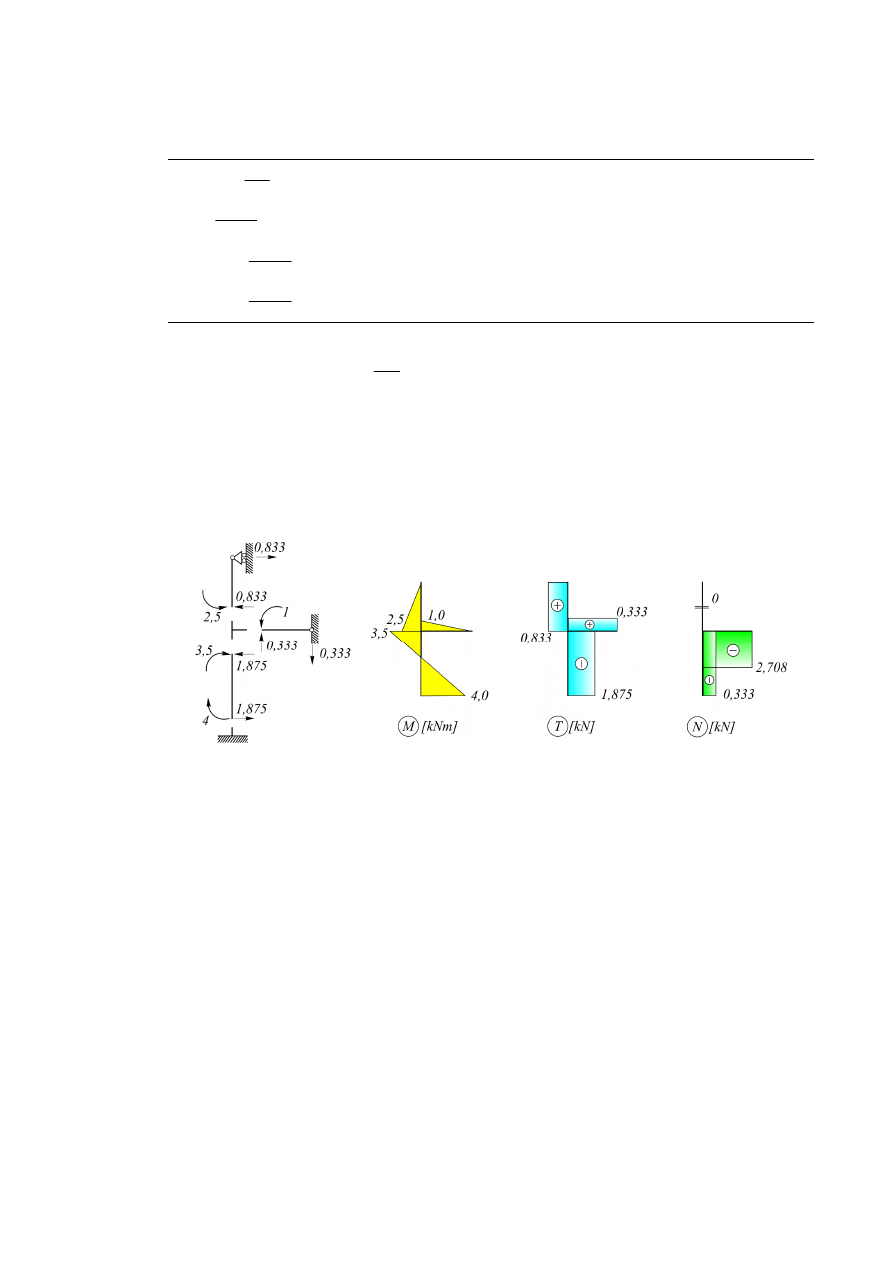
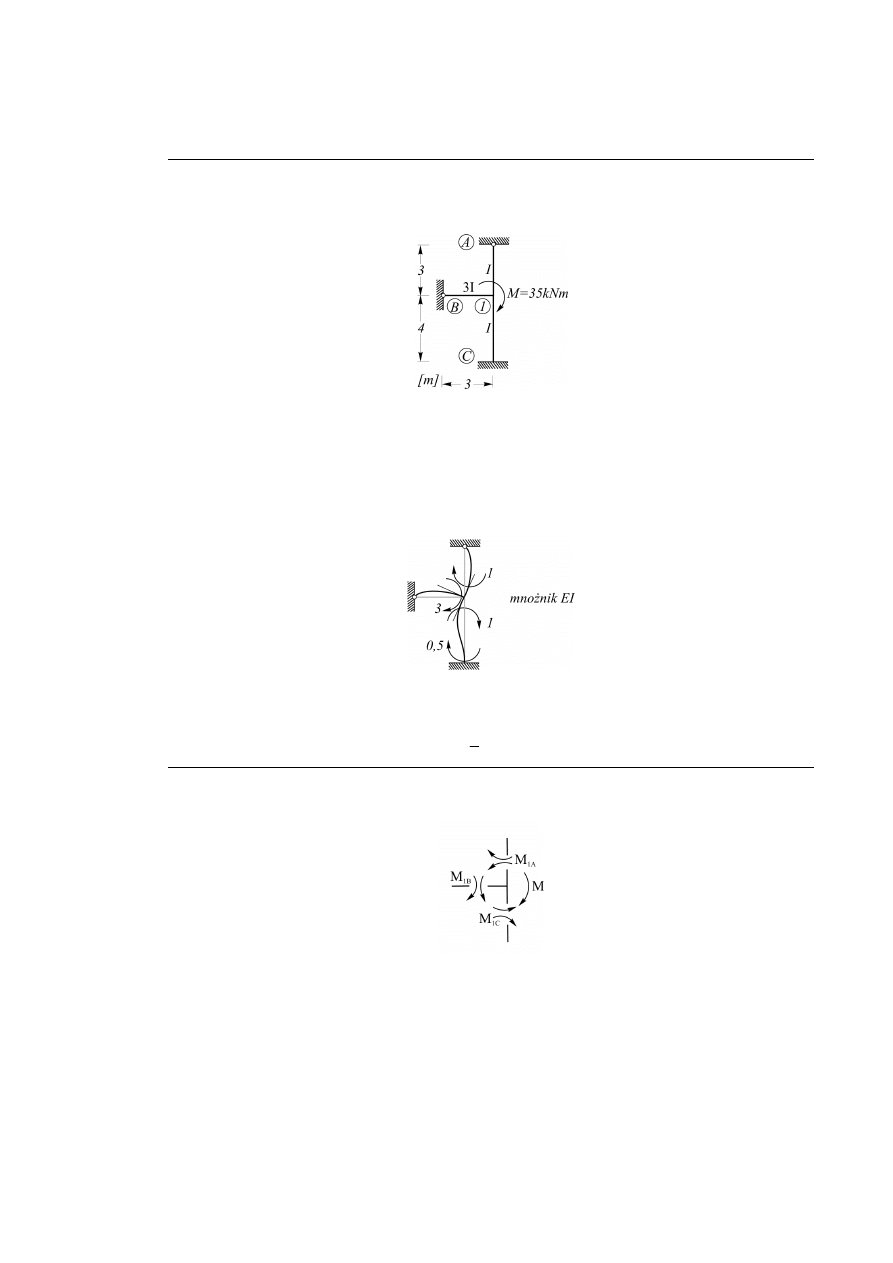
Rozwiązanie:
Rys. 6.2.3.
v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
74
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
Zad.4.3
Dany jest układ ramowy przedstawiony na rysunku 6.3.1.Sporządzić wykresy sił wewnętrznych N, T, M.
Rys.6.3.1.
Układ jest jednokrotnie geometrycznie niewyznaczalny.
1( )
g
n
ϕ
=
Ponieważ jedynym obciążeniem jest moment skupiony przyłożony w węźle, wyjściowe momenty
przywęzłowe są zerowe.
Wpływ wymuszonego kąta obrotu
1
ϕ
=
:
Rys. 6.3.2.
Momenty przywęzłowe pochodzące od kata obrotu
1
ϕ
=
:
1
1
1
1
1
3
2
A
B
C
C
M
EI
M
EI
M
EI
M
EI
ϕ
ϕ
ϕ
ϕ
=
=
=
=
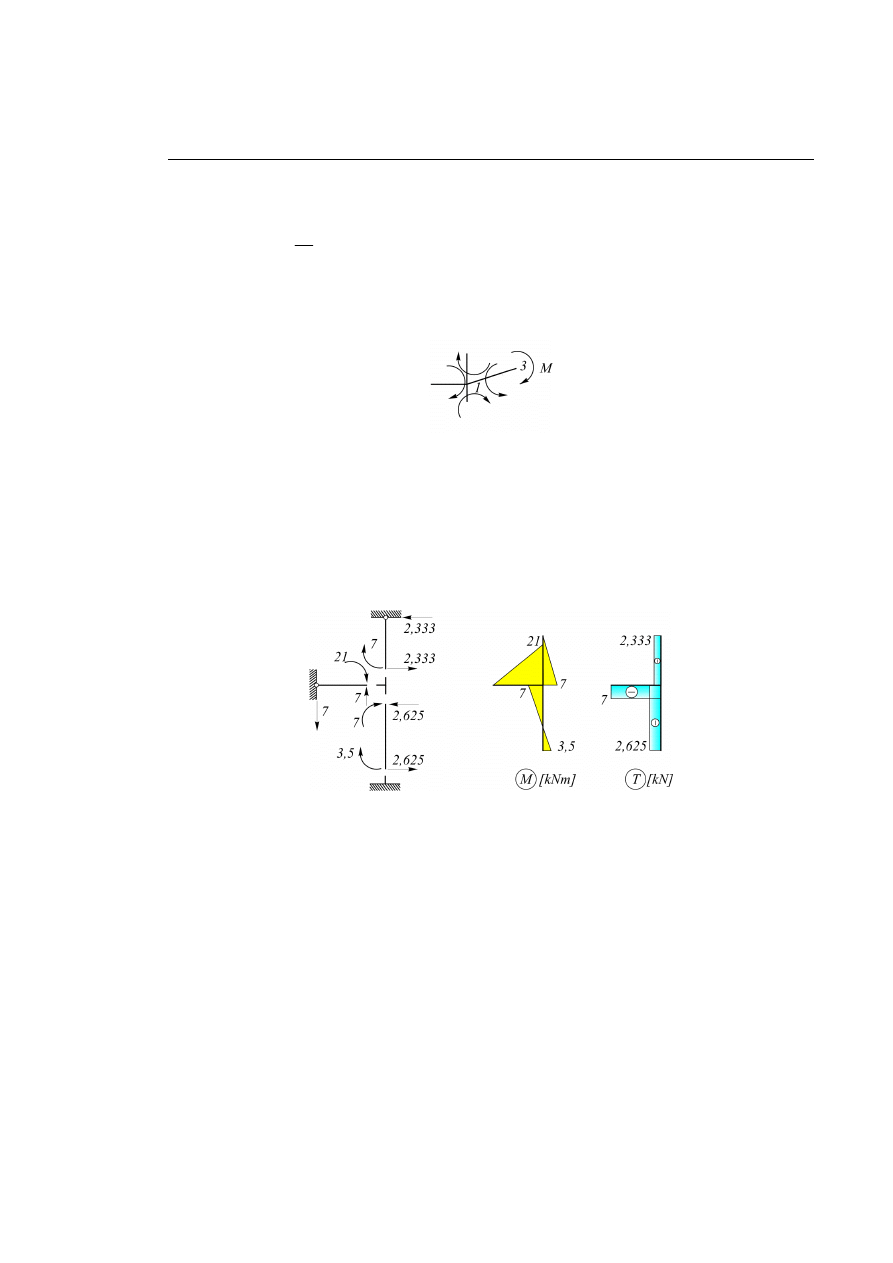
Równanie równowagi wyciętego węzła 1 – suma momentów przywęzłowych oraz skupionego momentu
węzłowego jest równa zeru:
Rys. 6.3.3.
v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
75
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
1
1
1
1
1
1
1
0
lub
A
B
C
A
B
C
M
M
M
M
M
M
M
M
M
Σ
= −
−
−
+
=
+
+
=
Stąd:
7
5
35
0
EI
EI
ϕ
ϕ
−
=
=
Inna interpretacja:
dodatkowy element 1-3 obciążony momentem skupionym
M
,w elemencie tym powstaje moment
wyjściowy
13
M
M
= −
Rys. 6.3.4
Wartości momentów przywęzłowych:
1
1
1
1
7 [
]
21[
]
7[
]
3, 5 [
]
A
B
C
C
M
kNm
M
kNm
M
kNm
M
kNm
=
=
=
=
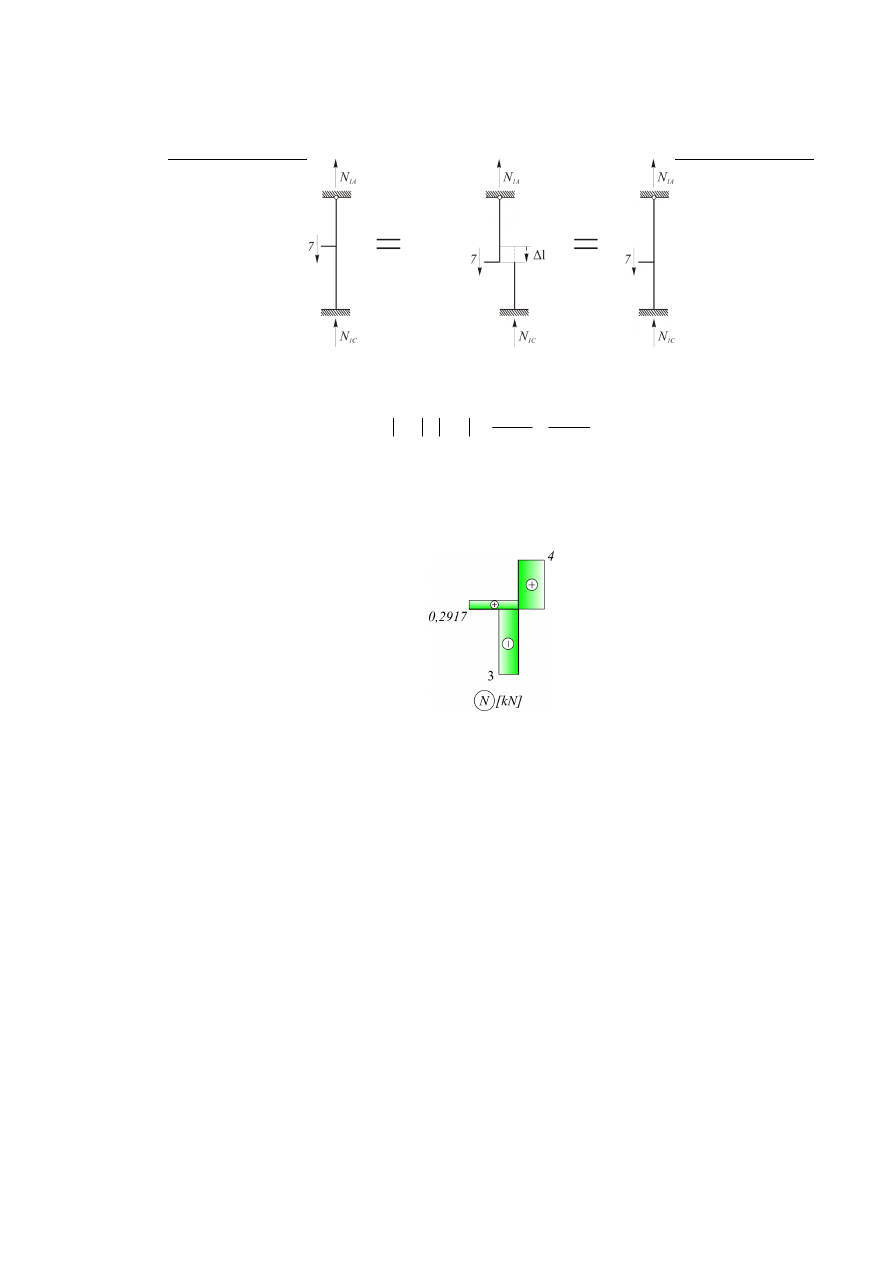
Rozwiązanie:
Rys. 6.3.5
Obliczenie sił normalnych w elementach A - 1 i 1 - C:
Przyjmujemy że siła
1A
N
jest rozciągająca, zaś siła
1C
N
ściskająca.
v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
76
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
Rys. 6.3.7
Równanie równowagi:
1
1
0
7
(1)
y
A
C
P
N
N
∑
=
⇒
+
=
Warunek zgodności przemieszczeń:
1
1
1
1
1
1
4
3
3
4
(2)
C
A
A
C
A
C
N
N
l
l
N
N
EA
EA
⋅
⋅
∆
= ∆
⇒
=
=
Z równań (1) i (2) mamy:
[ ]
1
1
1
4
3 [
]
Dodatkowo
2, 625 2, 333
0, 2917 [
]
A
C
B
N
kN
N
kN
N
kN
=
=
=
−
=
Rys. 6.3.8.
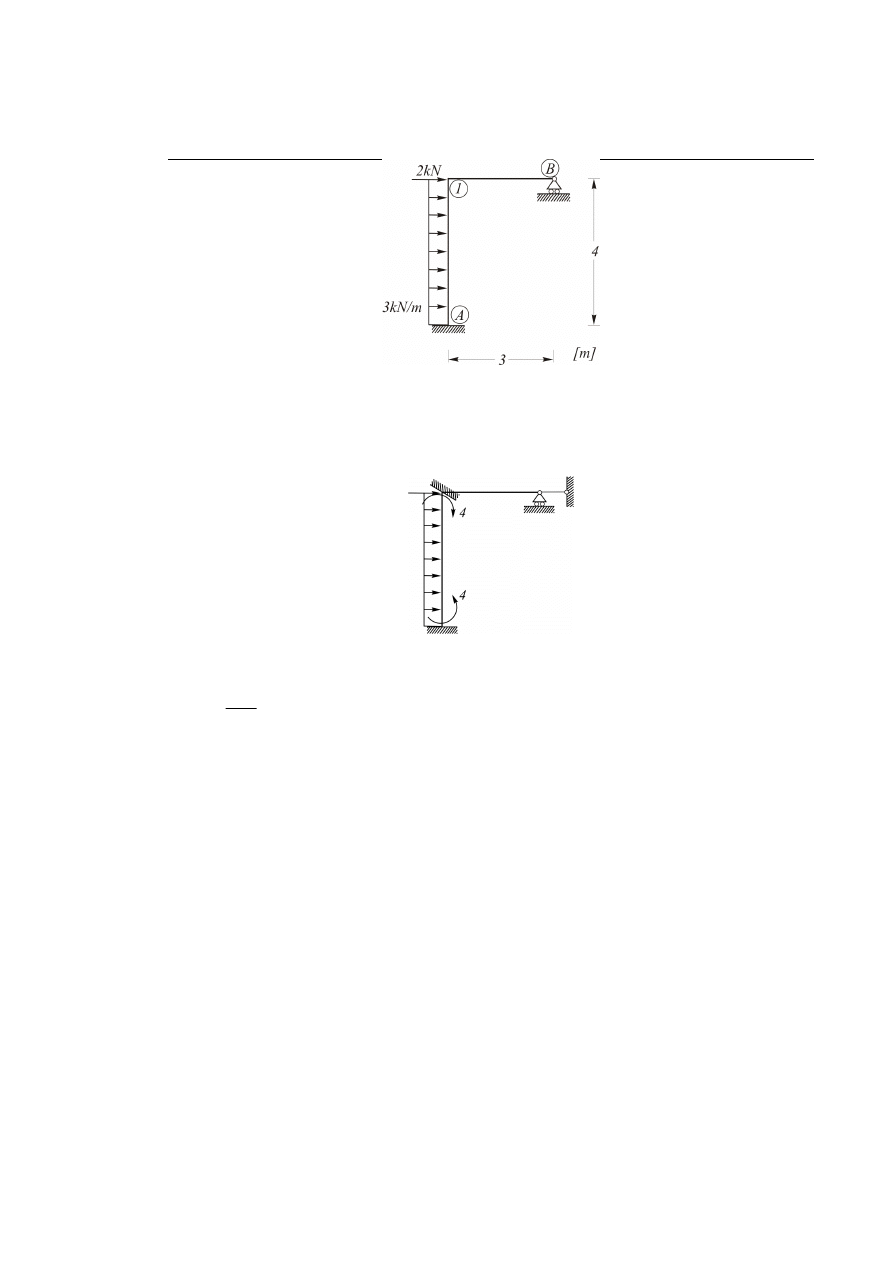
Zad. 6.4
Dany jest układ ramowy przedstawiony na rysunku 6.4.1. Sporządzić wykresy sił wewnętrznych. Przyjąć
EI=const.
v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
77
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
Rys. 6.4.1.
Układ jest dwukrotnie geometrycznie niewyznaczalny, przesuwny.
2 ( , )
g
n
ϕ
=
∆
Schemat geometrycznie wyznaczalny z obciążeniem zewnętrznym:
Rys. 6.4.2.
Momenty wyjściowe:
2
0
1
0
1
3 4
4 [
]
12
4 [
]
A
A
M
kNm
M
kNm
⋅
= −
= −
=
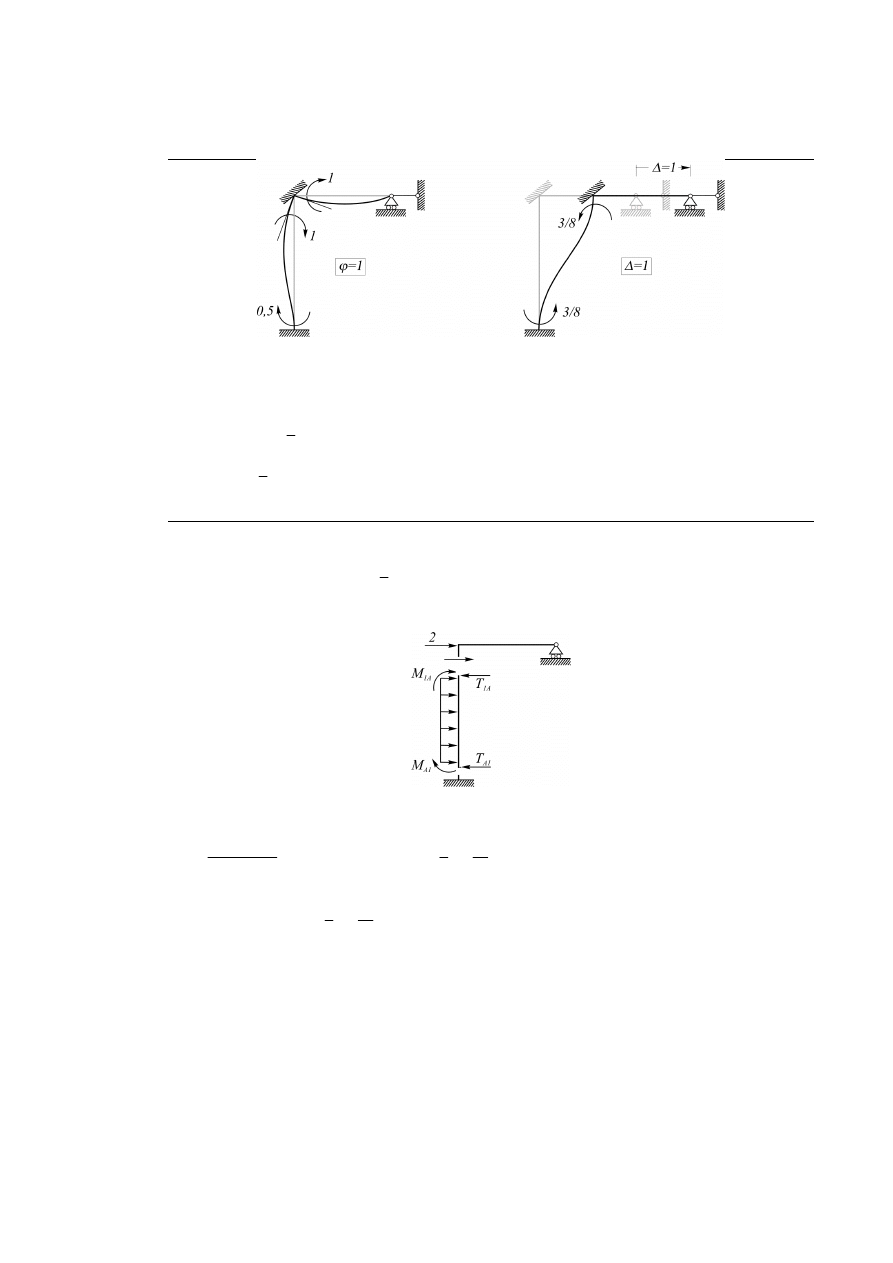
W obliczeniach poniżej przyjmujemy EI=1. Momenty zginające w układzie geometrycznie wyznaczalnym
wywołane jednostkowymi wymuszeniami
1
1
i
ϕ
=
∆ =
v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
78
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
Rys. 6.4.3.
W obliczeniach przyjmujemy
1
EI
=
.
Sumaryczne momenty przywęzłowe:
1
1
1
3
4 0, 5
8
3
4
8
A
A
B
M
M
M
ϕ
ϕ
ϕ
= − +
− ∆
= + − ∆
=
Równania równowagi :
(1) suma momentów w węźle 1
1
1
1
3
0
2
4
0
16
3
32
(1)
8
A
B
M
M
M
ϕ
ϕ
Σ
=
+
=
⇒
− ∆ + =
⇒
− ∆ = −
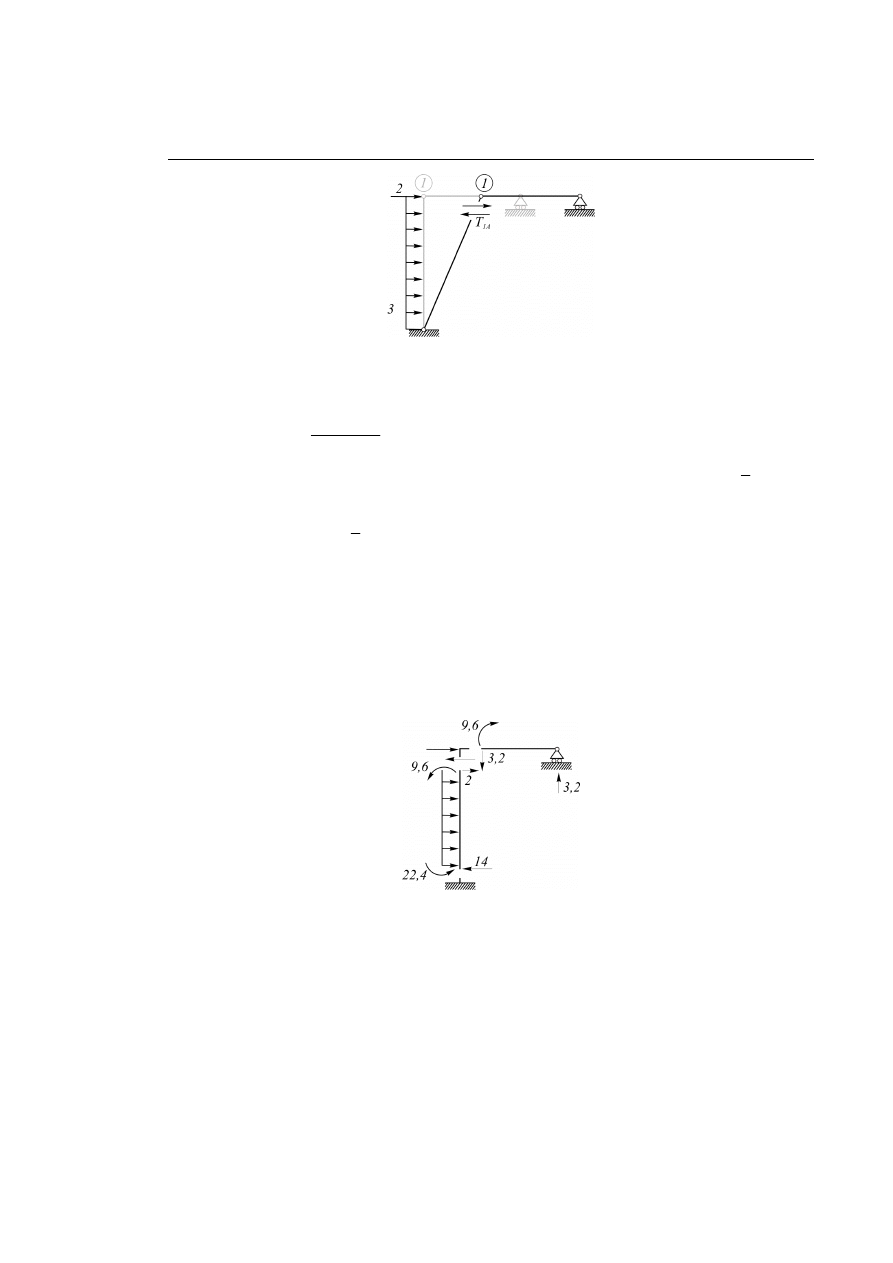
(2) Równowaga sił w wyciętym elemencie 1 - B
Rys. 6.4.4.
Przywęzłowe siły tnące:
0
0
1
1
1
1
1
1
1
3
3
,
6;
6
4
8
16
Równanie równowagi
3
3
0
2
0
8
0
6
3
128
(2)
8
16
A
A
A
A
A
A
x
A
M
M
T
T
T
T
P
T
ϕ
ϕ
ϕ
+
=
+
=
=
−
∆ +
Σ =
⇒
+ =
⇒
−
∆ + =
⇒
− ∆ = −
Równanie (2) można otrzymać inna drogą - tworząc układ przegubowy (mechanizm) i zadając w nim
przemieszczenie wirtualne
∆
=1
v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
79
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
Rys. 8.4.5.
Równanie równowagi wyciętego elementu 1 – B:
1
0
1 2 1
0
x
A
P
T
=
⇒
⋅ + ⋅ =
∑
(
1A
T
- od strony węzła)
Po podstawieniu
1
1
1
6
4
A
A
A
M
M
T
+
=
+
otrzymujemy równanie (2)
Do tego samego rezultatu można dojść wprowadzając wielkość kąta obrotu pręta A-1:
1
1
4
A
−
Ψ
=
i
zapisując równanie pracy wirtualnej:
1
1
1
1
(
)
2 1 3
1 4
0
(2)
2
A
A
A
M
M
−
Ψ
⋅
+
+ ⋅ + ⋅ ⋅ ⋅ =
⇒
Z układu równań (1) i (2) dostajemy
9, 6
61,8667
ϕ
⇒
=
∆ =
Wartości momentów przywęzłowych:
1
1
1
4
4,8 23, 2
22, 4 [
]
4 9, 6 23, 2
9, 6 [
]
9, 6 [
]
A
A
B
M
kNm
M
kNm
M
kNm
= − +
−
= −
= +
−
= −
= −
Rozwiązanie:
Rys. 6.4.6.
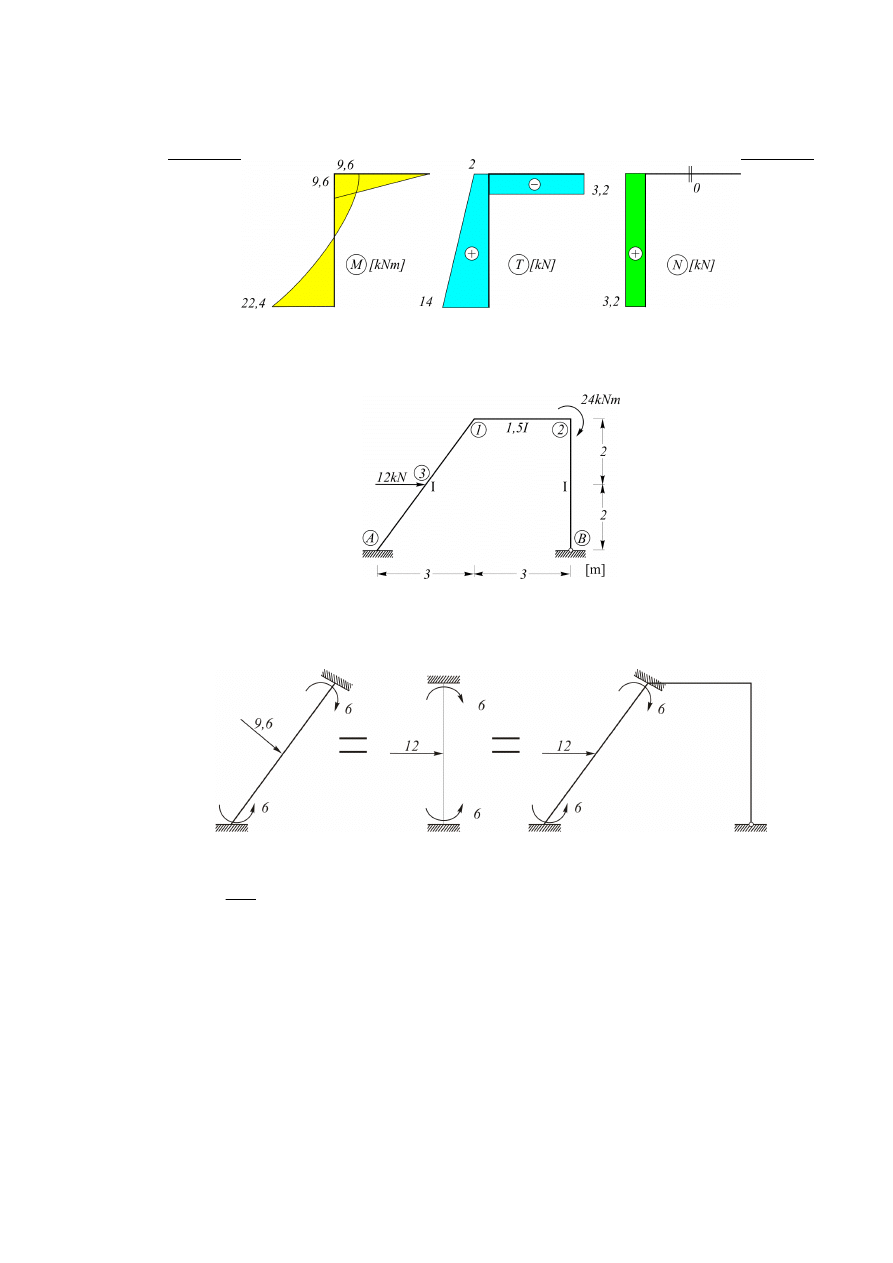
Wykresy sił wewnętrznych:
v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
80
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
Rys. 6.4.7
Zad. 6.5
Dany jest układ ramowy przedstawiony na rysunku 6.5.1. Sporządzić wykresy sił wewnętrznych.
Rys. 6.5.1.
Układ jest trzykrotnie geometrycznie niewyznaczalny, przesuwny.
1
2
3( , , )
g
n
ϕ ϕ
=
∆
Rys. 6.5.2.
Momenty wyjściowe:
0
1
0
1
12 4
6 [
]
8
6 [
]
A
A
M
kNm
M
kNm
⋅
= −
= −
=
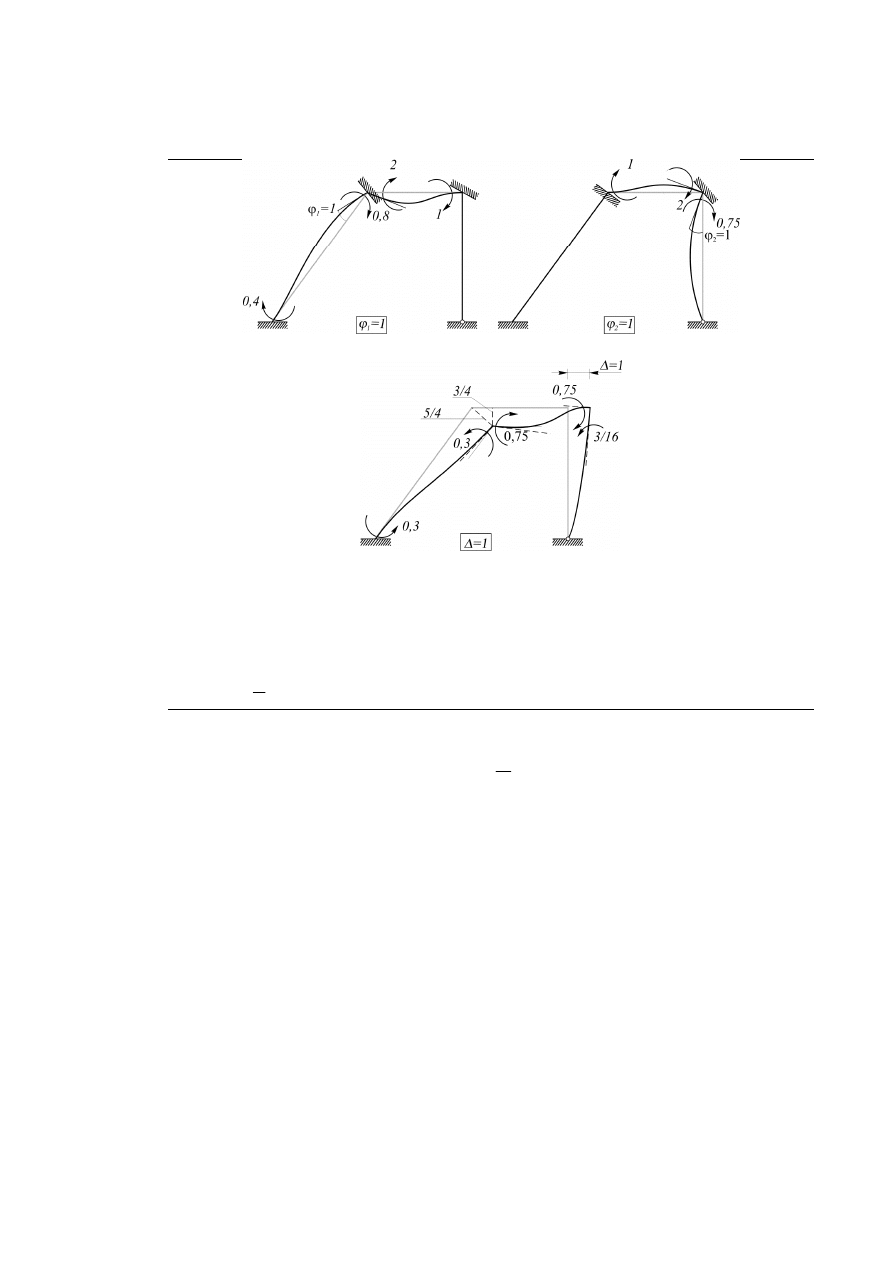
Momenty przywęzłowe w układzie geometrycznie wyznaczalnym wywołane wymuszeniami:
1
2
1,
1,
1
ϕ
ϕ
=
=
∆ =
:
v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
81
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
Rys. 6.5.4.
Sumaryczne momenty przywęzłowe:
1
1
1
1
12
1
2
21
1
2
2
2
6 0, 4
0, 3
6 0,8
0, 3
2
0, 75
2
0, 75
3
0, 75
16
A
A
B
M
M
M
M
M
ϕ
ϕ
ϕ ϕ
ϕ
ϕ
ϕ
= − +
−
∆
= +
−
∆
=
+
+
∆
=
+
+
∆
=
−
∆
Równania równowagi :
(1)
1
1
12
1
2
0
2,8
0, 45
6
(1)
A
M
M
M
ϕ ϕ
Σ
=
+
=
⇒
+
+
∆ = −
(2)
2
21
2
1
2
9
24
2, 75
24
(2)
16
B
M
M
M
M
ϕ
ϕ
Σ
=
+
=
=
⇒
+
+
∆ =
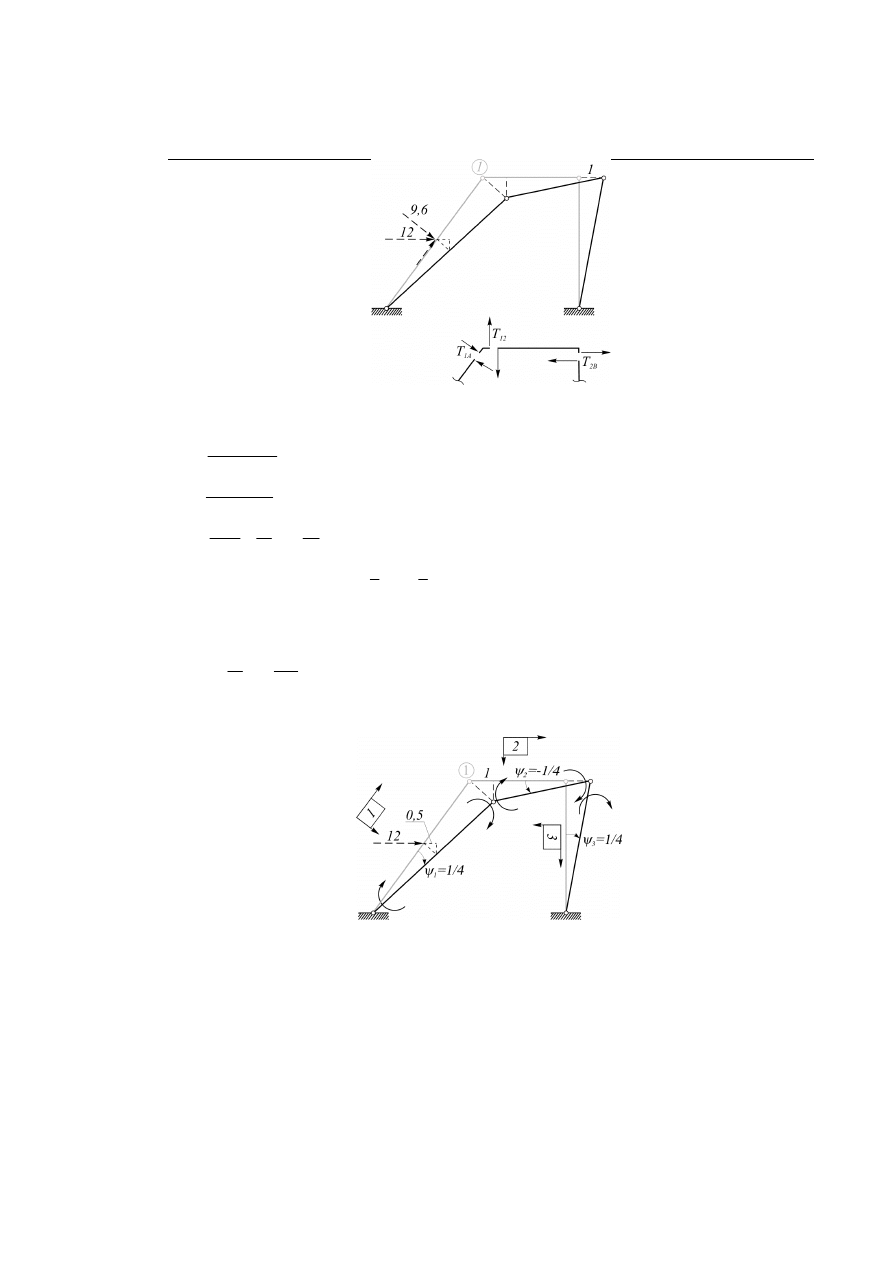
(3) Równanie sumy rzutów w wyciętym elemencie 1 – 2 na kierunku przesuwu – by je otrzymać,
tworzymy układ przegubowy i zadajemy przemieszczenie wirtualne
1
∆ =
v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
82
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
Rys. 6.5.5.
Przywęzłowe siły tnące:
1
1
1
1
12
21
12
1
2
2
2
2
4,8
0, 24
0,12
4,8
5
0, 5
3
3
3
4
16
64
A
A
A
B
B
M
M
T
M
M
T
M
T
ϕ
ϕ ϕ
ϕ
+
=
+
=
−
∆ +
+
=
=
+
+
∆
=
=
−
∆
Równanie pracy wirtualnej:
1
12
2
5
3
1
0
4
4
A
B
T
T
T
⋅ −
⋅ +
⋅ =
W równaniu tym zwrot sił przyjmujemy od strony węzłów, w przypadku braku obciążenia węzłowego
można podstawić siły T od strony elementów)
Po podstawieniu otrzymujemy:
1
2
9
183
0, 45
6
(3)
16
320
ϕ
ϕ
+
+
∆ =
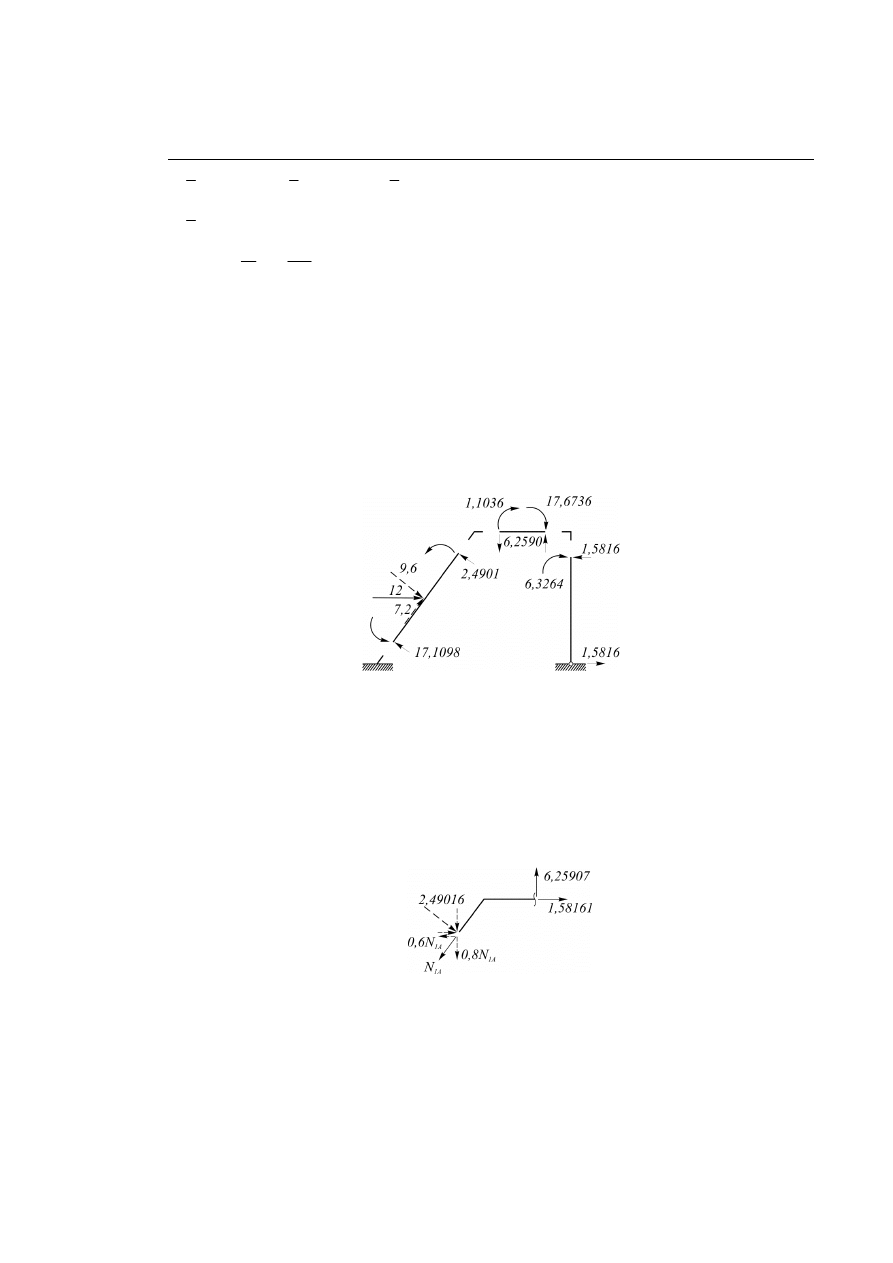
Inny wariant: obliczamy kąty obrotu poszczególnych prętów układu przegubowego (mechanizmu)
.
Rys. 6.5.6
Równanie pracy wirtualnej:
v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
83
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
1
1
21
12
2
1
1
21
12
2
1
2
1
1
1
(
)
(
)
12 0,5
0
4
4
4
1
(
)
6
0
4
9
183
0, 45
6
(3)
16
320
A
A
B
A
A
B
M
M
M
M
M
M
M
M
M
M
ϕ
ϕ
+
−
+
+
+ ⋅
=
+
−
−
+
+ =
+
+
∆ =
Po rozwiązaniu układu równań (1), (2), (3) otrzymujemy:
1
2
6, 64506,
9,92489,
5,95861
ϕ
ϕ
= −
=
∆ =
Momenty przywęzłowe:
1
1
12
21
2
10, 4456 [
]
1,1036 [
]
1,1036 [
]
17, 6736 [
]
6, 3264 [
]
A
A
B
M
kNm
M
kNm
M
kNm
M
kNm
M
kNm
= −
= −
=
=
=
Rozwiązanie:
Rys. 6.5.7
Siły normalne w elementach 2 – B i 1 – 2 uzyskujemy z równowagi węzła 2:
2
12
0
6, 25907
0
1,58161
y
B
x
P
N
kN
P
N
kN
=
⇒
= −
=
⇒
=
∑
∑
Siłę normalną
1
A
N
uzyskujemy z równowagi węzła 1
1
1
0
0, 6
0,8 2, 49016 1, 58161
0
5,9562
x
A
A
P
N
N
kN
=
⇒
−
+
⋅
+
=
=
∑
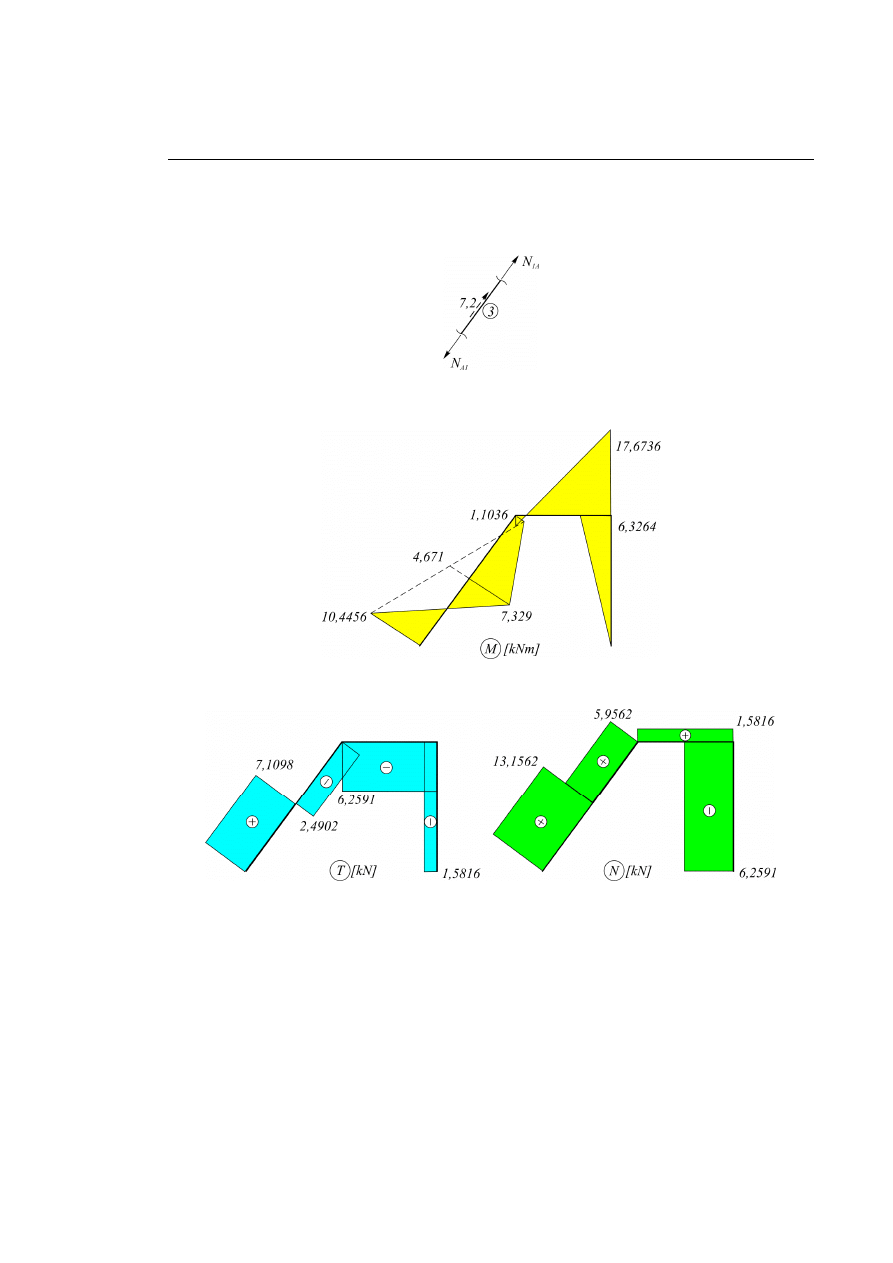
Rys.6.5.8.
v.2009
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
84
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel
się swoimi spostrzeżeniami pisząc na adres e-mail: jasina@pg.gda.pl, z góry dziękujemy. Autorzy
sprawdzenie:
0
y
P
=
∑
Z równowagi węzła 3 otrzymujemy siłę normalną
1
A
N
:
1
1
7, 2
13,1562kN
A
A
N
N
=
+
=
Rys. 6.5.9.
Wykresy sił wewnętrznych:
Rys. 6.5.10.
Rys. 6.5.11.
Wyszukiwarka
Podobne podstrony:
MB Cwiczenia Met przemieszczen cz 1
MB Cwiczenia Przemieszczenia w ukladach stytycznie wyznaczalnych cz 2
MB Cwiczenia Przemieszczenia w ukladach statycznie wyznaczalnych cz 1
MB ćwiczenia 24 04 2010 (02)
Cwiczenia z ochrony gleby cz 1a Nieznany
MB ćwiczenia 29 05 2010 (02)
Plyometria w ćwiczeniach z wykorzystaniem skrzyni cz 1
Ćwiczenia 4 Środki trwałe cz 2
proc met ekstr 3 cz 3
Projekt belka met przemieszczen
cwiczenie 7 -met.i sr, Ogrodnictwo UP Lbn, Ochrona roślin. Metody i środki
cwiczenie 6-met. sr, Ogrodnictwo UP Lbn, Ochrona roślin. Metody i środki
ćwiczenia koncentracji - aura cz.3, ĆWICZENIA do medytacji koncentracji oddychania i widzenia aury
więcej podobnych podstron