POLITECHNIKA ŚLĄSKA

Wydział elektryczny

Laboratorium

Inżynierii materiałów elektrotechnicznych.

Studia niestacjonarne zaoczne

Kierunek: EL

Rok akademicki: 2007/2008

Semestr: 3

Temat ćwiczenia:

Pomiar konduktywności elektrycznej materiałów przewodowych.

Studenci:

1. Dresler Adam

2. Zymela Dawid

3. Żemła Krzysztof

4. Poloczek Krzysztof

5. Mielcarz Mikołaj

Data: 26.10.2007

Grupa: 1

Sekcja: I

Prowadzący: dr inż. Rafał Sosiński

1. Cel i zakres badań.

Celem ćwiczenia jest poznanie własności przewodnictwa materiałów

elektrotechnicznych oraz sposobu pomiaru konduktywności.

W ćwiczeniu dokonano pomiarów rezystancji dwóch próbek, z aluminium oraz miedzi

przy użyciu mostka Thomsona. Następnie przeliczono uzyskane wyniki na wielkość

konduktywności badanych próbek.

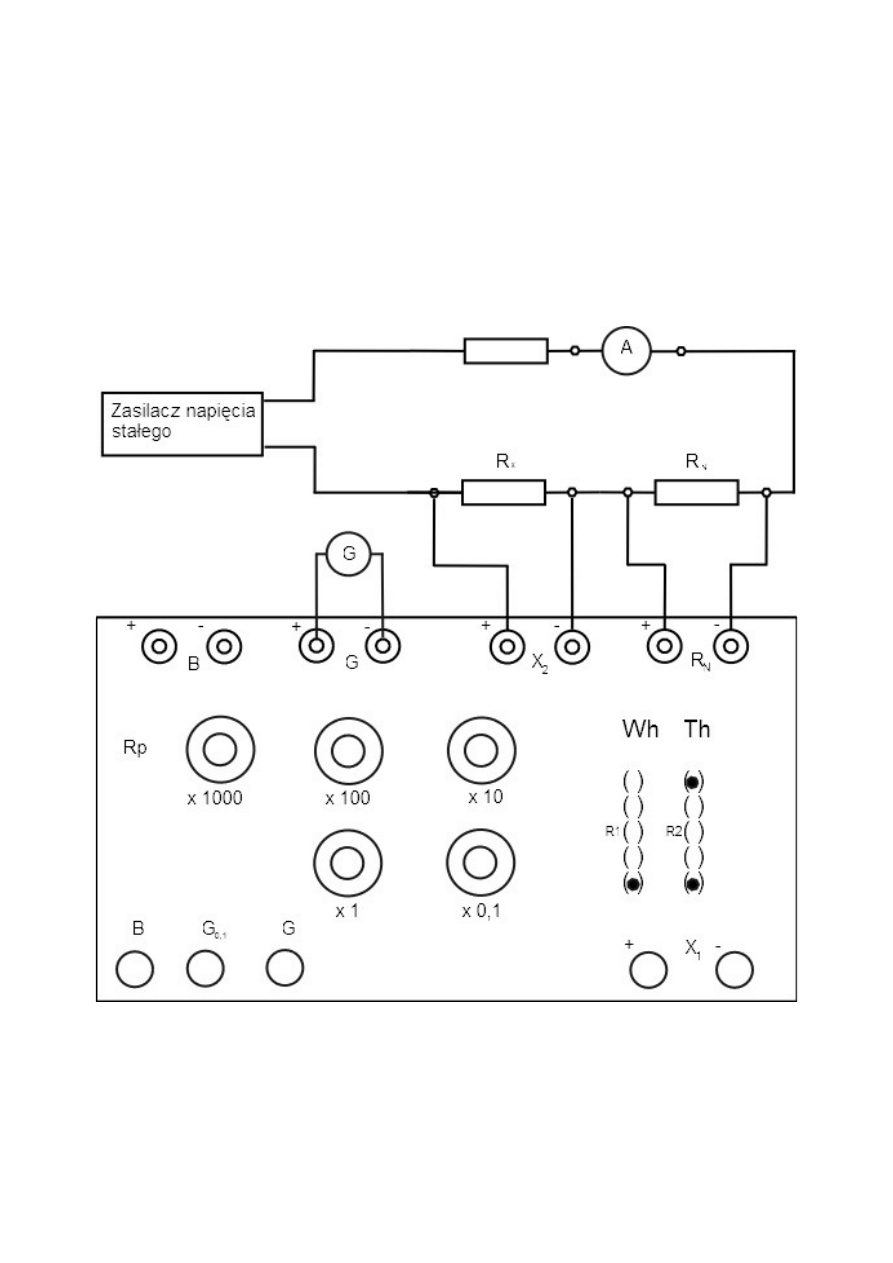
2. Układ pomiarowy.

Rys 1. Schemat układu pomiarowego konduktywności przewodników.

3. Przyrządy pomiarowe wykorzystane w ćwiczeniu

a) Mostek Weatstone`a – Thompsona MWT 77a

b) Amperomierz magnetoelektryczny LM-1 kl.0,5

c) Galwanometr GL-2 kl.1,5

d) Rezystor wzorcowy 0,001[Ω] (R

N

)

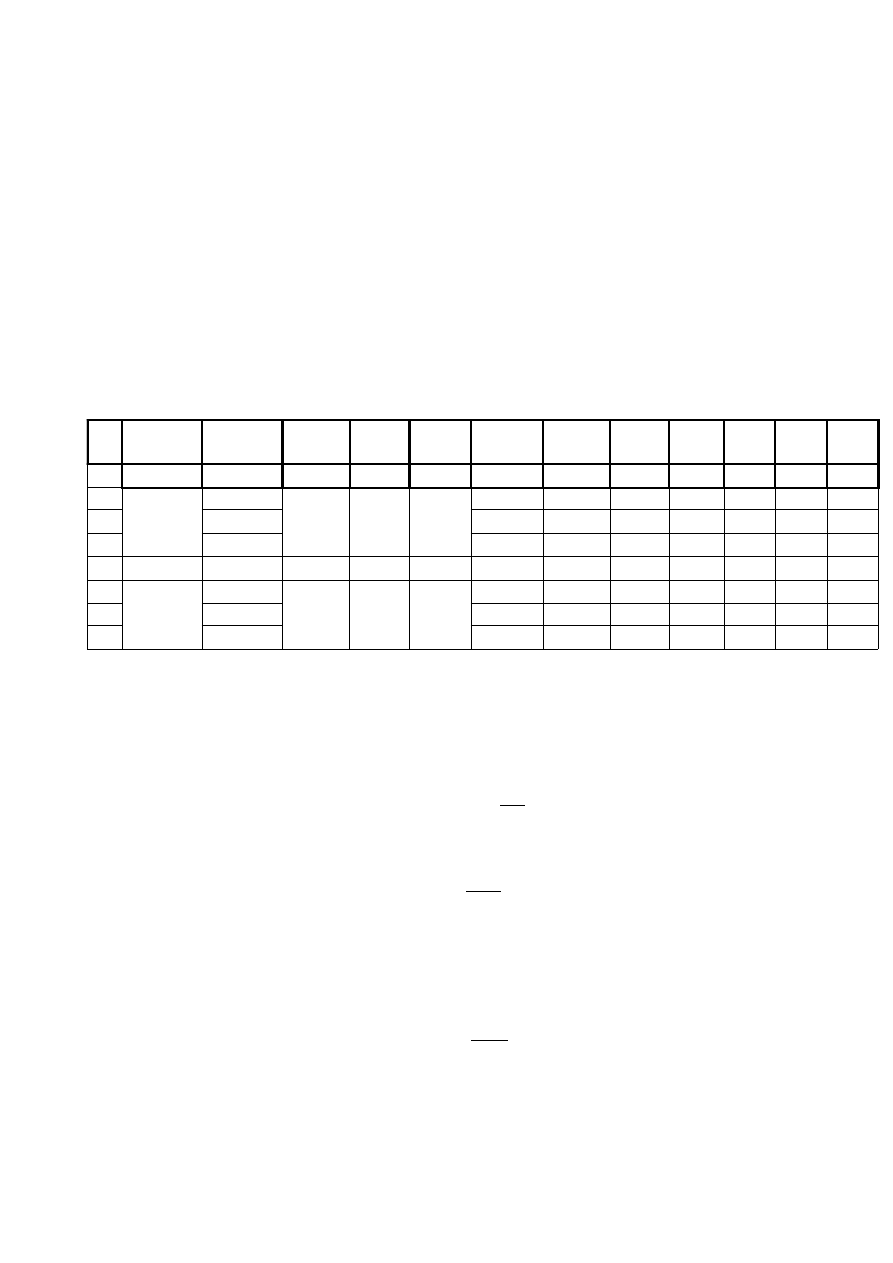
4. Tabele pomiarowe, obliczenia, wykresy.

4.1. Tabela pomiarowa.

Pomiary konduktywności wykonywano przy temperaturze 20ºC oraz przepływie prądu

przez próbkę 10 [A].

4.2. Wzory użyte do obliczenia, konduktywności oraz błędów i niepewności pomiarów.

Do wyznaczenia konduktywności zastosowano następujące zależności:

–

obliczenie wartości rezystancji próbki

R

x

=R

p

⋅

R

N

R

a

(4.1)

–

wyznaczenie konduktywności próbki

=

L

R

x

⋅s

(4.2)

Przy pomiarze mostkiem Thompsona występuje błąd rozdzielczości oraz błąd

pobudliwości:

–

błąd pobudliwości



p

=

R

x

R

x

(4.3)

gdzie ΔR

x

– próg pobudliwości

Lp

L

Ra

Rp

Rx

uc(Rx)

δp

γ

[mm]

[mm]

[Ω]

[Ω]

[Ω]

[MS/m]

[Ω]

1

AL

325

4,6

10000

0,001

5560

556,00

0,45

0,01

0,01

35,19

0,45

2

235

4000

400,00

0,33

0,01

0,01

35,37

0,45

3

160

2780

278,00

0,23

0,01

0,01

34,65

0,45

1

CU

340

4,4

10000

0,001

3720

372,00

0,30

0,01

0,01

60,14

0,80

2

260

2840

284,00

0,30

0,01

0,01

60,24

0,80

3

150

1550

155,00

0,23

0,01

0,01

63,68

0,87

Oznaczenie

próbki

Φsr

R

N

δr

u

c

(y)

10

-6

[Ω]

10

-6

[Ω] 10

-6

[Ω] 10

-6

[Ω]

–

błąd rozdzielczości δ

r

– wynika ze skwantowania elementu regulacyjnego,

w przypadku wykorzystanego do ćwiczenia mostka wynosi 0,1 [Ω] ( w

odniesieniu do R

x

,0,01*10

-6

[Ω].

Względną złożoną niepewność standardową pomiaru wartości rezystancji R

x

oszacowano na podstawie wzoru :

u

c

R

x

=R

x

⋅



u

r

 R

p



2

u

r

R

a



2

u

r

 R

N



2

(4.4)

niepewność poszczególnych rezystancji oszacowano z wzoru:

u

r

R

i

=

u

R

i



R

i

(4.5)

u

R

i

=

R

i



3

(4.6)

Niepewność konduktywności badanych próbek wyznaczono jako niepewność

standardową złożona pomiarów rezystancji, długości oraz przekroju badanej

próbki :

u

c

=⋅



u

r

R

x



2

u

r

L

2

u

r

s

2

(4.7)

5. Wnioski.

Pomiar konduktywności jest pośrednim pomiarem tzn. mierząc rezystancję próbki oraz

jej długość i średnicę możemy określić jej konduktywność.

Sposób jaki stosowaliśmy w ćwiczeniu jest obarczony pewnymi błędami wynikającymi

z samej konstrukcji mostka Thompsona (elementów rezystancyjnych), błędami

pomiaru długości próbki liniałem oraz błędem pomiaru średnicy próbki.

Pomiar rezystancji próbki jest obarczony błędem wynikającym z niedokładności

wykonania rezystancji dekad R

p

, rezystancji wzorcowej R

N

oraz rezystancji zakresowej

mostka R

a

.

Największy wpływ na dokładności pomiaru konduktywności ma prawidłowy pomiar

długości oraz przekroju próbki.

Jak wynika z pomiarów im przewodnik ma większą konduktywność tym jego

rezystancja maleje oznacza to że jest lepszym przewodnikiem jest lepszym

przewodnikiem.