2005-12-19

© Lesław ŁADNIAK

KLASYFIKACJA ELEMENTÓW OBWODU..........................2

1.1.1 Element obwodu. Dwójnik..............................................2

1.1.2 Elementy o parametrach rozłożonych i skupionych .......3

1.1.3 Elementy stacjonarne .....................................................4

1.1.4 Elementy liniowe i nieliniowe.........................................5

1.1.5 Impedancja .....................................................................7

1.1.6 Elementy symetryczne.....................................................8

RÓWNOWAŻNOŚĆ I APROKSYMACJA ...............................9

1.1.7 Równoważność elementów .............................................9

1.1.8 Aproksymacja elementów ...............................................9

1.1.9 Linearyzacja odcinkowa ...............................................10

1.1.10 Łączenie elementów....................................................11

1.1.11 Dzielnik napięcia ........................................................12

1.1.12 Dzielnik prądu ............................................................12

ELEMENTY AKTYWNE ..........................................................13

1.2

Ź

RÓDŁA SIŁY ELEKTROMOTORYCZNEJ

................................13

1.2.1 Energia źródła ..............................................................14

1.2.2 Moc źródła....................................................................14

1.2.3 Sprawność źródła .........................................................14

1.2.4 Charakterystyka napięciowo-prądowa źródła sem ......15

1.2.5 Idealne źródła napięcia i prądu....................................15

1.2.6 Maksimum mocy źródła................................................17

1.2.7 Generator – prawo Faradaya.......................................18

ELEMENTY PASYWNE ...........................................................19

1.3

O

DBIORNIKI ENERGII ELEKTRYCZNEJ

..................................19

1.3.1 Bilans energii................................................................20

1.3.2 Dobroć elementu ..........................................................20

1.3.3 Idealny przemiennik energii elektrycznej .....................21

1.3.4 Idealny element magazynujący energię elektryczną.....22

2

© Lesław ŁADNIAK

K

LASYFIKACJA ELEMENTÓW OBWODU

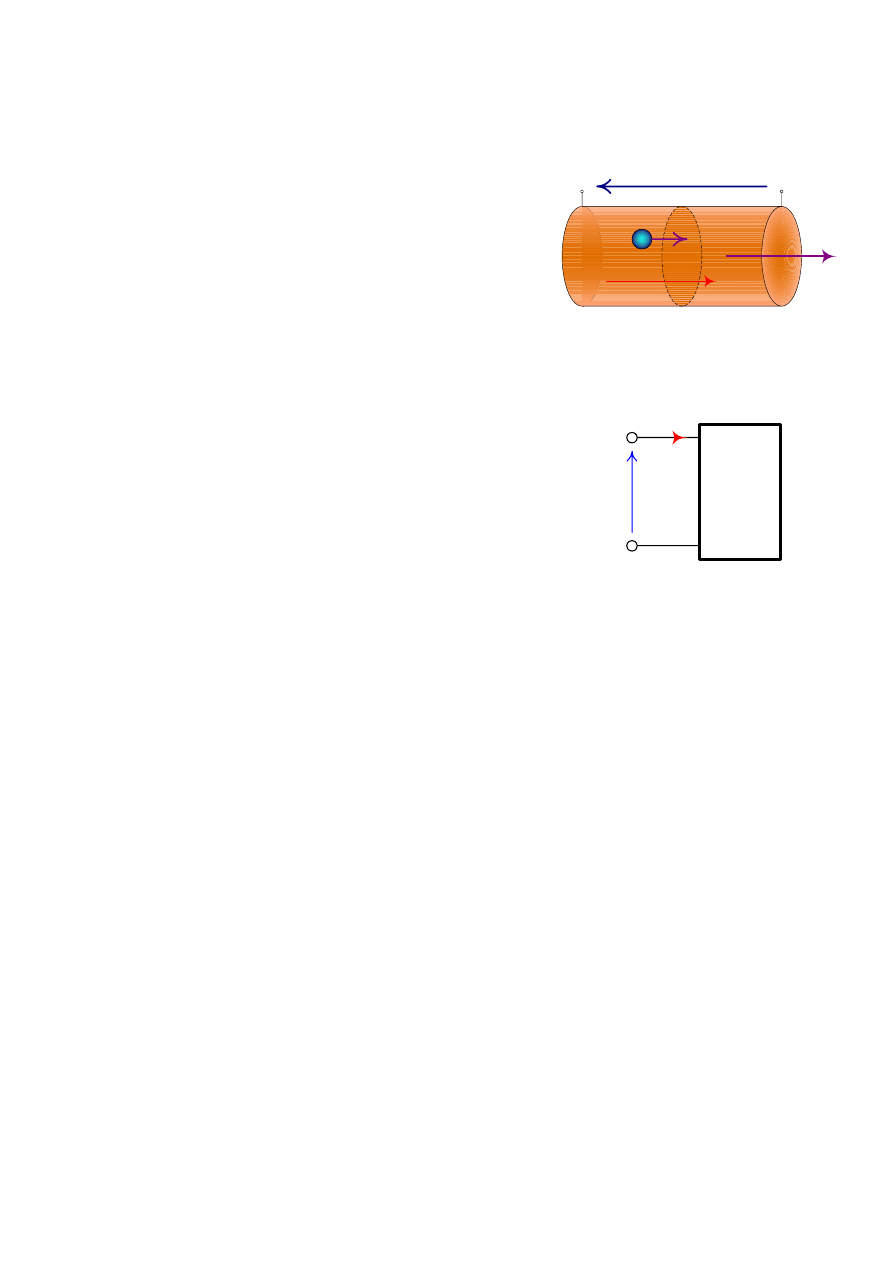
1.1.1 Element obwodu. Dwójnik.

Fragment przestrzeni, w której przemieszczają się ładunki
elektryczne lub rozprzestrzeniania się fala elektromagnetyczna,
czyli gdzie zachodzi przemiana energii elektrycznej, nazywamy
elementem obwodu elektrycznego (Rys. 1).

Njaprostrzym elementem obwodu elektrycznego jest dwójnik,
który posiadaja jedna parę zacisków służącą do doprowadzenia i
odprowadzenia energii elektrycznej. Na Rys. 2 przedstawiono
symbol dwójnika.

Napięcie i prąd na zaciskach dwójnika zaznaczamy pamiętając,
że strzałka napięcia wskazuje zacisk o wyższym potencjale, a
strzałka prądu wskazuje kierunek ruchu dodatnich ładunków.

W celu scharakteryzowania elementu obwodu elektrycznego
podaje się równanie opisujące ten element lub przedstawia
charakterystykę napięciowo-prądową tego elementu.

i(t) = f(u,

ε

,

μ

,

γ

,x,r,t)

Współczynniki wiążące prąd płynący przez rozpatrywany
element z napięciem na zaciskach tego elementu lub pochodne
tych wielkości nazywamy parametrami elementów obwodu
elektrycznego.

Wartość parametrów elementów obwodu elektrycznego zależy
od wymiarów geometrycznych elementów, własności materiału, z
jakiego jest z budowany element oraz własności ośrodka, w którym
ten element się znajduje.

Podstawowymi parametrami charakteryzującymi środowisko, w
którym obserwujemy przepływ prądu elektrycznego są
przenikalność elektryczna

ε

[F/m] oraz przenikalność

magnetyczna

μ

[H/m]. Dodatkową wielkością umożliwiającą

ocenę własności elektrycznych materiału jest przewodność
właściwa

γ

[S/m].

Wartości parametrów elementów obwodu można obliczyć lub
wyznaczyć na drodze eksperymentalnej badając charakterystykę
napięciowo-prądową elementu.

V

A

V

B

E

S

I

U

AB

q

U

AB

= V

A

- V

B

+

Rys. 1.

Element obwodu

Dwójnik

u

AB

(t)

i(t)

B

A

Rys. 2.

Dwójnik

3

© Lesław ŁADNIAK

1.1.2 Elementy o parametrach rozłożonych i skupionych

Analizując zjawiska zachodzące w poszczególnych
fragmentach obwodu elektrycznego należy pamiętać, że prędkość
rozchodzenia się w przestrzeni wszelkich zjawisk fizycznych jest
ograniczona. Prędkości rozprzestrzeniania się fali
elektromagnetycznej w próżni jest podstawową stałą fizyczną i
wynosi:

c =

1

ε

o

μ

o

= 2,997925 10

8

≅

3 10

8

m/s

gdzie

ε

o

jest przenikalnością elektryczną, a

μ

o

jest przenikalnością

magnetyczną próżni:

ε

o

=

1

36

π

10

-9

F/m

μ

o

= 4

π

10

-7

H/m

Prędkość fali elektromagnetycznej w ośrodku innym niż
próżnia jest zawsze mniejsza i wynosi:

v

2

=

c

2

ε

r

μ

r

gdzie

ε

r

jest względną przenikalnością elektryczną, a

μ

r

jest

względną przenikalnością magnetyczną danego ośrodka.

Ponieważ prędkość fali elektromagnetycznej ma określoną
wartość, to przejście fali przez element o zadanych wymiarach
geometrycznych wymaga czasu. W praktyce nie wyznacza się
czasu przejścia fali elektromagnetycznej przez element. Porównuje
się natomiast wymiary geometryczne elementu z długością fali

λ

,

czyli drogą, jaką przebywa fala w ciągu jednego okresu T:

λ

= v T =

v

f

gdzie v jest prędkością fali, a f =

1

T jest częstotliwością fali.

Element obwodu, w którym uwzględniamy czas potrzebny na
rozprzestrzenienie się fali elektromagnetycznej nazywamy
elementem o parametrach rozłożonych i opisujemy równaniami
różniczkowymi cząstkowymi, w których uwzględnia się zależność
wartość sygnałów nie tylko od czasu, ale także od odległości.

Jeżeli długość fali jest dużo razy większa od wymiarów
geometrycznych elementu, to można pominąć zjawiska falowe i
przyjąć, że parametry elementu są skupione. Elementy o
parametrach skupionych są opisywane równaniami różniczkowymi
zwyczajnymi.

Rys. 3. Fala elektromagnetyczna

Radiowe

Mikro

TV, FM

Długie

Gamma

X - ray

Częstotliwość, Hz

Długość fali

Ultrafiolet

Podczerwień

Widzialne

Średnie

10

22

10

21

10

20

10

19

10

18

10

17

10

16

10

15

10

14

10

13

10

12

10

11

10

10

10

9

10

8

10

7

10

6

10

5

10

4

10

3

1 A

1 nm

1

μ

m

1 cm

1 m

1 km

o

Rys. 4. Spektrum fal elektromagnetycznych

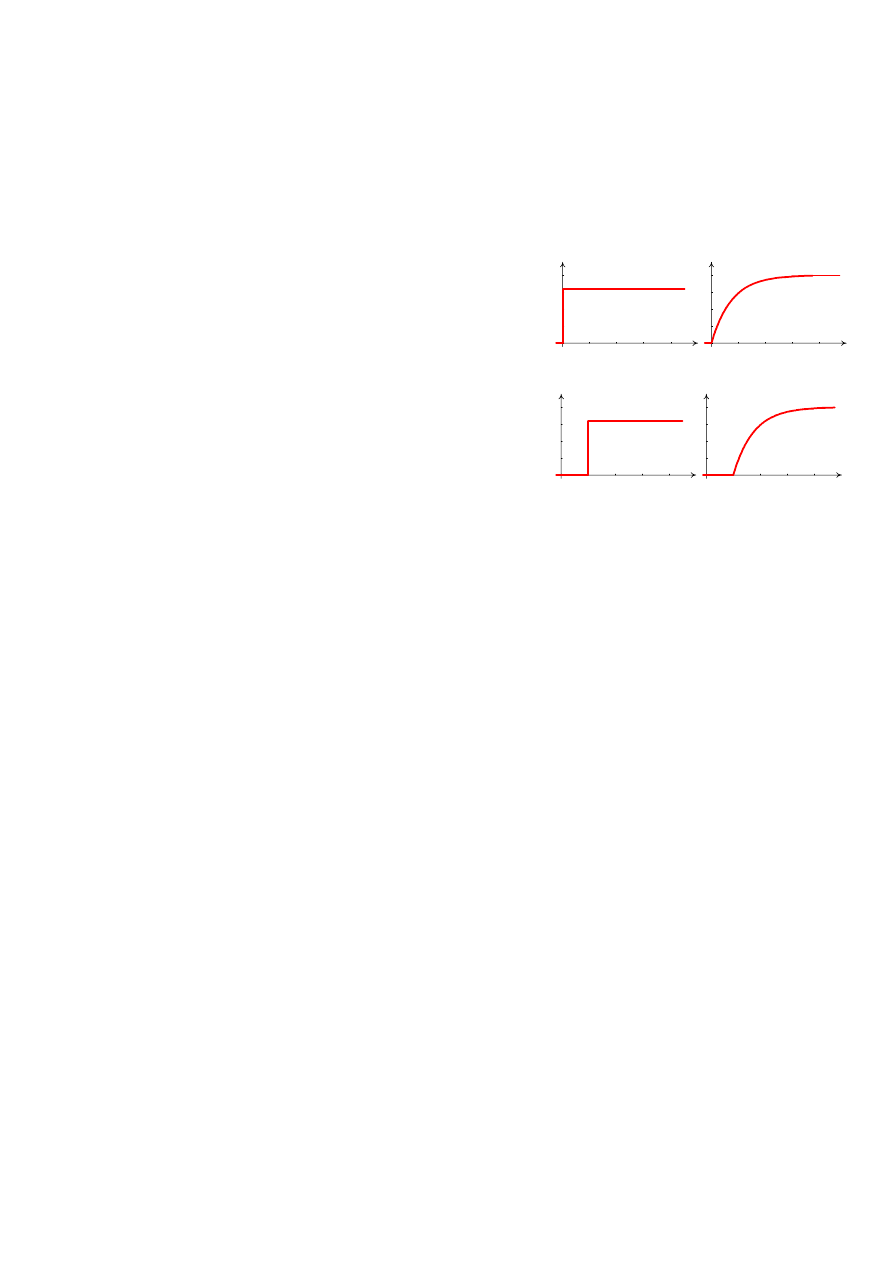
4

© Lesław ŁADNIAK

1.1.3 Elementy stacjonarne

Element obwodu elektrycznego, którego parametry lub
charakterystyka nie zmieniają się w czasie jest elementem
stacjonarnym. Element nie spełniający, tego warunku nazywamy
elementem niestacjonarnym lub parametrycznym. Warunkiem
stacjonarności elementu jest nie zmienność w czasie wymiarów
geometrycznych elementu oraz niezależność stałych fizycznych
ośrodka od czasu. W praktyce parametry elementów są
niestacjonarne. Jeżeli jednak szybkość zmian parametrów w czasie
jest niewielka w porównaniu do czasu obserwacji układów, to takie
elementy można rozpatrywać jak elementy o parametrach
stacjonarnych.

Element stacjonarny ma taką własność, że jeżeli wymuszenia
x(t) oraz x(t-

Δ

t) są takiej samej postaci, ale są przesunięte w czasie

o dowolną wartość

Δ

t, to odpowiedzi elementu na te wymuszenia

y(t) oraz y(t-

Δ

t) mają taką samą postać i są przesunięte w czasie o

tą samą wartość czasu

Δ

t, co wymuszenia (Rys. 5).

a)

t

x(t)

1

2

3

4

0

t

y(t)

1

2

3

4

0

b)

t

x(t-

Δ

t)

1

2

3

4

0

t

1

2

3

4

0

y(t-

Δ

t)

Rys. 5.

Odpowiedzi elementu stacjonarnego

5

© Lesław ŁADNIAK

1.1.4 Elementy liniowe i nieliniowe

Element jest elementem liniowym, jeżeli relacja pomiędzy
sygnałami na zaciskach elementu spełnia warunek
proporcjonalności i addytywności. Element nie spełniający tych
warunków nazywamy elementem nieliniowym. Relacja między
sygnałami na zaciskach elementu liniowego opisana jest liniowym
równaniem algebraicznym lub liniowym równaniem
różniczkowym.

Element

spełnia warunek proporcjonalności, gdy wymuszenie x

wywołuje odpowiedź y, a wymuszenie

α

x wywołuje odpowiedź

α

y, gdzie

α

jest dowolną stałą.

Element jest addytywny, gdy wymuszenia x

1

oraz x

2

wywołują

odpowiedzi układu odpowiednio y

1

oraz y

2

, a wymuszenie

x = x

1

+ x

2

będące sumą wymuszeń wywołuje odpowiedź

y = y

1

+ y

2

.

Warunkiem

liniowości elementu jest nie zależność stałych

fizycznych ośrodka, czyli przenikalności elektrycznej

ε

,

przenikalności magnetycznej

μ

oraz przewodności właściwej

γ

od

natężenia pola elektrycznego oraz natężenia pola magnetycznego.

Charakterystyka

napięciowo-prądowa elementu liniowego jest

linią prostą przechodzącą przez początek układu współrzędnych
(Rys. 6).

U

I

Rys. 6. Charakterystyka elementu liniowego

U

I

Rys. 7. Charakterystyka elementu nieliniowego

6

© Lesław ŁADNIAK

Przykład. Odpowiedź elementu liniowego

Rozpatrzmy element, którego charakterystyka napięciowo-
prądowa jest opisana funkcją:

I = A U

Jeżeli do zacisków tego elementu doprowadzimy napięcie u(t)
będące sumą składowej stałej napięcia U

o

oraz składowej zmiennej

napięcia u

~

:

u(t) = U

0

+ u

~

to przez ten element popłynie prąd opisany następującym
równaniem:

i(t) = A (U

0

+ u

~

) = A U

0

+ A u

~

= I

0

+ i

~

Jak wynika z powyższego równania prąd płynący przez
rozpatrywany element też zawiera składową stałą I

o

oraz składową

zmienną i

~

. Kształt prądu jest taki sam jak kształt napięcia.

Rozpatrywany element jest elementem liniowym.

Przykład. Odpowiedź elementu nieliniowego

W przypadku, gdy charakterystyka napięciowo-prądowa
elementu jest opisana funkcją:

I = A U

2

to gdy do zacisków tego elementu doprowadzimy napięcie u(t)
postaci:

u(t) = U

0

+ u

~

to prąd płynący przez rozpatrywany element będzie opisany
następującym równaniem:

i(t) = A (U

0

+ u

~

)

2

= A U

0

2

+ 2A U

0

u

~

+ A u

2

~

=

=

I

0

+ i

2

~

+ A U

0

u

~

W tym przypadku, postać prądu jest inna niż postać napięcia.
Prąd płynący przez element zawiera oprócz składowej stałej I

o

dwie składowe zmienne i

2

(t) oraz AU

0

u(t). Warto zwrócić uwagę

na postać drugiej składowej zmiennej, której wartość zależy
zarówno od wartości składowej stałej jak i składowej zmiennej
napięcia. Rozpatrywany element jest elementem nieliniowym.

U

I

u(t)

i(t)

t

t

t

1

t

2

t

3

t

1

t

2

t

3

Rys. 8. Odpowiedź elementu liniowego

U

I

u(t)

i(t)

t

t

t

1

t

2

t

3

t

1

t

2

t

3

Rys. 9. Odpowiedź elementu nieliniowego

7

© Lesław ŁADNIAK

1.1.5 Impedancja

Przyjmijmy,

że napięcie u(t) na zaciskach elementu jest funkcją

prądu i(t) płynącego przez ten element oraz parametru K
opisującego ten element:

u = f(i,K)

Przyrost napięcia na zaciskach elementu można opisać
równaniem:

du =

∂

f(i,K)

∂

i

di +

∂

f(i,K)

∂

K

dK

Przyrost napięcia będzie proporcjonalny tylko do zmian prądu,

jeżeli

∂

f(i,K)

∂

K

= 0, czyli gdy funkcja opisująca zmiany napięcia jest

co najwyżej pierwszego stopnia dla parametru K.

Jeżeli przyjmujemy, że napięcie u(t) na zaciskach elementu jest
tyko funkcją prądu i(t) płynącego przez ten element, czyli

u = f(i)

to przyrost napięcia na zaciskach elementu można opisać
równaniem:

du =

∂

f(i)

∂

i

di =

∂

u

∂

i

di

Wielkość

∂

u

∂

i

będąca pochodną napięcia względem

prądu nazywamy impedancją.

Całkując obustronnie równanie opisujące związek między
przyrostami napięcia i prądu można napisać:

u(t) =

∂

u

∂

i

i(t)

Korzystając z zależności między napięciem a prądem dla
wartości chwilowych moc elementu obwodu elektrycznego jest
opisana równaniem:

p(t) = u(t) i(t) =

∂

u

∂

i

i

2

(t) =

∂

u

∂

i

u

2

(t)

W

związku z powyższym elementarna

ilość energii dostarczana do elementu jest
opisana równaniem:

dW = p(t) dt =

∂

u

∂

i

i

2

dt =

∂

i

∂

u

u

2

dt

Ilość energii dostarczanej do elementu
jest proporcjonalna do kwadratu napięcia lub
prądu.

8

© Lesław ŁADNIAK

1.1.6 Elementy symetryczne

Elementy obwodu elektrycznego mogą być symetryczne
(odwracalne) lub niesymetryczne (nieodwracalne). Element
symetryczny (odwracalny) ma takie same właściwości niezależnie
od kierunku przepływu energii przez element, czyli sposobu
połączenia elementu w obwodzie oraz biegunowości przyłożonego
napięcia (porównać charakterystyki napięciowo-prądowej
rezystora oraz diody)
Każdy symetryczny element obwodu jest elementem
odwracalnym, ale nie koniecznie odwrotnie.

9

© Lesław ŁADNIAK

R

ÓWNOWAŻNOŚĆ I APROKSYMACJA

Pojęcie równoważności i aproksymacji ma duże znaczenie
praktyczne, ponieważ często musimy zastąpić jeden lub kilka
elementów innym elementem, nie powodując zmian napięć i
prądów w obwodzie.

1.1.7 Równoważność elementów

Dwa elementy obwodu są równoważne, gdy pełnia tą samą
funkcję w obwodzie, czyli równania lub charakterystyki opisujące
te elementy są takie same.

1.1.8 Aproksymacja elementów

Aproksymacja polega na zastąpieniu danego elementu innym
elementem, o charakterystyce tak dobranej, aby przy takim samym
wymuszeniu odpowiedzi obu elementów nie różniły się bardziej od
zadanej wartości.

Najczęściej do oceny różnicy między charakterystykami
elementów wykorzystywane jest kryterium błędu
średniokwadratowego:

⌡

⌠

-

∞

∞

[y

1

(x)

−

y

2

(x)]

2

dx <

ε

gdzie

ε

jest liczbą rzeczywistą dodatnią oznaczającą maksymalny

dopuszczalny błąd.

10

© Lesław ŁADNIAK

1.1.9 Linearyzacja odcinkowa

Charakterystykę napięciowo-prądową elementu nieliniowego
można przybliżyć wielomianem potęgowym:

y = a

o

+ a

1

x + a

2

x

2

+ a

3

x

3

+ ...

Pierwsze dwa wyrazy pozwalają na aproksymację liniową. W
wielu praktycznych przypadkach pierwsze trzy wyrazy szeregu
dają zadawalające przybliżenie charakterystyki elementu
nieliniowego.

Przykład. Dioda. Napięcie i prąd.

Do zacisków diody prostowniczej jest doprowadzone napięcie
sinusoidalnie zmienne u = U

m

cos

ω

t. Należy wyznaczyć kształt

prądu płynącego przez diodę.

Przyjmiemy,

że charakterystykę napięciowo-prądową diody

można odwzorować wielomianem potęgowym trzeciego stopnia:

i = a

o

+ a

1

u + a

2

u

2

Ponieważ nie płynie prąd przez diodę i = 0, gdy napięcie na
zaciskach diody jest równe zeru u = 0, to pierwszy współczynnik
wielomianu ma wartość równą zeru a

o

= 0.

Przy takich założeniach prąd płynący przez diodę jest opisany
równaniem:

i = a

1

U

m

cos

ω

t + a

2

U

m

2

cos

2

ω

t

czyli

i = a

1

U

m

cos

ω

t +

1
2 a

2

U

m

2

(1 + cos 2

ω

t) =

=

1
2 a

2

U

m

2

+ a

1

U

m

cos

ω

t +

1
2 a

2

U

m

2

cos 2

ω

t

Z

powyższego równania wynika, że prąd płynący przez diodę

posiada składową stałą, składową podstawową o częstotliwości
napięcia oraz drugą harmoniczną o nie występującej w napięciu
częstotliwości 2

ω

.

I

U

I

D

U

D

I

2

I

1

U

1

U

2

Rys. 10.

Aproksymacja charakterystyki diody

11

© Lesław ŁADNIAK

1.1.10 Łączenie elementów

Cechą charakterystyczną przy szeregowym połączeniu
elementów jest fakt, że przez każdy element płynie ten sam prąd:

i

1

(t) = i

2

(t) = i(t)

a całkowite napięcie na szeregowo połączonych elementach jest
równe sumie napięć na każdym z elementów:

u(t) = u

1

(t) + u

2

(t)

W przypadku równoległego połączenia elementów na każdym z
tych elementów występuje to samo napięcie:

u

1

(t) = u

2

(t) = u(t)

a prąd płynący przez wszystkie równolegle połączone elementy
jest sumą prądów płynących przez każdy z nich.

i(t) = i

1

(t) + i

2

(t)

Łącząc w dowolny sposób pojedyncze elementy obwodu można
tworzyć dowolne układy wielozaciskowe (n-wrotniki), z których
najważniejszą rolę dogrywają dwójniki i czwórniki.

u(t)

u

2

(t)

A

B

C

i(t)

u

1

(t)

Rys. 11.

Szeregowe połączenie elementów

i

1

(t)

i

2

(t)

i(t)

u(t)

Rys. 12.

Równoległe połączenie elementów

12

© Lesław ŁADNIAK

1.1.11 Dzielnik napięcia

Rozpatrzmy dwa szeregowo połączone elementy o rezystancji
R. Jeżeli skorzystamy z faktu, że przez dwa szeregowo połączone
elementy płynie ten sam prąd:

i

1

(t) = i

2

(t) = i(t)

to możemy napisać, że

u

1

(t)

R

1

=

u

2

(t)

R

2

=

u(t)

R

w

gdzie u(t) jest sumą napięć na elementach

u(t) = u

1

(t) + u

2

(t)

a R

w

jest rezystancją wypadkową gałęzi równą sumie rezystancji

poszczególnych elementów.

Napięcie na jednym z szeregowo połączonych rezystorów

u

k

(t) =

R

k

R

w

u(t)

jest proporcjonalne do wartości rezystancji tego rezystora.

1.1.12 Dzielnik prądu

Przy

równoległym połączeniu

elementów, napięcie na dowolnym
elemencie, jest równe napięciu na każdym z
nich.

u

1

(t) = u

2

(t) = u(t)

Możemy napisać, że

i

1

(t)

G

1

=

i

2

(t)

G

2

=

i(t)

G

w

gdzie i(t) jest sumą prądów płynących przez
wszystkie elementy

i(t) = i

1

(t) + i

2

(t)

a G

w

jest wypadkową przewodnością

wszystkich elementów.

Wartość prądu płynącego jedną z
równolegle połączonych gałęzi

i

k

(t) =

G

k

G

w

i(t)

jest proporcjonalna do przewodności tej
gałęzi.

Dla dwóch elementów rezystancyjnych
połączonych równolegle otrzymujemy:

R

1

i

1

(t) = R

w

i(t)

gdzie

R

1

=

1

G

1

oraz R

w

=

R

1

R

2

R

1

+ R

2

Stąd

i

1

(t) =

R

2

R

1

+ R

2

i(t)

13

© Lesław ŁADNIAK

E

LEMENTY AKTYWNE

1.2 Źródła siły elektromotorycznej

Elementy aktywne są przestrzenią, gdzie siły zewnętrzne
powodują ukierunkowane przemieszczanie się ładunków
elektrycznych, czyli dochodzi do przemiany dostarczanej do
elementu energii na energię elektryczną.

W wyniku przemieszczenia ładunków wewnątrz elementu
aktywnego na zaciskach tego elementu pojawia się napięcie zwane
siłą elektromotoryczną. Wartość siły elektromotorycznej jest
proporcjonalna do ilości energii dostarczanej do elementu
aktywnego w celu wytworzenia napięcia na zaciskach tego
elementu:

e

AB

(t) =

W

AB

(t)

q

Wartość siły elektromotorycznej informuje o ilości pracy , jaką
wykonują siły zewnętrzne w celu przemieszczenia ładunku
dodatniego od zacisku A do zacisku B elementu aktywnego.

Przepływ prądu elektrycznego przez element aktywny, czyli
spowodowanie wyjścia ładunków z elementu aktywnego, oznacza
przekazywanie energii z elementu aktywnego do otoczenia.
Wymaga to dostarczania do elementu aktywnego dodatkowej
energii dW

D

. Ta dodatkowa energia dW

D

ulega w elemencie

aktywnym tylko częściowej przemianie na energię elektryczną
dW

E

. Wynika to z faktu, że część dostarczanej energii dW

D

jest

wykorzystywana do wykonania pracy dW

P

związanej z

przemieszczeniem ładunków wewnątrz elementu aktywnego.

Ilość energii elektrycznej dostarczanej przez źródło siły
elektromotorycznej wyznaczamy znając napięcie i prąd na
zaciskach źródła:

dW

E

= u

E

(t) i

E

(t) dt

Źródłem siły elektromotorycznej są elementy aktywne, w
których dochodzi do przemiany dostarczanej do elementu energii
na energię elektryczną, co umożliwia przepływ prądu w obwodzie
elektrycznym. Warunkiem funkcjonowania każdego źródła siły
elektromotorycznej jest działanie czynnika elektromotorycznego
wywołanego przez reakcje chemiczne, zjawiska cieplne, zjawiska
magnetyczne, oddziaływania mechaniczne.

i(t)

u(t)

Element
aktywny

Energia

Energia

elektryczna

Energia

przemiany

A

B

Rys. 13.

Element aktywny

Rys. 14.

Źródła siły elektromotorycznej

14

© Lesław ŁADNIAK

1.2.1 Energia źródła

Z bilansu energii wynika, że ilość energii elektrycznej
uzyskanej w wyniku przemiany w elemencie aktywnym będącym
źródłem siły elektromotorycznej jest zawsze mniejsza niż ilość
energii dostarczonej do układu przemiany:

dW

E

= dW

D

−

dW

P

gdzie:
dW

E

- ilość energii elektrycznej dostarczanej do obwodu

elektrycznego przez element aktywny, czyli przemiennik energii,
dW

D

- ilość energii dostarczonej do przemiennika,

dW

P

- ilość energii przeznaczonej na wykonanie pracy

związanej z przemianą energii elektrycznej dW

E

.

1.2.2 Moc źródła

Szybkość przemiany energii w elemencie aktywnym opisuje
moc będąca stosunkiem ilość energii elektrycznej dostarczanej
przez element aktywny do czasu przemiany:

p

E

(t) =

dW

E

(t)

dt

moc źródła =

ilość energii elektrycznej

czas przemiany

Ponieważ zmiany energii układu są opisane funkcją ciągłą w

czasie, to moc elementu aktywnego ma zawsze skończoną
wartość.

1.2.3 Sprawność źródła

Podstawowym parametrem charakteryzującym dane źródło siły
elektromotorycznej jest sprawność źródła rozumiana jako stosunek
ilości energii elektrycznej pobieranej ze źródła do ilości energii
dostarczanej do źródła:

η

=

dW

E

dW

D

sprawność =

ilość energii elektrycznej

ilość energii dostraczonej do przemiennika

Sprawność idealnego źródła napięcia jest równa jedności.

15

© Lesław ŁADNIAK

1.2.4 Charakterystyka napięciowo-prądowa źródła sem

Jeżeli przyjmiemy, że ilość energii W

D

(t) dostarczanej do źródła

siły elektromotorycznej, czyli układu przemiany, jest
proporcjonalna do natężenia prądu pobieranego z układu, a praca
W

P

(t) potrzebna na przemianę energii jest proporcjonalna do

kwadratu prądu płynącego przez układ:

W

D

(t) = k i

E

(t) t W

P

(t) = r i

E

2

(t) t

to korzystając z bilansu energii otrzymujemy:

p

E

(t) =

1

dt (dW

D

– dW

P

) = k i

E

(t) - r i

E

2

(t) = u

E

(t) i

E

(t)

Jak wynika z powyższego równania, napięcie na zaciskach
układu przemiany jest w rozpatrywanym przypadku opisane
równaniem liniowym o postaci:

u

E

(t) = k - r i

E

(t)

Pamiętając o tym, że w przypadku, gdy prąd pobierany ze
źródła siły elektromotorycznej jest równy zeru, to napięcie na
zaciskach tego źródła u

E

(t) jest równe sile elektromotorycznej e(t)

oraz przyjmując, że współczynnik r odwzorowujący straty energii
w źródle spowodowane przepływem prądu i

E

(t) jest rezystancją

wewnętrzną źródła R

w

, to równanie opisujące zmiany napięcia na

zaciskach źródła przyjmuje następującą postać:

u

E

(t) = e(t) - R

w

i

E

(t)

Jeżeli zmiany prądu płynącego przez źródło siły
elektromotorycznej wyrazimy w zależności od napięcia na
zaciskach tego elementu, to otrzymamy równanie:

i

E

(t) =

1

R

w

e(t)

−

1

R

w

u

E

(t) = i

ź

−

G

w

u

E

(t)

gdzie i

ź

jest nazywane wydajnością prądową źródła, a G

w

przewodnością wewnętrzną źródła.

Jak wynika z przedstawionych zależności źródło siły
elektromotorycznej można nazwać źródłem napięcia lub
źródłem prądu w zależności od równania, które przyjmiemy do
opisu układu przemiany.

1.2.5 Idealne źródła napięcia i prądu

Jeżeli przyjmiemy, że ilość energii
dostarczanej do źródła siły
elektromotorycznej, jest proporcjonalna do
natężenia prądu pobieranego z tego źródła, a
praca potrzebna na przemianę energii ma
wartość równą zeru niezależnie od ilości
energii elektrycznej dostarczanej przez
źródło:

W

D

(t) = e(t) i

E

(t) t oraz W

P

(t) = 0

to moc źródła siły elektromotorycznej jest
opisana równaniem:

p

E

(t) =

1

dt (dW

D

– dW

P

) = e(t) i

E

(t) = u

E

(t)

i

E

(t)

Jak wynika z powyższego równania
wartość napięcia na zaciskach źródła nie
zależy od natężenia prądu pobieranego z
tego

źródła i jest równe sile

elektromotorycznej źródła:

u

E

(t) = e(t)

Jeżeli napięcie na zaciskach źródła jest
równe sile elektromotorycznej niezależnie
od wartości prądu pobieranego ze źródła,
czyli ilość i szybkość dostarczanej przez
źródło energii może mieć dowolną wartość,
to jest to idealne źródło napięcia.

Idealnym

źródłem prądu nazywamy takie

źródło siły elektromotorycznej, której
wydajność prądowa nie zależy od wartości
napięcia na zaciskach źródła.

16

© Lesław ŁADNIAK

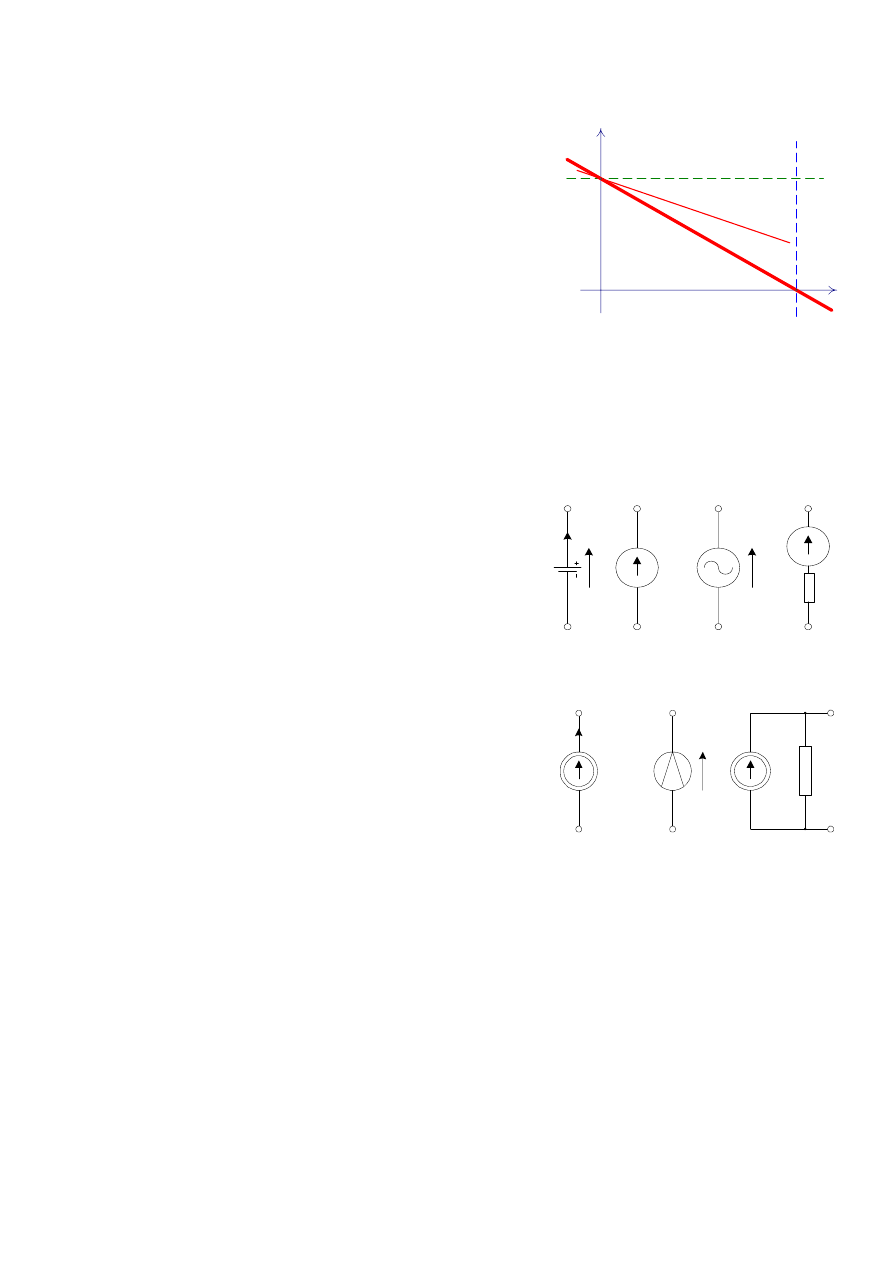
Na Rys. 15 przedstawiono wykres zmian napięcia na zaciskach
źródła siły elektromotorycznej funkcji zmian natężenia prądu
pobieranego z tego źródła. Jak wynika z tego wykresu
charakterystyka prądowo-napięciowa

źródła siły

elektromotorycznej jest opadającą liną prostą, której nachylenie
jest proporcjonalne do wartości rezystancji wewnętrznej źródła R

w

.

W przypadku idealnego źródła napięcie lub idealnego źródła
prądu charakterystyka źródła jest linią prostą, która jest równoległa
do osi prądu lub osi napięcia.
Punkt

przecięcia charakterystyki prądowo-napięciowej źródła

siły elektromotorycznej z osią napięcia odpowiada stanowi
jałowemu źródła, czyli gdy zaciski źródła są rozwarte, a prąd
pobierany ze źródła ma wartość równą zeru. Napięcie na zaciskach
źródła w stanie jałowym jest równe sile elektromotorycznej. Drugi
charakterystyczny punkt, to przecięcie charakterystyki prądowo-
napięciowej z osią prądu. Punkt ten odpowiada stanowi zwarcia
źródła. Prąd pobierany ze źródła siły elektromotorycznej, gdy
zaciski źródła są zwarte (bezpośrednio połączone) nazywamy
prądem zwarcia. W tym przypadku, napięcie między zaciskami
elementu jest równe zeru. Pobierany ze źródła prąd I

z

, jest

ograniczany jedynie przez wartość rezystancji wewnętrznej źródła
R

w

. Wartość płynącego w tym przypadku prądu jest równa

wydajności prądowej źródła I

ź

.

Wartość napięcia na zaciskach źródła w stanie jałowym oraz
wydajność prądowa źródła są podstawowymi parametrami
charakteryzującymi źródło siły elektromotorycznej. W energetyce
do opisu źródła siły elektromotorycznej stosuje się często wielkość
nazywaną mocą zwarciową źródła będącą iloczynem napięcia w
stanie jałowym i prądu w stanie zwarcia.

Teoretyczna maksymalna szybkość przekazywania energii z
jednego układu do drugiego jest równa iloczynowi napięcia w
stanie jałowym i prądu w stanie zwarcia. Wielkość ta jest
nazywana mocą zwarciową.

E

I

idealne źródło napięcia

U

I

ź

= E/R

w

ide

alne

ź

ró

dł

o p

rą

du

Rys. 15.

Charakterystyka prądowo-napięciowa

źródła siły elektromotorycznej

Na Rys. 16 oraz Rys. 17 przedstawiono
symbole graficzne źródeł siły
elektromotorycznej.

I

E

E

E

E

R

w

Rys. 16.

Symbole graficzne źródeł napięcia

I

ź

I

ź

I

ź

R

w

Rys. 17.

Symbole graficzne źródeł prądu

17

© Lesław ŁADNIAK

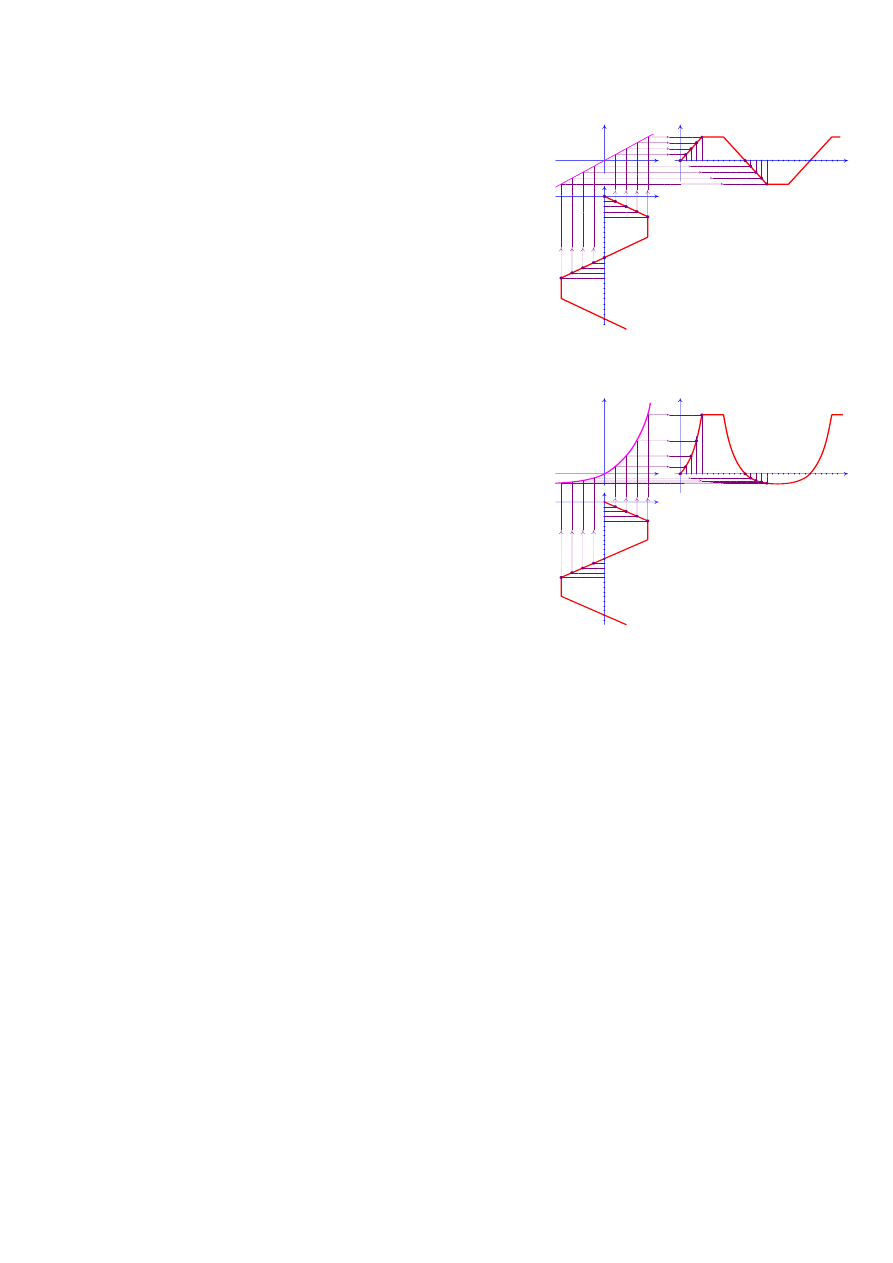
1.2.6 Maksimum mocy źródła

W

przypadku

źródła siły elektromotorycznej, dla którego ilość

energii dostarczanej W

D

(t) do układu przemiany, jest

proporcjonalna do natężenia prądu pobieranego z układu, a praca
W

P

(t) potrzebna na przemianę energii jest proporcjonalna do

kwadratu prądu płynącego przez układ, to równanie opisujące
zmiany mocy źródła ma następującą postać:

p

E

(t) = e(t) i

E

(t) – R

w

i

E

2

(t)

Maksymalna szybkość przemiany energii dostarczanej do
źródła siły elektromotorycznej zostanie osiągnięta, gdy pochodna
mocy względem prądu źródła będzie równa zeru:

dp

E

(t)

di

E

= e(t) – 2 R

w

i

E

(t) = 0

Jak wynika z powyższego równania, źródło osiąga maksymalną
moc, gdy prąd pobierany ze źródła ma wartość:

i

E

(t) =

e(t)

2 R

w

Jeżeli w równaniu na moc źródła uwzględnimy, że wartość
maksymalna siły elektromotorycznej jest równa napięciu U

o

w

stanie jałowym na zaciskach źródła oraz fakt, że wartość prądu
zwarcia I

z

jest równa napięciu w stanie jałowym U

o

podzielona

przez rezystancje wewnętrzną źródła R

w

, to maksymalna szybkość

przemiany energii wynosi:

p

Emax

=

1
4 U

o

I

z

Jak wynika z powyższego równania, maksymalną szybkość
przekazywania energii ze źródła siły elektromotorycznej do
obwodu elektrycznego uzyskamy, gdy napięcie na zaciskach
źródła jest równe połowie napięcia w stanie jałowym, a prąd
pobierany ze źródła jest równy połowie prądu zwarcia.

Należy podkreślić, że otrzymana zależność jest słuszna tylko w
przypadku, gdy istnieje liniowa zależność między napięciem na
zaciskach źródła, a wartością prądu pobieranego ze źródła.
Ponadto, przedstawiona na Rys. 18 charakterystyka zmian mocy
dostarczanej przez źródło siły elektromotorycznej została
wyznaczona przy założeniu, że ilość energii dostarczanej do źródła
w jednostce czasu może mieć dowolną wartość. W przypadku, gdy
szybkość dostarczania energii do układu przemiany może wzrastać

tylko do określonej wartości,
charakterystyka prądowo-napięciowa źródła
jest linią łamaną, co przedstawiono na
Rys. 19.

0

0,25

0,5

0,75

1

0

0,25

0,5

0,75

1

Rys. 18.

Charakterystyka prądowo-napięciowa oraz

charakterystyka mocy pobieranej ze źródła

0

0,25

0,5

0,75

1

0

0,25

0,5

0,75

1

Rys. 19.

Wzrost moc dostarczanej do źródła ma

ograniczoną wartość

Znając charakterystykę prądowo-
napięciową źródła można w łatwy sposób
wyznaczyć wartość mocy źródła przy danym
napięciu na zaciskach źródła i prądzie
pobieranym ze źródła. Ponieważ moc źródła
jest iloczynem napięcia i prądu na zaciskach
źródła, to pole powierzchni prostokąta o
bokach U

x

oraz I(U

x

) jest miarą mocy źródła.

Maksymalną wartość pola powierzchni
prostokąta uzyskamy, gdy jego boki będą
maiły długość U

o

/2 oraz I

z

/2

.

18

© Lesław ŁADNIAK

1.2.7 Generator – prawo Faradaya

Powszechnie

wykorzystywanymi

źródłami siły

elektromotorycznej są generatory napięć sinusoidalnie zmiennych,
w których zachodzi przemiana energii mechanicznej ruchu
obrotowego ramki obwodu elektrycznego w polu magnetycznym
na energię elektryczną.

Zgodnie z prawem Faradaya, siła elektromotoryczna
samoindukcji e(t) jest równa:

(A.1)

e(t) =

−

d

Φ

(t)

dt

gdzie

Φ

(t) jest strumieniem magnetycznym przenikającym

powierzchnię S, wzdłuż krawędzi której obliczamy siłę
elektromotoryczną e(t).

Ponieważ strumień magnetyczny

Φ

jest równy iloczynowi

skalarnemu wektora indukcji magnetycznej B oraz wektora
powierzchni S:

d

Φ

= d(B

o

S)

to w celu wywołania zmian tego strumienia musi wystąpić
przynajmniej zmiana:
- indukcji magnetycznej,
- powierzchni przenikanej przez pole magnetyczne,
-

kąta zawartego między liniami sił pola magnetycznego, a

polem powierzchni obwodu elektrycznego.

Rozpatrzmy przypadek, gdy fragment obwodu elektrycznego w
kształcie prostokątnej ramki o powierzchni S znajduje się w polu
magnetycznym o indukcji B. Powierzchnia obwodu jest nachylona
względem linii sił pola magnetycznego pod kątem

α

. W tym

przypadku obwód przenika strumień magnetyczny o wartości:

Φ

= B

o

S = B S cos

α

W przypadku, gdy rozpatrywany fragment obwodu zostanie
wprawiony w ruch obrotowy z prędkością kontową

ω

wzdłuż

swojej osi symetrii, to zmiany wielkości powierzchni, przez którą
przenika pole magnetyczne można opisać równaniem:

S(t) = S cos

ω

t

Przenikający obwód strumień
magnetyczny jest opisany równaniem:

Φ

(t) =B S cos

ω

t

a szybkość zmian tego strumienia:

d

dt

Φ

(t) =

ω

B S sin

ω

t

Wartość siły elektromotorycznej
indukowanej w obwodzie zmienia się
sinusoidalnie zgodnie z równaniem:

e(t) =

ω

B S sin

ω

t = U

m

sin

ω

t

gdzie U

m

=

ω

B

S jest wartością maksymalną

napięcia.

W celu otrzymania siły

elektromotorycznej opisanej funkcją
sinusoidalnie zmienną:

e(t) = U

m

sin

ω

t

należy obwód elektryczny umieścić w
wirującym z prędkością kątową

ω

w

polu magnetycznym o indukcji
magnetycznej B.

19

© Lesław ŁADNIAK

E

LEMENTY PASYWNE

1.3 Odbiorniki energii elektrycznej

Elementem pasywnym lub odbiornikiem energii elektrycznej
nazywamy przestrzeń, w której następuje przemiana energii
elektrycznej przenoszonej przez poruszające się ładunki
elektryczne lub falę elektromagnetyczną na inną postać energii.

Jeżeli energia kinetyczna przemieszczających się w elemencie
ładunków elektrycznych lub fali elektromagnetycznej jest
zamieniana na energię pola elektrycznego lub energię pola
magnetycznego, to można w łatwy sposób dokonać z powrotem
przemiany tej energii na energie elektryczną w wyniku działania
siły Culomba lub siły Lorentza. W przypadku, gdy energia
elektryczna jest zamieniona na ciepło, a ciepło ulega
odprowadzeniu z elementu, to proces przemiany jest praktycznie
nieodwracalny. Przyjmuje się, że ilość energii elektrycznej
zamienionej na ciepło jest energią, która ulga rozproszeniu.

O

ilości energii elektrycznej ulegającej przemianie na ciepło

oraz ilości energii ulegającej przemianie na energię pola
elektrycznego lub pola magnetycznego decydują parametry
elementu oraz parametry środowiska, w jakim ten element się
znajduje.

Należy zdawać sobie sprawę z faktu, że każdym elemencie
obwodu elektrycznego zachodzi jednocześnie, choć w różnych
proporcjach, proces przemiany i magazynowania energii.

Odbiornik

energii

elektrycznej

i(t)

u(t)

Energia

Energia

elektryczna

Energia

elektryczna

Rys. 20.

Odbiornik energii elektrycznej

20

© Lesław ŁADNIAK

1.3.1 Bilans energii

Ponieważ w każdy element pasywny może energię elektryczną
rozpraszać lub magazynować, to bilans energii dla tego elementu
ma postać:

dW

E

= dW

R

+ dW

M

gdzie:
dW

E

- ilość energii elektrycznej dostarczonej do elementu,

dW

R

- ilość energii ulegającej rozproszeniu,

dW

M

- ilość energii magazynowanej.

1.3.2 Dobroć elementu

Podstawowym parametrem elementu pasywnego jest jego
dobroć, czyli stosunek energii magazynowanej do ilości energii
przekazywanej (rozpraszanej) przez ten element:

Q

E

=

dW

M

dW

R

dobroć =

ilość energii magazynowanej

ilość energii przekazanej

Element obwodu jest idealnym elementem pasywnym, jeżeli w
danym elemencie zachodzi tylko rozpraszanie energii elektrycznej
lub tylko gromadzenie tej energii.

Wprowadzenie

pojęcia elementu idealnego umożliwia podział

obwodu elektrycznego na części, w których zachodzi tylko jeden
rodzaj przemiany energii.

21

© Lesław ŁADNIAK

1.3.3 Idealny przemiennik energii elektrycznej

Element obwodu jest idealnym przemiennikiem energii
elektrycznej na inną energię nazywanym często elementem
rozpraszającym energię elektryczną, wtedy i tylko wtedy, gdy dla
każdej chwili czasu, ilość energii elektrycznej dostarczonej do
elementu jest większa od zera:

dW = p(t) dt = u(t)

⋅

i(t) dt

> 0

Warunek ten będzie spełniony, gdy dla każdej chwili czasu moc
chwilowa jest większa od zera, czyli napięcie na zaciskach
elementu oraz prąd płynący przez ten element mają zawsze taki
sam znak. Oznacza to, że współczynnik wiążący wartości
chwilowe napięcia i prądu R(t) lub G(t) w każdej chwili czasu ma
wartość dodatnią:

u(t) = R(t) i(t) lub

i(t) = G(t) u(t)

Ponieważ wartość chwilowa mocy idealnego elementu
rozpraszającego energię jest zawsze większa od zera, to moc
czynna takiego elementu jest też zawsze dodatnia.

P

=

1

T

⌡

⌠

0

T

p(t) dt > 0

Elementem obwodu elektrycznego, w którym zachodzi tylko
przemiana energii elektrycznej na ciepło jest idealny rezystor.
Dobroć idealnego rezystora jest równa zeru.

Odbiorniki

rezystancyjny

i

R

(t)

u

R

(t)

Energia

elektryczna

Energia

Rys. 21.

Odbiornik rozpraszający energię

22

© Lesław ŁADNIAK

1.3.4 Idealny element magazynujący energię elektryczną

Elementem obwodu jest idealnym elementem magazynującym
energię elektryczną, jeżeli ilość energii dostarczonej do elementu i
otrzymanej z elementu, w ciągu czasu T będącego okresem
powtarzania napięcia i prądu, jest równa zeru.

W(0,T) =

⌡

⌠

0

T

p(t) dt = 0

Moc czynna idealnego elementu magazynującego energię jest
równa zeru, ponieważ ilość energii dostarczonej do elementu jest
równa zeru:

P

=

1

T

⌡

⌠

0

T

p(t) dt =

W(0,T)

T

= 0

Ponieważ interesuje nas przypadek, gdy moc chwilowa jest
różna od zera p(t) ≠ 0, z wyjątkiem skończonej liczby punków, to
musi być przedział czasu, gdy energia jest dostarczana do elementu
i przedział czasu, gdy uprzednio dostarczona do elementu energia
jest w całości oddawana do obwodu:

W(0,T)

=

⌡

⌠

0

t

x

p(t) dt +

⌡

⌠

t

x

T

p(t)

⋅

dt = 0

Odbiorniki

inukcyjny

i

L

(t)

u

L

(t)

Energia

elektryczna

Energia

elektryczna

Odbiorniki

pojemnościowy

i

C

(t)

u

C

(t)

Energia

elektryczna

Energia

elektryczna

Rys. 22.

Odbiorniki magazynujące energię

elektryczną