II zasada dynamiki - ruch obrotowy
druga zasada dynamiki ruchu obrotowego -
sformułowanie
II zasady dynamiki
dla ruchu
obrotowego
bryły sztywnej
wokół stałej (nie obracającej się w przestrzeni) osi. Dotyczy np. sytuacji,
gdy oś obrotu jest wymuszona przez zewnętrzne więzy. Mówi ona, że jeśli na pewne ciało,
o
momencie bezwładności
względem tej osi równym I, działają zewnętrzne siły, które wywierają na to
ciało wypadkowy
moment siły
M
, to w wyniku tego ciało będzie obracać się z
przyspieszeniem
kątowym
takim, że:
Moment siły M i przyspieszenie kątowe ε są wektorami osiowymi (
pseudowektorami
) a ich
kierunek i zwrot są takie same.
Granicznym przypadkiem drugiej zasady dynamiki dla ruchu obrotowego jest sytuacja, gdy
wypadkowy moment sił działających na ciało równy jest 0 (pierwsza zasada dynamiki dla ruchu
obrotowego). Ze wzoru wynika, że wówczas przyspieszenie kątowe również będzie równe 0 a
bryła obracać się będzie ze stałą
prędkością kątową
.
2) Przyspieszenie w ruchu postępowym
a=V/t
3)Energia Kinetyczna w ruchu obrotowym
Ek=Iw^2/2
4)Moment siły:
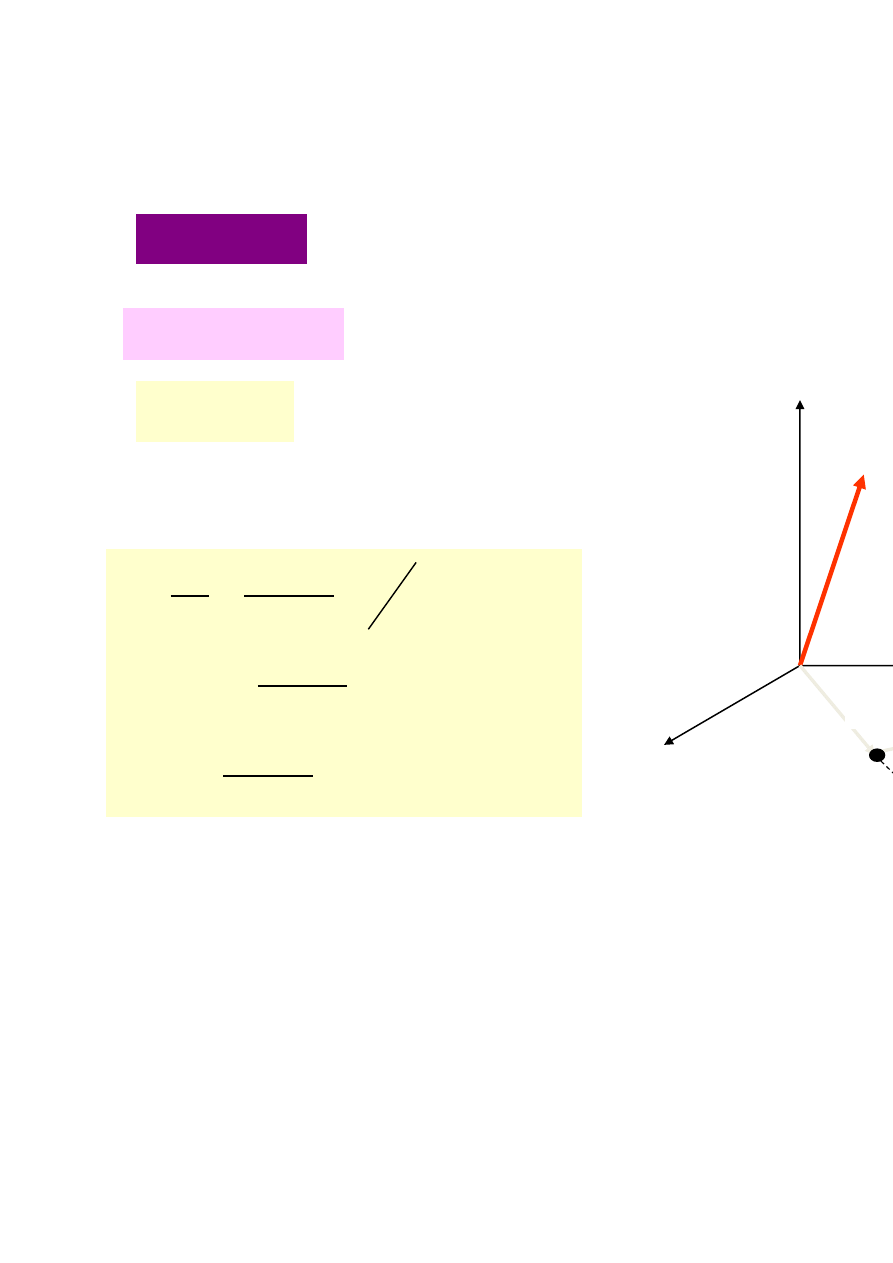
F
r
M
czyli
dt
v
m
d
r
M
dt
v
m
d
r
F
r
r
dt
v
m
d
dt
p
d
F
)
(
,
)
(
,
)
(
Jeżeli siła F działa na cząstkę w punkcie P odległym o r względem pewnego punktu odniesienia 0, to
moment siły M
względem początku układu
definiujemy jako
Wiemy, że
F
r
M
r
–
wektor
wodzący
punktu
przyłożenia
działającej
siły,
określa
położenie
cząstki
wzgl.
wybranego
inercjalnego układu odniesienia (lub ramię siły)
M – moment siły względem pkt. 0.,
θ – kąt między r i F,
sin
rF
M
r
F
M
,
z
0
θ
m
5) Prawo Coulomba
4. Prawo Coulomba
Siła oddziaływania dwóch ładunków q
1
i q
2
(naładowanych ciał)
2
2
1
r
q
q
k
F
gdzie stała
Prawo Coulomba
0
4
1
k
Ogólnie stałą k zapisujemy w postaci
0
= 8,854·10
-12
C
2
/(Nm
2
)
-
przenikalność elektryczna próżni (stała dielektryczna
próżni).
0
4
1
k
-
stała dielektryczna substancji lub względna przenikalność elektryczna ośrodka
jest
wielkością charakterystyczna dla danego ośrodka, zawsze większa od
jedności (
>1).
Dla wody
= 81, dla
próżni
= 1, a dla powietrza
= 1,0006.
Za
pomocą prawa Coulomba można opisać:
• oddziaływania między poszczególnymi elektronami atomu oraz pomiędzy
elektronami a
jądrem atomowym
• siły oddziaływania między atomami tworzącymi cząsteczkę chemiczną
• siły oddziaływania między atomami ciała stałego.
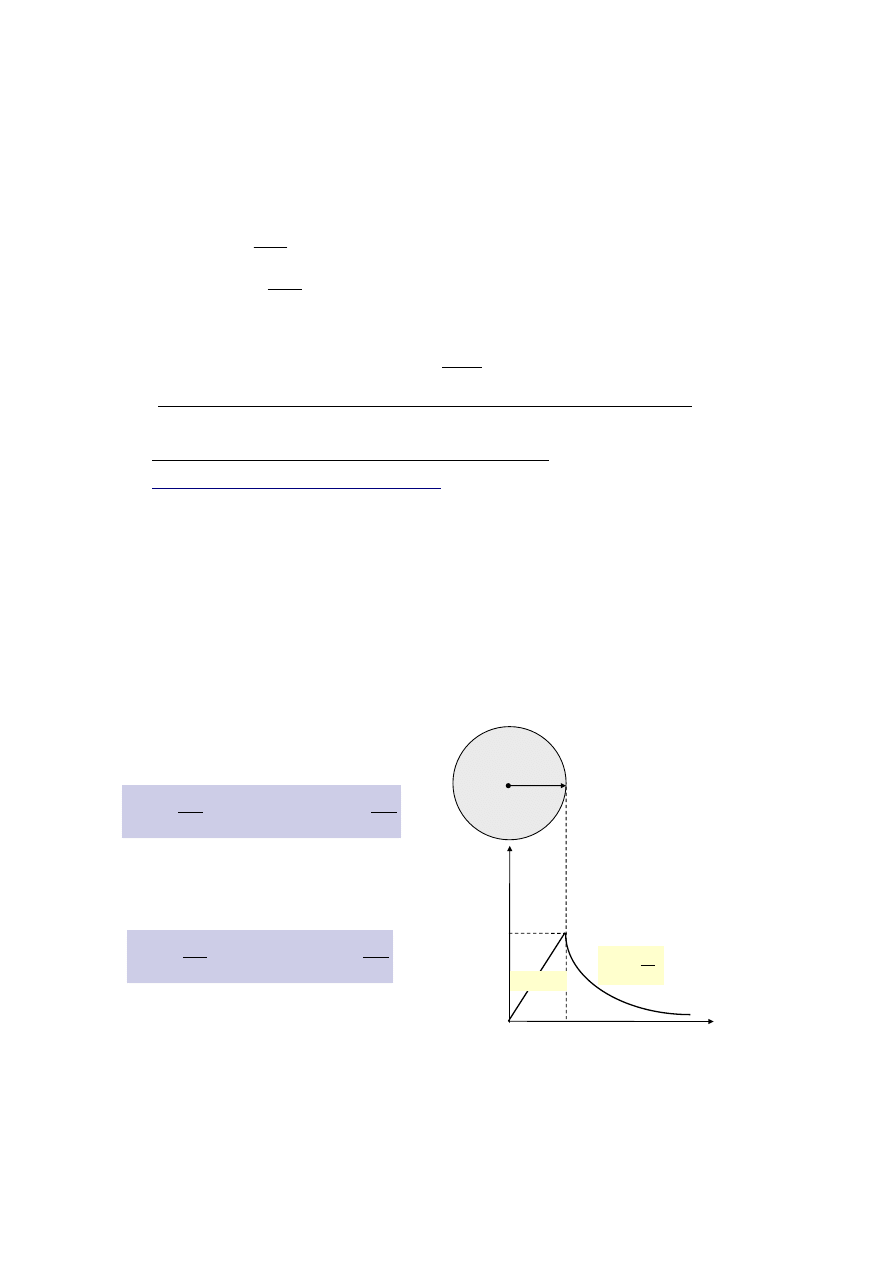
6) Natężenie pola grawitacyjnego ( wzór, wykres E=f(r))
-
wewnątrz kuli
-
rośnie
~ r
2
2
R
M
G
E
r
M
G
E
R
r
2
3
R
M
G
E
r
R
M
G
E
R
r
Wykres zależności natężenia pola grawitacyjnego
, wytwarzanego przez
masę M i promieniu R,
od odległości r
(rys. 5) :
-
na zewnątrz kuli
- maleje
~ r
2
M
E
max
=g
r
Rys. 5
r = R
)
(r
f
E
a
g
2
1
r
f
E
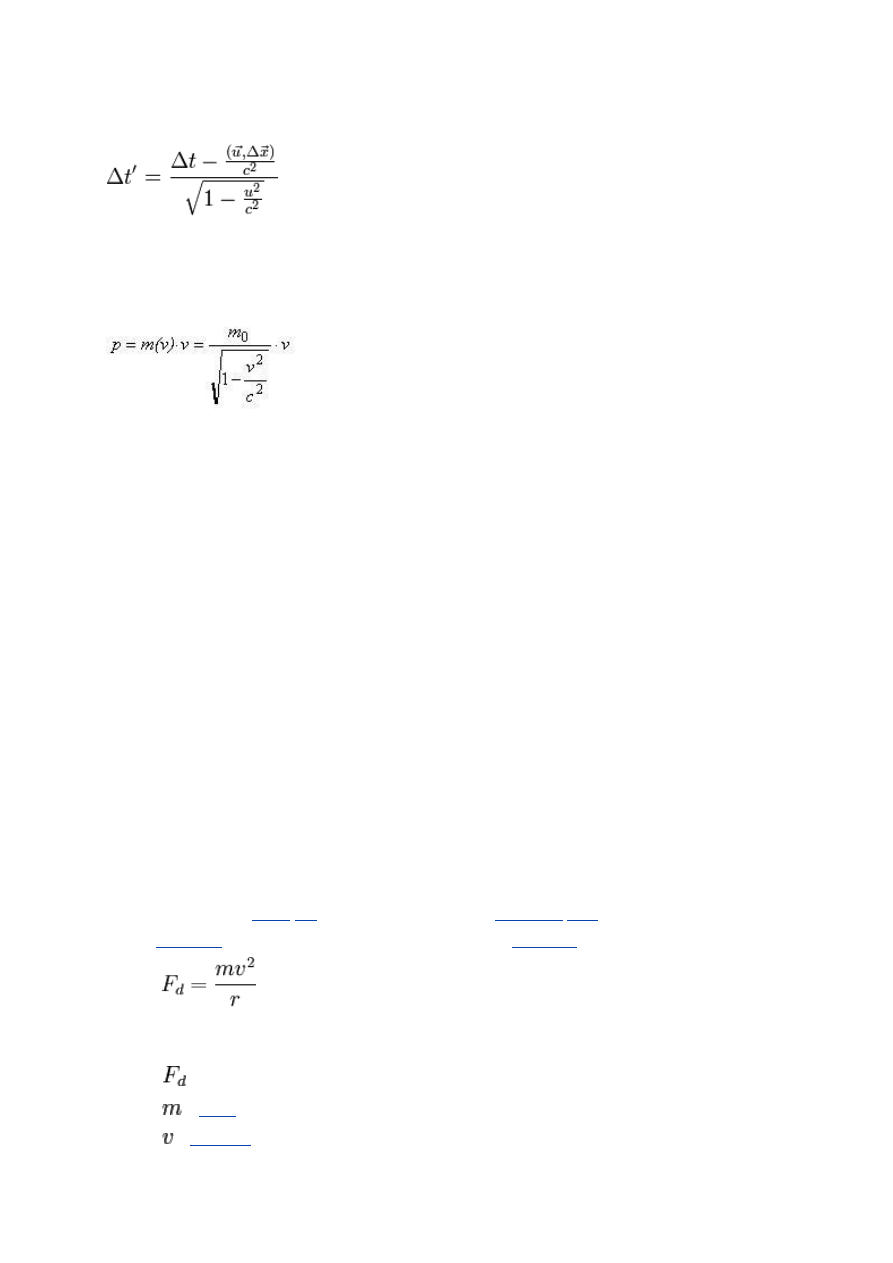
7)Dylatacja długości:
8)Pęd relatywistyczny:
• Pęd relatywistyczny uwzględnia zmiany masy ciała poruszającego się. Obliczamy go ze wzoru:
gdzie: p – pęd relatywistyczny ciała mierzony w spoczywającym układzie U; m(v) – masa
relatywistyczna; m
0
– masa spoczynkowa;
c – prędkość światła w próżni.
9) Ruch harmoniczny tłumiony (równ., rozw.)
m·d
2
x/dt
2
=-kx-k
1
·dx/dt,
k
1
współczynnik oporu środka, czyli
d
2
x/dt
2
+k/m·x+k
1
/m·dx/dt=0 i k/m=ω
0
, k
1
/m=2β wtedy
d
2
x/dt
2
+ ω
0
x+2β·dx/dt=0,
x=x
0
e
-βt
cos(ω
1
t+α) gdzie β=k
1
/2m, ω
1
=√ω
0
2
-β
2
,
ω
0
=√k/m, (ω
0
2
> β
2
), tłumienie λ (T okres ruchu
harmonicznego tłumionego, δ dekrement tłumienia)
λ=x(t)/x(1+t)=e
βT
gdzie T=2π/ω i δ=lnλ=βT
10) Siła odśrodkowa
siła dośrodkowa - w
fizyce
siła
powodująca zakrzywianie
toru ruchu
ciała
, skierowana
wzdłuż
normalnej
(prostopadle) do toru, w stronę środka jego
krzywizny
. Wartość siły określa wzór:
gdzie:
– siła dośrodkowa,
–
masa
ciała,
–
prędkość
ciała,
–
promień krzywizny
toru ruchu.
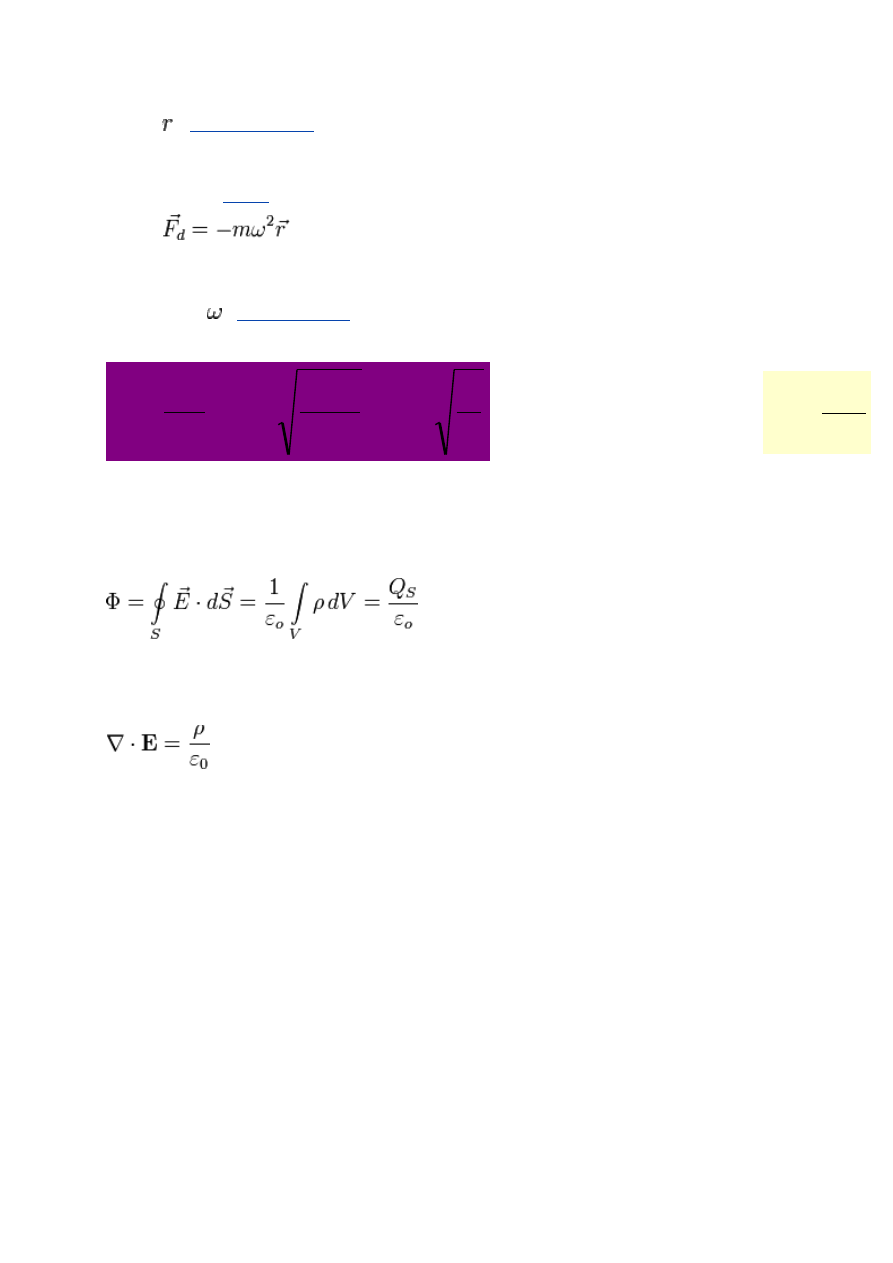
Siła dośrodkowa nie zmienia wartości prędkości ciała.
W ruchu po
okręgu
, powyższy wzór można wyrazić:
gdzie:
–
prędkość kątowa
.
11) Wahadło fizyczne ( opis, wzór na okres)
l
r
– długość zredukowana wahadła fizycznego, określa ona odległość takich dwóch osi
(niesymetrycznie położonych względem środka ciężkości), wokół których wahadło waha się z
jednakowym okresem.
12) Prawo Gaussa dla pkt. magnetycznego ( całk.,różn.,interp.)
wektor dS jest wektorem powierzchni,
współczynnikiem proporcjonalności jest przenikalność elektryczna próżni ε
o
.
∇ · E – dywergencja natężenia pola elektrycznego,
ρ – gęstość ładunku.
13) Uogólnione prawo Ampera ( całk., różn., interp.)
g
l
mga
I
T
r
2
2
2
ma
I
l
r
r
F
Całka dla pola E równała się wypadkowemu ładunkowi wewnątrz powierzchni, a
w przypadku pola B jest
równa całkowitemu prądowi otoczonemu przez kontur
(dowolny), co zapisujemy
I
0
d
l
B
Prawo Ampera
gdzie dl
– element konturu,
0
= 4
k/c
2
= 4
·10
-7
Tm/A, jest
przenikalnością
magnetyczną próżni
.
Tak jak w przypadku prawa Gaussa wynik
był prawdziwy dla dowolnej
powierzchni
zamkniętej tak dla prawa Ampera wynik nie zależy od kształtu
konturu
zamkniętego.
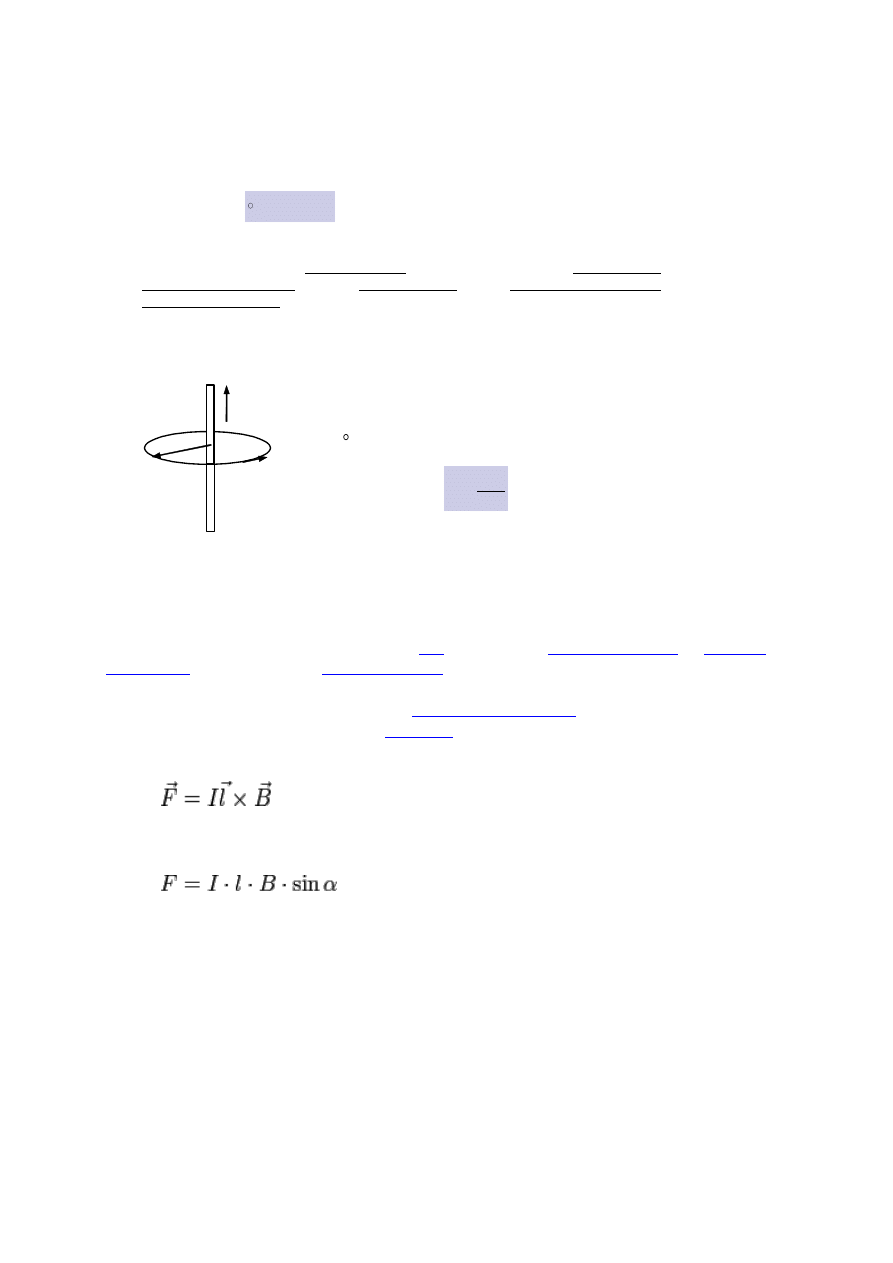
Przykład
Obliczmy pole
wokół nieskończenie długiego prostoliniowego przewodnika w
odległości r od niego.
I
r
dl
Z prawa Ampera wynika,
że dla konturu kołowego
I
0
d
l
B
B2
r =
0
I
s
tąd
r
I
B
2
0
14) Siła elektrodynamiczna:
Siła elektrodynamiczna (magnetyczna) -
siła
, z jaką działa
pole magnetyczne
na
przewód
elektryczny
, w którym płynie
prąd elektryczny
.
Na umieszczony w polu magnetycznym o
indukcji magnetycznej
B prostoliniowy przewodnik
o długości l, przez który płynie prąd o
natężeniu
I, działa siła F, którą wektorowo określa
wzór:
czyli jej wartość wynosi:
15) Elektryczny moment dipolowy:
11. Elektryczny moment dipolowy jest to wektorowa wielkość fizyczna charakteryzująca
dipol elektryczny. Dipol jest układem dwóch ładunków o tych samych wartościach
bezwzględnych, ale przeciwnych znakach
P=qd
x