Microsoft PowerPoint 04 algebra relacji i rachunek relacyjny

Algebra relacji i rachunek relacyjny



Meaning of the term relational completeness.



How to form queries in relational algebra.



How to form queries in tuple relational

calculus.



How to form queries in domain relational

calculus.



Categories of relational DML.



Relational algebra and relational calculus are

formal languages associated with the

relational model.



Informally, relational algebra is a (high-level)

procedural language and relational calculus a

non-procedural language.



However, formally both are equivalent to one

another.



A language that produces a relation that can

be derived using relational calculus is

relationally complete.



Operacje algebry relacji są realizowane na jednej

lub wielu relacjach, a ich wynik może definiować

nowe relacje bez zmiany relacji bazowych.



Zarówno argumenty jak i wyniki są relacjami, tak

więc wynik jednej operacji może stać się

argumentem kolejnej.



Pozwala to na zagnieżdżanie wyrażeń, tak jak w

przypadku wyrażeń arytmetycznych. Dzięki tej

własności można powiedzieć, że relacje są

domknięte.



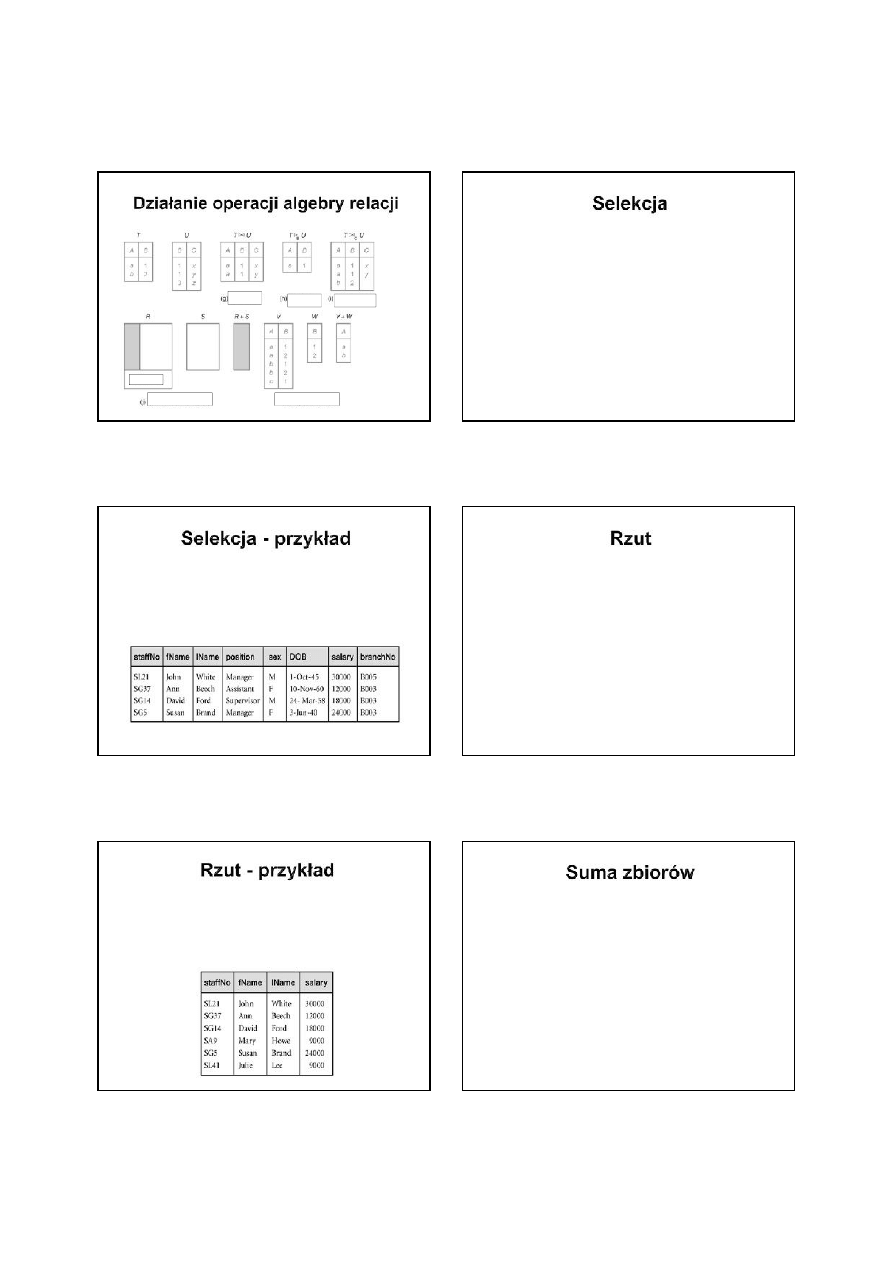
Pięć podstawowych operacji to: selekcja, rzut,

iloczyn kartezjański, suma oraz różnica zbiorów.



Pozwalają wykonać większość operacji

wyszukiwania danych.



Istnieją także dodatkowe operacje: złączenie,

przekrój oraz iloraz, które można wyrazić za

pomocą pięciu operacji podstawowych.

Selekcja

Rzut

Iloczyn

kartezjański

Suma

Przekrój

Różnica zbiorów

Złączenie

naturalne

Półzłączenie

Lewostronne

złączenie

zewnętrzne

Reszta

Iloraz

Przykład ilorazu





predykat

(R)



Operacja selekcji działa na jednej relacji R i daje w

wyniku relację zawierającą jedynie te krotki R,

które spełniają podany warunek (predykat).



Podaj wszystkich pracowników, którzy mają pensję

wyższą niż 10 000 funtów.



salary > 10000

(Staff)





a1, . . . , an

(R)



Działa na jednej relacji R i daje w wyniku relację,

która zawiera „pionowy” wycinek R powstały

przez wybranie wartości określonych atrybutów R

i pominięcie duplikatów krotek.



Podaj listę zawierającą pensje wszystkich

pracowników. Na liście mają być tylko staffNo,

fName, lName, oraz pensja (salary).



staffNo, fName, lName, salary

(Staff)



R  S



Suma dwu relacji R i S definiuje relację

zawierającą wszystkie krotki R jak i S, przy czym

duplikaty krotek są eliminowane.



R i S muszą mieć zgodne schematy.



Jeżeli R i S mają odpowiednio I oraz J krotek, to ich

sumę otrzymujemy łącząc obie relacje w jedną ,

zawierającą maksymalnie (I + J) krotek.



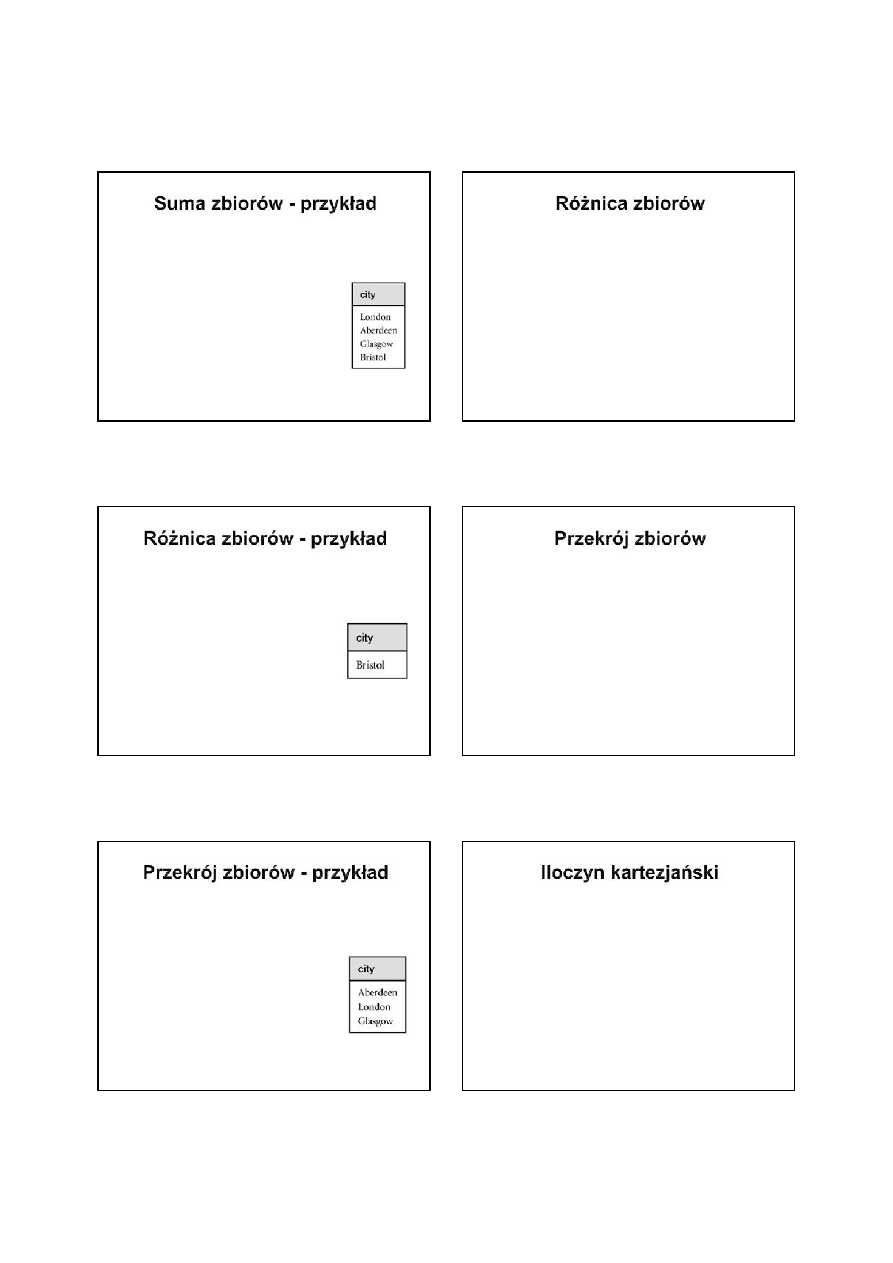
Podaj wszystkie miasta, w których znajduje się biuro

firmy lub nieruchomość do wynajęcia.



city

(Branch) 



city

(PropertyForRent)



R – S



Definiuje relację składającą się ze wszystkich

krotek zawartych w relacji R, ale nie należących

do relacji S.



R i S muszą mieć zgodne schematy.



Podaj wszystkie miasta, w których znajdują się biura

firmy, ale nie ma żadnej nieruchomości do

wynajęcia.



city

(Branch) –



city

(PropertyForRent)



R  S



Definiuje relację składającą się ze wszystkich

krotek należących zarówno do relacji R jak i do

relacji S.



R i S muszą mieć zgodne schematy.



Można go określić korzystając z podstawowych

operacji:

R  S = R – (R – S)



Podaj wszystkie miasta, w których znajduje się i

biuro firmy i nieruchomość do wynajęcia.



city

(Branch) 



city

(PropertyForRent)



R X S



Operacja iloczynu kartezjańskiego definiuje

relację, która zawiera konkatenację każdej krotki z

relacji R z każdą krotką relacji S.



Podaj nazwiska wszystkich klientów, którzy oglądali

nieruchomości, oraz zgłoszone przez nich uwagi.

(

clientNo, fName, lName

(Client)) X

(

clientNo, propertyNo, comment

(Viewing))



(

clientNo, fName, lName

(Client)) X (

clientNo,

propertyNo, comment

(Viewing))

itd.



Wykonajmy więc operację selekcji, by wybrać tylko

te krotki, dla których:



Client.clientNo = Viewing.clientNo.

Client.clientNo =

Viewing.clientNo

((

clientNo, fName,

lName

(Client))  (

clientNo,

propertyNo, comment

(Viewing)))



Iloczyn kartezjański i selekcję można sprowadzić do

jednej operacji zwanej Złączeniem.



Client.clientNo = Viewing.clientNo

((

clientNo, fName,

lName

(Client))  (

clientNo, propertyNo,

comment

(Viewing)))



Złączenie jest operacją pochodną iloczynu

kartezjańskiego.



Polega na wykonaniu selekcji na argumencie

będącym iloczynem kartezjańskim dwu relacji –

argumentów złączenia.



Jeden z trudniejszych problemów implementacji

DBMS i często pogarsza sprawność ich działania.



Odmiany operacji złączeń:



Teta-złączenie



Równozłączenie (szczególny

przypadek teta-złączenia)



Złączenie naturalne



Złączenie zewnętrzne



Półzłączenie





Wynikiem operacji teta-złączenie jest relacja

zawierająca krotki iloczynu kartezjańskiego R i

S spełniające warunek F.



Warunek F jest w postaci R.a

 S.b

gdzie 

jest jednym z operatorów porównania (<, , >,

, =, ).



Teta-złączenie można wyrazić za pomocą

podstawowych operacji selekcji i iloczynu

kartezjańskiego:

S = 

(R  S)



Krotność teta-złączenia jest sumą krotności relacji

składowych R i S. Jeżeli predykat F zawiera tylko

równość (=), to teta-złączenie nosi nazwę

równozłączenia.



Podaj nazwiska wszystkich klientów, którzy oglądali

nieruchomości, oraz zgłoszone przez nich uwagi.

(

clientNo, fName, lName

(Client))

Client.clientNo = Viewing.clientNo

(

clientNo,

propertyNo, comment

(Viewing))



R S



Złączenie naturalne jest równozłączeniem dwu

relacji R i S według wszystkich wspólnych

atrybutów x. Jedno z wystąpień każdego ze

wspólnych atrybutów jest eliminowane z relacji

wynikowej.



Podaj nazwiska wszystkich klientów, któzy oglądali
nieruchomości, oraz zgłoszone przez nich uwagi.

(

clientNo, fName, lName

(Client))

(

clientNo, propertyNo, comment

(Viewing))



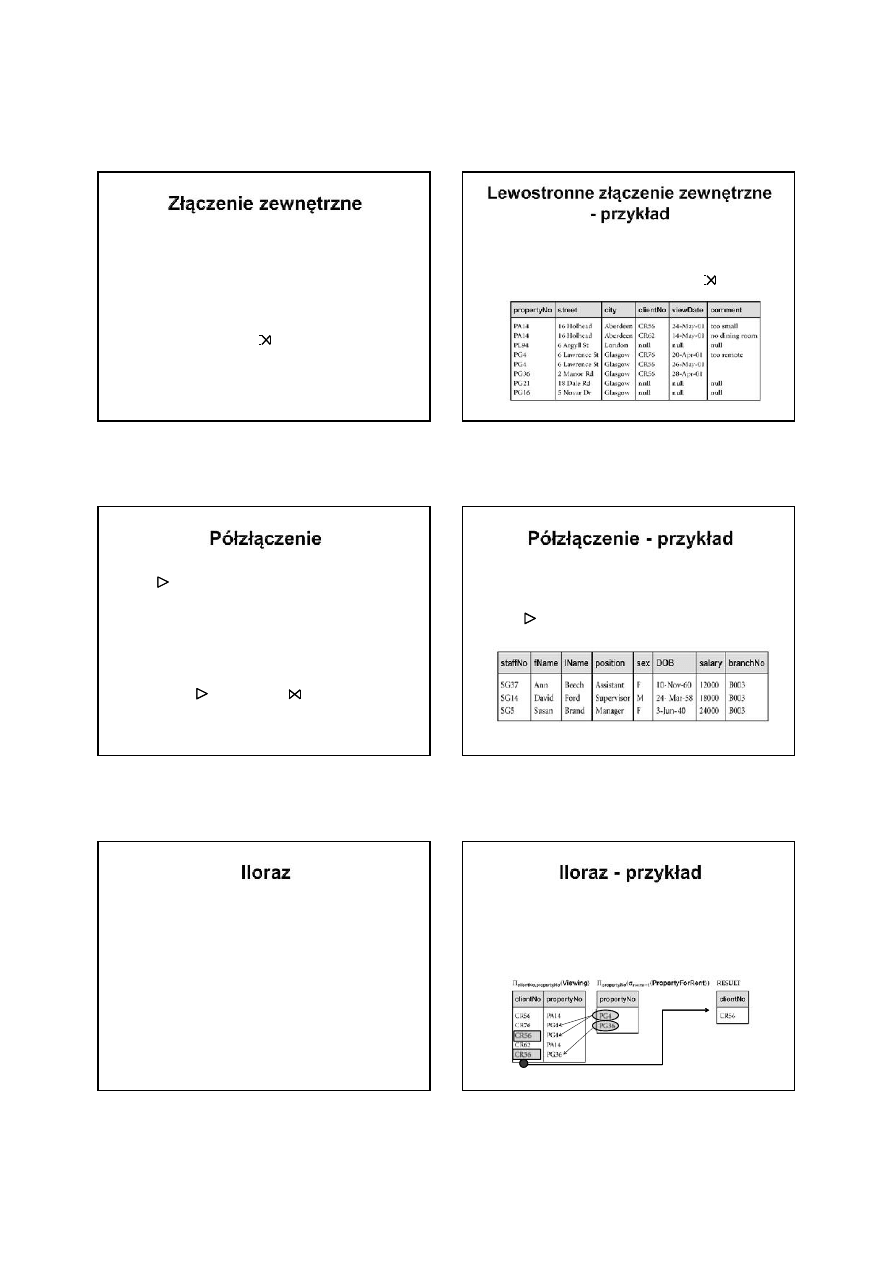
Złączenie zewnętrzne (lewostronne) to

złączenie, w którym do relacji wynikowej są

włączane również takie krotki z relacji R, dla

których w relacji S nie występują wartości

wspólnych atrybutów.



Podaj raport na temat wizyt we wszystkich

nieruchomościach.



propertyNo, street, city

(PropertyForRent)

Viewing





Wynikiem operacji półzłączenia jest relacja

zawerająca te krotki relacji R, które weszłyby

do złączenia R i S.



Półzłączenie można zapisać za pomocą operacji rzutu i

złączenia:

S =





Podaj kompletną informację o pracownikach biura w

Glasgow

Staff

Staff.branchNo=Branch.branchNo

(

city=‘Glasgow’

(Branch))



R  S



Wynikiem ilorazu jest relacja posiadająca atrybuty

C i zawierająca zbiór takich krotek z relacji R, które

w połączeniu z każdą krotką z relacji S stworzą

kombinację (krotkę) występującą w relacji R.



Można to przedstawić za pomocą operacji

podstawowych:

 

(R)

 

((S

) – R)

T  T

– T



Znajdź wszystkich klientów, którzy odwiedzili

wszystkie lokale trzypokojowe.
(



clientNo, propertyNo

(Viewing))



(



propertyNo

(



rooms = 3

(PropertyForRent)))





(R)



Applies aggregate function list, AL, to R to define a

relation over the aggregate list.



AL contains one or more (<aggregate_function>,

<attribute>) pairs .



Main aggregate functions are: COUNT, SUM,

AVG, MIN, and MAX.



How many properties cost more than £350 per

month to rent?



(myCount) 

COUNT propertyNo

(σ

rent > 350

(PropertyForRent))

 GA



(R)



Groups tuples of R by grouping attributes, GA, and

then applies aggregate function list, AL, to define a

new relation.



AL contains one or more (<aggregate_function>,

<attribute>) pairs.



Resulting relation contains the grouping attributes,

GA, along with results of each of the aggregate

functions.



Find the number of staff working in each branch

and the sum of their salaries.



(branchNo, myCount, mySum)

branchNo



COUNT staffNo, SUM salary

(Staff)



Relational calculus query specifies

what is to

be retrieved rather than

how to retrieve it.



No description of how to evaluate a query.



In first-order logic (or predicate calculus),

predicate is a truth-valued function with

arguments.



When we substitute values for the arguments,

function yields an expression, called a

proposition, which can be either true or false.



Jeżeli warunek zawiera zmienną (np. ‘x jest

pracownikiem’), to musi istnieć ograniczenie

dziedziny dla x.



Po podstawieniu za x pewnych wartości z tej

dziedziny zdanie może być prawdziwe, a po

podstawieniu innych danych – może być fałszywe.



W odniesieniu do baz danych rachunek relacyjny

może występować jako rachunek krotek lub

rachunek dziedzin.



Interesuje nas znalezienie krotek, dla których

warunek jest prawdziwy. Rachunek ten jest oparty na

zastosowaniu zmiennych krotkowych.



Zmienna krotkowa to zmienna, która „przebiega”

wskazaną relację; tzn. zmienna, której wartościami

mogą być tylko krotki danej relacji.



Np. określmy , że dziedziną zmiennej krotkowej S jest

relacja Staff:

Staff(S)



Zapytanie: znajdź zbiór wszystkich krotek S, dla

których jest prawdziwy warunek P(S) można wyrazić:

{S | P(S)}



Podaj dane pracowników zarabiających ponad

10,000 funtów:

{S | Staff(S)  S.salary > 10000}



Aby uzyskać wartość konkretnego atrybutu, jak na

przykład pensja (salary), możemy napisać:

{S.salary | Staff(S)  S.salary > 10000}



Można używać dwu rodzajów kwantyfikatorów, by

określić, dla jak wielu przypadków warunek (zdanie)

jest prawdziwy:



Kwantyfikator egzystencjalny $(‘istnieje’)



Kwantyfikator ogólny "(‘dla każdego’)



Zmienne krotkowe „objęte” kwalifikatorem "lub $

nazywamy zmiennymi związanymi, pozostałe

zmienne nazywamy zmiennymi wolnymi.



Kwantyfikator egzystencjalny stosuje się w

formułach, które muszą być prawdziwe dla

przynajmniej dla jednego przypadku, np.:

Staff(S)  (

∃

B)(Branch(B) 

(B.branchNo = S.branchNo)  B.city = ‘London’)



Co oznacza: ‘Istnieje krotka w relacji Branch, która

ma taki sam numer branchNo jak aktualnie

rozważana krotka S relacji Staff i jej atrybut city ma

wartość „Londyn”’ .



Kwantyfikator ogólny stosowany jest w zdaniach,

które powinny zachodzić dla każdego przypadku, np.:

(∀

B) (B.city  ‘Paris’)



Oznacza to, że: ‘Wszystkie krotki relacji Branch mają

wartość atrybut city inną niż „Paris”’ .



Można też wyrazić to inaczej:

∃

B) (B.city = ‘Paris’)

co znaczy: ‘nie istnieją biura w Paryżu’ .



Formuły to takie sformułowania, które są

jednoznaczne i sensowne.



Formuła (dobrze zbudowana) składa się z formuł

atomowych:

 R(S

)

, gdzie

jest zmienną krotkową, a

jest relacją

 S



Stosując te reguły można rekurencyjnie budować z

formuł atomowych kolejne formuły:



Formuła atomowa jest formułą.



Jeżeli

są formułami, to formułami są także ich:



koniunkcja -

 F2



dysjunkcja -

 F2



negacja



Jeżeli

jest formułą oraz

jest zmienną wolną w

, to

(

$X)(F)

oraz

(

"X)(F)

także są formułami.



Podaj nazwiska wszystkich dyrektorów, którzy zarabiają

więcej niż 25.000 funtów.

{S.fName, S.lName | Staff(S) 

S.position = ‘Manager’  S.salary > 25000}



Podaj wszystkich pracowników, którzy nadzorują

nieruchomości w Glasgow.

{S | Staff(S)  (

∃

P) (PropertyForRent(P) 

(P.staffNo = S.staffNo)  P.city = ‘Glasgow’)}



Podaj nazwiska pracowników, którzy obecnie nie

nadzorują żadnej nieruchomości.

{S.fName, S.lName | Staff(S)  (~(

∃

(PropertyForRent(P)(S.staffNo = P.staffNo)))}

Można to też sformułować inaczej:

{S.fName, S.lName | Staff(S)  ((P)

(~PropertyForRent(P) 

~(S.staffNo = P.staffNo)))}



Podaj nazwiska klientów, którzy oglądali

nieruchomości w Glasgow.

{C.fName, C.lName | Client(C)  ((

∃

V)(

∃

(Viewing(V)  PropertyForRent(P) 
(C.clientNo = V.clientNo) 
(V.propertyNo=P.propertyNo) 

P.city =‘Glasgow’))}



Za pomocą formuły relacyjnego rachunku krotek

można zapisać zbiór nieskończony. Na przykład

formuła:

{S | ~Staff(S)}

oznacza ona zbiór wszystkich krotek, które nie

należą do relacji Staff. Taką formułę nazywamy

niebezpieczną.



Należy więc dodawać ograniczenie stanowiące, że

wszystkie wartości występujące w relacji wynikowej

muszą pochodzić z dziedziny formuły E, oznaczanej

jako dom(E).



Uses variables that take values from domains

instead of tuples of relations.



If F(

, . . . ,

) stands for a formula

composed of atoms and

, . . . ,

represent

domain variables, then:

{

, . . . ,

| F(

, . . . ,

)}

is a general domain relational calculus expression.



Find the names of all managers who earn more

than £25,000.

{fN, lN | ($sN, posn, sex, DOB, sal, bN)

(Staff (sN, fN, lN, posn, sex, DOB, sal, bN) 

posn = ‘Manager’ sal > 25000)}



List the names of staff who currently do not

manage any properties for rent.

{fN, lN | ($sN)

(Staff(sN,fN,lN,posn,sex,DOB,sal,bN) 
(

($sN1) (PropertyForRent(pN, st, cty, pc, typ,

rms, rnt, oN, sN1, bN1) (sN=sN1))))}



List the staff who manage properties for rent

in Glasgow.

{sN, fN, lN, posn, sex, DOB, sal, bN |

($sN1,cty)(Staff(sN,fN,lN,posn,sex,DOB,sal,bN) 

PropertyForRent(pN, st, cty, pc, typ, rms,

rnt, oN, sN1, bN1) 

(sN=sN1) cty=‘Glasgow’)}



List the names of clients who have viewed a

property for rent in Glasgow.

{fN, lN | ($cN, cN1, pN, pN1, cty)

(Client(cN, fN, lN,tel, pT, mR) 

Viewing(cN1, pN1, dt, cmt) 

PropertyForRent(pN, st, cty, pc, typ,

rms, rnt,oN, sN, bN) 

(cN = cN1)  (pN = pN1) cty = ‘Glasgow’)}



When restricted to safe expressions, domain

relational calculus is equivalent to tuple

relational calculus restricted to safe

expressions, which is equivalent to relational

algebra.



Means every relational algebra expression has

an equivalent relational calculus expression,

and vice versa.



Relacyjny rachunek dziedzin.



Języki transformacji, np. SQL.



Języki o interfejsie graficznym, np. QBE.



Języki czwartej generacji (4GL).



Języki piątej generacji (5GL).



4GLs can create complete customized

application using limited set of commands in a

user-friendly, often menu-driven environment.



Some systems accept a form of natural

language, sometimes called a 5GL, although this

development is still at an early stage.

Wyszukiwarka

Podobne podstrony:
Microsoft PowerPoint 04 Analiza otoczenia konkurencyjnego ppt
Microsoft PowerPoint 03 model relacyjny id 299067
Nowy Prezentacja programu Microsoft PowerPoint 5
Rola rynku i instytucji finansowych INowy Prezentacja programu Microsoft PowerPoint
ZADANIA PiP Prezentacja Microsoft PowerPoint
Nowy Prezentacja programu Microsoft PowerPoint ppt
Microsoft PowerPoint IP5 klasyfikacje tryb zgodnosci
Microsoft PowerPoint IP tryb zgodnosci
Microsoft PowerPoint 02 srodowisko bazy danych, modele
(Microsoft PowerPoint 2 KONWENCJA WIEDENSKAid 1358 (2)
Microsoft PowerPoint IP5 bazydanych tryb zgodnosci
Microsoft PowerPoint znaki
(Microsoft PowerPoint E12 Rynek pieniadzaid 1360 (2)
(Microsoft PowerPoint E14 Inflacjaid 1361
Microsoft PowerPoint Wyklad 1 Wstep do informatyki i
Microsoft PowerPoint Wyklad 2 Wstep do informatyki i

więcej podobnych podstron