Algorytmy grafowe
Grafy
G = (V,E) – graf
Gdzie:
V – zbiór wierzchołków
E – zbiór krawędzi
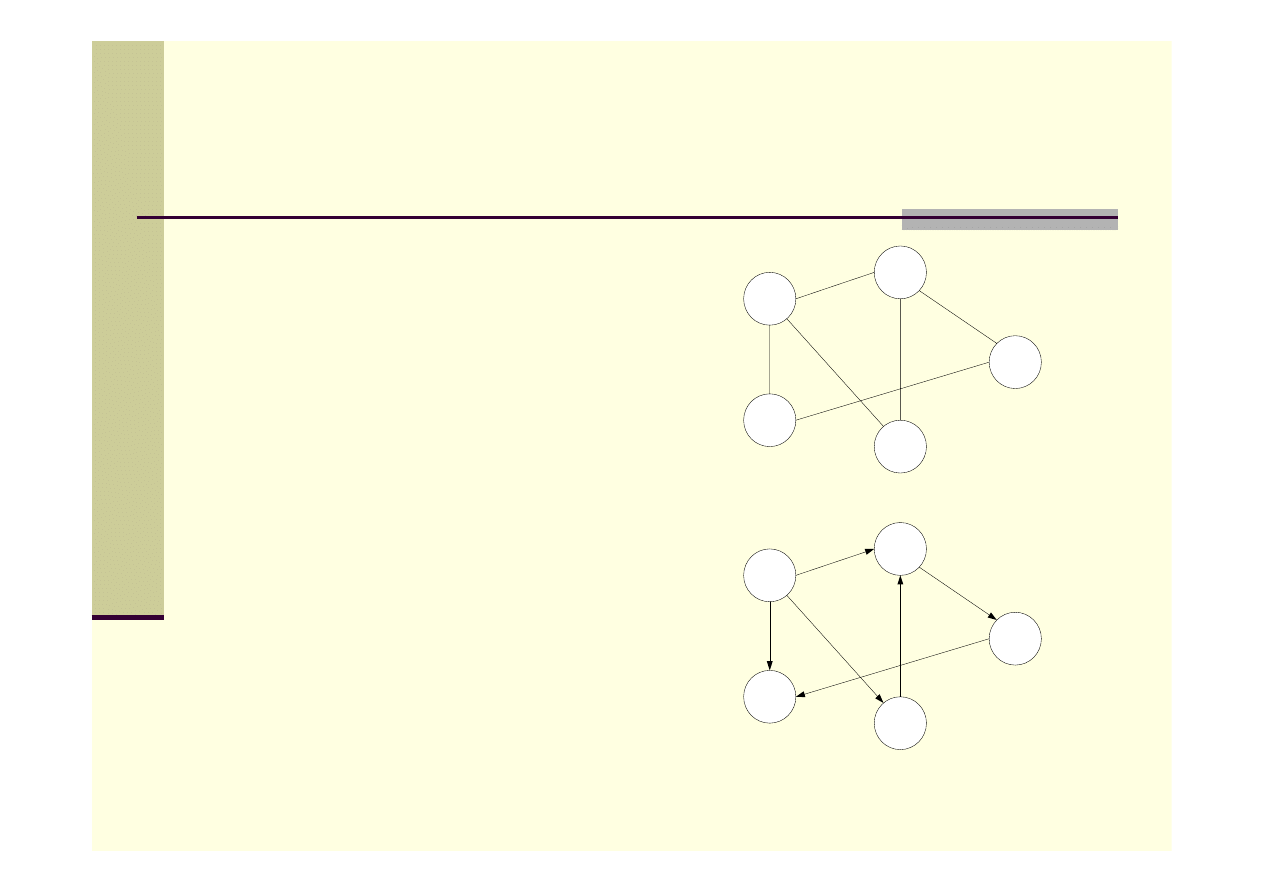
Grafy:
Skierowane
Nieskierowane
Spójność grafu
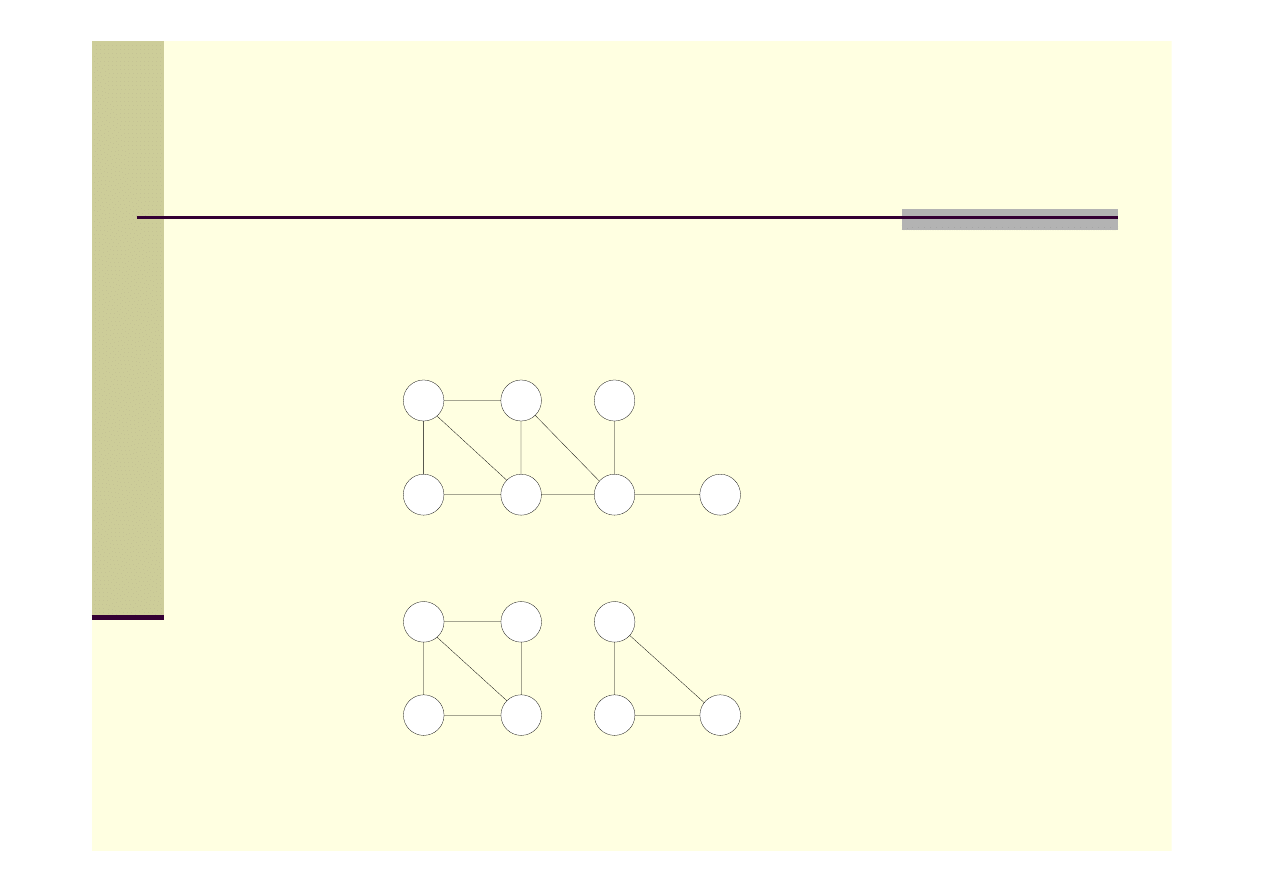
Graf G jest spójny, jeśli każde dwa wierzchołki można połączyć
ścieżką.
a)
Graf spójny
b)
Graf niespójny
Dwuspójność grafu
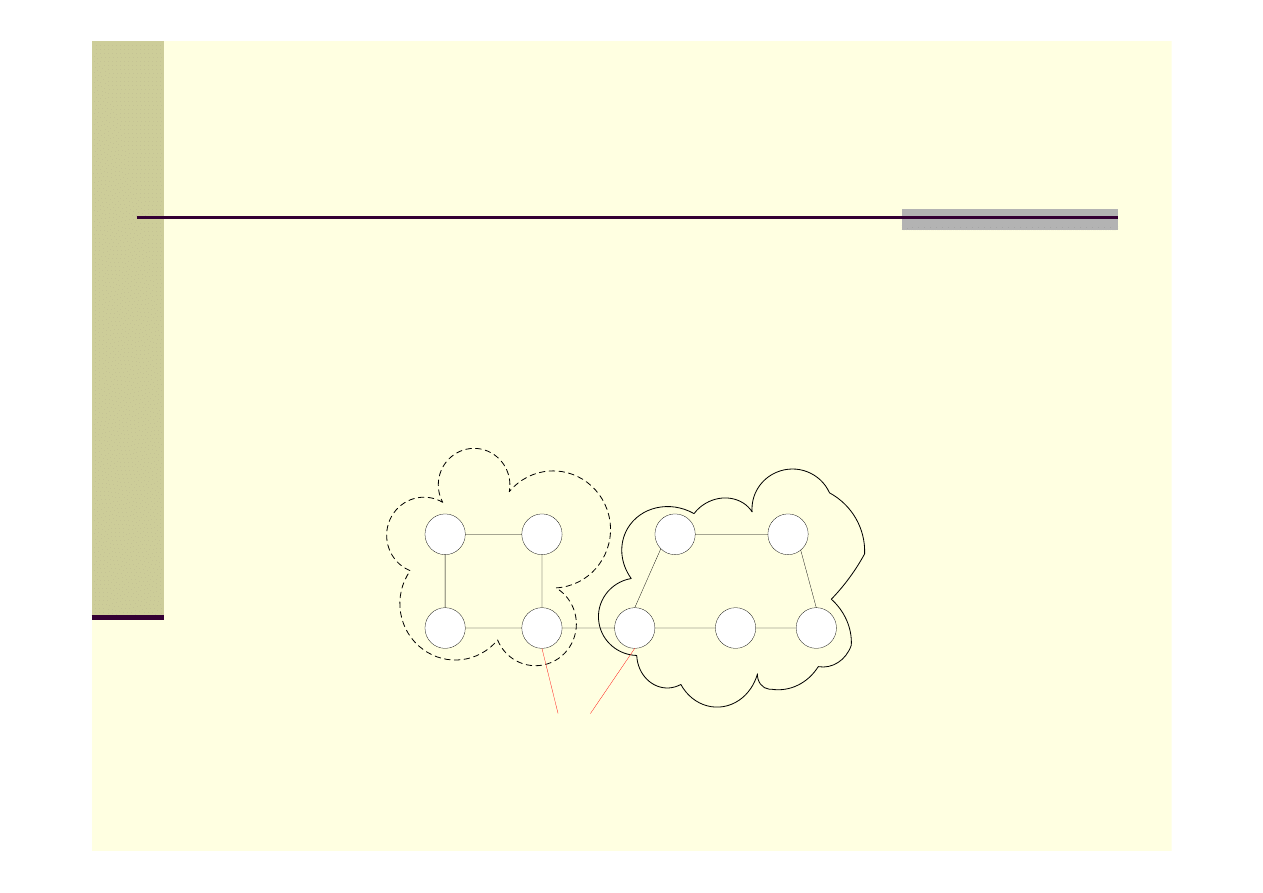
Graf G jest dwuspójny, jeśli między każdymi dwoma wierzchołkami
istnieją dwie różne ścieżki. Jeśli graf zawiera tylko 2 węzły, to jest
dwuspójny.
Punkt artykulacji (wierzchołek rozdzielający) – jego usunięcie
„rozspujnia” graf (dzieli na dwuspójne składowe).
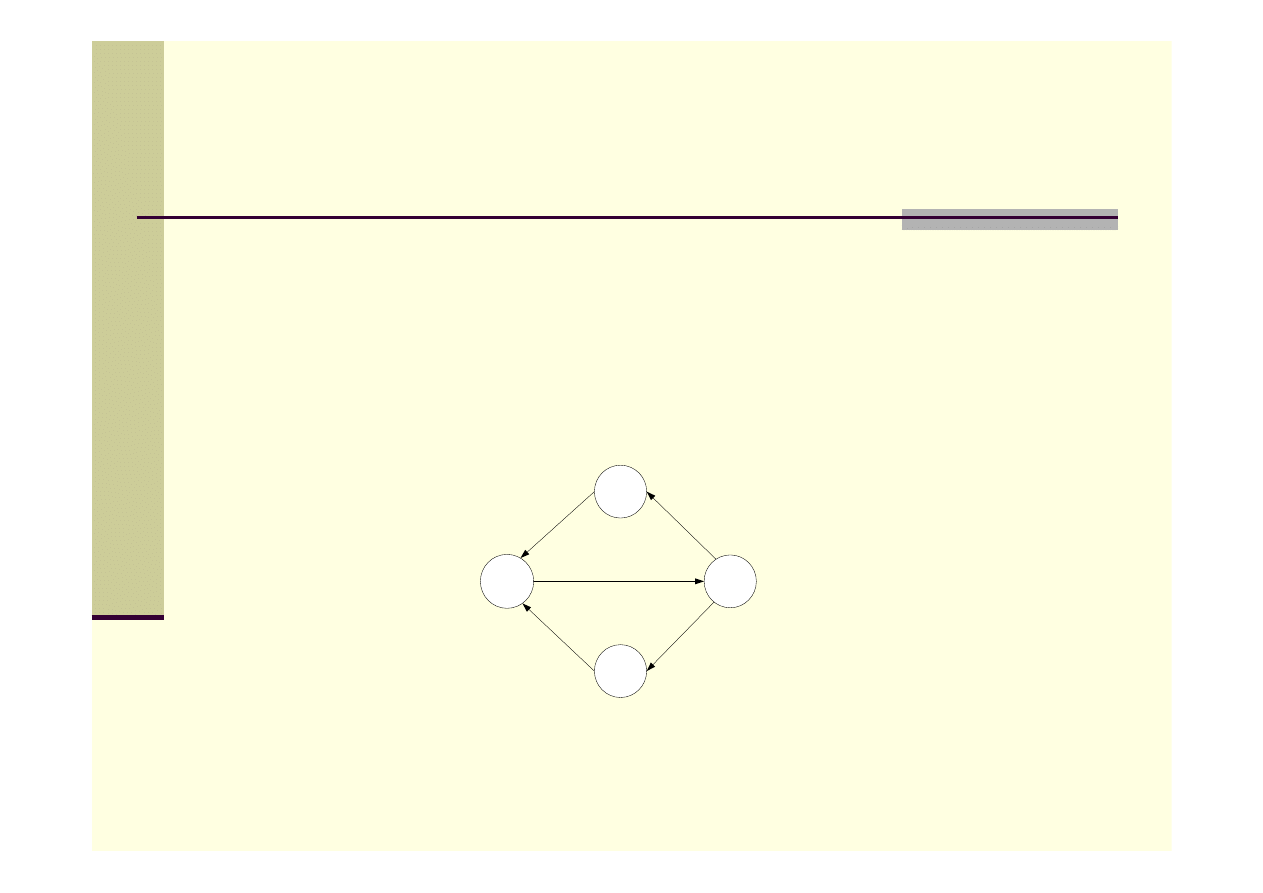
Silna spójność grafu
Graf skierowany G jest silnie spójny, jeśli dla każdych dwóch
wierzchołków v i w grafu G istnieją ścieżki skierowane z v do w oraz z
w do v.
Jeśli G nie jest silnie spójny, to można podzielić go na co najmniej dwie
silnie spójne składowe.
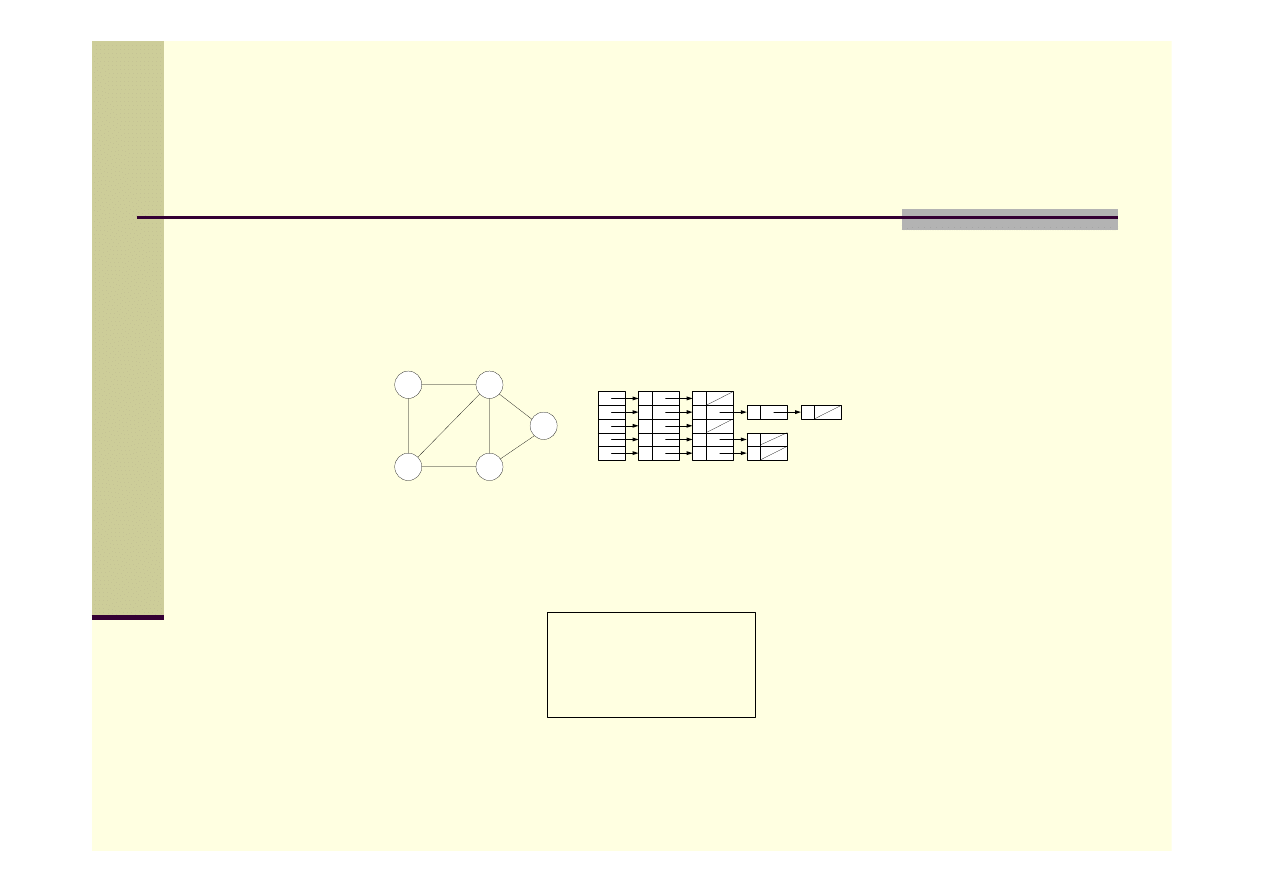
Reprezentacja grafu
Są dwie możliwości prezentacji
grafów w komputerze:
a) Lista sąsiedztwa
b) Macierz sąsiedztwa

Cykl, cykl prosty
W grafie skierowanym cyklem nazywamy ścieżkę <v0, v1, …, vk> która
zaczyna się i kończy w tym samym wierzchołku i zawiera co najmniej
jedną krawędź.
W cyklu prostym dodatkowo wierzchołki v1, v2, …, vk są różne.
W grafie nieskierowanym cyklem nazywamy ścieżkę <v0, v1, …, vk>,
gdzie v0=vk i v1, v2, …, vk są różne oraz k ≥2.
Graf nie zawierający cykli nazywamy acyklicznym.
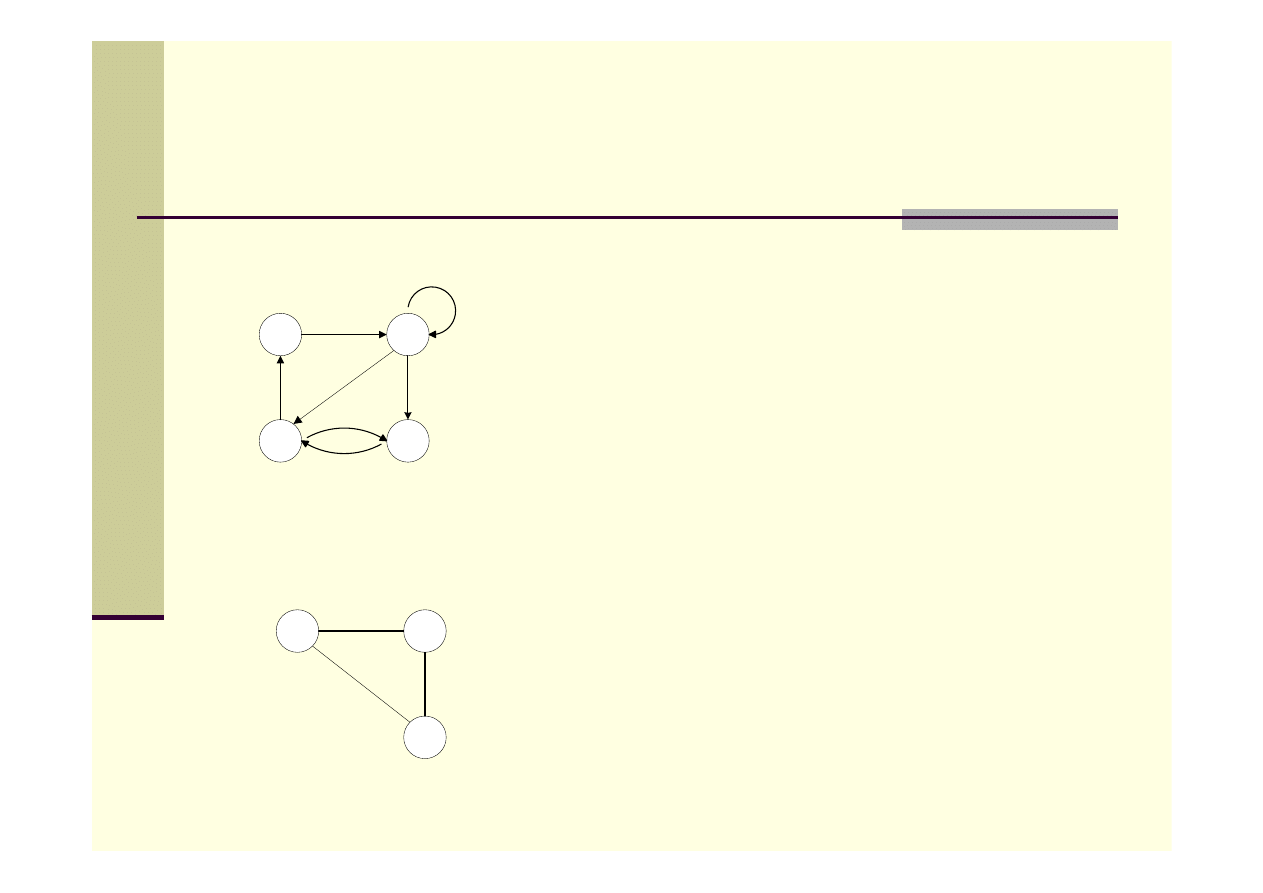
Cykl – przykłady grafów
<1,2,4,3,4,1> - cykl
<1,2,4,1> - cykl prosty
<2,2> - pętla
1
3
2
4
Graf skierowany:
Graf nieskierowany:
<1,2,3,1> - cykl
1
3
2
Cykl Eulera
Cykl Eulera przechodzi przez każdą krawędź grafu dokładnie raz (ale
może odwiedzać wielokrotnie ten sam wierzchołek). Warunkiem istnienia
cyklu jest:
spójność grafu,
dla grafu skierowanego należy sprawdzić czy ilość krawędzi
wchodzących do danego wierzchołka jest równa ilości krawędzi
wychodzących,
dla grafu nieskierowanego z każdego wierzchołka musi wychodzić
parzysta liczba krawędzi.
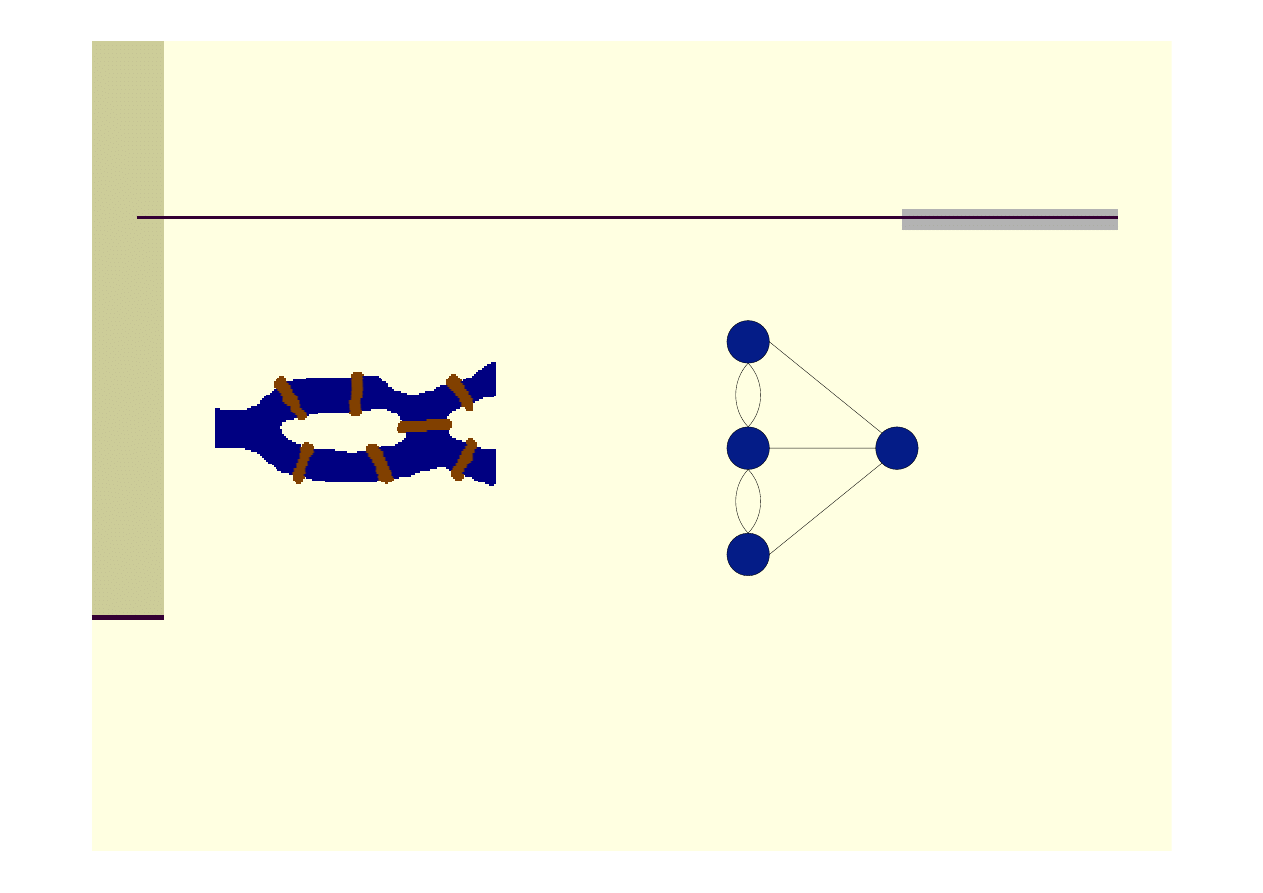
Cykl Eulera c.d.
Do powstania cyklu Eulera przyczynił się tzw. problem mostów
królewieckich.
Mosty na rzece Pregole
Odpowiadający im graf nieskierowany
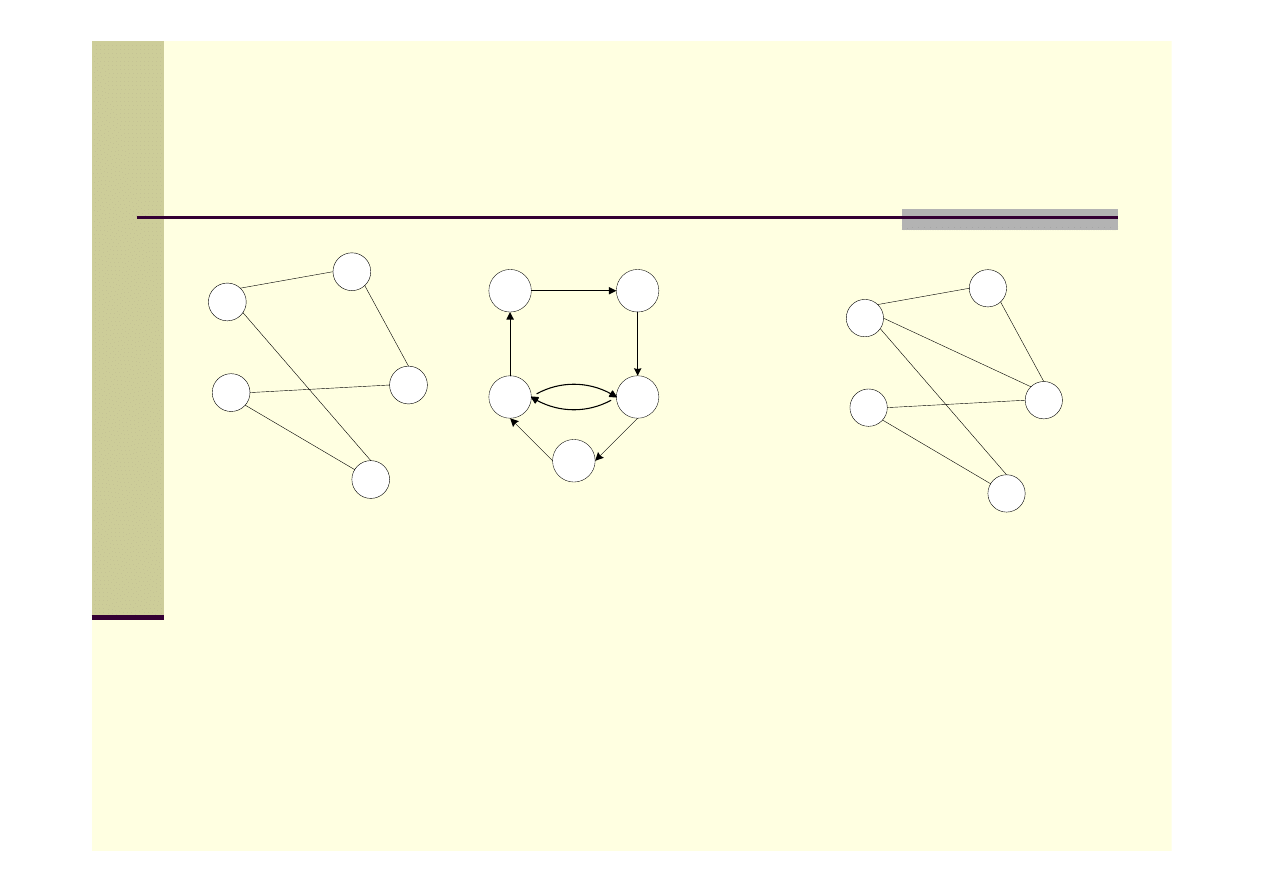
Cykl Eulera c.d.
1
5
3
4
2
1
5
3
4
2
1
3
2
4
5
Grafy z cyklem
Eulera
Graf bez cyklu
Eulera
Algorytm znajdujący cykl Eulera w grafie to algorytm Fleury’ego.

Algorytm Fleury’ego
Oznaczenia:
G = (V, E) – graf nieskierowany
V(G) – zbiór wierzchołków
C – ciąg zawierający kolejne wierzchołki grafu, tak aby tworzyły one
cykl Eulera
m – liczba krawędzi
Krawędź incydentna: jeśli (u,v) jest krawędzią grafu nieskierowanego
G=(V,E), to (u,v) jest incydentna z wierzchołkami u i v.
Stopień wierzchołka: stopniem wierzchołka w grafie nieskierowanym jest
liczba incydentnych z nim krawędzi.
Most: mostem w grafie G jest każda krawędź, której usunięcie rozspójnia
graf.

Algorytm Fleury’ego – c.d.
( )
( , ),
Fleury G
C
v
dowolny wierzcholek z V[G]
w grafie krawędzie incydentne z v
wybierz dowolną krawędź v w
wybierajać krawędzie będące mostami jedynie w ostat
← ∅
←
∃
while
do
\ ( , )
( , )
ecznosci
v
w
G G u v
C C
u v
ciąg C zawiera wszystkie krawędzie grafu G
zostala wyznaczona w nim droga Eulera
droga nie zostala wyznaczona
←
=
= ∪
if
then
else
Złożoność obliczeniowa:
O(m
2
)
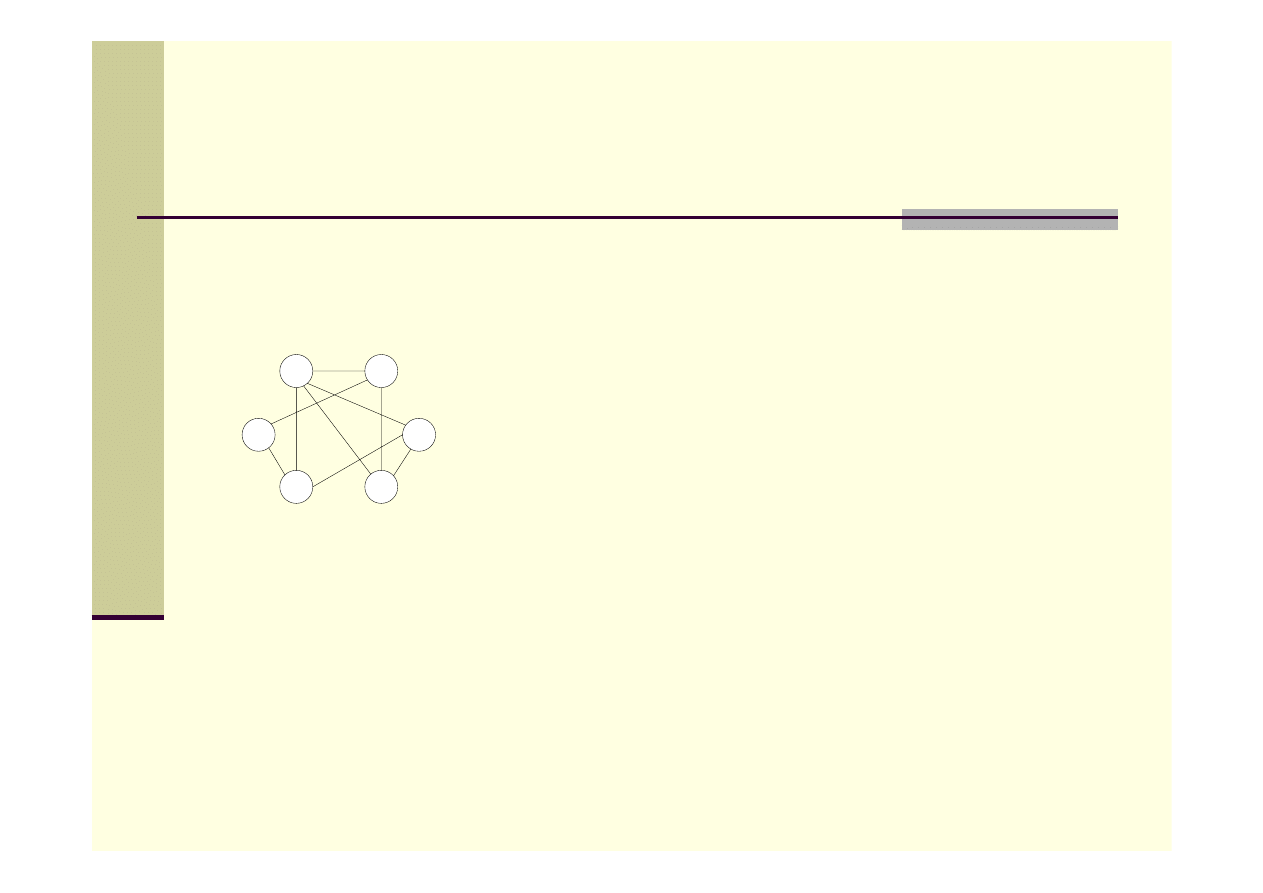
Cykl Hamiltona
Cykl Hamiltona to taki cykl w grafie, w którym każdy wierzchołek grafu
występuje dokładnie jeden raz.
Przykładowe cykle Hamiltona:
<1,2,6,5,3,4,1>
<1,5,6,2,4,3,1>
1
6
3
4
2
5
Nie istnieje żaden algorytm rozwiązujący ten problem w czasie
wielomianowym. Algorytmy znajdujące cykl Hamiltona należą do klasy
NP-zupełnych.
Stosuje się często algorytmy genetyczne, heurystyczne lub algorytmy
przybliżone, które nie wymagają rozważenia dużej liczby przypadków,
ale nie zawsze zwracają też rozwiązanie optymalne.
Cykl Hamiltona – c.d.
Znalezienie cyklu Hamiltona o minimalnej sumie wag krawędzi jest
równoważne rozwiązaniu problemu komiwojażera (TSP).
Stosowane rozwiązania:
Wyznaczenie minimalnego drzewa rozpinającego (alg. Kruskala oraz
Prima) i przeglądnięcie go metodą preorder
Algorytmy genetyczne
Algorytm Nearest Neighbour for TSP
Algorytm Greedy TSP

Nearest Neighbour for TSP
Oznaczenia:
G = (V, E) – graf pełny nieskierowany
V(G) – zbiór wierzchołków
Π – permutacja miast
a
j,k
– koszt przejazdu z miasta j do miasta k
n – liczba wierzchołków (miast)
Nearest Neighbour for TSP( )
(1)
(i-1),k
G
dowolne miasto
i = 2 do n
(i)
min{a
: k {V(G)\ { (1),... (i - 1}}}
π
π
π
π
π
←
←
∈
for
do
Złożoność obliczeniowa: O(n
2
)

Greedy TSP
Oznaczenia:
G = (V, E) – graf pełny nieskierowany
E(G) – zbiór krawędzi
Π – permutacja krawędzi
e
i
– krawędź
m – liczba krawędzi (połączeń między miastami)
Złożoność obliczeniowa: O(mlog(m))
Greedy TSP( )
i
G
posortuj krawędzie z E niemalejąco względem kosztów
i = 1 do m
(i)
e jeżeli dolaczenie krawędzi nie stworzy podcyklu
π
←
for
do

Wyszukiwanie najkrótszej ścieżki w grafie

Algorytm Dijkstry
Algorytm służy do rozwiązywania problemu najkrótszych ścieżek z
jednym źródłem w Grafie. Wagi są nieujemne – np. mogą
reprezentować odległości między miastami.
Użyte symbole:
G = (V, E) – graf ważony skierowany
w(u,v) ≥ 0 dla każdej krawędzi grafu G (wagi są nieujemne)
s – wierzchołek startowy
S – zbiór zawierający wierzchołki, dla których wagi najkrótszych
ścieżek ze źródła s zostały już obliczone
Q – kolejka priorytetowa (kluczami są aktualne odległości od s),
Q = V – S
Adj [u] – następniki wierzchołka u

Algorytm Dijkstry c.d.
Złożoność obliczeniowa -
( , , )
[ ]
MIN(Q)
{ }
każdy wierzcholek
[ ]
RELAKSACJA(u, v, w)
Dijkstra G w s
S
Q
V G
Q
u
S
S
u
v Adj u
← ∅
←
≠ ∅
←
← ∪
∈
while
do
for
do
2
(
)
O V

Algorytm Dijkstry c.d.
Relaksacja krawędzi (u,v) polega na sprawdzeniu, czy przechodząc
przez wierzchołek u, można znaleźć krótszą od dotychczas najkrótszej
ścieżki do v. Procedura relaksacji wygląda następująco:
Gdzie: - dotychczas najkrótsza ścieżka od źródła do v
- poprzednik v
( , , )
[ ]
[ ]
( , )
[ ]
[ ]
( , )
[ ]
RELAKS u v w
d v
d u
w u v
d v
d u
w u v
v
u
π
>
+
←
+
←
if
then
[ ]
d v
[ ]
v
π

Algorytm Dijkstry c.d.
W algorytmie Dijkstry pamiętany jest zbiór S zawierający te wierzchołki,
dla których wagi najkrótszych ścieżek ze źródła s zostały już obliczone.
Algorytm polega na wielokrotnym powtarzaniu operacji:
Wybraniu wierzchołka o najmniejszym oszacowaniu wagi najkrótszej
ścieżki od zbioru S
Dodaniu tego wierzchołka do S
Wykonaniu przeliczenia oszacowań z uwzględnieniem nowo dodanego
wierzchołka – tzw. Relaksacja problemu.
W poniższym przykładzie wierzchołki czarne należą do zbioru S.
Czerwone krawędzie pokazują oszacowania dróg.
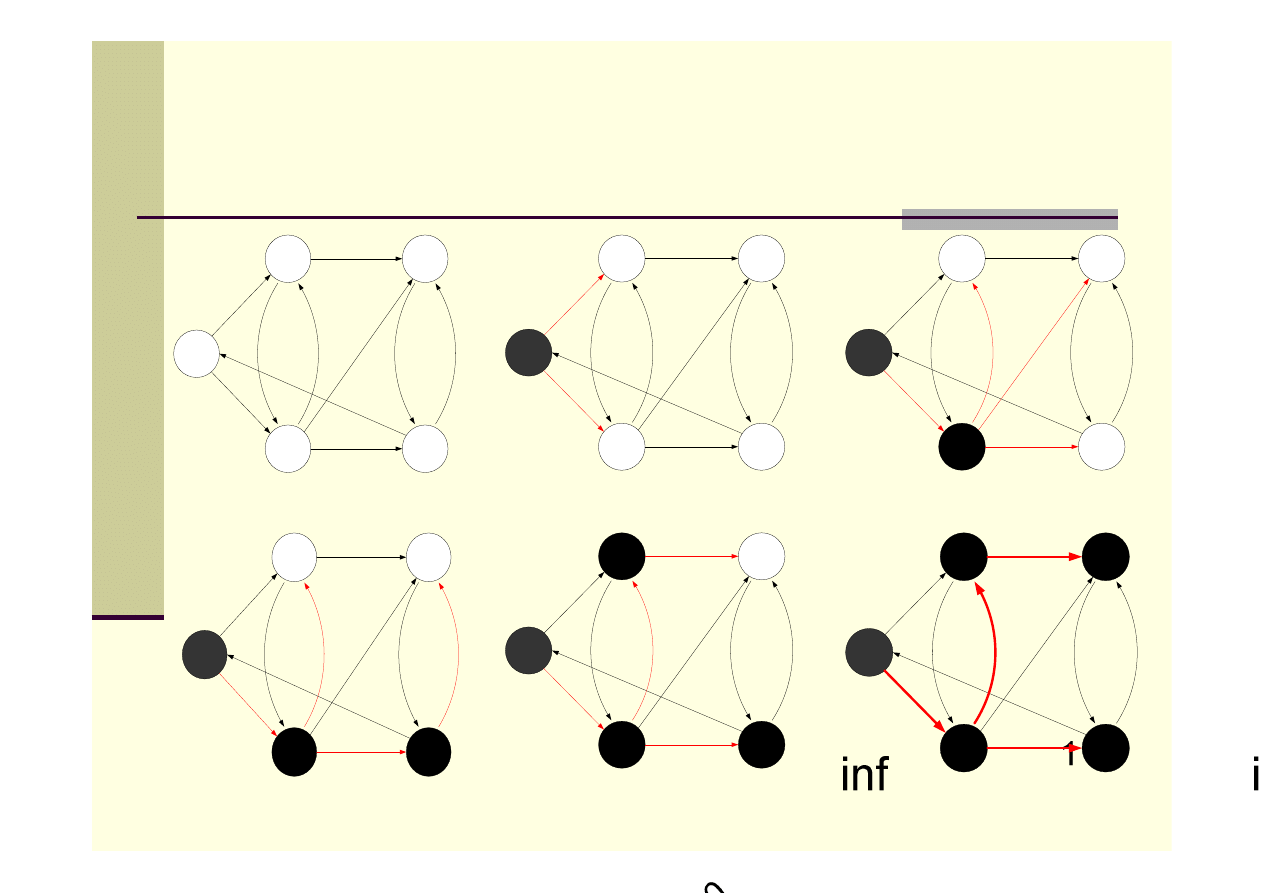
Algorytm Dijkstry - przykład

Algorytm Bellmana-Forda
Algorytm służy do rozwiązywania problemu najkrótszych ścieżek z
jednego źródła w ogólnym przypadku, gdzie wagi mogą być ujemne (
w(u,v) ).
Algorytm zwraca wartość FALSE, jeśli w grafie istnieje cykl o ujemnej
wadze osiągalny ze źródła.
W przeciwnym wypadku oblicza najkrótsze ścieżki i ich wagi.
Użyte symbole:
oznaczenia jak w algorytmie Dijkstry
∈

Algorytm Bellmana-Forda c.d.
Interpretacja:
Wagi pomiędzy wierzchołkami można traktować np. jako koszt
przejazdu między dwoma miastami.
Wagę ujemną traktujemy jako zwrot kosztów podróży.
W takim przypadku istnieje niebezpieczeństwo powstania cyklu
zamkniętego, po którym podróż dawałaby nieskończone zyski.
Oczywiście w rzeczywistym przypadku taka sytuacja nie jest możliwa.
Z tego powodu algorytm wykrywa te cykle i zwraca wartość FALSE.
Algorytm Bellmana-Forda c.d.
Złożoność obliczeniowa -
( , , )
1
[ ] 1
każda krawędź ( , )
[ ]
RELAKSACJA( , , )
każda krawędź ( , )
[ ]
[ ]
[ ]
( , )
FALSE
TRUE
Bellman Ford G w s
i
V G
u v
E G
u v w
u v
E G
d v
d u
w u v
−
←
−
∈
∈
>
+
for
to
do for
do
for
do if
then return
return
(
)
O VE

Algorytm Bellmana-Forda c.d.
Podobnie jak w algorytmie Dijkstry, w algorytmie Bellmana-Forda
wykorzystuje się metodę relaksacji, zmniejszając stopniowo
oszacowanie d[v] na wagę najkrótszej ścieżki ze źródła s do każdego
wierzchołka, aż zostanie osiągnięta rzeczywista waga najkrótszej
ścieżki.
W poniższym przykładzie czerwone krawędzie oznaczają tymczasowe,
„najlepsze” krawędzie do wierzchołków od źródła. Wartości w
wierzchołkach to aktualne oszacowania najkrótszej drogi.
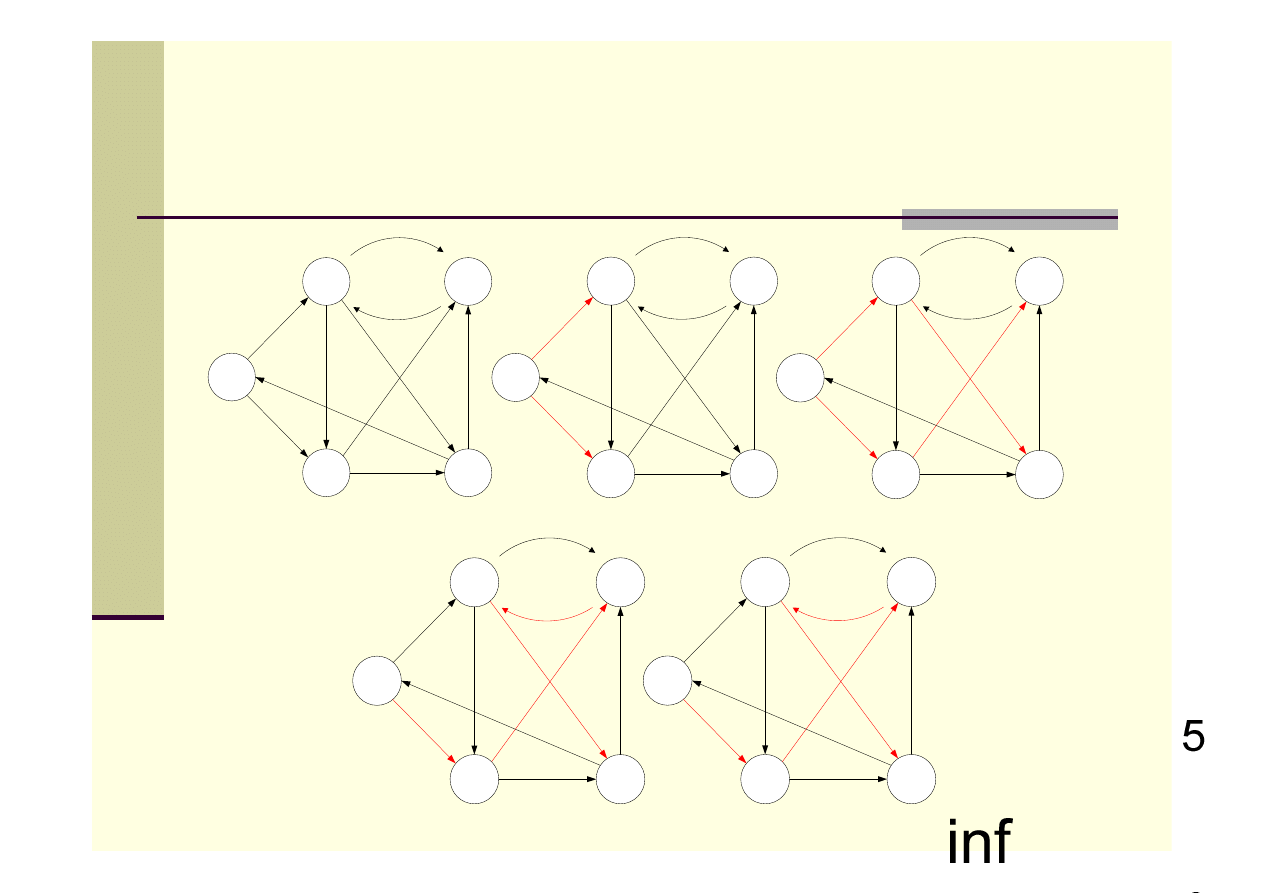
Algorytm Bellmana-Forda - przykład

Algorytm Floyda-Warshalla
Algorytm znajduje najkrótsze ścieżki między wszystkimi parami
wierzchołków skierowanych w grafie skierowanym G = (V,E).
Zakłada się, że wagi mogą być ujemne, ale brak jest cykli z wagami
ujemnymi.
Algorytm wylicza rekurencyjnie macierz najkrótszych ścieżek .
Użyte symbole:
waga najkrótszej ścieżki z wierzchołka i do j, której wszystkie
wewnętrzne wierzchołki należą do zbioru {1,2, …, k}
W – macierz sąsiedztwa, gdzie:
( )
n
D
( )
n
ij
d
(
)
0,
jeżeli
( , ), jeżeli
i ( , )
jeżeli
i ( , )
ij
ij
W
w
i
j
w
waga krawędzi i j
i
j i j
E
i
j i j
E
=
=
=
≠
∈
∞
≠
∉

Algorytm Floyda-Warshalla c.d.
Do konstruowania najkrótszej ścieżki buduje się macierz poprzedników :
(0)
( )
(
1)
(
1)
(
1)
( )
( )
1
1
1
min(
,
)
k
k
k
k
ij
ij
ik
kj
n
Floyd Warshall W
n
rozmiar grafu
D
W
k
n
i
n
j
n
d
d
d
d
D
−
−
−
−
←
←
←
←
←
←
+
for
to
do for
to
do for
to
return
∏
(0)
(
1)
( )
(
1)
(
1)
( )
(
1)
( )
(
1)
(
1)
,
jeżeli
lub
,
jeżeli
lub
jeżeli
jeżeli
ij
ij
ij
k
k
k
k
ij
ij
ik
kj
k
ij
k
k
k
k
kj
ij
ik
kj
NIL
i
j
w
i
i
j
w
π
π
π
π
π
π
π
π
π
π
−
−
−
−
−
−
=
= ∞
=
≠
< ∞
≤
+
=
>
+
Algorytm Floyda-Warshalla c.d.
Działanie algorytmu polega na badaniu w każdej iteracji czy
dołożenie wierzchołka k do ścieżki między każdymi dwoma
wierzchołkami nie polepszy oszacowania odległości między nimi.
Jeśli tak, oszacowanie jest zmniejszane.
( )
k
ij
d
( )
k
ij
d
(
1)
k
ik
d
−
(
1)
k
kj
d
−
Algorytm Floyda-Warshalla - przykład
(0)
(0)
(1)
(1)
0
3
8
4
1
1
1
0
1
7
2
2
4
0
3
2
5 0
4
4
6
0
5
0
3
8
4
1
1
1
0
1
7
2
2
4
0
2
5
5 0
2
6
0
NIL
NIL
NIL NIL NIL
D
NIL
NIL NIL NIL
NIL
NIL NIL
NIL NIL NIL
NIL
NIL
NIL
NIL NIL NIL
D
∞ −
∞
∞
=
∏ =
∞
∞ ∞
∞ −
∞
∞ ∞ ∞
∞ −
∞
∞
=
∏ =
∞
∞ ∞
−
−
∞ ∞ ∞
3
4
1
4
1
5
NIL
NIL NIL NIL
NIL
NIL NIL NIL
NIL
(2)
(2)
(3)
(3)
0
3
8
4
4
1
1
2
1
0
1
7
2
2
4
0
5 11
3
2
2
2
5
5 0
2
4
1
4
1
6
0
5
0
3
8
4
4
1
1
2
1
0
1
7
2
2
4
0
5 11
3
2
2
1
5 0
2
6
0
NIL
NIL NIL NIL
D
NIL
NIL
NIL
NIL NIL NIL
NIL
NIL
NIL NIL NIL
D
NIL
NIL
−
∞
∞
=
∏ =
∞
−
−
∞ ∞ ∞
−
∞
∞
=
∏ =
∞
−
−
−
∞ ∞ ∞
(4)
(4)
(5)
2
4
3
4
1
5
0
3
1 4
4
1
4
2
1
3
0
4 1
1
4
4
2
1
7
4
0
5
3
4
3
2
1
2
1
5 0
2
4
3
4
1
8
5
1
6
0
4
3
4
5
0
1
3 2
4
3
0
4 1
1
7
4
0
5
3
2
1
5 0
2
8
5
1
6
0
NIL
NIL NIL NIL
NIL
NIL
NIL
D
NIL
NIL
NIL
D
−
−
−
−
=
∏ =
−
−
−
−
−
−
−
=
∏
−
−
−
(5)
3
4
5
1
4
4
2
1
4
3
2
1
4
3
4
1
4
3
4
5
NIL
NIL
NIL
NIL
NIL
=
Algorytm Floyda-Warshalla - przykład
(5)
(5)
0
1
3 2
4
3
4
5
1
3
0
4 1
1
4
4
2
1
7
4
0
5
3
4
3
2
1
2
1
5 0
2
4
3
4
1
8
5
1
6
0
4
3
4
5
NIL
NIL
D
NIL
NIL
NIL
−
−
−
−
=
∏ =
−
−
−
Np.:
Koszt ścieżki z 1 do 3: -3.
Ścieżka: 1->5->4->3

Drzewa rozpinające

Drzewa rozpinające
Drzewem rozpinającym grafu G nazywamy drzewo, które zawiera
wszystkie wierzchołki grafu G, zaś zbiór krawędzi drzewa jest podzbiorem
zbioru krawędzi grafu.
Minimalnym drzewem rozpinającym nazywamy drzewo rozpinające, dla
którego suma wag krawędzi jest najmniejsza z możliwych.

Drzewa rozpinające – c.d.
Zastosowania drzew rozpinających:
Znajdywanie optymalnych połączeń dla sieci telefonicznych,
wodociągów, energetycznych, komunikacyjnych etc.
Rozwiązywanie problemu komiwojażera
Do wyznaczania minimalnego drzewa rozpinającego służą algorytmy:
Kruskala
Prima

Algorytm Kruskala
Oznaczenia:
G = (V, E) – graf spójny nieskierowany
V(G) – zbiór wierzchołków
w: E → R – funkcja wagowa, gdzie w(u,v) ≥ 0 dla każdej krawędzi grafu
A – zbiór będący podzbiorem drzewa minimalnego
m – liczba krawędzi

Algorytm Kruskala – c.d.
Algorytm Kruskala – skrócony opis
1.
Dla każdego wierzchołka grafu tworzone jest drzewo jednostkowe
(zawierające tylko i wyłącznie dany wierzchołek).
2.
Wszystkie krawędzie są sortowane niemalejąco względem wag.
3.
W każdej iteracji do rozwiązania dodawana jest krawędź
o najmniejszej możliwej wadze, pod warunkiem, że nowy wierzchołek
nie był już wcześniej dodany do drzewa.
Sprawdzenie to odbywa się w instrukcji:
DRZEWO(u)≠DRZEWO(v)
Złożoność obliczeniowa: O(mlogm)

Algorytm Kruskala – c.d.
( , )
[ ]
_
_
( )
ę
ę
ż
ę ź ( , )
,
ą
Kruskal G w
A
każdy wierzcholek v V G
STWORZ DRZEWO 1 WIERZCHOLKOWE v
posortuj kraw dzie z E niemalejaco wzgl dem wag w
ka da kraw d u v
E w kolejnosci nie malej cych wag
← ∅
∈
−
∈
for
do
for
do ( )
( )
then
{( , )}
_
( , )
DRZEWO u
DRZEWO v
A
A
u v
ZŁĄCZENIE DRZEW u v
A
≠
← ∪
if
return
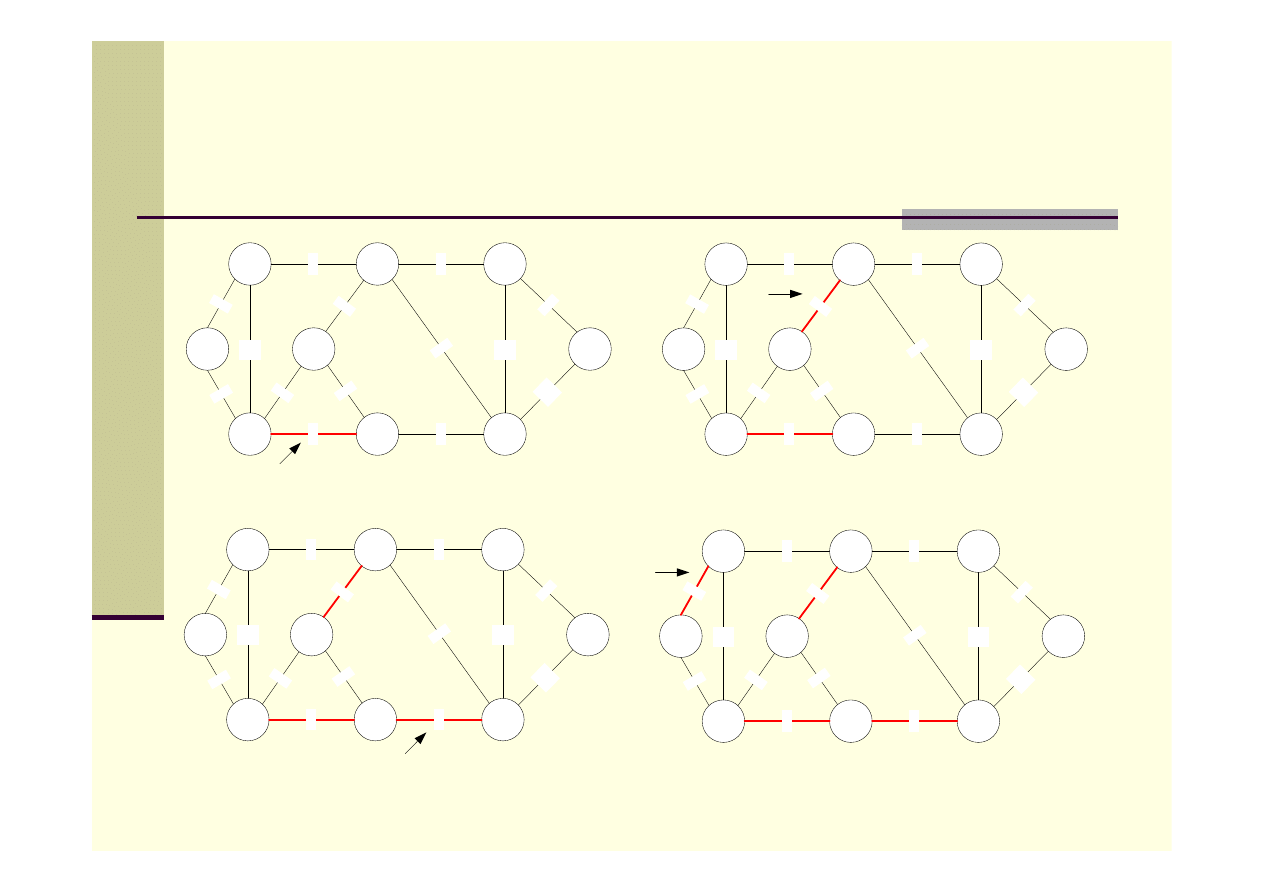
Algorytm Kruskala – przykład
a
h
b
i
g
e
f
d
c
7
1
2
2
6
4
9
10
7
8
1)
4
8
11
7
14
2
6
4
9
10
4
8
11
7
14
2
6
4
9
10
4
8
11
7
14
2
6
4
9
10
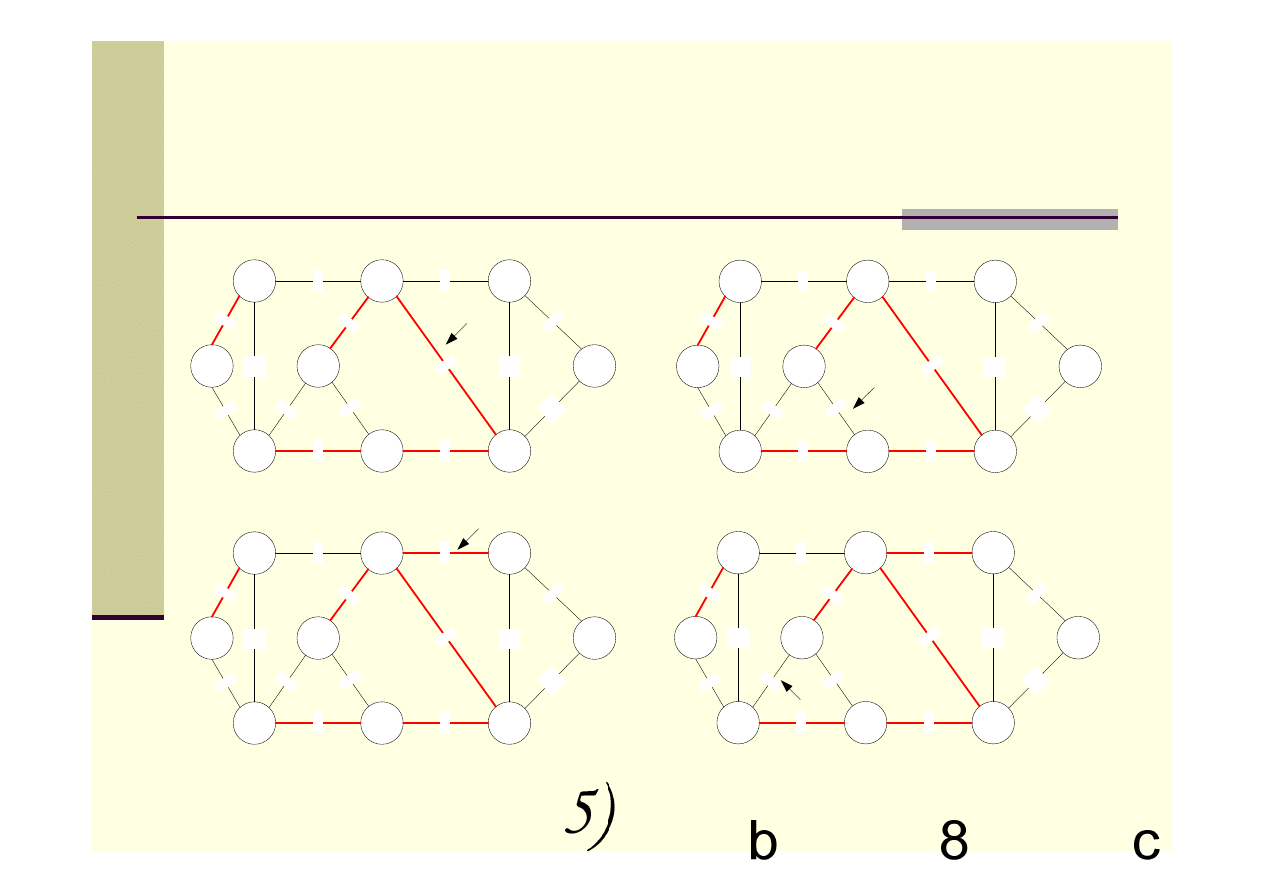
Algorytm Kruskala – przykład c.d.
4
8
11
7
14
2
6
4
9
10
4
8
11
7
14
2
6
4
9
10
4
8
11
7
14
2
6
4
9
10
4
8
11
7
14
2
6
4
9
10
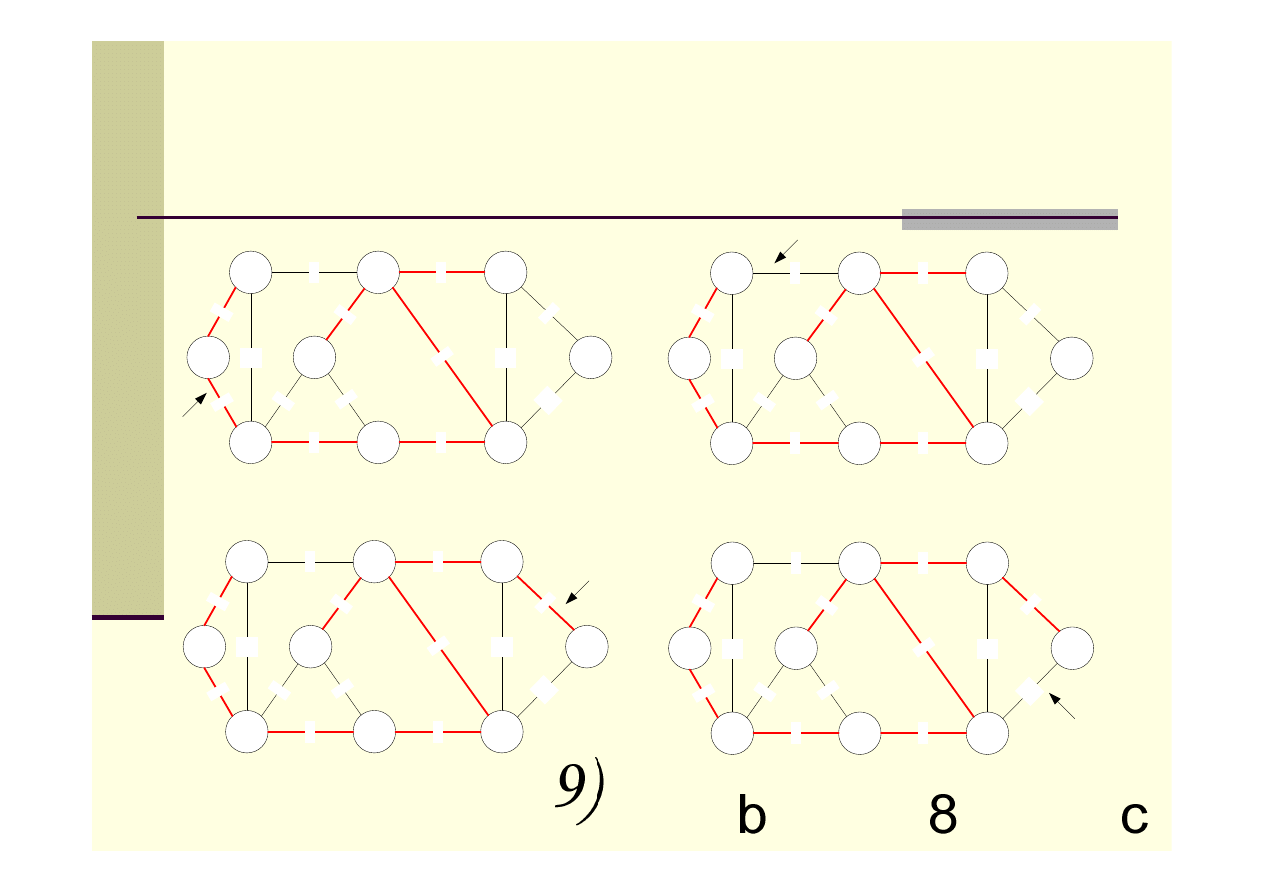
Algorytm Kruskala – przykład c.d.
4
8
11
7
14
2
6
4
9
10
a
h
b
i
g
e
f
d
c
4
8
11
7
1
2
14
2
6
4
9
10
7
8
10)
4
8
11
7
14
2
6
4
9
10
4
8
11
7
14
2
6
4
9
10
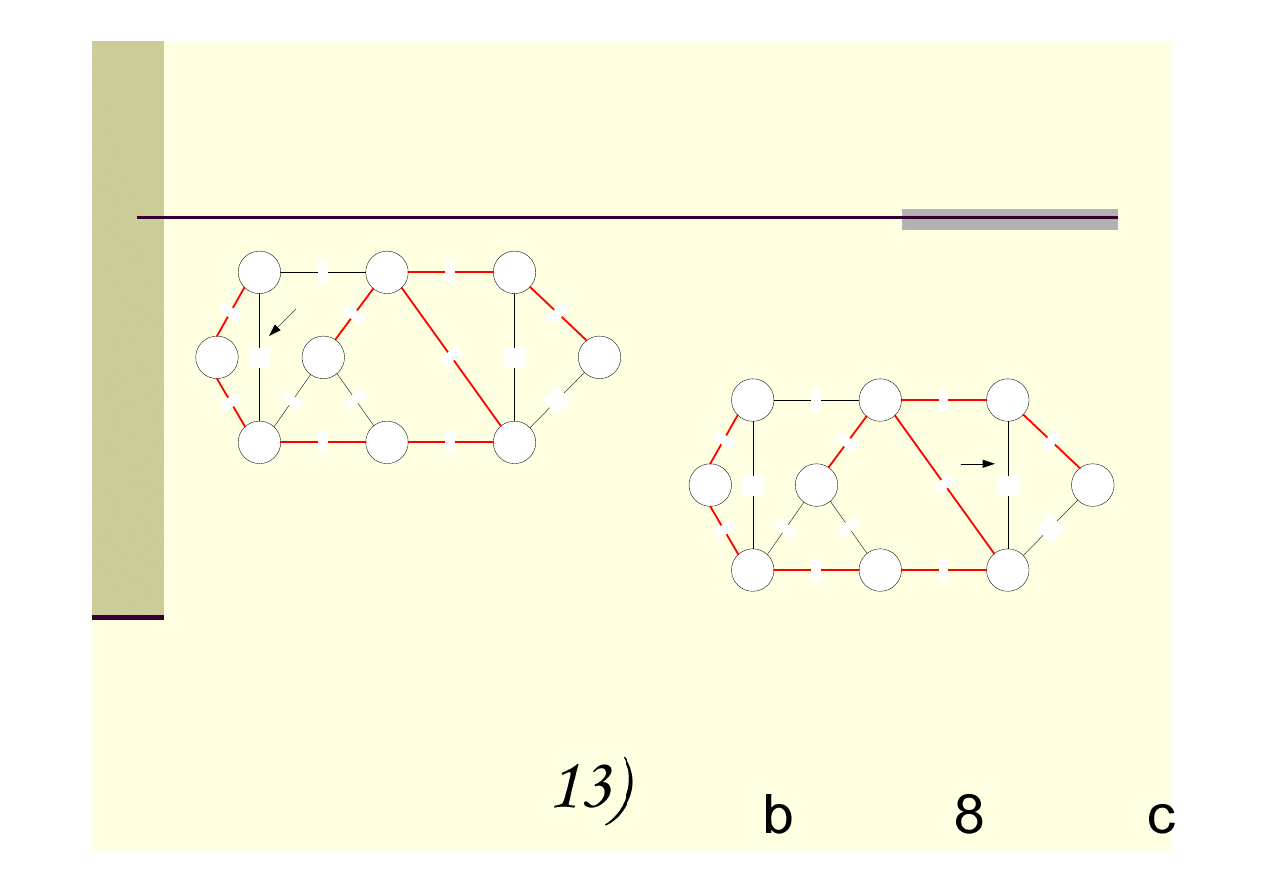
Algorytm Kruskala – przykład c.d.
4
8
11
7
14
2
6
4
9
10
4
8
11
7
14
2
6
4
9
10
Suma wag krawędzi dla minimalnego
drzewa rozpinającego wynosi 37.

Algorytm Prima
Oznaczenia:
G = (V, E) – graf spójny nieskierowany
w: E → R – funkcja wagowa, gdzie w(u,v) ≥ 0 dla każdej krawędzi grafu
V(G) – zbiór wierzchołków
r – wierzchołek startowy, korzeń
Q – kolejka priorytetowa (kluczem key[v] dla każdego wierzchołka v jest
minimalna waga spośród krawędzi łączących v z wierzchołkami
drzewa)
(V-Q) – zbiór zawierający wierzchołki budowanego drzewa
Π[v] – ojciec wierzchołka v
Adj [u] – sąsiedzi wierzchołka u
m – liczba krawędzi
n – liczba wierzchołków

Algorytm Prima – c.d.
Algorytm Prima – skrócony opis
1.
Inicjowanie kolejki priorytetowej (kluczem wierzchołka początkowego
r jest 0, pozostałych ∞, korzeń r nie ma ojca, więc Π(r)=NIL)
2.
W procedurze MIN(Q) zwracany jest wierzchołek o najmniejszej
wartości klucza key[i] oraz usuwany jest ze zbioru Q.
3.
Następnie aktualizowane są wartości pół key i Π, dla każdego
wierzchołka v spoza drzewa, który sąsiaduje z u.
Złożoność obliczeniowa: O(mlogn)

Algorytm Prima – c.d.
( , , )
[ ]
[ ]
[ ]
0
[ ]
( )
[ ]
( , )
[ ]
Prim G w r
Q
V G
każdy u Q
key u
key r
r
NIL
Q
u
MIN Q
każdy v Adj u
v Q i w u v
key v
π
←
∈
← ∞
←
←
≠ ∅
←
∈
∈
<
for
do
while
do
for
do if
the [ ]
[ ]
( , )
v
u
key v
w u v
π
←
←
n
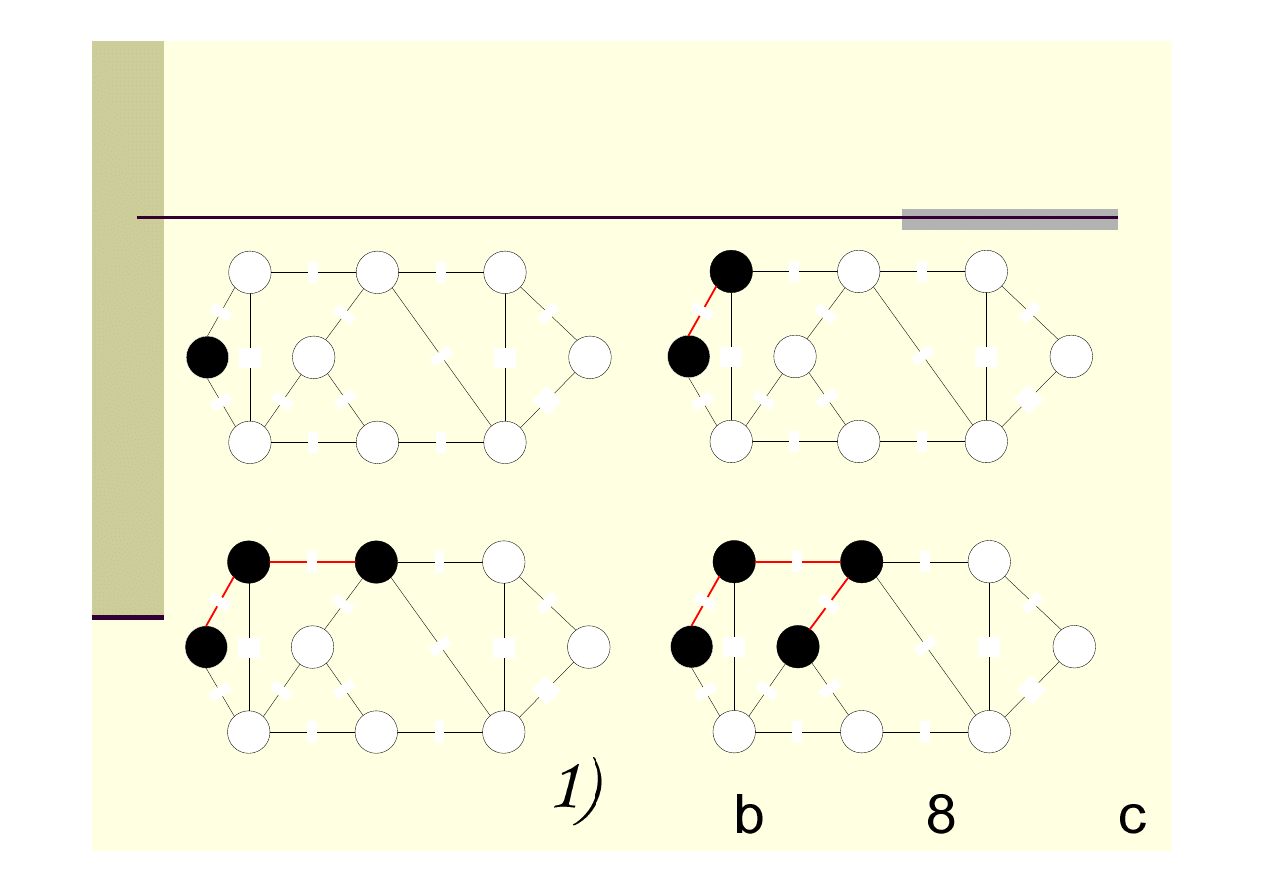
Algorytm Prima – przykład
4
8
11
7
14
2
6
4
9
10
4
8
11
7
14
2
6
4
9
10
4
8
11
7
14
2
6
4
9
10
4
8
11
7
14
2
6
4
9
10
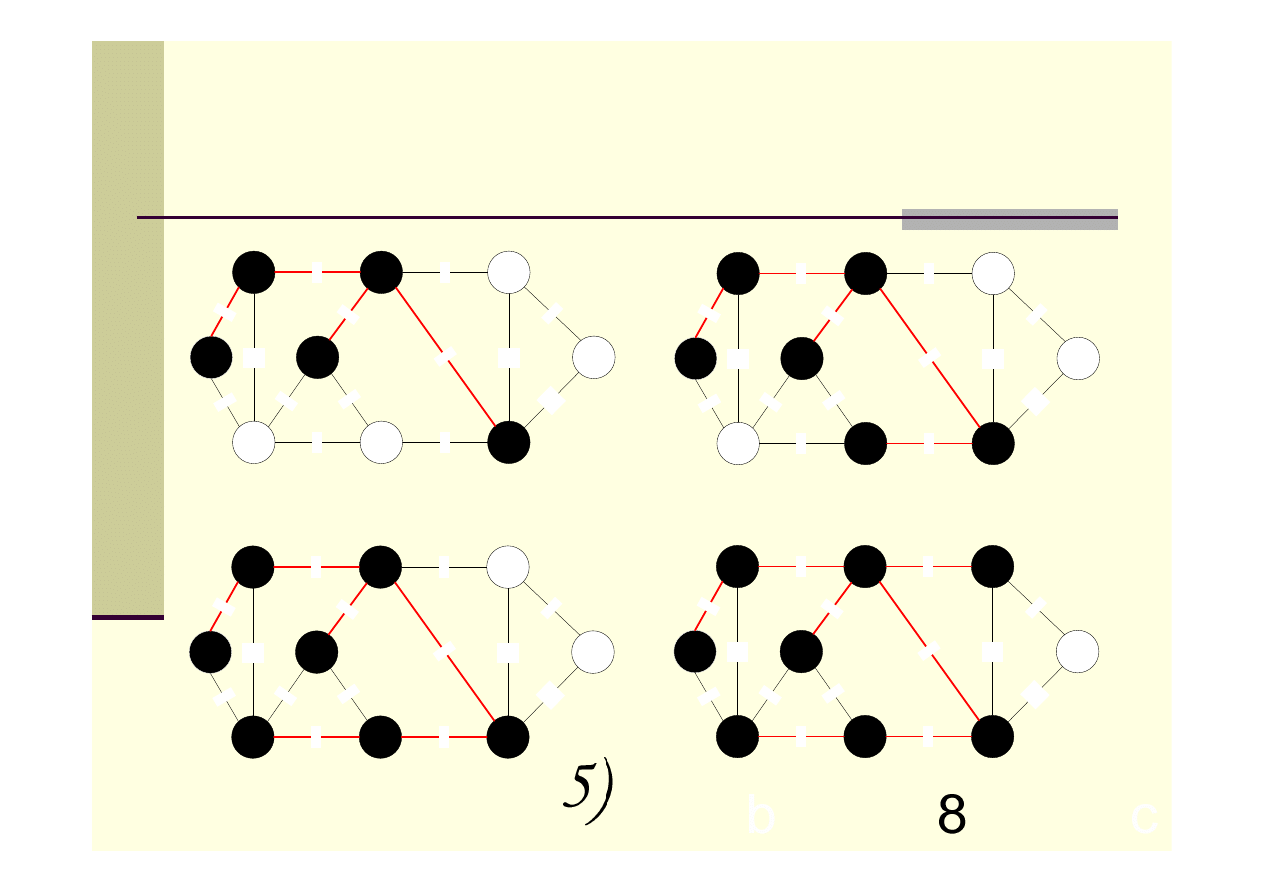
Algorytm Prima – przykład c.d.
4
8
11
7
14
2
6
4
9
10
4
8
11
7
14
2
6
4
9
10
4
8
11
7
14
2
6
4
9
10
4
8
11
7
14
2
6
4
9
10
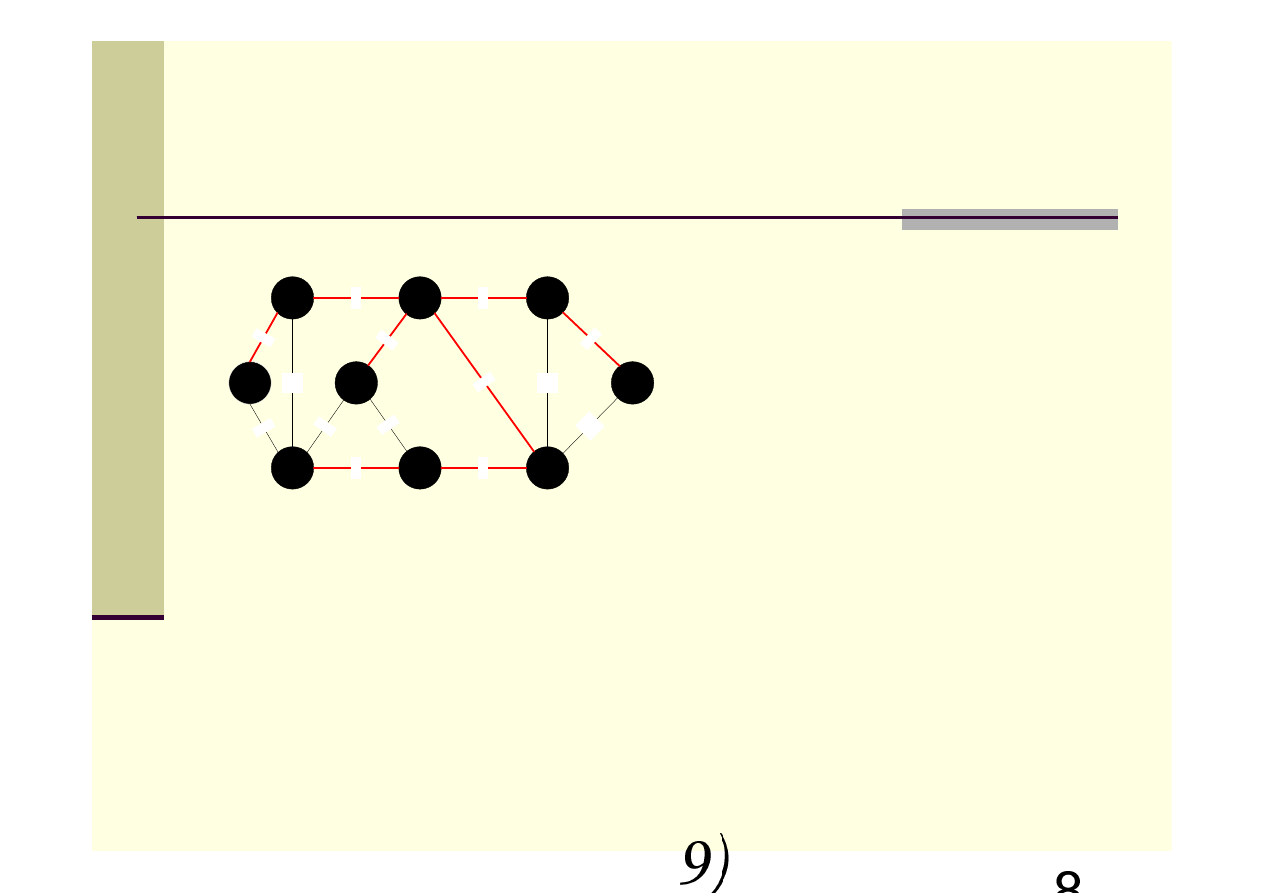
Algorytm Prima – przykład c.d.
4
8
11
7
14
2
6
4
9
10
Suma wag krawędzi dla minimalnego
drzewa rozpinającego wynosi 37.

Algorytmy przepływowe
Algorytmy przepływowe
Każdą krawędź skierowaną w grafie można interpretować jako kanał,
którym coś płynie (woda w rurociągu, prąd w przewodzie…).
Każdy kanał ma ustaloną przepustowość, wyznaczającą maksymalną
szybkość, z jaką następuje przepływ w tym kanale.
Musi być spełniona własność zachowania przepływu – szybkość
wpływania do wierzchołka musi być taka sama jak szybkość
wypływania.
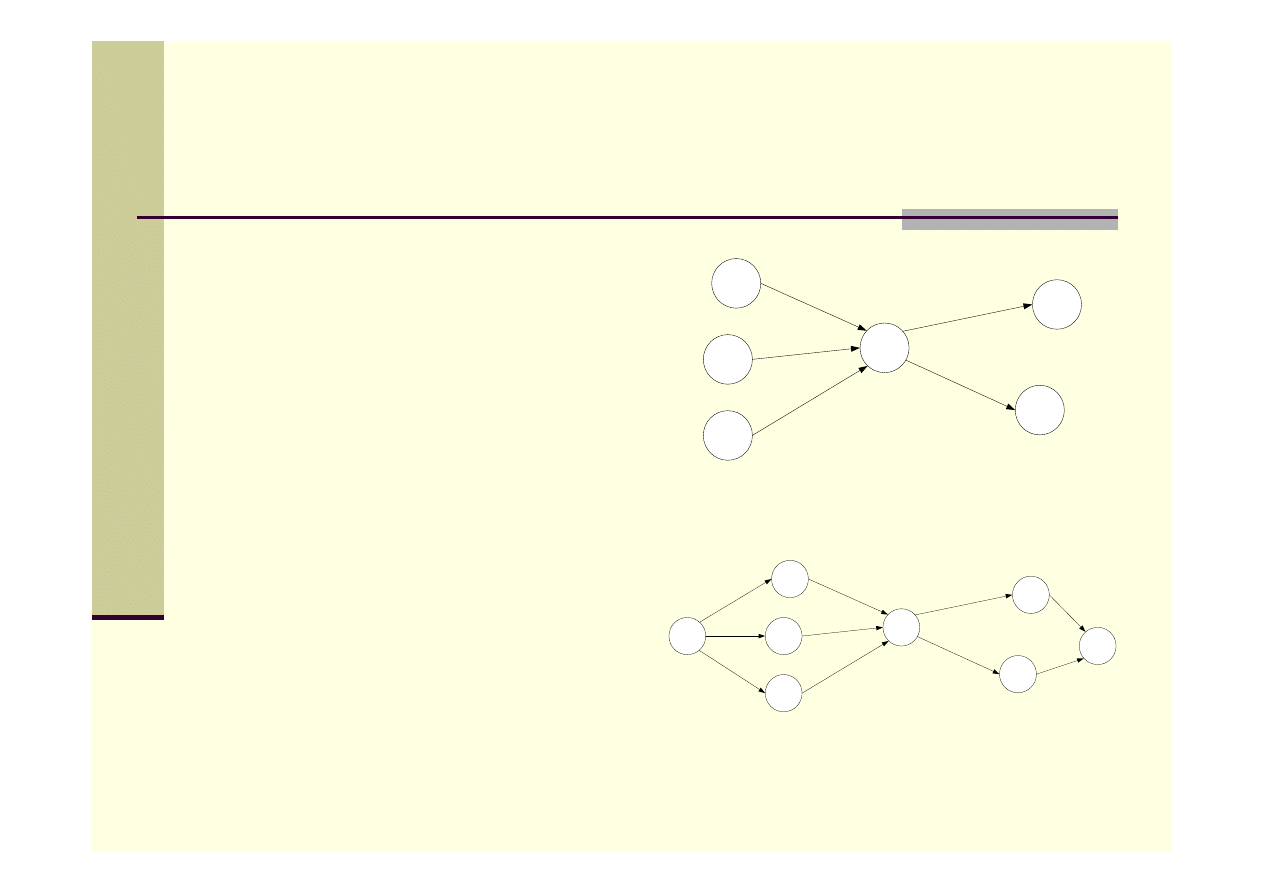
Algorytmy przepływowe c.d.
Sieci z wieloma źródłami i
ujściami
W celu ułatwienia problemu
wprowadza się superźródło
oraz superujście
∞
∞
∞
∞
∞

Metoda Forda-Fulkersona
Najczęściej spotykanym problemem jest problem maksymalnego
przepływu.
Metoda Forda-Fulkersona rozwiązuje ten problem.
Użyte pojęcia:
f(u,v) – wielkości przepływu między węzłami u i v
ścieżka powiększająca – jest to ścieżka ze źródła do ujścia, po której
możemy przesłać większy przepływ

Metoda Forda-Fulkersona c.d.
Ford- Fulkerson( , , )
inicjowanie na 0
istniejesciezka powiekszajaca
powieksz przeplyw wzdluz
G s t
f
p
f
p
f
while
do
return

Metoda Forda-Fulkersona c.d.
Praktyczny algorytm Forda-Fulkersona może wyglądać następująco:
Ford- Fulkerson( , , )
kazda krawedz ( , )
[ ]
[ , ]
0
[ , ]
0
istniejesciezka z do
( )
min{ ( , ) : ( , ) jest na }
kazda krawedz ( , ) na
[ , ]
[ , ]
( )
[ , ]
[ , ]
f
f
f
G s t
u v
E G
f u v
f v u
p s
t
c p
c u v
u v
p
u v
p
f u v
f u v
c p
f v u
f u v
∈
←
←
←
←
+
← −
for
do
while
do
for
do
Maksymalny przepływ określa całkowity wypływ z wierzchołka końcowego.
Złożoność obliczeniowa -
3
( )
O V

Metoda Forda-Fulkersona c.d.
W metodzie Forda-Fulkersona w każdej iteracji znajdujemy dowolną
ścieżkę powiększającą p i zwiększamy przepływ f wzdłuż p o
przepustowość residualną
. W następującej implementacji tej
metody obliczamy maksymalny przepływ w grafie G=(V,E), aktualizując
przepływ netto f[u,v] między każdą parą wierzchołków u,v połączonych
krawędzią w G.
Przepustowość residualną obliczamy ze wzoru:
( )
f
c p
( , )
( , )
( , )
f
c u v
c u v
f u v
=
−
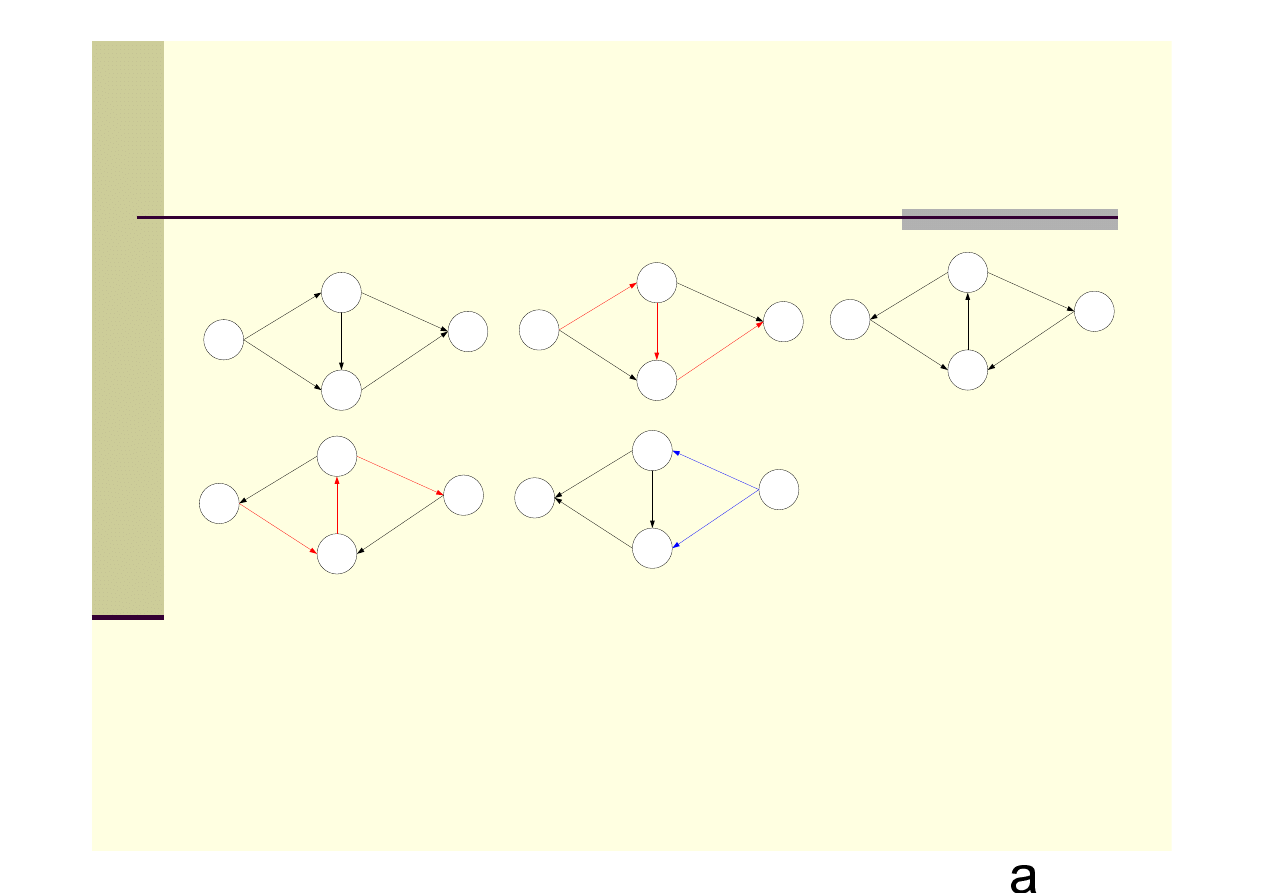
Metoda Forda-Fulkersona - przykład
Maksymalny przepływ wynosi 2.

Kolorowanie grafu
Kolorowanie grafu
Kolorowanie grafu to przyporządkowanie wierzchołkom grafu liczb
naturalnych w taki sposób, aby końce żadnej krawędzi nie miały
przypisanej tej samej liczby (koloru).
Optymalnym pokolorowaniem grafu nazywamy pokolorowanie
zawierające najmniejszą możliwą liczbę kolorów.
Liczbą chromatyczną grafu G nazywamy liczbę χ(G) równą minimalnej
liczbie kolorów wystarczającej do prawidłowego pokolorowania
wierzchołków grafu G.
Problem znalezienia optymalnego pokolorowania a także znalezienia
liczby chromatycznej jest NP zupełny.

Kolorowanie grafu - zastosowania
Ustalanie planów i harmonogramów zajęć
Przypisywanie częstotliwości w telefonach komórkowych
Ustalanie wartości wpisów w rejestrach komputera
Rozpoznawanie wzorców
Analiza danych w biologii i archeologii

Kolorowanie grafu – c.d.
Do kolorowania grafu służą następujące algorytmy:
Algorytm zachłanny
Algorytm DSATUR
Algorytm MAXIS

Algorytm zachłanny
Algorytm zachłanny - przechodząc kolejno wszystkie wierzchołki
grafu, kolorujemy każdy z nich najmniejszym możliwym kolorem, tzn.
takim, który dotychczas nie został użyty dla żadnego z sąsiadów
rozważanego wierzchołka.
G = (V, E) – graf
c(u) – funkcja kolorująca, przypisująca kolor do wierzchołka
Adj[u] – sąsiedztwo wierzchołka u
n – liczba wierzchołków
Greedy Algorithm( )
( ), ( )
( )
[ ]
\{ }
G
V
wybierz wierzcholek u V
u
c u c u
c v
v Adj u
V
V
u
≠ ∅
∈
←
≠
∀ ∈
←
while
do
Złożoność obliczeniowa:
O(m
2
)
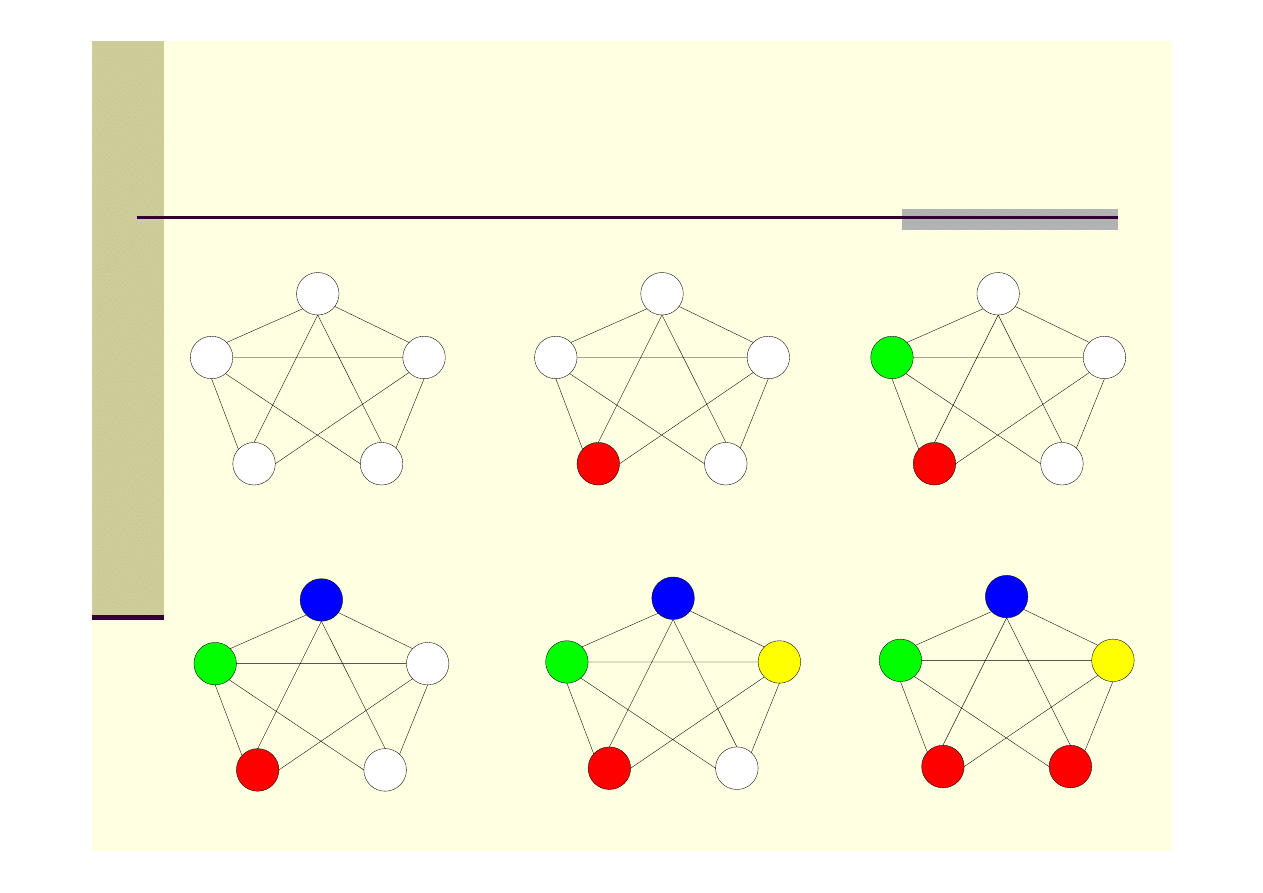
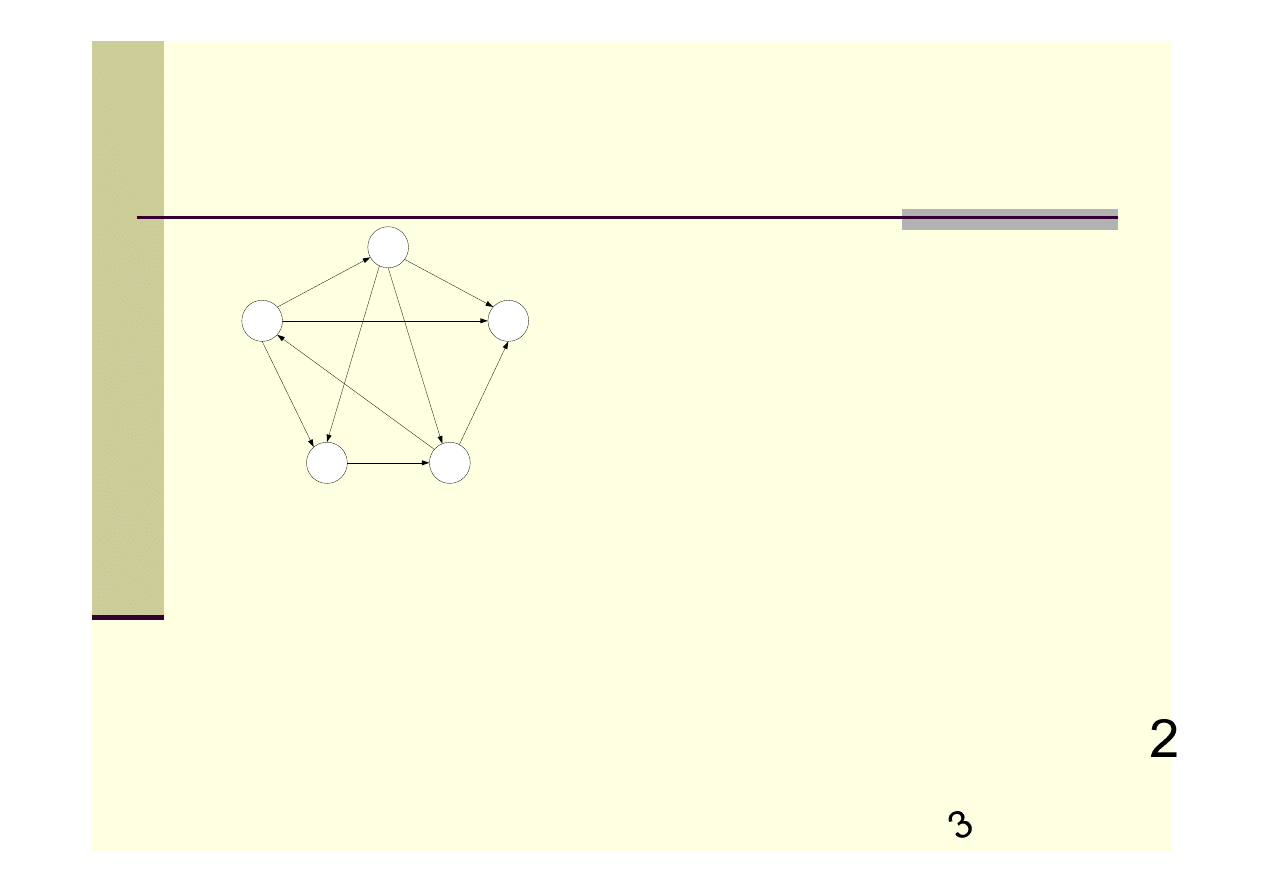
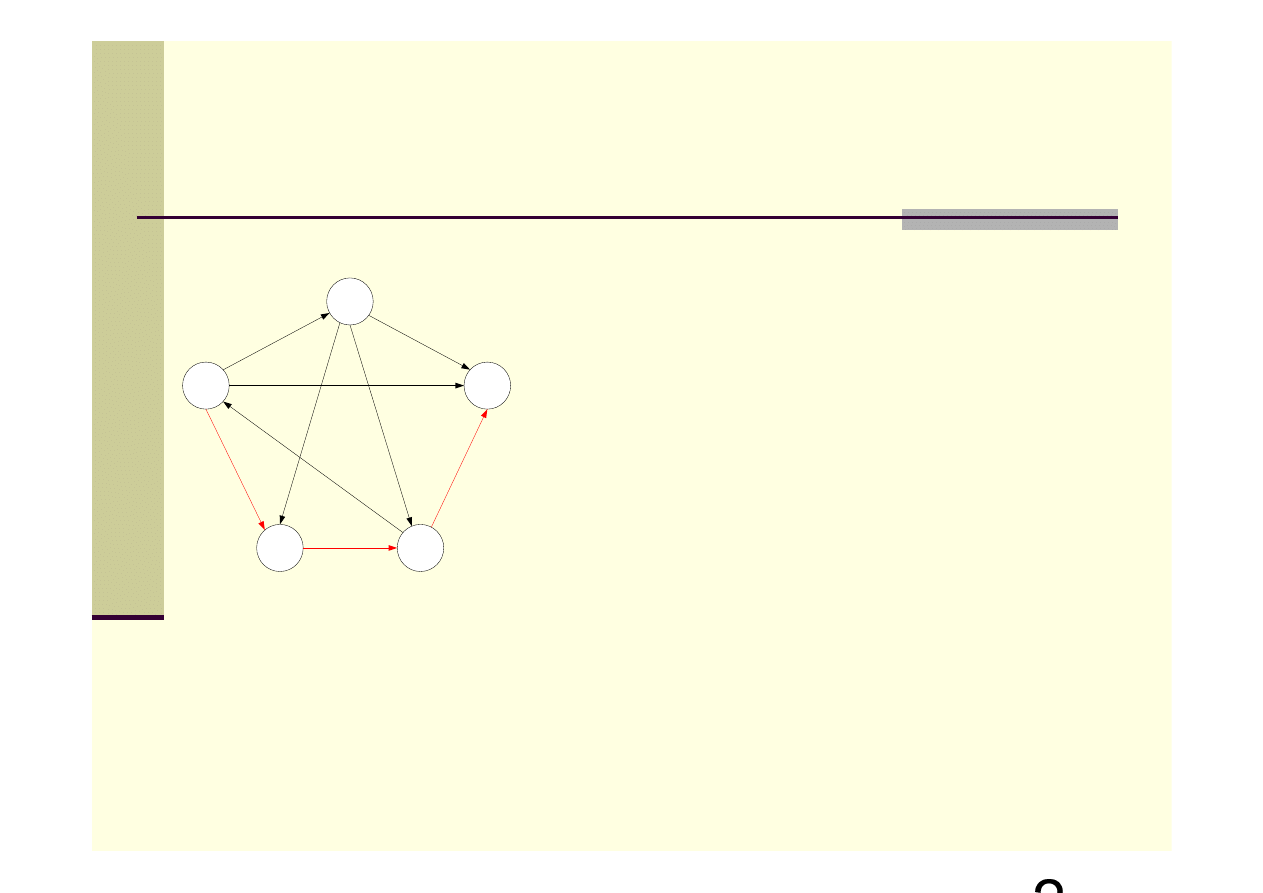
Algorytm zachłanny – przykład
3
2)
5
1
4
2
3
3)
5
1
4
2
3
1)
5
1
4
2
3
4)
5
1
4
2
3
5)
5
1
4
2
3
6)
5
1
4
2

Algorytmy DSATUR i MAXIS
Algorytm DSATUR działa podobnie jak algorytm zachłanny ale
kolejność rozpatrywania wierzchołków grafu wyznaczana jest
dynamicznie w zależności od liczby kolorów, które mogą być użyte do
pomalowania poszczególnych wierzchołków. Najpierw kolorowane są
te wierzchołki, dla których jest najmniej możliwości.
Algorytm MAXIS opiera się na algorytmie znajdującym największy
zbiór niezależny wśród wierzchołków danego grafu (żadne dwa
wierzchołki takiego zbioru nie sąsiadują ze sobą).

Algorytm MAXIS – c.d.
G = (V, E) – graf
MIS(U) – funkcja wyznaczająca najliczniejszy zbiór niezależny
MIN(U) – funkcja zwracająca wierzchołek o minimalnym stopniu
c(u) – funkcja kolorująca
( )
[ ]
0
1
( )
( )
\
Maxis G
U
V G
k
U
k
k
W
MIS U
każdy u W
c u
k
U
U W
←
←
≠ ∅
← +
←
∈
←
←
while
do
for
do
( )
'
'
( ')
{ }
'
'\{ } \{
' : ( , )
}
procedura MIS U
U
U
W
U
u
MIN U
W
W
u
U
U
u
v U
u v
E
W
←
← ∅
≠ ∅
←
←
∪
←
∈
∈
while
do
return
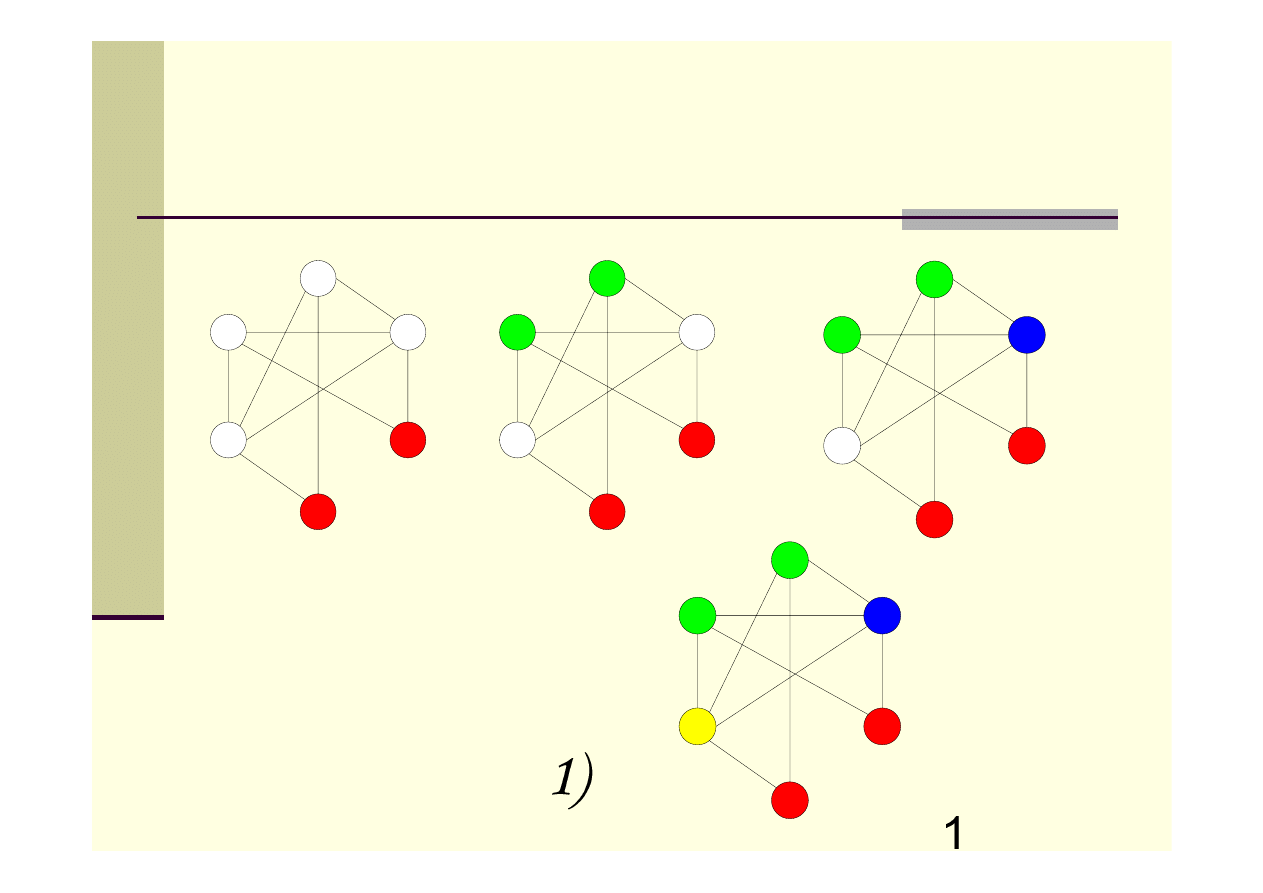
Algorytm MAXIS – przykład
1
2)
4
5
2
6
3
Kolorowanie grafu – c.d.
Kolorowanie grafów ma wiele odmian, m.in.:
Kolorowanie krawędzi – jest to przyporządkowywanie krawędziom liczb
naturalnych symbolizujących kolory
Listowe kolorowanie – kolorowanie wierzchołków, przy czym każdy wierzchołek
posiada odpowiadającą mu listę kolorów
Całkowite kolorowanie – kolorowanie wierzchołków oraz krawędzi
Harmoniczne kolorowanie – kolorowanie wierzchołków, gdzie każda para
kolorów użyta jest co najwyżej raz w stosunku do sąsiadującej pary
wierzchołków
Kompletne kolorowanie - kolorowanie wierzchołków, gdzie każda para kolorów
użyta jest co najmniej raz w stosunku do sąsiadującej pary wierzchołków
Dokładne kolorowanie - kolorowanie wierzchołków, gdzie każda para kolorów
użyta jest dokładnie raz w stosunku do sąsiadującej pary wierzchołków
Literatura
1.
Thomas H. Cormen, Charles E. Leiserson – Wprowadzenie do
algorytmów
2.
http://en.wikipedia.org/wiki/Main_Page
- Wikipedia, the free
encyclopedia
3.
http://www.algorytm.cad.pl
- Algorytmy i struktury danych
4.
http://mat.gsia.cmu.edu/COLOR/general/ccreview/node2.html
-
Sample applications of graph coloring
5.
http://www.cs.ualberta.ca/~joe/Coloring/Colorsrc/manual.html
- Graph
coloring
6.
J. Sikorski – Matematyka dyskretna – wykłady
7.
A. Drozdek i D. Simons – Struktury danych w języku C
8.
L.Banachowski, K. Diks i W. Rytter – Algorytmy i struktury danych
Wyszukiwarka
Podobne podstrony:
Algorytmy grafowe
4 algorytmy grafowe z przykladami
Algorytmy grafowe(1)
lichtenstein,Struktury danych i złożoność obliczeniowa,Badanie efektywności algorytmów grafowych w z
kozik,projektowanie algorytmów,TEORIA GRAFÓW
Układy Napędowe oraz algorytmy sterowania w bioprotezach
5 Algorytmy
5 Algorytmy wyznaczania dyskretnej transformaty Fouriera (CPS)
Tętniak aorty brzusznej algorytm
Ruciński A Teoria Grafów 1, wyklad6
Algorytmy rastrowe
Algorytmy genetyczne
Teorie algorytmow genetycznych prezentacja
Algorytmy tekstowe
Algorytmy i struktury danych Wykład 1 Reprezentacja informacji w komputerze
ALGORYTM EUKLIDESA
więcej podobnych podstron