Algorytmy grafowe

•Minimalne drzewa rozpinające

•Algorytm Kruskala
•Algorytm Prima

•Wyszukiwanie najkrótszych ścieżek z

jednym źródłem

•Algorytm Dijkstry
•Algorytm Bellmana-Forda

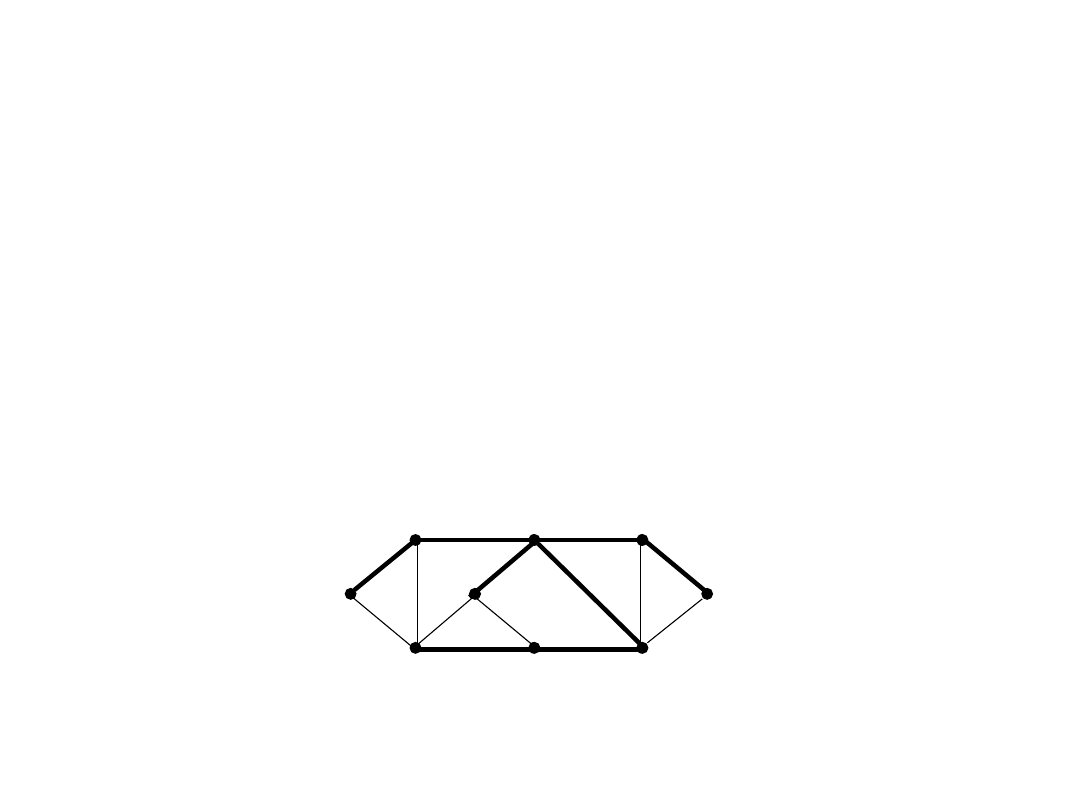
Minimalne drzewa

rozpinające

Podgraf T spójnego grafu G nazywa się jego
drzewem rozpinającym, jeśli T jest acykliczny i
łączy wszystkie wierzchołki G. Jeśli krawędziom
przypisane są wagi, i suma wag krawędzi T jest
minimalna, T nazywamy minimalnym drzewem
rozpinającym.

4

8

7

9

14

10

2

1

11

2

7

8

4

6

Przykład minimalnego drzewa
rozpinającego

Algorytm Kruskala

MST-Kruskal(G, w)
1 A := 
2 for każdy wierzchołek vV[G]
3

do Make-Set(v)

4 posortuj krawędzie z E niemalejąco względem wag w
5 for każda krawędź (u,v)  E, w kolejności niemalejących

wag

6

do if Find-Set(u)  Find-Set(v)

7

then A := A  {(u,v)}

8

Union(u,v)

9 return A

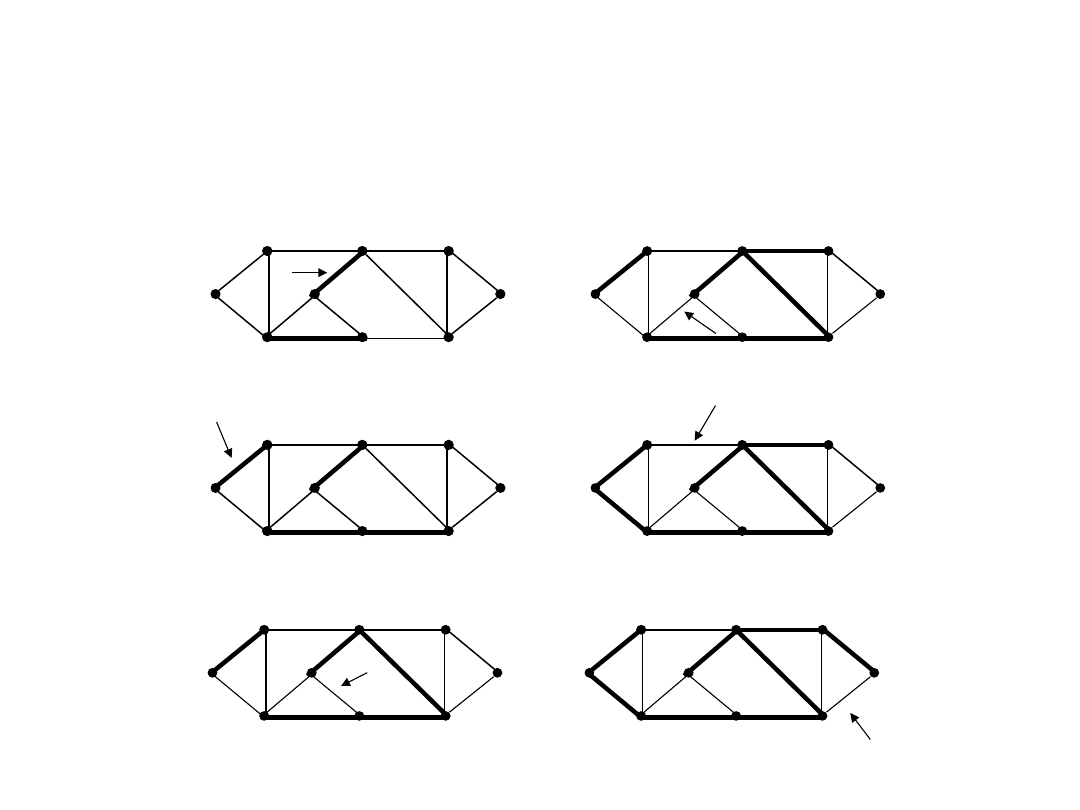
Algorytm Kruskala

(przykład)

4

8

7

9

14

10

2

1

1
1

2

7

8

4

6

4

8

7

9

14

10

2

1

1
1

2

7

8

4

6

4

8

7

9

14

10

2

1

1
1

2

7

8

4

6

4

8

7

9

14

10

2

1

1
1

2

7

8

4

6

2

1

4

8

7

9

10

1
1

2

7

8

4

6

4

8

7

9

14

10

2

1

1
1

2

7

8

4

6

Algorytm Prima

MST-Prim(G, w, r)
1 Q := V[G]
2 for każdy uQ
3

do key[u] := 

4 key[r] := 0
5



[r] := NIL

6 while Q  
7

do u := Extract-Min(Q)

8

for każdy v  Adj[u]

9

do if vQ i w(u,v) < key[v]

10

then



[v] := u

11

key[v] := w(u,v)

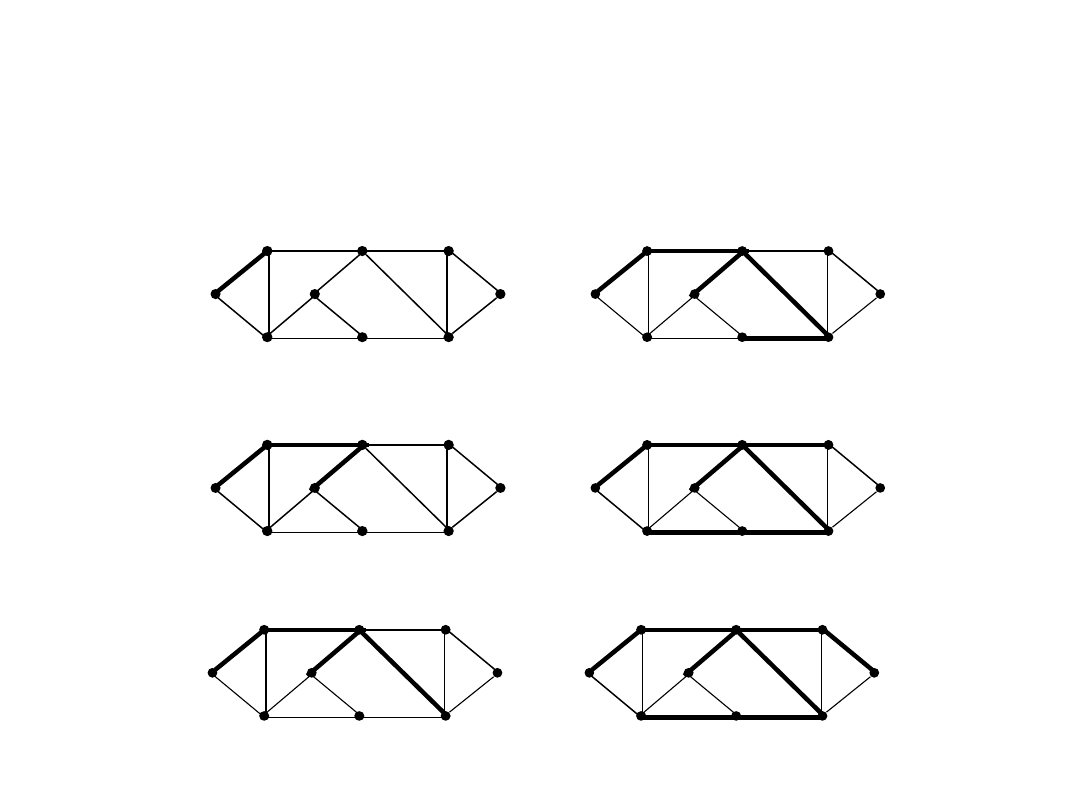
Algorytm Prima (przykład)

8

7

4

9

14

10

2

1

1
1

2

7

8

4

6

4

8

7

9

14

10

2

1

1
1

2

7

8

4

6

4

8

7

9

14

10

2

1

1
1

2

7

8

4

6

4

8

7

9

14

10

2

1

1
1

2

7

8

4

6

2

1

4

8

7

9

10

1
1

2

7

8

4

6

8

7

2

1

4

9

14

10

1
1

2

7

8

4

6

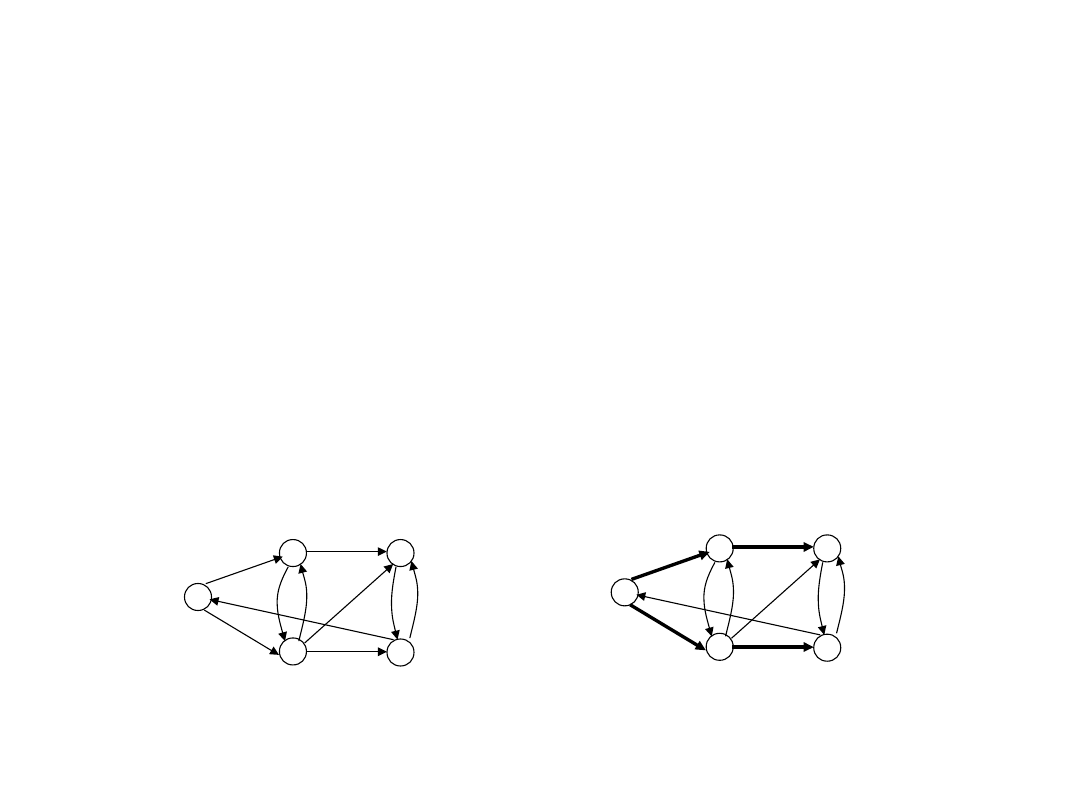
Najkrótsze ścieżki z

jednym źródłem

Dany jest ważony graf skierowany G=(V,E) i
wyróżniony wierzchołek sV, nazywany źródłem;

dla każdego wierzchołka vV należy znaleźć

najkrótszą ścieżkę z s do v. Wagą ścieżki jest
suma wag tworzących ją krawędzi. Najkrótszą
ścieżką jest ścieżka o najmniejszej wadze.

s

6

3

5

7

11

9

3

5

0

2

1

6

2

4

3

Ważony graf skierowany Drzewo najkrótszych ścieżek

s

6

3

5

7

9

3

5

0

2

1

6

2

4

3

1
1

Najkrótsze ścieżki z

jednym źródłem

d[v] - oszacowanie wagi najkrótszej ścieżki, [v] -

poprzednik v

Initialize-Single-Source(G, s)
1 for każdy wierzchołek vV[G]

2

do d[v] := 

3

[v] := NIL

4 d[s] := 0

Relaksacja krawędzi - ewentualne zmniejszenie

oszacowania wagi najkrótszej ścieżki d[v]

Relax(u, v, w)
1 if d[v] > d[u] + w(u, v)
2

then d[v] := d[u] + w(u, v)

3

[v] := u

Algorytm Dijkstry

Dijkstra(G, w, s)
1 Initialize-Single-Source(G, s)
2 S := 
3 Q := V[G]
4 while Q  
5

do u := Extract-Min(Q)

6

S := S  {u}

7

for każdy wierzchołek v  Adj[u]

8

do Relax(u, v, w)

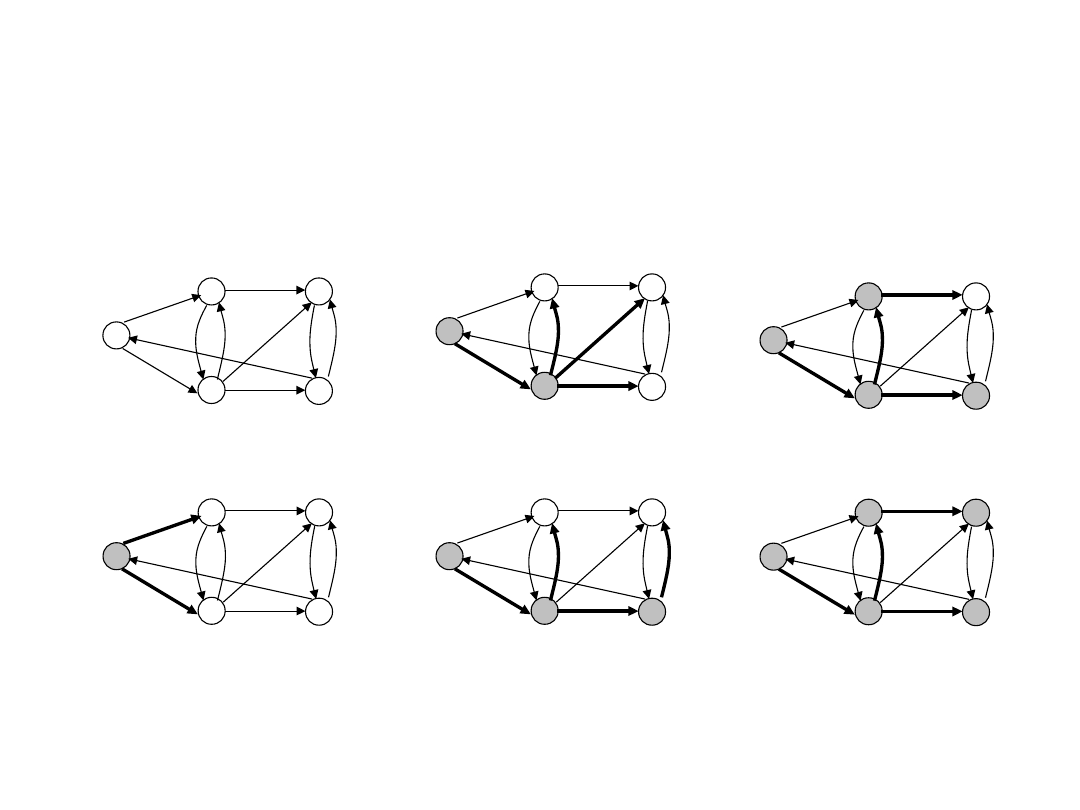
Algorytm Dijkstry

(przykład)

s

1

1
0

5

6









0

2

3

2

4

9

7

s

1

1
0

5

6





10

5

0

2

3

2

4

9

7

s

1

1
0

5

6

7

14

8

5

0

2

3

2

4

9

7

s

1

1
0

5

6

7

13

8

5

0

2

3

2

4

9

7

s

1

1
0

5

6

7

9

8

5

0

2

3

2

4

9

7

1

s

1
0

5

6

7

9

8

5

0

2

3

2

4

9

7

Algorytm Bellmana-Forda

Bellman-Ford(G, w, s)
1 Initialize-Single-Source(G, s)
2 for i = 1 to |V[G]| - 1
3

do for każda krawędź (u, v)  E[G]

4

do Relax(u, v, w)

5 for każda krawędź (u, v)  E[G]
6

do if d[v] > d[u] + w(u, v)

7

then return FALSE

8 return TRUE

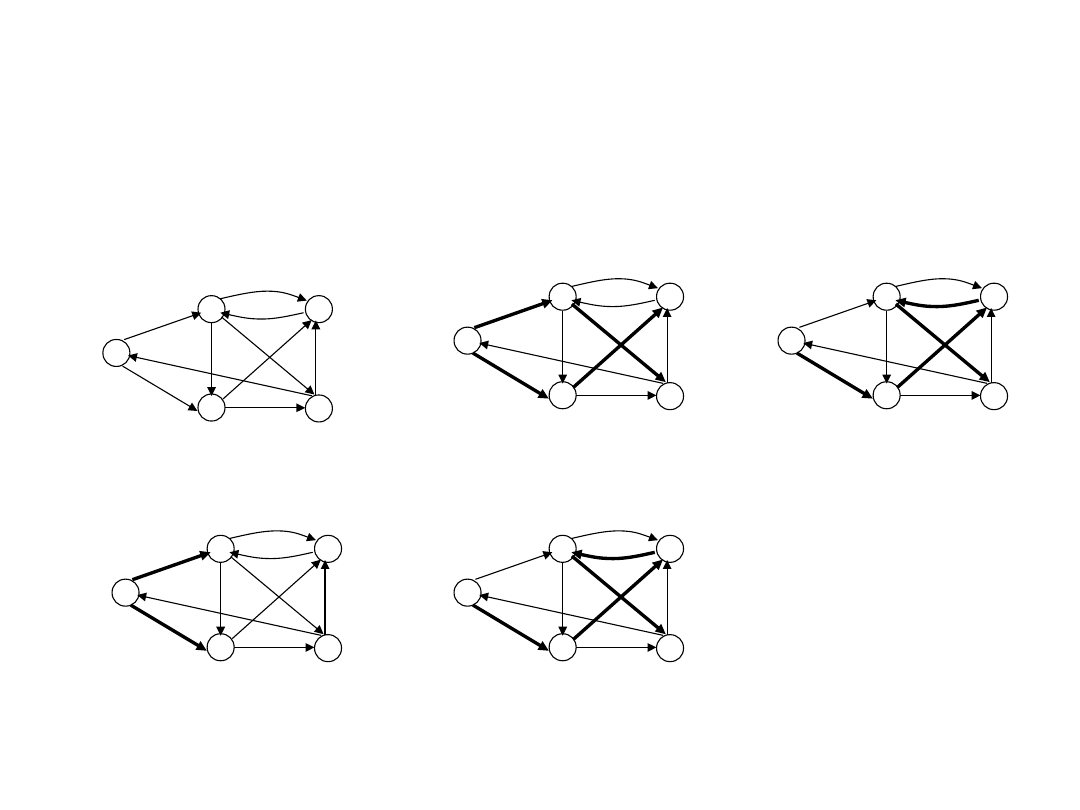
Algorytm Bellmana-Forda

(przykład)

s

5

6

7

7









0

8

3

9

-4

-2

2

-3

s

5

6

7

7





6

7

0

8

3

9

-4

-2

2

-3

s

5

6

7

7

2

4

6

7

0

8

3

9

-4

-2

2

-3

9

s

5

6

7

7

2

4

2

7

0

8

3

-4

-2

2

-3

s

5

6

7

7

-2

4

2

7

0

8

3

-4

-2

2

-3