Przykład AT-3.
Wyznaczyć poprawiony (o mniejszych kosztach całkowitych) plan dostaw dla rozwiązania
startowego z przykładu AT-2.

Rozwiązanie:

Wyznaczony w przykładu AT-2 startowy, bazowy plan dostaw był następujący:

Odbiorca „j”

Dostawca „i”

1

O

2

O

3

O

4

O

podaż

1

D

210

90

0

0

300

2

D

0

80

70

0

150

3

D

0

0

290

140

430

popyt

210

170

360

140

880

Na trasie

)

1

,

3

(

otrzymaliśmy

1

31

−

=

∆

- oznacza to, że kierując jednostkową dostawę

na trasę

)

1

,

3

(

obniżamy całkowite koszty transportu o 1 jednostkę. Zatem, jeśli w nowym

planie dostaw zmienna

31

x

będzie zmienną bazową to

31

31

x

KC

⋅

∆

=

∆

.

Należy teraz ustalić, która z poprzednich zmiennych bazowych zostanie z bazy

usunięta oraz wartość dla nowej zmiennej bazowej

31

x

. Odpowiednia procedura polega

znalezienia cyklu, który tworzy pole

)

1

,

3

(

z pozostałymi polami odpowiadającymi

niewiadomym bazowym. W tablicy zaznaczamy pola (zacieniowane), którym odpowiadają
niewiadome bazowe oraz znakiem „+” pole na które kierujemy dostawę.

1

O

2

O

3

O

4

O

1

D

-

+

2

D

-

+

3

D

+

-

Przenosząc dostawę na trasę

)

1

,

3

(

musimy: zmniejszyć dostawę na trasie

)

1

,

1

(

(co

zaznaczamy znakiem „.

-

”) oraz zwiększyć dostawę na trasie

)

2

,

1

(

(co zaznaczamy znakiem

„.+

”), następnie zmniejszyć dostawę na trasie

)

2

,

2

(

oraz zwiększyć dostawę na trasie

)

3

,

2

(

i konsekwentnie zmniejszyć dostawę na trasie

)

3

,

3

(

. Ponieważ liczba znaków „.+

” i „.

-

” jest

w każdym wierszu i w każdej kolumnie taka sama to szukany cykl został znaleziony.

Aby ustalić wartość dostawy

31

x

, korzystamy z warunku

0

≥

ij

x

: dla pól oznaczonych

znakiem „

-

” wielkości dostaw nie mogą być ujemne stąd:

80

}

290

,

80

,

210

min{

}

,

,

{

min

33

22

11

31

=

=

=

x

x

x

x

Aby otrzymać poprawiony plan dostaw musimy dodać po 80 do wielkości dostaw na polach
oznaczonych znakiem „ +

” oraz odjąć po 80 od wielkości dostaw na polach oznaczonych

znakiem „

-

”.

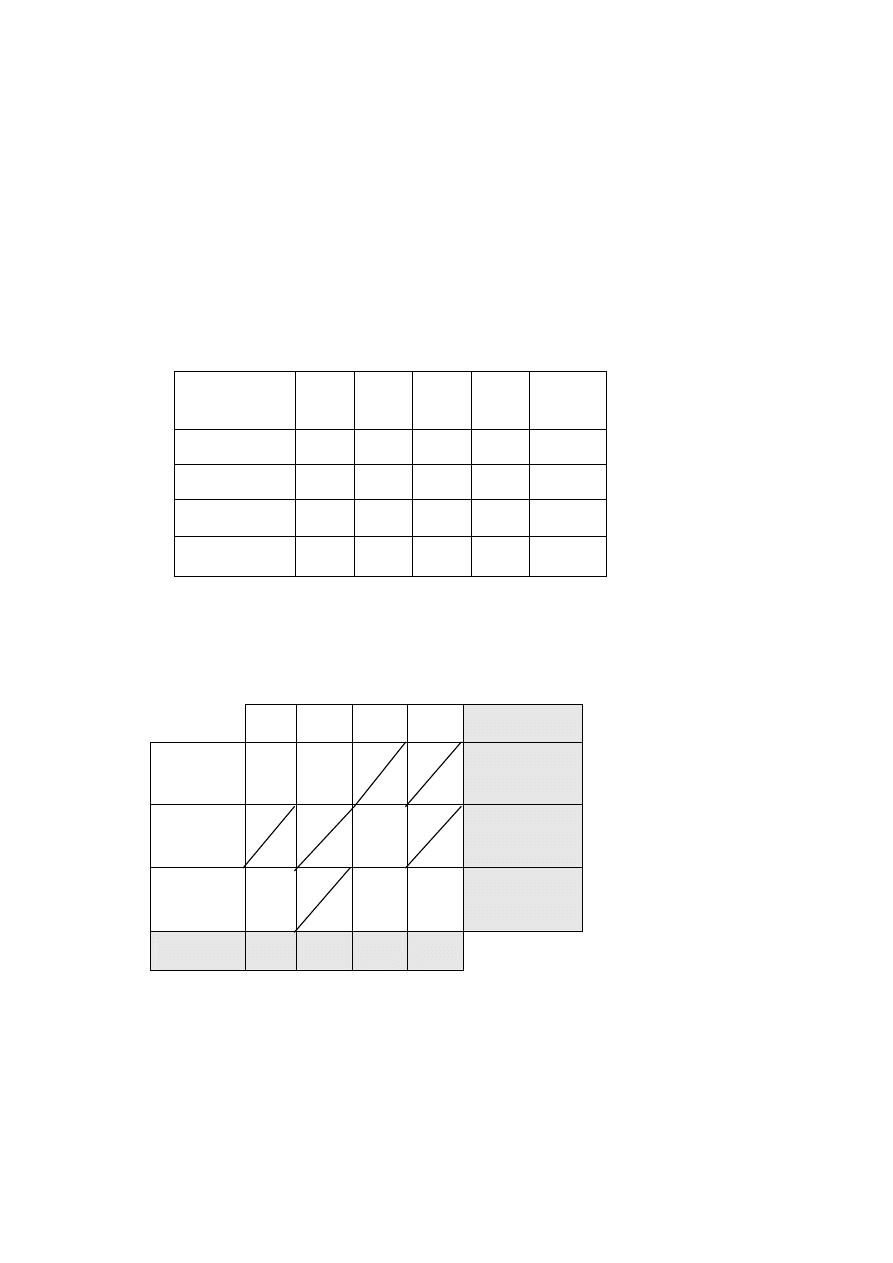
Nowy (poprawiony) plan przewozów jest zatem następujący

Odbiorca „j”

Dostawca „i”

1

O

2

O

3

O

4

O

podaż

1

D

130

170

0

0

300

2

D

0

0

150

0

150

3

D

80

0

210

140

430

popyt

210

170

360

140

880

Dla

nowego

poprawionego

planu

dostaw

2840

80

)

1

(

2920

=

⋅

−

+

=

∆

+

KC

KC

.

Dociekliwa Osoba zauważy, że to rozwiązanie otrzymaliśmy metodą minimalnego elementu
macierzy kosztów (był to oczywiście przypadek a nie reguła).

Sprawdzając optymalność nowego rozwiązania otrzymamy:

Na trasie

)

1

,

2

(

otrzymaliśmy ujemną wartość wskaźnika optymalności

1

21

−

=

∆

co oznacza,

ż

e wyznaczone rozwiązanie nie jest optymalne. Wyznaczenie nowego planu przewozów (po

skierowaniu dostawy na trasę

)

1

,

2

(

) pozostawiamy Osobie studiującej.

1

O

2

O

3

O

4

O

i

u

1

D

6

3

3

+5

1

+5

0*

2

D

5

-1

2

+1

2

0

+5

-1

3

D

6

3

+2

3

1

0

j

v

6

3

3

1