Zadanie 1

Trzech rolników dostarcza mleko do trzech mleczarni. Rolnicy owi dostarczają odpowiednio 200, 150, 220 hl mleka. Poszczególne mleczarnie mogą przyjąć następujące ilości: 100, 300 i 150 hl. Koszty przewiezienia jednego hl mleka (zł) między rolnikami a mleczarniami przedstawia macierz:

C=

Opracować plan dostarczenia całego mleka tak, aby łączny koszt przewozu był jak najmniejszy (wykorzystać metodę kąta północno-zachodniego).

Zadanie 2

Trzy cementownie zaopatrują w cement cztery budowy. Cementownie dysponują odpowiednio 20, 30 i 40 tonami cementu, podczas gdy zapotrzebowanie na budowach wynosi: 15, 20, 20 i 30 ton. Macierz jednostkowych kosztów przewozu (zł) jest następująca:

C=

Opracować plan dostaw minimalizujący koszty transportu używając metody kąta północno-zachodniego.

Zadanie 3

Czterech producentów dostarcza do 2 kontrahentów wyroby metalowe. Dysponują oni odpowiednio 50, 30, 45 i 23 tonami wyrobów, podczas gdy zapotrzebowanie wynosi u każdego z odbiorców po 60 ton. Macierz jednostkowych kosztów przewozu (zł) jest następująca:

C=

Z powodu remontu, droga między drugim producentem a drugim odbiorcą jest całkowicie nieprzejezdna.

Opracować plan dostaw minimalizujący koszty transportu używając metody kąta północno-zachodniego.

Zadanie 4

Trzy autobusy muszą rozwieźć ludzi w trzy różne miejsca. Pojemności autobusów, liczbę osób mających znaleźć się w punktach docelowych oraz macierz kosztów jednostkowych (zł) podaje poniższa tabela:

	Miejsce 1	Miejsce 2	Miejsce 3	a
Autobus 1	2,5	3	1,5	31
Autobus 2	1,2	1,3	3	30
Autobus 3	3,2	3,3	4	28
b	27	42	20

Opracować plan dostaw minimalizujący koszty transportu używając metody kąta północno-zachodniego.

Zadanie 5

Dwa duże gospodarstwa rolne zaopatrują w buraki cukrowe cztery punkty skupu. W tym roku pierwsze gospodarstwo dostarczy 75 a drugie 60 ton buraków. Punkty skupu skłonne są przyjąć odpowiednio: 40, 30, 32, 29 ton buraków. Macierz jednostkowych kosztów przewozu (zł) jest następująca:

	Punkt skupu 1	Punkt skupu 2	Punkt skupu 3	Punkt skupu 4
Gospodarstwo 1	2,5	2,3	2,7	2,3
Gospodarstwo 2	2,9	3	2,1	2,1

Na trasie z gospodarstwa 2 do trzeciego punktu skupu zorganizowano objazd, w związku z czym można na tej trasie przewieźć do 25 ton ładunku.

Opracować plan dostaw minimalizujący koszty transportu używając metody kąta północno-zachodniego.

Zadanie 6

Konserwy z trzech wojskowych magazynów mają trafić do trzech jednostek. Z magazynu pierwszego wyjedzie 20, z drugiego 30, a z trzeciego 24 tony konserw. Do jednostek ma trafić odpowiednio: 28, 26, 20 ton. Macierz jednostkowych kosztów przewozu (zł) jest następująca:

C=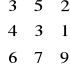

Trasa z magazynu 1 do jednostki 3 jest całkowicie nieprzejezdna

Opracować plan dostaw minimalizujący koszty transportu używając metody kąta północno-zachodniego.

Zadanie 7

Producenci serialu „A jak alabaster” zamówili u dwóch dostawców elementy dekoracji, które tymczasowo mają znaleźć się w jednym z czterech magazynów wytwórni. Dostawca 1 może zapewnić 200 a drugi 180 kg owych elementów. W pierwszym magazynie ma się znaleźć 120, w drugim 80, w trzecim 110 a w czwartym 70 kg elementów. Z powodu koczowania licznej grupy fanów, trasa od pierwszego dostawcy do trzeciego magazynu jest nieprzejezdna. Macierz jednostkowych kosztów przewozu jest następująca:

C=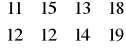

Opracować plan dostaw minimalizujący koszty transportu używając metody kąta północno-zachodniego.

---