Zadanie 1

Dane jest zadanie programowania liniowego:

max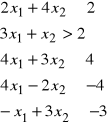

.

Rozwiąż je metodą graficzną. Naszkicuj zbiór rozwiązań dopuszczalnych, rozwiązania dopuszczalne i rozwiązanie optymalne.

Zadanie 2

Przedsiębiorstwo może wytwarzać 3 typy maszyn: A, B, C zużywając przy tym m.in. energię
(co najwyżej 220 kWh tygodniowo) i stal (co najwyżej 160 kg tygodniowo). Jednostkowe zapotrzebowanie na energię i stal oraz zyski ze sprzedaży gotowych wyrobów przedstawia tabela.

Maszyna	Energia	Stal	Przychód
A	3	1	11
B	2	5	16
C	4	2	5

Zakład zainteresowany jest maksymalizacją swego przychodu. Treść zadania zapisz w postaci zadania programowania liniowego i rozwiąż je za pomocą programu MATLAB.

Zadanie 3

Na podstawie rozwiązania optymalnego zadania dualnego do zadania:

max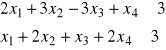

wyznacz rozwiązanie zadanie pierwotnego. Zadanie dualne rozwiąż za pomocą programu MATLAB.

Zadanie 4. (15)

Załóżmy, że dostawcami mąki do piekarń są jej bezpośredni producenci -młyny: M1, M2
i M3. Zdolności produkcyjne młynów osiągają odpowiednio wielkości: 100, 20, 80 ton mąki, a koszty produkcji 1 tony (w zł) dla każdego z młynów wynoszą 1080, 1060, 1100. Koszty transportu opisane są w tabeli.

MŁYNY	CZAS NIEZBĘDNY DO PRODUKCJI MĄKI
	P1 P2 P3 P4
M1	50	40	50	20
M2	40	80	70	30
M3	60	40	70	80

Miesięczne zapotrzebowanie piekarń na mąkę jest następujące: 40, 60, 50 i 50 ton. Zakładając, że młyny będą produkować dokładnie tyle ile wynosi zapotrzebowanie odbiorców podać optymalny (łączny) plan produkcji i transportu mąki z młynów do piekarń tak, aby zminimalizować łączne kwoty produkcji i transportu. Wykorzystując oprogramowanie proszę napisać jakie dane zostają wprowadzone i jaką postać ma funkcja wykonawcza programu.

1

ZADANIA RÓŻNE - ZESTAW 1

---