Przykład AT-1
Wyznaczyć startowy, dopuszczalny i bazowy plan przewozów dla zadania transportowego:
Trzej producenci:
1
D
,
2
D
,
3
D półfabrykatów zaopatrują cztery place budowy:
1
O ,
2
O ,
3
O ,
4
O . Półfabrykaty są przewożone w zestawach. Podaż dostawców wynosi
odpowiednio: 300, 150, 430 [zestawów]; zapotrzebowanie odbiorców jest następujące: 210,
170, 360, 140 [zestawów]. Macierz jednostkowych kosztów ma postać:
1
3
5
6
5
2
3
4
6
8
3
6
=
C
Obliczyć łączne koszty dla wyznaczonego planu przewozów
Rozwiązanie:
Zadanie jest zamkniętym zadaniem transportowym (łączny popyt jest równy łącznej
podaży). Plan dostaw będziemy zapisywać w tablicy, w której: w
i-tym wierszu wpisujemy
przewozy zestawów półfabrykatów od dostawcy
i
D (
3
,
2
,
1
=
i
) do wszystkich odbiorców; w
j-tej kolumnie wpisujemy przewozy zestawów półfabrykatów do odbiorcy
j
O
(
4
,
3
,
2
,
1
=
j
)
od wszystkich dostawców. W tablicy notujemy także popyt odbiorców i podaż dostawców.
1. Wyznaczanie startowego planu dostaw metodą kąta północno zachodniego
Na początek, dla ustalenia uwagi, wpiszemy do tablicy wielkości dostaw jako
niewiadome
ij
x
dla
3
,
2
,
1
=
i
oraz
4
,
3
,
2
,
1
=
j
.
Odbiorca „j”
Dostawca „i”
1
O
2
O
3
O
4
O
podaż
1
D
11
x
12
x
13
x
14
x
300
2
D
21
x
22
x
23
x
24
x
150
3
D
31
x
32
x
33
x
34
x
430
popyt
210
170
360
140
880
Ustalanie startowego planu dostaw rozpoczynamy od określenia dostawy od dostawcy
1
D
do odbiorcy
1
O
, przyjmujemy:
210
}
210
,
300
{
min
}
,
{
min
1
1
11
=
=
=
b
a
x
. Dostawa ta
jest równa zapotrzebowaniu odbiorcy
1
O
, zatem
0
21
=
x
i
0
31
=
x
. Mamy więc ustalone
liczby w pierwszej kolumnie.
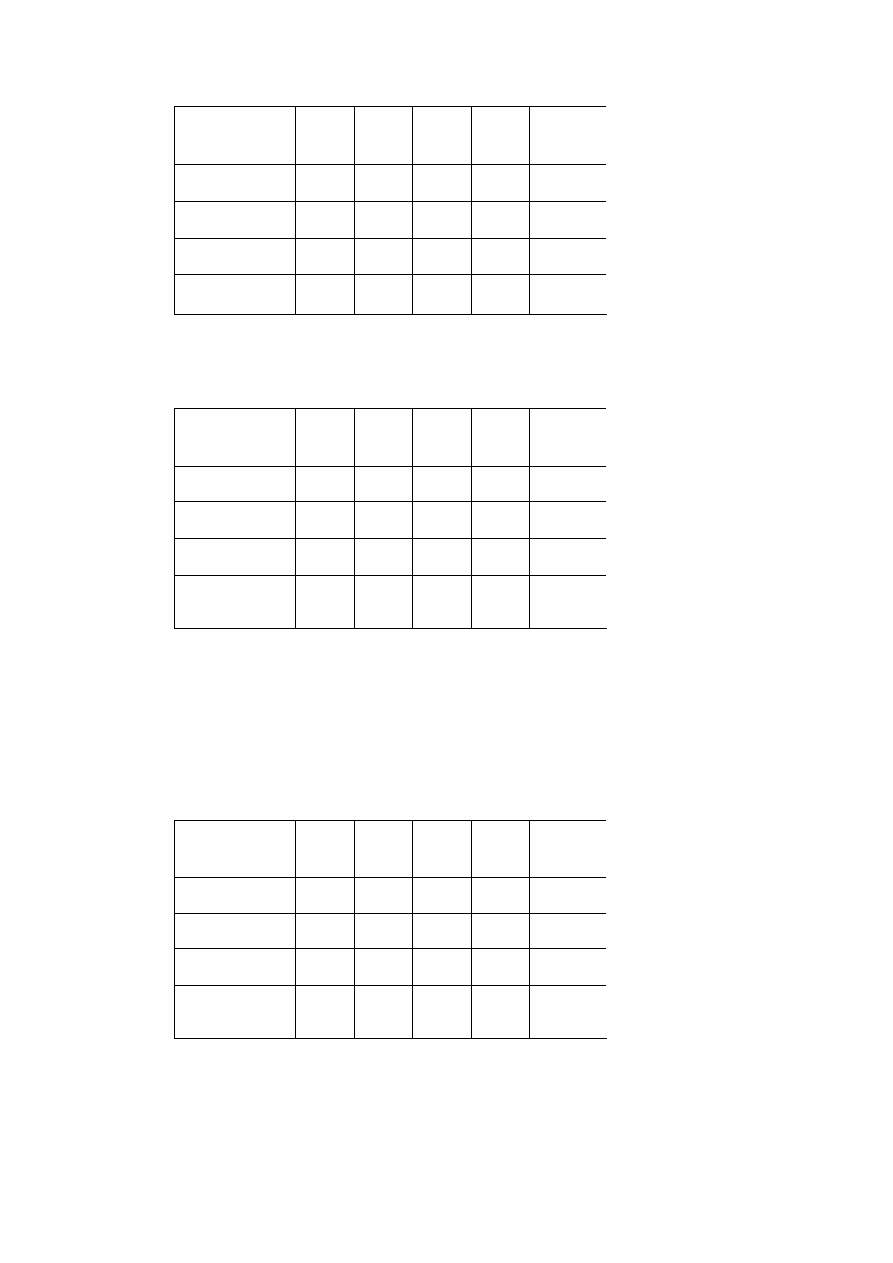
Odbiorca „j”
Dostawca „i”
1
O
2
O
3
O
4
O
podaż
1
D
210
12
x
13
x
14
x
300
2
D
0
22
x
23
x
24
x
150
3
D
0
32
x
33
x
34
x
430
popyt
210
170
360
140
880
Wyznaczamy teraz wielkość dostawy
12
x jako:
90
}
210
,
90
min{
}
,
210
min{
1
1
=
=
−
b
a
.
Ponieważ
11
x +
12
x =
0
0
300
14
13
1
=
∧
=
⇒
=
x
x
a
.Zapis w tablicy będzie następujący:
Odbiorca „j”
Dostawca „i”
1
O
2
O
3
O
4
O
podaż
1
D
210
90
0
0
300
2
D
0
22
x
23
x
24
x
150
3
D
0
32
x
33
x
34
x
430
popyt
210
170
360
140
880
880
Dalsze rachunki są następujące:
0
80
}
80
,
150
min{
}
,
min{
32
12
2
2
22
=
⇒
=
=
−
=
x
x
b
a
x
;
0
70
}
360
,
70
min{
}
,
min{
24
3
22
2
23
=
⇒
=
=
−
=
x
b
x
a
x
;
140
}
,
min{
290
}
290
,
430
min{
}
,
min{
4
33
3
34
23
3
3
33
=
−
=
⇒
=
=
−
=
b
x
a
x
x
b
a
x
Ostatecznie startowy plan dostaw wyznaczony metodą kąta północno zachodniego jest
następujący:
Odbiorca „j”
Dostawca „i”
1
O
2
O
3
O
4
O
podaż
1
D
210
90
0
0
300
2
D
0
80
70
0
150
3
D
0
0
290
140
430
popyt
210
170
360
140
880
880
Zwróćmy uwagę, w tym planie dostaw, liczba dostaw dodatnich wynosi
N=6= m+n-1,
jest to bazowy plan dostaw. Wyznaczając plan dostaw nie braliśmy pod uwagę wartości
jednostkowych kosztów transportu.
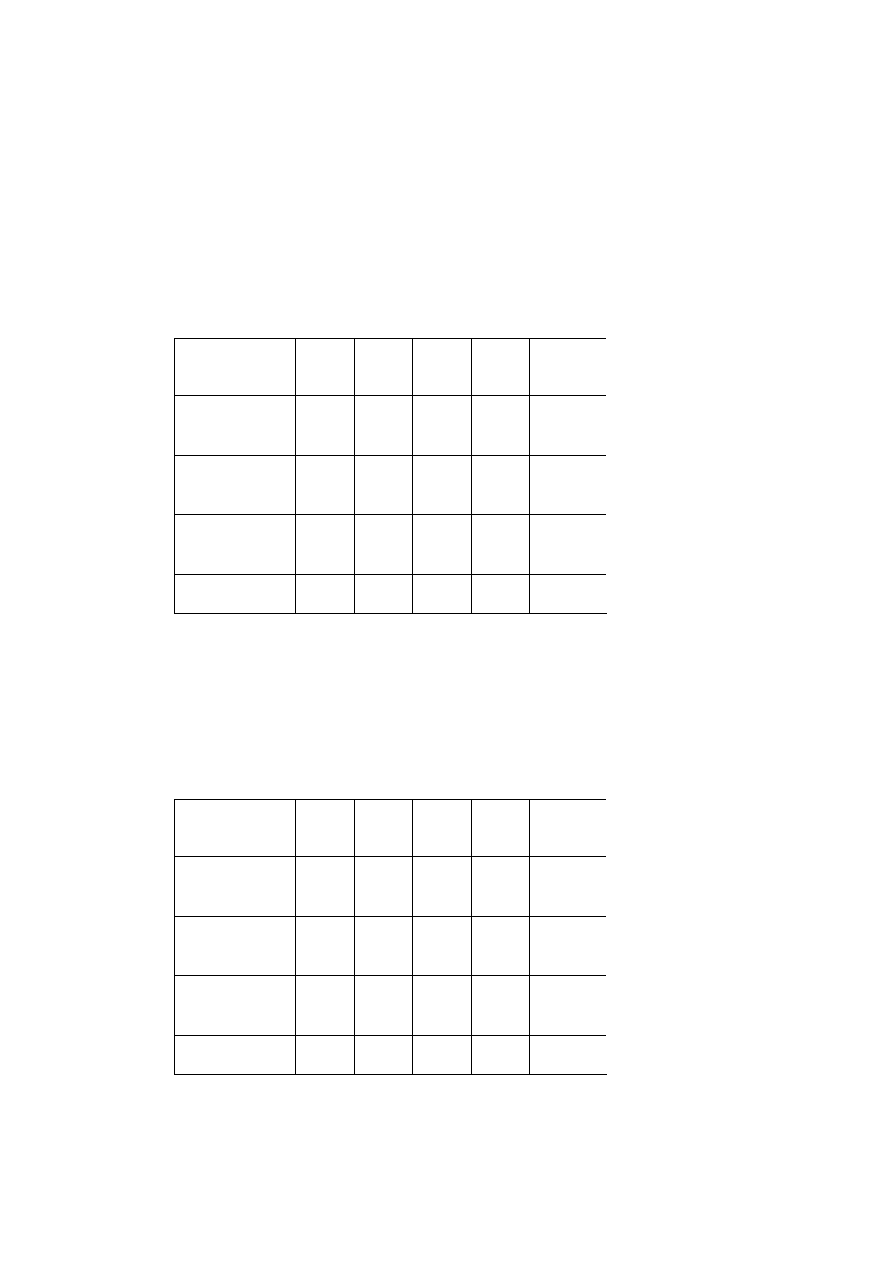
Łączne koszty przewozów dla tego planu wynoszą:
2920
140
1
290
3
70
2
80
3
90
3
210
6
=
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
KC
.
2. Wyznaczanie startowego planu dostaw metodą minimalnego elementu
macierzy kosztów
W tej metodzie wyznaczania startowego, bazowego planu dostaw bierzemy pod uwagę
wartości jednostkowych kosztów transportu. Dlatego wpiszemy je do tablicy (w lewych
górnych rogach poszczególnych kratek – do odróżnienia w kolorze czerwonym), w której
plan budujemy.
Odbiorca „j”
Dostawca „i”
1
O
2
O
3
O
4
O
podaż
1
D
6
11
x
3
12
x
8
13
x
6
14
x
300
2
D
4
21
x
3
22
x
2
23
x
5
24
x
150
3
D
6
31
x
5
32
x
3
33
x
1
34
x
430
popyt
210
170
360
140
880
Budowę planu rozpoczynamy o ustalenia wielkości dostawy na tej trasie, na której
jednostkowy koszt transportu jest najmniejszy. Ponieważ
1
}
{
min
34
=
=
c
c
ij
, ustalamy
dostawę
34
x jako
140
}
140
,
430
{
min
=
. Zatem
34
x =140, co odpowiada zapotrzebowaniu
odbiorcy
4
O , czyli
14
x = 0 i
24
x = 0.
W tablicy mamy teraz następujący zapis:
Odbiorca „j”
Dostawca „i”
1
O
2
O
3
O
4
O
podaż
1
D
6
11
x
3
12
x
8
13
x
6
0
300
2
D
4
21
x
3
22
x
2
23
x
5
0
150
3
D
6
31
x
5
32
x
3
33
x
1
140
430
popyt
210
170
360
140
880
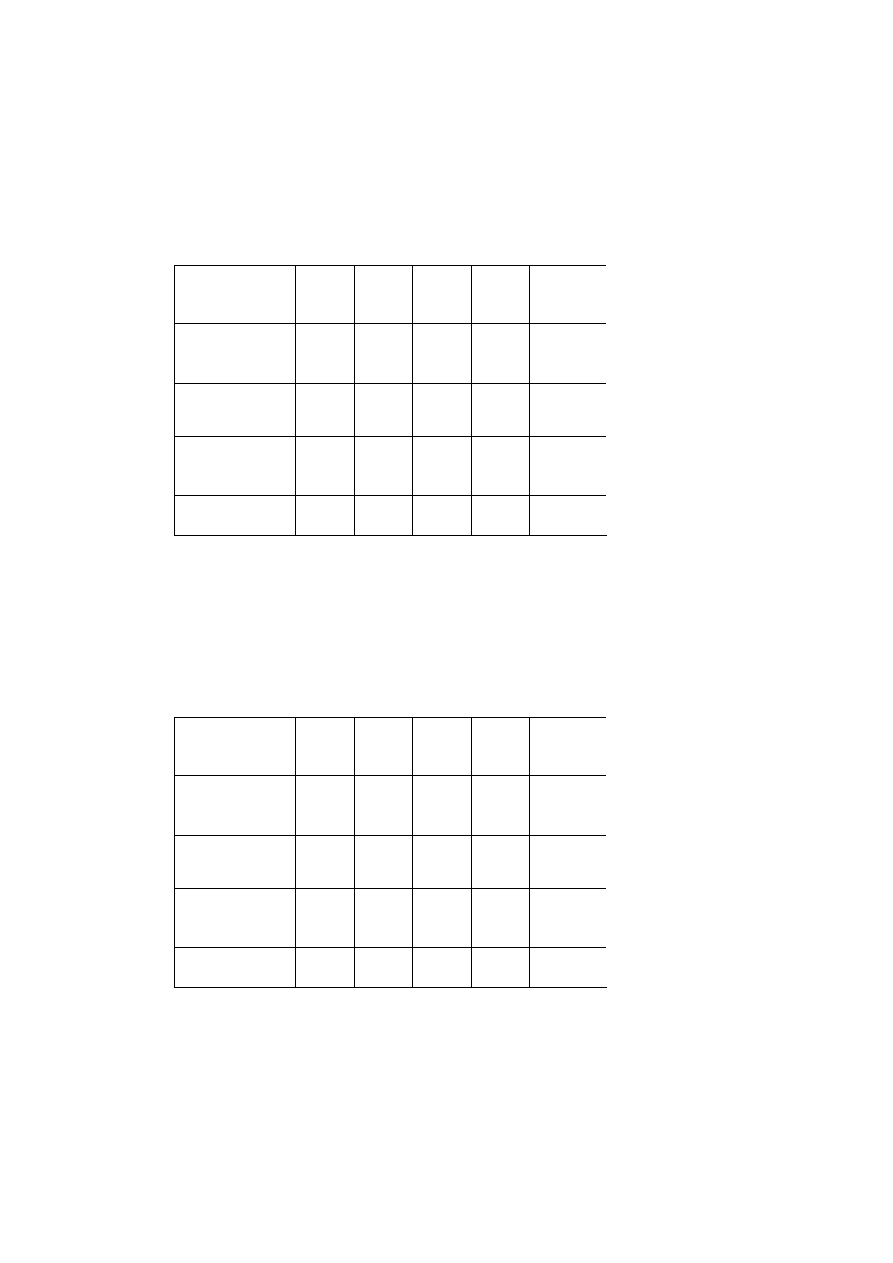
Spośród elementów macierzy kosztów w trzech pierwszych kolumnach wybieramy
element
najmniejszy,
jest
nim
2
23
=
c
,
to
ustalamy
wielkość
dostawy:
150
}
360
,
150
min{
23
=
=
x
. Wówczas
0
22
21
=
=
x
x
.
Wyznaczyliśmy w ten sposób wielkości dostaw w kolumnie czwartej i w wierszu drugim.
Odbiorca „j”
Dostawca „i”
1
O
2
O
3
O
4
O
podaż
1
D
6
11
x
3
12
x
8
13
x
6
0
300
2
D
4
0
3
0
2
150
5
0
150
3
D
6
31
x
5
32
x
3
33
x
1
140
430
popyt
210
170
360
140
880
Dalej postępujemy analogicznie: wybieramy najmniejszy koszt jednostkowy dla
pozostałych „kratek”, uwzględniamy tylko te trasy
)
,
( j
i
dla których nie określiliśmy dostaw.
Ponieważ:
33
12
33
32
31
13
12
11
3
}
,
,
,
,
,
min{
c
c
c
c
c
c
c
c
=
=
=
, to wybieramy trasę
)
2
,
1
(
lub
)
3
,
3
(
.
Wybierzmy najpierw
)
2
,
1
(
, wówczas
0
170
}
170
,
300
min{
32
12
=
⇒
=
=
x
x
.
Odbiorca „j”
Dostawca „i”
1
O
2
O
3
O
4
O
podaż
1
D
6
11
x
3
170
8
13
x
6
0
300
2
D
4
0
3
0
2
150
5
0
150
3
D
6
31
x
5
0
3
33
x
1
140
430
popyt
210
170
360
140
880
Ustalamy
teraz
wielkość
dostawy
na
trasie
)
3
,
3
(
jako:
210
}
150
360
,
140
430
min{
33
=
−
−
=
x
. Zatem
13
x =0. Pozostało nam jeszcze wyznaczyć
brakujące dostawy w pierwszej kolumnie:
11
x
i
31
x . Mamy więc:
11
x
=300-170=130 oraz
31
x =210-130=80.
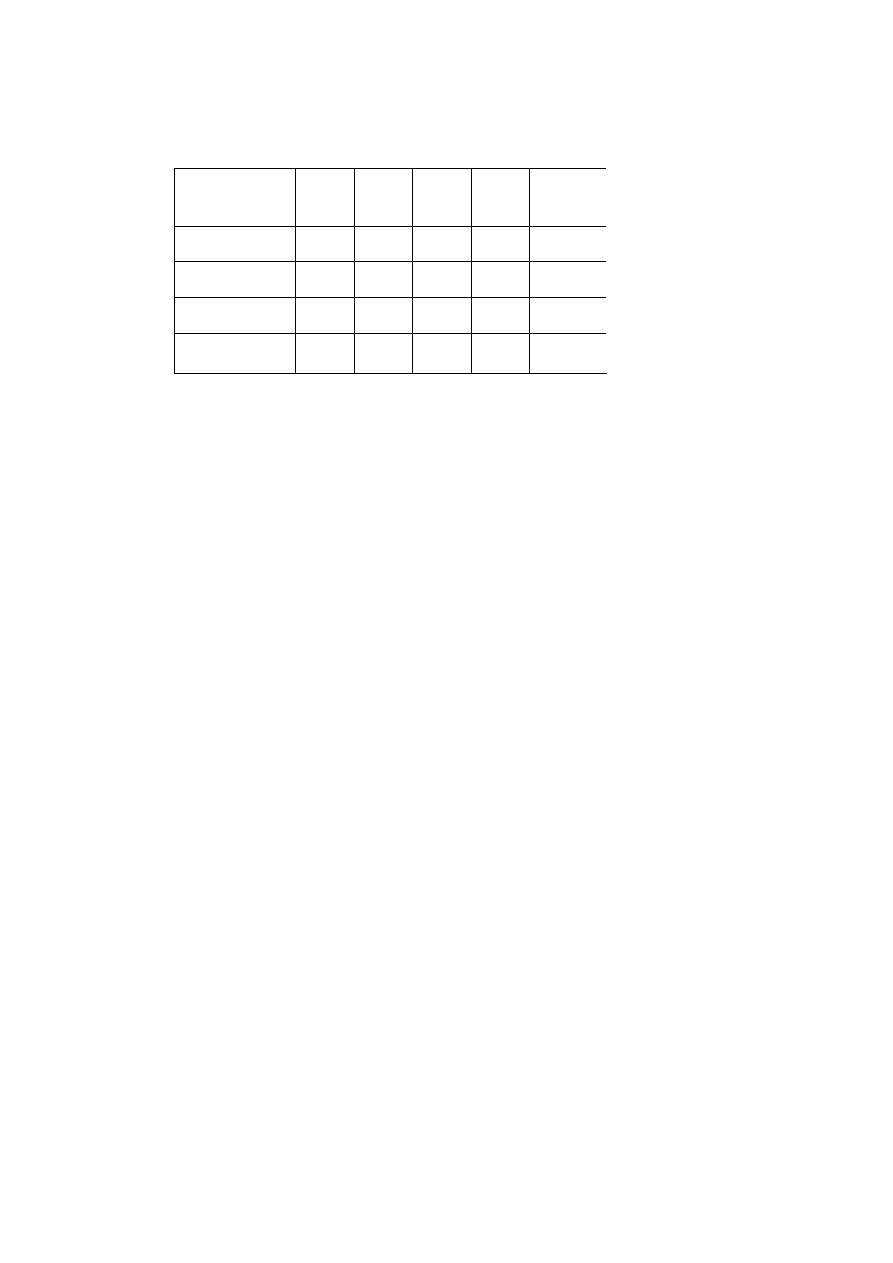
Wyznaczony plan dostaw, metodą minimalnego elementu macierzy kosztów,
zapiszemy w tablicy końcowej:
Odbiorca „j”
Dostawca „i”
1
O
2
O
3
O
4
O
podaż
1
D
130
170
0
0
300
2
D
0
0
150
0
150
3
D
80
0
210
140
430
popyt
210
170
360
140
880
Łączne koszty transportu dla tego planu dostaw wynoszą:
KC=2840. Plan ten jest
lepszy niż poprzednio wyznaczony (łączne koszty są niższe).