05 Wytrzymałość materiałów

73

WYTRZYMAŁOŚĆ MATERIAŁÓW

MECHANIKA CIAŁA ODKSZTAŁCALNEGO

Podstawą wytrzymałości materiałów są prawa statyki

oraz wnioski wypływające z doświadczenia.

Pomostem łączącym mechanikę ciał sztywnych z wytrzyma-

łością jest wspomniana już zasada zesztywnienia.

P

ojęcie „wytrzymałość materiałów” m ożna traktować jako

ce

chę, właściwość ciał stałych, polegającą na przeciwstawianiu

się niszczącemu działaniu sił.

Zadania

„wytrzymałość materiałów” jako przedmiotu opisują-

cego zachowanie się ciał odkształcalnych:
 określanie nośności konstrukcji (odpowiedniej wytrzymałości),
 wyznaczanie przemieszczeń konstrukcji wywołanych obcią-

żeniami (określanie sztywności konstrukcji).

Wytrzymałość materiałów jest częścią mechaniki o praktycz-
nym, inżynierskim charakterze. W rozwiązywaniu konkretnych
zadań wykorzystuje się pewne uogólnienia i uproszczenia.
Uproszczenia dotyczą opisu właściwości materiału i opisu
kształtu elementu konstrukcyjnego. Dzięki uproszczeniom rze-
czywisty obiekt zostaje przekszta

łcony w pewien model, który

umożliwia rozwiązanie problemu za pomocą określonego
schematu obliczeniowego. Model (schemat obliczeniowy)
musi zachowywać istotne dla rozwiązywanego problemu cechy
i właściwości rzeczywistego obiektu.

UPROSZCZ

ENIA W WYTRZYMAŁOŚCI MATERIAŁÓW:

 modelu ciała  ciało jednorodne,

 właściwości materiału  ciało izotropowe, którego właści-

wości we wszystkich kierunkach są identyczne (ciało ani-
zotropowe –

różne właściwości), ciało sprężyste

 sposobu rozwiązywania  uproszczenia inżynierskie.

05 Wytrzymałość materiałów

74

Wytrzymałość materiałów posługuje się modelem cia-
ła jednorodnego, izotropowego, idealnie sprężystego
i charakteryzuje się praktycznym, inżynierskim podej-
ściem do rozwiązywanych problemów.

Wytrzymałość materiałów bada przede wszystkim siły

wewnętrzne, będące wynikiem oddziaływania między po-
szczególnymi cząstkami ciała jednorodnego.

Jednym z głównych zadań wytrzymałości materiałów jest roz-

wiązywanie zadań statycznie niewyznaczalnych, w których
liczba niewiadomych jest większa od liczby równań równowagi.
W

praktyce inżynierskiej spotyka się przede wszystkim zadania

statycznie niewyznaczalne.

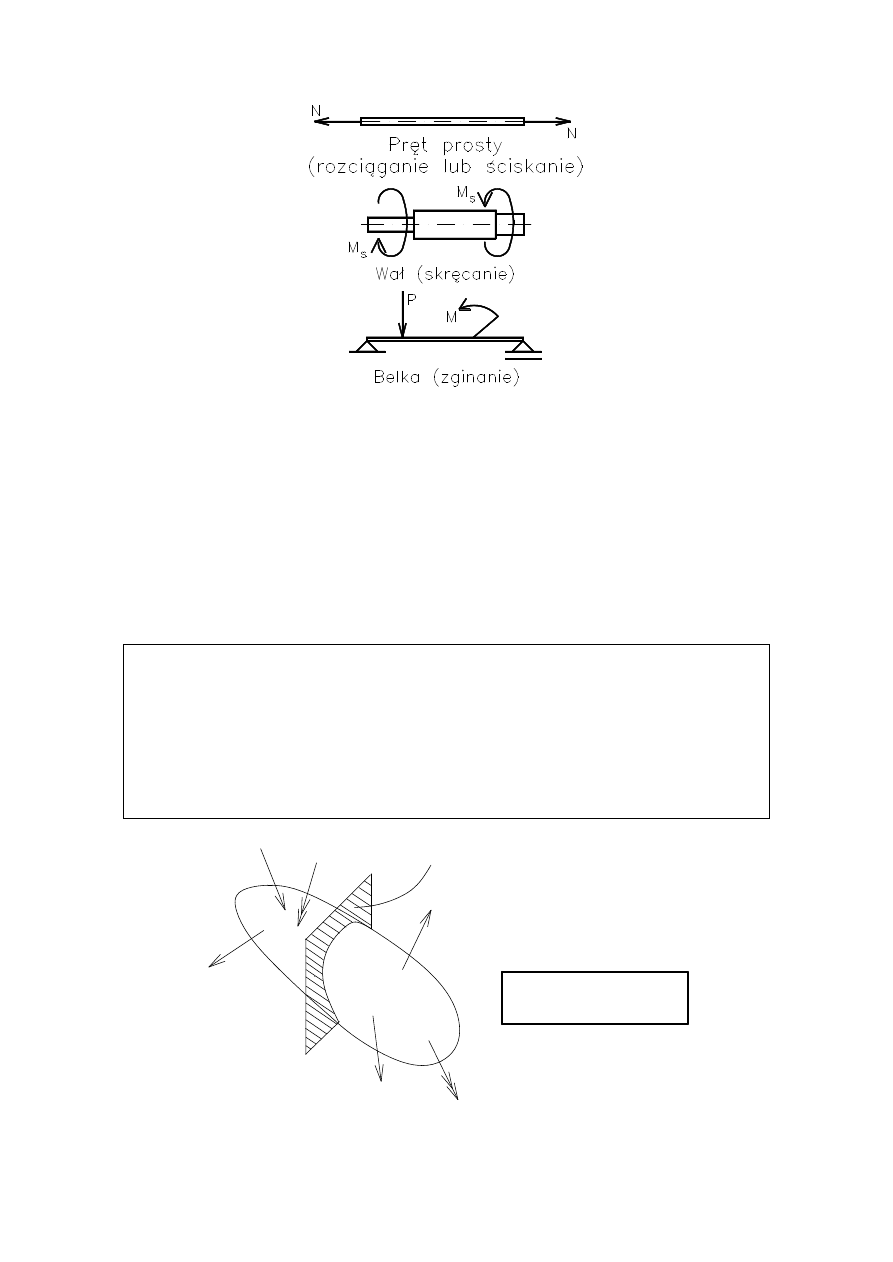
PODSTAWOWYMI MODELAMI NOMINALNYMI W WY-

TRZY

MAŁOŚCI MATERIAŁÓW SĄ PRĘTY, WAŁY I BELKI.

Model nominalny (fizyczny) w sposób uproszczony powinien

wiernie przedstawiać badany fragment rzeczywistości (muszą
być spełnione prawa podobieństwa modelowego). Korzysta on
ze zbioru pojęć właściwych dla badanej rzeczywistości. Uprosz-
czenia, będące istotnym elementem wytrzymałości materiałów,
muszą być w modelu nominalnym odpowiednio uzasadnione i
doświadczalnie zweryfikowane.

PRĘTY – ROZCIĄGANIE

WAŁY – SKRĘCANIE

BELKI –ZGINANIE

05 Wytrzymałość materiałów

75

Podstawowe modele konstrukcji pro

stych w wytrzymałości materiałów

SIŁY WEWNĘTRZNE

W wytrzymałości materiałów siły zewnętrzne czynne są siłami
ob

ciążającymi konstrukcję. Siły zewnętrzne bierne ujawniają się

po uwolnieniu konstrukcji od więzów. Dla ujawnienia sił we-
wnętrznych korzysta się z tzw. zasady myślowych przekro-
jów.

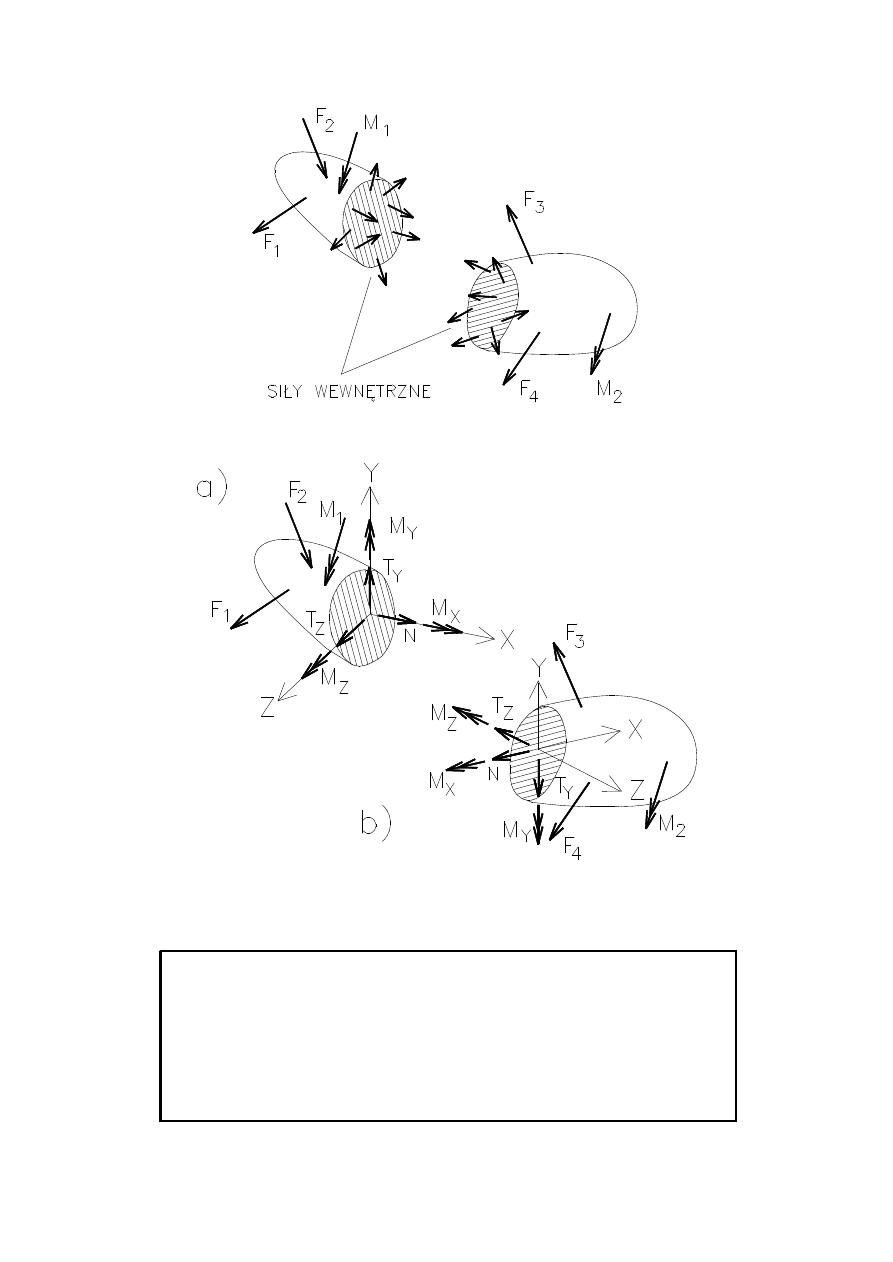
Zasada myślowych przekrojów polega na dokonaniu my-
ślowego (wirtualnego) przekroju konstrukcji i myślowego
(wirtualnego)

rozdzielenia ciała na dwie części. Dzięki te-

mu rozdzieleniu ujaw

niają się siły wewnętrzne, które muszą

być w równowadze z siłami zewnętrznymi, działającymi na
rozpatrywaną część ciała.

PŁASZCZYZNA MYŚLOWEGO PRZEKROJU

- siły zewnętrzne
czynne i bierne

1

F

3

F

M

1

M

2

4

F

2

F

M

i

F

i ,

Idea myślowych przekrojów

05 Wytrzymałość materiałów

76

Siły wewnętrzne w myślowo podzielonym ciele stałym

Uporządkowane siły wewnętrzne

N –

siła normalna (siła osiowa),

T

Y

, T

Z

–

siły poprzeczne (siły tnące, siły ścinające),

M

X

–

moment skręcający,

M

Y

, M

Z

– momenty zgi

nające.

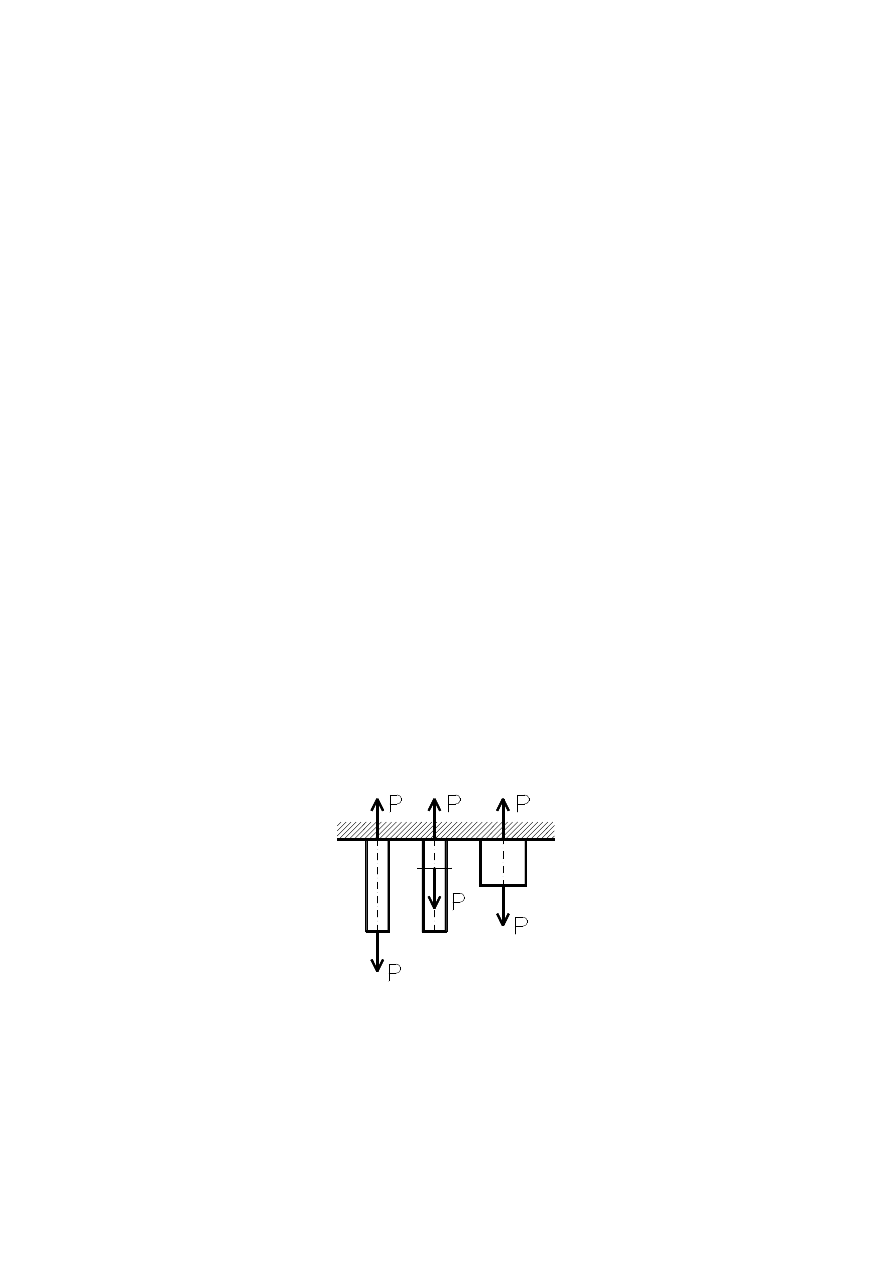
05 Wytrzymałość materiałów

77

PROSTE PRZY

PADKI OBCIĄŻEŃ:

 rozciąganie (ściskanie), gdy działa tylko siła N; siła N skie-

rowana na zewnątrz rozpatrywanego przekroju jest siłą do-
datnią, powodującą rozciąganie (znak „+”); siła N skierowana
do wewnątrz powoduje ściskanie (znak „–”);

 ścinanie, gdy działa jedna z sił poprzecznych T

Y

lub T

Z

;

 skręcanie, gdy działa moment skręcający M

X

;

 zginanie, gdy działa jeden z momentów zginających; mo-

ment M

Z

powoduje zginanie przekroju w płaszczyźnie XY

(pionowej), natomiast moment M

Y

zginanie w płaszczyźnie

XZ (poziomej).

W praktyce inżynierskiej najczęściej spotyka się złożone

przypadki obciążenia, będące kombinacją wymienionych wy-
żej prostych przypadków. Złożone przypadki obciążeń są ko-
lejną charakterystyczną cechą wytrzymałości materiałów.

NAP

RĘŻENIA

Statycznie równo

ważne układy sił

STATYKA CIAŁA SZTYWNEGO – analiza sił zewnętrznych.
WYTRZYMAŁOŚC MATERIAŁÓW – analiza „wytrzymałości”
konstrukcji.

05 Wytrzymałość materiałów

78

Do oceny wytrzymałości danego przekroju

wprowadzono po

jęcie naprężenia.

Def

inicja naprężenia

Naprężeniem w punkcie C nazywa się wektor zdefiniowa-
ny

zależnością:

dA

dN

A

N

lim

A















0

.

Jednostką naprężenia jest paskal [Pa]:

 

2

m

niuton





.

PRAKTYKA INŻYNIERSKA: megapaskal, 1 MPa = 10

6

Pa.

Związki między siłami wewnętrznymi i naprężeniami

Równania statyki dla przestrzennego układu sił (6 równań):

UWAGA:

równania statyki można formułować tylko dla sił.



















A

A

A

xz

z

xy

y

x

dA

T

,

dA

T

,

dA

P

,

05 Wytrzymałość materiałów

79





























A

A

x

z

x

y

A

xy

xz

x

.

ydA

M

,

dA

M

,

dA

z

y

M

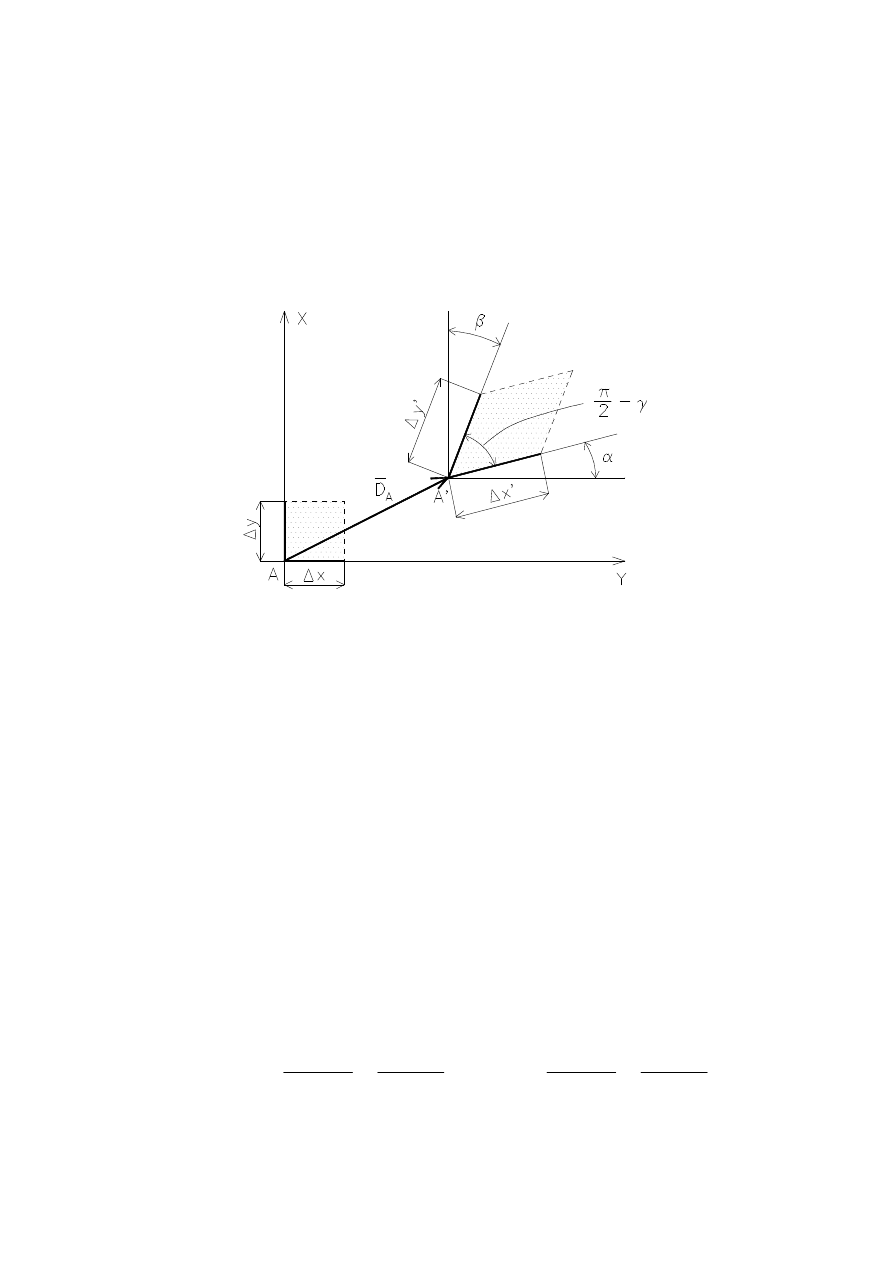
ODKSZTAŁCENIA I PRZEMIESZCZENIA

Działanie sił – odkształcenia i przemieszczenia.

Odkształcenia i przemieszczenia

RODZAJE ODKSZTAŁCEŃ:

–

liniowe

, które są określane jako wektor o początku w pew-

nym punkcie ciała nieodkształconego i końcu w tym samym
punkcie ciała odkształconego,

–

kątowe, które są określane za pomocą kąta zawartego
po

między dowolnie krótkim odcinkiem związanym z rozpa-

try

wanym ciałem przed odkształceniem i po jego odkształ-

ceniu.

Przemieszczenia ciała są wynikiem odkształceń.

Wydłużenie liniowe (odkształcenie wzdłużne, wydłużenie
względne, jednostkowe, właściwe) określa się z zależności

.

dy

dy

'

dy

y

y

'

y

lim

,

dx

dx

'

dx

x

x

'

x

lim

y

y

x

x









































0

0

05 Wytrzymałość materiałów

80

Odkształcenia postaciowe (odkształcenie poprzeczne, kąt
od

kształcenia postaciowego) są określone:

.

y

x

,

xy

0



















DOŚWIADCZALNE PODSTAWY

WYTRZYMAŁOŚCI MATERIAŁÓW

STATYCZNA PRÓBA ROZCIĄGANIA.

– określa związek pomiędzy naprężeniami i odkształceniami,
– dostarcza podstawowych informacji o właściwościach wy-

trzymałościowych materiałów,

– umożliwia prowadzenie obliczeń wytrzymałościowych wyko-

rzystujących warunek wytrzymałościowy.

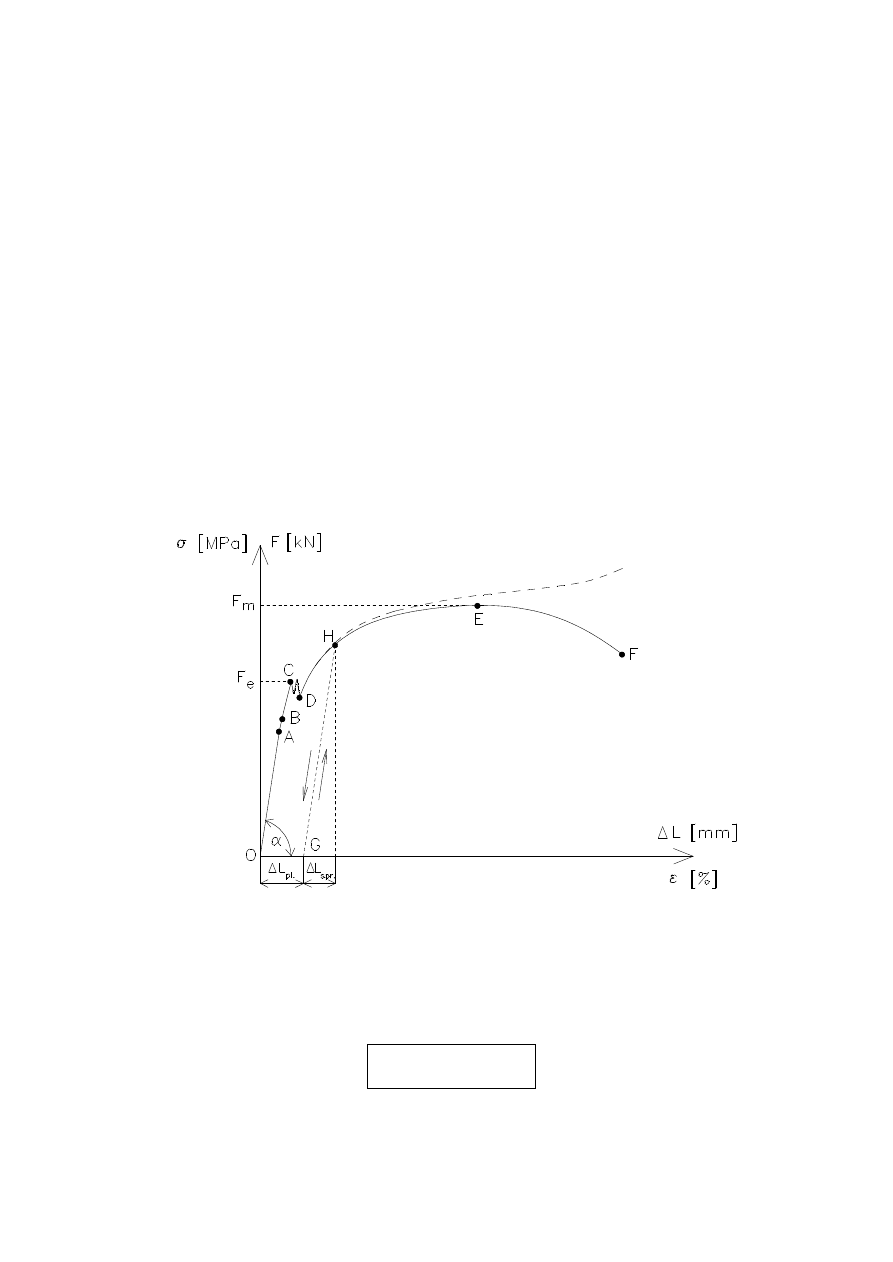
Wykres

rozciągania dla materiału z wyraźną granicą plastyczności

Odcinek OA – liniowa

zależność między obciążeniem i wy-

dłużeniem. Jest to więc zakres ważności prawa Hooke'a. Pra-
wo

Hooke’a to związek fizyczny:









E

 = F/A

0

, –

naprężenie, A

0

–

początkowy przekrój próbki;

05 Wytrzymałość materiałów

81

 = L/L

0

, –

wydłużenie względne próbki,

L

0

– początkowa długość próbki;

E –

współczynnik proporcjonalności, charakteryzujący od-

kszta

łcalność materiału, moduł (współczynnik) sprężystości

wzdłużnej, moduł Younga [MPa].

Punkt A

– granica

proporcjonalności.

Punkt B

– granica

sprężystości.

Punkt C, D – granica plastycz

ności.

Punkt E

–

wytrzymałość na rozciąganie

(wytrzymałość doraźną).

Za pomocą statycznej próby rozciągania określa się podsta-
wowe

właściwości mechaniczne (wytrzymałościowe) stosowa-

nych w praktyce inżynierskiej materiałów konstrukcyjnych:

– moduł Younga E [MPa,

– współczynnik Poissona, wyrażona jako stosunek wydłużenia

poprzecznego do wzdłużnego, oznaczona symbolem 

,

'









 – wydłużenie wzdłużne, ' – wydłużenie po-
przeczne; liczba Poissona mieści się w prze-
dziale 0 <  < 0,5 ( = 0 – korek, beton,  = 0,5
– kauczuk);

– granica plastyczności R

e

[MPa];

– wytrzymałość na rozciąganie R

m

[MPa],

– wydłużenie, zdefiniowane zależnością

,

%

L

L

L

A

u

100

0

0





gdzie: L

0

–

długość początkowa próbki, L

u

–

długość próbki

po zerwaniu;

– przewężenie, zdefiniowane zależnością

,

%

A

A

A

Z

u

u

100

0





gdzie: A

0

–

początkowy przekrój próbki, A

u

– przekrój próbki

po zerwaniu.

PRAWO HOOKE’A:

E







.

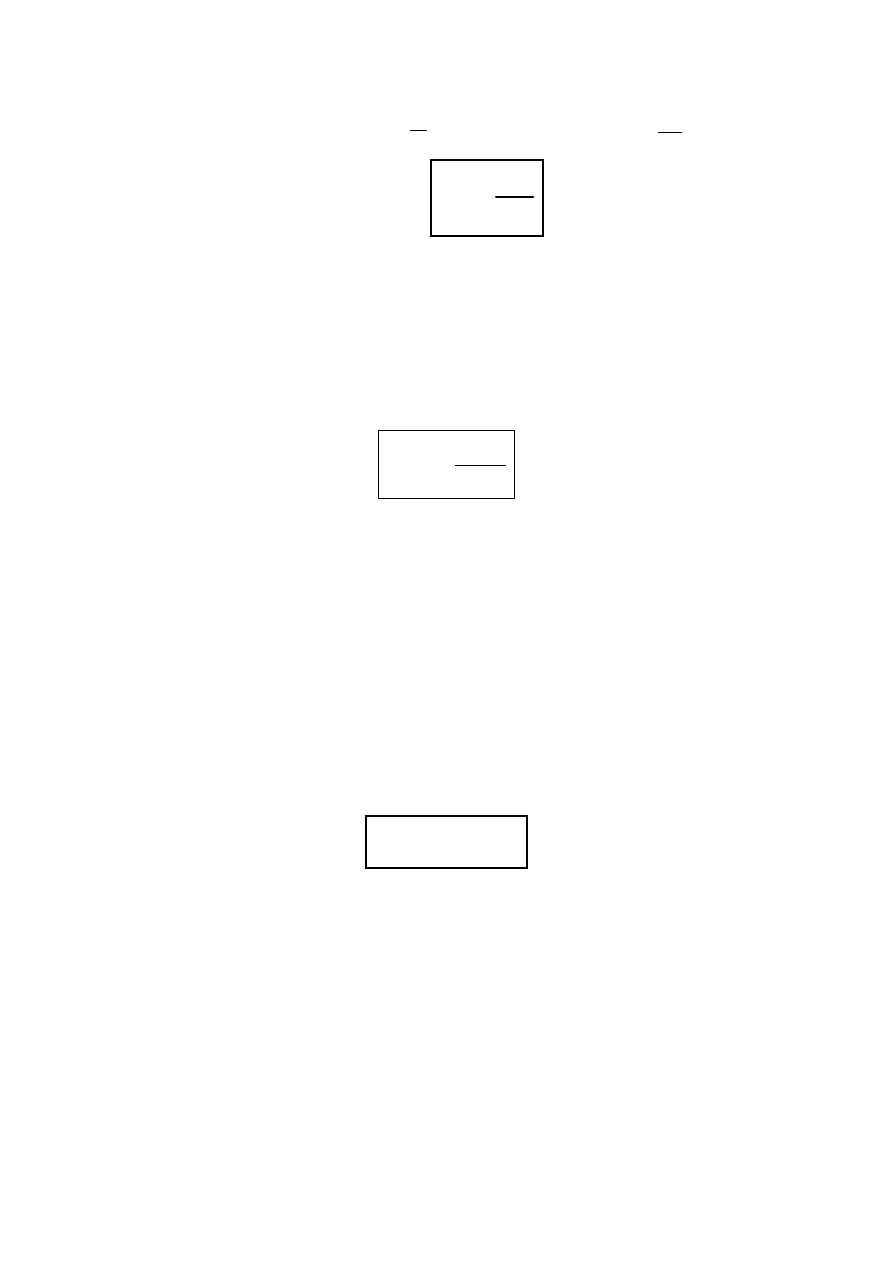
05 Wytrzymałość materiałów

82

Naprężenie:

A

P





,

wydłużenie:

L

L







,

Dr

uga postać prawa Hooke’a:

.

A

E

L

P

L 



EA – sztywno

ść przekroju na rozciąganie.

WARUNEK WYTRZYMAŁOŚCIOWY

Miarą wytężenia materiału (zdolności do przenoszenia obcią-

żeń) są naprężenia . Graniczną miarą wytężenia są naprę-
żenia dopuszczalne.

,

n

nieb

dop







gdzie: 

nieb

–

naprężenie przyjęte za niebezpieczne (granica

plastyczności),

n

–

współczynnik bezpieczeństwa.

Współczynnik bezpieczeństwa n musi być większy od 1.

Dobór

współczynnika bezpieczeństwa – znaczenie ekono-

miczne.

WARUNEK WYTRZYMAŁOŚCIOWY:

.

dop

max







Warunek wytrzymałościowy stanowi podstawę obliczeń wy-

trzymałościowych na naprężenia dopuszczalne. Korzystanie
z niego umożliwia zrealizowanie obu zadań wytrzymałości ma-
teriałów, czyli:
– określenie dopuszczalnych obciążeń konstrukcji o zna-

nych wymiarach,

– określenie koniecznych wymiarów konstrukcji dla zada-

nego ob

ciążenia.

05 Wytrzymałość materiałów

83

Jest oczywiste, że postawą obliczeń wytrzymałościowych na

napr

ężenia dopuszczalne są właściwości materiału uzyskane

za pomocą statycznej próby rozciągania.

WARUNEK SZTYWNOŚCI

.

l

l

dop







ZASADA SUPERPOZYCJI

Podstawa: prawo Hooke’a

(liniowy związek między obciąże-

niem i odkształceniem).

Rezultaty działania kilku sił są równe sumie

(algebraicznej lub geometrycznej) rezultatów,

otrzymywanych w wyniku działania każdej siły oddzielnie.

ZADANIA STATYCZNIE WYZNACZALNE

I STATYCZNIE NIEWYZNACZALNE

W wytrzymałości materiałów przeważają zagadnienia sta-

tycznie niewyznaczalne, tzn. takie, gdzie liczba niewiadomych
p

rzekracza liczbę równań równowagi, które mogą być napisane

dla tego zagadnienia. Różnica między liczbą niewiadomych a
liczbą równań równowagi określa tzw. stopień statycznej nie-
wyznaczalności zadania.

Rozwiązanie zadania statycznie niewyznaczalnego:
– określenie stopnia statycznej niewyznaczalności zadania

i

wielkości statycznie niewyznaczalnych,

– utworzenie odpowiedniej liczby tzw. równań geometrycz-

nych

z wykorzystaniem warunków nierozdzielności (łączno-

ści) konstrukcji.

05 Wytrzymałość materiałów

84

STOPIEŃ STATYCZNEJ NIEWYZNACZALNOŚCI ZALEŻY

OD SPOSOBU PODPARCIA KONSTRUKCJI.

INTERPRETACJA ZNAKÓW W RÓWNANIACH STATYKI w

wytrzymałości materiałów wymaga bezwzględnego prze-
strzegania

zasady zgodności odkształceń elementów kon-

struk

cji ze znakami sił założonymi w równaniach statyki.

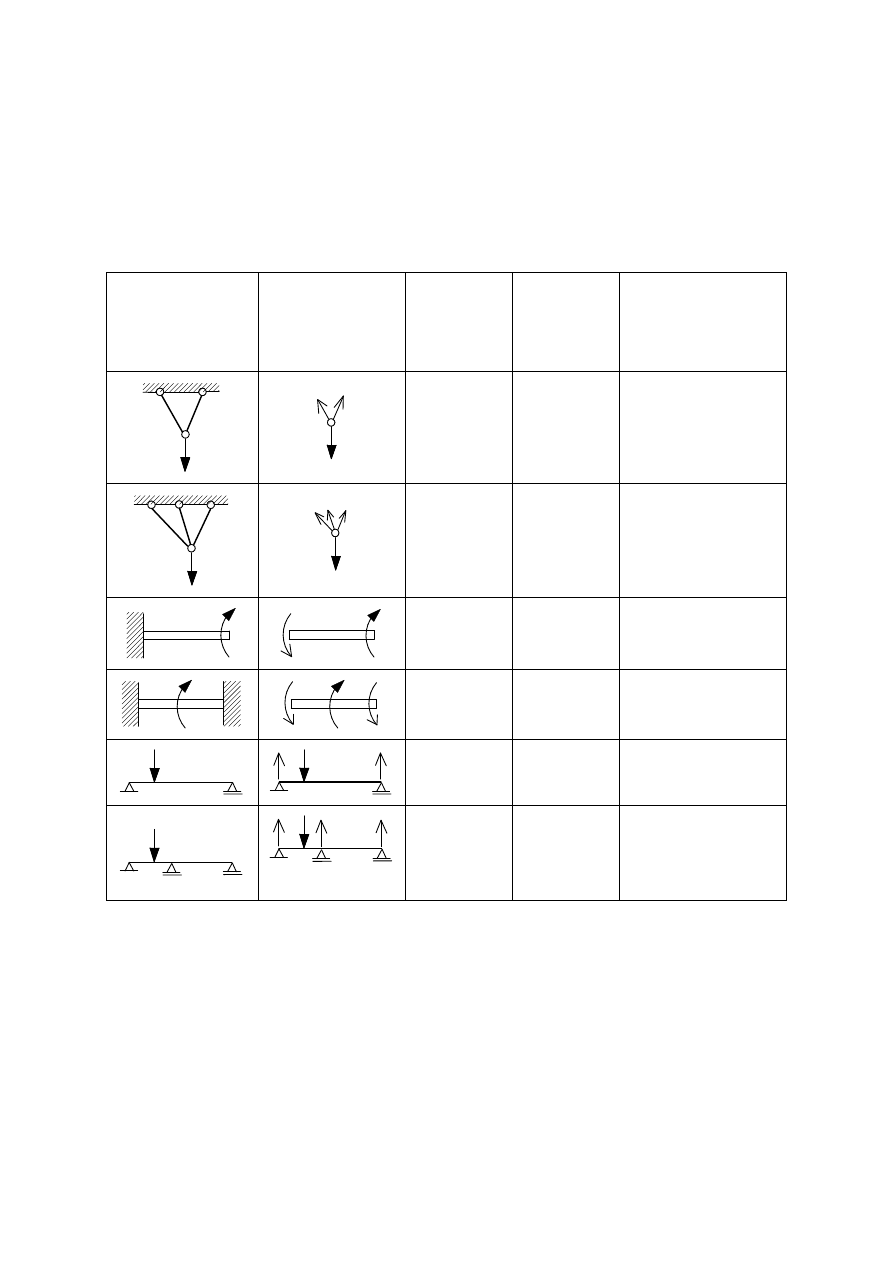
05 Wytrzymałość materiałów

85

Zadania statycznie wyznaczalne i niewyznaczalne

Schemat kon-

strukcji

Schemat sił

Liczba

rów

nań

statyki

RS

Liczba

niewia-

domych

n

Stopień sta-

tycznej niewy-

znaczalno

ści

X = n – RS

2

2

0

2

3

1

1

1

0

1

2

1

2

2

0

2

3

1

05 Wytrzymałość materiałów

86

RACHUNEK JEDNOSTEK

Wielokrotno

ści i podwielokrotności jednostek podstawowych:

mega (M)  10

6

 1000000

kilo (K)  10

3

 1000

centy (c)  10

–2

 0,01

mili (m)  10

–3

 0,001

mikro ()  10

–6

 0,000001

nano (n)  10

–9

 0,000000001

PRZELICZNIK JEDNOSTEK

KONTROLA POPRAWNOŚCI WZORÓW

P

RZYKŁAD

Za pomocą prawa Hooke'a obliczyć przelicznik jednostek, je-

żeli P jest wyrażone w kiloniutonach [kN], L w metrach [m], E w
megapaskalach [MPa], A w centymetrach kwadratowych [cm

2

].





 

.

mm

m

mm

m

cm

kN

MN

cm

MN

m

kN

cm

m

MN

m

kN

L

,

mm

EA

PL

L

4

3

2

2

4

3

2

3

2

2

10

1

10

1

10

10

1

















































P

RZYKŁAD

Określić związek pomiędzy momentem skręcającym, mocą i

liczbą obrotów wału przenoszącego tę moc.

Z dynamiki znany jest wzór: N = M , gdzie N [kW] – moc,

M

S

[Nm] – moment skręcający,  [rad/s] – prędkość kątowa.

Po podstawieniu:  = 2, gdzie  [1/s] – częstość kątowa, n =
60 [obr/min], otrzymuje się:

 

.

m

N

m

N

,

m

N

s

min

obr

kW

s

m

N

min

obr

kW

n

N

M

S

































































9550

3

9549

2

10

60

1

60

2

1

1

10

3

3