1.

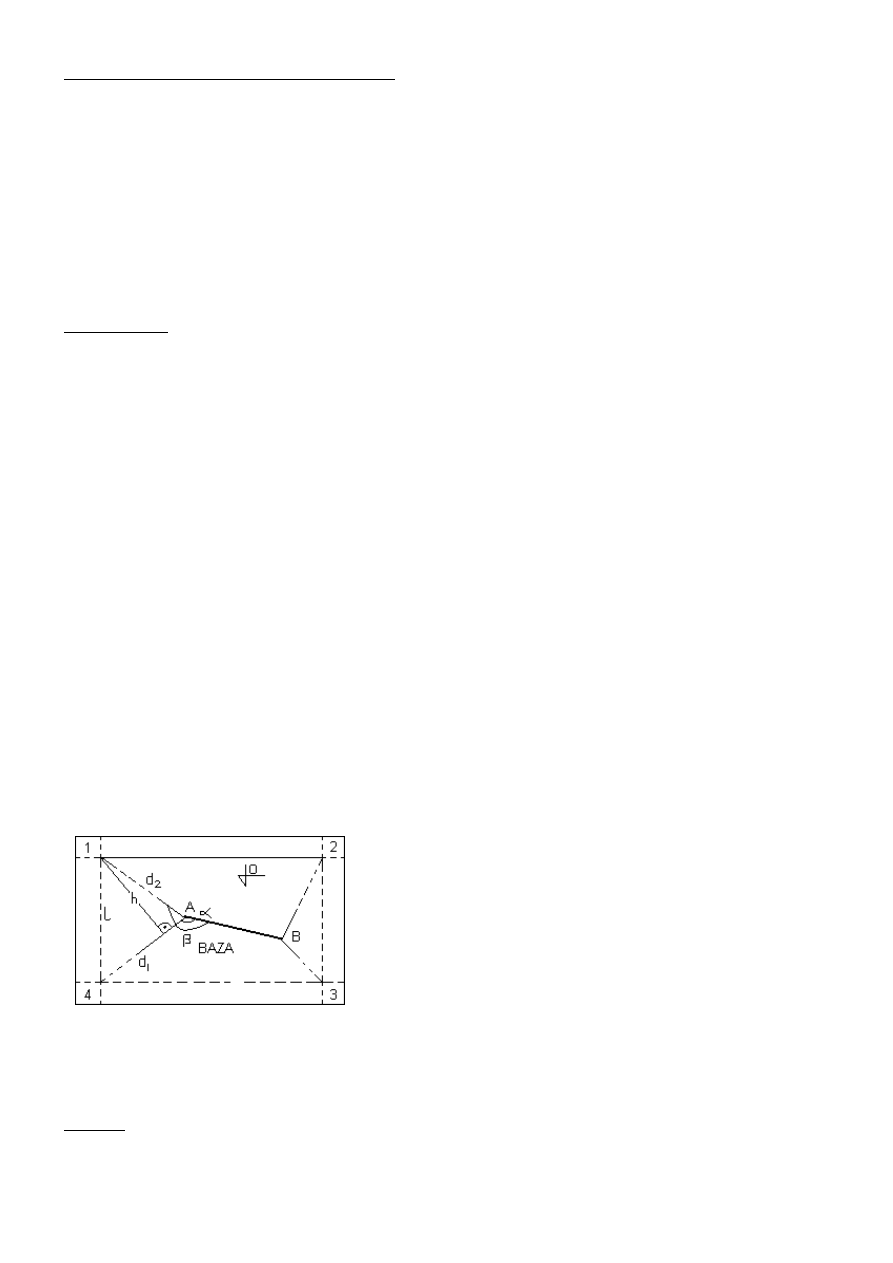
Budownictwo wieżowe, wyznaczenie odchyleń od pionowości metodą kątową wraz z analizą dokładności.

metoda kątowa = metoda kierunkowa = metoda dwusiecznej
Pomiar polega na wyznaczeniu kierunków stycznych (lewej K

L

i prawej K

P

) do obiektu w każdym z przekroju, z każdego stanowiska

obserwacyjnego.
Średnia z każdej pary kierunków określa położenie osi budowli w poszczególnych przekrojach:
K=(K

l

+K

p

)/2

Natomiast DKi=Ki-

K1 jest różnicą między położeniem osi na poziomie i oraz na poziomie najniższym – najbliższym podstawie budowli (

przyjmowany za poziom zerowy)

i pozwala z zależności

d

– odległość między stanowiskiem a osią obiektu

obliczyć składowe wychylenia osi budowli od pionowości w kierunku prostopadłym do celowych z poszczególnych stanowisk obserwacyjnych
Liczba stanowisk od 2 do 5, najlepiej 3, a kąt między poszczególnymi stanowiskami a kierunkiem do osi obiektu 2pi/n, n - liczba stanowisk
obserwacyjnych.

m

u

2

=(du/dd)

2

*m

d

2

+(du/dDα)

2

*mDα

2

+(du/dα

0

)

2

*mα

0

+(du/dαi)

2

*mα

i

mα=mDα
m

u

=√((m

d

/d)

2

+(m

α

/Dα)

2

)

mu=(um

d

√2)/Dα

(m

d

/d)^2 Jest bardzo małe i pomijamy

2.Metoda bezpośredniego rzutowania:
met.stos.gdy obserwowany obiekt ma niewielkie poziome rozmiary u podstawy i jest widoczny z co najmniej 2kier. Obserwacje kat owe-
>liniowymi. W tym celu umieszczamy prostopadle late do kierunku osi budowli-stanowisko. Celujemy teodolitem na wybrany pkt.i opuszczamy
lunete, odczytujemy na lacie polozenie pionowej kreski krzyz. Obserwacje prowadzimy dla 2 stycznych w każdym przekroju,a ich Sr.okresla
Pol.osi obiektu w tym przekroju. Porównanie serdnich dla poszcz.poziomow z poziomem odniesienia pozwalaokreslic składowe wych ylenia osi
prostopadle do kier.wcinajacego. łata usytuowana jest w odl. „d” od stanowiska odległego o wlk.D od osi obiektu. To roznica średnich odchyleń
na łacie”ui” jest mniejsza D/drazy od wielkości składowej wych/osi obiektu U., dwa rysunki (jeden z tw Talesa) i zapisanie U/D=u/d co daje
U=D*(u/d)=K*(O

i

-O

0

) (K-

stałe dla stanowiska), analiza dokładności: m

d

/d=m

D

/D oraz m

D

=m

o

można zapisać m

U

2

=2(m

o

/D)

2

U

2

+2K

2

m

o

2

wpływ

błędu pomiaru długości mały zatem: m

U

=Km

o

sqrt2

Wpływ błędów instrumentalnych: A-niepionowość osi głównej instrumentu (wpływa na

mierzony kierunek) m

K

=r tgα sinβ (r-wychylenie osi instrumentu, α-kąt nachylenia osi celowej, β-azymut osi celowej) przy β=100

g

błąd jest

maksymalny->m

K

=r tgα=r H/D, m

K

na długości D powoduje błąd M

K

=m

K

/ρ *D po porównaniu stronami: M

K

=(rH)/ρ B-niepoziomowość łaty:

m

o

=O'-

O, O=O'cosα, zatem m

o

=O'-

O'cosα=1/2 O'(α/ρ)

2

, zatem wpływ α=sqrt{(2m

o

/O')}

ρ C-nieprostolinowość łaty m

o

2

=O'-O, x/(d+y)=O/d, przy

założeniu cosα=1, sinα=α, O'=O otzrymamy dO'=Od+(O')

2

(α/ρ), wpływ α=(dm

o

2

ρ)/(O')

2

3. Bud wiez

– oprac. wyn pomiar met anal – graf:

Metoda analityczno

– graficzna - jest jedną z metod stosowanych w pomiarach odchyleń osi budowli od pionowości, polegającą na częściowym

skartowaniu i częściowym obliczeniu wartości służących do określenia tych wychyleń.
Do metody należy:
-skartowanie stanowisk obserw.: 1,2,3
-

obliczenie wartości u

-

wykreślenie wstęg wahań w skali 1:1

-

określenie środka ciężkości trójkąta błędów

-

odczytanie wartości wychylenia

Część analityczna - polega na obliczeniu wartości wektorów u

i

przesunięć na poszczególnych wysokościach budowli:

liczona na trzech stanowiskach, gdzie:
d

i

– odległości mierzony pomiędzy poszczególnymi stanowiskami a osią budowli

Δα

i

– wychylenia kątowe osi budowli

Do części graficznej należy:
-skartowanie stanowisk obserwacyjnych (n

ajczęściej są to trzy stanowiska równomiernie rozłożone wokół osi budowli (lub dwa stanowiska

usytuowane pod kątem 90˚ względem siebie),
-

wykreślenie wstęg wahań w skali 1:1 (dokonujemy tego poprzez równoległe przesunięcie linii łączących oś budowli ze stanowiskiem o

obliczony wektor u),
-

określenie środka ciężkości trójkątów błędów,

-

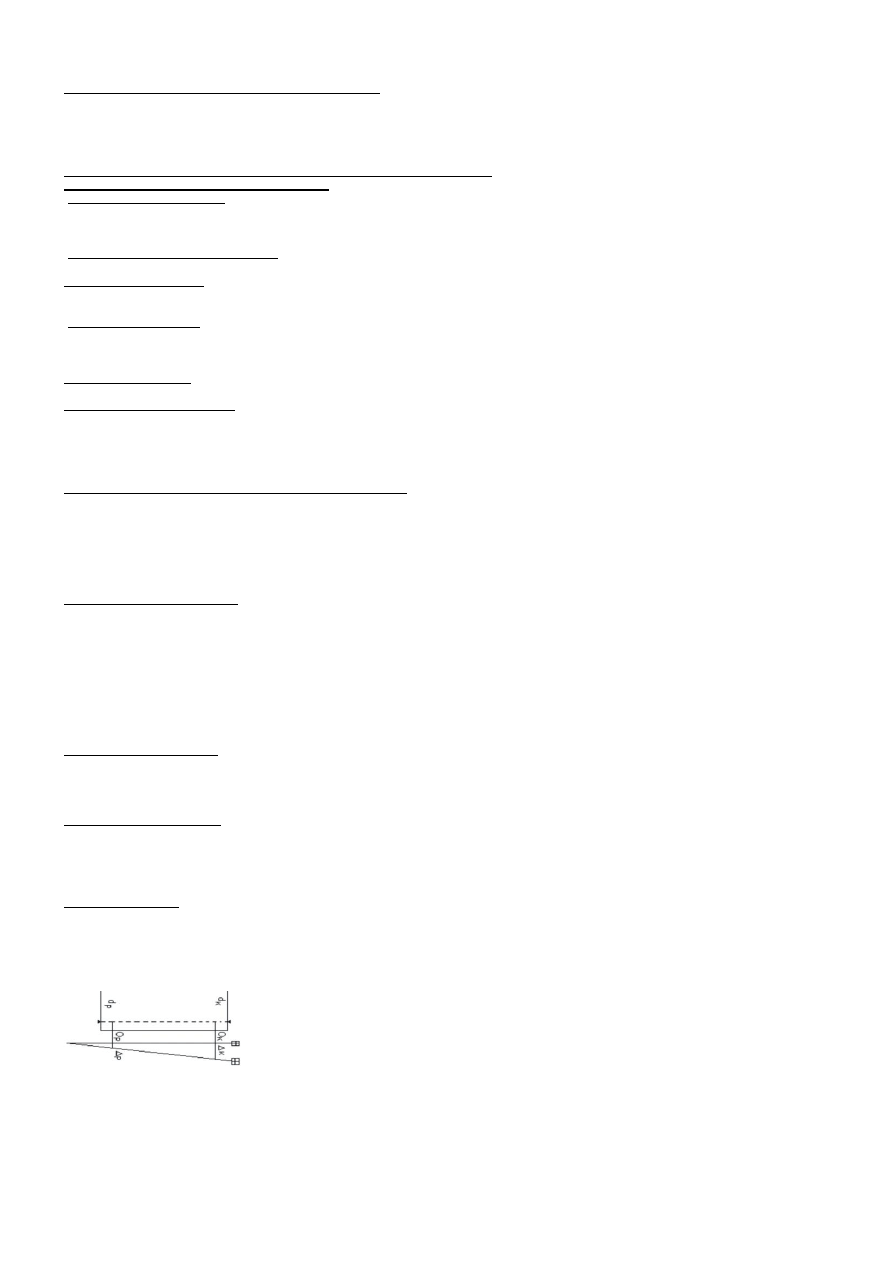
odczytanie wartości wychyleń na poszczególnych poziomach.

4. Opracowanie wyników pomiarów metodą analityczną:
Postępowanie: 1. obliczenie K

śr

2. obliczenie wartości kątowej wychylenia Δα=K

i

śr

=K

o

śr

3. obliczenie różnicy wysokości ΔH=d(tgβ

i

-

tgβ

o

)

4.obliczenie U, Kątowe przesunięcie można zapisać w postaci różniczkowej zupełnej: Δα=-sinφ/d ρu

x

+cosφ/d ρu

y

, dzielimy przez d/ρ i

otrzymujemy u=-

sinφ u

x

+ cosφ u

y

, zestawiamy równani

a poprawek i rozwiązujemy je stosując metodę najmniejszych kwadratów. Obliczamy u

x

i

u

y

a następnie u

2

=u

x

2

+u

y

2

5. CZYNNIKI WPŁYWAJĄCE DESTRUKCYJNIE NA BUDOWLE WYSMUKŁE:
WPŁYWY MECHANICZNE- zalicza się do nich :
-

CIĘŻAR WŁASNY BUDOWLI- ciężar trzonu lub powłoki, wykładziny żaroodpornej, zraszalnika, urządzeń dodatkowych. Ciężar ten decyduje o

stateczności budowli.
-

WPŁYW ODKSZTAŁCENIA PODŁOŻA GRUNTOWEGO- reakcja podłoża gruntowego na ciężar budowli i powstające z tej przyczyny

osiadanie gruntu może wywołać przechyły budowli.
-

WPŁYW EKSPLOATACJI GÓRNICZEJ- mechanizm tego zjawiska na budowle znajdujące się na powierzchni terenu związany jest z

powstawaniem niecki osiadań, będącej skutkiem przesuwania się frontu eksploatacji.
-

WPŁYWY DYNAMICZNE- budowle wieżowe są wrażliwe na obciążenia- drgania, których źródłem mogą być: procesy wibracyjne

przeprowadzane przez człowieka w celach technologicznych, urządzenia techniczne, wywołujące drgania skutkiem własnej pracy, zjawiska
losowe, niezależne od człowieka-przede wszystkim ruchy tektoniczne)
-

OBCIĄŻENIA WIATREM- duże powierzchnie boczne budowli wieżowych i ich znaczne wysokości sprawiają, że budowle te przejmują na

siebie olbrzymie obciążenia, powstałe od parcia wiatru co może wywołać przechyły budowli, a także zjawiska, które mogą mieć istotny wpływ na
pomiary geodezyjne wykonywane podczas wznoszenia budowli, z wpływem tym należy się również liczyć podczas wykonywania pomiarów
kontrolnych istniejących obiektów
WPŁYWY TERMICZNE- zalicza się do nich przede wszystkim wpływ nierównomiernego nasłonecznienia. Jest to zjawisko bardzo ważne
podczas obsługi wznoszenia budowli wieżowych oraz podczas wykonywania pomiarów kontrolnych.
WPŁYWY FIZYKOCHEMICZNE- zalicza się do nich przede wszystkim zjawiska, wywołujące zmiany strukturalne materiału konstrukcyjnego. Są
to w pierwszej kolejności reologia i relaksacja, wywołujące zjawiska skurczowe i starzeniowe, które występują w wyniku szkodliwego
oddziaływania na beton różnego rodzaju substancji chemicznych, zawartych w spalinach. Szkodliwe działanie związków chemicznych polega
na rozkładzie nierozpuszczalnego nie rozpuszczalnego w wodzie węglanu wapnia na czynniki rozpuszczalne, które są następnie wypłukiwane z
konstrukcji przez wody odpadowe. Prowadzi to w sposób powolny do pogo

rszenia się jakości materiału konstrukcyjnego.

6. TECHNOLOGIE WZNOSZENIA BUDOWLI WYSMUKŁYCH.
W zależności od rodzaju budowli rozróżniamy 4 różne technologie wznoszenia:
Dla kominów, wież i silosów:
1. przestawna- budowle o zmiennym przekroju poprzecznym
2.ślizgowa- budowle o stałym przekroju poprzecznym
Dla chłodni kominowych:
1.deskowania przestrzennego-

chłodnie hiperboliczne

2.klatkowa-

chłodnie hiperboliczne

TECHNOLOGIA PRZESTAWNA
Stosuje się ją przy budowie kominów, wież , silosów. Cecha charakterystyczna jest to, że budowla wznoszona jest segmentami o wys. 2,5-3m.
Urządzenie technologiczne do wznoszenia obiektu tą technologią zawieszone jest na wieży ustawione wewnątrz budowli.
Jest ono wykonane z rur lub kształtowników stalowych. Na wieży zawieszany jest pomost roboczy, do którego z kolei podwieszone jest kołowe
deskowanie, uformowane z odcinków blachy stalowej. Wznoszenie budowli wysmukłych odbywa się segmentami tzw. cyklami budowlanymi.
Fazy cyklu:
-

nadbudowa wieży i podniesienie pomostu maszynowego,

-

zwolnienie deskowania i podniesienie pomostu roboczego wraz z blachami formy zewnętrznej na poziom wyższy,-

-wykonanie zbrojenia,
-

ustawienie blach formy zewnętrznej i wewnętrznej w projektowanym promieniu

-zabetonowanie
TECHNOLOGIA ŚLIZGOWA
Urządzenie do nadawania budowli projektowanego kształtu opiera się na wykonanym już fragmencie obiektu. W żelbetonowej ścianie prowadzi
się na całym grube pręty ślizgowe, które stanowią oparcie dla urządzeń. Po prętach tych pełzną dźwigary hydrauliczne, zapewniające ruch
postępowy w 2-3 centymetrowych interwałach, co w praktyce stanowi ruch płynny. Technologia ślizgowa stosowana jest najczęściej przy
wznoszeniu budowli o stałym przekroju poprzecznym.
TECHNOLOGIA KLATKOWA
Charakteryzuje ją stosowanie systemów automatycznego podnoszenia dla elementów pomostów obwodowych wykonanych w postaci
charakterystycznych klatek. Stosuje się ją do wznoszenia chłodni kominowych. W technologii tej wyeliminowano wieżę przyścienną zastępując
ją dźwigiem ustawionym w osi pionowej chłodni. Eliminacja wieży przyściennej spowodowała utratę możliwości rozwijania osnowy realizacyjnej.
Spowodowało to konieczność przeniesienia osnowy realizacyjnej na wykonany fragment ściany i zawieszenie tam elementów deskowania.

7. Met. stałej prostej
a) stawiamy teodol. na p-kcie linii bazowej osnowy bud-

mont., celujemy na tarczę na końcu tej linii

b) poziomujemy teodol. przy każ-dym pomiarze
c) układamy łatę na stropie kondygnacji roboczej i ustawiamy ją prostopadle do płaszcz. celowania
d) łatę ustawiamy tak, by obraz tarczy sygn. znalazł się na pionowej kresce siatki celowniczej teodol.
e) zaznaczamy na stropie tyczony punkt. Czynności w 2 poł. lunety.

1) jeśli O

K

=O

P

to O

K

’-



K = O

P

’-



P

2)



K = d

K

/d

P

*



P O

K

’-O

P

’ = (d

K

/d

P

*



P) -



P

O

K

’-O

P

’ = (d

K

/d

P

-1)

*



P O

K

’-O

P

’ = [(d

K

-d

p

)/d

P

]

*



P

poprawki trasowania



P = [(O

K

’-O

P

’)/(d

K

-d

P

)]

*

d

P



K = [O

K

’-O

P

’] +



P

analiza dokładności
1.bł centrowania teodol. 0,4mm
2.bł centrowania sygnału 0,4mm
3.niepionowość osi obrotu teodol. 0,9mm
4.bł celowania na tarczę 0,3mm
5.bł wprowadzenia sygn. w oś celową 0,4mm
6.bł oznaczania wskaźnika 0,8mm
7.inne błędy 0,3mm
m =



(m

12

+m

2

2

+...m

7

2

) =



1,4mm

8) Suwnice podzial i rys.:
Suwnica

– jest samojezdnym urządzeniem transportowym, pracującym w obrębie hali produkcyjnej lub składu materiałów, elementów.

Wyróżniamy:
a) suwnice bramowe-

stosowane do składowania surowców, montażu dużych konstrukcji, np. stocznie

b)

suwnica półbramowa (półportalowa)- jako przyścienna na zewnątrz lub wewnątrz hali, służą do rozładunku, załadunku wagonów.

------------------------------------------------------------------------------------------------

a) b)
c)

przyścienne (wspornikowe)- do transportu niewielkich ciężarów.

d)pomostowe- stosowane w halach produkcyjnych.

-------------------------------------------------------

9.) Suwnice

– wymagania techniczne:

a)

wzajemna różnica poziomów główek szyn w jednym przekroju poprzecznym toru jezdnego nie powinna być większa niż:

-

na podporach (nad słupami) – 10mm

-

w przęśle (na środkach odcinków między słupami) -15mm,

b)

różnica poziomów główki szyny na słupach w tej samej osi podłużnej nie powinna przekraczać wartości b/1500, gdzie b – rozstaw słupów, i

jedno

cześnie nie może przekraczać 10mm,

c)

odchylenie w wymiarze prześwitu toru jezdnego w stosunku do projektu nie powinno różnić się więcej niż ±5mm (odchyłka rozstawu szyn

toru),
d)

odchyłka osi szyny od jej osi teoretycznej nie powinna być większa od 2,5mm,

e)

wzajemne przesunięcie czoła szyn w styku, w poziomie lub pionie, nie powinno być większe od 1mm,

f)

odchylenie osi górnego pasa belki suwnicowej w środku jej rozpiętości od płaszczyzny pionowej, przechodzącej przez środki podpór przy

wysokości belki h ,nie powinno być większe od h/500.

10. Analityczno - graficzna
Mając odczyty z łaty L i P obliczamy y

L

i y

P

praktyczne w układzie odniesienia (geodezyjnym). Obliczamy środek toru dla każdego

zasygnalizowanego p-ktu [y

0

=(y

L

+y

P

)/2] i wartość średnią położenia osi toru [y

śr

=(



Y

0

)/n]. Następnie obl. odchyłki ze wzoru: y

0

-y

śr

. Wrysowanie

na kalce milimetrowej y

o

4. odczytanie Y

o

z wrysowanej osi torów Obliczone odchyłki odejmujemy od teoretycznej wartości położenia osi toru

(Y

0

), po czym obliczamy Y

L

=Y

0

-S/2 i Y

P

=Y

0

+S/2. W końcu wyliczamy odchyłki osi belek w oznaczonych p-ktach od wypośrodkowanych osi

teoretycznych: V

YL

=y

L

-Y

L

; V

YP

=y

P

-Y

P

oraz odchyłki rozstawu osi belek w poszczególnych przekrojach V

ROZ

=V

YP

-V

YL

Met. analityczna
Różni się od anal-graf, że nie rysujemy wypośrodkowanej osi toru, ale obliczamy współczynniki tej osi oraz współrzędne Y0 przez podstawienie
ich do odpowiednich równań poprawek. Równania układa się wg wzoru: a

*

i+b = y

0

-y

śr

+v; i = d

i

/d

a,b -

współczynniki równania osi toru

di - odl p-ktu od

początku toru

d -

odl. między sąsiednimi p-ktami

y

0

-y

śr

- wyraz wolny równania

v - poprawka
Obliczone odchyłki p-któw oznaczonych na osiach belek od wypośrodkowanych teoretycz. osi szyn wykorzystywane są w ten sposób, że
odkłada się je od wspomnianych p-któw z odwrotnym znakiem, uzyskując na belkach miejsca wskaźników do montażu szyn. 1.obliczenie
równania prostej ai+b=y

o

-y

śr

+v 2. obliczenie poprawki v=ai+b-(y

o

-y

śr

) 3.wyznaczenie współczynników równania osi torów a i b X=(A

T

A)

-1

A

T

L

4.obliczenie poprawek v

5.obliczenie położenia osi torów Y

o

=y

o

-v 6.obliczenie Y

L

i Y

P

11. WYMIEŃ UKŁADY KONSTRUKCYJNE BUDYNKÓW, RYSUNKI.
Dla budownictwa mieszkaniowego i podobnego

– Część ścian nośnych może być w tym przypadku zastąpiona słupami. Słupy mają w tym

przypadku pr

zekrój płaski, mieszczący się w grubości ścian, tj. 15 cm słupy formowane są w deskowaniach układów ścianowych.

Dla budownictwa usługowego - Ściana nośna, nazywana również konstrukcyjną, przenosi na fundament lub inne konstrukcje elementy budowli
ciężar własny i obciążenie z elementów spoczywających na niej (np. obciążenie z dachu, obciążenie użytkowe stropów i ich ciężar własny).
Ściana konstrukcyjna oprócz przejmowanych obciążeń pionowych współpracuje ze stropami w przenoszeniu obciążeń poziomych, twor ząc
układy konstrukcyjne: podłużne, poprzeczne, krzyżowe.

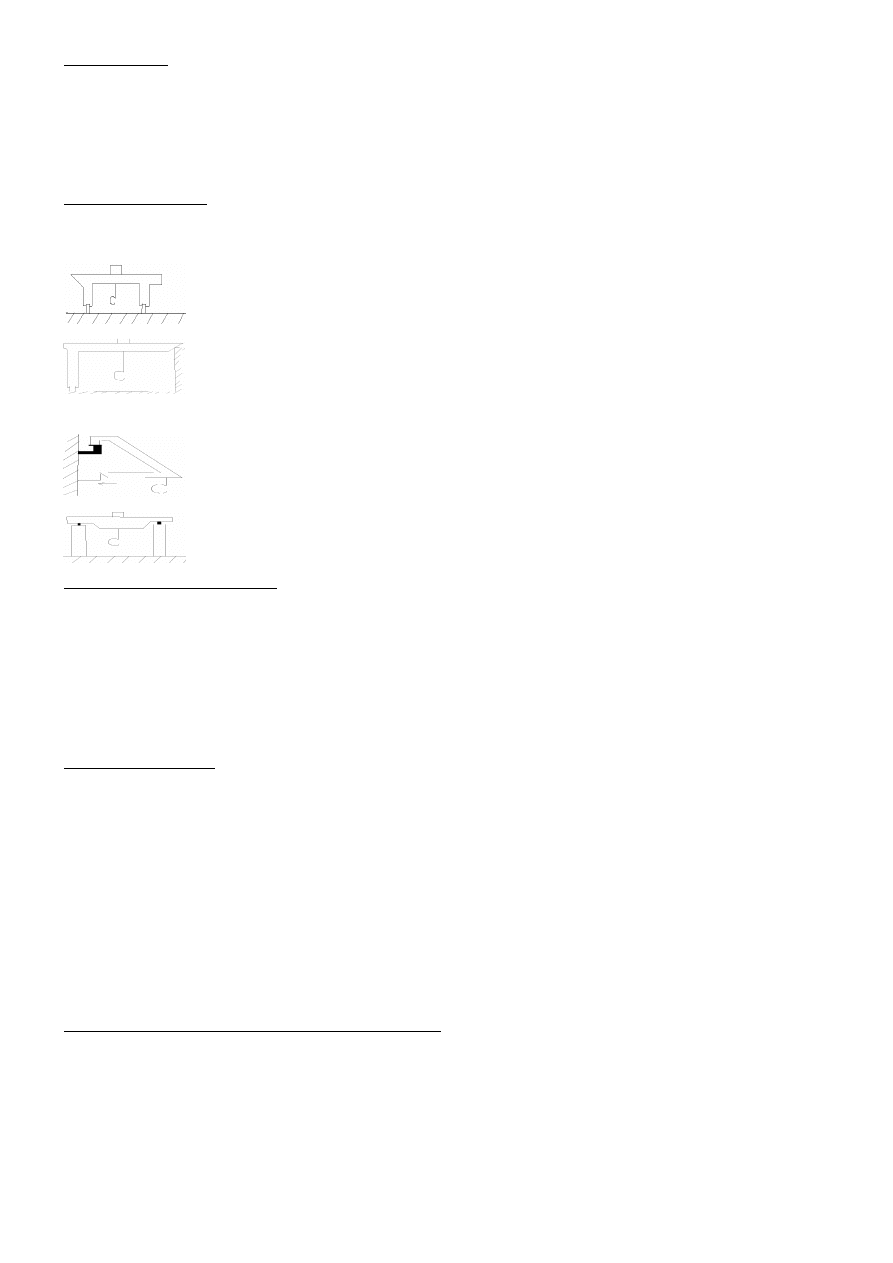
12.) Montaz wymuszony i swobodny:

Montaż swobodny – montaż elementów prefabrykowanych, wykonywany na styk prosty, bez pomocy części łączących, ograniczających
wielkości odchyłek montażu, pozwalający na swobodne, wzajemne przesunięcia względem siebie montowanych elementów.

Montaż wymuszony (przymusowy) – montaż elementów prefabrykowanych, wyposażonych w płaszczyznach stykowych w złącza montażowe
ograniczające odchyłki montażu, wyznaczające z dużą dokładnością miejsce usytuowania elementów w konstrukcji budynku.

System budowlany W-

70 (Wrocławska Wielka Płyta) - wielkowymiarowe elementy ścienne są tu zaopatrzone w tzw. urządzenia rektyfikacyjne.

Są to śruby rektyfikacyjne (śrubowe trzpienie) z nakrętkami, umieszczone w górnej części płyty w jej osi podłużnej oraz wnęki rektyfikacyjne z
tulejami, umieszczone w dolnej części płyty.

13.) Bud mieszk

– przeniesienie wskaz kontr met bezp rzutowania:

Metodą rzutowania można wyznaczyć osie konstrukcyjne lub linie równoległe do tych osi dla ścian zewnętrznych i wewnętrznych. Można też
przenosić na kondygnację roboczą wszystkie typy osnowy wewnętrznej.
W celu wyznaczenia wskaźników konstrukcyjnych na dowolnym poziomie roboczym metodą rzutowania, należy:
a

) ustawiony teodolit na stanowisku spoziomować i wycelować pionową kreskę siatki celowniczej na odpowiedni punkt celowania  czyli

wskaźnik wyjściowy oznaczony na budynku,
b) wyznaczyć w dwóch położeniach lunety wskaźnik na krawędzi stropu wg pionowej kreski siatki celowniczej teodolitu,
c) za każdym razem przed rozpoczęciem pracy w danym położeniu lunety doprowadzić libelę teodolitu dokładnie do poziomu,
d) z przeciwległego stanowiska wyznaczyć wskaźnik na krawędzi stropu z drugiej strony budynku.

Metodą rzutowania wykonuje się również pomiary kontrolne osiowości i pionowości ścian, sklepów i innych elementów konstrukcyjnych.
Zależność między odsunięciem od płaszczyzny konstrukcyjnej teodolitu i wskaźnika konstrukcyjnego.

Rys.1

Rys.2

Wpływ odsunięcia teodolitu od płaszczyzny konstrukcyjnej na dokładność wyznaczenia położenia wskaźnika metodą rzutowania zgodnie z rys.2
określa wzór:
q = p* (D/d)
D

– odl. Stanowiska teodolitu od ściany budynku

d

– odsunięcie płaszczyzny przenoszonego wskaźnika od ściany budynku

p

– wpływ odsunięcia stanowiska teodolitu od płaszczyzny konstrukcyjnej na wyznaczenie położenia wskaźnika

q

– dopuszczalne odsunięcie stanowiska teodolitu od płaszczyzny konstrukcyjnej.

Dokładność tyczenia:
m3 = 0,9 mm (bł. Niepionowości osi głównej teodolitu)
m4 = 0,3 mm (bł. Celowania)
m5 = 0,4 mm (wprowadzenie sygnału w płaszczyznę celowania)
m6 = 0,8 mm (ozn. Wskaźnika na stropie)

m

2

= m3

2

+ m4

2

+ m5

2

+ m6

2

m = 1,3 mm

14. PRZENOSZENIE WSKAŹNIKÓW KONSTRUKCYJNYCH

Przed przystąpieniem do obsługi geod. kondygnacji powtarzalnych i wyznacz. wskaźników konstrukcyjnych na poszczegól. poziomach robocz.
należy sporządzić szkic tyczenia, zawierający rozmieszcz. osi konstrukcyjnych zgodnie ze szkicem dokumentacyjnym oraz osnowę budowl.-
montaż. Osn. ta będzie służyć do przenoszenia osi konstrukcyjnych na poszczególne kondygnacje.

Met. stałej prostej
a) stawiamy teodol. na p-kcie linii bazowej osnowy bud-

mont., celujemy na tarczę na końcu tej linii

b) poziomujemy teodol. przy każ-dym pomiarze
c) układamy łatę na stropie kondygnacji roboczej i ustawiamy ją prostopadle do płaszcz. celowania
d) łatę ustawiamy tak, by obraz tarczy sygn. znalazł się na pionowej kresce siatki celowniczej teodol.
e) zaznaczamy na stropie tyczony punkt. Czynności w 2 poł. lunety.
1) jeśli O

K

=O

P

to O

K

’-



K = O

P

’-



P

2)



K = d

K

/d

P

*



P O

K

’-O

P

’ = (d

K

/d

P

*



P) -



P

O

K

’-O

P

’ = (d

K

/d

P

-1)

*



P O

K

’-O

P

’ = [(d

K

-d

p

)/d

P

]

*



P

poprawki trasowania



P = [(O

K

’-O

P

’)/(d

K

-d

P

)]

*

d

P



K = [O

K

’-O

P

’] +



P

analiza dokładności
1.bł centrowania teodol. 0,4mm
2.bł centrowania sygnału 0,4mm
3.niepionowość osi obrotu teodol. 0,9mm
4.bł celowania na tarczę 0,3mm
5.bł wprowadzenia sygn. w oś celową 0,4mm
6.bł oznaczania wskaźnika 0,8mm
7.inne błędy 0,3mm
m =



(m

12

+m

2

2

+...m

7

2

) =



1,4mm

Metoda rzutowania
Wyznacza się osie konstrukcyjne lub linie równoległe do tych osi dla ścian zewn. i wewn. Przenosi się też tą met. wszystkie t ypy osnowy wewn.
na kondygnację roboczą.
1)

teod. stawiamy na stanow., poziomujemy, celujemy pionową kreską na wskaźnik wyjściowy na bud.

2)

w 2 poł. lunety wyznaczamy wskaźnik na krawędzi stropu wg kreski pion.

3)

każdorazowo poziomujemy teod.

4)

analogicznie wyzn. wskaźnik z drugiej strony budynku

5)

wtyczyć teod. w linię przeniesionych wskaźników i za pomocą łaty realizacyjnej wyznaczamy wskaźniki ścian zewn.

ANALIZA:
niepionowość osi obrotu teod. 0,9mm
bł. celowania 0,3mm
bł. wprowadzenia sygnału w płaszcz. rzutowania 0,4mm
oznacz. wskaźnika na stropie 0,8mm
m

2

= m

1

2

+...m

4

2

= 1,3mm

Metoda biegunowa
Tyczenie wskaźników montażowych metodą biegunową odbywa się z punktów P i Q przenoszonych na strop kondygnacji roboczej za pomocą
pionowników (rys. ). Metoda ta polega na tym, że poszczególne punkty 1’, 2’, ..., n’ osi montażowych na kolejnych kondygnacjach wyznacza się
przez odkładanie od punktów końcowych bazy P

i

i Q

i

stałych kątów



1

,



2

,



3

,...,



n

oraz odcinków l

1

, l

2

, l

3

, ..., l

n

wcześniej pomierzonych na

poziomie zerowym. W tym celu na każdej kondygnacji nad punktami P

i

, Q

i

ustawia się teodolit, który powinien być starannie zorientowany,

zawsze na ten sam dobrze widoczny i odległy cel I, II ... itd. Następnie od kiedy na kierunkach wyznaczonych przez ramiona wymienionych
kątów odkłada się odcinki l

1

, l

2

, ..., l

n

, których końce określają położenie punktów osiowych 1’, 2’, ..., n’.

W związku z powyższym podczas lokalizacji punktów końcowych bazy pomiarowej P

0

i Q

0

powinny być spełnione następujące warunki:

*z punktów końcowych bazy (P

0

i Q

0

) muszą być dobrze widoczne na wszystkich kondygnacjach co najmniej po dwa stałe punkty służące do

zorientowania teodolitu (I, II, III ...),
*punkty P

0

i Q

0

powinny być tak zlokalizowane, aby odległości do tyczonych punktów osi montażowych nie przekraczały długości taśmy 20-

metrowej,

l

2

= d

1

2

+ d

2

2

– 2d

1

d

2

cos(



-



)

m

L

2

= cos

2



m

d1

2

+ cos

2



m

d2

2

+ h

2

m



2

+ h

2

m



2

ANALIZA
bł centrowania pionownika 0,3mm
bł poziomowania libelli 0,1mm
bł odczytu podziałki 0,7mm
bł oznaczenia p-ktu na tarczy 0,5mm
m = 0,5mm przy n kondygnacjach m

n

= 0,5



n

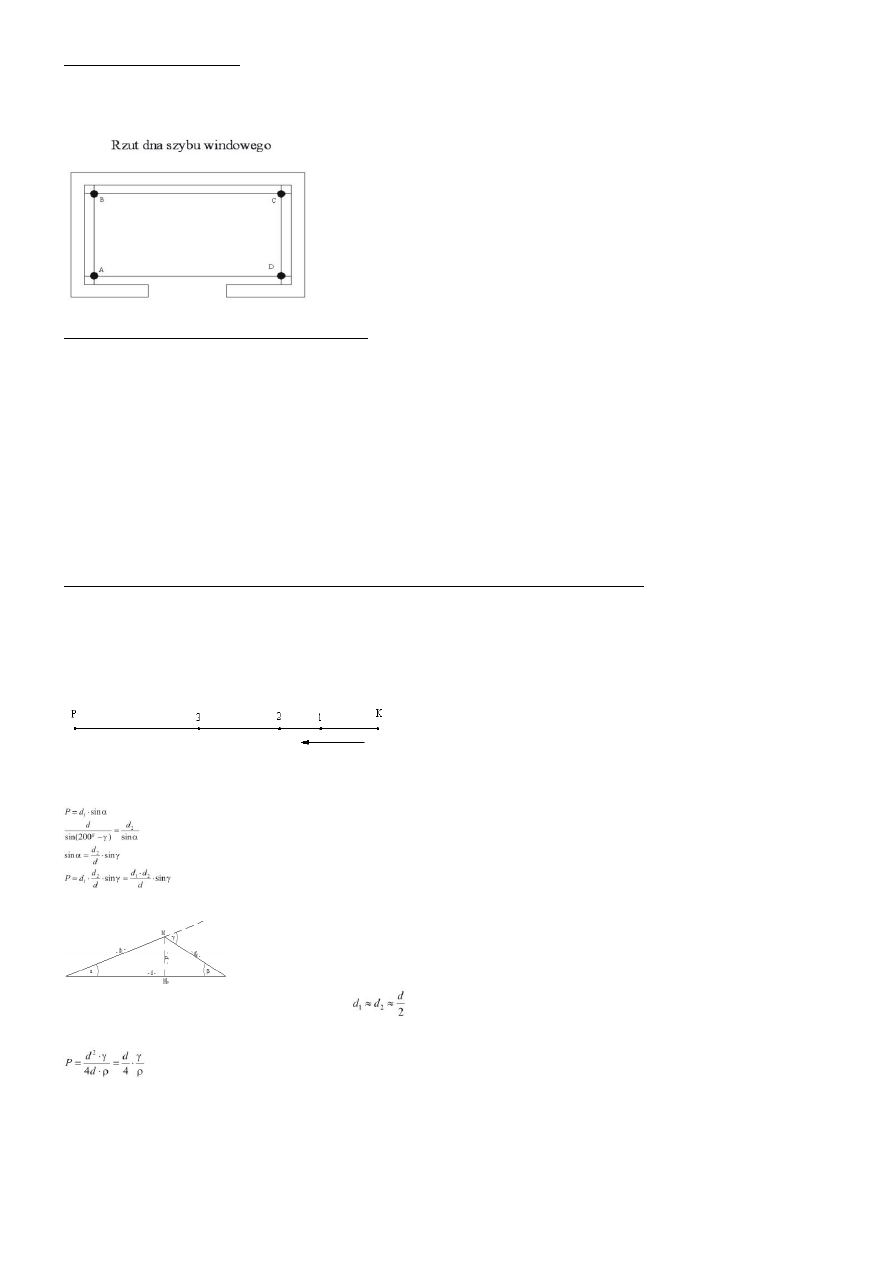
15.) Szyby windowe

– pomiary:

Na dnie szybu windowego zakładamy osnowę pomiarową (A, B, C, D) w odległościach równych od ścian szybu na tych punktach
ustawiamy pion optyczny poczym na każdym piętrze wykonujemy pomiar odległości ścian szybu od pionu postępujemy tak samo na
każdym kolejnym punkcie osnowy. Odchyłki od pionu nanosimy na rysunek. Pomiary wykonuje się w celu wpasowania szyn
windowych w szyb.

16.Szyby windowe. Opracowanie wyników pomiarów:

Metoda graficzna:

osnową pomiarową są w tym wypadku cztery punkty stanowiące wierzchołki prostokąta o znanych wymiarach. Przekroje

szybu na poszczególnych kondygnacjach orientuje się względem tego prostokąta i nanosi na jeden zbiorczy rysunek, podobnie jak przy
określaniu odchyłek kształtu szybu. W skali 1:10 nanosi się na kalce technicznej położenie osi prowadnic dźwigowych. Kalkę przykłada się do
wspomnianego rysunku zbiorczego i tak się przesuwa, aby rzuty prowadnic mieściły się swobodnie w powierzchni zawartej między liniami
poziomymi przekrojów wewnętrznych powierzchni ścian szybu. 16. Metoda analityczna: polega na określeniu optymalnych płaszczyzn, w
których zmontowane zostaną prowadnice. Matematyczną podstawą opracowania wyników pomiaru jest metoda parametryczna wyrównania z
warunkami wiążącymi parametry. W obliczeniach wagi dla poszczególnych równań wiążących są dużo większe od wag równań podstawowych.
Teoretyczne wagi powinny wynosić nieskończoność, a podstawienie konkretnych liczb spowodowane jest niemożliwością wykorzystania
nieskończoności w obliczeniach. W praktyce geodezyjnej inwentaryzację wykonuje się z dwóch punktów znajdujących się w pobliżu drzwi
wejściowych do szybu windowego. Teoretycznie inwentaryzacja wykonana z czterech punktów daje większe możliwości wpasowania nie tylko
osi prowadnic dźwigowych, ale całego szybu windowego. Obliczenia wykonuje się w układzie współrzędnych, gdzie osiami X i Y są krawędzie
ścian szybu w piwnicy budynku. W stosunku do tych osi odnosi się krawędzie ścian dla każdej kondygnacji. Współrzędne X i Y, które są
jednocześnie wyrazami wolnymi dla poszczególnych punktów każdej wyrażone są w układzie XOY. Tok postępowania: 1.obliczenie X,Y
punktów obserwacyjnych 2.ułożenie równań poprawek X

i

obs

+V

xi

=X

i

wyr

, Y

i

obs

+V

yi

=Y

i

wyr

3. nałożenie na niewiadome warunków równoległości:X

B

w

-

X

A

w

=S, X

c

w

-X

B

w

=S, Y

C

w

-Y

D

w

=h, Y

B

w

-Y

A

w

=h i prostopadłości: X

B

w

-X

A

w

=0, X

c

w

-X

B

w

=0, Y

C

w

-Y

B

w

=0, Y

D

w

-Y

A

w

=0

17.BUDOWNICTWO DROGOWE. TYCZENIE DŁUGICH ODCINKÓW PROSTYCH, METODY, dokładność.

Sposób tyczenia zależy od warunków terenowych, długości odcinka i wymaganej dokładności tyczenia.
I. Tyczenie przy możliwości celowania wzdłuż całego odcinka.
1. Jeżeli długość odcinka nie przekracza 2 km, można zastosować tyczenie zwykłe przy użyciu teodolitu. Na punkcie początkowym P
ustawiamy teodolit, a na punkcie końcowym K – dobrze widoczny sygnał. Tyczenie zaczynamy od punktu najdalszego i prowadzimy
je w kierunku „na siebie”. Punkty pośrednie 1, 2, 3, ...(zwane kierunkowymi) rozmieszczamy we wzajemnej odległości nie większej niż
300 m, aby później można było między nimi przetoczyć prostą nawet bez posługiwania się teodolitem. Punkty kierunkowe obieramy w
takich miejscach, gdzie nie będą narażone na zniszczenie. Sygnał wprowadzamy w płaszczyznę celowania.

Jeżeli punkt końcowy i punkt tyczony są jednocześnie w polu widzenia, to wyznaczenie punktu pośredniego można wykonać przy jednym
położeniu lunety, jeżeli natomiast punkty te znajdują się na różnych wysokościach, to tyczenie należy wykonać przy dwóch położeniach lunety.
2. W ce

lu dokładniejszego wytyczenia długiej prostej mniej więcej w pobliżu środka odcinka AB obieramy punkt M, mierzymy na nim kąt (200

g

-

γ)

i obliczamy przesunięcie P, które należy wykonać tak, aby punkt M znalazł się dokładnie na tyczonej prostej.

bo sin(200-

γ)=sinγ

Można przyjąć z bardzo dużym przybliżeniem, że:

oraz ze względu małą wartość kąta gama: singama=gama
Otrzymujemy wzór końcowy na wielkość przesunięcia:

Długości odcinków d

1

i d

2

wystarczy znać z takim przybliżeniem, jakie daje graficzne ich określenie z mapy. Jeżeli przyjmiemy, że np. d

1

= d

2

=2

km, a kąt γ = 10’ zmierzymy z dokładnością ±0,1’, to w celu wyznaczenia punktu pośredniego M

o

na prostej z dokładnością ± 5 cm wystarczy

znać odcinki d

1

i d

2

z dokładnością ± 20 m.

Po odmierze

niu odcinka P od punktu M wzdłuż dwusiecznej sprawdzamy, czy tak znaleziony punkt M

o

leży na prostej PK. W tum celu mierzymy

kąt PM

o

K

– powinien on być równy 200

g

.

II. Tyczenie prostej w terenie falistym.

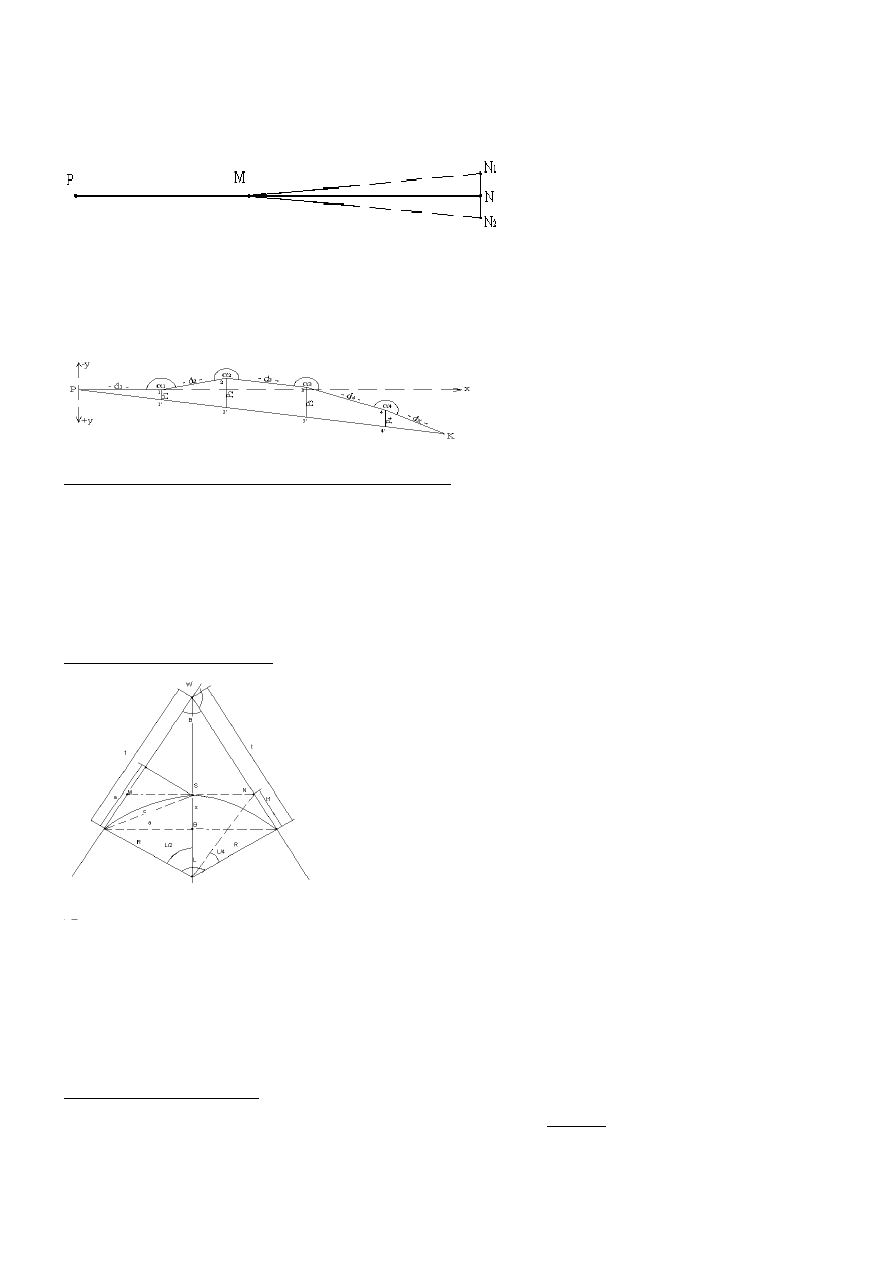
1.W terenie falistym zdarza się, np. przy tyczeniu przez doliny, że z punktu początkowego widać punkt końcowy i bliskie punkty pośrednie, lecz
dalsze są niewidoczne. Ponieważ mamy w tym wypadku dany kierunek prostej, więc wytyczamy najpierw możliwie najdalszy punkt pomocniczy
M. Jeżeli z punktu tego widać punkt końcowy K, to dla sprawdzenia możemy zmierzyć kąt PMK, który powinien być równy 200

g

.

Jeśli jednak z punktu M nie widać punktu K, to do tyczenia dalszych punktów stosujemy metodę przybliżeń. Na ostatnim wytyczonym punkcie M
ustawiamy teodolit, celuje

my na punkt P i po przerzuceniu lunety przez zenit wyznaczamy na kierunku MK możliwie daleko położony punkt N

1

.

Ze względu na błędy instrumentalne celujemy na punkt P ponownie przy drugim położeniu lunety i po przerzuceniu jej przez zenit wyznaczamy
punkt N

2

. Jeżeli punkty N

1

i N

2

nie pokrywają się, to właściwe położenie punktu N otrzymamy dzieląc odcinek N

1

N

2

na połowę.

2.Jeżeli z punktu początkowego nie widać punktu końcowego, a w terenie istnieje osnowa geodezyjna, to po nawiązaniu do niej kierunku
pro

jektowanej trasy można będzie obliczyć współrzędne punktów P i K. Pozwoli to wyznaczyć kąt, zawarty między tyczoną prostą a kierunkiem

na widoczny punkt triangulacyjny lub poligonowy.
3.Jeżeli punkty początkowy i końcowy nie są widoczne, lecz w terenie na kierunku tyczonej trasy istnieje dostatecznie zagęszczona sieć
poligonowa, to punkty kierunkowe można wyznaczyć przez obliczenie przecięć prostej PK z bokami poligonowymi albo przez obliczenie
domiarów prostokątnych lub biegunowych do określonych punktów. Jeżeli takiej osnowy nie ma, to w celu dokładnego wytyczenia długiego
odcinka prostego zakładamy wzdłuż trasy prostoliniowy ciąg poligonowy i obliczamy go w lokalnym układzie współrzędnych. Początek układu
przyjmujemy w punkcie P, a kierunek osi x wzdłuż pierwszego boku poligonowego.

18.) Bud drog

– tyczenie p posr luku kolowego jedna opisac szczeg:

-

Metoda rzędnych od stycznej dla równych odcinków na łuku

-

Metoda rzędnych od stycznej dla równych odcinków na stycznej

-Metoda biegunowa
-Metoda od prze

dłużonej cięciwy

Metoda rzędnych od stycznej dla równych odcinków na łuku:
Polega na wytyczeniu punktów pośrednich łuku kołowego w równych odstępach Δ l, poczynając od punktu początkowego. Dla założon ej
wartości odcinka łuku Δ l, należy wyznaczyć wartość kąta środkowego Δ α, a następnie wartości rzędnych i odciętych x i y.
Δα = ( Δ l / R)*( 200 / Л )
X = R * sin Σ Δ α i
Y = R ( 1-

cos Σ Δ α i )

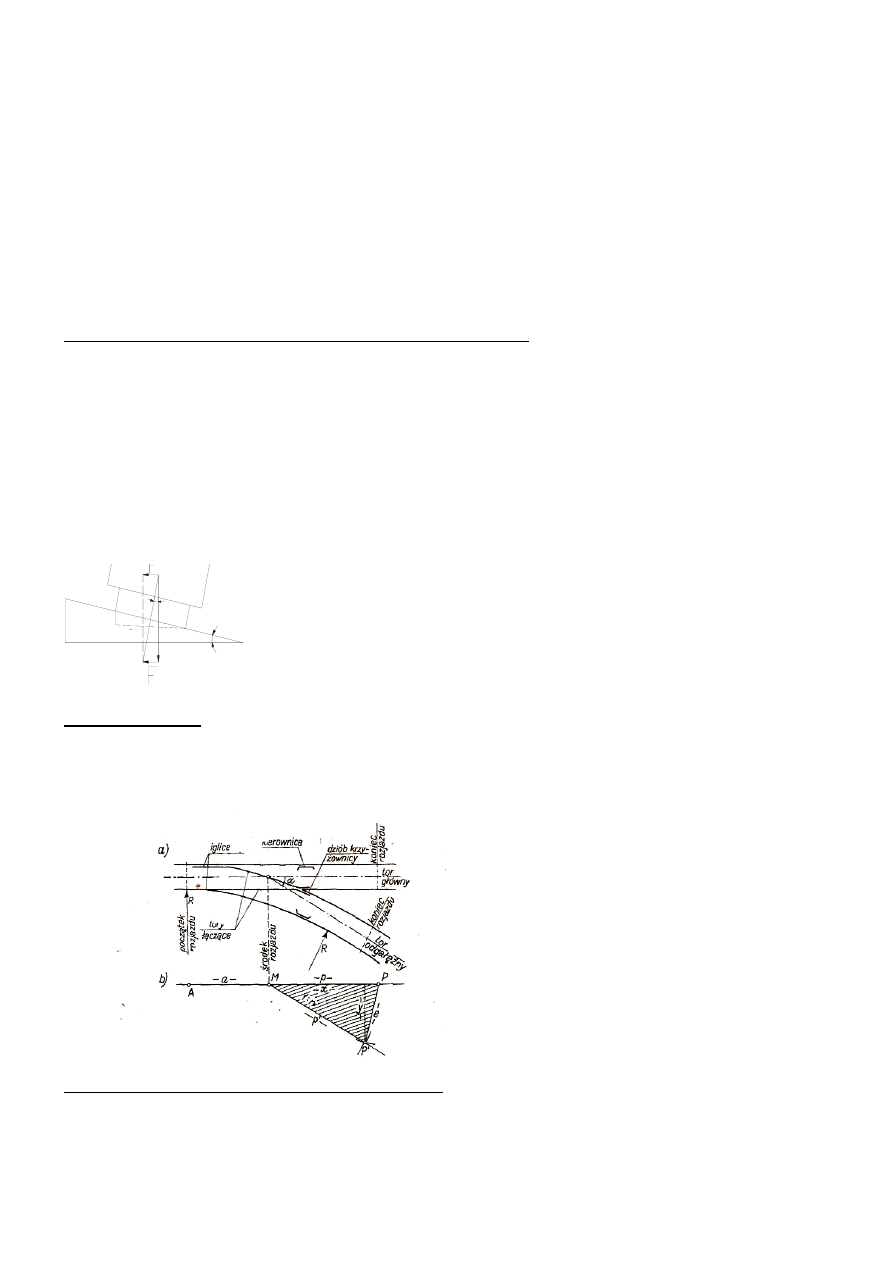
18.ŁUK KOŁOWY-PUNKTY GŁÓWNE

Dane: L -

kąt, R

Punktami głównymi łuku kołowego nazywa się punkty styczności łuku z prostymi głównymi trasy- P i K oraz punkt środkowy łuku S.
Wyznaczenie terenowe tych punktów wykonywane jest przez odłożenie odpowiednich miar kątowych i liniowych od punktu wierzchołkowego i
kierunków głównych trasy.
Punkt początkowy „P” i końcowy „K” zostanie wyznaczony w wyniku odłożenia wartości stycznej głównej „t” od punktu wierzchołkowego wzdłuż
kierunków głównych trasy.
t=PW=WK=R*tgL/2
WS=R(secL/2-1)
a=PB=BK=R*sinL/2
s=BS=R(1-cosL/2)
t1=R*tgL/4

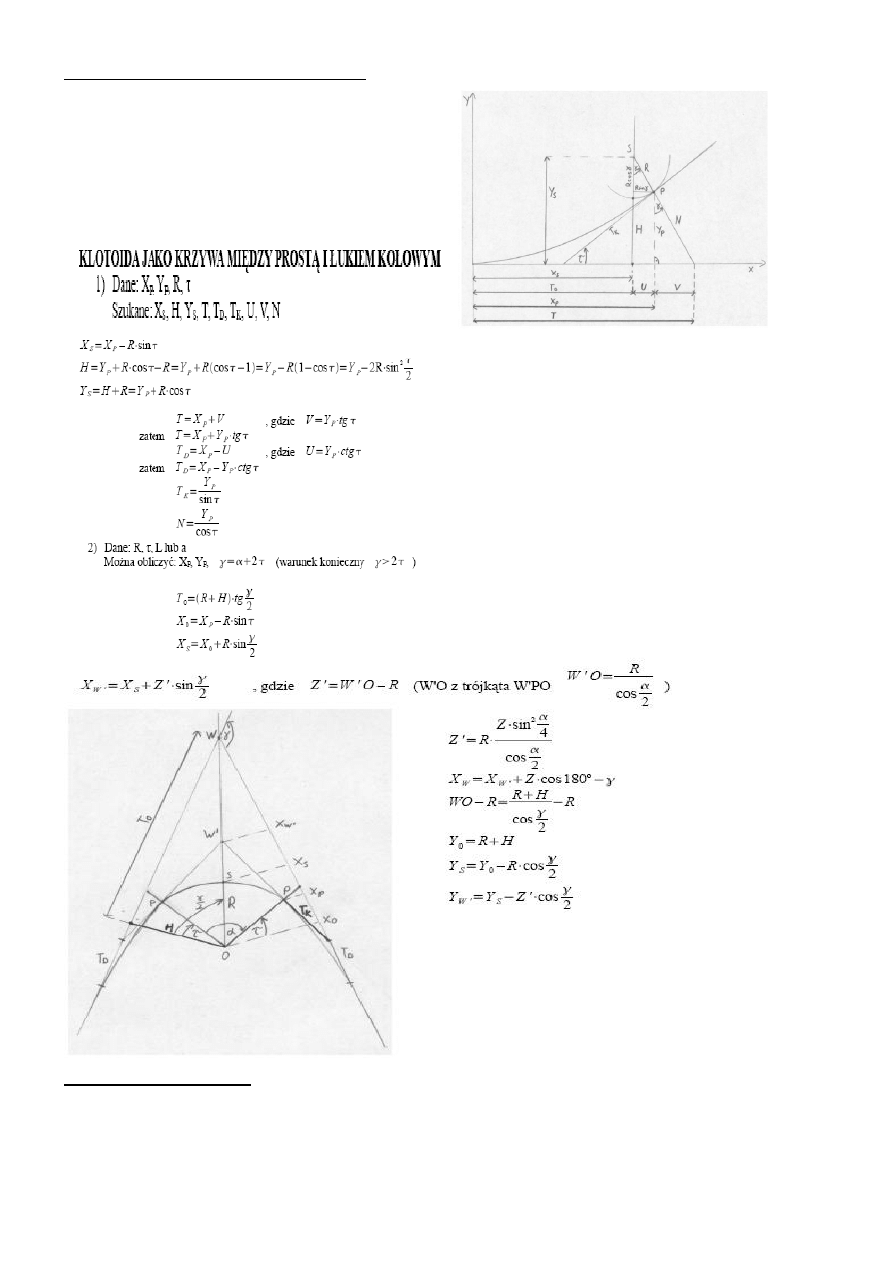
19. Tyczenie punktów pośrednich:

Metody: -biegunowe -

rzędnych od stycznej -rzędnych od cięciwy -od przedłużonej cięciwy; Biegunowe- jest często stos.bo można nia latwo

tyczyc pkt.w dowolnie dobranych odstępach. Stanowisko instrumentu może być obrane na pkt.gł. P,S,K lub na W. miara kontrolna jest wielkość
c. wytyczenie pkt.posrednich Pol.na obliczeniu kata i odległości d : 2φ=ΔL/R ρ-> φ=ΔL/2R ρ; d=2Rsinφ; c=2Rsinφ; Gdy warunki terenowe
pozwalają na pomiary liniowe można z dwóch stanowisk odkładać kierunki za pomocą dwóch teodolitów

20. Bud drogowe

– klotoida jako krzywa przejsciowa:

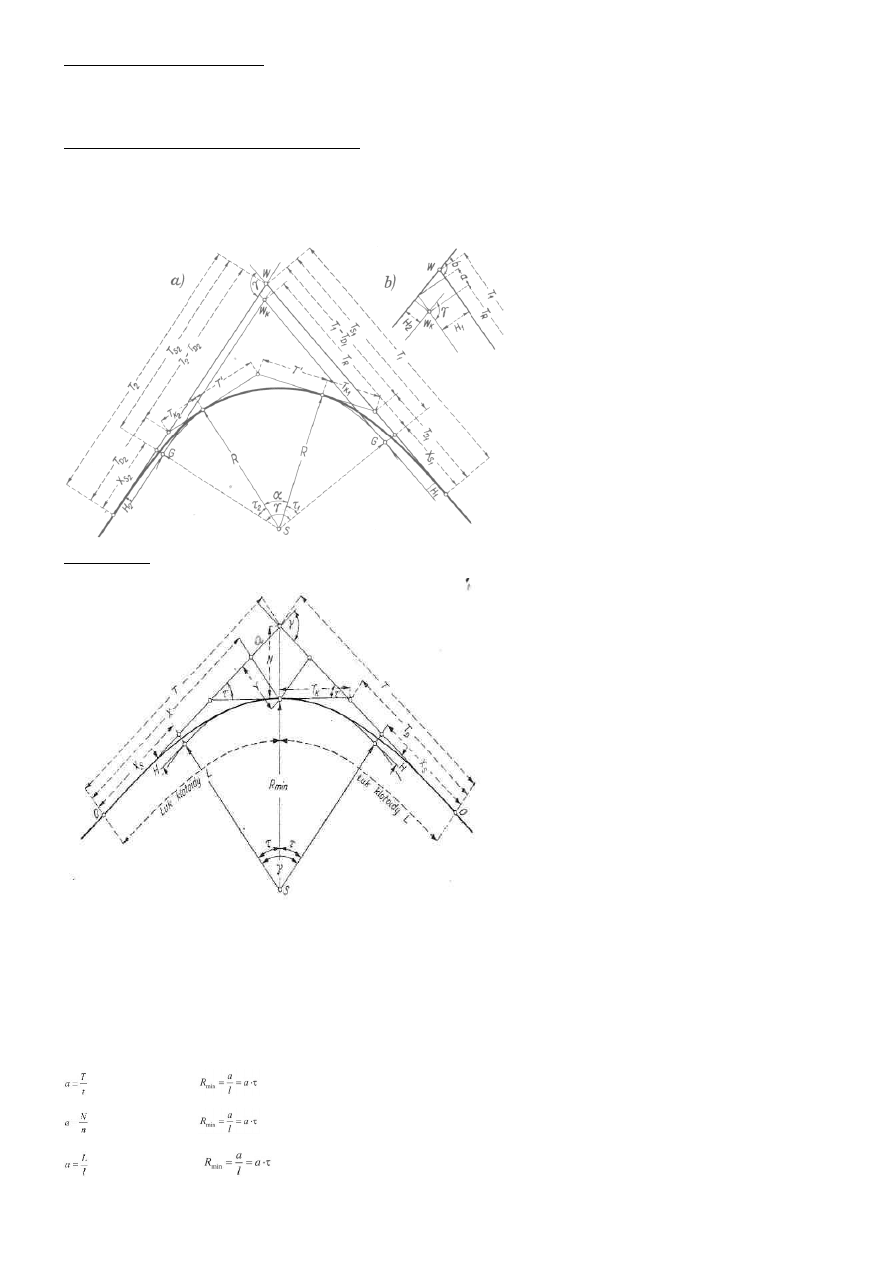
21. Równanie naturalne klotoidy:

tg

α=h/b oraz tgα=F/Q, zatem h=(Fb)/Q gdzie F=mv

2

K Q=mg, h=(bv

2

K)/g, wartość przechyłki h wprowadzana jest stopniowo h=iL, zatem

iL=(bv

2

K)/g->L=(bv

2

K)/ig, ostatecznie LR=a

2

22. Równanie różniczkowe klotoidy

LR=a

2

oraz R=1/K, można napisać L=a

2

K, gdzie K=dτ/dL, całkując wyrażenie LdL=a

2

dτ otrzymamy L

2

=2a^2τ, zestawiając równania L

2

=2a^2τ

oraz LR=a

2

możemy wyprowadzić związki pochodne; liczenie punktów pośrednich na klotoidzie: dx=dLcosτ i dy=dLsinτ oraz τ=L

2

/2a

2

, po

scałkowaniu i rozwinięciu w szereg: x=L-L

5

/40a

2

+L

9

/3456a

8

- oraz y=L

3

/6a

2

-L

7

/336a

6

+

23. Luk kołowy z niesymetrycznymi łukami klotoidy.

Jeśli z obu stron łuku kołowego zastosujemy jako krzywe przejściowe niejednakowo długie łuki róznych klotoid, to otrzymamy niesymetryczna
trase krzywo liniową o nierównych stycznych T

1

i T

2

. Orag o danym promieniu R jest w tym przypadku t

ez położony niesymetrycznie względem

prostoliniowych odcinkow trasy, a odsuniecie jego od stycznych gł. Będzie wynosilo dla jednej stycznej H

1

a dla drugiejH

2

. znając kąt , promień

R okreu i położenie jego środka S wzgl.obu stycznych, możemy wyznaczyć wartości H1 i H2, a nastepnie katy a także kąt :
Możemy obliczyc parametry a

1

i a

2

i wszystkie pozostałe wartości par.potrzebne do wyznaczenia w terenie tak zaprojektowanej trasy

krzywoliniowej.

24.) Biklotoida:

W celu przejścia z jednego kierunku prostoliniowego na drugi można używać nie tylko łuku kołowego zakończonego łukami klotoidy, lecz
jedynie dwóch łuków klotoidy bez wstawki kołowej. Zespół takich dwóch łuków nazywa się biklotoidą. Mogą być symetryczne o jednakowych
parametrach „a” bądź niesymetryczne o różnych parametrach „s”. O dopuszczalnej szybkości ruchu na takiej trasie będzie decydował promień
R

min

w wierzchołku, gdzie stykają się dwa łuki.

Biklotoidę stosuje się najczęściej wtedy, gdy kąt zwrotu stycznych jest mały i gdy promień R

min

jest duży. Obliczanie i tyczenie biklotoidy jest

znacznie łatwiejsze niż łuku kołowego zakończonego dwoma łukami klotoidy.
4-przypadki wyznaczenia parametru a:
a) dany Rmin, τ = gama/2, dla kąta τ znajdujemy: l,t,n,x,y
Parametr a obliczamy a = Rmin*l
Mnożąc elementy jednostkowe przez parametr a znajdziemy wielkości :L,T,N,X,Y potrzebne do wyznaczenia biklotoidy.
b) dane długość stycznej T i kąt τ, dla τ wyznaczamy t oraz obliczam :

c) dane odległość N, kąt τ, obliczamy:

d) dane długość L

1=

L

2

, τ, obliczamy :

25.

Łuki koszowe:

3 warunki matematyczne: sumα

i

=180-

β=α; t1=(r1-R2)sinα+(R2-R3)sin(α1+α2)+R3sin(α1+α2+α3)+t2cosβ; w 3 warunku zmienia się cosβ na

sinβ, Najczęściej spotykane są przypadki, gdy dane: 1.β, Ri i t1 szukene α

i

,t2 2.β,t1,t2,R1 szukane: R

i

,α

i

3.β,α1,R1,t1 szukane: R

i

,t2,α2

26. ŁUKI PIONOWE, PUNKTY GŁÓWNE I POŚREDNIE
Ukształtowanie pionowe trasy ma bardzo duży wpływ na bezpieczeństwo ruchu przyszłych użytkowników.

Obliczanie punktów głównych łuku pionowego:
Dane :
H

A

, H

B

, R, D

Szukane:
H

W

, H

1

, H

2

, i

1

, i

2

, t, WS, H

S

, H

P,

H

K

H

W

=H

A

+i

1*

D

1

H

W

= H

B

-i

2

(D-D

1

)

H

1

=H

W

-H

A

H

2

= H

W

-H

B

i

1

=

i

2

=

t=

WS=

H

s

=H

w

-WS

H

P

=H

W

-i

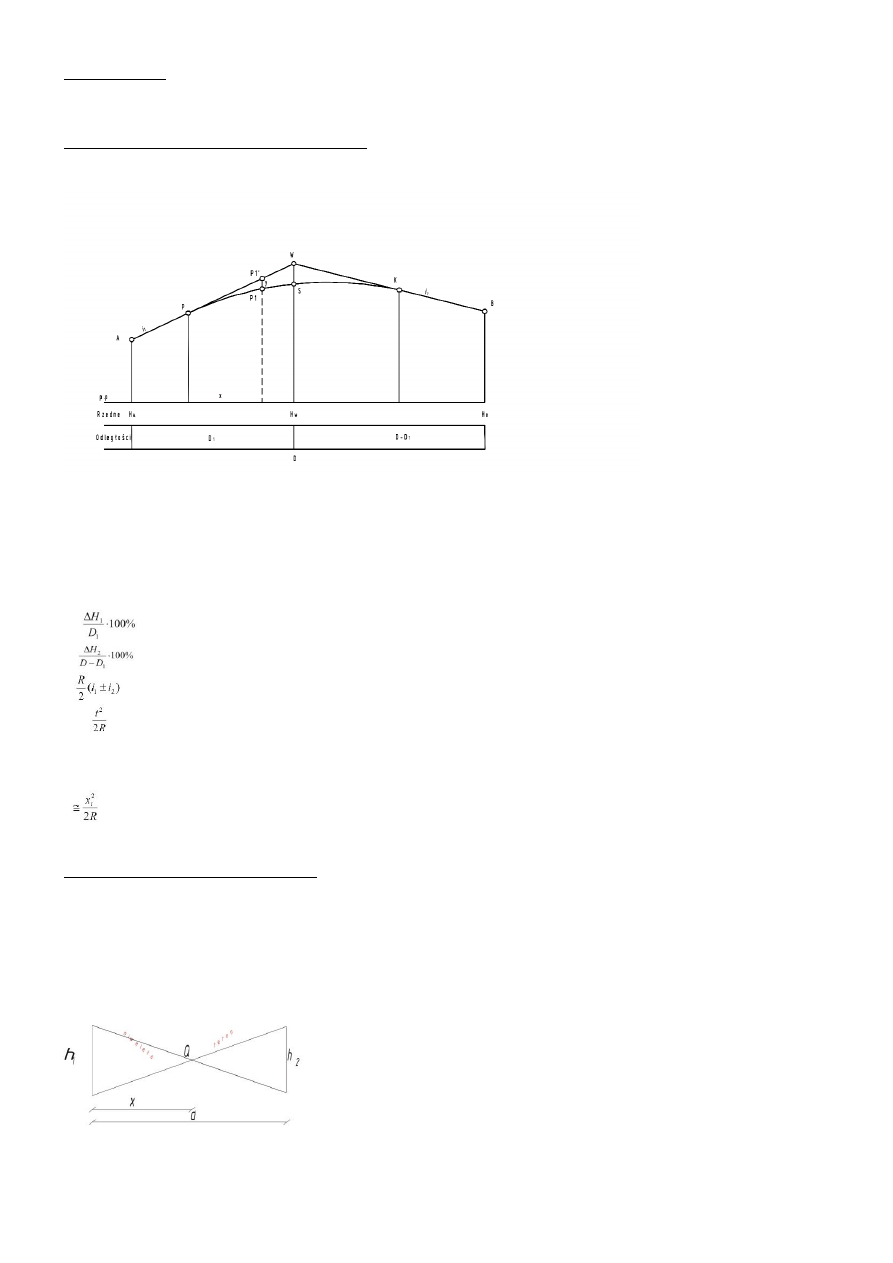
1*

t

H

K

= H

W

-i

2*

t

Punkty pośrednie łuku pionowego:

y

i

H

P1

= H

P

+i

1*

x

– y

27. PRZECIĘCIE SIĘ NIWELETY Z TERENEM

NIWELETA -

projektowany profil podłużny terenu (płaszczyzna pionowa), łączy punkty projektowanej osi drogi, dna rowu, spadku wyrobiska,

główki szyn kolejowych itp.
NIWELETA-

to obraz drogi w płaszczyźnie pionowej.

Podstawowe warunki, które powinny być spełnione przy projektowaniu niwelety to:
-

zachowanie parametrów żądanych spadków podłużnych,

-

niweleta powinna być jak najbardziej zbliżona do powierzchni terenu,

-

bilansowanie robót ziemnych, jak najmniejsze różnice,

-

przy spadkach większych niż 1% powinny zostać zaprojektowane łuki pionowe,

-

należy wyliczyć punkty robót zerowych, tzn. miejsca przecięcia się istniejącego terenu z projektowaną niweletą.

B

NIWELETA -

ISTNIEJĄCY TEREN= PRZEWYŻSZENIE

28. OBL. MAS ZIEMNYCH
Met. siatki kwadratów
pow.działki pokrywa się regularna siatka kw. o boku a. objętość V robot ziemnych jest suma objętości graniastosłupow ograniczonych od gory i
dołu powierzchniami topograficzną i projektowaną,z boku płaszczyznami przech.przez boki kwadratow. Gdy pow.projektowania jest płaszczyzną
poziomą, jej wts.liczy się:
H

I

-

wys.wierzchołków kw. Uczestniczących w obliczeniach pojedynczo na pow.topograficznej; H

II

-wys.uczest. w obliczeniach 2 razy; H

III

-

…3x;

H

IV

-

…4x; n-lp.kwadratow, na które podzielono pow.dz

Płaszczyzna projektowana,kt.wys.obliczono, dzieli obszar dzialki na pow.wykopów i nasypów. Linia przecięcia się pow.topograficznej z
pł.projektowana to linia zerowa robót ziemnych – H

o

.

Obj.pojedynczego gran

.liczy się: V=a^2/4*(h

1

+h

2

+h

3

=h

4

), h

1,2..

-

roznice wys.wierzchołkowkw h

i

=H

i

-H

o

; a^2-pow.kwadratu.

Suma objętości gran.obliczonych oddzielnie dla wykopow i nas. Jest calkowita obj.robót danej dz. V=V

w

+V

N

.

Gdy podstawe gran.przecina linia robot zer., to obj. Wykopu i nas. Jest: V

W

=(h

A

+h

B

/4)*S

w

S

w

-pow.wykopu/nas., h

A,C..

-

wys.naroży siatki liczone

od pł.projektowanej.
Tak to najpierw określamy róznice obj. V=a^2(h

A

+h

B

+h

C

-h

D

)/4, a nast. Obj.nasypu. V

N

=1/3*h

D

*S

N

, stad V

W

=V-V

N

.

Błąd wynikający z tego sposobu liczenia obj.bedzie zal.od dl a boku kwadratu, czyli od liczby n kwadratow skladających się na cala pow.dzialki.
E

max

=R-pierw.R^2-a^2/4.

Wpływ błedu wynikający ze sposobu obliczenia met.siatki kw.na dokł.obliczenia obj.gruntow liczymy: m

Va

=+-1/2*E

max

*a^2*pierw.n. sumaryczny

błąd określenia obj.
Met. przekrojów poprzecznych
Sposób ten jest powszechnie stosowany do obliczania robót ziemnych przy projektowaniu „budowli” o kształcie wydłużonym.
wzór ścisły na obliczenie objętości
1. V = d/3 (F

1

+ F

2

+



(F

1

F

2

))

2. wzór Simpsona
V = d/6 (F

1

+ F

2

+ 4F

ŚR

)

3. wzór Czepsena
V = d/2(F

1

+F

2

) - d/6 i (h

2

-h

1

)

i

– spadek terenu

F

1

, F

2

- pola powierzchni przekrojów poprzecznych;

d -

odległość między przekrojami

29.) Prace ziemne

– wpływ ukszt ter na dokl oblicz objet:

W praktyce projektowania dokładność obliczenia objętości mas ziemi jest ściśle związana z kosztami wykonania robót ziemnych, rozliczanych
za ilość jednostek objętości gruntu (m

3

).

W zależności od charakteru powierzchni terenu stosuje się znane klasyczne metody pomiaru:
-

niw. siatkową dla pow. płaskiej lub łagod. nachylonej

-niw. punktów rozproszonych dla pow. falistych
-

niwelację przekrojów podłużnych i poprzecznych dla tras komunikacyjnych

-

tachimetrię dla terenów o urozmaiconej rzeźbie

Za istotne

dla określenia dokładności objętości można przyjąć błąd ukształtowania powierzchni ( 4 cm dla rzędnych w siatce 40x40).

Oznaczmy:
m

k

– wpływ błędu ukształtowania powierzchni na dokładność określenia objętości;

Jeśli przyjmiemy maksymalna wielkość błędu ukształtowania powierzchni terenu ( oznaczoną przez m ), dla kwadratu o boku 40 m,
dopuszczonego norma techniczna, będziemy mieli:
m

k

= 40*40*0,04 = 64m

3

przyjmujemy te wielkość za błąd jednostkowy, oraz prawdopodobieństwo popełnienia błędu dodatniego i ujemnego P = ½ , wówczas dla całej
powierzchni s niwelowanej powierzchni będziemy mieli:

m

k

=

gdzie n-

liczba kwadratów o boku 40 m , mieszczących się w powierzchni S.

Ponieważ: n= S/1600, będzie:

30. Wpływ błędu zagęszczenia terenu
Wskaźnik lub stopień zagęszczenia gruntu zależy m.in. od rodzaju gruntu, jest definiowany jako stosunek objętości gruntu w wykopie do
objętości gruntu wbudowanego w nasyp po odpowiednim zagęszczeniu
D=V

W

/W

N

; V

W

=V

N

D



0,02D V

N

0,02D

– ustalona tolerancja stopnia zagęszczenia gruntu; wg Polskiej Normy 0,9<D<1,15

31. PROJEKTOWANIE PŁASZCZYZN BILANSUJĄCYCH
ROBOTY ZIEMNE
Każda płaszczyzna przechodząca przez środek ciężkości jest płaszczyzną bilansującą roboty ziemne.
1)

średnia wartość współrzędnych

X

S

=



x

i

/n Y

S

=



y

i

/n Z

S

=



z

i

/n

2)

jeżeli pł. bilansująca ma zadany kierunek najw. spadku



i wart. najw. spadku k

to równanie płaszcz. to:

(kcos



)x + (ksin



)y

– z + H

o

= 0

H

o

= - X

S

kcos



- Y

S

ksin



+ Z

S

3)

jeżeli projektowana płaszcz. ma przechodzić przez 2 p-kty

1=(x1, y1, z1) i 2=(x2, y2, z2) to
(x

1

-X

S

)kcos



+ (y

1

-Y

S

)ksin



- (z

1

-Z

S

) =0

(x

2

-X

S

)kcos



+ (y

2

-Y

S

)ksin



- (z

2

-Z

S

) =0

kcos



i ksin



dają tg



i liczymy



4)

jeżeli projektowana płaszcz. ma przechodzić przez 1 dany p-kt i ma określony max spadek wzdłuż kierunku



to mamy jedno r-nie;

(x

1

-X

S

)kcos



+ (y

1

-Y

S

)ksin



- (z

1

-Z

S

) =0

5)

jeżeli projektowana płaszcz. ma przechodzić przez 1 dany p-kt i ma określony max spadek k to mamy jedno r-nie;

(x

1

-X

S

)kcos



+ (y

1

-Y

S

)ksin



- (z

1

-Z

S

) =0

dołączamy równanie sin

2



+cos

2



=1 i wyliczamy



Projektowanie płaszcz. minimalizujących roboty ziemne

a) dla każdego p-ktu o znanych wsp. zestawiamy r-nie
v

i

= (x

1

-X

S

)kcos



+ (y

1

-Y

S

)ksin



- (z

1

-Z

S

)

r-

nie te wagujemy proporcjonalnie do powierzchni otaczającej dany p-kt i rozwiązujemy wg [pvv] = min

b)

projektowana płaszcz, ma zminimalizować roboty ziemne i zbilansować je. Wtedy dla każdego p-ktu o znanych X i Y zestawiamy następujące

r-

nie aproksymujące:

v

i

= e

X

x

i

+ e

y

y

i

+ z

0

- z

i

e

X

– nachylenie pł. wzdłuż osi OX

e

y

– nachylenie pł. wzdłuż osi OY

z

0

– przecięcie pł. z osią OZ

Metoda przekrojów poziomych z mapy warstwicowej

V = h/2



(S

i

+S

i+1

) +



h/3

*

S

n

Met. siatki trójkątów
V = a

2

/2

*

1/3(h

1

+h

2

+h

3

)

Met. p-tów rozproszonych
V = 1/3 S

1

(h

1

+h

2

+h

3

)

m

V

2

=(Vm

S

/S)

2

+(S/3)

2

3m

h

2

+m

Vu

2

m

Vu

2

= 0,6 Q S



b

Q

– współczynnik bogactwa mikro-rzeźby (0,005 – 0,01)

b

– średnia długość celowej

Na dokł określenia objętości składają się następujące błędy:
m

K

– bł. ukształt. pow. terenu

m

g

– bł. zagęszczenia gruntów

m

W

– wpływ dokł. materiałów wyjściowych.

m

K

– bł. ukształt. pow. terenu



= R

– x; x =



(R

2

-a

2

/4)

Błąd obliczonej objętości ze wzgl. na ukształtowanie terenu wynosi
m

Vu

2

= S



SR

= n a

2



SR

Wpływ błędu zagęszczenia terenu
Wskaźnik lub stopień zagęszczenia gruntu zależy m.in. od rodzaju gruntu, jest definiowany jako stosunek objętości gruntu w wykopie do
objętości gruntu wbudowanego w nasyp po odpowiednim zagęszczeniu
D=V

W

/W

N

; V

W

=V

N

D



0,02D V

N

0,02D

– ustalona tolerancja stopnia zagęszczenia gruntu; wg Polskiej Normy 0,9<D<1,15

Wpływ dokładności materiałów wyjściowych
Błędy określenia objętości gruntów.
Można wyróżnić dwa podstawowe źródła błędów określenia objętości: błędy pomiarów i opracowań map, na które składają się:
-

błąd odwzorowania terenu -błąd pomiaru rzeźby terenu -błąd opracowania mapy warstwicowej

błędy obliczania objętości, wynikające z przyjętego sposobu obliczeń Błąd odwzorowania terenu
Powierzchni terenu nie można odwzorować wiernie Każdy pomiar rzeźby terenu stanowi aproksymacje powierzchni terenu powierzchnią
topograficzną, czyli powierzchnią określoną zbiorem punktów o znanych współrzędnych w przyjętym układzie odniesienia. Geodeta, dokonując
pomiaru powierzchni terenu dzieli ją na szereg płaszczyzn, najczęściej trójkątnych, przez wyznaczenie współrzędnych wierzchołków figur. W
rzeczywistości pomiędzy trzema punktami tworzącymi płaszczyznę rozpięty jest pewien płat powierzchni terenu o nieregularnej krzywiźnie.
Punkty powierzchni terenu mogą względem danej płaszczyzny przyjmować różne położenia:

wszystkie nad płaszczyzną (powierzchnia wypukła)
wszystkie pod płaszczyzną (powierzchnia wklęsła)
cześć punktów nad, część pod, a wobec tego część również na płaszczyźnie
: V

i

= E(e

i

)S

i

W rozpatrywanym punkcie odległości e

i

są błędami prawdziwymi odwzorowania terenu i jak wiadomo mogą być z dostatecznym przybliżeniem

określone na drodze pomiaru. Z uwagi na skończoną liczbę punktów powierzchni, w których możemy dokonać pomiaru, wartość oczekiwaną
E(e

i

) zastąpimy średnim błędem odwzorowania terenu:

gdzie e

i

– odległość pomiędzy powierzchnią terenu a płaszczyzną powierzchni topograficznej, pomierzona w punkcie i z dokładnością

umożliwiającą uznać ją za błąd prawdziwy; n – liczba pomierzonych odległości.
Wpływ błędu odwzorowania terenu na dokładność obliczenia objętości gruntu będzie zależna od charakteru terenu. Jeżeli teren jest
zróżnicowany pod względem ukształtowania powierzchni, tzn. gdy wymienione pod (a), (b), (c) położenia powierzchni terenu względem
płaszczyzny topograficznej występują w przybliżeniu z jednakową częstotliwością na całym obszarze objętym robotami ziemnymi, wówczas ze
względu na jednakowe prawdopodobieństwo wystąpienia dodatnich i ujemnych błędów odwzorowania terenu e

i

można napisać:

gdzie:
m

Vz

– wpływ błędu odwzorowania terenu na dokładność obliczenia objętości gruntu

m

z

– średni błąd odwzorowania terenu

S

0

– pole średniego trójkąta utworzonego przez punkty pomiaru rzeźby terenu

n

– liczba trójkątów na obszarze o powierzchni S

32a

. CO TO JEST PRZEŚWIT, ROZSTAW I PRZECHYŁKA TORÓW KOLEJOWYCH:

Prześwit- jest to odległość między wewnętrznymi krawędziami szyn toru, mierzona na wysokości 14mm poniżej powierzchni tocznych.. Na
odcinkach prostych i łukach o R ≥ 300m wynosi. 1435mm. Dla R<300m prześwit należy powiększyć.
Rozstaw-

odległość między osiami dwóch sąsiednich torów. Na szlaku linii dwutorowej nie może być mniejszy od 3,5m.

Jeżeli R< 350m to rozstaw 3,5m należy powiększyć o poszerzenie. Rozstaw min. 3.5 m, 4.0 m do 4.7 m w przypadku ustawienia sygnałów
kolejowych. Jeżeli promień dwóch linii kolejowych leżących w łuku jest mniejszy od 350 m, to rozstaw powiększa się od 20 – 1100 mm.
Przechyłka torów – jest to różnica wysokości toków szyn w torze. Jej wartość zależy od: promienia łuku, prędkości, siły odśrodkowej i ciężaru
własnego.
Przechyłkę stosuje się dla łuków o R ≤ 4000 m.
Prz

echyłka toru:

h=b*tgα
F=c*tgα tgα=h/b=F/c
h=F/c*b, ponieważ: F=mv^2/R, c=m*g
h=(v^2/R*g)*b
Jeżeli h przyjmiemy w mm, a v w km/godz. b=1435~1.5 m
h=11.8 v^2/R lub h=600v/R (wzór doświadczalny)

h

b

c

32b. ROZJAZD PROSTY
W rozjeździe rozróżnia się dwa kierunki torów: kierunek toru zasadniczego (prosty) oraz kierunek toru odgałęźnego ( w łuku). Rozjazd
wyznaczają punkty zaznaczone na osi toru zasadniczego i odgałęźnego. Będą to punkty A-początek rozjazdu, PiP’- koniec rozjazdu, M-środek
rozjazdu α- kąt rozjazdu(zawarty między kierunkami obydwu osi).Wyrażany jest najczęściej za pomocą ułamka l:n, zwanego skosem rozjazdu.
Odległość od punktu początkowego do środka rozjazdu (odcinek a) oraz środka rozjazdu do punktów końcowych ( odcinki pip') zależy od typu
rozjazdu i jego konstrukcji. Typ rozjazdu podawany jest najczęściej w skróconej formie, np.S45-500-1:12,gdzie s- typ szyny, 500 – promień toru
odgałęźnego , 1:12 – skos rozjazdu

33. Połączenie torów równoległych rozjazdami o równych skosach
Kąt



zawarty między kierunkiem osi toru zasadniczego a kierunkiem osi toru odgałęzionego, nosi nazwę kąta rozjazdu. Wyrażany jest

najczęściej za pomocą ułamka 1:n, zwanego skosem rozjazdu.

Połączenie dwóch torów równoległych dwoma rozjazdami o jednakowym skosie
Tyczenie rozpoczyna się od wyznaczenia punktów A

1

, M

1

i P

1

wzdłuż osi toru 1.

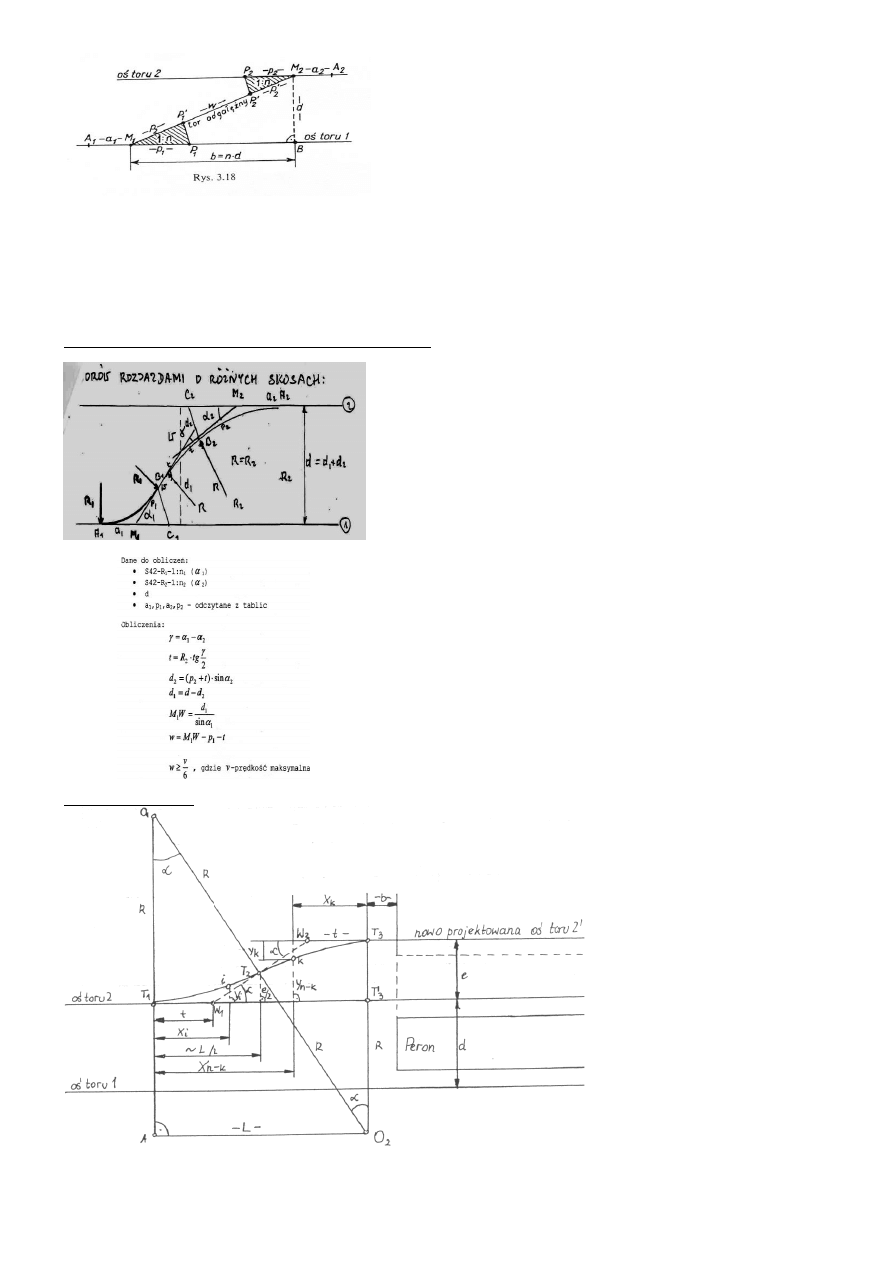
Następnie wyznacza się punkt M

2

przez wystawienie prostopadłej d (rozstaw osi toru 1 i 2) z punktu B, leżącego na osi toru 1 w odległości b = n



d od punktu M

1

.

Prawidłowość wyznaczenia punktu M

2

sprowadza się przez pomiar odcinka M

1

M

2

. Odcinek ten powinien być równy wielkości określonej z

wzoru M

1

M

2

= d / sin



.

Po wytyczeniu punktu M

2

wyznacza się punkty A

2

i P

2

, leżący na osi toru 2, w odległości a

2

i p

2

od punktu M

2

. Pozostałe punkty (P’

1

i P’

2

)

wyznacza się przez odmierzenie wzdłuż prostej M

1

M

2

odcinków p

1

’ od punktu M

1

i p

2

’ od punktu M

2

. Między punktami P’

1

i P’

2

powstanie prosta,

której długość będzie równa

w = M

1

M

2

-

(p’

1

+

p’

2

).

34. POŁĄCZENIE TORÓW ROZJAZDAMI O RÓŻNYCH SKOSACH

35) Poszerzenie torów:

Na stacjach istniejących może zachodzić potrzeba poszerzenia międzytorza. Większość poszerzenia e, o jaką należy zwiększyć rozstaw,
zostaje określona w projekcie przebudowy. Przejście od toru „z” do nowo projektowanego położenia toru ”z

,

” odbywa się po łuku odwrotnym.

Odcinek L, odpowiadający rzutowi długości łuku odwrotnego, przy większych poszerzeniach oraz większych szybkościach kursujących
pociągów nie powinien być krótszy od 200m. Dopuszcza się ewentualne zmniejszenie tej odległości do 100m. W celu wytyczenia przejścia do
nowo projektowanego toru należy określić promień łuku odwrotnego oraz długości odcinka L. Przy założeniu, że promienie te będą sobie równe,
wartości ich obliczamy ze wzoru:
R



V

2

gdzie:
V-

szybkość największa pociągu kursującego

Długość odcinka „L” wyznacza się na podstawie znanych wielkości e i R:

Położenie punktów głównych łuku odwrotnego określa się w stosunku do punktu T

3

, któr

ego położenie określone jest w projekcie. Punkt T

1

wyznacza się więc przez odłożenie po kierunku osi toru 2 odcinka L, począwszy od punktu T

3

’

.

Następnie określamy kąt



ze wzoru:

Jeśli zamiast R podstawimy

to otrzymamy:

Kąt



możemy wyznaczyć również z innego wzoru :

Z porównania powyższych wzorów otrzymujemy :

gdzie e- pomijamy
z tego

Mając długość stycznej określamy położenie punktu W

1

i W

2

.W

1

jest na osi toru 2 w odległości „t” od punktu „T

1

”, a punkt W

2

na osi toru 2

’

, a w

odległości „t” od punktu T

3

. Punkt T

2

będzie się znajdował w połowie odcinka W

1

W

2

, gdzie x= L/2, odkładane po osi toru 2 począwszy od

punktu T

1

, oraz y= e/2 . Oprócz punktów głównych łuku odwrotnego należy jeszcze wyznaczyć punkty szczegółowe. Ponieważ poszerzenie jest

zazwyczaj niewielkie, wszystkie punkty szczegółowe łuku odwrotnego są tworzone od jednej stycznej, za którą przyjmuje się oś toru 2.
Wielkości „y” dla pierwszego łuku obliczane są ze znanego wzoru:
y= x

2

/2R

Wielkość „y” możemy obliczyć również jako funkcje L i e. Więc można napisać:
i dalej

Rzędne drugiego łuku oblicza się na podstawie rzędnych łuku pierwszego z zależności:
y

n

= e

y

n-1

= e

– y

1

y

n-2

= e

– y

2

y

n-k

= e

– y

k

35. Regulacja osi torów metoda wykresu kątów.
Projekt regulacji krzywoliniowego

odcinka toru ma na celu ustalenie poprawnego przebiegu dla toru istniejącego i określenie wielkości

przesuniec, jakie należy nadac poszczególnym punktom toru aby przyjał on zalozone położenie.
Metoda ta polega na sporządzeniu wykresów krzywej toru istniejącego i krzywej projektowanej dla etgo toru, w odp.odwzorowaniu.na podst.
Tych 2 wykresow tworzy się trzeci.-tzw.wykres przesuniec, z kt.mozna w prosty sposób odczytac wielkośc przesunięć dla każdego pkt.krzywej
istniejącej.
Jeśli an osi x będą odkladane dł.odcinkow krzywej L

i

=i*del.L, a wzdłuż osi y odp.kąty zwrotu alfa

i

, to po połaczeniu wyznaczonych w ten sposób

pkt.otrzymamy inny obraz krzywej. Tak odwzorowana krzywa nazywa się wykresem kątów.
Przy odkladaniu dl.L i alfa trzeba zastosowac skale dł. C

x

oraz skale katow C

y

. dla nieskończenie malych odcinkow krzywej:

Dx=Cx*Dl; Dy=Cy*dalfa, bo dalfa=Dl/r, wiec Dy=CydL/r.

37. PRZENIESIENIE WYSOKOŚCI PRZEZ PRZESZKODY WODNE

Przy budowie mostów, zapór itp. zachodzi potrzeba przeniesienia wysokości przez przeszkody wodne. Stosuje się met. niwelacji geo-
metrycznej lub trygonometrycznej przy użyciu tarcz bisekcyjnych.
Met. niwelacji geometrycznej
Na łacie A wykonuje się odczyt wstecz, następnie (przy spoziomowanej osi celowej) celujemy na łatę na reperze B. Pomiarowy przesuwa tarczę
bisekcyjną do momentu pokrycia poziomej kreski krzyża i środka tarczy. Należy wykonać kilka serii pomiarów by wyeliminować błędy. Z różnicy
odczytów A i B otrzymuje się różnicę wysokości.

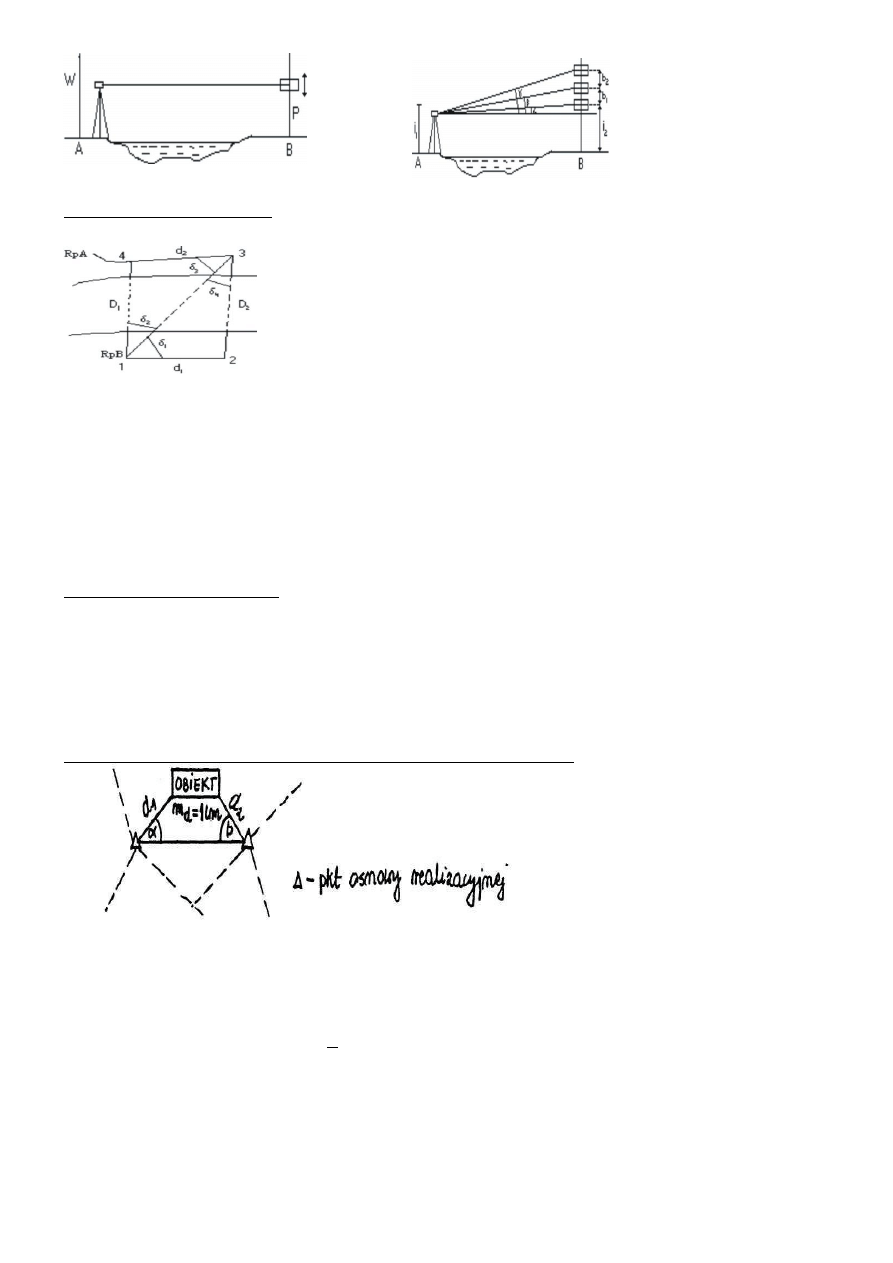
38. Met. niwelacji trygonometrycznej
zasada przedstawiona jest na rysunku.

Przewyższenie



H można obliczyć trzykrotnie na podst. kątów



,



,



. Chcąc zwiększyć dokładność wyznacz.



H należy przeprowadzić

obserwacje jednocześnie z dwóch stanowisk po obu brzegach przeszkody.
Na p-ktach 2 i 4 us

tawia się statywy z tarczami bisekcyjnymi i mierzy się wysokości tarcz nad p-ktami oraz między tarczami. Teodolity ustawia

się na p-ktach 1 i 3. Obserwacje kątów pionowych wykonuje się jednocześnie. Mierzy się również kąty poziome.
Dokł. określenia różnicy wys. tą met. oblicza się ze wzoru:
m

h

=



[(tg



+(1-K/r)D

0

)m

do

]

2

+(d

o

m/cos

2



)

2

+ (d

o

m

K

/2r)

2



-

kąt pionowy

K

– współczynnik refrakcji

r

– promień kuli ziemskiej

d

o

– odległość między p-ktami

Na błąd przyrostu wysokości największy wpływ ma błąd pomiaru kąta pionowego, wpływ odległości nie ma większego znaczenia.



H = i

t

+Dtg



- i

s

+ D

2

[(1-K)/2r]

39. osnowy realizacyjne podzial z g-3:

Sytuacyjne(XY),wysokościowe(H), przestrzenne(XYH). Wszystkie dzielą się na podstawowe – szczegółowe – budowlano-montażowe. Osn.
dzielą się na osn. dowolnego kształtu, regularne, układ baz, sieci wydłużone, zakładane techniką GPS.Podst. osn. real. wiąże tyczoną
inwestycję z otaczającym terenem i uzbrojeniem. Szczegół. osn. real. służy do bezpośredniego oparcia pomiarów realizacyjnych. Podst. osn.
real. to pozioma osn. II kl. i wysokościowa II kl. Projektowanie to 1)czynności wstępne. 2)prace projektowe. AD.1)analiza dan ych wyjściowych
(inform. o terenie, osnowie, plan realizacyjny inwestycji, założenia techniczne i dokładnościowe) projektu i przegląd stosowanych rozwiązań
danego zadania. AD.2)projektowanie obejmuje 3 etapy analiz i ustaleń (geometria sieci i obserwacje wiążące; dokładności obserwacji;
szczegóły realizacji i opracowania wyników). Do wykonania projektu sieci niezbędny jest plan realizacyjny danej inwestycji – zawiera
rozmieszczenie wszystkich zaprojektowanych obiektów i urządzeń na tym terenie. Projektując sieć należy tak usytuować jej p-kty w terenie, by
służyły do pomiarów przez cały okres realizacji inwestycji

40

. Zasady ustalania dokładności pomiaru osnów realizacyjnych na etapie projektowania.

Cel: ustalenie z jaka dokładnością pomierzyć kąty i długości w osnowie realizacyjnej oraz z jaką dokładnością odłożyć kąty α, β i długości dl,d2
żeby błąd wzajemnego położenia punktów 1,2 nie przekroczył 1cm.
m

td

2

= m

fd

2

+ m

2

d(

α,d)

gdzie: m

td

2

błąd tyczenia , m

fd

2

- blad osnowy podstawowej

[średni błąd wynikający z dokładności osnowy, średni błąd wynikający z

dokładności tyczenia (brak obserwacji nadliczbowej)]
m

td

2

= m

0

2

(F

d

T

QF

d

) + m

d

2

(

α,d) gdzie:m

0

-

średni błąd jednostkowy po wyrównaniu Q - macierz współczynników wagowych (macierz kowariancji

X, Y osnowy) F

d

- macierz funkcyjna -

macierz jednokolumnowa pochodnych cząstkowych funkcji d

2

= (x

j

– x

i

)

2

+ (y

j

– y

i

)

2

uzasadnienie drugiego wzoru

x

p

= X (xi, y

i

, βi, di) ; Y

P

= y (xi, yi,

βi, di) ®cov(x

p

,y

p

) = F

p

*cov(X, Y,

β, d) Fp

T

gdzie:

*cov(x

p

,y

p

) -

macierz kowariancji dla współrzędnych punktu P

*

cov(X, Y, β,d) kowariancja wsp. pkt. osnowy (X,Y) i dla elementów (β,d) odkładanych podczas tyczenia punktu P

*F

p

maciez pochodnych cząstkowych dla funkcji

41. OSNOWY REALIZACYJNE. OPRACOWANIE WYNIKÓW POMIARU METODĄ PARAMETRYCZNĄ, UKŁAD LOKALNY.

Mając daną osnowę z pomierzonymi kątami i długościami ustalamy liczbę obserwacji nadliczbowych i wybieramy parametry
f =n- r
Gdzie f to liczba obserwacji nadliczbowych
r- liczba obserwacji koniecznych
n- liczba niewiadomych
następnie obliczmy współrzędne przybliżone punktów osnowy. Ze współrzędnych przybliżonych obliczamy kąty i długości (przybliżone wartości
wielkości mierzonych), a następnie macierze A,L,P.
l=



obl

-



obs

l= d

obl

- d

obs

L to macierz wyrazów wolnych
P to macierz wag
c/m

2

0 0

P= 0 c/m

2

0

0 0 c/m

2

obliczamy wartości przyrostów dx oraz dy, możemy to zrobić dwiema metodami:
A

t

PAdx+ A

T

PL=0

metoda nieoznaczona: dx= -(A

T

PA)

-1

A

T

PL

metoda oznaczona: [A

T

PA| A

T

PL]= R

T

[R|L

R

]

Rdx+ L

R

=0 stąd obliczamy dx

Po obliczeniu przyrostów do współrzędnych dx i dy obliczamy poprawki V
V=Adx+L
Przyrosty dodajemy do współrzędnych przybliżonych, poprawki zaś do wartości obserwowanych.
Pierwszy etap kontroli: S=V

T

PV

S’= L

T

PL+ L

T

Padx

S=S’
Obliczamy wyrównane obserwacje. Np. d

wyr

= d

obs

+V

Obliczenie wyrównanyc współrzędnych X

wyr

= X

przybl

+dx

Drugi etap kontroli: sprawdzamy czy wartości obliczone z wyrównanych współrzędnych są równe wyrównanym po dodaniu poprawek
Analiza dokładności:
m

o

2

= (V

T

PV)/(n-r)

błędy średnie wyznaczonych parametrów dla metody nieoznaczonej
Cx= m

o

2

*( A

T

PA)

-1

= m

x

2

cov(x,y)

cov(x,y) m

y

2

błąd położenia punktu m

p

=



( m

x

2

+ m

y

2

)

błędy średnie wyrównanych wielkości metodą nieoznaczoną: m

i

2

= m

0

2

* F

T

(A

T

PA)

-1

F, gdzie:

F=



F/



x

1



F/



x

2

błędy średnie wyrównanych wielkości metodą oznaczoną
m

i

2

= m

0

2

*F

R

T

F

R, gdzie

R

T

F

R

= F

42. Odkształcenie obiektu
– zmiana kształtu lub objętości albo zmiana kształtu i objętości obiektu powodująca zmiany wzajemnych odległości jego punktów Rodzaje:
1.odkształcenie liniowe – względna zmiana długości odcinka między dwoma punktami
2. odkształcenia postaciowe – zmiana wartości kątów zawartych między kierunkami łączącymi punkty obiektu 3.odkształcenia objętościowe –
względna zmiana objętości obiektu na skutek jego odkształceń liniowych albo postaciowych lub jednocześnie liniowych i postaciowych
4.odkształcenia trwałe – odkształcenia, które po ustąpieniu przyczyny pozostają
5.odkształcenia sprężyste – odkształcenia, które po ustąpieniu przyczyny ustępują
6.odkształcenia graniczne – wielkość odkształcenia, której przekroczenie uniemożliwia montaż konstrukcji albo normalne użytkowanie
konstrukcji lub podłoża wobec utraty przez nie zdolności przenoszenia obciążeń

43. Przemieszczenie obiektu

– zmiana położenia obiektu, przesunięcie, obrót lub przesunięcie i obrót, przy którym wzajemne odległości wszystkich punktów obiektu nie
ulegają zmianie. Rodzaje przemieszczeń:
1.pzemieszczenia trwałe – przemieszczenia, które po ustąpieniu przyczyny pozostają
2.pzemieszczenia bezwzględne – zmiana położenia punktu zaistniała w rozpatrywanym okresie czasu i wyrażone przez wektor
przemieszczenie w stałym układzie odniesienia
3.pzemieszczenia względne – zmiana położenia punktu w okresie czasu i wyrażone przez wektor przemieszczenie w niestałym układzie
odniesieni
4.Stały układ odniesienia – układ współrzędnych, w których wyrażone są przemieszczenia punktów i obiektów, wyznaczonych przez
zastabilizowane punkty sieci kontrolnej zdefiniowane jako stałe
5.niestały układ odniesienia – układ współrzędnych, w których wyrażone są przemieszczenia punktów i obiektów, wyznaczonych przez
zastabilizowane punkty sieci kontrolnej, których stałości nie sprawdzono
6.przemieszczenie nietrwałe – przemieszczenie, które po ustąpieniu przyczyny ustaje
7.przemieszczenia graniczne

– wielkość przemieszczeń, której przekroczenie uniemożliwia montaż konstrukcji albo normalne użytkowanie

konstrukcji lub podłoża

44. METODY WYZNACZENIA PRZEMIESZCZEŃ OBIEKTÓW INŻYNIERSKICH:

Metoda pomiaru zastosowana do wyznaczenia przemi

eszczeń zależy od 3 czynników:

-

szybkości zmian zachodzących na badanym obiekcie

-

rodzaju wyznaczanych przemieszczeń: poziome(dwie składowe w płaszczyźnie poziomej i czas), pionowe(jedna składowa w linii pionu i czas),

przestrzenne(trzy składowe, X,Y,Z i czas), względne lub odniesione do stałych punktów.
-

wymaganej dokładności wyznaczanego przemieszczenia.

Metody te oparte są na stosowaniu następujących instrumentów pomiarowych:
-

ekstensometr, tensometr, pochyłomierz, szczelinomierz, klinometr, wahadło, inklinometr.

45. Przemieszczenia

– met oprac wyn pomiar:

Przemieszczenie

– prace projektowe, obliczeniowe, pomiarowe prowadzące do określenia: wektora zmiany położenia obserwowanych punktów

reprezentujący badany obiekt.
Metody opracowania: wyznaczamy funkcj

e el. Kątowych i liniowych w osnowie, wyznaczamy współrzędne p-ów kontrolowanych, po pół roku

znowu współrzędne,



,



, d

Opracowanie wyników pomiaru

– metoda parametryczna

Metoda parametryczna opracowanie wyników
1.Obserwowanie kierunków na j stanowiskach:

gdzie:

parametry to współrzędne przybliżone p-ów obserwowanych
V

jk

- poprawka do obserwacji kierunku

d

xk

d

yk

d

xj

d

yj

- poprawka do parametrów

S

j

-

niewiadoma określająca skręt pęk na stanowisku

K

jk

- kierunki obserwacji

K

jk

- kierunki obliczone na podstawie x

P

i y

p

2.Kąty poziome:

3.Długości:

-V+AX=L

*

Zgodnie z zasadą: V

T

PV minimalne rozwiązanie układu równań * pow. do funkcji macierzowej

Pochodna cząstkowa macierzy X przyrównujemy do 0 – układ równań normalnych

m- liczba r-

ań obserwacyjnych

n- liczba niewiadomych

46. LINIA NAPOWIETRZNA ZASADY POMIARU I OPRACOWANIA WYNIKÓW

DANE:
H

st

, H

i

, d, α, β

Kolejność obliczeń:

Wysokości punktów (H

1

, H

2

, H

3

):

Analogicznie obliczamy:

Jeżeli:

to,

47. RODZAJE INWENRATYZACJI, OMÓW JE:

-

inwentaryzacja pełną (kompletną)-polega na opracowaniu kompletnej dokumentacji obiektu; dokumentacji podobnej do tej, na podstawie,

której obiekt został zbudowany. Wynikiem pełnej są zwykle oprócz mapy sytuacyjnej, rzuty poziome, przekroje pionowe, rysunki elewacji,
rysunki detali architektonicznych,
-

inwentaryzacja częściowa- może obejmować tylko niektóre części obiektu np. rzut poziomy przyziemia lub rysunek jednej elewacji. Jest zwykle

wykonywana, gdy zachodzi potrzeba opracowań projektu nadbudowy lub projektu budowli, która ma być realizowana w bezpośrednim
sąsiedztwie z danym obiektem
-

inwentaryzacje branżową” i inwentaryzacje geodezyjną”, dla podkreślenia rodzaju elementów, które mają być przede wszystkim uwzględnione

przy inwentaryzacji danego obiektu.
Zwykłe pomiary inwentaryzacyjne wykonywane są z dokładnością ±1÷3 cm.(budynki,mosty,wiadukty).
± 10 cm- budowle ziemne, przewodów podziemnych (przed zasypaniem ±1÷3 cm.
± 2÷3 mm- inwentaryzacja torów kolejowych lub suwnicowych oraz budowli zabytkowych, wykonywana do celów badawczych.

48.INWENTARYZACJA. METODA INDUKCYJNA, ZASADY POMIARU.

Przez podziemne uzbrojenie terenu rozumiemy istniejące w terenie urządzenia sieci przewodów: wod., kanal., ciepln., gaz., elektr., telekom. i
inn

ych. Urządzenia te, zgodnie ze standardami, powinny być geodezyjnie zinwentaryzowane w trakcie prac, przed ich zasypaniem.

Inwentaryzacji urządzeń (przewodów) podziemnych dokonuje się na dwa sposoby:
-pomiar w wykopie,
-

pomiar na podstawie wskazań aparatury wykrywającej przewody podziemne.

Przekopy wykonuje się w sytuacji występowania zakłóceń pola elektromagnetycznego przewodów i niemożności określenia ich położenia
wykrywaczem oraz przy dużej liczbie przewodów na różnych głębokościach, równoległych i krzyżujących się.
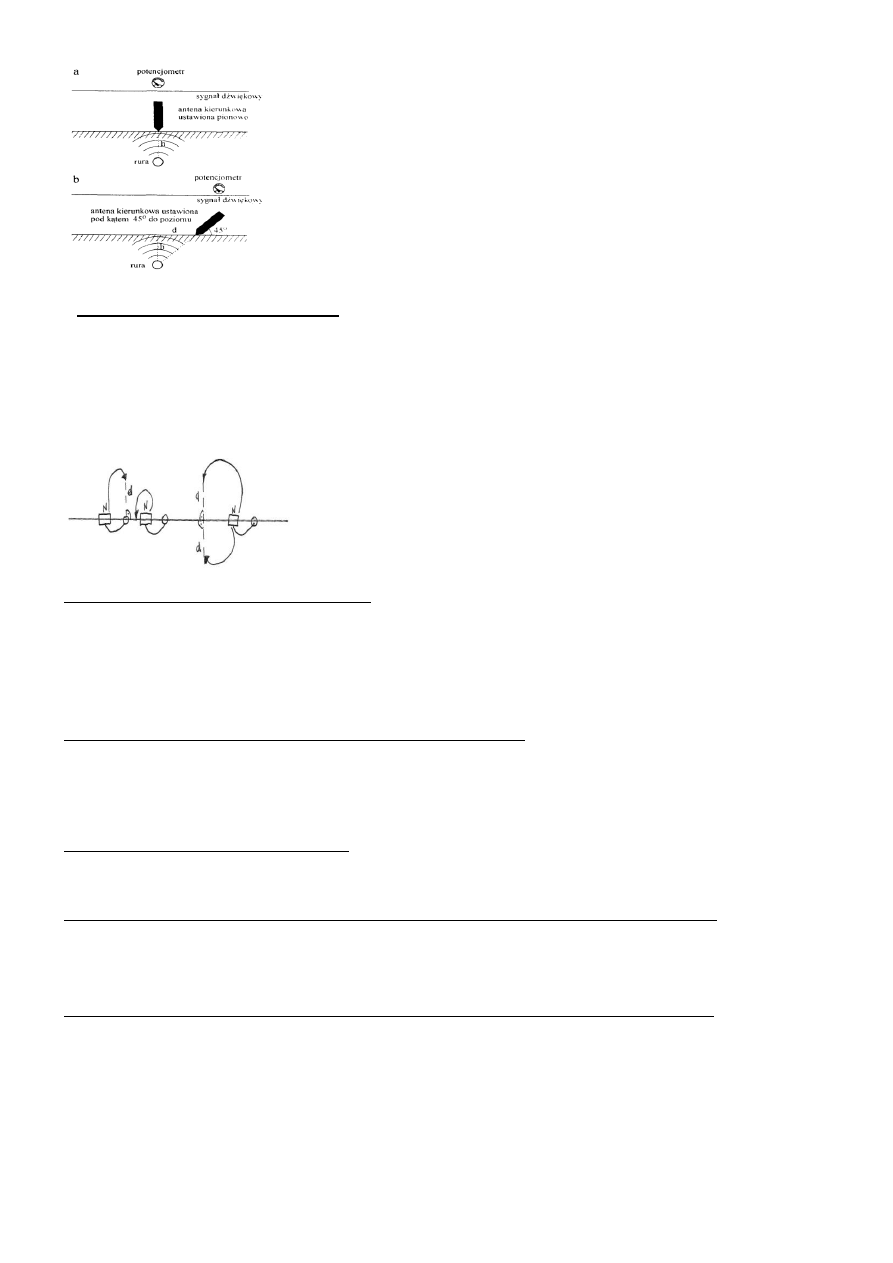
Wykrywacze mogą działać na różnych zasadach, ale najpopularniejsza jest metoda indukcyjna.
Nadajnik lokalizatora (postawiony nad przewodem) wytwarza zmienne pole magnetyczne, które jest zakłócane przez badany przewód,
lokalizacja położenia przewodu polega na przemieszczaniu anteny ustawionej pionowo w dół, nad powierzchnią terenu i śledzenie reakcji
odbiornika.
Gdy antena lokalizatora przybliża się do miejsca, pod którym znajduje się przewód, odczyt wskaźnika potencjometru wzrasta, a sygnał
dźwiękowy staje się bardziej intensywny. Następnie, gdy antena jest już nad przewodem zarówno wskaźnik potencjometru, jak i s ygnał
dźwiękowy maleją do minimum. W ten sposób określamy miejsce, pod którym znajduje się przewód.
Aby określić głębokość zalegania przewodu, ustawiamy antenę pod kątem 45° stosunku do poziomu i przesuwamy nad terenem, aż do
uzyskania efektów jak przednio. Ponieważ antena ustawiona była pod kątem 45° w stosunku do poziomu to odległość anteny od osi przewodu
jest identyczna jak głębokość zalegania przewodu (bo tangens 45°=1). W celu sprawdzenia tych wskazań powinniśmy czynność powtórzyć z
drugiej strony lokalizowanego przewodu

49METODA GALWANICZNA, ZASADY POMIARU

wymaga ona łączenia nadajnika bezpośrednio z przewodem. Stosując tę metodę przed uruchomieniem nadajnika , należy jeden z wyjściowych
zacisków połączyć za pośrednictwem przewodnika z dowolnym dostępnym punktem poszukiwanego przewodu , a drugi z wyjściowych
zacisków należy uziemić. Odległości pomiędzy odbiornikiem, miejscem uziemienia i miejscem połączenia z szukanym przewodem nie mogą być
zbyt małe. Szczególnie należy starać się o większe oddalenie od miejsca uziemienia.
Wyznaczenie trasy przewodu zaczynamy zwykle od ustawienia nadajnika, uziemiacza i wykonania połączeń, po czym obchodzimy miejsce
połączenia nadajnika z szukanym przewodem w promieniu od 2 do 15 m ( zależnie od warunków miejscowych wskaże bliskość przewodu
podziemnego ). Dalszy tok postępowania przedstawia rysunek:

50 INWENTARYZACJA PRZEWODÓW PODZIEMNYCH
Bezpośrednia (przed zasypaniem) i pośrednia (pomiar rzędnej osi przewodu) tachimetrem. Dzieli się na szczegółową i zbiorczą, a oprócz tego
inwent. może być schematyczna lub bramowa. Metody inwent pośredniej: 1. indukcyjna (wykorzystuje zmienne pole elektryczne oraz
generator drgań i nadajnik)
b

1

=(a

1

+h)tgalfa; b

2

=(a

2

+h)tgalaf; a

1

=a

2

=a; h=h

1

+h

2

/2

2. galwaniczna (podłączenia przewodu). Met galwaniczna jest nieznacznie dokładniejsza od indukcyjnej. Wyzn poł przewodu met ind.

1. sygnał w momencie natrafienia na przewód (nadajnik wysyła fale w promieniu 5m, ciągle przesuwamy nadajnik i w ten sposób wykrywamy
przewód) 2. siatka kwadratów

– nadajnik na kolejnych narożnikach siatki 3. wyzn kierunku podłączenia lub załamania przewodu 4. wyzn poł

przewodów leżących blisko siebie (gdy d>1m można wyzn poł, gdy d<1m – poł przybliżone).

51. Metody opracowania geodezyjnego planów realizacyjnych, wymień, omów je.
analityczne -

mapa numeryczna projektowana w oparciu o związki matematyczne, graficzne - mapa analogowa, dane do wyniesienia

odczytane z mapy ,
analityczno-graficzne -

mapa analogowa, dane do wyniesienia częściowo odczytane z mapy częściowo odczytane i obliczone z warunków

geometrycznych np.: linii zabudowy, osi konstrukcyjnych, osi dróg itp. Ogolnie: 1. ustaleni

e lokalnego ukł. wsp. osn. realiz. i obl. wsp. 2. wyz-

nacz. danych geod. do określenia transf. X’ Y’ planu realiz. na wsp. w ukł. geod. 3. obl. XYZ p-tów ok.-reślających główne elementy planu realiz.
4. obl. bł. elem. liniowych i kątowych służących do wyznacz. p-tów. 5. obl. elem. Kontrolnych

52. Geodezyjne opracowanie planu realizacyjnego
Metody opracowania geodezyjnego: a)Analityczna

– mapa numeryczna, projektowanie w oparciu o związki matematyczne b)Graficzna – mapa

analogowa, dane do wyniesienia odczytane z mapy c)Analityczno

– graficzna – mapa analogowa, dane do wyniesienia częściowo odczytane z

mapy, częsiowo obliczone z warunków geometrycznych, np. linii zabudowy, osi konstrukcyjnych , osi dróg, itp

53. Podaj zasady ustalenia dokładności tyczenia sytuacyjnego obiektów inż. bez uwzględnienia błędności osnowy.
x

P

=x

P

(β,d)

y

P

=y

P

(β,d)

m

x

=√(dx/dd)

2

m

d

2

+(dx/dβ)

2

m

β

2

m

y

=...

m

p

=m

x

2

+m

y

2

54. Podaj zasady ustalenia dokładności tyczenia sytuacyjnego obiektów inż. z uwzględnieniem błędności osnowy.
x

P

=x

p

(X,Y,

β,d) (1)

y

P

=y

P

(X,Y,

β,d) (1)

gdzie:
X,Y-

współrzędne p-tów osnowy

β,d- elementy kątowe i liniowe odkładane podczas tyczenia
cov(x

P,

y

P)

= F

P

cov(X,Y,

β,d) F

P

T (2)

gdzie:
cov(x

P,

y

P)

- macierz kowariancji dla X,Y punktów osnowy oraz

dla odkładanych podaczas tyczenia elementów(β,d)

F

P

-

macierz pochodnych cząstkowych dla funkcji (1)

Lub w formie blokowej: