B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

PODSTAWY SZYFROWANIA INFORMACJI

W swiecie wymiany informacji, w którym obecnie króluje globalna siec Internet, coraz

czesciej pojawia sie zagadnienie tajnosci danych przesylanych w sieci. Prawde mówiac problem

ten nie jest nowy, nie zrodzil sie on wraz z era maszyn liczacych i sieci komputerowych. Borykali

sie z nim juz starozytni i oni tez opracowali pierwsze sposoby ochrony informacji przed oczyma

niepowolanych osób. Metoda byla bardzo prosta: szyfrowanie.

Wyróznia sie dwa sposoby szyfrowania informacji: za pomoca szyfrów przestawieniowych oraz

za pomoca szyfrów podstawieniowych. W wyniku zlozenia tych dwu metod otrzymujemy nowa

klase szyfrów, szyfry kaskadowe, które sa znacznie bezpieczniejsze od swych poprzedników.

1.1. Szyfry przestawieniowe

Szyfry przestawieniowe zmieniaja porzadek znaków wedlug pewnego schematu.

Przestawienia tego dokonuje sie za pomoca pewnej figury geometrycznej, do której wpisuje sie

tekst w sposób okreslony sciezka zapisu, a potem odczytuje sie tekst zgodnie z pewna sciezka

odczytu.

Tekst jawny

→Figura→Tekst zaszyfrowany

zapis odczyt

Przykladem takiego szyfru jest szyfr plotkowy. Tekst zaszyfrowany otrzymuje sie przez zapis

w ksztalcie „plotka”, a nastepnie odczytuje sie wierszami informacje. Klucz K tego szyfru

okreslony jest wysokoscia tego „plotka”.

Przyklad (dla K = 3):

BEZPIECZENSTWO_SIECI_KOMPUTEROWYCH

tekst jawny

B

EZP

I

ECZ

E

NST

W

O_S

I

ECI

_

KOM

P

UTE

R

OWY

C

H

B

E

Z

P

I

E

C

Z

E

N

S

T

W

O

_

S

I

E

C

I

_

K

O

M

P

U

T

E

R

O

W

Y

C

H

figura

BE

Z

PIE

C

ZEN

S

TWO

_

SIE

C

I_K

O

MPU

T

ERO

W

YCH

BIEWI_PRCEPEZNTOSEIKMUEOYHZCS_COTW

wiadomosc zaszyfrowana

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

2

Czesto figura jest macierz dwuwymiarowa. Tekst jawny zapisuje sie do macierzy wierszami.

Tekst zaszyfrowany powstaje przez odczytanie kolumn w okreslonym porzadku.

Przyklad: Uzywajac macierzy 3x4 szyfrujemy slowo „MARCYPANKOWY”.

1

2

3

4

Tekst zaszyfrowany po odczycie kolumn w kolejnosci 2-4-1-3

M. A R

C

Bedzie mial postac:

Y

P

A

N

APOCNYMYKRAW

K

O W Y

Macierz moze byc n-wymiarowa.

Wiele szyfrów przestawieniowych zmienia kolejnosc znaków tekstu przy zastosowaniu

pewnego stalego okresu d. Niech Z

d

jest zbiorem liczb calkowitych od 1 do d, a f: Z

d

→ Z

d

permutacja na zbiorze Z

d

. Kluczem takiego szyfru jest para K=(d, f). Kolejne bloki d znaków sa

szyfrowane przez dokonanie permutacji znaków zgodnie z f.

Przyklad:

d=4

f jest permutacja

i: 1 2 3 4

f(i): 2 4 1 3

UWAGA_SCISLE_TAJNA_WIADOMOSC

tekst jawny

WGUA_CASSEILTJ_AAWN_AOIDOCMS

wiadomosc zaszyfrowana

W rzeczywistosci dwa poprzednie sposoby szyfrowania sa szczególnymi przypadkami

trzeciego. Bardzo latwo jest rozpoznac, czy dany szyfr jest szyfrem przestawieniowym.

Czestotliwosc wystepowania liter w tekscie jawnym jest taka sama jak czestotliwosc

wystepowania tych samych liter w tekscie zaszyfrowanym.

1.2. Szyfry podstawieniowe

Szyfry podstawieniowe dzielimy na cztery typy: monoalfabetyczne, homofoniczne,

wieloalfabetyczne i poligramowe.

1.2.1. Szyfry monoalfabetyczne

Szyfry monoalfabetyczne zamieniaja kazdy znak uporzadkowanego alfabetu jawnego na

odpowiedni znak uporzadkowanego alfabetu szyfru. Bardzo czesto alfabet szyfru powstaje

z alfabetu jawnego przez prosta zamiane kolejnosci znaków w alfabecie jawnym (permutacja).

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

3

Jesli alfabet jawny ma a

1

, a

2

, ..., a

N-1

,

wtedy alfabet szyfru ma postac f(a

1

), f(a

2

), ..., f(a

N-1

), przy

czym f jest odwzorowaniem wzajemnie jednoznacznym (bijekcja). Kluczem jest alfabet szyfru lub

funkcja f.

Przyklad:

alfabet jawny: A B C D E F G H I J K L M N O P R S T U W X Y Z

alfabet szyfru: D E F G H I J K L M N O P R S T U W X Y Z A B C

tekst jawny:

SYSTEM

tekst zaszyfrowany:

WBWXHP

Powyzszy przyklad jest szczególnym przypadkiem szyfru podstawieniowego, gdyz szyfr

powstal na „alfabecie przesunietym” zwanym tez szyfrem Cezara [1, 2, 3].

Funkcja f ma wtedy postac:

f(a) = (a+k) mod N

gdzie:

N – dlugosc alfabetu,

k – przesuniecie w prawo,

a – oznacza pozycje litery w alfabecie.

Innym przypadkiem szyfru podstawieniowego jest szyfr oparty na mnozeniach zwany

„przerzedzonym”. Funkcja f ma postac:

f(a) = (s*k) mod N

przy czym k oraz N sa wzglednie pierwsze. Jesli k i N nie sa liczbami wzglednie pierwszymi, to

wielu literom tekstu jawnego bedzie odpowiadac ta sama litera tekstu zaszyfrowanego.

Dwie powyzsze metody mozna polaczyc i otrzymamy wtedy szyfr „afiniczny”.

f(a) = (a * k

1

+ k

0

)

mod N

gdzie:

k

0

– przesuniecie w prawo,

k

1

– wspólczynnik przerzedzenia.

Ogólny wzór przeksztalcenia wyzszego rzedu otrzymuje sie z przeksztalcen wielomianowych

stopnia t

f(a) = (a

t

*k

t

+ a

(t-1)

*k

(t-1)

+ ... a*k

1

+ k

0

) mod N

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

4

1.2.2. Szyfry homofoniczne

Szyfry homofoniczne odwzorowuja kazdy znak a

i

alfabetu jawnego A na zestaw elementów

tekstu zaszyfrowanego, zwanych homofonami. W ten sposób odwzorowanie tekstu jawnego na

zaszyfrowany mozna okreslic jako funkcje:

f: A

→B

gdzie B jest alfabetem szyfrujacym, skladajacym sie z podzbiorów b

i

, bedacych zbiorami

homofonów odpowiadajacych a

i

Tekst jawny M=m

1,

m

2

, ... podlega szyfrowaniu jako b=c

1

, c

2

, ... gdzie znak c

i

wybierany jest

losowo ze zbioru homofonów f(m

i

).

Przyklad:

Litera Homofony

A

17 19 34 41 56 60 67 83

I

08 22 53 65 88 90

L

03 44 76

N

02 09 15 27 32 40 59

O

10 11 23 28 42 54 70 80

P

33 91

T

05 10 20 29 45 58 64 78

Tekst jawny:

P I L O T

Tekst zaszyfrowany: 91 53 03 80 64

lub:

33 08 76 80 05

Szyfry homofoniczne moga byc duzo trudniejsze do zlamania niz zwykle szyfry

podstawieniowe, szczególnie w przypadkach, gdy liczba homofonów przydzielonych literze jest

proporcjonalna do wzglednej czestosci jej wystepowania. Oczywiscie im wiecej homofonów

przydzielimy literom, tym silniejszy tworzymy szyfr.

W wiekszosci szyfrów jest mozliwe jego zlamanie, gdy posiadamy odpowiednio duza ilosc

tekstu zaszyfrowanego [4]. Wynika to z faktu, ze istnieje tylko jeden klucz K, którego uzycie do

deszyfrowania daje w wyniku zrozumialy tekst jawny. Istnieje jednak mozliwosc stworzenia

szyfru homofonicznego wyzszego stopnia, dla którego kryptogram mozna zdeszyfrowac na wiecej

niz jeden sensowny tekst.

Aby skonstruowac taki szyfr drugiego stopnia (kazdemu tekstowi zaszyfrowanemu

odpowiadaja dwa teksty jawne), nalezy macierz K(NxN) wypelnic losowo liczbami od 1 do N

2

.

Wiersze i kolumny odpowiadaja znakom alfabetu jawnego. Dla kazdego znaku a tekstu jawnego

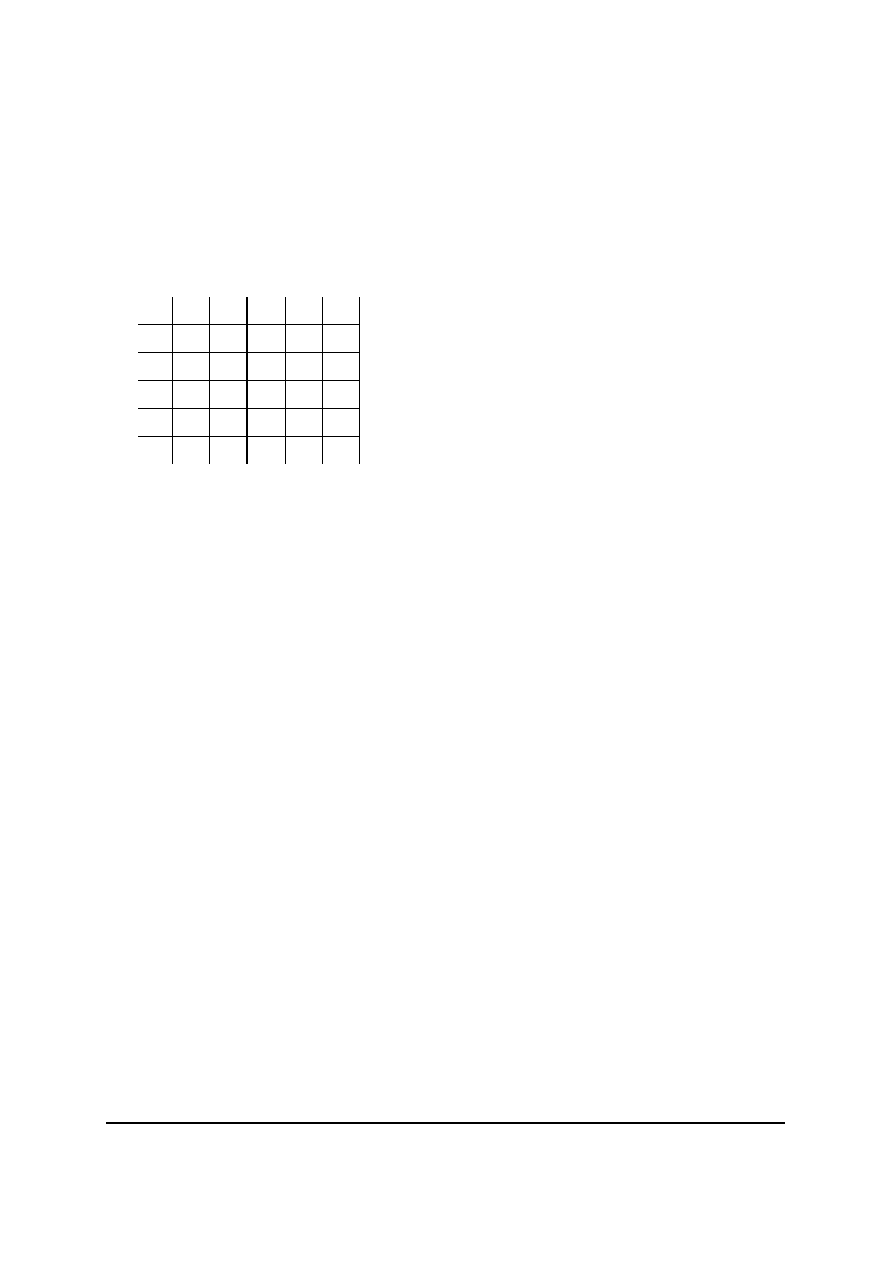
B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

5

wiersz a macierzy tworzy jeden zbiór homofonów f

1

(a), zas kolumna a tworzy zbiór f

2

(a).

Wlasciwy tekst jawny M=m

1

, m

2

,... szyfrujemy z tekstem falszywym X=x

1

, x

2

,..., tworzac

kryptogram C=c

1

, c

2

,..., gdzie c

i

= K(m.

i

, x

i

) dla i = 1, 2, ...

Przyklad:

N=5, {A, I, K, L}

\

A

I

J

K

L

Tekst „lalka” szyfrujemy tekstem falszywym „kajak”.

A 10 22 18 02 11

Tekst zaszyfrowany:

I

12 01 25 05 20

L A L K A

J

19 06 23 13 07

K A J A K

K 03 16 08 24 15

14 10 21 03 02

L

17 09 21 14 04

1.2.3. Szyfry wieloalfabetyczne

Szyfry monoalfabetyczne zachowuja rozklad czesciowy wystepowania znaków tekstu

jawnego. Szyfr homofoniczny ukrywa ten rozklad przez przypisanie danej literze wielu symboli

(homofonów). Szyfr wieloalfabetyczny takze ukrywa ten rozklad, ale robi to przez uzycie wielu

podstawien. Twórca szyfrów wieloalfabetycznych jest Leon Batista Alberti [5, 6, 7, 8, 9].

Skonstruawal on dysk szyfrowy, skladajacy sie z dwóch kól. Na zewnetrznym znajdowaly sie

litery alfabetu jawnego (24 znaki), na wewnetrznym ruchomym znajdowaly sie litery alfabetu

szyfrowego. Dzieki temu dysk ten definiuje 24 mozliwe podstawienia (zamiana tekstu jawnego na

litery kryptogramu z kola wewnetrznego), które oczywiscie mozemy zmienic co pewien okres d

(znak tekstu) przez obrót kola.

Przykladem szyfru podstawieniowego wieloalfabetycznego jest szyfr Vigene’a [5]. Klucz

szyfru K tworzy sekwencja liter K=k

1

, k

2

, ... k

d

, gdzie k

i

(i=1, ... d) daje liczbe przesuniec w i-tym

alfabecie:

f

i

(a) = (a + k

i

) mod N

Przyklad:

Szyfrujemy slowo „lekkoatletka” z uzyciem klucza czad.

Tekst jawny:

L E K K O A T L E T K A

Klucz:

C Z A D C Z A D C Z A D

Tekst zaszyfrowany:

N D K N Q Z T O G S K D

Pomocna przy szyfrowaniu i deszyfrowaniu jest tablica Vigenere’a. Czesc tej tablicy

przedstawiona jest ponizej:

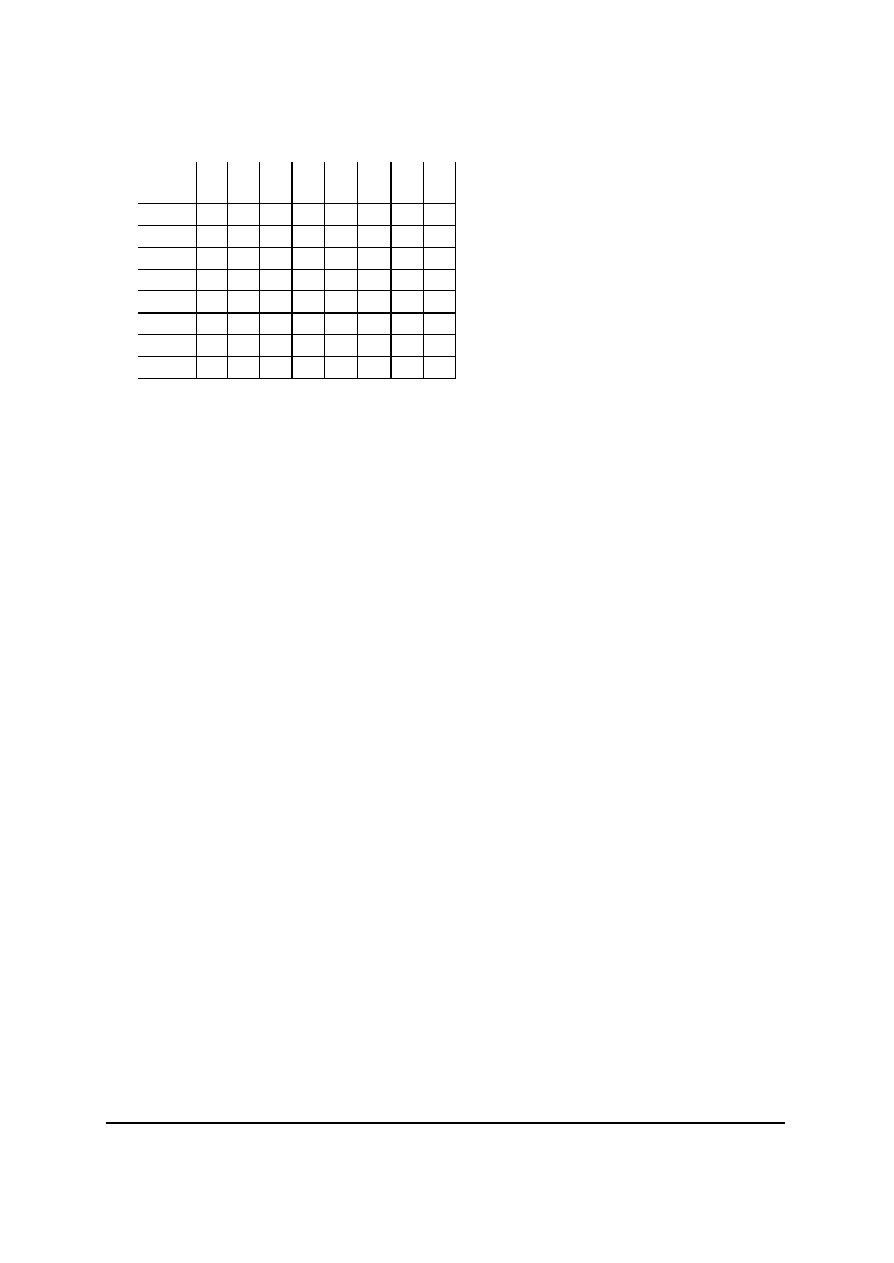
B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

6

A B C D E

F

G ...

→tekst jawny

A

A B C D

E

F

G

...

B

B

C D E

F

G H

...

Dla litery tekstu jawnego d i litery klucza d

C

C D E

F

G H I

...

litera kryptogramu c jest znak z kolumny d

D

D E

F

G

H I

J

...

i wiersza d, czyli znak g.

E

E

F

G H

I

J

... ...

F

F

G H I

J

K ... ...

Bardzo podobny do szyfru Vigenere’a jest

G

G H I

J

K ... ... ...

szyfr Beauforta, dla którego odwzorowanie

...

... ... ... ... ... ... ... ...

przybiera postac:

Ζ
klucz

f

i

(a) = (k

i

– a) mod N

Inna odmiana szyfru podstawieniowego wieloalfabetycznego jest szyfr z kluczem biezacym.

Jest to szyfr, w którym dlugosc klucza jest równa dlugosci tekstu jawnego. Jedna z metod jest

uzycie tekstu z jakiejs ksiazki lub dokumentu jako szyfru podstawieniowego. Kluczem jest tytul

ksiazki lub dokumentu i punkt startowy. Szyfr ten gwarantuje prawie doskonala poufnosc

szyfrowania. Mozna go zlamac wykorzystujac fakt, ze teksty, które sa kluczami np. w jezyku

angielskim, cechuje pewna redundancja. Najlepiej nadaje sie do tego metoda Friedmana[8].

Innym rozwiazaniem sa maszyny rotowe [6, 10], w których stosuje sie podstawienie

wieloalfabetyczne o dlugim okresie. Maszyna taka jest zbudowana z szeregu kól (rotorów). Na

obwodzie kazdego kola, po obu stronach, znajduje sie po 26 styków. Kazdy styk na jednej stronie

polaczony jest z jednym ze styków po drugiej stronie. Polaczenie to definiuje nam odwzorowanie

f

i

liter tekstu jawnego na litery kryptogramu. Kolo (rotor) moze sie obracac, kazde nowe polozenie

rotora odpowiada innemu odwzorowaniu. Gdy rotor jest w pozycji i-tej, to funkcja opisujaca

odwzorowanie przyjmuje postac:

F

i

= (f

i

(a-j

i

) mod 26 + j

i

) mod 26

Sygnal odpowiadajacy literze tekstu jawnego wchodzi do zespolu rotorów, przechodzi przez

nie i pojawia sie z drugiej strony. Jesli w maszynie znajduje sie kilka rotorów, to szyfr

podstawieniowy sklada sie z kilku szyfrów odpowiadajacych kolejnym rotorom. Funkcja

odwzorowujaca litere przyjmuje postac:

E

ki

(a) = F

i

°...° F

2

°F

1

(a)

przy czym k

i

zalezy od f

1

, ...,f

i

zaszytych w polaczeniach miedzy stykami dla odpowiednich

rotorów oraz od pozycji j

1

, ..., j

i

poszczególnych rotorów. Poczatkowy klucz tego szyfru jest

okreslony poczatkowym ustawieniem rotorów oraz ich okablowaniem (polaczeniami), nastepnie

sposobem zmiany klucza, czyli zmiany pozycji (obracanie) poszczególnych rotorów. Maszyna

z trzema rotorami ma okres dlugosci 17.546, z czterema 456.976, a z piecioma az 11.881.376.

Mimo ze okresy (klucze) sa tak dlugie, nie sa one calkiem losowe i szyfry te moga zostac zlamane,

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

7

co dowiedli wybitni polscy przedwojenni matematycy, którzy zlamali kod maszyny szyfrujacej

„Enigma” stosowanej przez Niemców w czasie drugiej wojny swiatowej. „Enigma” jest

przykladem maszyny rotowej z trzema rotami, w której ruch rotorów odbywal sie jak w liczniku, a

kluczem bylo poczatkowe polozenie tych rotorów.

Prawdopodobnie najlepszym tego typu szyfrem jest szyfr z kluczem jednokrotnym.

KLucz jest losowa sekwencja znaków, bez powtórzen i jest uzywany tylko raz. Gilbert

Verman jako pierwszy zastosowal ten szyfr dla 32-znakowego kodu Baudota stosowanego

w dalekopisach firmy AT&T (American Telegraph Copany). Uzycie kazdego innego

losowego klucza daje nam jeden z najtrudniejszych do zlamania szyfrów. Niedogodnoscia tej

metody jest bardzo dlugi klucz.

1.2.4. Szyfry poligramowe

Szyfry przestawieniowe i podstawieniowe szyfruja krokowo po jednej literze tekstu jawnego.

Szyfry poligramowe szyfruja w jednym kroku wieksze grupy liter i to wlasnie powoduje, ze

zlamanie takiego szyfru jest duzo trudniejsze, a to dzieki zachwianiu równowagi pomiedzy

czestotliwoscia wystepowania liter w tekscie jawnym i zaszyfrowanym.

Jednym z szyfrów poligramowych jest szyfr Playfaira [6], który jest digramowym szyfrem

podstawieniowym. Szyfr ten byl stosowany przez Anglikow w czasie pierwszej wojny swiatowej.

Kluczem jest macierz o wymiarach 5x5 skladajaca sie z liter (bez litery J).

H

A

R P S

I

C

O D B

E

F

G K L

M

N

Q T

U

V

W X Y

Z

Kazda pare liter tekstu jawnego m

1

m

2

szyfruje sie wedlug podanych regul:

1. Jesli litery m1 i m2 sa w tym samym wierszu, to c1 i c2 sa znakami polozonymi z prawej

strony m1 i m2;

2. Jesli litery m1 i m2 znajduja sie w tej samej kolumnie, to c1 i c2 sa znakami polozonymi

ponizej m1 i m2;

3. Jezeli m1 i m2 znajduja sie w tej samej kolumnie, to c1 i c2 sa brane z przeciwleglych rogów

prostokata wyznaczonego przez m1 i m2, przy czym c1 pochodzi z wiersza zawierajacego m1,

a c2 z wiersza zawierajacego m2.

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

8

4. Jesli m1 = m2, to do tekstu jawnego miedzy te litery wstawia sie nieznaczaca litere (np. X), co

eliminuje powtórzenia.

5. Jesli tekst jawny ma nieparzysta liczbe znaków, to na koncu tekstu jawnego dopisuje sie

nieznaczaca litere.

Pierwsza kolumne macierzy traktuje sie jako polozona na prawo od ostatniej kolumny,

a pierwszy wiersz jako lezacy pod ostatnim wierszem.

Przyklad:

Za pomoca szyfru Playfaira kodujemy slowa „POLITECHNIKA”, „PANNA”.

PO LI TE CH NI KA

tekst jawny

RD EB MK IA MC FP tekst zaszyfrowany

PA NX NA

tekst jawny (wstawienie znaku nieznaczacego miedzy litery)

SR QW WC

tekst zaszyfrowany

Inny szyfr zwany Hilla przeksztalca liniowo d znaków tekstu jawnego na d znaków tekstu

zaszyfrowanego. Opis metody szyfrowania dla przypadku, gdy d=2 oraz M=m

1

m

2

. Tekst jest

szyfrowany jako C = E

K

(M) = c

1

c

2

, gdzie:

c

1

= (k

11

* m

1

+ k

12

* m

2

) mod n

c

2

= (k

21

* m

1

+ k

22

* m

2

) mod n

Traktujac M i C jako wektory oraz K jako macierz przeksztalcenia mozna zapisac:

C = K*M mod n:

Deszyfrowanie jest bardzo proste i dokonuje sie przez uzycie macierzy odwrotnej K

-1

:

D

K

(C) = K

-1

KM mod n = M mod n = M.

Ze wzgledu na to, ze przeksztalcenie jest liniowe, mozna bardzo latwo odtworzyc klucz, majac

zaszyfrowana i jawna postac zaledwie kilkunastu znaków tekstu. Majac kawalki tekstu jawnego

i odpowiadajace im kawalki tekstu zaszyfrowanego M

1

= (m

1

m

2

), M

2

= (m

3

m

4

), C

1

=

(c

1

c

2

) oraz C

2

= (c

3

c

4

) i przyjmujac, ze M = (M

1,

M

2

), C = (C

1,

C

2,

), mozna znalezc macierz K korzystajac ze

wzoru: K = CM

-1

mod n.

1.3. Szyfry kaskadowe

Szyfr kaskadowy jest zlozeniem i funkcji (szyfrów) F

1

, F

2

, ..., F

i, ,

gdzie F

i

jest permutacja

albo podstawieniem. Maszyny rotorowe sa przykladem szyfrów kaskadowych. Funkcja

przeksztalcenia ma postac:

E

ki

(a) = F

i

°...° F

2

° F

1

(a)

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

9

Szyfrowanie podstawieniowo-permutacyjne jest polaczeniem róznego rodzaju funkcji. Twórca

tej koncepcji jest Shannon. Przeksztalcenie mozna tworzyc laczac przestawienie z sekwencja na

przemian wykonywanych podstawien i prostych operacji liniowych.

Przed era komputerowa kryptografia zajmowala sie szyframi dzialajacymi na pojedynczych

znakach. Byly to algorytmy dokonujace podstawienia znaków. Jeszcze lepsze wyniki uzyskano,

mieszajac wielokrotnie obie techniki.

Rzeczy skomplikowaly sie w erze komputerowej, lecz istota problemu nie ulegla zmianie.

Podstawowa zmiana jest zmiana jednostki przetwarzania; obecnie jest nia bit, a nie znak. Fakt ten

spowodowal zmiane rozmiarów alfabetu: z 26 znaków do 2, ale nic poza tym. Wiekszosc dobrych

algorytmów kryptograficznych nadal laczy elementy podstawiania i przestawiania.

L

ITERATURA

1.

B. S

CHNEIER

, Kryptografia dla praktyków. Protokoly, algorytmy i programy zródlowe w jezyku C. Wydawnictwa

Naukowo-Techniczne, Warszawa 1995.

2. C. E. S

HANNON

, Predication and Entropy in Printed English. Bell System Technical Journal, v. 30, n. 1, 1951,

str. 50-64.

3.

S. P

ELEG AND

A. R

OSENFIELD

, Breaking Substitution Ciphers Using a Relaxation Algorithm. Communications of

the ACM, v. 22,n. 11, Nov 1979.

4.

F. P

RATT

, Secret and Urgent. Blue Ribbon Books, 1942

5.

D. E. R

OBLING

D

ENING

, Kryptografia i ochrona danych. Wydawnictwa Naukowo-Techniczne, Warszawa 1993.

6.

D. K

AHN

, The Codebreakers: The Story of Secret Writing, New York: Macmillan, 1967.

7.

B. S. K

ALISKI

, R. L. R

IVERS AND

A. T. S

HERMAN

, Is the Data Encryption Standard a Group?. Journal of

Cryptology, v. 1, n. 1, 1988, str. 3-36.

8.

W. F. F

RIEDMAN

, The Index of Coincidence and Its Applications in Cryptography, Riverbank Publication No. 22,

Riverbank Labs, 1920.

9.

H. F. G

AINES

, Cryptoanalysis, American Photographic Press, 1937.

10. A. S

CHERBIUS

, Ciphering Machine, U.S. Patent 1, 657, 411, 24 Jan 1928.

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

KLASYFIKACJA ALGORYTMÓW

Algorytmów szyfrujacych jest bardzo wiele. Mozna je klasyfikowac w bardzo rózny sposób.

W poprzednim rozdziale wyróznilismy dwie grupy szyfrów, ze wzgledu na metody szyfrowania

informacji, podstawieniowe i przestawieniowe. Najbardziej jednak funkcjonalny wydaje sie

podzial ze wzgledu na sposób, w jaki algorytmy przeksztalcaja tekst jawny w szyfrogram. Ze

wzgledu na ten parametr wyróznia sie dwa typy algorytmów: strumieniowe (rozdzial 1.4)

i blokowe (rozdzial 1.6).

1.4. Szyfry strumieniowe

Niech M oznacza wiadomosc tekstowa, zwana równiez tekstem jawnym. Szyfry

strumieniowe dziela tekst M na znaki lub bity m

1

, m

2

, ..., a nastepnie kazdy i-ty element m

i

jest

szyfrowany kluczem k

i

nalezacym do strumienia kluczy K = k

1

, k

2

, ...; tzn.

E

k

(M) = E

k1

(m

1

)E

k2

(m

2

)...

Szyfr strumieniowy jest okresowy, jesli strumien klucza powtarza sie po d znakach, dla

danego ustalonego d. W przeciwnym przypadku szyfr jest nieokresowy (tego typu szyfry sa

bezpieczniejsze od okresowych i w dalszej czesci tego podrozdzialu zajmiemy sie wlasnie nimi).

Jak nietrudno zauwazyc, bezpieczenstwo szyfrów strumieniowych calkowicie zalezy od

generatora strumienia kluczy (rys. 6). Mozna sobie wyobrazic sytuacje, w której generator

strumienia klucza wytwarza nieskonczenie wiele zer, co sprawi, ze na wyjsciu otrzymamy

szyfrogram taki sam jak tekst jawny. Moze sie tez zdarzyc, ze generator bedzie wytwarzal

powtarzajacy sie wzorzec (efekt niedopuszczalny w przypadku szyfrów nieokresowych), co

sprawi, ze nasz caly zlozony system bedzie zwyklym sumatorem modulo dwa. Trzeba by wiec

stworzyc generator, który wytwarzalby nieskonczony strumien bitów losowych. W ten sposób

otrzymamy klucz jednorazowy i doskonale zabezpieczenie. W rzeczywistosci generatory ciagów

klucza wytwarzaja strumienie bitów, które sa zdeterminowane. Moga wiec one byc w stosunkowo

latwy sposób odtworzone przez kryptoanalityków. Jedynym rozwiazaniem wydaje sie stworzenie

generatora, który wytwarzalby losowo wygladajacy ciag bitów, zadanie to jednak nie nalezy do

latwych.

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

11

Generator

ciagu kluczy

Ciag klucza

Generator

ciagu kluczy

Ciag klucza

Tekst jawny

Tekst jawny

Szyfrogram

C

i

P

i

P

i

K

i

K

i

Szyfrowanie

Deszyfrowanie

Rys. 6. Generator strumienia klucza

W kategorii szyfrów strumieniowych mozna wyróznic synchroniczne szyfry strumieniowe

oraz samosynchronizujace szyfry strumieniowe

.

W pierwszym przypadku mamy do czynienia

z sytuacja, w której klucz jest generowany niezaleznie od strumienia wiadomosci. Po obu

stronach, szyfrujacej i deszyfrujacej, generatory strumieni kluczy wytwarzaja identyczne

strumienie bitów klucza. Wszystko dziala poprawnie do chwili, gdy oba generatory sa

zsynchronizowane. Moze jednak nastapic „zagubienie” bitu podczas przesylania lub jeden z

generatorów „przeskoczy” cykl; wówczas od tego momentu kazdy znak szyfrogramu bedzie

zdeszyfrowywany niepoprawnie. By owa pomylke wyeliminowac, nadawca i odbiorca musza

ponownie zsynchronizowac swoje generatory strumieni kluczy. Nie jest to jednak takie proste,

jakby sie na pozór wydawalo; musza dokonac tego w taki sposób, aby nie powtórzyla sie zadna

czesc ciagu klucza. Nie wystarczy wiec ponowna inicjacja obu generatorów.

Pozytywna strona tego rozwiazania jest to, ze synchroniczne szyfry strumieniowe nie

rozsiewaja bledów transmisji.

Szyfry strumieniowe pracuja w dwu trybach:

•

tryb sprzezenia zwrotnego wyjsciowego – gdy klucz wplywa na funkcje nastepnego stanu;

funkcja wyjscia jest prosta i nie zalezy od klucza,

•

tryb licznikowy – gdy mamy do czynienia z prostymi funkcjami stanu wewnetrznego

i skomplikowanymi funkcjami wyjscia, które sa zalezne od klucza.

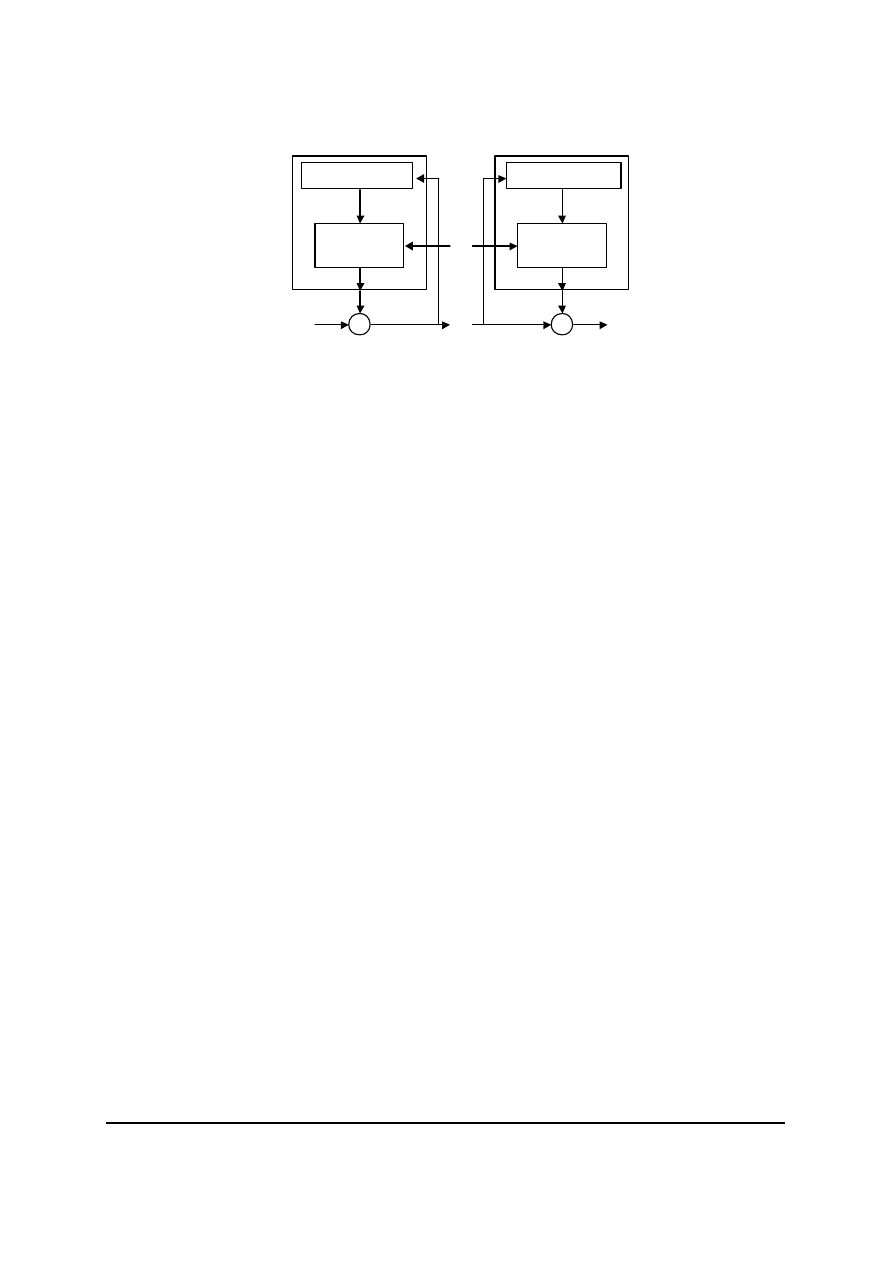
W samosynchronizujacych szyfrach strumieniowych kazdy bit ciagu szyfrujacego jest funkcja

pewnej stalej liczby poprzednich bitów szyfrogramu. Najczesciej te szyfry strumieniowe pracuja

w trybie sprzezenia zwrotnego szyfrogramu. Na rys. 7 przedstawiony jest schemat dzialania szyfru

strumieniowego w trybie sprzezenia zwrotnego szyfrogramu.

Poniewaz stan wewnetrzny zalezny jest od n poprzednich bitów szyfrogramu, wiec generator

strumienia klucza do deszyfrowania bedzie automatycznie zsynchronizowany z generatorem

strumienia klucza do szyfrowania po odebraniu n bitów szyfrogramu.

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

12

Stan wewnetrzny

Funkcja

wyjsciowa

Stan wewnetrzny

Funkcja

wyjsciowa

K

C

i

P

i

P

i

Rys. 7. Samosynchronizujacy szyfr strumieniowy

Niestety, ujemna strona samosynchronizujacych sie szyfrów strumieniowych jest propagacja

bledów. Jezeli wystapi blad jednego bitu w czasie przesylania, to po stronie deszyfrujacej

otrzymamy n niepoprawnych bitów [1, 2, 3, 4].

1.5. Generatory ciagów losowych

W rozdziale wczesniejszym stwierdzilismy, ze szyfry strumieniowe latwo mozna zlamac, gdy

lancuch klucza sie powtarza lub zawiera redundancje. Intuicyjnie oznacza to, ze kazdy element

z alfabetu klucza powinien byc równomiernie rozmieszczony w calym lancuchu klucza i nie

powinno byc dlugich powtarzajacych sie ciagów ani tez innych wzorców.

Okazuje sie jednak, ze zaden algorytm skonczony nie moze generowac prawdziwie losowych

ciagów. Nie wyklucza to jednak mozliwosci generowania kluczy przy uzyciu generatorów liczb

pseudolosowych.

1.5.1. Liniowe generatory kongruencyjne

Liniowymi generatorami kongruencyjnymi (ang. Linear Congruential Generator)
nazywamy generatory ciagów pseudolosowych pracujace wg wzoru kongruencyjnego:

(

)

X

aX

b

m

n

n

=

+

−1

mod

,

gdzie:

X

n

– liczba o numerze n w ciagu,

a, b, m – wielkosci stale,
a

– mnoznik,

b

– przyrost,

m

– modulo,

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

13

X

0

– ziarno generatora – wartosc poczatkowa.

Jak latwo zauwazyc, generator ten ma okres nie wiekszy niz m.
Jezeli liczby a, b i m sa odpowiednio dobrane, to generator bedzie generatorem
maksymalnego okresu i bedzie mial okres m, np. gdy m i b wzglednie pierwsze [5].

Tabela 1 zawiera liste dobrych stalych dla liniowych generatorów kongruencyjnych.

Zapewniaja one, ze generatory wytwarzaja ciagi maksymalnego okresu.

Tabela 1. Stale dla liniowych generatorów kongruencyjnych

Przepelnienie przy

a

b

m

2

20

106

1283

6075

2

21

211

1663

7875

2

22

421

1663

7875

2

23

430

2531

11979

936

1399

6655

1366

1283

6075

2

24

171

11213

53125

859

2531

11979

419

6173

29282

967

3041

14406

2

25

141

28411

134456

625

6571

31104

1541

2957

14000

1741

2731

12960

1291

4621

21870

205

29573

139968

2

26

421

17117

81000

1255

6173

29282

281

28411

134456

2

27

1093

18257

86436

421

54773

259200

1021

24631

116640

1021

25673

121500

2

28

1277

24749

117128

741

66037

312500

2041

25673

121500

2

29

2311

25367

120050

1807

45289

214326

1597

51749

244944

1861

49297

233280

2661

36979

175000

4081

25673

121500

3661

30809

145800

2

30

3877

29573

139968

3613

45289

214326

1366

150889

714025

cd. tabeli 1

2

31

8121

28411

134456

4561

51349

243000

7141

54773

259200

2

32

9301

49297

233280

4096

150889

714025

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

14

2

33

2416

374441

177185

2

34

17221

107839

510300

36261

66037

312500

2

35

84589

45989

217728

Zaleta liniowych generatorów kongruencyjnych jest duza szybkosc ich realizacji, gdyz

wymagaja tylko kilku generacji na jeden bit wytwarzanego ciagu.
Niestety liniowe generatory kongruencyjne nie moga byc wykorzystywane w szyfrach
strumieniowych, poniewaz ciagi przez nie wytwarzane sa przewidywalne.

Po raz pierwszy liniowe generatory kongruencyjne zostaly zlamane przez Joan Boyar [6].

Zlamala ona równiez generatory kwadratowe i szescienne postaci

(

)

(

)

X

aX

bX

c

m

X aX

bX

cX

d

m

n

n

n

n

n

n

n

=

+

+

+

+

+

−

−

−

−

−

1

2

1

1

3

1

2

1

mod

mod

Dalsi badacze rozszerzyli te metode na dowolne wielomianowe generatory kongruencyjne.

Nastepnie badacze tacy, jak Wichmann, Hill, Pierre, L`Eayer badali kombinacje liniowych
generatorów kongrencyjnych. Generatory bedace wynikiem ich pracy maja dluzsze okresy
i zachowuja sie lepiej w testach losowosci, lecz nie sa obecnie kryptograficznie bezpieczne.

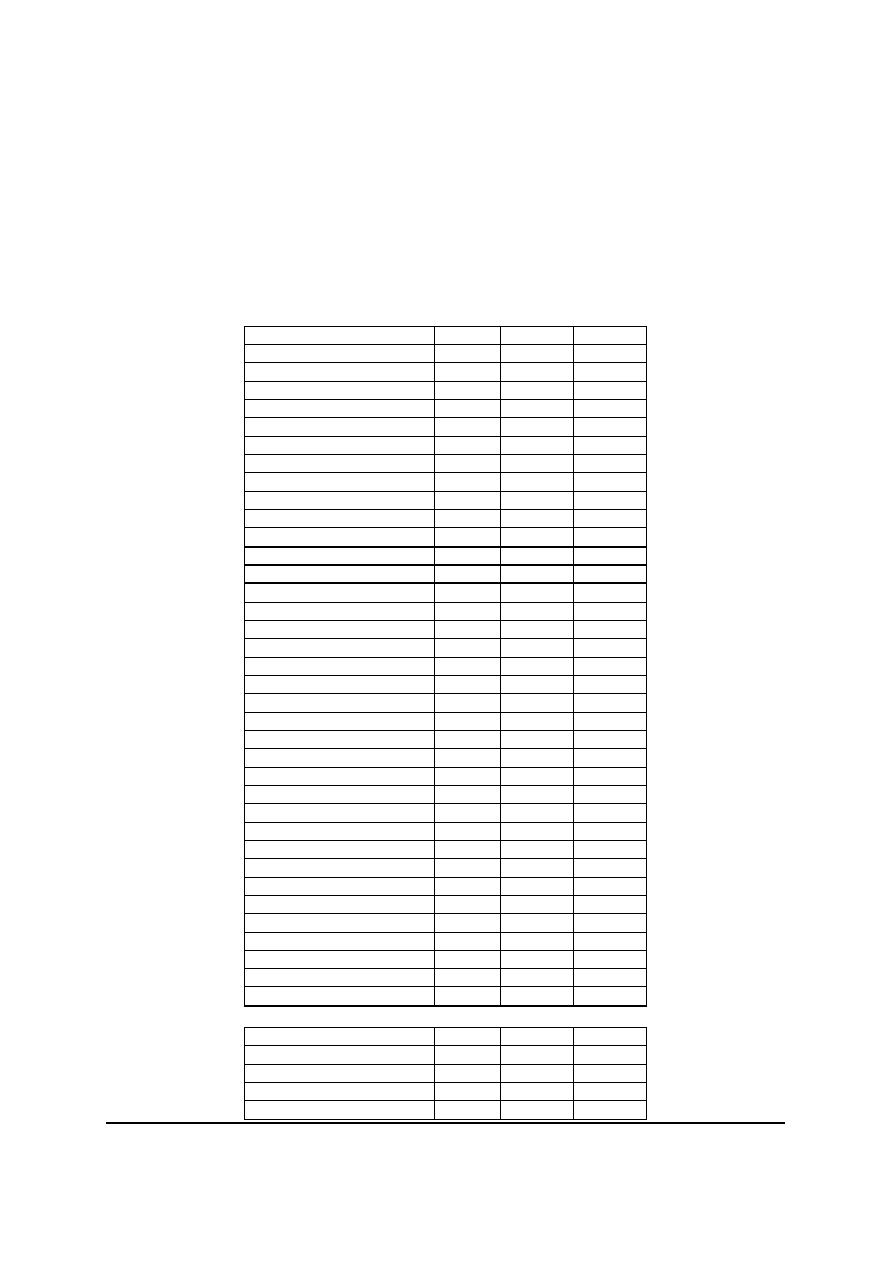
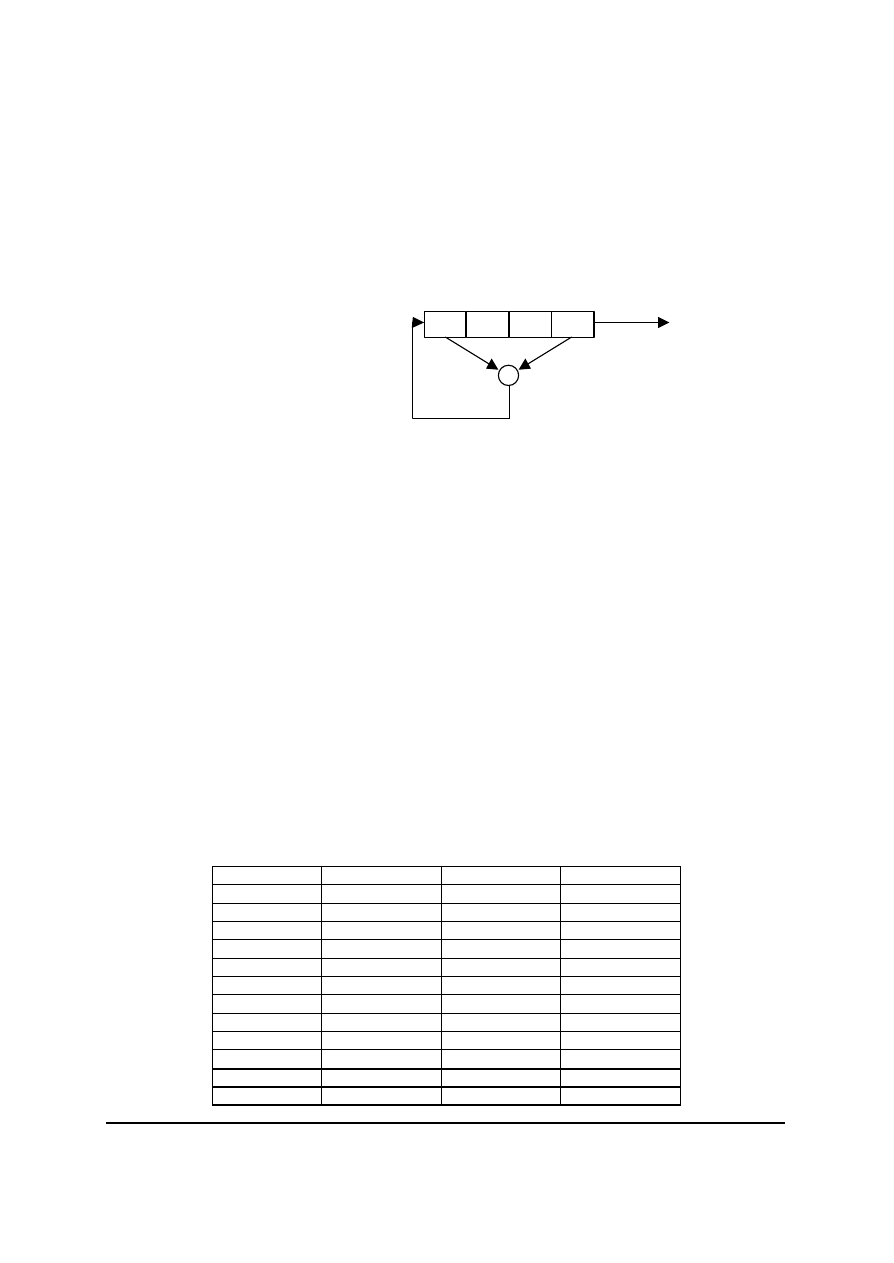
1.5.2. Rejestry przesuwajace z liniowym sprzezeniem zwrotnym

Rejestry przesuwajace z liniowym sprzezeniem zwrotnym (ang. Linear Feedback Shift

Register, rys. 8) sa zbudowane z dwóch czesci: rejestru przesuwajacego i ciagu odczepów.
Rejestr przesuwajacy moze byc przedstawiony jako ciag bitów. Pojawienie sie bitów na
wyjsciu rejestru wyznaczone jest przez impulsy (zegarowe), które powoduja, ze wszystkie
bity w rejestrze sa przesuwane o jedna pozycje w prawo i na wyjsciu rejestru przesuwajacego
z liniowym sprzezeniem zwrotnym pojawia sie najmniej znaczacy bit. Nowy najbardziej
znaczacy bit jest obliczany przez sumowanie modulo 2 innych bitów w rejestrze zgodnie
z ciagiem odczepów.

b

n

b

n-1

.....................

b

4

b

3

b

2

b

1

bit
wyjsciowy

Rys. 8. Rejestr przesuwajacy z liniowym sprzezeniem zwrotnym

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

15

Teoretycznie n-bitowy rejestr przesuwajacy z liniowym sprzezeniem zwrotnym moze
wytworzyc pseudolosowy ciag bitów o okresie powtarzania równym 2

n

-1. Dowód tego faktu

mozna znalezc w pracy [7].

Przyklad:

4-bitowy Rejestr przesuwajacy z liniowym sprzezeniem zwrotnym (rys. 9) majacy odczepy

na pierwszej i czwartej pozycji i wartosc poczatkowa 1111 wytwarza nastepujacy ciag stanów:

1

0011

0

0110

1

1101

0

1010

1

0101

1

1011

1

0111

1

1111

→

→

→

→

→

→

→

→

1001

1

0100

0

0010

0

0001

1

1000

0

1100

0

1110

0

→

→
→

→
→
→
→

b

4

b

3

b

2

b

1

Λ

bit

wyjsciowy

Rys. 9. Rejestr przesuwajacy z liniowym

sprzezeniem zwrotnym

Twierdzenie 1.
Aby dany Rejestr przesuwajacy z liniowym sprzezeniem zwrotnym byl rejestrem

maksymalnego okresu, wielomian utworzony z elementów ciagu odczepów musi byc
wielomianem pierwotnym modulo 2.

Twierdzenie 2.
Wielomianem pierwotnym stopnia n jest wielomian nieredukowalny bedacy podzielnikiem

dwumianu x

n

2

1

1

−

+

, lecz nie bedacy podzielnikiem dwumianu

x

d

+

1

dla zadanej wartosci

d, która jest podzielnikiem liczby

2

1

n

−

.

Tabela 2 zawiera liste wielomianów pierwotnych modulo 2. Sa one napisane w formie np.

ciagu (32, 7,5, 3, 2, 1, 0), oznacza to w zapisie matematycznym wielomian postaci:

x

x

x

x

x

x

32

7

5

3

2

1

+

+

+

+

+ +

Tabela 2. Lista wielomianów pierwotnych modulo 2

1,0

32,7,6,2,0

58,6,5,1,0

85,8,2,1,0

2,1,0

33,13,0

59,7,4,2,0

86,6,5,2,0

3,1,0

33,16,4,1,0

59,6,5,4,3,1,0

87,13,0

4,1,0

34,8,4,3,0

60,1,0

87,7,5,1,0

5,2,0

34,7,6,5,2,1,0

61,5,2,1,0

88,11,9,8,0

6,1,0

35,2,0

62,6,5,3,0

88,8,5,4,3,1,0

7,1,0

36,11,0

63,1,0

89,38,0

7,3,0

36,6,5,4,2,1,0

64,4,3,1,0

89,51,0

8,4,3,2,0

37,6,4,1,0

65,18,0

89,6,5,3,0

9,4,0

37,5,4,3,2,1,0

65,4,3,1,0

90,5,3,2,0

10,3,0

38,6,5,1,0

66,9,8,6,0

91,8,5,1,0

11,2,0

39,4,0

66,8,6,5,3,2,0

91,7,6,5,3,2,0

12,6,4,1,0

40,5,4,3,0

67,5,2,1,0

92,6,5,2,0

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

16

13,4,3,1,0

41,3,0

68,9,0

93,2,0

14,5,3,1,0

42,7,4,3,0

68,7,5,1,0

94,21,0

15,1,0

42,5,4,3,2,1,0

69,6,5,2,0

94,6,5,1,0

16,5,3,2,0

43,6,4,3,0

70,5,3,1,0

95,11,0

17,3,0

44,6,5,2,0

71,6,0

95,6,5,4,2,1,0

17,5,0

45,4,3,1,0

71,5,3,1,0

96,10,9,6,0

17,6,0

46,8,7,6,0

72,10,9,3,0

96,7,6,4,3,2,0

18,7,0

46,8,5,3,2,1,0

72,6,4,3,2,1,0

97,6,0

18,5,2,1,0

47,5,0

73,25,0

98,11,0

19,5,2,1,0

48,9,7,4,0

73,4,3,2,0

98,7,4,3,1,0

20,3,0

48,7,5,4,2,1,0

74,7,4,3,0

99,7,5,4,0

21,2,0

49,9,0

75,6,3,1,0

100,37,0

22,1,0

49,6,5,4,0

76,5,4,2,0

100,8,7,2,0

23,5,0

50,4,3,2,0

77,6,5,2,0

101,7,6,1,0

24,4,3,1,0

51,6,3,1,0

78,7,2,1,0

102,6,5,3,0

25,3,0

52,3,0

79,9,0

103,9,0

26,2,1,0

53,6,2,1,0

79,4,3,2,0

104,11,10,1,0

27,5,2,1,0

54,8,6,3,0

80,9,4,2,0

105,16,0

28,3,0

54,6,5,4,3,2,0

80,7,5,3,2,1,0

106,15,0

29,2,0

55,24,0

81,4,0

107,9,7,4,0

30,6,4,1,0

55,6,2,1,0

82,9,6,4,0

108,31,0

31,3,0

56,7,4,2,0

82,8,7,6,1,0

109,5,4,2,0

31,6,0

57,7,0

83,7,4,2,0

110,6,4,1,0

31,7,0

57,5,3,2,0

84,13,0

111,10,0

31,13,0

58,19,0

84,8,7,5,3,1,0

111,49,0

112,11,6,4,0

142,21,0

164,12,6,5,0

236,5,0

113,9,0

143,5,3,2,0

165,9,8,3,0

250,103,0

113,15,0

144,7,4,2,0

166,10,3,2,0

255,52,0

113,30,0

145,52,0

167,6,0

255,56,0

114,11,2,1,0

145,69,0

170,23,0

255,82,0

115,8,7,5,0

146,5,3,2,0

172,2,0

258,83,0

116,6,5,2,0

147,11,4,2,0

174,13,0

266,47,0

117,5,2,1,0

148,27,0

175,6,0

270,133,0

cd. tabeli 2

118,33,0

149,10,9,7,0

175,16,0

282,35,0

119,45,0

150,53,0

175,18,0

282,43,0

119,8,0

151,3,0

175,57,0

286,69,0

120,9,6,2,0

151,9,0

177,8,0

286,73,0

121,18,0

151,15,0

177,22,0

294,61,0

122,6,2,1,0

151,31,0

177,88,0

322,67,0

123,2,0

151,39,0

178,87,0

333,2,0

124,37,0

151,43,0

183,56,0

350,53,0

125,7,6,5,0

151,46,0

194,87,0

366,29,0

126,7,4,2,0

151,51,0

198,65,0

378,43,0

127,1,0

151,63,0

201,14,0

378,107,0

127,7,0

151,66,0

201,17,0

390,89,0

127,15,0

151,67,0

201,59,0

462,73,0

127,30,0

151,70,0

201,79,0

521,32,0

127,63,0

152,6,3,2,0

202,55,0

521,48,0

128,7,2,1,0

153,1,0

207,43,0

521,158,0

129,5,0

153,8,0

212,105,0

521,168,0

130,3,0

154,9,5,1,0

218,11,0

607,105,0

131,8,3,2,0

155,7,5,4,0

218,15,0

607,147,0

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

17

132,29,0

156,9,5,3,0

218,71,0

607,273,0

133,9,8,2,0

157,6,5,2,0

218,71,0

1279,216,0

134,57,0

158,8,6,5,0

218,83,0

1279,418,0

135,11,0

159,31,0

225,32,0

2281,715,0

135,16,0

159,34,0

225,74,0

2281,915,0

135,22,0

159,40,0

225,88,0

2281,1029,0

136,8,3,2,0

160,5,3,2,0

225,97,0

3217,67,0

137,21,0

161,18,0

225,109,0

3217,576,0

138,8,7,1,0

161,39,0

231,26,0

4423,271,0

139,8,5,3,0

161,60,0

231,34,0

9689,84,0

140,29,0

162,8,7,4,0

234,31,0

141,13,6,1,0

163,7,6,3,0

234,103,0

Kontynuujac przyklad, ciag (32, 7,5, 3, 2, 1, 0) oznacza, ze wezmiemy 32-bitowy rejestr

przesuwajacy, i bedziemy wytwarzac bity wyjsciowe, sumujac modulo 2, bity: 32,7,5,3,2,1;
wówczas tak utworzony rejestr bedzie rejestrem maksymalnego okresu, który przebiega
wszystkie

2

1

32

−

stany rejestru przed ich powtórzeniem.

Rejestry przesuwajace z liniowym sprzezeniem zwrotnym sa czesto wykorzystywane
w szyfrach strumieniowych, a tak duzy zbiór wielomianów umozliwia wybranie róznych
wielomianów pierwotnych.

Twierdzenie 3.

Jezeli wielomian p(x) jest wielomianem pierwotnym, to wielomian

x p

x

n

1

χ

χ



ρ

jest takze

wielomianem pierwotnym.

Przyklad:
Niech ciag (a,b,0) okresla wielomian pierwotny, to na mocy twierdzenia 3 ciag (a,a-b,0)

okresla takze wielomian pierwotny.
W zapisie matematycznym:

x

x

x

x

a

b

a

a b

+

+

←

Τ

+

+

←

−

1

1

wielomian pierwotny

wielomian pierwotny

Odniesienie do szyfrów strumieniowych

Glówna zaleta generatorów ciagów pseudolosowych kryptograficznie bezpiecznych jest to,
ze sa one doskonale dla szyfrów strumieniowych.
Ciag wyjsciowy tych generatorów jest nieodróznialny od ciagów losowych wytwarzanych
przez generatory fizyczne.
Po prostu sumujac modulo 2, bity z wyjscia generatora z bitami tekstu jawnego, otrzymujemy
dobry szyfr strumieniowy.
Rainer Rueppel podal cztery praktyczne podejscia do konstrukcji generatorów ciagów
pseudolosowych kryptograficznie bezpiecznych:

-

na gruncie teorii informacji,

-

systemowo – teoretyczne,

-

bazujace na teorii zlozonosci,

-

randomizowalne.

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

18

Podejscie systemowo-teoretyczne

Przy podejsciu do szyfrów strumieniowych kryptograf projektuje generatory ciagu klucza

w taki sposób, aby mialy one testowalne wlasciwosci zapewniajace bezpieczenstwo: okres,
rozklad pewnych ukladów bitów, zlozonosc liniowa itd., zamiast wnikania w teorie
matematyczna.

W ciagu lat stosowania podejscie to zaowocowalo zbiorem kryteriów projektowych dla

generatorów ciagu klucza. Zostaly one naszkicowane przez Rueppela – wyjasnia on

szczególy teoretyczne uzasadniajace te kryteria:

•

dlugi okres, brak powtórzen,

•

kryteria zlozonosci liniowej: duza zlozonosc liniowa, profil zlozonosci liniowej, lokalna
zlozonosc liniowa itd. (Zlozonosc liniowa generatora jest zdefiniowana jako dlugosc
najkrótszego rejestru przesuwajacego ze sprzezeniem zwrotnym, który moze wytworzyc
taki sam ciag jak ten generator. Zlozonosc liniowa jest miara losowosci generatora),

•

kryteria statystyczne, takie jak idealny rozklad czestosci wystepowania wszystkich
mozliwych ciagów k bitów,

•

mieszanie: kazdy bit w ciagu klucza musi byc w zlozony sposob zalezny od wszystkich
lub od wiekszosci bitów klucza,

•

rozpraszanie: nadmiarowosc zawarta w podstrukturach musi byc rozproszona na statystyki
dlugozakresowe,

•

kryteria nieliniowe dla funkcji Boole`a, takie jak odpornosc na korelacje rzedu m,
odleglosc od funkcji liniowych, kryterium lawiny itd.

Glównym problemem zwiazanym z tego rodzaju systemami kryptograficznymi jest to, ze

nie mozna udowodnic ich bezpieczenstwa [8].

Podejscie bazujace na teorii zlozonosci

Przy tym podejsciu do szyfrów strumieniowych kryptograf próbuje wykorzystac teorie
zlozonosci do udowodnienia, ze jego generatory sa kryptograficznie bezpieczne.
Konsekwencja tego jest to, ze generatory staja sie coraz bardziej skomplikowane, a tym
samym wolniejsze i mniej poreczne [1].

Podejscie bazujace na teorii informacji

Przy tym podejsciu zaklada sie, ze kryptoanalityk dysponuje nieograniczonym czasem i moca
obliczeniowa. Jedynym praktycznym szyfrem strumieniowym, który jest zabezpieczony
przed takim przeciwnikiem, jest szyfr z kluczem jednorodnym. Niekiedy zamiast okreslenia
klucz jednorodny stosuje sie okreslenie tasma jednorodna. Dwie tasmy magnetyczne, jedna
dla strony szyfrujacej, a druga dla strony deszyfrujacej, maja zapisany ten sam losowy ciag
klucza. Przy szyfrowaniu dokonuje sie po prostu poelementowego sumowania modulo 2
bitow tekstu jawnego i bitow klucza na tasmie. Przy deszyfrowaniu dokonuje sie równiez
poelementowego sumowania modulo 2 bitow szyfrogramu z bitami klucza zapisanymi na
drugiej, identycznej tasmie. Poniewaz ciag klucza jest w pelni losowy, nie wolno nigdy uzyc
tego samego klucza dwukrotnie. Jezeli po wykorzystaniu tasmy zostana spalone, to
osiagniemy tajnosc doskonala [1].

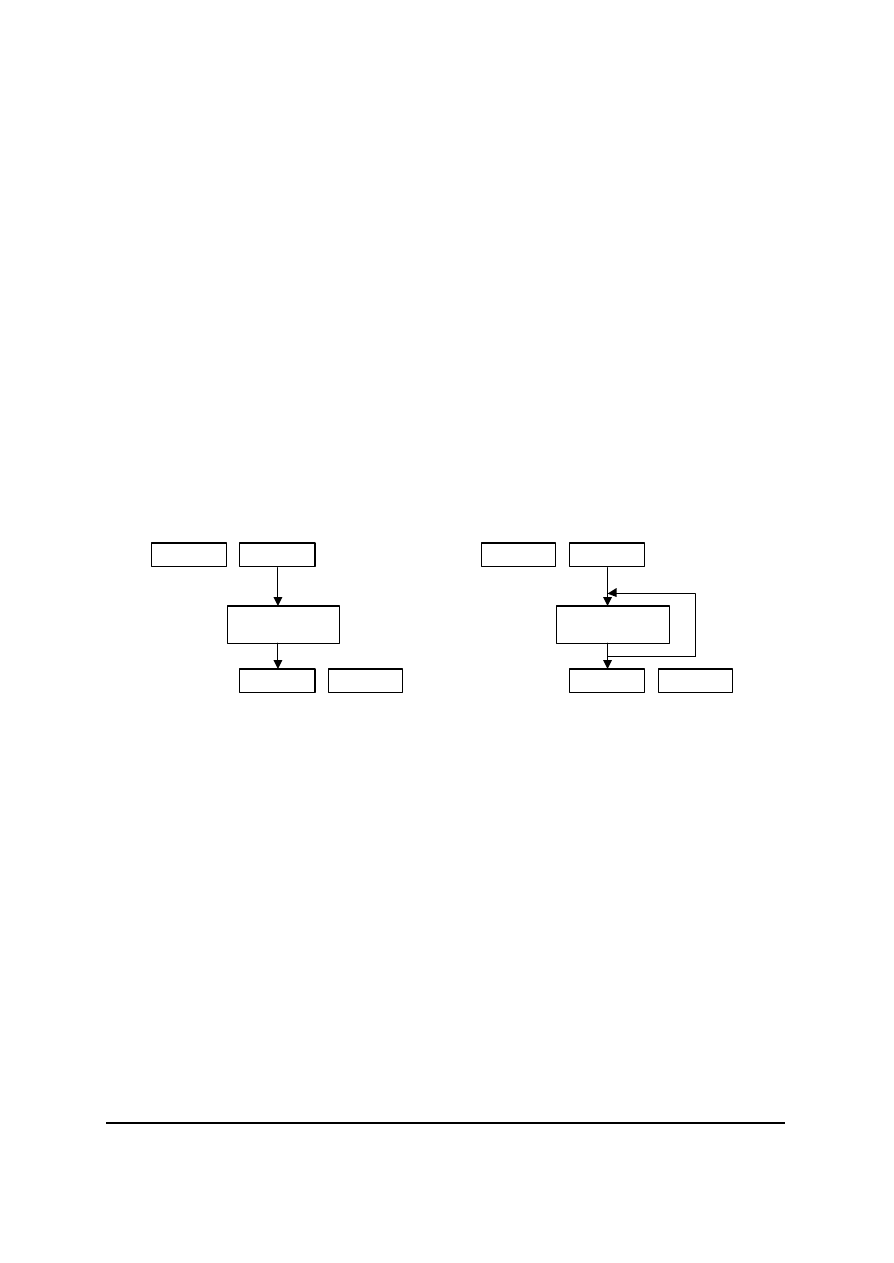
B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

19

1.6. Szyfry blokowe

Algorytmy blokowe dzialaja z reguly na blokach tekstu jawnego lub szyfrogramu dlugosci 64
bitów. Mozna w ich pracy wyróznic cztery podstawowe tryby:

•

Tryb elektronicznej ksiazki kodowej (ang. electronic codebook ECB) [1, 9, 2] – jest

najlatwiejszym i najszybszym trybem do zastosowania w szyfrach blokowych (rys. 10).
Jego zaleta jest mozliwosc niezaleznego szyfrowania kazdego bloku tekstu jawnego. Nie
musimy liniowo szyfrowac pliku. Ta cecha jest istotna dla plików, w których musi byc
zastosowana mozliwosc dostepu losowego, na przyklad w bazach danych.

Wada jest jednak to, ze jest on najslabszy (najlatwiejszy do zlamania). Nie powinno sie

wiec z tego trybu korzystac.

•

Tryb wiazania bloków zaszyfrowanych (ang. cipher block chaining CBC) [1, 9]

– tekst jawny jest przed szyfrowaniem sumowany modulo dwa z poprzednimi blokami
szyfrogramów. Dzialanie CBC przedstawia rys. 11.

W tym trybie nie mozna zaczac szyfrowania, zanim nie odbierze sie calego bloku danych.

Jest nieprzydatny, jezeli dane musza byc przetwarzane w porcjach wielkosci bajtu.

Szyfrator

Tekst jawny

Tekst zaszyfrowany

Rys. 10. Elektroniczna ksiazka kodowa

Szyfrator

Tekst jawny

Tekst zaszyfrowany

Rys.11. Wiazania bloków zaszyfrowanych

•

Tryb sprzezenia zwrotnego szyfrogramu (ang. cipher feedback CFB) [1, 9] – ten

tryb pozwala na szyfrowanie informacji w jednostkach mniejszych niz rozmiar bloku. Na

przyklad moze to byc jeden znak ASCII na raz, co przedstawia rysunek 12. Moze to byc

równiez blok jednobitowy, idea pozostaje ta sama. Na rys. 12 przedstawiony jest schemat

dzialania trybu 8-bitowego CFB. W pierwszym kroku rejestr jest wypelniany wartoscia

poczatkowa. Po zaszyfrowaniu zawartosci rejestru 8 bitów skrajnych z lewej strony dodaje

sie modulo dwa z pierwszym 8-bitowym znakiem tekstu jawnego w celu uzyskania

pierwszego znaku 8-bitowego szyfrogramu. Ten znak moze byc nastepnie przeslany. Tych

samych 8 bitów przesuwa sie na 8 bitów skrajnych z prawej strony kolejki, a wszystkie

pozostale bity sa przesuwane o 8 pozycji w lewo. Odrzuca sie najbardziej znaczacych 8

bitów. Nastepny bit szyfruje sie dokladnie w ten sam sposób. Ten tryb pracy jest

wolniejszy od swoich poprzedników.

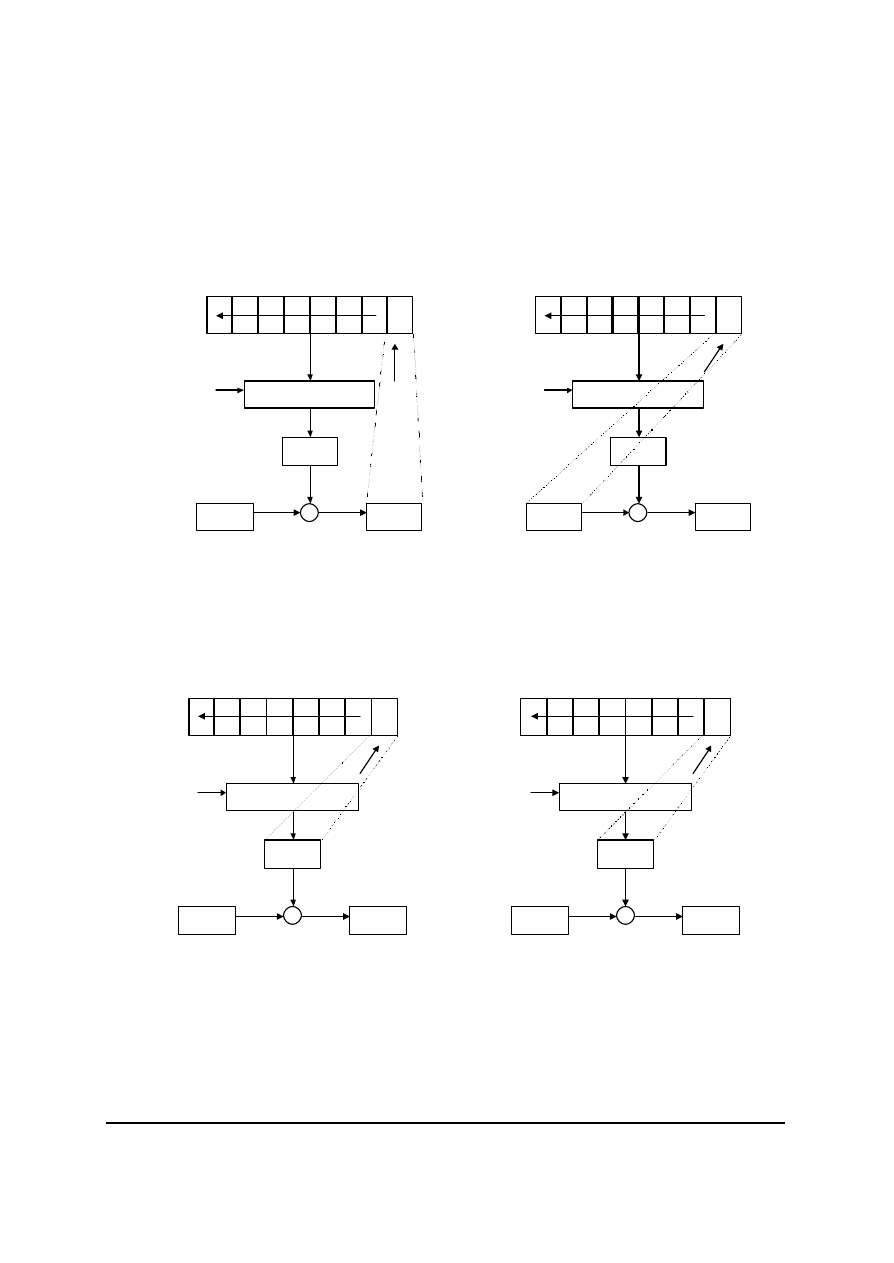
B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

20

•

Tryb sprzezenia zwrotnego wyjsciowego (ang. output feedback OFB) [1, 9] – jest

podobny do trybu CFB. Róznica polega na tym, ze czesc poprzedniego bloku wyjsciowego jest
kierowana na skrajne prawe pozycje rejestru. Schemat dzialania tego trybu przedstawia rys. 13.

Ostatnich 8 bajtów

Rejestr przesuwajacy

Szyfrator

KLUCZ K

C

i-1

P

i

C

i

Lewy skrajny bajt

(a) Zaszyfrowanie

Ostatnich 8 bajtów

Rejestr przesuwajacy

Szyfrator

KLUCZ K

C

i-1

C

i

P

i

Lewy skrajny bajt

(b) Odszyfrowanie

Rys. 12. Tryb sprzezenia zwrotnego szyfrogramu

Ostatnich 8 bajtów

Rejestr przesuwajacy

Szyfrator

KLUCZ K

C

i-1

P

i

C

i

Lewy skrajny bajt

(a) Zaszyfrowanie

Ostatnich 8 bajtów

Rejestr przesuwajacy

Szyfrator

KLUCZ K

C

i-1

C

i

P

i

Lewy skrajny bajt

(b) Odszyfrowanie

Rys. 13. Tryb sprzezenia zwrotnego wyjsciowego

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

21

1.7. Porównanie szyfrów strumieniowych z blokowymi

Róznica pomiedzy szyframi strumieniowymi i blokowymi ma charakter raczej

praktyczny anizeli teoretyczny.

Szyfry strumieniowe:

•

szyfruja i deszyfruja po jednym bicie danych na raz, co w praktyce oznacza, ze nie sa
odpowiednie do implementacji programowej (operacje na bitach sa czasochlonne),

•

algorytmy sa latwe do analizy matematycznej,

•

pojedyncze znieksztalcenie szyfrogramu powoduje znieksztalcenie tylko jednego bitu
tekstu jawnego,

•

nadaje sie do szyfrowania danych typu ASCII z terminalu komputerowego; blokowy
algorytm szyfrowania w tym wypadku nie spelni stawianych przed nim oczekiwan.
Szyfry blokowe:

•

w przeciwienstwie do szyfrów strumieniowych sa latwiejsze do implementacji,

•

ich algorytmy sa silniejsze w dzialaniu,

•

pojedyncze znieksztalcenie szyfrogramu powoduje znieksztalcenie danych co najmniej
wielkosci bloku,

•

doskonale w przypadku, gdy dane sa zapisywane i odczytywane w postaci bloków.

L

ITERATURA

1.

B. S

CHNEIER

, Kryptografia dla praktyków. Protokoly, algorytmy i programy zródlowe w jezyku C. Wydawnictwa

Naukowo-Techniczne, Warszawa 1995.

2.

C. M. C

AMPBELL

, Design and Specification of Cryptographic Capabilities. Computer Society Magazine, v. 16, n.

6, Nov 1978, str. 15-19.

3.

W. D

IFFIE AND

M. E. H

ELLMAN

, Privacy and Autentication: An Introduction to Cryptogaphy. Proceedings of

IEEE, v. 67, n. 3, Mar 1979, str. 387-427.

4.

M. E. H

ELLMAN

, On DES-Based Synchronous Enkryption. Departament of Electrical Engineering, Stanford

University, 1980.

5.

D

. K

NUTH

, The Art of Computer Programming. Volume Z, Seminomerical Algorithmw, 2nd edition Adelison –

Wesley, 1981.

6. B. P

LUMSTEAD

, Inferning a Sequence Generated by a Linear Congruence. Proceding of the 23rd IEE5

Symposium on the Foundation of Computer Sience, 1982, pp. 153 – 159.

7. W. G

OLOMB

, Shift Register Sequences, Sun Francisko: Holden-Day, 1967.

8. L. & S. T. K

ENT

, Security Mechanizms in High – Level Networks. ACM Computing Group v. IS, n.2 Jun.

1983, pp. 135 – 140

9.

D. E. R

OBLING

D

ENING

, Kryptografia i ochrona danych. Wydawnictwa Naukowo-Techniczne, Warszawa 1993.

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

2. ALGORYTMY KOMPUTEROWE

Wsród wielu algorytmów kryptograficznych najczesciej stosowane sa cztery:

•

DES (ang. Data Encryption Standard) – obecnie najpopularniejszy komputerowy

algorytm szyfrujacy. Jest to standardowy algorytm szyfrujacy rzadu USA, zostal przyjety

przez armie USA do szyfrowania informacji „nie utajnionej, ale waznej” (w oryginale

Unclassified but Sensitive). Jest to algorytm symetryczny, z tym samym kluczem

uzywanym do szyfrowania i deszyfrowania.

•

IDEA (ang. Improved Proposed Encryption Standard) – jest to, podobnie jak DES,

algorytm blokowy, symetryczny, przez wielu uwazany za najbezpieczniejszy sposród

dostepnych algorytmów.

•

RSA (nazwa jest zlozeniem pierwszych liter nazwisk autorów – Rivest, Shamir i

Adleman) – najpopularniejszy algorytm z kluczem jawnym (Algorytmy klucza jawnego

charakteryzuja sie tym, ze do szyfrowania i deszyfrowania wykorzystywane sa dwa rózne

klucze. Tekst jawny szyfrowany jest tzw. kluczem publicznym adresata, ogólnie

dostepnym. Natomiast zaszyfrowana informacja moze byc zdeszyfrowana tylko przy

wykorzystaniu klucza prywatnego adresata, który to klucz jest znany tylko jemu). Moze

byc zastosowany zarówno do szyfrowania, jak i do podpisów cyfrowych.

•

DSA (ang. Digital Signature Algorithm, zastosowany w DSS – ang. Digital Signature

Standard) inny niz RSA algorytm z kluczem jawnym, ale moze byc stosowany tylko do

podpisów cyfrowych.

W niniejszym rozdziale zostana omówione trzy sposród wczesniej wymienionych: DES,

IDEA i RSA.

2.1. Standard szyfrowania DES

Powstal w latach siedemdziesiatych i zostal przyjety jako standard szyfrowania przez
Amerykanski Narodowy Instytut Standaryzacji (ang. American National Standards Institute –
ANSI) 23 listopada 1976 roku [1, 2, 3, 4, 5, 6, 7, 8, 9, 10].

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

23

Permutacja poczatkowa

Permutacja

IP

-1

Szyfrogram

Tekst

jawny

IP

L

0

R

1

= L

0

Λ

f(R

0

,K

1

)

R

0

L

1

= R

0

L

2

= R

1

L

15

= R

14

R

2

= L

1

Λ

f(R

1

,K

2

)

R

15

= L

14

Λ

f(R

14

,K

15

)

R

16

= L

15

Λ

f(R

15

,K

16

)

L

16

= R

15

Λ

f

K

1

Λ

f

K

2

Λ

f

K

16

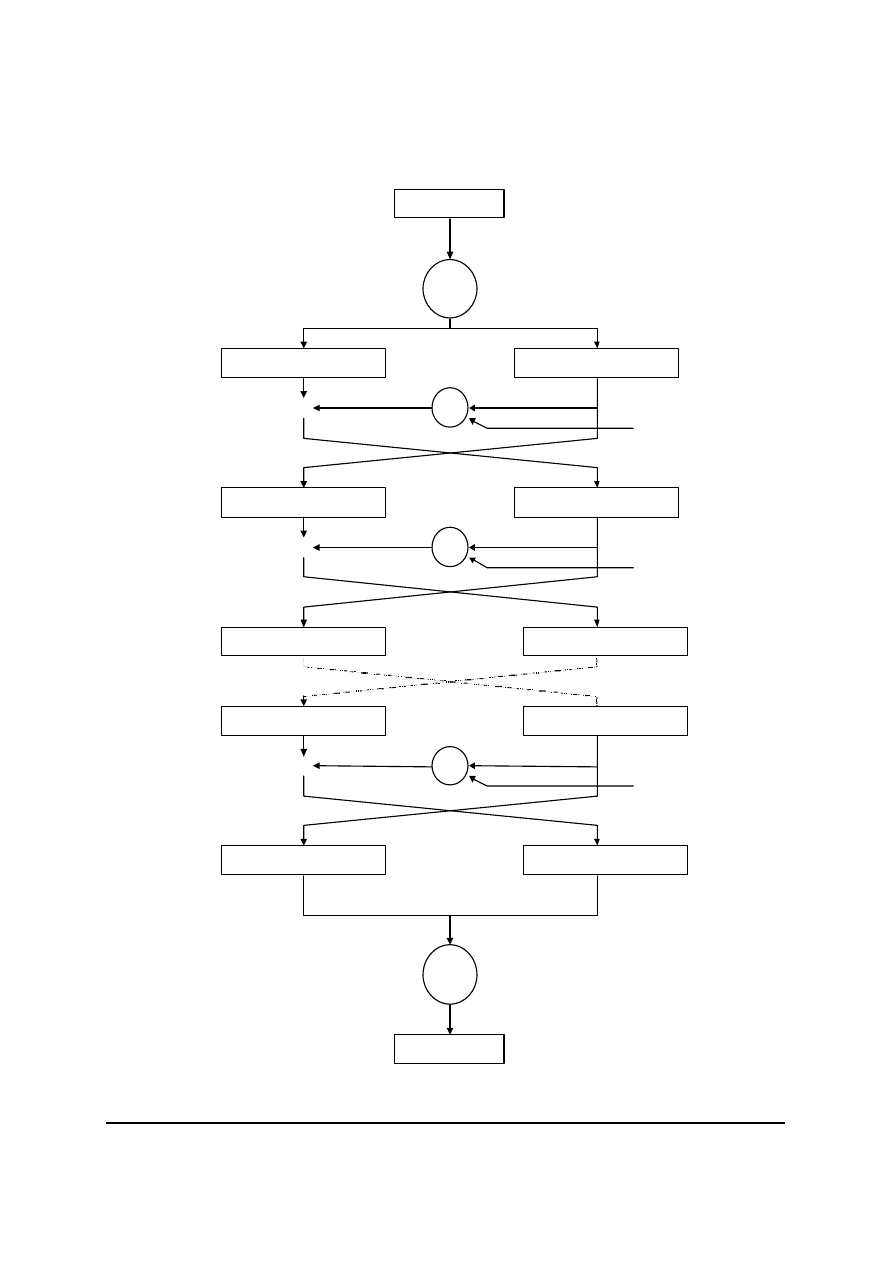
Rys.14. Schemat blokowy algorytmu DES

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

24

DES jest szyfrem blokowym, pracujacym na 64-bitowych pakietach danych. Zarówno do

szyfrowania, jak i deszyfrowania stosuje sie ten sam algorytm. Klucz jest 64-bitowy, przy

czym informacja uzyteczna zajmuje 56 bitów (co ósmy bit w ciagu klucza jest bitem

parzystosci). Cale bezpieczenstwo spoczywa wlasnie na nim.

Algorytm DES to kombinacja dwu podstawowych technik: mieszania i rozpraszania.

2.1.1. Opis algorytmu

Tekst jawny (64-bitowy blok) poddawany jest permutacji wstepnej (tabela 3, blok oznaczony
IP). Potem dzielony jest na dwa podciagi 32-bitowe (rys. 14). Nastepnie wykonywanych jest
16 cykli jednakowych operacji, nazywanych funkcjami f. Po szesnastym cyklu lewa i prawa
strona sa laczone i poddawane permutacji koncowej (tabela 4).

Tabela 3. Permutacja poczatkowa IP

58 50 42 34 26 18 10 2 60 52 44 36 28 20 12 4
62 54 46 38 30 22 14 6 64 56 48 40 32 24 16 8
57 49 41 33 25 17

9

1 59 51 43 35 27 19 11 3

61 53

5

37 29 21 13 5 63 55 47 39 31 23 15 7

Tabela 4. Permutacja koncowa IP-1

40 8 48 16 56 24 64 32 39 7 47 15 55 23 63 31
38 6 46 14 54 22 62 30 37 5 45 13 53 21 61 29
36 4 44 12 52 20 60 28 35 3 43 11 51 19 59 27
34 2 42 10 50 18 58 26 33 1 41

9

49 17 57 25

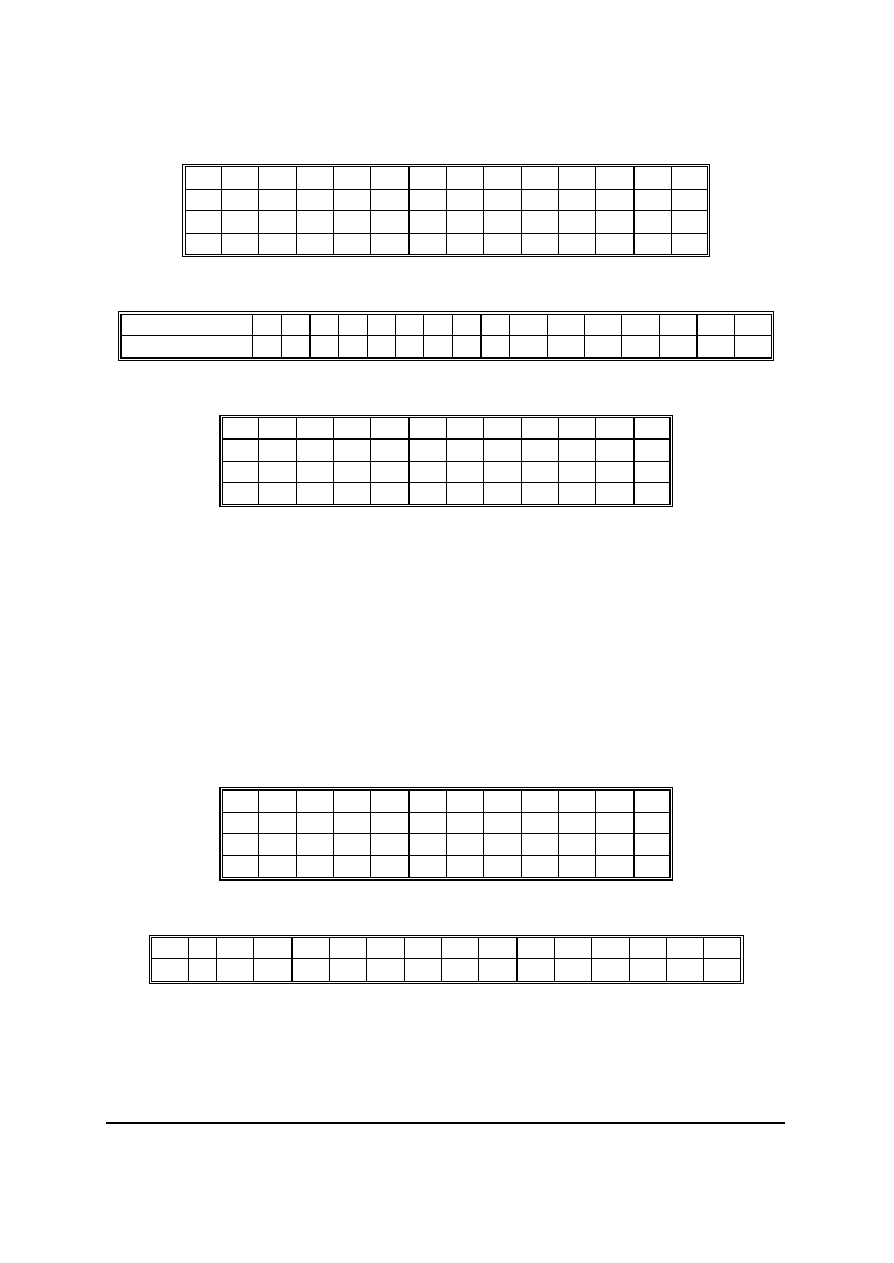
2.1.2. Jak powstaje klucz?

Poniewaz klucz jest 64-bitowy, redukowany jest do klucza 56 bitów przez pominiecie co

ósmego bitu parzystosci. Tak przygotowany ciag bitów poddawany jest permutacji
wejsciowej (tabela 5), po czym dzielony jest na dwa podciagi 28-bitowe. Nastepnie polowy
te przesuwane sa w lewo o jeden lub dwa bity, zaleznie od numeru cyklu (tabela 6).

Po polaczeniu nowo powstalych ciagów wybiera sie 48 z 56 bitów (tabela 7, permutacja

z kompresja). Tak otrzymujemy klucz dla i-cyklu (gdzie i jest numerem cyklu), i = 1, ...,16.

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

25

Tabela 5. Permutacja klucza

57 49 41 33 25 17

9

1

58 50 42 34 26 18

10

2

59 51 43 35 27 19 11

3

60 52 44 36

63 55 47 39 31 23 15

7

62 54 46 38 30 22

14

6

61 53 45 37 29 21 13

5

28 20 12

4

Tabela 6. Tablica przesuniec polówek klucza

NR ITERACJI I 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Liczb. Przes.

1 1 2 2 2 2 2 2 1 2

2

2

2

2

2

1

Tabela 7. Tablica permutacji kompresji

14 17 11 24

1

5

3

28 15

6

21 10

23 19 12

4

26

8

16

7

27 20 13

2

41 52 31 37 47 55 30 40 51 45 33 48
44 49 39 56 34 53 46 42 50 36 29 32

2.1.3. Realizacja funkcji f

W funkcji f (rys. 15) prawa polowa bloku danych jest poddawana permutacji z

rozszerzeniem (tabela 8, E), czyli z 32 do 48 bitów. Nastepnie, nowo powstaly podciag
bitów, laczony jest za pomoca poelementowej sumy modulo 2 z 48 bitami przesunietego i
spermutowanego klucza. Po tej operacji otrzymany ciag dzielony jest na 8 czesci i
wprowadzany do skrzynek S-bloków (tabela 10), gdzie z 6-bitowych podciagów na wyjsciu
otrzymujemy 4-bitowe podciagi, które laczymy ze soba. Nowo powstaly ciag jest na wyjsciu
poddany permutacji (tabela 9, P) i otrzymujemy zaszyfrowany ciag 32-bitowy.

Tabela 8. Tabela permutacji rozszerzenia

32 1

2

3

4

5

4

5

6

7

8

9

8

9

10 11 12 12 12 13 14 15 16 17

16 17 18 19 20 21 20 21 22 23 24 25
24 25 26 27 28 29 28 29 30 31 32 1

Tabela 9. Tabela permutacji P-bloku

16 7 20 21 29 12 28 17 1

15 23 26 5

18 31 10

2

8 24 14 32 27 3

9

19 13 30 6

22 11 4

25

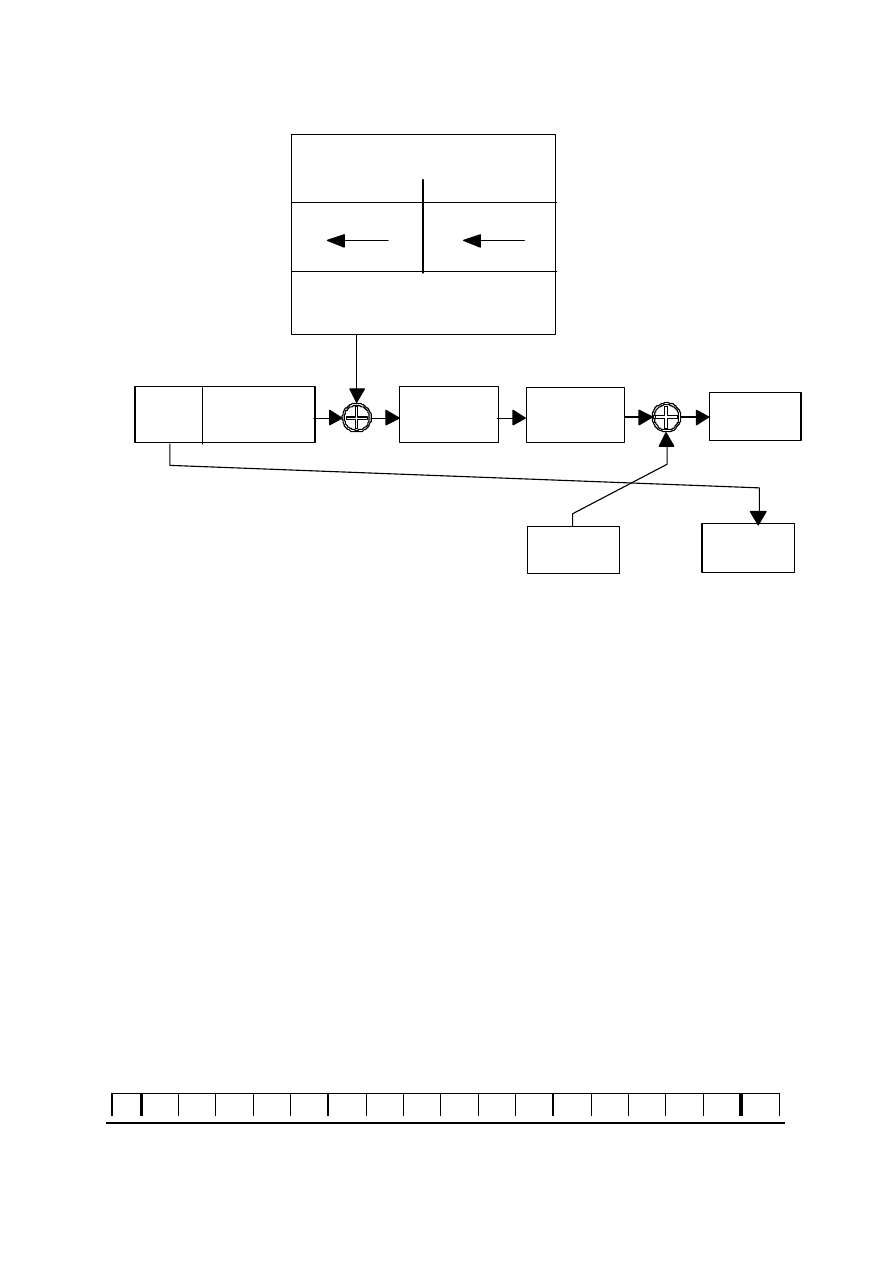
B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

26

Klucz

28 bitów

56 bitów

Wybranie do permutacji

48 bitów

28 bitów

28 bitów

Przesuniêcie

28 bitów

Przesuniêcie

Rj-1
32 bity

Permutacja

z rozszerzeniem

48 bitów

Podstawienie

w S- bloku

32 bity

Permutacja
w P-bloku

Rj

L j

Lj-1

32 bity

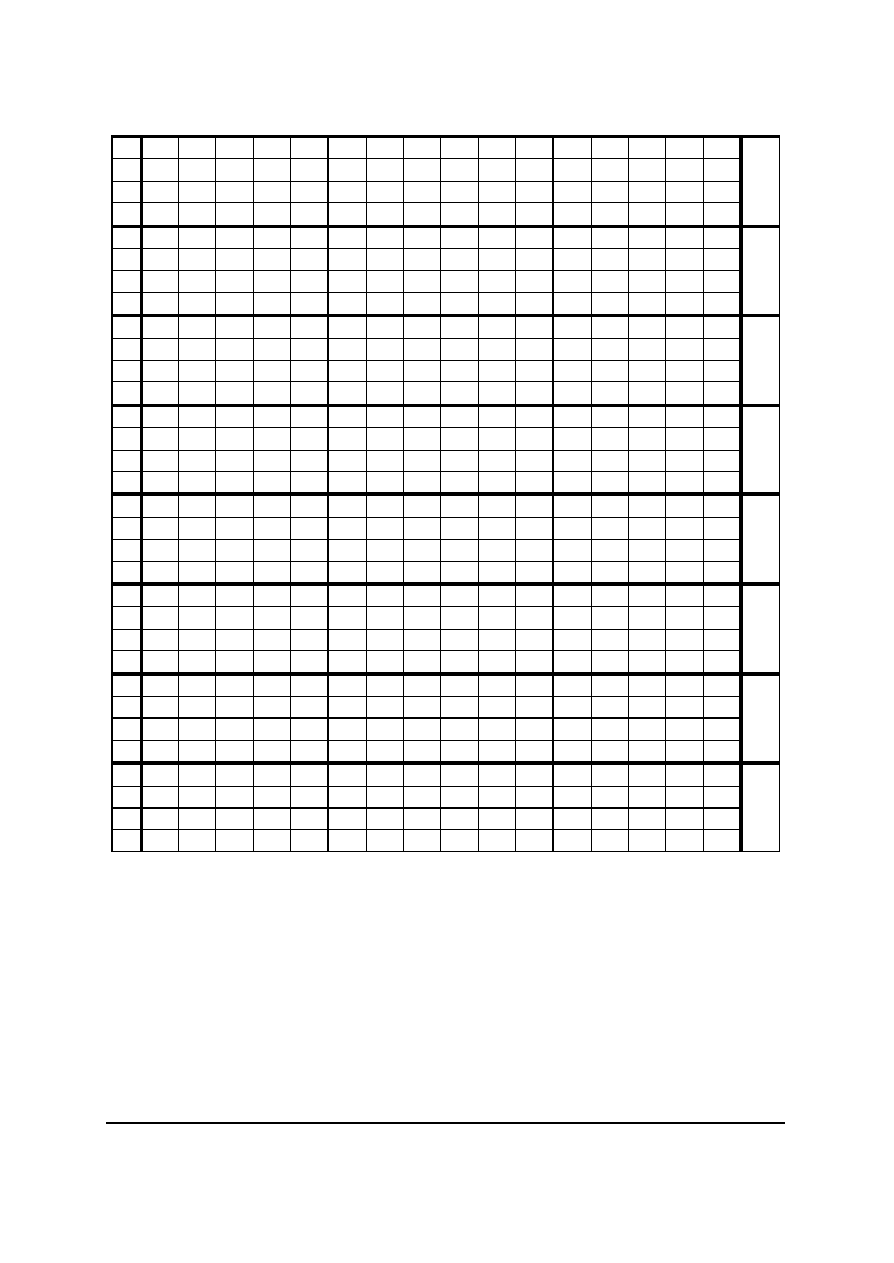
Rys. 15. Metoda wyznaczania wartosci funkcji f dla DES

Przeksztalcenie 6-bitowego bloku na 4-bitowy w skrzynce odbywa sie w ten sposób, ze

liczba b1b6 okresla wiersz tablicy, a bity b2b3b4b5 okreslaja kolumne.

2.1.4. Tryby pracy DES

DES pracuje w czterech trybach pracy:

1. tryb elektronicznej ksiazki kodowej (Electronic Codebook – ECB),

2. tryb wiazania bloków zaszyfrowanych (Cipher Block Chaining – CBC),

3. tryb sprzezenie zwrotne wyjscia (Output Feedback – OFB),

4. tryb sprzezenie zwrotne szyfrogramu (Cipher Feedback – CFB).

Bankowe standardy ANSI specyfikuja [6, 7, 8, 9, 10]:

•

ECB i CBC do szyfrowania,

•

CBC i CFB do uwierzytelniania.

Najczesciej oferowanym, gotowym komercyjnym oprogramowaniem jest elektroniczna

ksiazka kodowa, mimo ze jest najbardziej podatna na ataki.

Tabela 10. Tablica S-bloków

0

1

2

3

4

5

6

7

8

9

10 11 12 13 14 15

Permutacja kompresji

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

27

0 14 4

13 1

2

15 11 8

3

10 6

12 5

9

0

7

S1

1 0

15 7

4

14 2

13 1

10 6

12 11 9

5

3

8

2 4

1

14 8

13 6

2

11 15 12 9

7

3

10 5

0

3 15 12 8

2

4

9

1

7

5

11 3

14 10 0

6

13

0 15 1

8

14 6

11 3

4

9

7

2

13 12 0

5

10 S2

1 3

13 4

7

15 2

8

14 12 0

1

10 6

9

11 5

2 0

14 7

11 10 4

13 1

5

8

12 6

9

3

2

15

3 13 8

10 1

3

15 4

2

11 6

7

12 0

5

14 9

0 10 0

9

14 6

3

15 5

1

13 12 7

11 4

2

8

S3

1 13 7

0

9

3

4

6

10 2

8

5

14 12 11 15 1

2 13 6

4

9

8

15 3

0

11 1

2

12 5

10 14 7

3 1

10 13 0

6

9

8

7

4

15 14 3

11 5

2

12

0 7

13 14 3

0

6

9

10 1

2

8

5

11 12 4

15 S4

1 13 8

11 5

6

15 0

3

4

7

2

12 1

10 14 9

2 10 6

9

0

12 11 7

13 15 1

3

14 5

2

8

4

3 3

15 0

6

10 1

13 8

9

4

5

11 12 7

2

14

0 2

12 4

1

7

10 11 6

8

5

3

15 13 0

14 9

S5

1 14 11 2

12 4

7

13 1

5

0

15 10 3

9

8

6

2 4

2

1

11 10 13 7

8

15 9

12 5

6

3

0

14

3 11 8

12 7

1

14 2

13 6

15 0

9

10 4

5

3

0 12 1

10 15 9

2

6

8

0

13 3

4

14 7

5

11 S6

1 10 15 4

2

7

12 9

5

6

1

13 14 0

11 3

8

2 9

14 15 5

2

8

12 3

7

0

4

10 1

13 11 6

3 4

3

2

12 9

5

15 10 11 14 1

7

6

0

8

13

0 4

11 2

14 15 0

8

13 3

12 9

7

5

10 6

1

S7

1 13 0

11 7

4

9

1

10 14 3

5

12 2

15 8

6

2 1

4

11 13 12 3

7

14 10 15 6

8

0

5

9

2

3 6

11 13 8

1

4

10 7

9

5

0

15 14 2

3

12

0 13 2

8

4

6

15 11 1

10 9

3

14 5

0

12 7

S8

1 1

15 13 8

10 3

7

4

12 5

6

11 0

14 9

2

2 7

11 4

1

9

12 14 2

0

6

10 13 15 3

5

8

3 2

1

14 7

4

10 8

13 15 12 9

0

3

5

6

11

2.1.5. Sprzetowe i programowe implementacje DES

DES jest algorytmem, który powstal z mysla o implementacjach sprzetowych. Uklad

skonstruowany przez Digital Equipment Corporation, zbudowany z 50 tysiecy tranzystorów

na podlozu z GaAs, zawiera zespól bramek realizujacych tryby ECB i CBC. Dane moga byc

szyfrowane i deszyfrowane z szybkoscia 1 Gbit/s, co jest równowazne 15,6 milionom bloków

na sekunde. Jest to imponujaca liczba [1, 2, 3, 11, 12, 13, 14, 15].

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

28

Implementacje programowe sa znacznie wolniejsze i przegrywaja w konkurencji z

rozwiazaniami sprzetowymi. Tabela 11 przedstawia szybkosci realizacji algorytmu DES
przez rózne mikroprocesory.

Tabela 11. Szybkosc realizacji algorytmu DES przez rózne mikroprocesory

Procesor

Czestotliwosc zegara

procesora (w Mhz)

Szerokosc szyny

(w bitach)

Szybkosc szyfrowania

(bloki DES na sekunde)

8088

4,7

8

370

68000

7,6

16

900

80286

6,0

16

1100

68020

16,0

32

3500

68030

16,0

32

3900

80386

25,0

16

5000

68030

50,0

32

9600

68040

25,0

32

23200

80486

33,0

32

40600

2.1.6. Bezpieczenstwo algorytmu DES

Okazuje sie, ze z powodu sposobu, w jaki jest modyfikowany klucz dla kolejnych cykli

algorytmu, niektóre z nich sa kluczami slabymi (tabela 12), tzn.ze klucz uzyty w jednym cyklu

algorytmu bedzie taki sam we wszystkich pozostalych, a co za tym idzie tekst jawny nie zostanie

zaszyfrowany.

Istnieja równiez pary kluczy, które szyfruja tekst jawny do jednakowych szyfrogramów.

Innymi slowy, jeden klucz z pary moze sluzyc do deszyfrowania wiadomosci zaszyfrowanej

drugim kluczem z tej pary. Zamiast generowac 16 róznych podkluczy, generowane sa dwa. Kazdy

z nich jest wykorzystywany 8 razy w algorytmie. Klucze takie nazywamy kluczami pólslabymi

(tabela 13) [1, 2, 3, 16].

Tabela12. Klucze slabe algorytmu DES (zapis szesnastkowy)

Pierwotny ciag slabego klucza Faktyczny ciag klucza

0101 0101 0101 0101

0000000 0000000

FEFE FEFE FEFE FEFE

FFFFFFF FFFFFFF

1F1F 1F1F 1F1F 1F1F

0000000 FFFFFFF

E0E0 E0E0 F1F1 F1F1

FFFFFFF 0000000

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

29

Tabela 13. Klucze pólslabe algorytmu DES

01FE 01FE 01FE

01FE

1FE0 1FE0 0EF1

0EF1

01E0

01E0

01F1

01F1

1FFE 1FFE 0EFE 0EFE
011F

011F

010E

010E

E0FE E0FE F1FE F1FE

FE01 FE01 FE01

FE01

E01F E01F F10E

F10E

E001

E001

F101

F101

FE1F FE1F FE0E FE0E
1F01

1F01

0E01

0E01

FEE0 FEE0 FEF1 FEF1

W 1990 roku Eli Biham i Adi Shamir opublikowali metode kryptoanalizy róznicowej [17].

Atak przy wykorzystaniu tej metody okazal sie bardzie skuteczny od dotad stosowanego ataku

brutalnego. Metoda ta przy znanym tekscie jawnym dziala przeciw DES w dowolnym trybie pracy

– ECB, CBC, CFB oraz OFB. DES moze byc ulepszony przez zwiekszenie liczby cykli. Okazuje

sie, ze juz przy 19 cyklach metoda wyczerpujacego przeszukiwania jest efektywniejsza niz analizy

róznicowej (tabela 14).

Tabela 14. Zlozonosc ataku na DES metoda kryptoanalizy róznicowej

Liczba cykli

Wybrane teksty

jawne

Znane teksty

jawne

Analizowane

teksty jawne

Zlozonosc analizy

8

2

14

2

38

4

2

9

9

2

24

2

44

2

2

32

10

2

24

2

43

2

14

2

15

11

2

31

2

47

2

2

32

12

2

31

2

47

2

21

2

21

13

2

39

2

52

2

2

32

14

2

39

2

51

2

29

2

29

15

2

47

2

56

2

7

2

37

16

2

47

2

55

2

36

2

37

2.1.7. Modyfikacje algorytmu DES

Poniewaz za sprawa Eli Biham i Adi Shamir znaleziono dosc skuteczna metode lamania szyfru

DES, a postep techniki zrzadzil, ze nawet w przypadku lamania brutalnego, czas potrzebny na

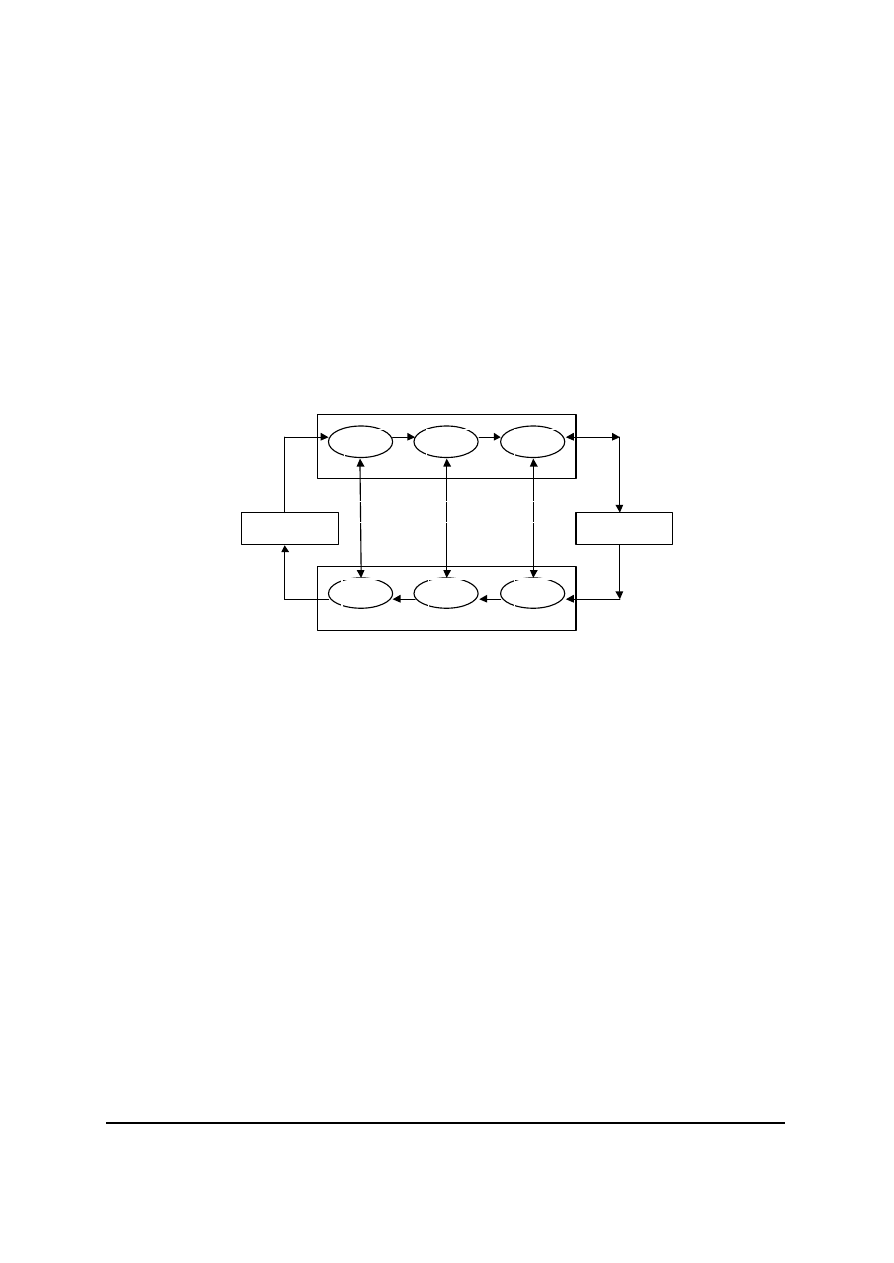
B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

30

sprawdzenie wszystkich kombinacji klucza nie rozciaga sie w nieskonczonosc, postanowiono

zmodyfikowac algorytm DES.

Wielokrotny DES

Poniewaz DES nie tworzy grup, mozna go wykorzystac wielokrotnie. W komercyjnych

rozwiazaniach wykorzystuje sie trzykrotny DES (rys. 16). Uzyskany szyfrogram jest duzo

trudniejszy do zlamania metoda wyczerpujacego przeszukiwania: 2

112

prób zamiast 2

56

. Co wazne

potrójne DES opiera sie kryptografii róznicowej [1, 2, 3].

Tekst jawny

Szyfrogram

DES

DES

DES

DES-1

DES-1

DES-1

K1

K2

K1

Szyfrowanie

Deszyfrowanie

Rys. 16. Trzykrotny DES

Uogólniony DES

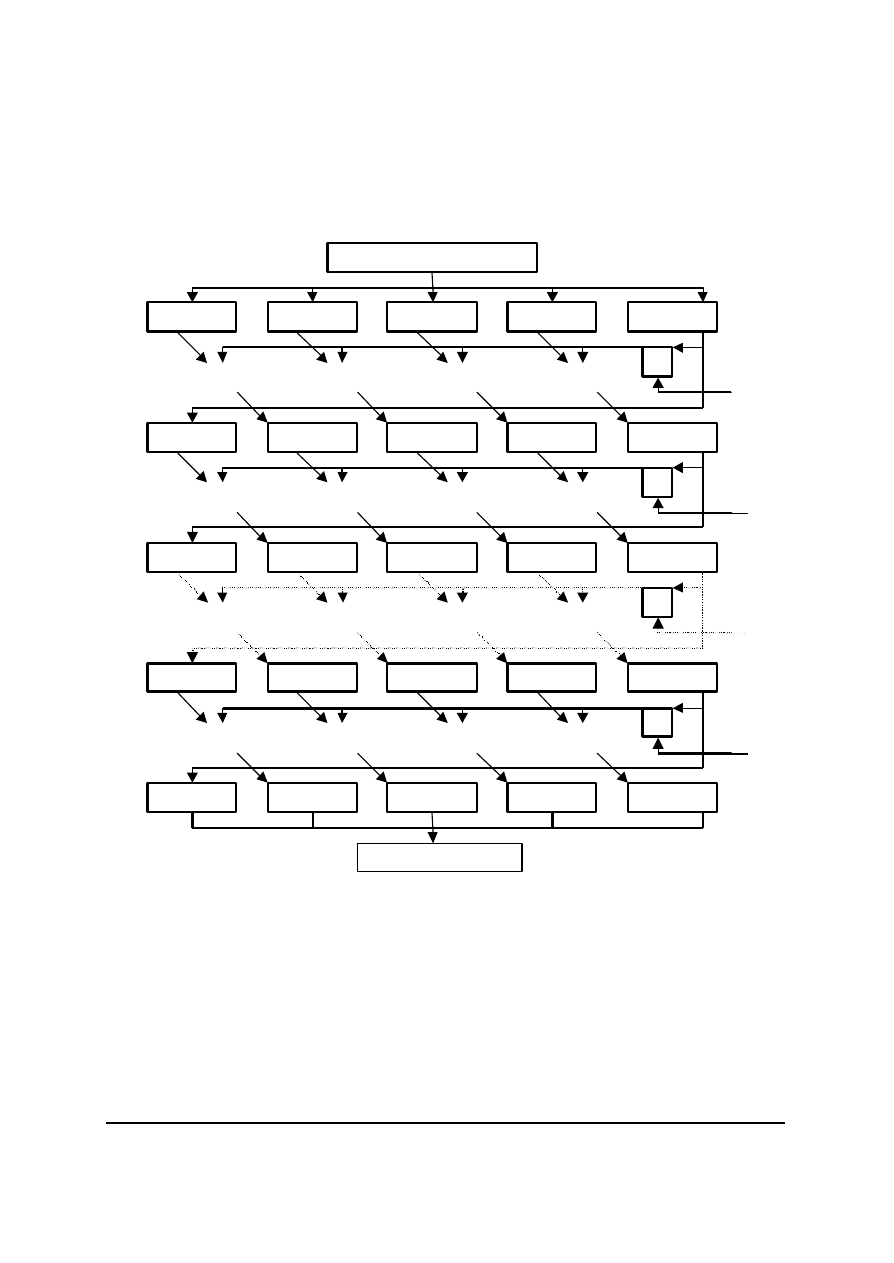
Uogólniony DES (Generalized DES – GDES), charakteryzuje sie wzrostem dlugosci bloku

i niezmieniona funkcja f (rys. 17).

Szyfrowane bloki sa dzielone na q 32-bitowych podbloków. Zazwyczaj liczba q jest równa

dlugosci bloku podzielonego przez 32. Jak widac ze schematu, funkcja f liczona jest tylko raz na

cykl, dla podbloku lezacego najbardziej na prawo[1, 2].

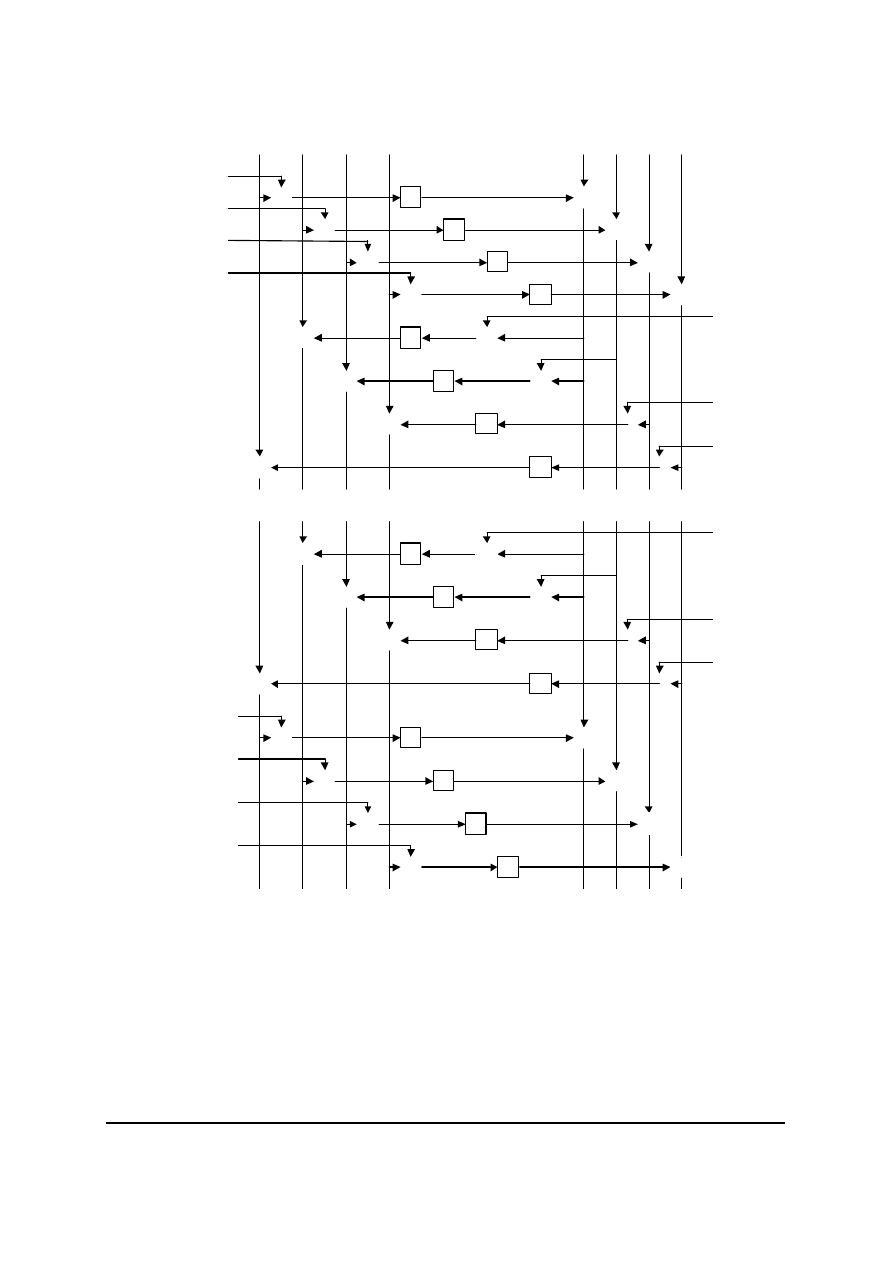
2.1.8. NewDES

NewDES (rys. 18) zostal zaprojektowany przez Roberta Scotta, w roku 1985, jako nastepca

DES. Blok tekstu jawnego nadal ma 64 bity, zmienila sie natomiast dlugosc klucza, 120 bitów.

Scott zrezygnowal w swojej wersji algorytmu z permutacji poczatkowej i koncowej, co

w znacznym stopniu uproscilo sam algorytm. Wszystkie operacje sa wykonywane na calych

bajtach, a sam algorytm nigdy nie czyta, nie zapisuje, nie permutuje zadnych pojedynczych bitów.

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

31

Funkcja f zostala zaprojektowana na podstawie tekstu Deklaracji Niepodleglosci. Szczególy

mozna znalezc w [18].

Tekst jawny

B

0

(1)

B

0

(2)

B

0

(3)

B

0

(4-1)

B

0

(4)

B

1

(1)

B

1

(2)

B

1

(3)

B

1

(4-1)

B

1

(4)

B

2

(1)

B

2

(2)

B

2

(3)

B

2

(4-1)

B

2

(4)

B

n-1

(1)

B

n-1

(2)

B

n-1

(3)

B

n-1

(4-1)

B

n-1

(4)

B

n

(1)

B

n

(2)

B

n

(3)

B

n

(4-1)

B

n

(4)

Λ

Λ

Λ

Λ

f

Λ

Λ

Λ

Λ

f

Λ

Λ

Λ

Λ

f

Λ

Λ

Λ

Λ

f

K

1

K

2

K

i

K

n

Szyfrogram

Rys. 17. Schemat blokowy algorytmu GDES

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

32

f

f

f

f

f

f

f

f

Λ

Λ

Λ

Λ

Λ

Λ

Λ

Λ

Λ

Λ

Λ

Λ

Λ

Λ

Λ

Λ

B0

B1

B2

B3

B4

B5

B6

B7

K0

K1

K2

K3

K4

K5

K6

Cykl 1

Cykl 2

Cykl 3-15

f

f

f

Λ

Λ

Λ

Λ

Λ

Λ

K9

K10

Cykl 16

Λ

f

Λ

K8

Cykl 17

Λ

f

Λ

Λ

f

Λ

Λ

f

Λ

Λ

f

Λ

K11

K12

K13

K14

B7

B0

B1

B2

B3

B6

B5

B4

Rys. 18. Schemat algorytmu NewDES

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

33

Z

p

Yi

X

4

X

3

X

1

X

2

Z

4(1)

Z

3(1)

Z

2(1)

Z

1(1)

Z

5(1)

Z

6(1)

1(9)

Z

2(9)

Z

3(9)

Z

4(9)

Y

2

Y

3

Y

4

siedem
ozostal ych

cykl i

pierwszy

cykl

Y

1

X i

Zi (r)

- 16 bitów podbl oku tekstu jaw nego

- 16 bitów podbloku te kstu szyfrogramu

- 16 bitów podbloku klucza

- poele ment ow a suma modul o 2 pojedync zych bitów

lub ciagów 16-bitowych

- suma modulo 2

16

li czb 16-bitowych

- il ocz yn modulo 2

16

+ 1 li czb 16-bitowych

ciag wyjsciowy

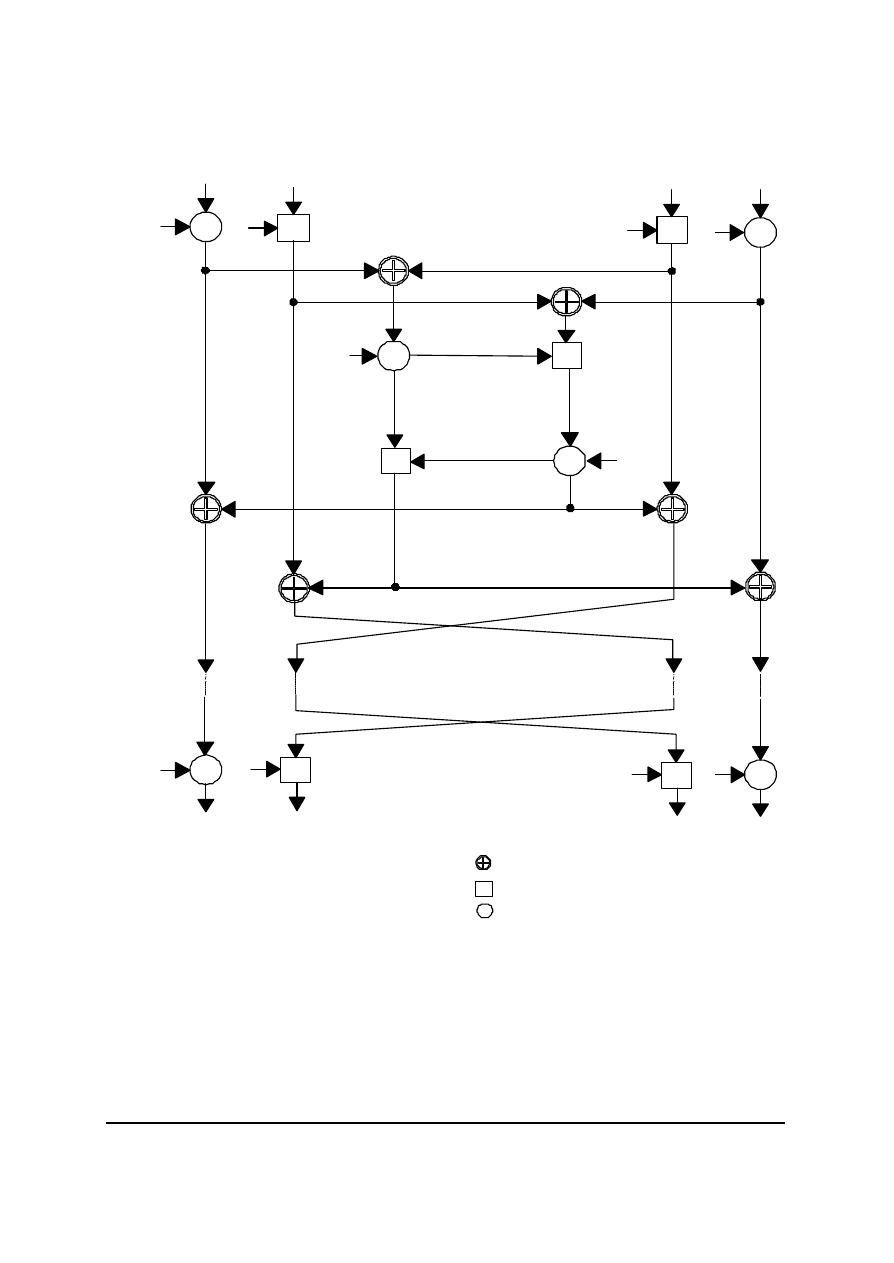
Rys. 19. Schemat blokowy algorytmu IDEA

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

34

Algorytm IDEA

Algorytm IDEA (ang. Improved Proposed Encryption Standard), podobnie jak DES, byl
tworzony z mysla o implementacjach sprzetowych. Przez wielu uwazany jest za
najbezpieczniejszy z algorytmów blokowych dostepnych na rynku [19, 20, 21].
Pracuje na bloku dlugosci 64 bitów i operuje kluczem 128-bitowym. Stosowany jest zarówno
do szyfrowania, jak i deszyfrowania.

2.1.9. Opis algorytmu

Rysunek 19 przedstawia ogólny schemat blokowy algorytmu. Jak widac, blok danych

dzielony jest na cztery podbloki (16-bitowe), które stanowia wejscie do pierwszego cyklu

algorytmu. Wykonywanych jest osiem cykli. Jak nietrudno zauwazyc, algorytm wykorzystuje

az 52 podklucze o dlugosci 16 bitów kazdy. Uzyskujemy je dzielac nasz klucz wejsciowy na

osiem podciagów. W rezultacie tego dzialania otrzymamy osiem pierwszych podkluczy. By

uzyskac kolejne, przesuwamy cyklicznie klucz wejsciowy o 25 bitów w lewo i ponownie

wykonujemy dzielenie. Operacje te powtarzamy tak dlugo, az bedziemy mieli wszystkie

potrzebne nam podklucze.

2.1.10.Tryby pracy IDEA

IDEA pracuje w czterech trybach pracy:

1. tryb elektronicznej ksiazki kodowej (Electronic Codebook – ECB),

2. tryb wiazania bloków zaszyfrowanych (Cipher Block Chaining – CBC),

3. tryb sprzezenie zwrotne wyjscia (Output Feedback – OFB),

4. tryb sprzezenie zwrotne szyfrogramu (Cipher Feedback – CFB).

2.1.11.Implementacje sprzetowe

Przeprowadzone testy dla realizacji programowych algorytmu IDEA wykazuja, ze sa one

prawie tak szybkie jak implementacje standardu DES. Na komputerze z mikroprocesorem
386 i zegarem 33 MHz dane sa szyfrowane z szybkoscia 880 Kbit/s. W przypadku VAX
9000 szybkosc ta jest prawie cztery razy wieksza.

Implementacja sprzetowa algorytmu IDEA zrealizowana jako uklad VLSI, opracowany

w ETH Zurich, szyfruje z szybkoscia 177 Mbit/s, przy czestotliwosci taktowania 25 MHz [22].

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

35

2.1.12.Bezpieczenstwo IDEA

Jak dotad nie znaleziono skuteczniejszej metody ataku na algorytm IDEA jak atak brutalny.

Uzyskanie klucza wymagaloby przeprowadzenia 2

128

(10

38

) szyfrowan. Jak dotad nie stworzono

takiej maszyny, która moglaby wykonac tyle prób w rozsadnym czasie. Przy zalozeniu ze mamy

uklad scalony, który testowalby miliard kluczy w ciagu sekundy i gdybysmy uzyli do rozwiazania

naszego problemu miliard takich ukladów, to zajeloby to 10

13

lat, czyli czas dluzszy od trwania

wszechswiata.

Istnieje kilka grup akademickich i wojskowych aktualnie pracujacych nad kryptoanaliza IDEA.

Dotychczas zadna z nich nie odniosla sukcesu (i nie oglosila takiego faktu publicznie). Szyfr

blokowy IDEA jest opatentowany w Europie [23] i oczekuje na patent w Stanach Zjednoczonych.

Algorytm RSA

Osoby prowadzace korespondencje stosuja ten sam algorytm szyfrowania i ten sam klucz.
Ale jak rozwiazac problem przekazania klucza w sposób pewny i tajny, zwlaszcza gdy
abonentów dziela tysiace kilometrów. Powstal wiec pomysl zastosowania asymetrycznych
algorytmów kryptograficznych. W algorytmach tych istnieja dwa klucze: szyfrujacy
i deszyfrujacy. Co wiecej, pelnia one te funkcje zamiennie: jesli zaszyfrujemy wiadomosc
przy uzyciu klucza A, to bedzie ja mozna odczytac tylko i wylacznie przy uzyciu klucza
B i na odwrót. Jednym z takich algorytmów jest powstaly w 1977 roku RSA (nazwa jest
zlozeniem pierwszych liter nazwisk autorów – Rivest, Shamir i Adleman). Jest on chroniony
patentem tylko w USA, objety miedzynarodowa norma ISO/IEC9796.

2.1.13.Historia

Autorami algorytmu sa: Ron Rivest, Adi Shamir i Leonard Adelman. W dniu opublikowania
algorytmu przedstawili oni postulat, ze mimo znajomosci 110-cyfrowej liczby n i klucza
jawnego adresata, przykladowa wiadomosc nie zostanie nigdy rozszyfrowana. Nie
przewidzieli oni jednak tak szybkiego postepu w technice cyfrowej. Obecne komputery sa
wielokrotnie szybsze niz te stosowane w latach 70. Z ich pomoca, a takze przy wspólpracy
kilkuset ochotników-uzytkowników sieci Internet, zespól naukowców amerykanskich w 1995
roku oglosil odczytanie wiadomosci. Czas potrzebny na zlamanie szyfru napawa jednak
optymizmem: po takim okresie przestaje byc celowa ochrona duzej czesci danych, nawet
o znaczeniu strategicznym. Oczywiscie klucze 100-cyfrowe przestaja byc bezpieczne.
Specjalisci szacuja, ze zastosowanie kluczy ponad 300-cyfrowych (sa uzywane juz dzisiaj)
pozwoli na utrzymywanie poufnosci danych jeszcze przez okolo 10 lat. Koszt zlamania
szyfru z takim kluczem oceniany jest, w chwili obecnej, na astronomiczna kwote rzedu 10

20

$

USA. Szacuje sie, ze zlozonosc problemu odczytania zaszyfrowanej wiadomosci jest tak
duza jak zlozonosci problemu faktoryzacji duzych liczb. Do tej chwili algorytm RSA

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

36

skutecznie opieral sie wszelkim metodom kryptoanalizy i jest prawdopodobne, ze bedzie tak
jeszcze przez wiele lat [1, 2, 3].

2.1.14.Generacja kluczy

Algorytm generacji pary kluczy (publiczny-prywatny) mozemy podzielic na nastepujace fazy:

•

Szukamy 2 liczb pierwszych p i q, a nastepnie wyliczamy ich iloczyn:

n = pq

Wszystkie dzialania na wiadomosciach odbywac sie beda „modulo n”.

•

Wybieramy klucz szyfrujacy (publiczny) e taki, ze e oraz (p-1)(q-1) sa liczbami
wzglednie pierwszymi (tzn. nie maja wspólnego dzielnika róznego od 1).

•

Szukamy liczby d takiej, ze jest ona odwrotnoscia liczby e „modulo n”, tzn.:

d = e

-1

mod (p-1)(q-1),

czyli

xe + yd = 1

Mozemy do tego celu wykorzystac rozszerzony algorytm Euklidesa (rozszerzenie algorytmu
znajdowania najwiekszego wspólnego dzielnika [1]). Liczba d bedzie kluczem deszyfrujacym.

•

Publikujemy liczby e i n, które pelnia funkcje klucza jawnego (klucz publiczny).

•

Utajniamy liczbe d, to jest naszym kluczem tajnym (klucz prywatny).

•

Liczby p i q nalezy wymazac i nigdy nie ujawniac zadnej z nich.

2.1.15.Szyfrowanie i deszyfrowanie

Sam algorytm szyfrowania i deszyfrowania opiera sie jedynie na 2 operacjach: potegowaniu
(mnozeniu) i dzieleniu „modulo n”. W celu szyfrowania dzielimy wiadomosc na jak
najwieksze bloki m

i

, takie ze posiadaja jednoznaczna interpretacje „modulo n” (np. jesli

wiadomoscia bedzie 200-elementowy ciag cyfr, a liczba n jest 50-cyfrowa, to powstana co
najmniej 4 bloki po co najwyzej 50 cyfr) i wyliczamy wartosc wyrazenia:

c

i

= m

i

e

mod n

Cala zaszyfrowana wiadomosc bedzie sie wiec skladac z bloków c

i

:

c= c

1

c

2

... c

k

Deszyfrowanie odbywa sie w sposób analogiczny – tym razem bloki c

i

poddajemy

potegowaniu i dzieleniu „modulo n” i skladamy zdeszyfrowany tekst:

m

i

= c

i

d

mod n

m = m

1

m

2

...m

k

Zauwazmy, ze mimo prostoty matematycznego zapisu algorytmu szyfrowania
i deszyfrowania, jego rzeczywiste implementacje wymagaja dzialan na liczbach

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

37

ponadstucyfrowych i wymagaja specjalnych reprezentacji liczb i algorytmów operowania na
nich.

2.1.16.Rozwiazania sprzetowe

Wkrótce po opublikowaniu algorytmu RSA pojawily sie scalone uklady szyfrujace
przyspieszajace i ulatwiajace szyfrowanie [24]. Jak pokazuje praktyka, uzyskane rezultaty sa,
jak dotychczas, znacznie gorsze niz w przypadku ukladów do szyfrowania symetrycznego
(uklady te sa ok. 100 razy wolniejsze od ukladów szyfrujacych z uzyciem algorytmu DES.
Przy zastosowaniu programowej implementacji, algorytm RSA jest ok. 1000 razy
wolniejszy). Prawdopodobnie znaczacy wplyw na rozwój ukladów szyfrujacych mialo prawo
amerykanskie zabraniajace wywozenia poza granice kraju pewnych algorytmów i rozwiazan
technicznych (np. dla algorytmu RSA uklady z kluczem powyzej 512 bitów, a dla DES
powyzej 46 bitów). Obecnie w Japonii rozpoczeto produkcje ukladów clipper posiadajacych
mozliwosc szyfrowania z kluczem 102-bitowym (uklady pochodzace z USA – 512-bitowy).
Byc moze stanie sie to bodzcem do dalszego rozwoju ukladów szyfrujacych (Japonia jest
jednym z najwiekszych ich odbiorców, a jednoczesnie jest krajem posiadajacym bardzo
zaawansowane technologie – moze wiec podjac sie produkcji i badan nad nowymi ukladami).

2.1.17.Atak na algorytm RSA

Rozwazajac bezpieczenstwo danych przesylanych w sieci i chronionych algorytmem RSA,

nalezy rozwazyc kilka mozliwych scenariuszy przechwycenia i zdekodowania wiadomosci:

•

Napastnik N podszywa sie pod bank kluczy publicznych. Nadawca A chce przeslac do odbiorcy
B poufna wiadomosc. Zwraca sie wiec do banku kluczy z prosba o podanie publicznego klucza
B. Poniewaz transmisje kontroluje N, przesyla do A swój klucz publiczny. A ufa bankowi, w
zwiazku z czym bez watpliwosci szyfruje informacje za pomoca klucza publicznego N i przesyla
wiadomosc do B. N przechwytuje wiadomosc i dekoduje ja za pomoca swojego klucza
prywatnego. Nastepnie pobiera z banku klucz publiczny B, koduje wiadomosc za jego pomoca i
przesyla do rzeczywistego adresata. Jest jednak w posiadaniu tekstu wiadomosci.

•

Napastnik N przechwycil zaszyfrowana wiadomosc c od A (zna wiec c, n i e). Wybiera
wiec r<n i oblicza:

x=r

e

mod n -> r=x

d

mod n -> t=x

-d

mod n

y = x*c mod n

t=r

-1

mod n

Teraz N przesyla do A wiadomosc y z prosba o jej podpisanie – A musi podpisac cala
wiadomosc, a nie jej skrót. W zwiazku z tym N otrzymuje u=y

d

mod n. Teraz wystarcza

juz tylko proste obliczenia, aby zlamac szyfr A:

t*u mod n = x

-d

*y

d

mod n = x

-d

*x

d

*c

d

mod n = c

d

mod n = p.

•

Grupa pracowników jakiegos przedsiebiorstwa posluguje sie tym samym modulem n, ale
kazdy z nich ma wlasne klucze e i d. Napastnik N przechwytuje dwie wiadomosci c

1

i c

2

.

Nastepnie pobiera e

1

, e

2

– klucze jawne obydwu pracowników oraz modul n, którym sie

oni posluguja. Poniewaz e

1

i e

2

sa (a raczej powinny byc) wzglednie pierwsze, to szukamy

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

38

liczb r i s spelniajacych zaleznosc r*e

1

+s*e

2

=1. Jesli zalozymy, ze r jest ujemne, to

otrzymujemy [1]:

(c

1

-1

)

-r

*c

2

s

=p mod n.

2.1.18.Ostrzezenia i zalecenia

W tym miejscu zebrano kilka rad i ostrzezen dotyczacych korzystania z algorytmu RSA,
istotnych ze wzgledu na bezpieczenstwo naszych danych przesylanych w sieci publicznej:

•

Nie nalezy nigdy podpisywac wiadomosci z niesprawdzonego zródla – jesli juz wystapi
taka koniecznosc, nalezy zastosowac jednokierunkowa funkcje skrótu lub inny algorytm
podpisu cyfrowego.

•

Nie nalezy uzywac identycznego modulu w grupie uzytkowników korzystajacych z sieci
innej niz wewnetrzna w przedsiebiorstwie.

•

Nalezy uzywac jak najwiekszych wartosci kluczy e i d – im wieksze one beda, tym

trudniej bedzie odczytac wiadomosc przez osoby do tego niepowolane.

•

Znajomosc jednej pary wykladników szyfrowania/deszyfrowania dla danego modulu

umozliwia atakujacemu faktoryzacje modulu.

•

Znajomosc jednej pary wykladników szyfrowania/deszyfrowania dla danego modulu

umozliwia atakujacemu obliczenie innych par wykladników szyfrowania/deszyfrowania

bez koniecznosci faktoryzacji n.

•

Jesli istnieje potrzeba szczególnej ochrony informacji przesylanej w sieci publicznej,

nalezy zmieniac co pewien czas modul i klucze. Eliminuje to zwiekszanie

prawdopodobienstwa odczytania wiadomosci (pozbawiamy napastnika próbek tekstu

zaszyfrowanego za pomoca tego samego klucza).

2.1.19.Praktyka szyfrowania z uzyciem algorytmu RSA

W praktyce zawsze poszukuje sie rozwiazania optymalnego: bezpiecznego i szybkiego.

Algorytm RSA zapewnia tylko pierwsza z tych cech, DES obie, ale pod warunkiem

bezpiecznego przekazania klucza. Aby wiec zapewnic idealne warunki przesylania danych

poufnych miedzy koncówkami sieci, stosuje sie kombinacje algorytmów DES-RSA. Polega

ona na tym, ze klucz do szyfrowania-deszyfrowania dla DES przesyla sie szyfrujac go za

pomoca algorytmu RSA. Dane szyfrowane sa juz przy uzyciu algorytmu DES, który jako

algorytm synchroniczny z kluczem dlugosci 64 bitów jest znacznie szybszy od RSA.

Poniewaz obecny stan techniki obliczeniowej pozwala na biezaca faktoryzacje liczb

110-cyfrowych (512-bitowe), do przesylu poufnych informacji stosuje sie klucze ponad

200-cyfrowe (w niektórych zastosowaniach nawet 308 cyfr – liczby 1024-bitowe).

Specjalisci oceniaja, ze zastosowanie kluczy 1024-bitowych pozwoli na spelnienie wszelkich

warunków bezpieczenstwa jeszcze przez okolo 10 lat [25].

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

39

Glosariusz

FAKTORYZACJA

– rozklad liczby na czynniki pierwsze (np. poddanie faktoryzacji liczby

1001 daje w rezultacie 3 liczby: 7, 11 i 13).

JEDNOKIERUNKOWA FUNKCJA SKRÓTU – argumentem funkcji H(M) jest M(wia-

domosc) dowolnej dlugosci, wynikiem jest h ustalonej dlugosci (skrót). Wlasciwosci funkcji H(M):

•

majac dane M, latwo jest obliczyc h,

•

majac dane h, trudno jest obliczyc M,

•

majac dane M, trudno jest obliczyc M’, takie ze H(M)=H(M’),

•

„trudno” oznacza koniecznosc wykonania co najmniej 2

64

operacji.

ROZSZERZONY ALGORYTM EUKLIDESA OBLICZANIA NWD x i n:

u*u

1

+v*u

2

=1

static void Update (int *un, int *vn, int q)
{

int tn;

tn = *un – *vn * q;

*un = *vn;

*vn = tn;

}

int rozsz_Euklides (int u, int v, int *u1wy, int u2wy)

{

int u1=1;

int u3=u;

int v1=0;

int v3=v

int q;

while (v3 > 0)

{

q=u3/v3;

Update(&u1, &v1, q);

Update(&u3, &v3, q);

}

*u1wy=u1

*u2wy=(u3-u1*u)/v;

return u3;

}

ZARZADZANIE KLUCZAMI – klucz jawny moze byc pobierany bezposrednio od
wlasciciela lub z centralnej bazy danych. W przypadku centralnej bazy danych stosuje sie
dodatkowo certyfikaty – informacja zaszyfrowana za pomoca klucza prywatnego urzedu
poswiadczajacego, ze pobrany klucz nalezy dokladnie do tej osoby, z która chcemy sie
skontaktowac (jest to osobny problem zwiazany z uwierzytelnianiem i certyfikatami
omawiany w dalszej czesci tego skryptu).

L

ITERATURA

1.

B. S

CHNEIER

, Kryptografia dla praktyków. Protokoly, algorytmy i programy zródlowe w jezyku C. Wydawnictwa

Naukowo-Techniczne, Warszawa 1995.

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

40

2.

D. E. R

OBLING

D

ENING

, Kryptografia i ochrona danych. Wydawnictwa Naukowo-Techniczne, Warszawa 1993.

3.

J. S

TOKLOSA

, Algorytmy kryptograficzne. OWN – Osrodek Wydawnictw Naukowych, Poznan 1994.

4.

ANSI X3.92, American National Standard for Data Encryption Algorithm (DEA). American National Standards

Institute, 1981.

5.

ANSI X3.105, American National Standard for Information Systems – Data Link Encryption. American National

Standards Institute, 1983.

6.

ANSI X9.8, American National Standard for Personal Information Number (PIN) Menagement and Security.

American Bankers Association, 1982.

7.

ANSI X9.9, American National Standard for Financial Institution Message Autentication (Wholesale). American

Bankers Association, 1986.

8.

ANSI X9.23, American National Standard for Financial Institution Message Encryption. American Bankers

Association, 1988.

9.

ANSI X9.24, American National Standard for Retail Key Management. American Bankers Association, 1988.

10. ANSI X9.26, American National Standard for Financial Institution Sign-On Autentication for Wholesale

Financial Transaction. American Bankers Association, 1990.

11. D. M

AC

M

ILLAN

, Single Chip Encrypts Data at 14Mb/s. Electronics, v. 54, n. 12, 16 June 1981, str. 161-165.

12. S. K. B

ANERJEE

, High Speed Implementation of DES. Computers and Security, v. 1, 1982, str. 261-267.

13. R. C. F

AIRFIELD

, A. M

ATUSEVICH AND

J. P

LANY

, An LSI Digital Encryption Processor (DEP). Advances in

Cryptology – CRYPTO’84 Proceedings, Springer-Verlag, Berlin 1985, str. 115-143.

14. R. C. F

AIRFIELD

, A. M

ATUSEVICH AND

J. P

LANY

, An LSI Digital Encryption Processor (DEP). IEEE

Communications, v. 23, n.7, Jun 1985, str. 30-41.

15. M. D

AVIO

, Y. D

ESMENDT

, J. G

OUBERT

, F. H

OORNAERT AND

J. J. Q

UISQUATER

, Efficient Hardware and

Implementation of the DES. Advances in Cryptology – CRYPTO’84 Proceedings, Springer-Verlag, Berlin,

1985, str. 144-146.

16. D. W. D

AVIES

, Some Regular Properties of the DES. Advances in Cryptology: Proceedings of Crypto 82, Plenum

Press, 1983, str. 89-96.

17. E. B

IHAM

, A. S

HAMIR

, Differential Cryptoanalysis of the DES. Springer-Verlag, Berlin 1993.

18. S

COTT

, Wide Open Encription Design Offers Flexible Implementations. Cryptologia, v. 9, n. 1, Jan 85, str. 75-90.

19. X. L

AI

, J. M

ASSEY AND

S. M

URPHY

, Markov Ciphers and Differential Cryptanalysis. Advances in Cryptology –

EUROCRYPT’91 Proceedings, Springer-Verlag, Berlin 1991, str. 17-38.

20. X. L

AI

, J. M

ASSEY

, A Proposal for New Block Encryption Standard. Advances in Cryptology – EUROCRYPT’90

Proceedings, Springer-Verlag, Berlin 1991, str. 389-404.

21. X.L

AI

, Detailed Description and a Software Implementation of the IPES Cipher. Preprint 8 Nov 1991.

22. X L

AI

, Personal communication.

23. J. L. M

ASSEY AND

X. L

AI

, Device for Converting a Digital Block and the Use Thereof. Interntional Patent

PCT/CH91/00117, 28 Nov 1991.

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

41

24. E. F. B

RICKELL

, Survey of Hardware Implementations of RSA. Advances in Cryptology – CRYPTO’89

Proceedings, Springer-Verlag, Berlin 1990, str. 368-370.

25. T. B

ETH

, M. F

RISCH AND

G. J. S

IMMONS

,

EDS

., Lecture Notes in Computer Science 578; Public-Key

Cryptography: State of the Art. And Future Directions, Springer-Verlag, Berlin 1992.

B S K

K A T A R Z Y N A T Y B I C K A - F R A N C I K

42