- 1 -
Wersja 4.7.0.
9.11.2015
Instalka
http://www.fx-calc.de/index_en.html
Uniwersalny kalkulator naukowy
dla Windows
Przekład
Robert Wi
ś
niewski
http://chomikuj.pl/bobwis
FX-Calc jest jednym z najbardziej zaawansowanych kalkulatorów przeznaczonych do definiowania,
wizualizacji i obliczania funkcji naukowych. Pozwala na definiowanie i natychmiastowe obliczanie
funkcji zawieraj
ą
cych do 5 zmiennych. Działa równie
ż
na liczbach zespolonych. Rozwi
ą
zuje równania
i analizuje funkcje z graficzn
ą
prezentacj
ą
wyników w formacie 2D i 3D. Wyznacza ekstrema lokalne,
punkty przegi
ę
cia, styczne oraz przeprowadza analiz
ę
regresji liniowej i interpolacje. Dokumentacja
(w j, angielskim) znajduje si
ę
w pliku PDF. Aplikacja działa w systemie Windows XP.
- 2 -
SPIS TRE
Ś
CI
1. Fx-Calc – Uniwersalny kalkulator naukowy
1.1. Unikalne mo
ż
liwo
ś
ci
2. Instalacja
3. Podstawowe koncepcje
4. Skrócona tablica składni wprowadzanych obiektów
5. Obliczenia przykładowe
6. Obliczenia z funkcjami i nawiasami
7. Funkcje definiowane przez u
ż
ytkownika
7.1. Obliczanie przy korzystaniu z pami
ę
ci
8. Sumy i iloczyny
9. Inne operacje
9.1. Analiza funkcji
9.2. Obliczanie stycznych
9.3. Wykresy funkcji 2D
9.4. Wykresy funkcji 3D
9.5. Regresja liniowa
10. Baza danych warto
ś
ci stałych
10.1. Obliczanie pierwiastków
10.2. Pierwiastki dla argumentów innych ni
ż
0
10.3. Warto
ś
ci ekstremalne
10.4. Całki oznaczone
10.5. Punkty nieokre
ś
lone
10.6. Punkty brakuj
ą
ce, pierwiastki i ekstrema
11. Od Autora.
- 3 -
1. Fx-Calc – Uniwersalny kalkulator naukowy
Program fx-Calc jest aktualnie jednym z z najbardziej zaawansowanych kalkulatorów pulpitowych dla
oblicze
ń
naukowych w
ś
rodowisku Windows. Pocz
ą
wszy od prostego okna oblicze
ń
, pozwala na
korzystanie z wbudowanych funkcji, sum i iloczynów.
Przykładowo, kilka klikni
ęć
myszk
ą
uruchamia iteracj
ę
Leibnitza do obliczania warto
ś
ci liczby
ππππ
.
Program fx-Calc pozwala na definiowanie, analizowanie i obliczanie funkcji naukowych i jest
doskonałym zamiennikiem starego kalkulatora Windows.
Niezale
ż
nie od oblicze
ń
i wizualizacji, mo
ż
na analizowa
ć
i rozwi
ą
zywa
ć
funkcje naukowe oraz
przeprowadza
ć
analiz
ę
regresji liniowej.
Chocia
ż
koncepcja Windows nie pozwala na zaawansowany wygl
ą
d interfejsu, du
żą
zalet
ą
programu
jest mo
ż
liwo
ść
wielokrotnego otwierania okien i porównywania wyników w razie potrzeby.
Aplikacja ta wymaga mniej ni
ż
750 kB pami
ę
ci i jest mniejsza od programu calc.exe wbudowanego
w Windows.
Aby skorzysta
ć
z interpretera DLL we własnych projektach, mo
ż
na uzyska
ć
jego kopi
ę
oraz
dokumentacj
ę
bezpo
ś
rednio od autora programu.
1.1. Unikalne mo
ż
liwo
ś
ci
•
Definiowanie i po
ś
rednie obliczanie funkcji maj
ą
cych do 5 zmiennych
•
Rozwi
ą
zywanie równa
ń
•
Analiza funkcji w poł
ą
czeniu z graficzna prezentacj
ą
wyników
•
Obliczanie parametrycznych sum i iloczynów
•
Wbudowana biblioteka funkcji
•
Wbudowana biblioteka stałych naukowych
•
Wykresy 2D zawieraj
ą
ce zło
ż
one grafiki
•
Mechanizm Open GL przy
ś
pieszaj
ą
cy tworzenie wykresów 3D
•
Wielokrotne okna wykresów i analiz w celu porównywania ró
ż
nych charakterystyk funkcji
•
Interaktywny moduł analizy regresji liniowej
•
Zautomatyzowana historia polece
ń
•
Wy
ś
wietlanie aktualnej warto
ś
ci pami
ę
ci w osobnym polu
•
Wbudowane przykłady
•
Obsługa liczb zespolonych
•
Obliczanie punktów nieokre
ś
lonych
- 4 -
2. Instalacja
Wymagania systemowe:
Procesor CPU
X86 Dual Core poczwszy od 1,6 GHz
Pami
ęć
RAM
5123 MB
Dysk twardy HDD
3 MB
Karta grafkii
Wymagana Open GL 2,0
Systemy operacyjne
Windows Vista, Windows 7, Windows 8 (32 i 64 bit),
Windows XP (w ograniczeniu, ale działa)
Fx-Calc wymaga Microsoft dotNET v. 4.0 lub wy
ż
szej.
Instalacja jest bardzo prosta i przeprowadzana w sposób standardowy.
Wymagane jest tylko jedno ustawienie: Lokalizacja.
- 5 -
Instalator tworzy odpowiedni wpis w menu Start i oferuje opcjonalne utworzenie ikony programu na
pulpicie. Istniej
ą
ce dane z wcze
ś
niejszej wersji s
ą
automatycznie przenoszone do nowej wersji.
Niezale
ż
nie od ikony programu, mo
ż
na utworzy
ć
skrót do pliku dokumentacji w formacie PDF.
Fx-Calc zawiera funkcj
ę
automatycznego sprawdzania aktualizacji. Gdy dost
ę
pna jest nowa wersja,
wówczas program oferuje skrót do
ś
ci
ą
gania nowej wersji po zamkni
ę
ciu aplikacji. Taki rodzaj
komunikacji internetowej jest tylko do czytania, tzn. Fx-Calc nie wysyła
ż
adnych danych z komputera
do Internetu.
3. Podstawowe koncepcje
Ka
ż
de obliczenie wymaga wprowadzenia danych w polu edycji. Fx-Calc oblicza natychmiast wyniki
podczas wpisywania. Format wyra
ż
e
ń
matematycznych jest podobny do BASIC, a wbudowana
klawiatura ułatwia wprowadzane funkcji. W razie popełnienia pomyłki w wyra
ż
eniu matematycznym,
program wy
ś
wietli odpowiedni komunikat o bł
ę
dzie. Zniknie on automatyczne po wprowadzeniu
korekty.
Interpreter rozró
ż
nia du
ż
e i małe litery ! Korzystaj
ą
c z klawiatury mo
ż
na wstawia
ć
poprawne nazwy
funkcji w polu edycji.
WA
Ż
NE
Fx-Calc korzysta z normalnej logiki oblicze
ń
naukowych o nazwie DAL (Direct Algebraic Logic).
Tak wi
ę
c mno
ż
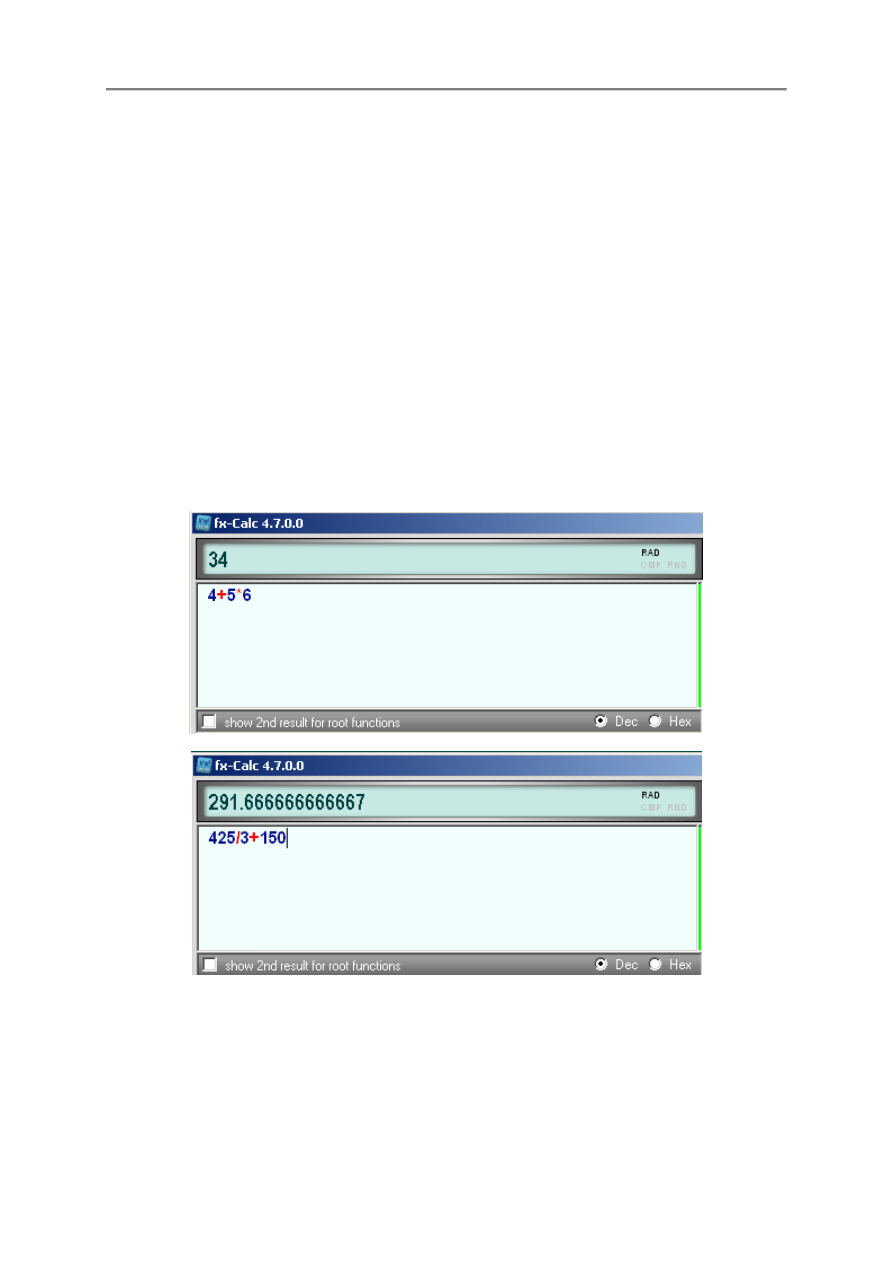
enie * oraz dzielenie / jest wykonywane przed dodawaniem + i odejmowaniem -, np:
4 + 5 * 3 = 19, a nie 27
Z tego powodu wyra
ż
enia matematyczne obliczane s
ą
krok po kroku w zale
ż
no
ś
ci od hierarchii
operatorów.
- 6 -
4. Skrócona tablica składni wprowadzanych obiektów
Poni
ż
sza tablica zawiera przegl
ą
d składni wprowadzanych obiektów:
Temat
Podtemat
Przykłady
Komentarze
Liczby
proste
1; 2,579; 3,14256;
0,0015
Jako separator dziesi
ę
tny mo
ż
na stosowa
ć
przecinek lub kropk
ę
Format
naukowy
4e-4; 6.623e-23
Litera e poprzedza wykładnik pot
ę
gi
o podstawie 10
Liczby
Liczby
zespolone
1+1i; 0-4i; 6e-12+i8e3;
(12-i3e-5)
Liczby zespolone w wyra
ż
eniu musz
ą
zawsze
zawiera
ć
oba elementy: rzeczywisty i urojony.
Gdy cz
ęść
urojona jest zerwa, wpisujemy 0
+
5+3.14; 546+3+6
Ka
ż
dy operator * lub / wykonywany jest wcze
ś
niej
-
5-3.14; 546-3-6
Ka
ż
dy operator * lub / wykonywany jest wcze
ś
niej
*
5*3.14; 546*3*6
Operator ten ma pierwsze
ń
stwo przed + lub -
W poni
ż
szych przypadkach operator mno
ż
enia
nie jest wymagany:
•
Mno
ż
enie dwóch zmiennych x*y jest takie
samo jak xy
•
Liczba i otwarty nawias 2,5*( ... jest takie
samo jak 2,5 (...
•
Funkcja 2,5*sin(30) jest taka sama jak
2,5sin(30)
•
Zmienna 2,5*x jest taka sama jak 2,5x
•
Nawias zamkni
ę
ty i otwarty ...)*(... jest taki
sam jak ...)(...
/
5/3.14; 546/3*6
Operator ten ma pierwsze
ń
stwo przed + lub -
Przykłady
pierwsze
ń
stwa
4+3*6 = 40
7+1/2 = 7,5
Najpierw obliczane jest 3*6 przed dodaniem 4
Dzielenie jest wykonywane przed dodaniem 7
Operatory
^
x^n; 4^3 = 64
5,23^2,77 = 97,77
W celu podniesienia liczby x do pot
ę
gi n, liczby te
mog
ą
by
ć
całkowite, ułamkowe
a nawet zespolone
Korzystanie
z funkcji
sin(30); f(x)=sin(x)
3^(1.2); 4^2
Ona te przykłady pokazuj
ą
jak korzysta si
ę
z funkcji. Zwykle zaczynamy od identyfikatora
funkcji. po czym nast
ę
puje argument funkcji
w nawiasach Jest to bardzo podobne do składni
j
ę
zyka BASIC. Wyj
ą
tkiem od tej zasady jest
funkcja pot
ę
gowa z której mo
ż
na korzysta
ć
za
pomoc
ą
operatora ^
Funkcje
wbudowane
Wszystkie wbudowane
funkcje
ln(x), exp(x), log(x), x^y, sqrt(x), abs(x), fac(x)
(facult), sin(x), cos(x), tan(x), cotan(x), pi,
arcsin(x), arccos(x), arctan(x), sinh(x), cosh(x),
tanh(x), Con(i); Rec(i);
Stopnie
i radiany
Funkcje
trygonometryczne
Dla funkcji trygonometrycznych mo
ż
na wybra
ć
argumenty w stopniach lub w radianach przy
korzystaniu z przycisków radiowych w górnym
prawym rogu kalkulatora
Funkcje
Funkcje
definiowane
f(x)=sin(x);
f(hight)=sqrt(hight*9,91
Wszystkie funkcje definiowane zaczynaj
ą
si
ę
od f(,
po czym nast
ę
puje do 5 parametrów, przy czym
ich separatorem jest przecinek, a na ko
ń
cu
znajduje si
ę
nawias zamykaj
ą
cy i znak równo
ś
ci
oraz wyra
ż
enie z tymi parametrami:
f(argument 1, argument 2,...) = Wyra
ż
enie
Program fx-Calc rozpoznaje te argumenty oraz
uaktywnia automatycznie odpowiednie pola.
- 7 -
O czym nale
ż
y pami
ę
ta
ć
:
•
Ogólna zasada jest taka,
ż
e gdy mamy w
ą
tpliwo
ś
ci co do operatorów lub nawiasów, lepiej
skorzysta
ć
z nawiasów aby wyra
ż
enie było bardziej zrozumiałe
•
Obowi
ą
zuje hierarchia operatorów
•
Wej
ś
cia rozró
ż
niaj
ą
wielko
ś
ci liter
•
Liczby zespolone musz
ą
zawsze zawiera
ć
cz
ęść
rzeczywist
ą
i urojon
ą
– nawiasy mog
ą
pomóc przy ich wpisywaniu, ale nie s
ą
konieczne
•
Kalkulator ten jest bardzo tolerancyjny na brak operatorów mno
ż
enia, ale korzystanie z nich
zmniejsza mo
ż
liwo
ść
popełnienia bł
ę
du,
5. Obliczenia przykładowe
W celu wykonywania prostych oblicze
ń
, wprowadza
ć
wymagane zadania w polu tekstowym – wyniki
oblicze
ń
b
ę
d
ą
pojawiały si
ę
w miar
ę
wpisywania danych. Program fx-Calc przetwarza wyra
ż
enia
korzystaj
ą
c z hierarchii operatorów, np.:
lub:
Mo
ż
na korzysta
ć
z naukowego formatu liczb, np. 5e-5, co jest równe 0,00005. Ponadto, fx-Calc
obsługuje liczby zespolone korzystaj
ą
c z poni
ż
szego formatu:
r +/- i z
gdzie r jest cz
ęś
ci
ą
rzeczywist
ą
, z jest cz
ęś
ci
ą
urojon
ą
, znak plus lub minus przed liter
ą
i definiuje
znak składowej z., np.:
4-ie-3 lub 0+2i
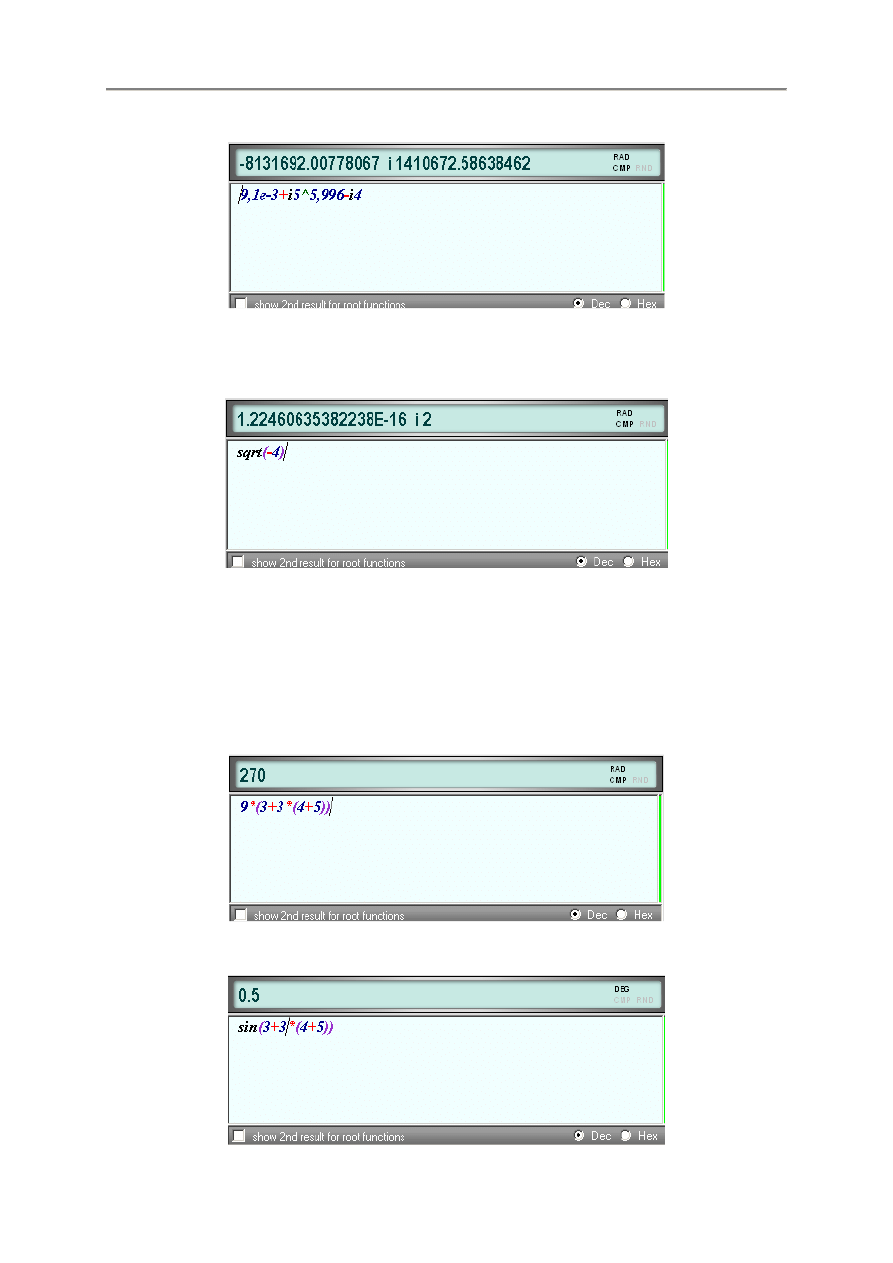
- 8 -
Poni
ż
ej podano przykład takich oblicze
ń
na liczbach zespolonych:
W celu wykonania zło
ż
onych oblicze
ń
na liczbach zespolonych, fx-Calc oferuje funkcje sprz
ęż
enia
liczb zespolonych i obliczania odwrotno
ś
ci liczb zespolonych. Typowym przykładem jest obliczanie
pierwiastka kwadratowego z liczby ujemnej:
6. Obliczenia z funkcjami i nawiasami
Podstaw
ą
jest równie
ż
porównywanie prostych operacji arytmetycznych bez zbytniej komplikacji.
Takie funkcje wymagaj
ą
ce korzystania z nawiasów mo
ż
na wstawia
ć
w polu tekstowym pry korzystaniu
z odpowiednich przycisków. Pami
ęć
dynamiczna pozwala przynajmniej teoretycznie na stosowanie
nieograniczonych poziomów nawiasów w wyra
ż
eniach matematycznych. Przy dzisiejszych rozmiarach
pami
ę
ci, nie ma
ż
adnych ogranicze
ń
w tym zakresie, np.:
lub przy korzystaniu z funkcji sinus:
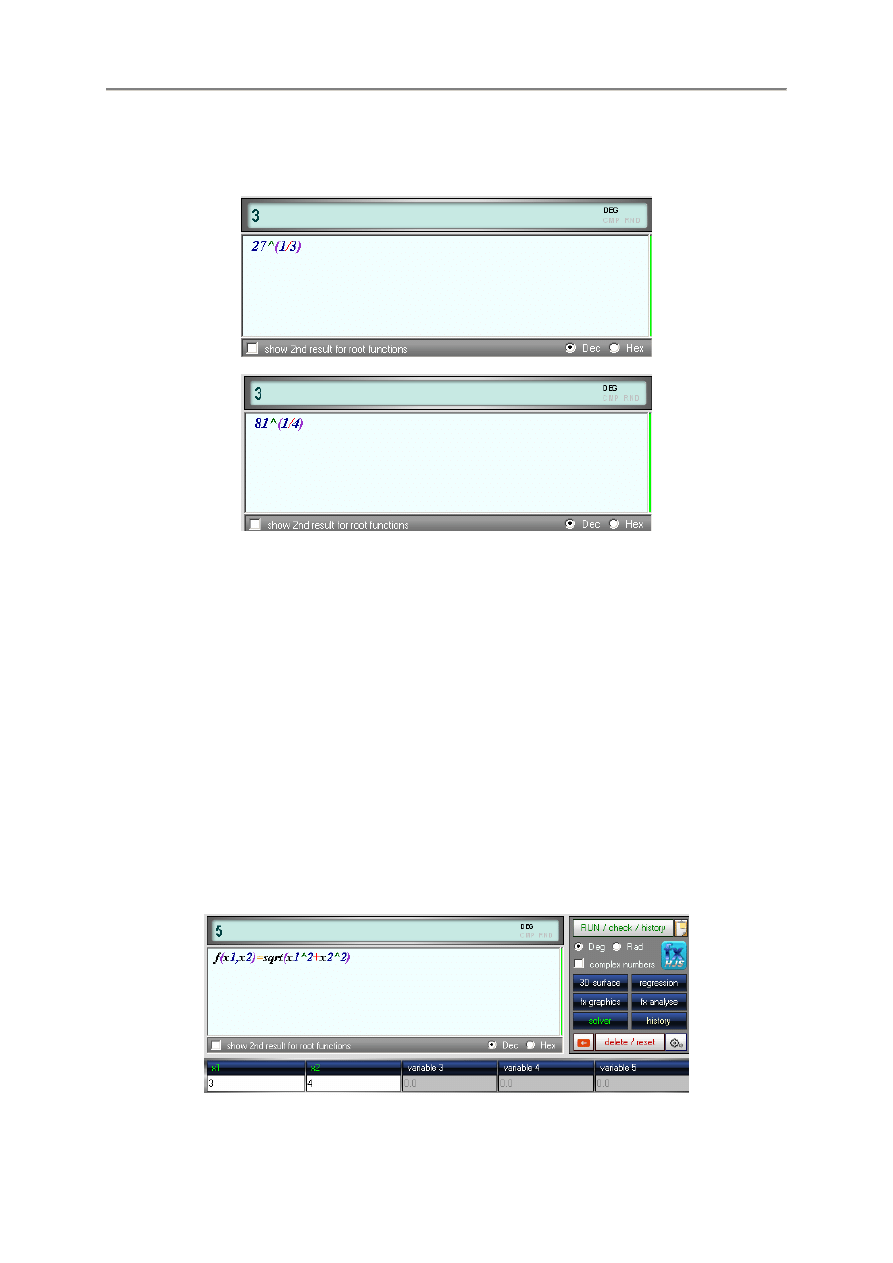
- 9 -
Wszystkie zaimplementowane funkcje wyst
ę
puj
ą
ce w wi
ę
kszo
ś
ci kalkulatorów naukowych mo
ż
na
znale
źć
wskazuj
ą
c kursorem przycisk funkcyjny. Szczególnym przypadkiem jest obliczanie
pierwiastków innych ni
ż
kwadratowe. Poni
ż
sze dwa przykłady pokazuj
ą
jak to mo
ż
na w prosty sposób
wykona
ć
korzystaj
ą
c z funkcji pot
ę
gowej y^x (np. do obliczenia pierwiastka 3-go i 4-go stopnia):
7. Funkcje definiowane przez u
ż
ytkownika
Krotko mówi
ą
c, funkcje te definiuj
ą
jak mo
ż
na obliczy
ć
okre
ś
lony wynik na podstawie pewnych
parametrów lub zmiennych. Takie zmienne mog
ą
mie
ć
własne nazwy, a fx-Calc mo
ż
e zarz
ą
dza
ć
funkcjami definiowanymi korz6staj
ąć
z własnej, malej bazy danych. Program pozwala na korzystanie
do 5 zmiennych w tych funkcjach.
Ka
ż
da nazwa zmiennej musi zaczyna
ć
si
ę
liter
ą
i musi by
ć
inna od nazwy wbudowanej funkcji, np.
takiej jak sin lub ln. Zmienne s
ą
automatycznie wykrywane podczas ich wpisywania w polu tekstowym
przy czym jednocze
ś
nie aktywowane s
ą
odpowiednie pola (pod polem tekstowym) zgodne z nazwami
zmiennych.
Nale
ż
y pami
ę
ta
ć
,
ż
e wszystkie funkcje definiowane zaczynaj
ą
si
ę
od f(, po czym nast
ę
puje do
5 parametrów, przy czym ich separatorem jest przecinek, np w postaci f(a1,b2,c3,.... Na ko
ń
cu
znajduje si
ę
nawias zamykaj
ą
cy oraz znak równo
ś
ci i wyra
ż
enie z tymi parametrami, npi:
f(a1, b2, c3) = a1*b2*c3
Najłatwiej to zapami
ę
ta
ć
na podstawie przykładów:
Wszystkie warto
ś
ci zmiennych (w naszym przykładzie x1 i x2) mo
ż
na zmienia
ć
w celu obliczania
nowego wyniku funkcji.
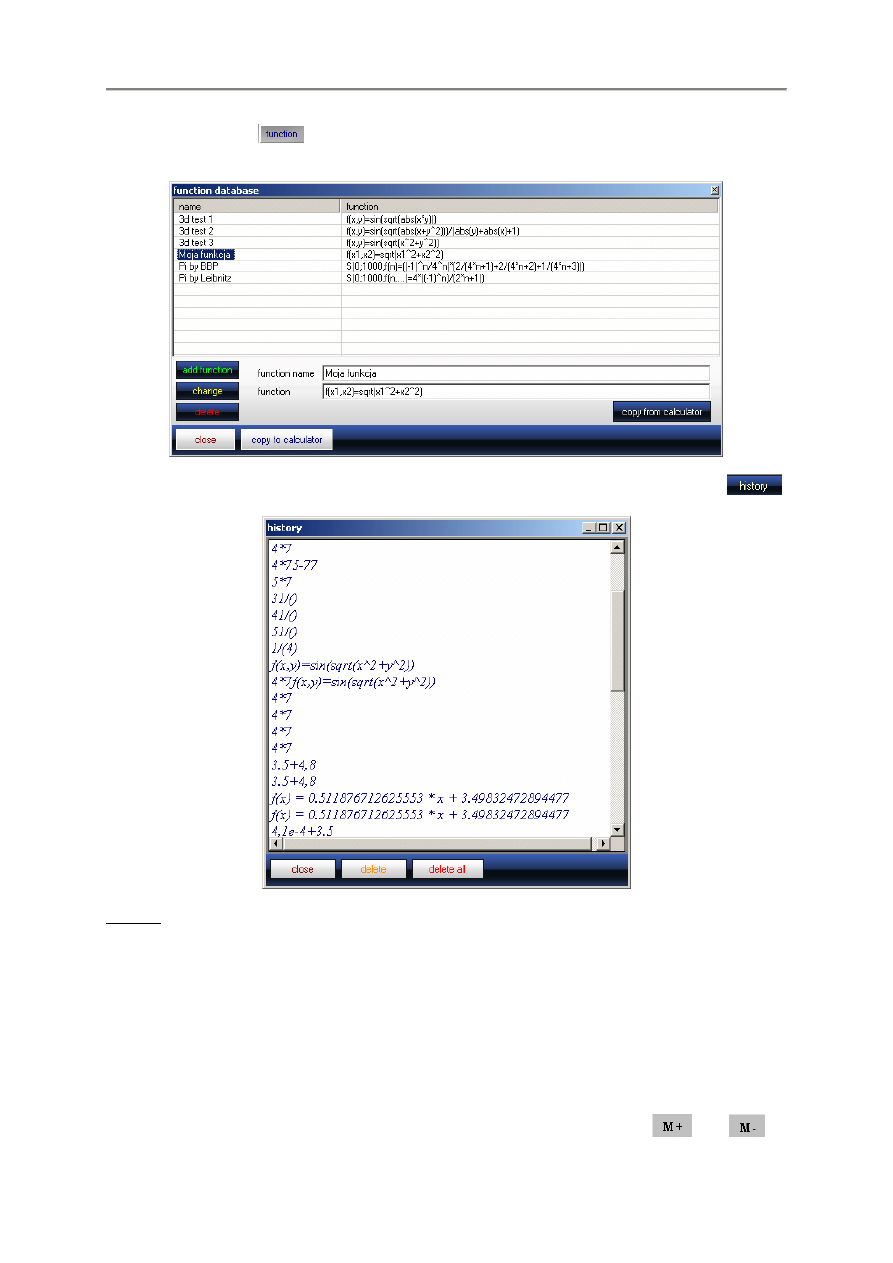
- 10 -
Ka
ż
da funkcja definiowana jest przechowywana bazie danych funkcji Function Database (otwieranej
po klikni
ę
ciu przycisku
), co pozwala na ich wywoływanie przez podwójne klikni
ę
cie wymaganej
funkcji
Inn
ą
mo
ż
liwo
ś
ci
ą
jest wywołanie historii polece
ń
, po klikni
ę
ciu przycisku Calculation History
WA
Ż
NE :
Po podwójnym klikni
ę
ciu zaznaczonej pozycji, zostanie ona natychmiast wstawiona do kalkulatora.
Odnosi si
ę
to do wszystkich okienek baz danych.
7.1. Obliczanie przy korzystaniu z pami
ę
ci
Program fx-Calc obsługuje rozszerzon
ą
manipulacj
ę
aktualnej warto
ś
ci w pami
ę
ci za pomoc
ą
czterech podstawowych operacji. Aktualna zawarto
ść
pami
ę
ci jest wy
ś
wietlana w dolnym prawym
rogu głównego okna Value in Memory.
Warto
ść
pocz
ą
tkowa wynosi 0 i mo
ż
na j
ą
przede wszystkim zmienia
ć
przyciskami
oraz
.
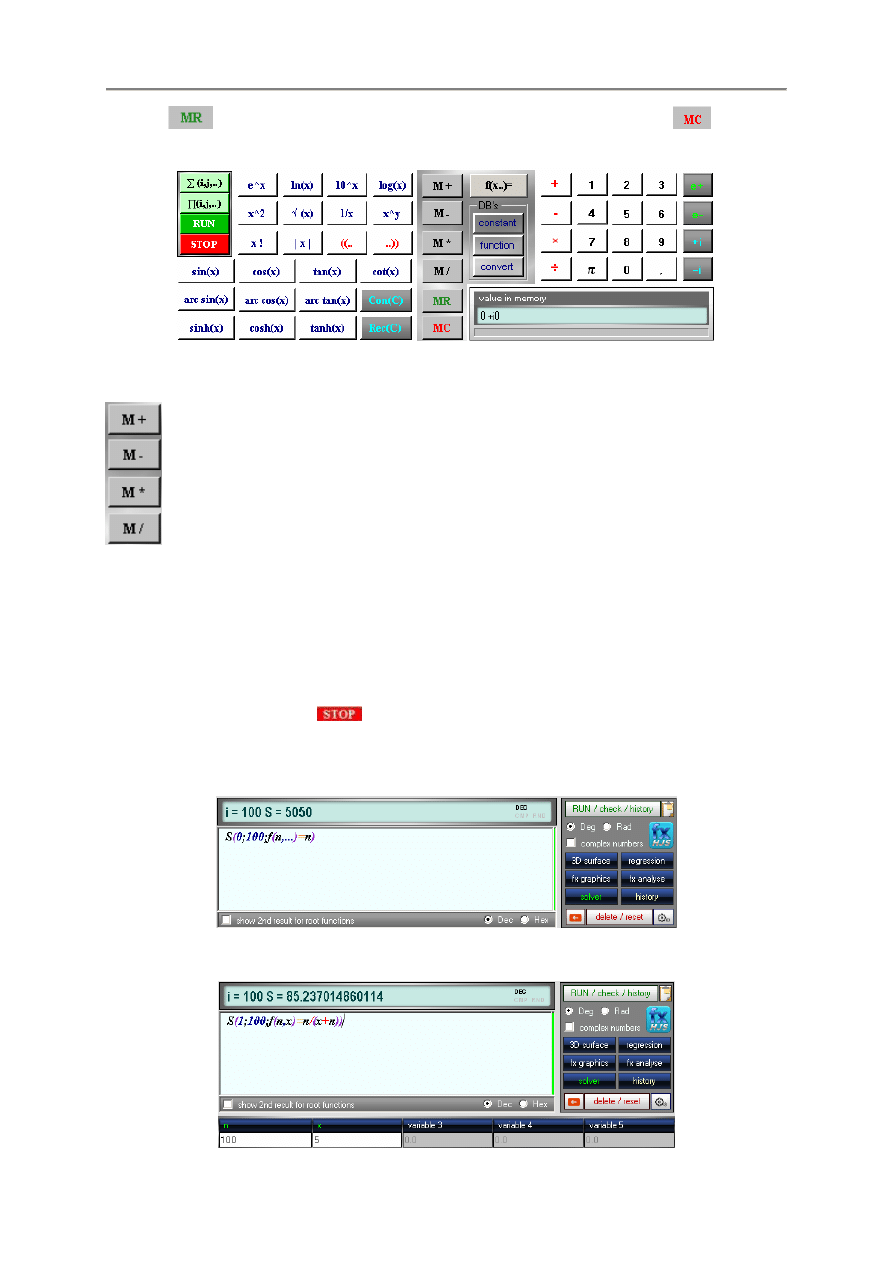
- 11 -
Przycisk
wywołuje zawarto
ść
pami
ę
ci wstawia j
ą
w polu edycji, a przycisk
oczyszcza
zawarto
ść
pami
ę
ci nadaj
ą
c jej warto
ść
0.
Program fx-Calc wykonuje poni
ż
sze obliczenia na pami
ę
ci:
Dodaje wynik do pami
ę
ci
Odejmuje wynik z pami
ę
ci
Mno
ż
y wynik w pami
ę
ci
Dzieli wynik w pami
ę
ci
8. Sumy i iloczyny
Sumy i iloczyny s
ą
nieco bardziej zło
ż
one ni
ż
definiowane funkcje. W odró
ż
nieniu od wyra
ż
enia
funkcji, sumy i iloczyny wymagaj
ą
punktu startowego oraz liczy iteracji. Chocia
ż
samo sumowanie jest
proste, to punkt startowy = 0 nie zawsze jest poprawny dla iloczynu
nnym wa
ż
nym aspektem jest obserwowanie jak zachowuje si
ę
okre
ś
lone wyra
ż
enie i program musi
mie
ć
znale
źć
koniec iteracji podany przez u
ż
ytkownika. Mo
ż
na to sprawdzi
ć
ustawiaj
ą
c liczb
ę
iteracji
na 0 lub wciskaj
ą
c przycisk
gdy chcemy zatrzyma
ć
proces oblicze
ń
. Najlepiej to ilustruj
ą
poni
ż
sze przykłady.
Aby zsumowa
ć
wszystkie liczby od 0 do 100, wystarczy wprowadzi
ć
poni
ż
sze wyra
ż
enie:
Poni
ż
szy przykład ilustruje korzystanie z wyra
ż
enia funkcyjnego:
- 12 -
Warto
ść
mo
ż
na ustawi
ć
w odpowiednim polu zmiennej je
ś
li nie jest aktywowane automatycznie Nawet
je
ś
li n jest rozpoznawane i prezentowane w polu zmiennej, wszelkie warto
ś
ci tego pola b
ę
d
ą
ignorowane i nadpisywane przez warto
ś
ci z wyra
ż
enia.
Wyra
ż
enie S
(0
;
100
;f
(
n
,
x
)
=
n
/
(
x
+
n
))
zawiera poni
ż
sze elementy:
•
S = suma (P = iloczyn)
•
Licznik n od 0
•
Licznik n do 100
•
Wyra
ż
enie to korzysta z funkcji f
(
n
,
x
)
=
n
/
(
x
+
n
))
Jak wspomniano wcze
ś
niej, obowi
ą
zuje to równie
ż
dla iloczynu za wyj
ą
tkiem zmiany litery S na P.
Drugi parametr naszego przykładu jest ustawiony na 0, a program oblicza sum
ę
lub iloczyn do chwili
klikni
ę
cia przycisku
przez u
ż
ytkownika (oczywi
ś
cie, zatrzymanie nast
ę
puje automatycznie po
zako
ń
czeniu oblicze
ń
).
Wszystkie cztery przyciski sumy i iloczynu znajduj
ą
si
ę
w lewym górnym rogu klawiatury kalkulatora.
Chocia
ż
ten kalkulator wykonuje wszystkie obliczenia w trakcie wprowadzania danych, to jednak nie
ma to miejsca w przypadku sum i iloczynów. Powód jest oczywisty. Obliczenia wymagaj
ą
iteracji.
Dlatego trzeba klikn
ąć
zielony przycisk
w celu uruchomienia oblicze
ń
..
Poni
ż
ej przytoczono przykład stosowania sumy do obliczania liczby
π
:
S(0;1000;f(n)=((-1)^n/4^n)(2/(4n+1)+2/(4n+2)+1/(4n+3)))
9. Inne operacje
Program fx-Calc pozwala na:
•
Wykre
ś
lanie funkcji w 2D i 3D`
•
Rozwi
ą
zywanie i analizowanie funkcji
•
Przeprowadzanie analizy regresji liniowej.
Ka
ż
dy z tych modułów zaczyna si
ę
wbudowanym przykładem, który ilustruje stosowane parametry
oraz składni
ę
modułu.
Wszystkie przykłady mo
ż
na łatwo zmienia
ć
i stosowa
ć
wg uznania.
- 13 -
Wa
ż
ne wskazówki:
Wszystkie moduły zawieraj
ą
metody sprawdzania wprowadzanych danych. Gdy wpis zawiera
niepoprawne dane, wowczas obliczenia zostan
ą
przerwane i zasygnalizowany jest bł
ą
d, który nale
ż
y
skorygowa
ć
.
Bł
ę
dy sygnalizowane s
ą
przez:
•
Czerwony kolor tekstu w polach edycji`
•
Tekst informuj
ą
cy w osobnym polu pod polem edycji.
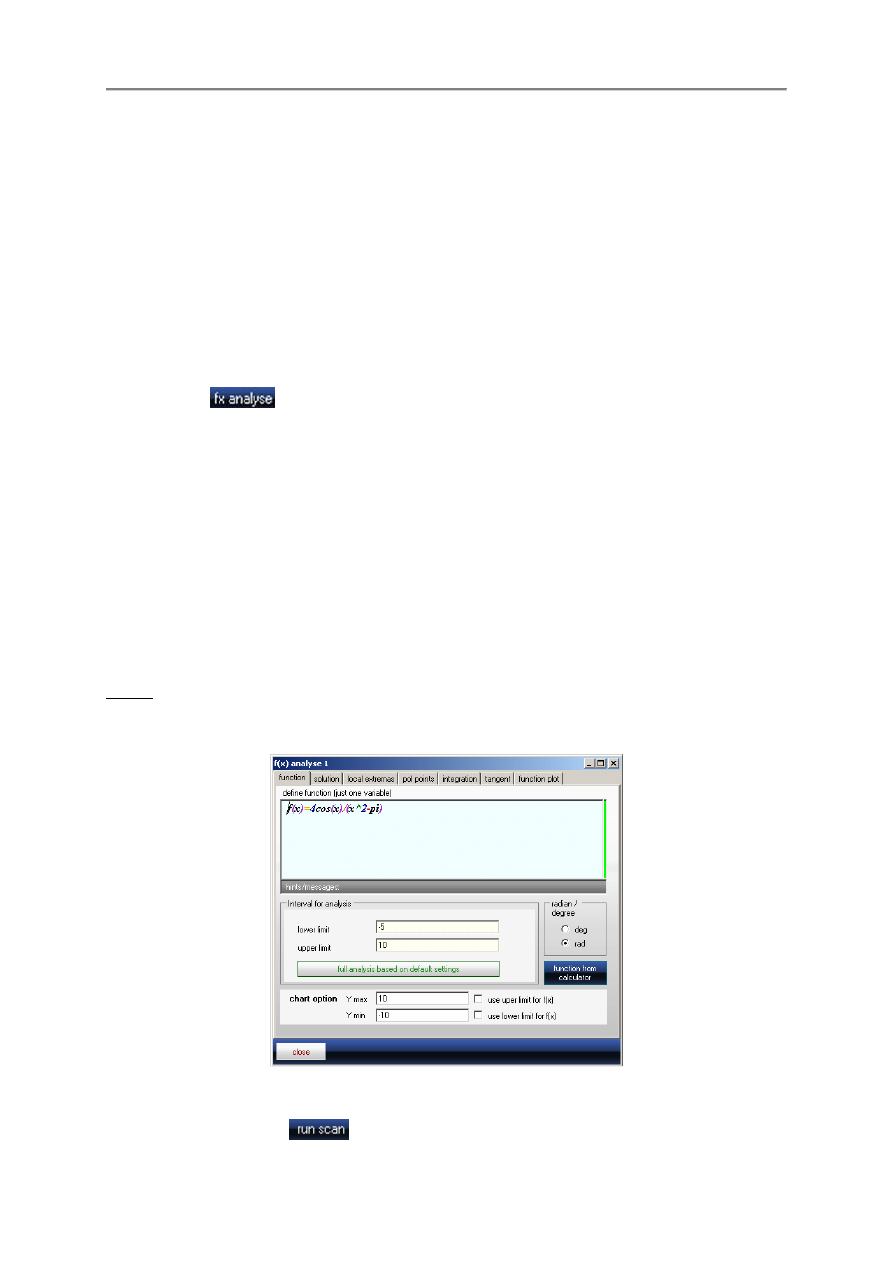
9.1. Analiza funkcji
Analiza funkcji
mo
ż
e by
ć
czasochłonna, zwłaszcza przy bardziej zło
ż
onych wyra
ż
eniach.
Program oferuje mo
ż
liwo
ść
ogl
ą
dania wielu pierwiastków i ekstremów lokalnych w
ś
ci
ś
le
zdefiniowanym przedziale. Obliczenia oparte s
ą
na algorytmach numerycznych co ułatwia skanowanie
przedziałów i zmiany ich znaków lub pochodnych funkcji. Jest bardzo elastyczne i stabilne, ale ma
pewne ograniczenia. W szczególno
ś
ci nale
ż
y korzysta
ć
z odpowiednich przedziałów i parametrów.
Ponadto mo
ż
na korzysta
ć
z wykresów funkcji w celu weryfikacji rozwi
ą
za
ń
.
Moduł analizy oblicza:
•
Pierwiastki funkcji
•
Ekstrema lokalne
•
Punkty przegi
ę
cia
•
Interaktywn
ą
iteracj
ę
Newtona
•
Całki oznaczone
Wa
ż
ne: Zakładka definicji funkcji Function mo
ż
e by
ć
stosowana równie
ż
dla innych zakładek.
Tak wi
ę
c gdy chcemy zmieni
ć
funkcj
ę
lub jej przedział, mo
ż
na korzysta
ć
z tej pierwszej zakładki.
Rozwi
ą
zywanie równa
ń
jest bardzo proste. Wystarczy wybra
ć
zakładk
ę
Solution, zmieni
ć
warto
ść
docelow
ą
i klikn
ąć
przycisk
:
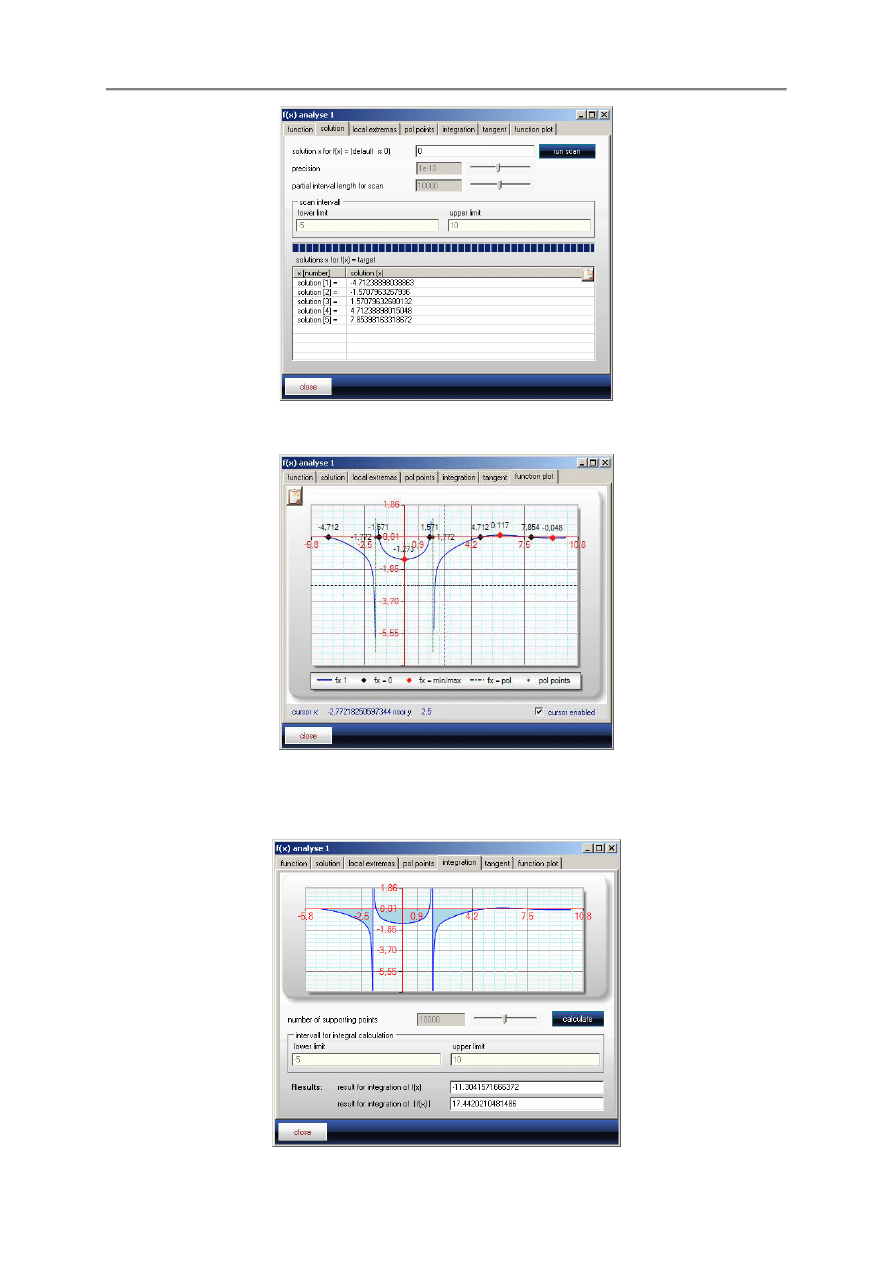
- 14 -
Korzystaj
ą
c z zakładki Function Plot, mo
ż
na łatwo zweryfikowa
ć
wszystkie wyniki na wykresie:
Na koniec, moduł ten pozwala w zakładce Integration na obliczanie całki oznaczonej funkcji.
Program umo
ż
liwia jednoczesne otwieranie wielu instancji tego okna w celu porównywania ró
ż
nych
scenariuszy
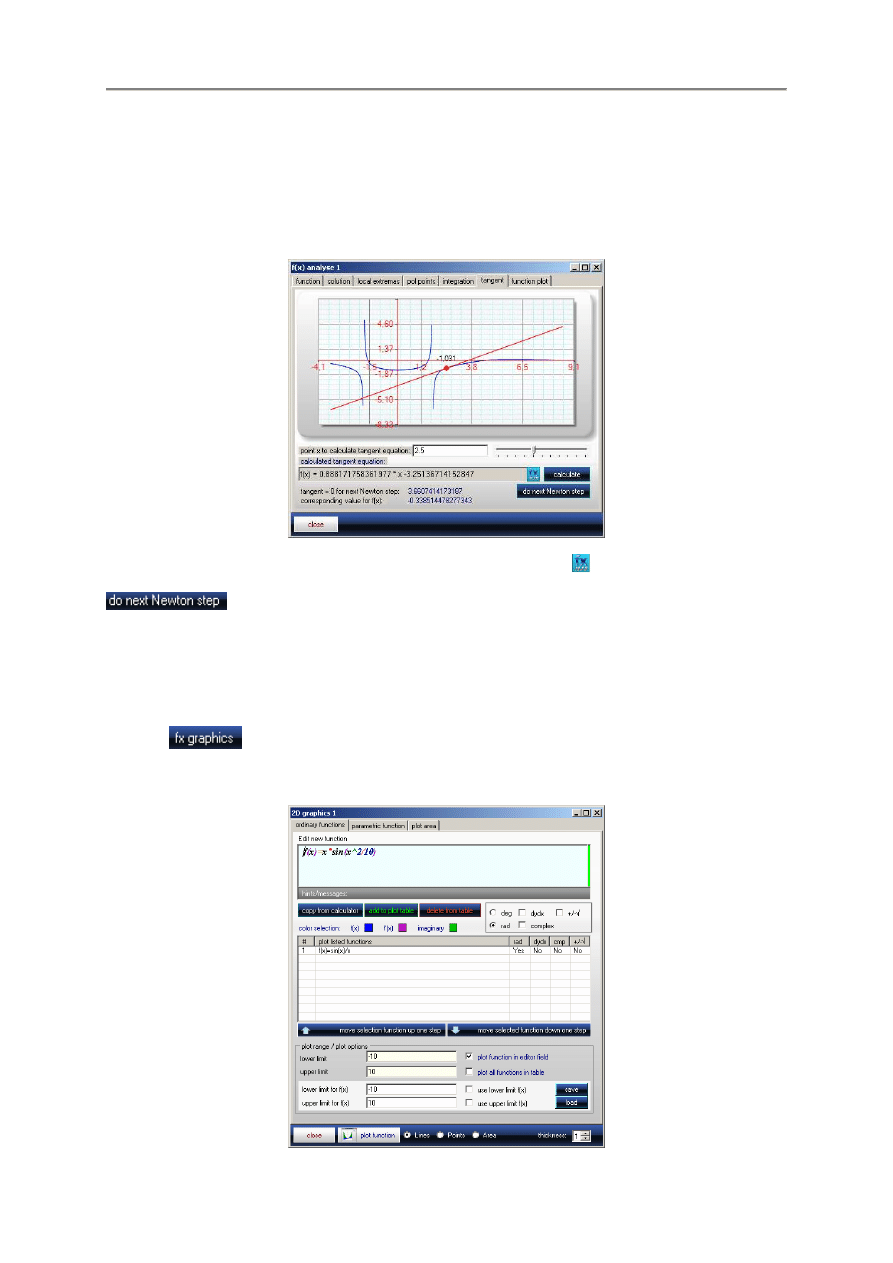
- 15 -
9.2. Obliczanie stycznych
Obliczanie stycznych do równa
ń
w zakładce Tangent jest oparte na obliczeniach numerycznych
pierwszej pochodnej danej funkcji w okre
ś
lonym punkcie x danych. Punkt startowy x jest zwykle
ś
redni
ą
z przedziału analizowanej funkcji i mo
ż
e by
ć
łatwo zmieniony przez ustawienie jego warto
ś
ci
w pierwszym polu tekstowym. Uzyskanie poprawnych wyników wymaga aby dana funkcja była
ró
ż
niczkowalna w wybranym przedziale.
Program fx-Calc oblicza styczn
ą
do równania za pomoc
ą
przycisku
oferuje mo
ż
liwo
ść
transferu
uzyskanego równania bezpo
ś
rednio do okna kalkulatora. Na dole tego okna znajduje si
ę
przycisk
pozwalaj
ą
cy na wykonanie nast
ę
pnej iteracji Newtona. Podczas tej operacji mo
ż
na
obserwowa
ć
jak styczna zbli
ż
a si
ę
do nast
ę
pnego rozwi
ą
zania danej funkcji. Zwykle proces tej jest
szybko zbie
ż
ny i najcz
ęś
ciej wystarczy 5 kroków aby uzyska
ć
wynik ko
ń
cowy.
9.3. Wykresy funkcji 2D
Przycisk
w prawym górnym rogu kalkulatora otwiera okno wykresów dwuwymiarowych
2D Graphics z aktywn
ą
zakładk
ą
Ordinary Function pozwalaj
ą
ce na wykre
ś
lanie jednej lub kilka
zwykłych funkcji. Program mo
ż
e wy
ś
wietla
ć
tabel
ę
zawarto
ś
ci i pole zawarto
ś
ci edytora.
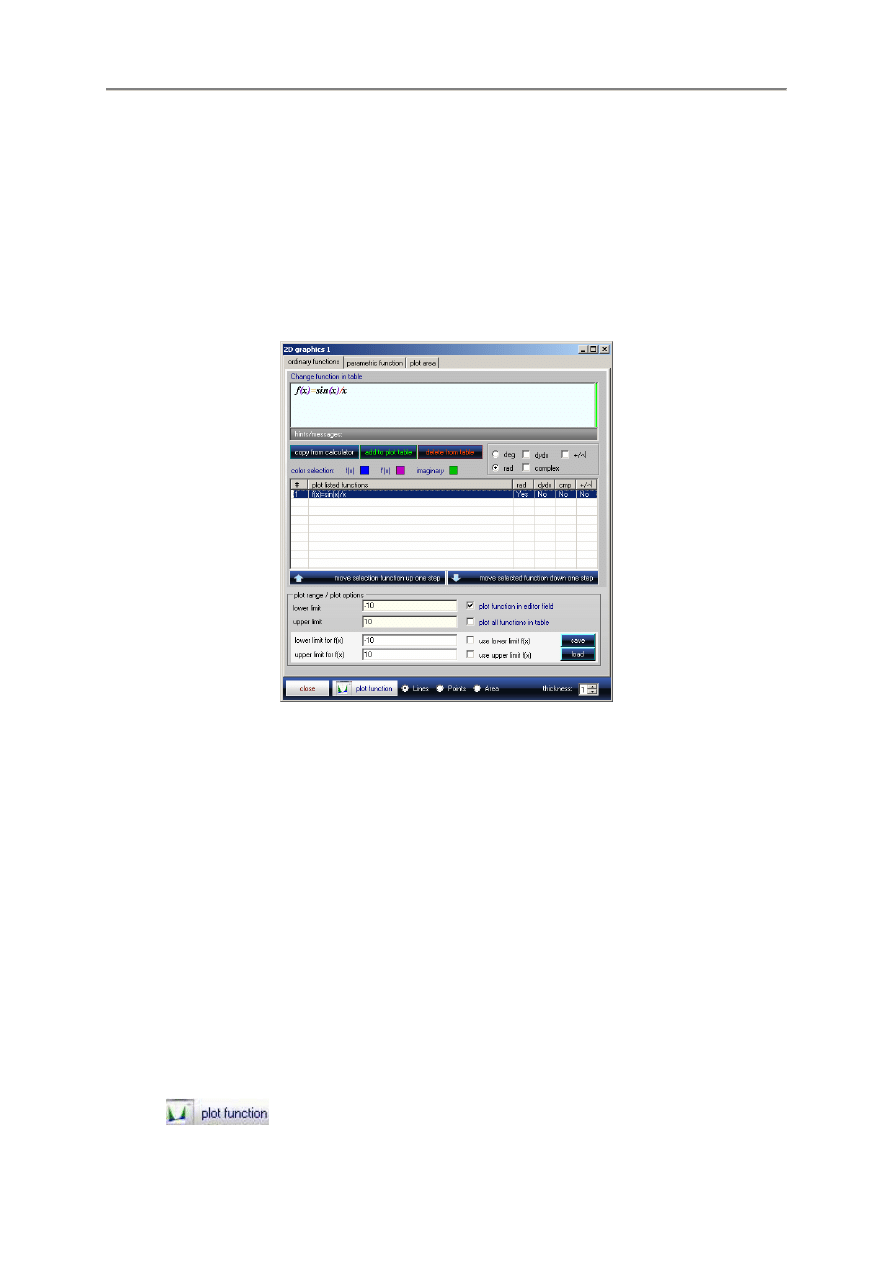
- 16 -
Korzystaj
ą
c z pól zaznaczania na dole tego okna, mo
ż
na wybiera
ć
poni
ż
sze opcje:
•
Wykres funkcji zawarty w polu edycji Plot function in editor field (opcja domy
ś
lna)
•
Wykresy funkcji zawartych w tabeli Plot functions in table
•
Wykresy z edytora i z tabeli funkcji
Korzystaj
ą
c z dolnych i górnych granic funkcji, mo
ż
na wizualizowa
ć
funkcje i istotnych ró
ż
nicach. Inn
ą
mo
ż
liwo
ś
ci
ą
jest wykre
ś
lanie funkcji parametrycznych, co pozwala na wizualizacj
ę
okre
ś
lonych
wła
ś
ciwo
ś
ci funkcji w zale
ż
no
ś
ci od wybranych parametrów. W celu zmiany funkcji lub jej opcji, klikn
ąć
funkcj
ę
w dolnej tabeli. Zawarto
ść
górnego pola edycji automatycznie zmieni si
ę
wy
ś
wietlaj
ą
c klikni
ę
t
ą
funkcj
ę
. Ka
ż
da zmiana opcji, zmieni natychmiast odpowiedni pola tabeli. Tryb ten jest wskazywany
przez zmian
ę
koloru tła i nagłówka pola edytora.
W celu opuszczenie tego trybu, wystarczy klikn
ąć
w pustym miejscu tabeli.
Inn
ą
now
ą
opcj
ą
jest wykre
ś
lanie funkcji przy korzystaniu z liczb zespolonych. W tym przypadku
program wykre
ś
la dwa wykresy funkcji: jeden dla składowej rzeczywistej a drugi dla składowej
urojonej. Ponadto, mo
ż
na wzbogaca
ć
wykresy dodaj
ą
c do nich wykresy pochodnych. Tak wi
ę
c
obydwie linie mo
ż
na wizualizowa
ć
na jednym diagramie:
•
Kilka funkcji (pole edytora i tabela)
•
Ka
ż
da z nich mo
ż
e mie
ć
poni
ż
sze opcje:
Pochodna funkcji
Rozszerzenie zespolone (cz
ęść
urojona)
Drugi wynik pierwiastka kwadratowego
Stopnie lub radiany dla funkcji trygonometrycznych
•
W razie potrzeby, mo
ż
na zmniejszy
ć
zdefiniowane granice.
Przyciski radiowe na dole tego okna pozwalaj
ą
na prezentacj
ę
wykresów w postaci linii, punktów lub
wypełnie
ń
kolorami.
Przycisk
wykre
ś
la odpowieni wykres:
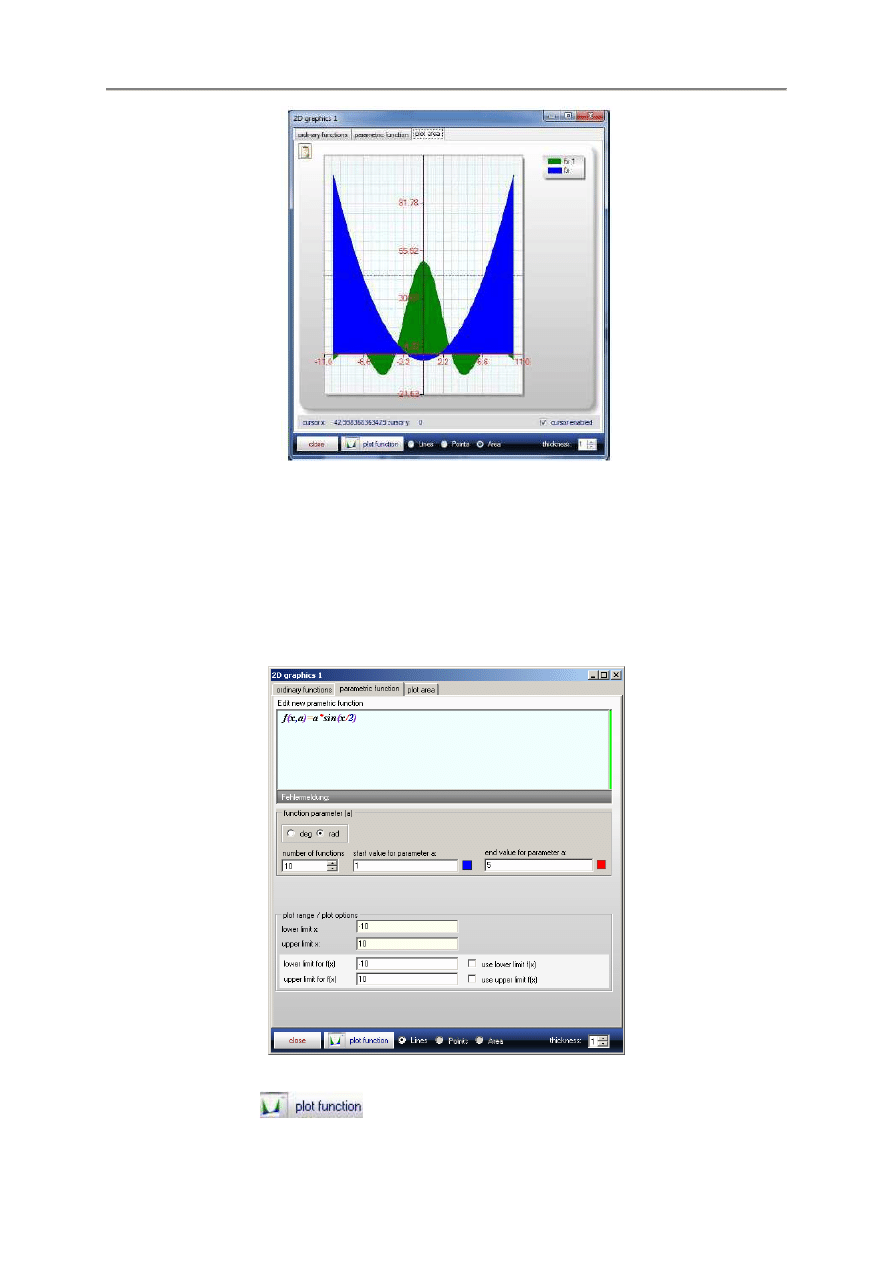
- 17 -
W celu wizualizacji funkcji parametrycznej, druga zakładka Parametric Function otwiera okienko
dialogowe pozwalaj
ą
ce na definiowanie poni
ż
szych wielko
ś
ci:
•
Liczby wy
ś
wietlanych funkcji
•
Warto
ś
ci pocz
ą
tkowej ka
ż
dego parametru
•
Warto
ś
ci ko
ń
cowej ka
ż
dego parametru
•
Kolorów
•
Przedziału
•
Warto
ś
ci granicznych
Po klikni
ę
ciu przycisku
uzyskujemy poni
ż
szy diagram:
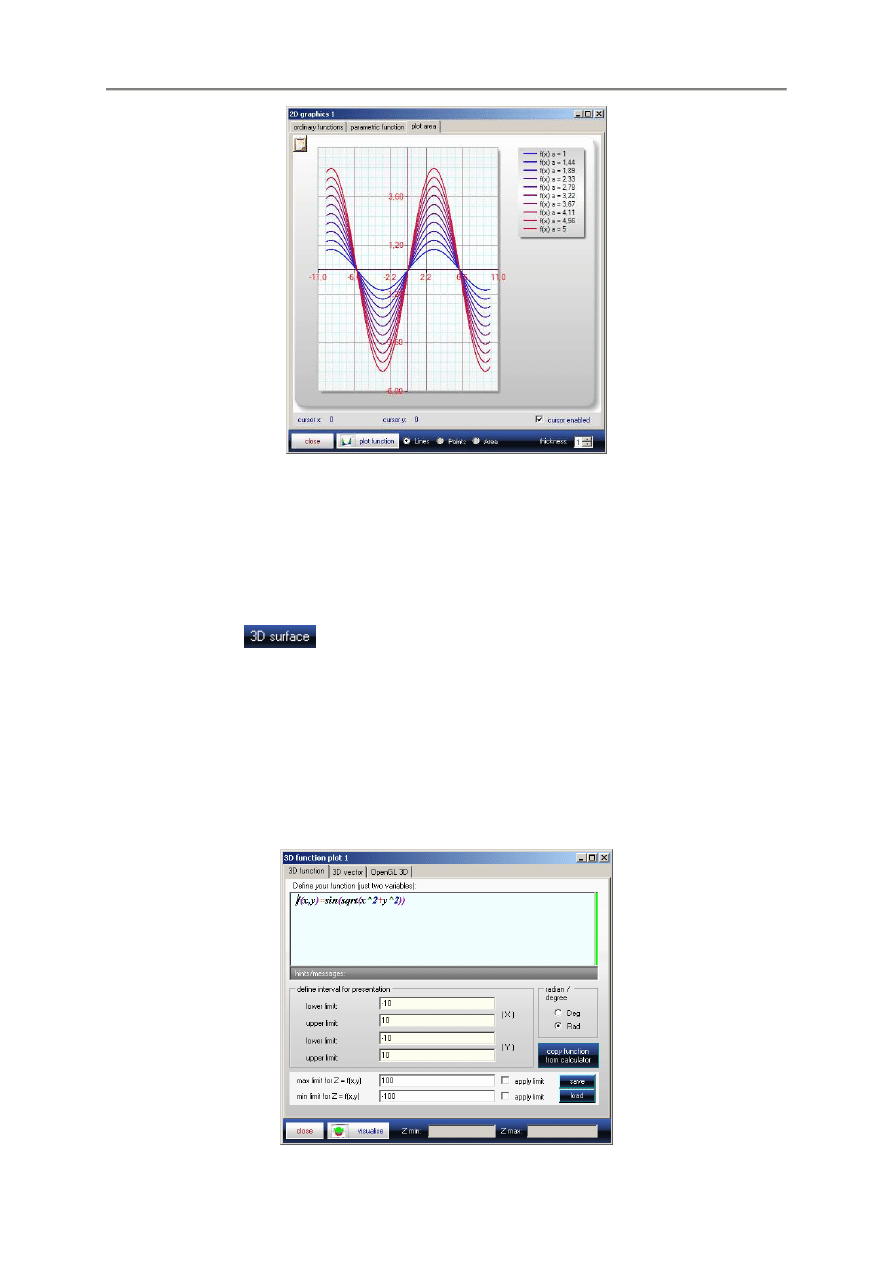
- 18 -
Na diagramie funkcji parametrycznej, program pozwala na wstawienie do 40 kroków parametrów na
jednym wykresie. Kursor graficzny umo
ż
liwia ogl
ą
danie współrz
ę
dnych okre
ś
lonych punktów. Program
fx-Calc pozwala na otwieranie wielu instancji wykresów parametrycznych w tym oknie w celu
porównywania ró
ż
nych scenariuszy.
9.4. Wykresy funkcji 3D
Klikni
ę
cie przycisku
w prawym górnym rogu kalkulatora otwiera okno 3D Function Plot
pozwalaj
ą
ce na tworzenie wykresów powierzchni trójwymiarowych Z = f(x,y). Sterownik Open GL
pozwala na manipulacj
ę
wykresów w czasie rzeczywistym przy korzystaniu z przyspieszanego
sprz
ę
towo interfejsu graficznego komputera.
Program fx-Calc oferuje dwie metody definiowania obiektów 3D:
•
Definiowanie obiektów w postaci funkcji Z = f(x,y)
•
Definiowanie x, y, z jako wektorów za pomoc
ą
współrz
ę
dnych biegunowych r oraz phi (
φ
).
Nie działa to w komputerach bez zainstalowanego sterownika Open GL.
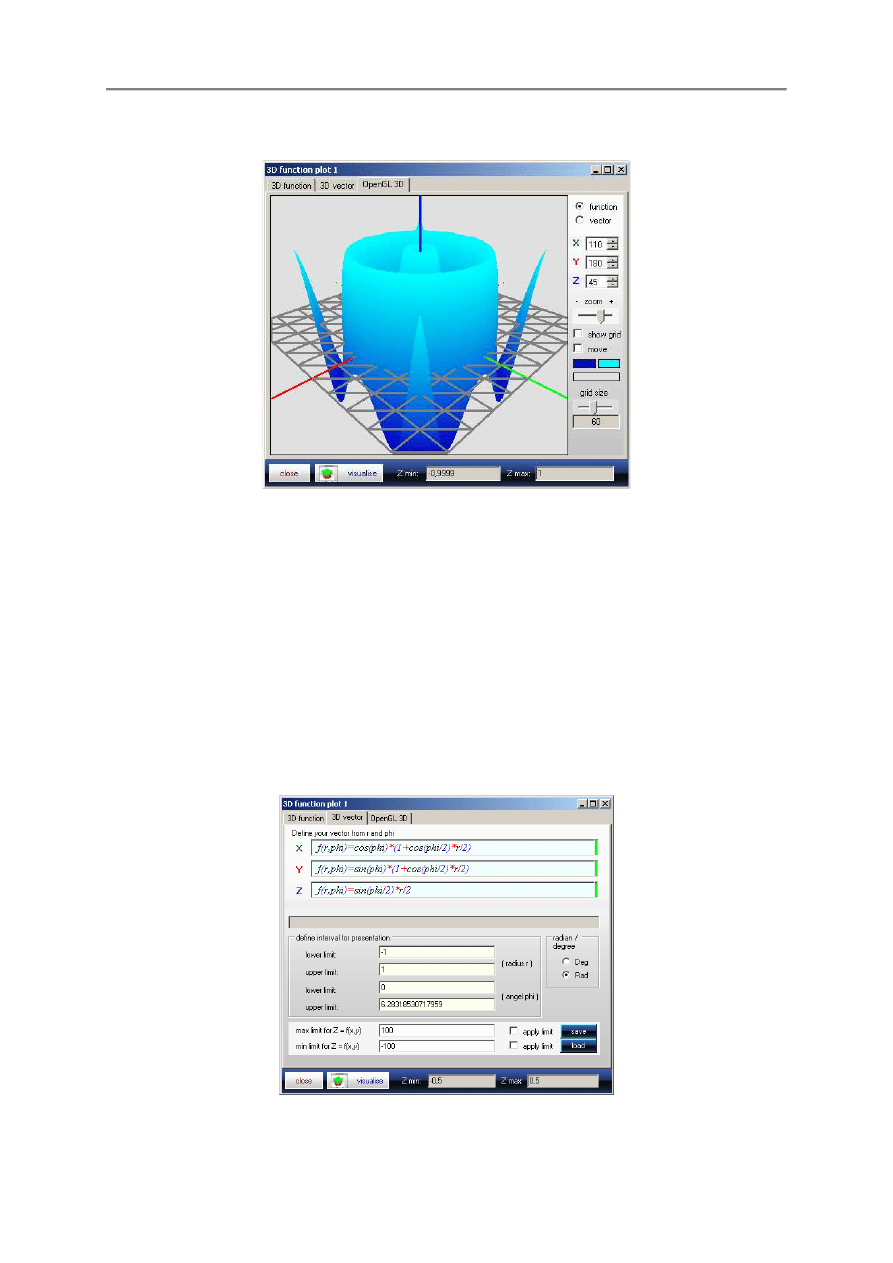
- 19 -
Podobnie do wykresów 2D,m wykresy 3D oferuj
ą
mo
ż
liwo
ść
ustawiania granic warto
ś
ci Z Klikni
ę
cie
zakładki OpenGL 3D pozwala na uzyskanie poni
ż
szego wykresu funkcyjnego.
W oknie tym mo
ż
na:
•
Obraca
ć
r
ę
cznie wykres 3D myszk
ą
przy wci
ś
ni
ę
tym jej lewym klawiszu
•
Wy
ś
wietla
ć
siatk
ę
zamiast powierzchni gładkiej
•
Przybli
ż
a
ć
(powi
ę
ksza
ć
) i oddala
ć
(pomniejsza
ć
)
•
Uruchamia
ć
automatyczne obracanie
W przypadku modelu biegunowego (zakładka 3D vector) otwiera si
ę
poni
ż
sze okno: deklarowania
ustawie
ń
:
Natomiast klikni
ę
cie zakładki OpenGL 3D wy
ś
wietla odpowiadaj
ą
cy wykres wektorowy:
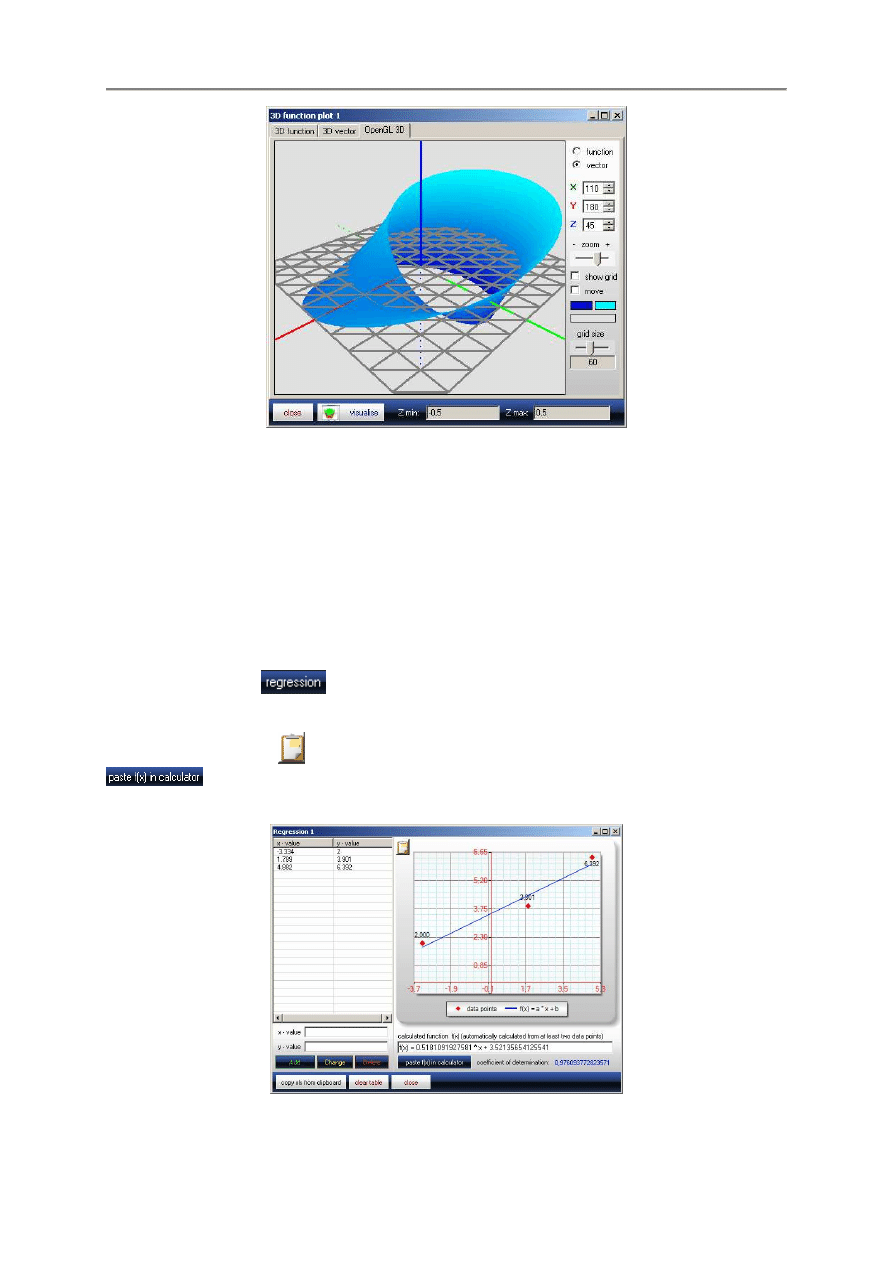
- 20 -
Program fx-Calc pozwala na otwieranie wielu instancji wykresów w tym oknie w celu porównywania
ró
ż
nych scenariuszy.
9.5. Regresja liniowa
W statystyce, prosta regresja liniowa jest estymacj
ą
metod
ą
najmniejszych kwadratów modelu regresji
liniowej o jednej zmiennej obja
ś
niaj
ą
cej. Inaczej mówi
ą
c, prosta regresja liniowa dopasowuje lini
ę
prost
ą
do zestawu punktów w taki sposób, aby suma kwadratów reszt modelu (tzn. pionowych
odległo
ś
ci mi
ę
dzy punktami zestawu danych a dopasowan
ą
lini
ą
) była mo
ż
liwie jak najmniejsza.
Po klikni
ę
ciu przycisku
w prawym górnym rogu kalkulatora, otwiera si
ę
okno analizy regresji
Regression zawieraj
ą
ce dwie pary warto
ś
ci danych x i y. Program oblicza funkcj
ę
liniow
ą
oraz tworzy
odpowiedni wykres.
Korzystaj
ą
c z przycisku
mo
ż
na kopiowa
ć
uzyskany wykres do schowka, a klikaj
ą
c przycisk
mo
ż
na wklei
ć
aktualn
ą
funkcj
ę
wynikow
ą
do pola edycji kalkulatora w celu jej
wykorzystania w dalszych obliczeniach.
Program fx-Calc pozwala na otwieranie wielu instancji wykresów w tym oknie w celu porównywania
ró
ż
nych scenariuszy.
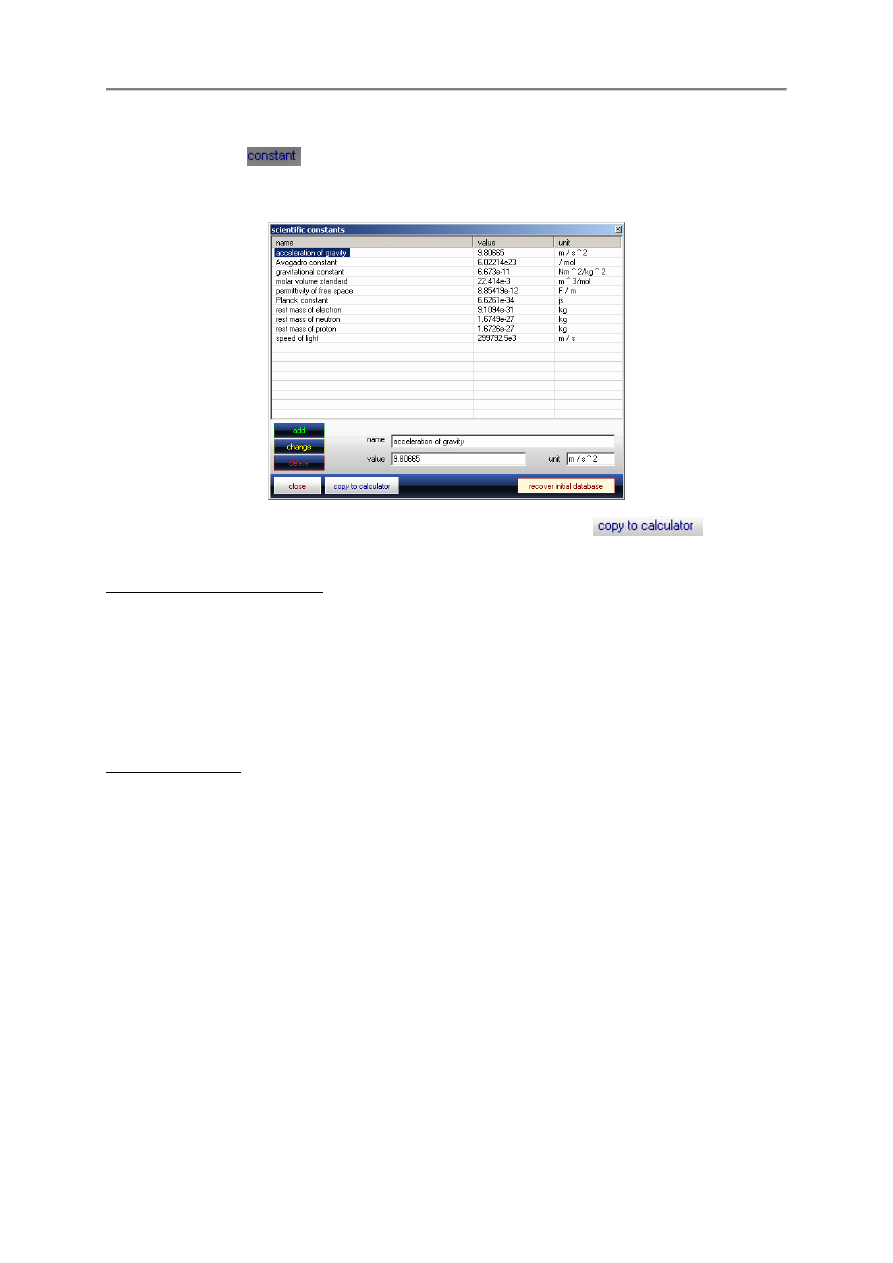
- 21 -
10. Baza danych warto
ś
ci stałych
Klikni
ę
cie przycisku
z lewej strony klawiatury kalkulatora otwiera okno Scentific Constants
zawieraj
ą
ce mał
ą
baz
ę
stałych naukowych. Podwójne klikni
ę
cie dowolnej stałej kopiuje j
ą
do pola
edycji kalkulatora i okno bazy danych zostaje zamkni
ę
te.
W celu skopiowania stałej do kalkulatora mo
ż
na równie
ż
klikn
ąć
przycisk
.
Obliczenia i metody numeryczne
W celu wykonywania oblicze
ń
, program fx-Calc musi interpretowa
ć
wszystkie wej
ś
cia. Realizuje si
ę
to
za pomoc
ą
specjalnie ładowanego programu, który przekształca wej
ś
cia na szybszy kod wykonawczy.
Kod ten jest nast
ę
pnie wykorzystywany w obliczeniach i w indywidualnych iteracjach.
Program fx-Calc korzysta tylko z metod numerycznych do rozwi
ą
zywania równa
ń
, całek oznaczonych
oraz do wyznaczania warto
ś
ci ekstremalnych. Metody te s
ą
dobrze znane i dostosowane specjalnie
dla fx-Calc. Zarówno interpreter jak i metody obliczeniowe s
ą
składnikami tego programu.
Metody numeryczne
Do obliczania pierwiastków, rozwi
ą
za
ń
, całek oznaczonych i ekstremów, istniej
ą
na ogół dwa sposoby.
Pierwszy z nich analizuje wyra
ż
enie matematyczne (symboliczne), rozwi
ą
zuje je oblicza. Tworzy to
najbardziej dokładne wyniki i zawiera reguły stosowane do wszystkich funkcji. Wad
ą
tej metody jest
rosn
ą
ca zło
ż
ono
ść
przy zagnie
ż
d
ż
aniu funkcji i w wyra
ż
eniach trudniejszych do analizy. Dotyczy to
zwłaszcza całek oznaczonych, ale pierwiastki równa
ń
s
ą
obliczane szybko. Program fx-Calc korzysta
najcz
ęś
ciej z tej metody do rozwi
ą
zywania wi
ę
kszo
ś
ci zada
ń
. W pozostałych przypadkach program
korzysta z metod numerycznych. Jednak i te metody maj
ą
swoje zalety i wady.
Te ostatnie s
ą
ni
ż
ej wymienione:
•
Konieczno
ść
zdefiniowania analizowanego przedziału (nic poza nim nie b
ę
dzie wynikiem)
•
Okre
ś
lona niedokładno
ść
(kryterium przerwania oblicze
ń
w przypadku iteracji)
•
Pierwiastki wy
ż
szych rz
ę
dów nie s
ą
definiowane jako takie.
Zalet
ą
metod numerycznych jest ich uniwersalno
ść
. Tak wi
ę
c s
ą
one bardzo przydatne do
weryfikowania wyników na podstawie wykresów, które pozwalaj
ą
natychmiast na porównywanie
wszystkich wyników.
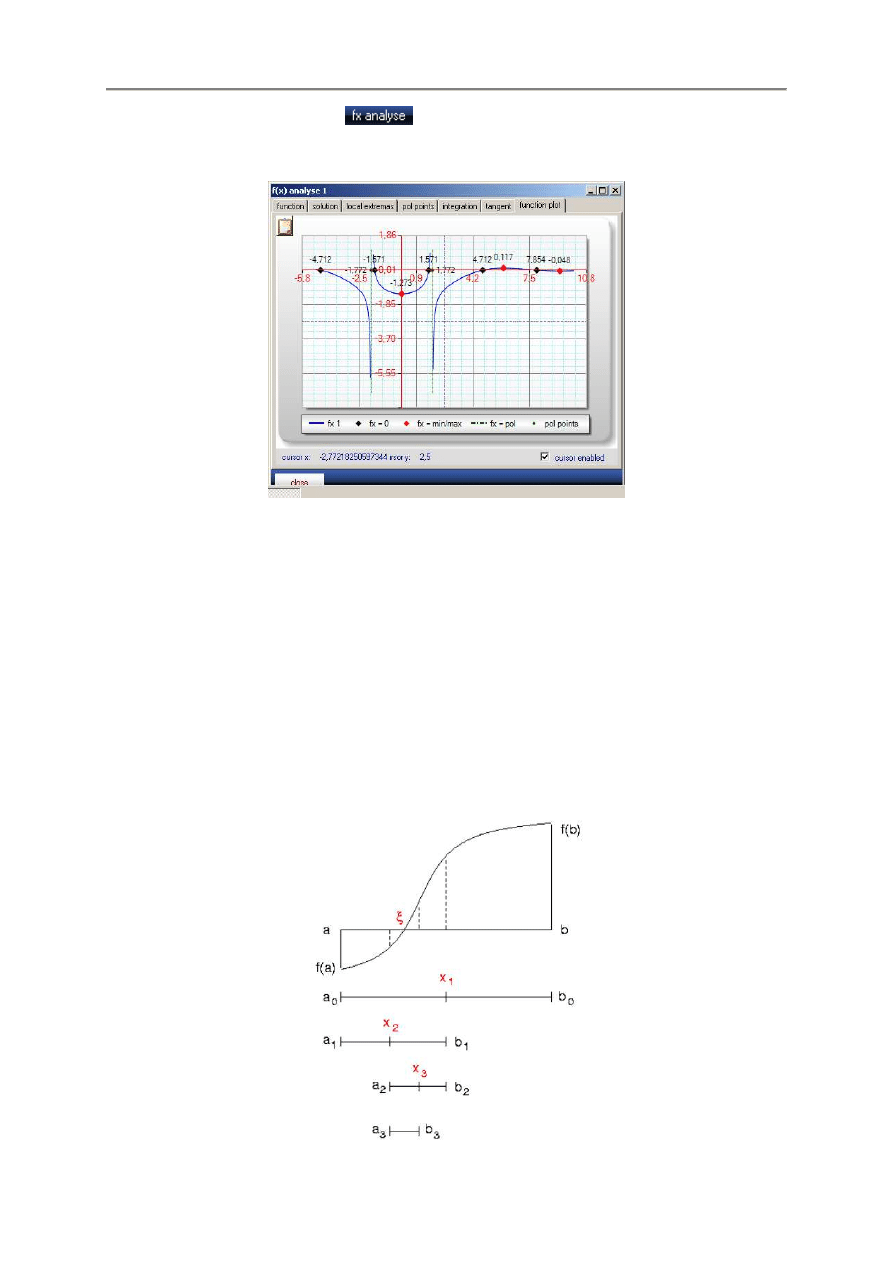
- 22 -
Przykładowo, klikni
ę
cie przycisku
w prawym górnym rogu głównego okna kalkulatora
otwiera okno analizy funkcji f(x) Analyse (patrz rozdział 9.1).
Klikni
ę
cie w nim zakładki Function Plot otwiera okno aktualnego wykresu z wynikami analizy funkcji.
W odró
ż
nieniu od weryfikacji wyników, wykres ten ilustruje zachowanie si
ę
funkcji.
10.1. Obliczanie pierwiastków
Obliczanie pierwiastków równa
ń
(w postaci f(x) = 0) jest bardziej zło
ż
one ni
ż
mo
ż
na s
ą
dzi
ć
na
pierwszy rzut oka. Niezale
ż
nie od zmiany znaku, istniej
ą
tutaj specjalne sytuacje:
•
Wierzchołki funkcji, które nie wykazuj
ą
zmiany znaku
•
Funkcje o małym zakresie analizowanego przedziału
Przy poszukiwania pierwiastków, funkcja jest analizowana w celu wyznaczenia zakresu warto
ś
ci oraz
opcjonalnie jest odpowiednio przekształcana. Program korzysta przy tym z metody zagnie
ż
d
ż
ania
przedziałów (metoda bisekcji), która sprawdza zmiany znak funkcji w przedziale.
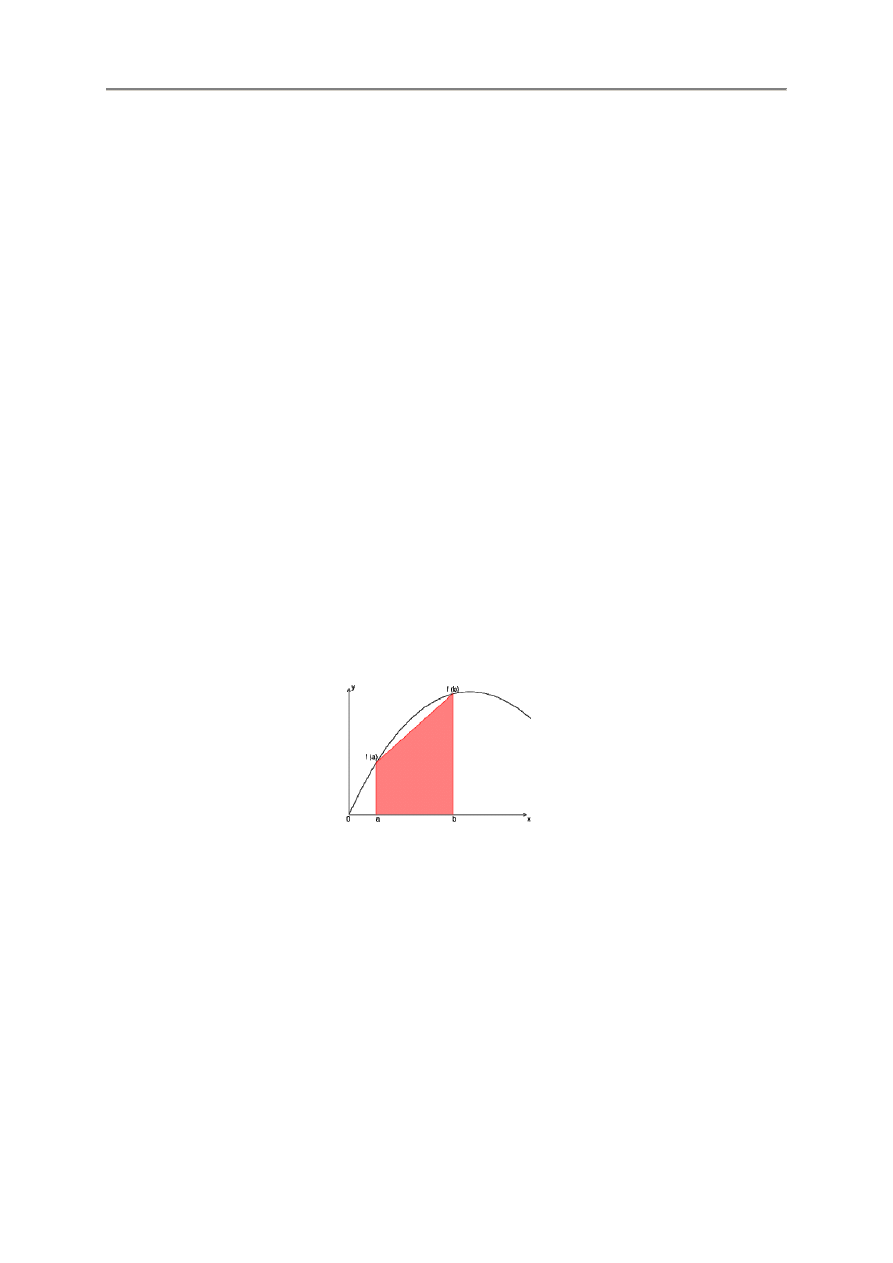
- 23 -
Nast
ę
pnie wyznaczane s
ą
wierzchołki funkcji – równie
ż
numerycznie. Jest to numeryczne szukanie
ró
ż
nic. Odnajdywane s
ą
przy tym pierwiastki. Metoda Newtona jest tutaj nieprzydatna, poniewa
ż
nie
zawsze uzyskuje si
ę
zbie
ż
no
ść
je
ś
li funkcje nie s
ą
ci
ą
gle ró
ż
niczkowalne.
10.2. Pierwiastki dla argumentów innych ni
ż
0
Obliczanie pierwiastków ma równie
ż
miejsce przy szukaniu rozwi
ą
za
ń
równania fx(x), nawet je
ś
li
funkcja jest zdefiniowana jako:
0 = f(x) - stała
Jest ona analizowana pry korzystaniu z tej samej metody jak przy poszukiwaniu pierwiiastków
10.3. Warto
ś
ci ekstremalne
Obliczanie ekstremów pozwala na szybkie sprawdzenie rozmieszczenia pierwiastków oraz na
stosowanie transformacji. Jednak tworzenie drugiej pochodnej ró
ż
nic mo
ż
e by
ć
niestabilne i dlatego
pomija si
ę
je przy obliczaniu pików drugiej pochodnej. To równie
ż
tłumaczy dlaczego fx-Calc nie
oblicza punktów po
ś
rednich. W ka
ż
dym przypadku zmiana znaku pierwszej pochodnej odpowiada
realnym ekstremom.
10.4. Całki oznaczone
Całki oznaczone s
ą
cz
ęś
ciej przedmiotem metod numerycznych ni
ż
warto
ś
ci pierwiastków oraz
ekstremów, chocia
ż
rzadko wyst
ę
puj
ą
w analizie funkcji f(x). W tym konkretnym przypadku, fx-Calc
korzysta z metody trapezów, która dzieli badany obszar na 1000 podprzedziałów z du
żą
precyzj
ą
.
Przed ka
ż
dym obliczaniem całki, fx-Calc analizuje funkcj
ę
wyznaczaj
ą
c jej pierwiastki oraz ekstrema.
Program korzysta z tych wyników do definiowania cz
ą
stkowych zakresów całkowania w celu
uzyskania mo
ż
liwie jak najwi
ę
kszej dokładno
ś
ci.
10.5. Punkty nieokre
ś
lone
W celu obliczania nieokre
ś
lono
ś
ci funkcji gdy mianownik funkcji ułamkowej staje si
ę
zerem, program
łamie funkcj
ę
w mianowniku i w odpowiednich punktach. W takich przypadkach s
ą
to punkty
nieokre
ś
lone.
Istniej
ą
pewne ograniczenia dokładno
ś
ci przy obliczaniu tych punktów.
Program fx-Calc rozwi
ą
zuje ten problem numerycznie gdy warto
ść
bezwzgl
ę
dna mianownika jest
mniejsza od 1e-5. Inny przypadek nieokre
ś
lono
ś
ci ma miejsce przy trygonometrycznej funkcji tangens.
Program fx-Calc wyznacza ten punkt dla argumentu równego
ππππ
/2.
- 24 -
10.6. Punkty brakuj
ą
ce, pierwiastki i ekstrema
Wszystkie wcze
ś
niej opisane metody były testowane i dopasowane do najwi
ę
kszej przydatno
ś
ci.
Tym niemniej mog
ą
wyst
ą
pi
ć
pewne braki oczekiwanych wyników i dlatego warto je porównywa
ć
oraz
sprawdza
ć
korzystaj
ą
c z wykresów. Wy
ś
wietlaj
ą
one wyniki uzyskiwane metodami numerycznymi dla
najlepiej ustawionych parametrów.
•
Pierwszym sposobem jest zwi
ę
kszenie liczby podprzedziałów i wykonanie dokładnego
skanowania funkcji
•
Mo
ż
liwo
ś
ci te obejmuj
ą
:
Ustawienie pełnego przedziału funkcji
Zmiana dokładno
ś
ci parametrów.
Oczywi
ś
cie, kombinacja wszystkich mo
ż
liwo
ś
ci zwi
ę
ksza szanse powodzenia zgodnie z wybran
ą
precyzj
ą
. Dokładno
ść
odchyle
ń
mniejsza od 1e-15 jest praktycznie bezu
ż
yteczna nawet dla danych
podwójnej dokładno
ś
ci.
Krytyczne przypadki s
ą
funkcjami o bardzo małych lub bardzo du
ż
ych zakresach:
•
|F(x)| < 1e-50
•
|F(x)| < 1e+100
Program optymalizuje te przypadki przez odpowiedni
ą
transformacj
ę
warto
ś
ci funkcji Jednak nie
zawsze jest to skuteczne. Dokładne sprawdzanie wykresów pozwala na wykrywanie niezgodno
ś
ci.
11. Od Autora
Przede wszystkim pochodz
ę
z Niemiec i mam nadziej
ę
,
ż
e mój przekład jest wystarczaj
ą
cy. Je
ś
li nie,
prosz
ę
o kontakt ze mn
ą
.
Program fx-Calc mo
ż
e by
ć
bardzo silnym narz
ę
dziem w wi
ę
kszym stopniu do badania funkcji ni
ż
do
algebry. Wi
ę
kszo
ść
oblicze
ń
statystycznych i algebraicznych jest zwykle cz
ęś
ci
ą
typowych arkuszy
kalkulacyjnych, np. takich jak Excel lub Open Office i dlatego nie implementowano szerzej tych
zagadnie
ń
.
Moim drugim celem było utworzenie aplikacji mo
ż
liwie jak najłatwiejszej w stosowaniu. Mam nadziej
ę
,
ż
e zostało to osi
ą
gni
ę
te.
Bardzo prosz
ę
o nadsyłanie swoich uwag i propozycji, zwłaszcza w zakresie poprawy tej aplikacji
Ż
ycz
ę
powodzenia przy korzystaniu z fx-Calc,
Hans Jörg ;-)
Author: Hans Jörg Schmidt, Fasanenweg 10, 99869 Drei Gleichen, Germany
Google+
E-mail:
info@fx-calc.de