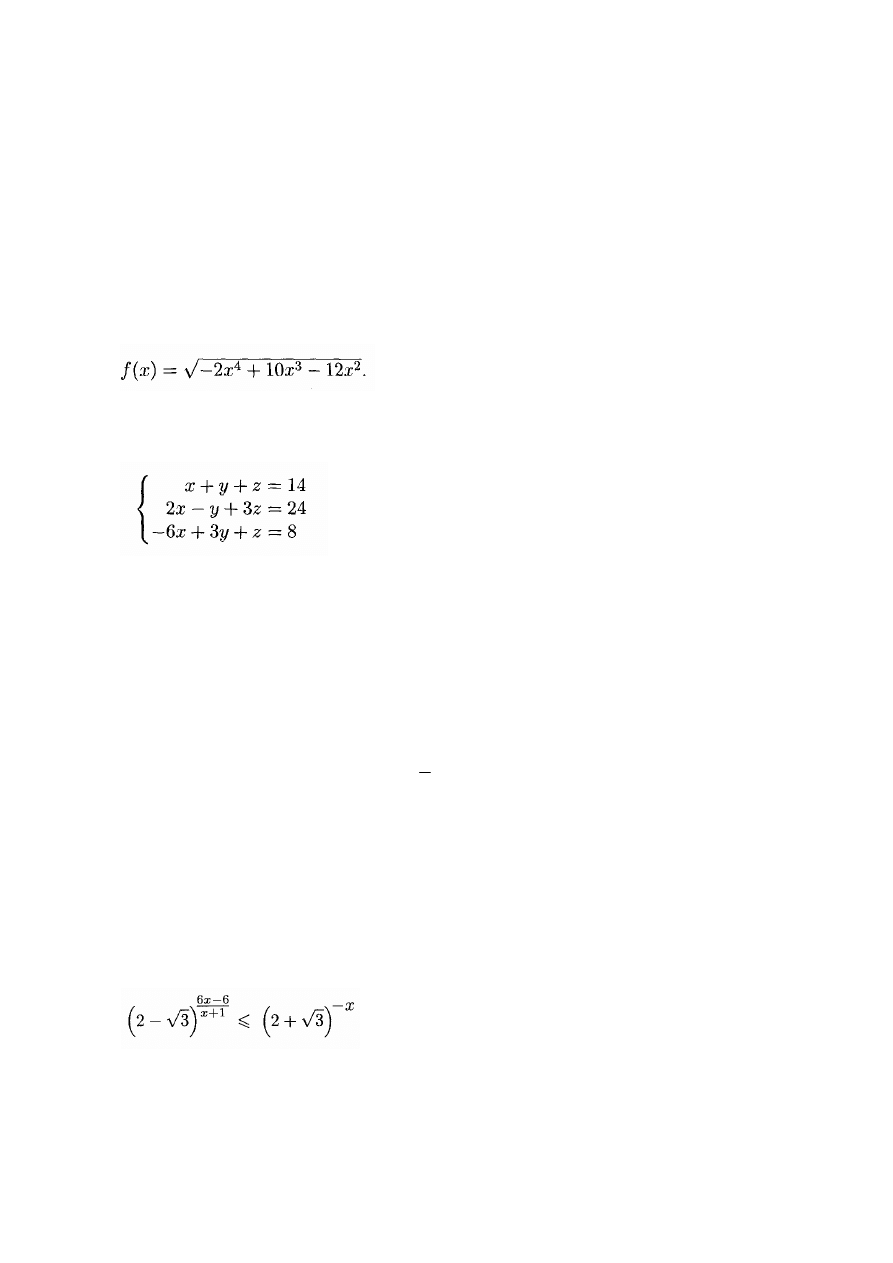
©Irek.edu.pl
1
Zestaw 1. Poziom rozszerzony
Zadanie 11 (7 pkt).
Znajdź równanie okręgu będącego obrazem okręgu
x
2
+ y
2
- 4x + 2y + 1 = O
w jednokładności o środku w punkcie A = (-2,3) i skali k= -4.
Zadanie 12 (5 pkt).
Wyznacz dziedzinę funkcji
Zadanie 13 (7 pkt).
Dany jest układ równań
a)
Rozwiąż go i sprawdź, czy ciąg (x, y, z) utworzony z rozwiązań tego
układu jest ciągiem geometrycznym.
b) Rozważmy nieskończony ciąg arytmetyczny, którego trzy pierwsze wyrazy
wynoszą odpowiednio x —3, y +2, z +5, gdzie x, y, z są rozwiązaniami
powyższego układu równań. Oblicz sumę 2005 początkowych wyrazów
tego ciągu.
Zadanie 14 (7 pkt).
Napisz równania tych stycznych do wykresu funkcji f(x) =x
3
- 8x,
które są prostopadle do prostej y =
2
1
x + 3.
Zadanie 15 (6 pkt).
Wykaż, że dla każdej liczby naturalnej n liczba
L
n
= ll
n+2
+ 12
2n+1
jest podzielna przez 133.
Zadanie 16 (8 pkt).
Rozwiąż nierówność
Zadanie 17 (10 pkt).
Przez punkt A = (2,5) poprowadź taką prostą k o współczynniku kierunkowym
ujemnym, aby pole trójkąta ograniczonego osiami układu współrzędnych i
prostą k było najmniejsze. Podaj wzór tej prostej i oblicz pole tego trójkąta.

©Irek.edu.pl
2
Zestaw 2. Poziom rozszerzony
Zadanie 10 (4 pkt).
Dany jest wielomian W(x) = x
4
+ x
3
- ax + b. Wiedząc, że x
o
= 1 jest
podwójnym pierwiastkiem tego wielomianu, znajdź resztę z dzielenia
wielomianu W przez dwumian x + 1.
Zadanie 11 (7 pkt).
Dla jakich wartości parametrów a i b funkcja
jest ciągła w zbiorze liczb rzeczywistych?
Zadanie 12 (8 pkt).
Wyznacz zbiór wartości parametru a, dla których funkcja
f(x)=
3
1
ax
3
- 2x
2
+ (a - 3)x + 1
jest malejąca w zbiorze liczb rzeczywistych.
Zadanie 13 (4 pkt).
Mamy dwie urny U
1
i U
2
. W urnie U
1
są 3 kule białe i 2 czarne, w urnie U
2
są
4 kule białe i 4 kule czarne. Losujemy jedną kulę z urny U
1
i, nie oglądając jej,
wrzucamy do urny U
2
. Następnie z urny U
2
losujemy 2 kule. Oblicz
prawdopodobieństwo, że obie kule wyjęte z urny U
2
będą czarne.
Zadanie 14 (9 pkt).
Dla jakich wartości parametru m równanie
(m+1)
.
9
x
- 2
.
3
x
+m - 1=O
ma dwa rozwiązania?
Zadanie 15 (4 pkt).
Rozważmy funkcje f(x) = 3
x
oraz g(x) = log
3
x. Wyznacz wzór funkcji f (g(x)),
określ jej dziedzinę i wykonaj wykres.
Zadanie 16 (5 pkt).
Oblicz współrzędne obrazu punktu A(3, 1) w symetrii względem prostej
y = 2x.
Zadanie 17 (9 pkt).
Określ liczbę rozwiązań układu
w zależności od parametru a.

©Irek.edu.pl
3
Zestaw 3. Poziom rozszerzony
Zadanie 12 (9 pkt).
Dana jest funkcja f określona wzorem f(x)= x
2
+ (p+2)x + 1. Wyznacz
wszystkie wartości parametru p, dla których pierwiastki x
1
, x
2
równania f(x) =
O spełniają warunek x
1
2
+ x
2
2
< 3x
1
x
2
.
Zadanie 13 (6 pkt).
Rozwiąż równanie
Zadanie 14 (8 pkt).
Dane są dwa okręgi: (x-1)
2
+(y - 1)
2
= 9 i (x - m)
2
+(y- 1)
2
= 4. Wyznacz
wszystkie wartości parametru m dla których te okręgi mają dokładnie jeden
punkt wspólny.
Zadanie 15 (5 pkt).
Wyznacz zbiór wartości funkcji
ℜ
∈
+
−
=
x
dla
x
x
x
f
1
sin
2
cos
3
)
(
2
Zadanie 16 (4 pkt).
Korzystając z definicji pochodnej, oblicz pochodną funkcji
f(x) =
3
2
+
x
w punkcie x
0
=1.
Zadanie 17 (7 pkt).
Z talii 52 kart losujemy 4 karty. Jakie jest prawdopodobieństwo, że wśród
wylosowanych kart będą 2 asy lub 2 króle? Podaj wynik z dokładnością
do 0,01.
Zadanie 18 (6 pkt).
Dane są proste: 1 o równaniu 3x — 4y + 2 = O i k o równaniu 4x + 3y - 7 = O.
Wyznacz równania dwusiecznych kątów utworzonych przez te proste.
Zadanie 19 (5 pkt).
Wykaż, że funkcja f(x) jest parzysta
f(x) =
x
x
x
+
−
2
2
log
3
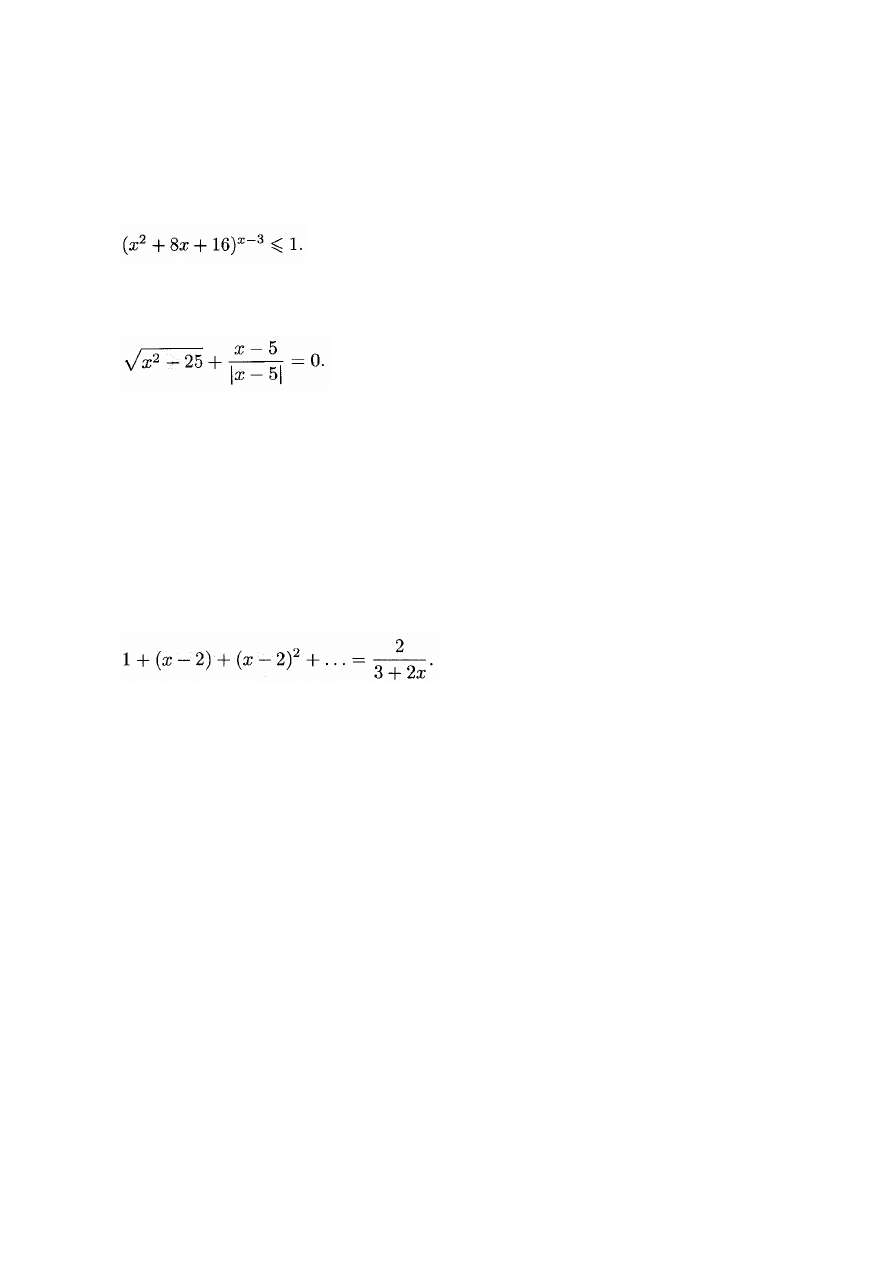
©Irek.edu.pl
4
Zestaw 4. Poziom rozszerzony
Zadanie 11 ( 13 pkt)
Rozwiąż nierówność
Zadanie 12 (7 pkt).
Rozwiąż równanie
Zadanie 13 (10 pkt).
Marcin ma w szafie 10 garniturów, w tym 3 brązowe, oraz 6 par butów, w tym
2 pary brązowych. Codziennie do pracy wkłada garnitur. Jakie jest
prawdopodobieństwo, że Marcin pójdzie do pracy przynajmniej 3 razy w
tygodniu w brązowym garniturze i brązowych butach? Przyjmij, że tydzień ma
pięć dni roboczych. Garnitur i buty Marcin wybiera losowo.
Zadanie 14 (7 pkt).
Rozwiąż równanie
Zadanie 15 (7 pkt).
Wyznacz i narysuj zbiór punktów płaszczyzny spełniających warunek
x
2
+ y
2
= 2|x| + 2y.
Zadanie 16 (6 pkt).
Długości podstaw trapezu równoramiennego wynoszą 4 i 6, a jego wysokość
jest równa 2. Oblicz objętość bryły powstałej w wyniku obrotu tego trapezu
wokół krótszej podstawy. Wykonaj odpowiedni rysunek.
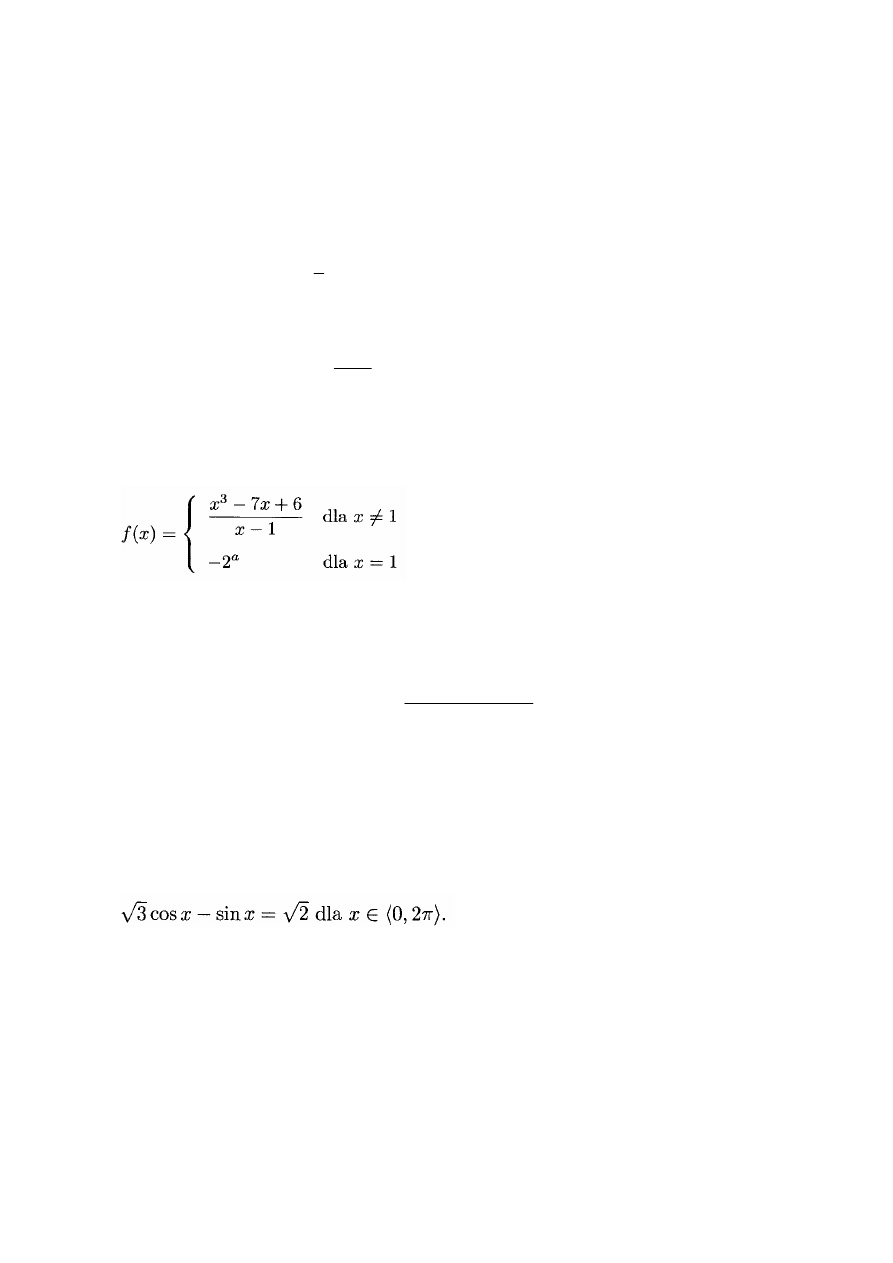
©Irek.edu.pl
5
Zestaw 5. Poziom rozszerzony
Zadanie 10 (8 pkt).
Dana jest funkcja f(x)= 3mx
2
- (m+1)x- 1. Rozwiąż metodą graficzną
nierówność f( |x|)
≥ 0, wiedząc, że osią symetrii paraboli będącej wykresem
funkcji f jest prosta x=
3
1
.
Zadanie 11 (6 pkt).
Wykaż, że funkcja f(x) =
2
3
−
+
x
x
jest różnowartościowa.
Zadanie 12 (4 pkt).
Dobierz taką wartość parametru a, aby funkcja f określona
wzorem
była ciągła w punkcie x
o
= 1.
Zadanie 13 (10 pkt).
Rozwiąż równanie
(
) (
)
n
n
n
x
x
x
n
3
9
6
3
1
2
3
lim
log
log
log
2
3
9
2
9
9
+
+
+
+
+
+
=
+
+
+
∞
→
K
K
Zadanie 14 (9 pkt).
Suma wysokości i promienia podstawy stożka wynosi 6. Wyznacz wysokość i
promień podstawy stożka, dla których objętość tej bryły jest największa.
Zadanie 15 (5 pkt).
Rozwiąż równanie
Zadanie 16 (8 pkt).
Miara kąta zawartego między najkrótszym a najdłuższym bokiem pewnego
trójkąta wynosi 60
0
. Oblicz długości boków tego trójkąta i długość promienia
okręgu na nim opisanego, wiedząc, że najdłuższy bok jest o 3cm dłuższy od
najkrótszego, a trzeci bok jest o 40% dłuższy od najkrótszego.

©Irek.edu.pl
6
Zestaw 6. Poziom rozszerzony
Zadanie 11 (6 pkt).
Rozwiąż równanie
(
)
12
2
5
6
log
12
1
log
+
=
x
x
Zadanie 12 (11 pkt).
Zbadaj przebieg zmienności i wykonaj wykres funkcji
K
+
−
+
−
=
7
5
3
)
(
x
x
x
x
x
f
Zadanie 13 (17 pkt).
Ze zbioru Z = {x
∈ C : 3
2x+1
- 244
.
3
x + 81
<0} losujemy ze zwracaniem trzy
liczby a, b, c i tworzymy funkcję y = ax
2
+ bx + c. Oblicz
prawdopodobieństwo zdarzeń:
a) A — „otrzymana funkcja jest rosnąca w
ℜ”
b) B „otrzymana funkcja jest parzysta”.
Zadanie 14 (8 pkt).
Znajdź wszystkie rozwiązania równania sin2x= |sinx| - sinx
należące do przedziału
π
π
4
,
2
.
Zadanie 15 (4 pkt).
Sprawdź, czy przekształcenie P(x, y) = (-x, y), gdzie x, y
∈ R, jest izometrią.
Zadanie 16 (4 pkt).
Pani Zosia zachorowała w Chinach na bardzo groźną chorobę zakaźną zwaną
SARS. Ponieważ nie poddała się kwarantannie i leczeniu, w pierwszej
godzinie po przyjeździe do kraju zaraziła dwie osoby. Każda z nowo
zakażonych osób zaraża w ciągu następnej godziny kolejne dwie osoby.
Oblicz, po ilu godzinach na SARS zachoruje całe 1,5-milionowe miasto.
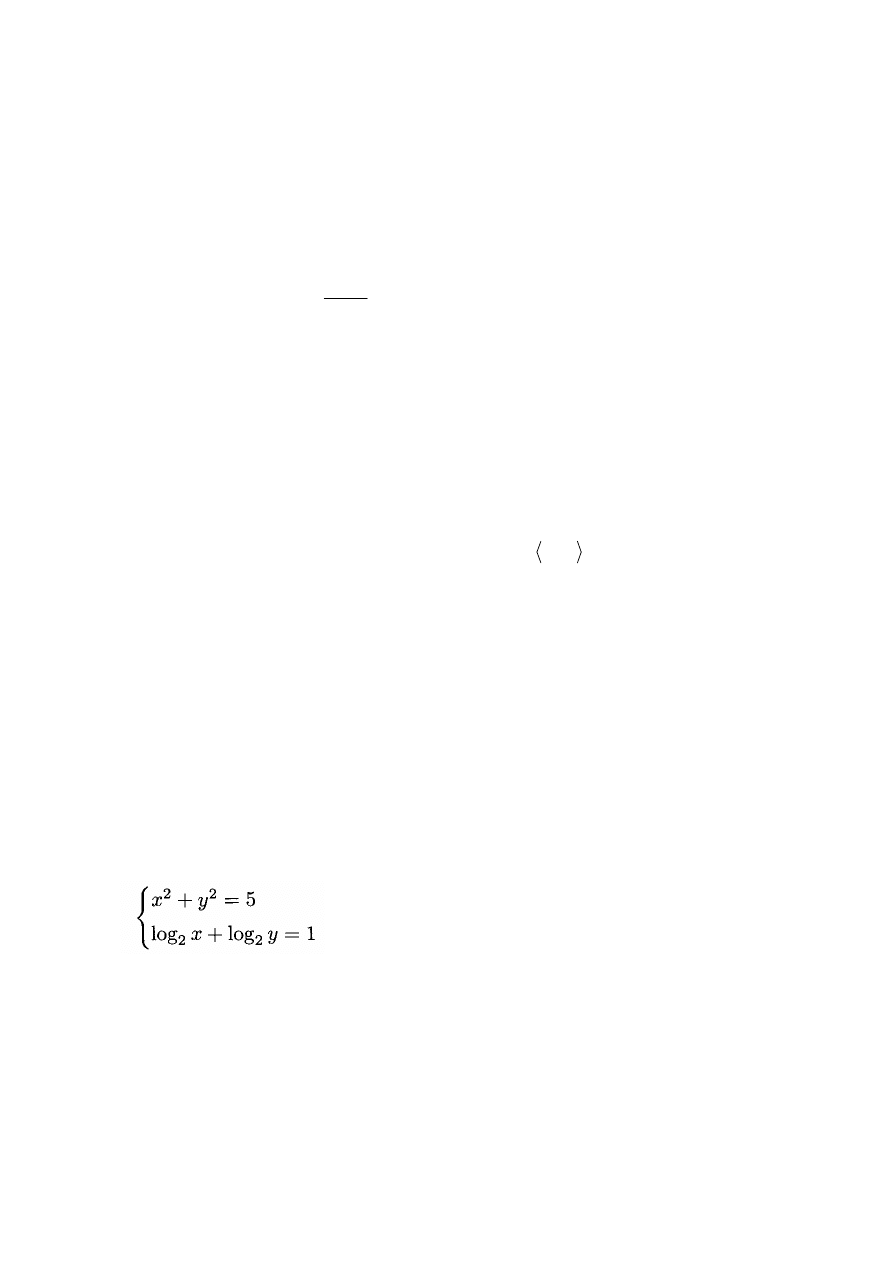
©Irek.edu.pl
7
Zestaw 7. Poziom rozszerzony
Zadanie 12 (5 pkt).
Rozwiąż równanie 3
4x-1
+ 2
.
9
x
- 9 =0.
Zadanie 13 (8 pkt).
Dana jest funkcja f(x) =
1
2
2
−
x
x
a) Wyznacz wzór funkcji g(x) = f(f(x)).
b) Określ dziedzinę funkcji g.
c) Wyznacz zbiór argumentów, dla których funkcja g przyjmuje wartości
ujemne.
d) Oblicz
)
(
lim
3
x
f
x
→
.
e) Oblicz
)
(
lim
x
f
x
∞
→
.
Zadanie 14 (7 pkt).
Rozwiąż równanie: cos3x - cosx = sin2x dla x
∈
π
2
,
0
Zadanie 15 (6 pkt).
Wykaż, że równanie x
3
+ 2x + 7 = 0 ma dokładnie jeden pierwiastek
rzeczywisty.
Zadanie 16 (6 pkt).
Wyznacz wszystkie wartości parametru m, dla których równanie
|x
2
- 2x – 3| = m ma:
a) trzy rozwiązania dodatnie i jedno ujemne,
b) dwa rozwiązania dodatnie i dwa ujemne.
Zadanie 17 (13 pkt).
Rozwiąż układ równań:
Zadanie 18 (5 pkt).
Sklep zaopatruje się w owoce cytrusowe pomarańcze i cytryny tylko w dwóch
hurtowniach: H
1
i H2, przy czym właściciel sklepu 40% towaru zamawia w
hurtowni H
1
, pozostałe 60% bierze z hurtowni H
2
. W tym tygodniu właściciel
kupił 12 kg cytryn i 48 kg pomarańczy w hurtowni H
1
oraz 40kg cytryn i 50kg
pomarańczy w hurtowni H
2
. Pani Małgorzata kupiła 1 kg cytryn. Jakie jest
prawdopodobieństwo, że zakupione cytryny pochodziły z hurtowni H1?
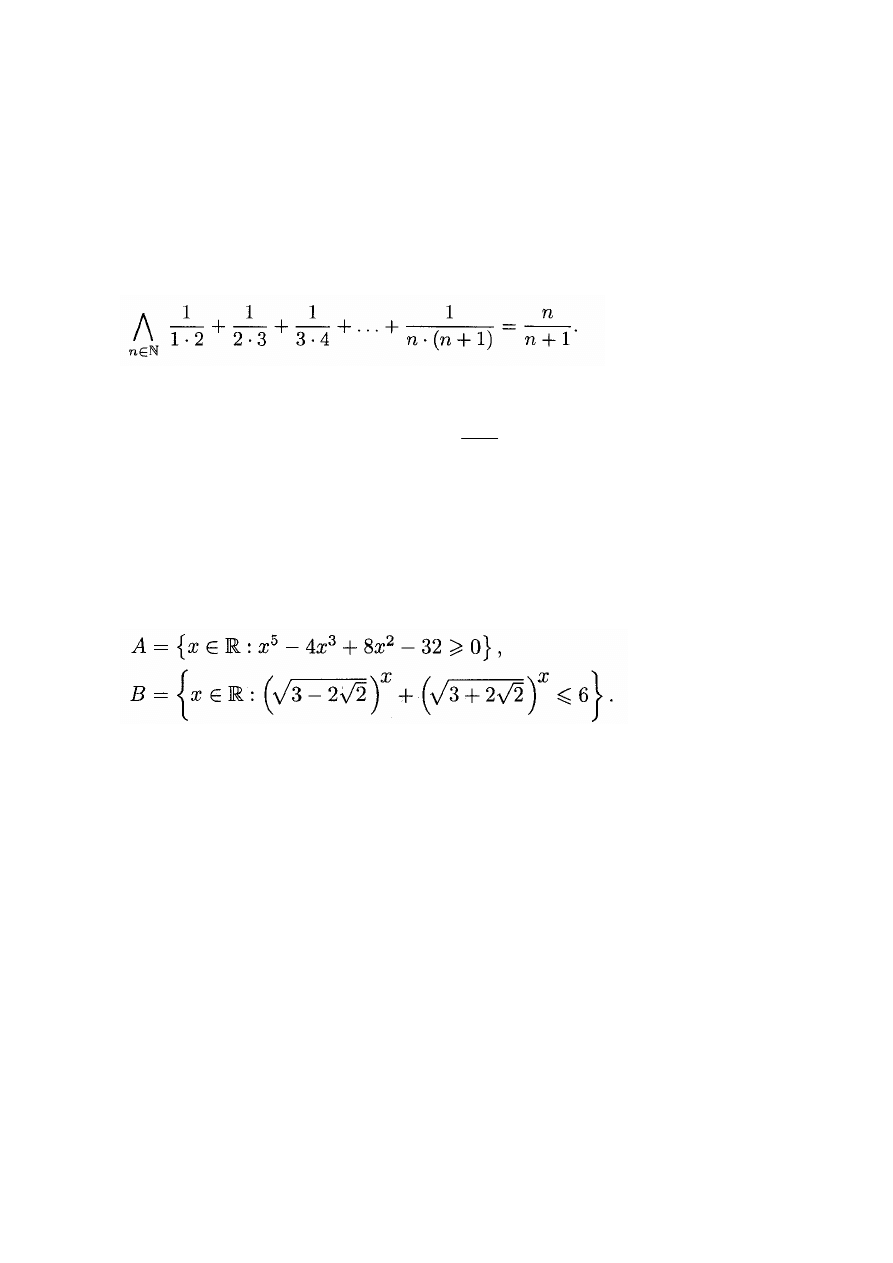
©Irek.edu.pl
8
Zestaw 8. Poziom rozszerzony
Zadanie 11 (6 pkt).
Rozwiąż równanie (|x – 1| - 3)
sin4x + cos4x – 1
=1
Zadanie 12 (7 pkt).
Udowodnij, korzystając z zasady indukcji matematycznej, że
Zadanie 13 (9 pkt).
a) Zbadaj liczbę rozwiązań równania x+
5
4
−
x
= b+5 w zależności od
parametru b.
b) Wykonaj wykres funkcji y = f(b) określającej zależność liczby rozwiązań
powyższego równania od parametru b.
c) Podaj wzór funkcji y = f(b).
Zadanie 14 (12 pkt).
Niech
Wyznacz zbiory A i B oraz A
∩ B.
Zadanie 15 (8 pkt).
Na podstawie definicji wykaż, że funkcja f(x)= x
2
- 4x jest rosnąca dla
każdego x
∈ (2, ∞).
Zadanie 16 (8 pkt).
Mleko o objętości V
0
należy wlać do naczynia w kształcie walca i przykryć
pokrywą kołową. Wyznacz taki promień podstawy, aby na wykonanie
naczynia zużyć jak najmniej materiału.
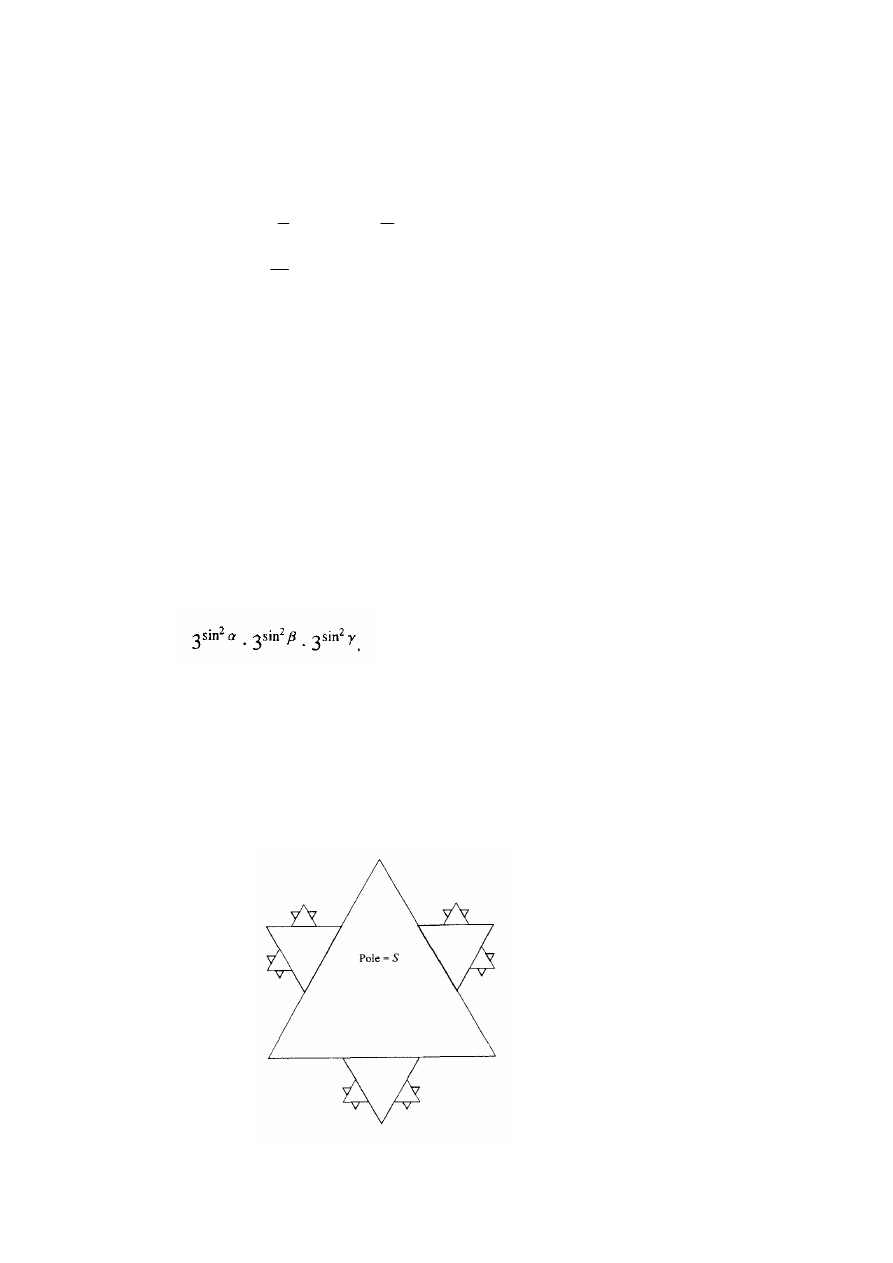
©Irek.edu.pl
9
Zestaw 9. Poziom rozszerzony
Zadanie 1.
Wiedząc, że tg
α =
3
4
i a
∈ (0,
2
π
)„ sprawdź, że liczby:
sin
α, cosα, tgα -
15
14
tworzą w podanej kolejności ciąg arytmetyczny.
Zadanie 2
Wiedząc, że wykres funkcji y = ax + b przechodzi przez punkt A = (6,4),
określ, dla jakich wartości parametru a
∈ R wykresy funkcji y = |x – 2| + 2
oraz y = ax + b nie mają punktów wspólnych.
Zadanie 3.
Dany jest wielomian: W(x) = x
3
+ 4mx
2
+ 4m
2
x.
Określ przedziały monotoniczności w zależności od wartości parametru m
≥
0.
Zadanie 4.
Wiedząc, że
α, β, y są kątami trójkąta prostokątnego, oblicz wartość
wyrażenia:
Zadanie 5.
Boki trójkąta równobocznego o polu S podzielono na trzy równe części i na
ś
rodkowych z nich zbudowano trójkąty równoboczne. W otrzymanych
trójkątach dwa boki tak samo podzielono na trzy równe części i zbudowano na
nich trójkąty równoboczne. Tak możemy postępować w nieskończoność.
Oblicz sumę pól wszystkich trójkątów.

©Irek.edu.pl
10
Zadanie 6.
Z punktu A leżącego na okręgu poprowadzono dwie cięciwy równej długości
AK i AM. Wiedząc, że KM =4 i że punkty Ki M dzielą okrąg na dwie części w
stosunku 1:5, oblicz pole koła ograniczonego tym okręgiem.
Zadanie 7.
Odcinek o końcach w punktach A= (2, -3) i B = (6, 1) jest podstawą
trójkąta równoramiennego, którego jedno z ramion zawiera się w prostej
x +2y - 8 = O. Wyznacz trzeci wierzchołek i pole tego trójkąta.
Zadanie 8.
Wykaż, że jeśli a
∈ (1;∞) i b ∈(l;∞), to log
a
b+log
b
a
≥
2.
Zadanie 9.
Prostokąt o wymiarach 5 i 12 zgięto wzdłuż przekątnej tak, że płaszczyzny
zawierające obie części prostokąta są prostopadłe. Po zgięciu wierzchołki
prostokąta wyznaczają czworościan. Oblicz objętość tego czworościanu oraz
pole powierzchni kuli opisanej na tym czworościanie.
Zadanie 10.
Ze zbioru liczb naturalnych dwucyfrowych losujemy trzy różne liczby.
a) Jakie jest prawdopodobieństwo, że ich suma jest liczbą parzystą?
b) Suma wylosowanych liczb jest parzysta. Jakie jest prawdopodobieństwo, że
wszystkie wylosowane liczby są parzyste?

©Irek.edu.pl
11
Zestaw 10. Poziom rozszerzony
Zadanie 1.
Wykaż, że dla każdej liczby naturalnej n liczba 2
4n+1
+ 3
4n+1
jest podzielna
przez 5.
Zadanie 2.
Wykonaj wykres funkcji:
x
x
f
2
1
log
2
)
(
=
Dla jakich a
∈ R wykresy funkcji f(x) i g(x)= ax + 1 mają dwa punkty
wspólne?
Zadanie 3.
Dla jakich wartości parametru m
∈ R zbiorem rozwiązań nierówności:
0
1
3
2
2
2
2
>
+
−
+
+
mx
x
x
x
jest zbiór wszystkich liczb rzeczywistych?
Zadanie 4.
Wyznacz najmniejszą wartość wyrażenia:
+
−
+
+
x
x
x
x
2
cos
sin
2
sin
cos
π
π
W przedziale
2
,
4
π
π
.
Zadanie 5.
Z miejscowości A do miejscowości B jest 60 km. Rowerzysta na drodze z A
do B jechał ze średnią prędkością 30 km/h. Z jaką średnią prędkością powinien
wracać z B do A, aby średnia prędkość na całej trasie w obie strony
wyniosła 20
Zadanie 6.
Liczbę 12 przestaw w postaci sumy nieskończenie wielu wyrazów ciągu
geometrycznego o ilorazie q =
3
2
−
Zadanie 7.
Wykaż, że jeżeli trzy kolejne kąty czworokąta wpisanego w okrąg tworzą ciąg
arytmetyczny, to co najmniej dwa kąty tego czworokąta są proste.

©Irek.edu.pl
12
Zadanie 8.
Napisz równanie stycznej do wykresu funkcji f(x)= 2x
3
- 3x
2
+ 5 w punkcie
o odciętej x =
2
1
−
Zadanie 9.
Dane są punkty: A = (2, -3) i B = (6, 1). Na prostej y = -2 znajdź taki
punkt C, aby pole trójkąta ABC było równe 8.
Zadanie 10.
Podstawą czworościanu ABCS jest trójkąt prostokątny ABC o
przeciwprostokątnej AB = 20 cm i przyprostokątnej BC = 16 cm. Krawędź CS
jest prostopadła do płaszczyzny podstawy i ma długość równą krawędzi AC.
Punkty K, L, M, N są odpowiednio środkami krawędzi AC, BC, BS, AS.
Oblicz pole przekroju czworościanu płaszczyzną wyznaczoną przez punkty K,
L, M, N.
Zadanie 11.
Ośmioosobową grupę przedszkolaków pani ustawia w sposób losowy W pary
(jedna za drugą). Oblicz prawdopodobieństwo tego, że ustalona dwójka dzieci:
a) będzie stała ze sobą w jednej parze,
b) nie będzie stała ze sobą w jednej parze.

©Irek.edu.pl
13
Zestaw 11. Poziom rozszerzony
Zadanie 1.
Aby liczbę 373 przedstawić w układzie dwójkowym, dzielimy kolejno przez 2
tę liczbę, a następnie otrzymane ilorazy. Wyniki możemy ująć w następującej
tabeli:
Wynika stąd, że:
373=1
.
2°+0
.
2
1
+1
.
2
2
+0
.
2
3
+1
.
2
4
+ 1
.
2
5
+1
.
2
6
+0
.
2
7
+1
.
2
8
= 101110101
2
.
Przeprowadź analogiczne rozumowanie i przedstaw liczbę 237 w układzie
dwójkowym.
Zadanie 2.
Odległości przedmiotu i obrazu od soczewki spełniają zależność:
g
b
f
1
1
1
−
=
gdzie:
f—ogniskowa soczewki,
g — odległość przedmiotu od soczewki,
b — odległość obrazu od soczewki.
Po przeprowadzeniu doświadczenia i wykonaniu pomiarów otrzymano
następujące wyniki:
b=73±0,5mm, g= 122±0,5mm. Oszacuj długość ogniskowej tej soczewki.
Zadanie 3.
Dla jakich wartości parametru b nierówność
5
3
5
2
+
+
−
−
b
x
b
x
< O jest spełniona przez
wszystkie liczby rzeczywiste x takie, że |x|
≤ 2?
Zadanie 4.
Wyznacz największy wyraz ciągu (a
n
) określonego wzorem a
n
=
100
2
2
+
n
n
Zadanie 5.
Rozwiąż równanie:
−
=
+
2
3
5
28
9
4
2
2
x
x
x
x
Wskazówka. Warto zastosować podstawienie
t
x
x
=
−
2
3
Zadanie 6.
Dane są zbiory:
A=(x,y): x
≥0 i y≥0
B = {(x,y) : y
≤-√3x + √3 )
a) Zaznacz na płaszczyźnie współrzędnych zbiór A
∩B.
b) Wyznacz promień największego okręgu zawartego w A
∩ B.
©Irek.edu.pl
14
Zadanie 7.
Znajdź liczbę x, która spełnia jednocześnie równanie:
(
)
(
)
[
]
a
x
a
x
a
x
a
−
+
+
=
∞
→
2
3
lim
i nierówność x
3
>x
Zadanie 8.
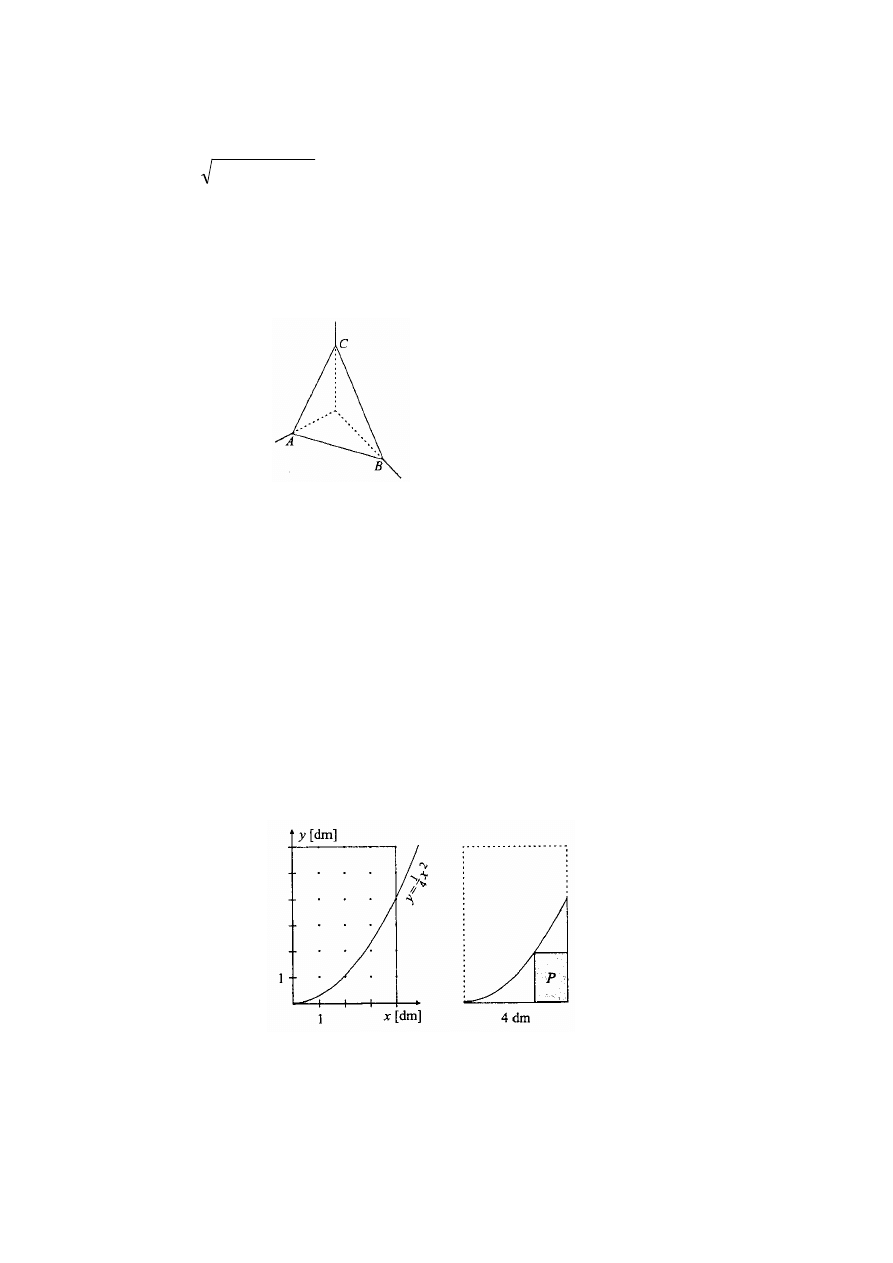
Trójkątna płytka ma szczelnie zakrywać róg prostopadłościennego pokoju, tak
jak to przedstawia rysunek.
Punkt A znajduje się w odległości 9cm od rogu, punkt B w odległości 12cm, a
C na wysokości 16cm nad podłogą. Znajdź długości boków trójkąta ABC i
oblicz jego pole.
Zadanie 9.
Wykres funkcji wielomianowej czwartego stopnia jest symetryczny względem
osi y i przechodzi przez punkt P = (0,4), natomiast styczna do wykresu w
punkcie Q = (4,0) jest równoległa do osi x. Znajdź wzór, którym ta funkcja jest
określona i naszkicuj jej wykres.
Zadanie 10.
Do prostokątnej tafli szkła o szerokości 4 dm przyłożono szablon w kształcie
paraboli, aby wyciąć fragment witraża. Z pozostałej części tafli artysta musi
jeszcze wykroić prostokąt o możliwie największej powierzchni. Opisaną
sytuację przedstawia rysunek.
Podaj wymiary tego prostokąta.
Zadanie 11.
Dwie kule o środkach A i B oraz promieniach równych odpowiednio 1 i 3
zawarte są w trzeciej, większej od nich kuli. Wykaż, że jeśli |AB| = 5, to
promień tej największej kuli jest większy lub równy 4,5.
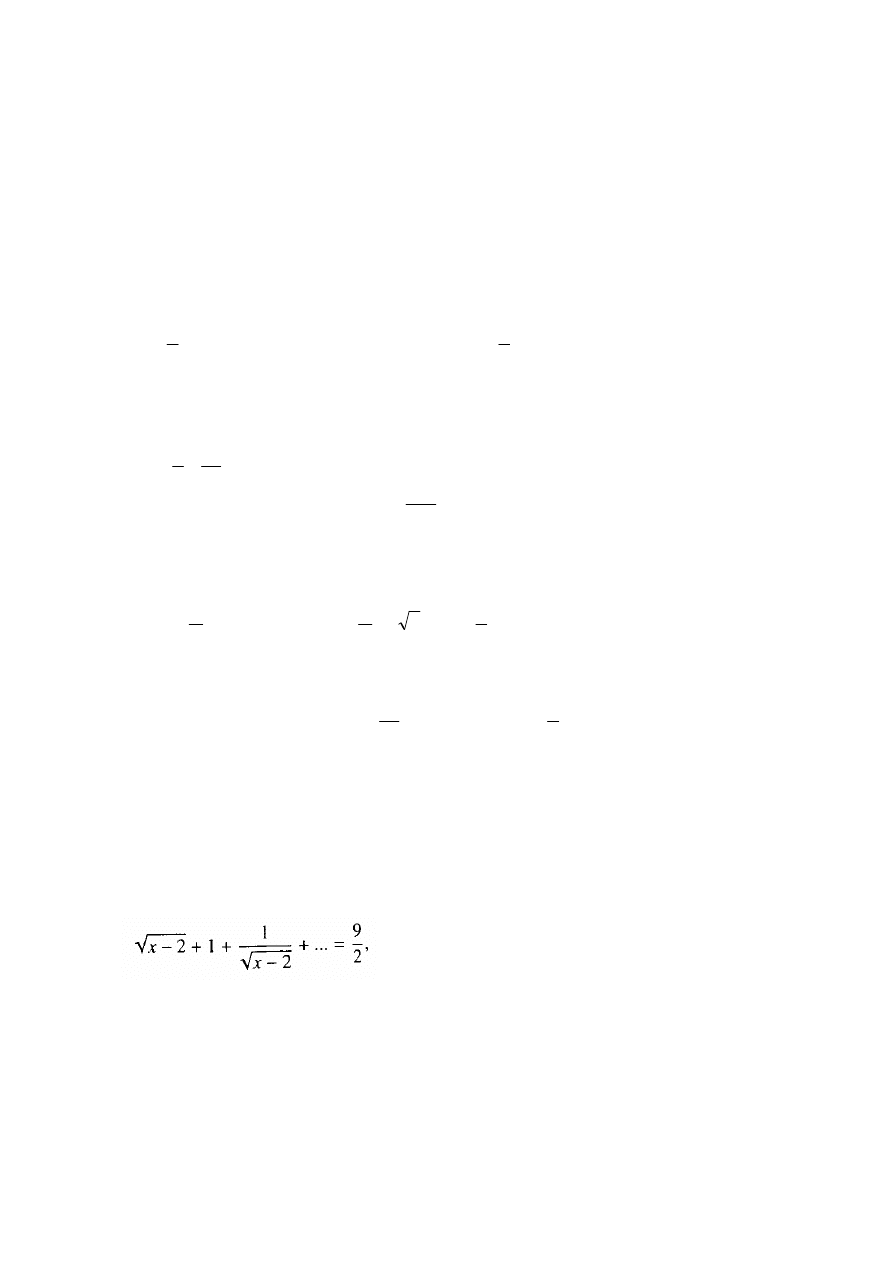
©Irek.edu.pl
15
Zestaw 12. Poziom rozszerzony
Zadanie 1.
Korzystając z własności funkcji wykładniczej, uzasadnij, że równanie
3
x
+ 4
x
= 5
x
ma dokładnie jedno rozwiązanie.
Zadanie 2.
Wykaż, że pole obszaru ograniczonego osią x oraz wykresami funkcji
f(x)=
2
6 −
x
i g(x)=-x
2
+4x-3 jest mniejsze niż
3
4
Zadanie 3.
Suma n początkowych wyrazów pewnego ciągu (a
n
) jest równa
S
n
=
4
3
4
1
n
+
−
Wykaż, że: a
1
.
a
2
.
a
3
.
…
.
a
n
=
(
)
n
n
n
−
−
⋅ 2
3
2
1
Zadanie 4.
Wyznacz wszystkie rozwiązania równania:
0
2
3
cos
2
4
sin
2
cos
4
sin
2
2
=
+
−
+
−
+
+
x
x
x
x
π
π
Zadanie 5.
Oblicz wartość wyrażenia x
3
+
3
1
x
wiedząc, że x +
x
1
= 3.
Zadanie 6.
Wyznacz wszystkie wartości parametru a, dla których nierówność:
1 + log
5
(x
2
+ 1)
≥log
5
(ax
2
+ 4x + a) jest spełniona dla każdego x
∈ R.
Zadanie 7.
Rozwiąż równanie:
w którym lewa strona jest zbieżnym szeregiem geometrycznym.
Zadanie 8.
Figurę geometryczną F opisaną nierównością:
x
2
+ y
2
+ 2x - 4y + 1
≤ 0
przekształcono symetrycznie względem osi Y. Oblicz pole figury będącej
sumą figury F i jej obrazu w podanej symetrii.
©Irek.edu.pl
16
Zadanie 9.
Trzyosobowa komisja kwalifikuje pisarzy do finału literackiej nagrody Nike.
Pisarz zostaje zakwalifikowany, gdy wszyscy członkowie komisji zgodnie
poprą jego kandydaturę. Jakie jest prawdopodobieństwo, że spośród pięciu
kandydatów przynajmniej jeden znajdzie się w finale?
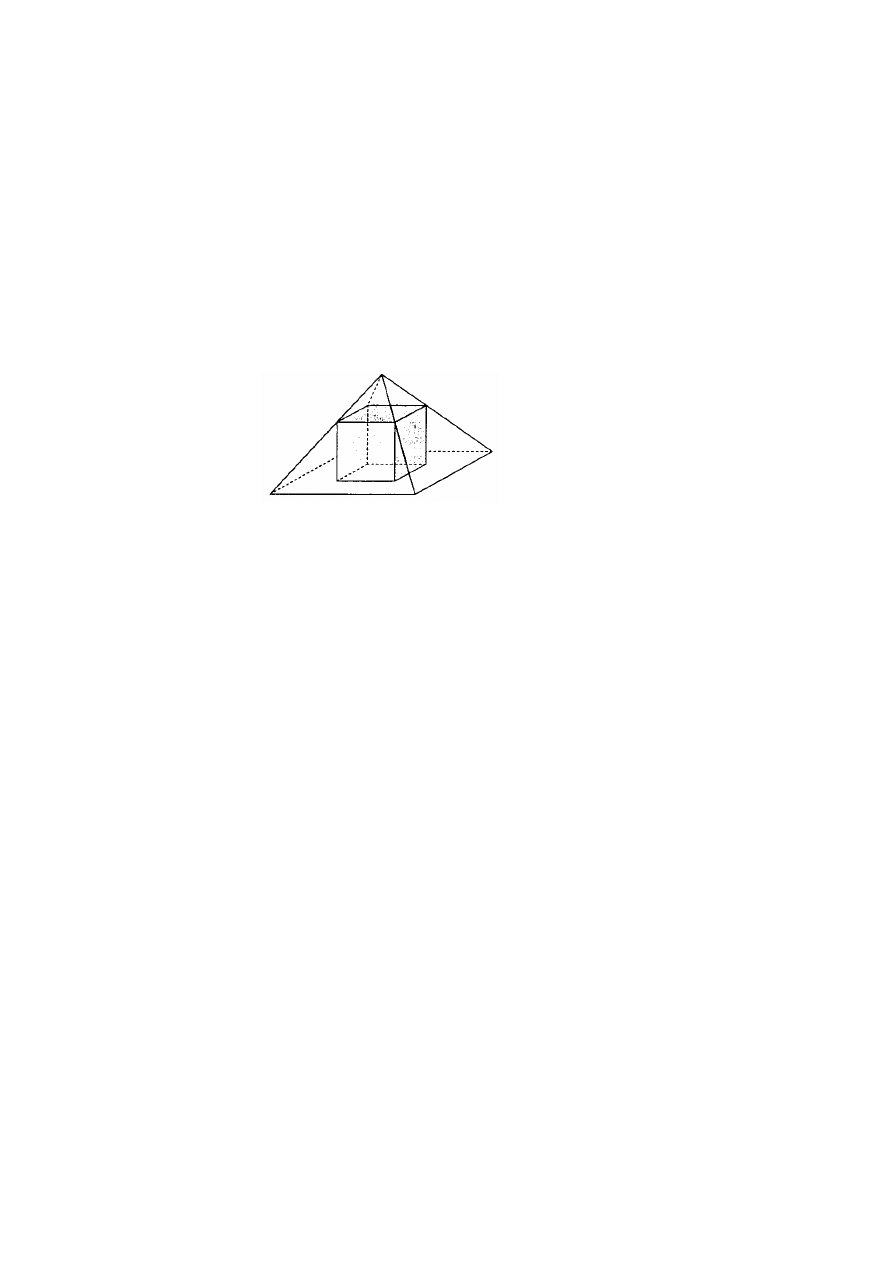
Zadanie 10.
Z ostrosłupa prawidłowego czworokątnego o krawędzi postawy długości 6 cm
i wysokości długości 6 cm wykonanego z cegły wycięto wpisany w niego
sześcian.
Czy otrzymana w ten sposób bryła będzie pływała w wodzie?
Uwaga. Ciało pływa w cieczy, gdy jego gęstość jest mniejsza niż gęstość
cieczy. Gęstość wody p = 10
3
kg/m
3
, gęstość cegły p = 1,5
.
l0 kg/m
3
. Masę
powietrza zawartego w otrzymanej bryle pomijamy.

©Irek.edu.pl
17
Zestaw 13. Poziom rozszerzony
Zadanie 1.
Niech
α i β będą kątami przedstawionymi na poniższym rysunku. Oblicz cosβ,
wiedząc, że sin
α =
5
4
Zadanie 2.
Rozwiąż równanie, którego lewa strona jest szeregiem geometrycznym:
Zadanie 3.
Wielkość gwiazdowa, tzw. magnitudo (w skrócie mag), jest to powszechnie
używana miara jasności widzialnej obiektów astronomicznych. Do
wyznaczania wielkości gwiazdowej służy wzór:
m = -2,5logE - 14,05,
gdzie:
m — wielkość gwiazdowa,
E — natężenie światła gwiazdy w luksach.
a) Gwiazda Polarna świeci z natężeniem 3,8
.
10
-7
luksa. Jaka jest wielkość
gwiazdowa Gwiazdy Polarnej?
b) Czy jaśniej świeci gwiazda o wielkości gwiazdowej 1 mag, czy o wielkości
2 mag?
c) Jeśli jedna z dwóch gwiazd świeci z natężeniem 100 razy większym niż
druga, to o ile mag różnią się ich wielkości gwiazdowe?
Zadanie 4.
Rzucamy dwiema kostkami do gry. Wynik z pierwszej kostki zapisujemy jako
współrzędną x, z drugiej — jako współrzędną y. Otrzymujemy w ten sposób
punkt (x, y) w układzie współrzędnych.
a) Oblicz prawdopodobieństwo, że otrzymany punkt należy do okręgu:
(x - 3)
2
+ (y - 4)
2
=5.
b) Rzut powtarzamy. Jeśli otrzymamy ten sam punkt, kończymy
doświadczenie, jeśli inny, to przez oba punkty prowadzimy prostą. Jakie jest
prawdopodobieństwo, że w wyniku tego doświadczenia narysujemy prostą
y = x — 2?
©Irek.edu.pl
18
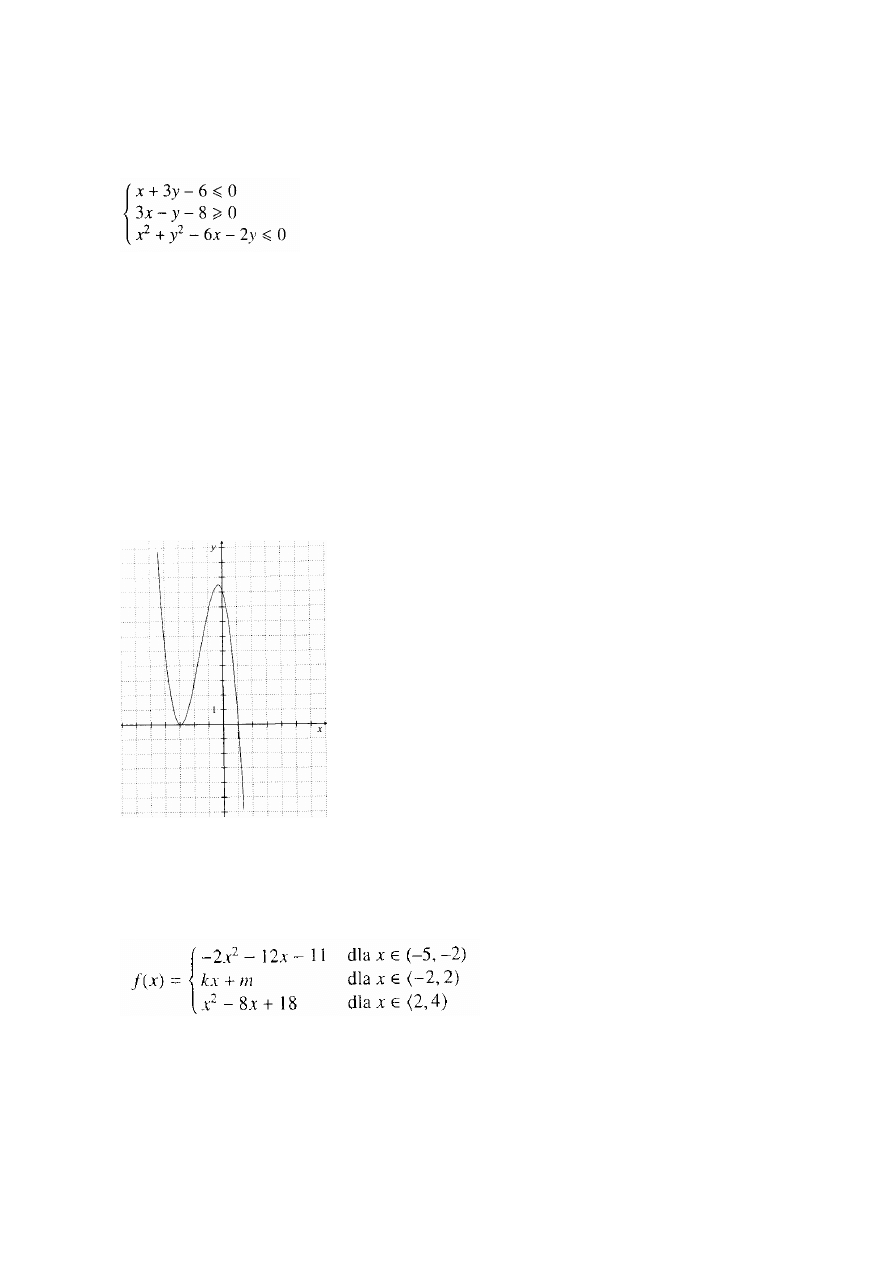
Zadanie 5.
Oblicz pole figury określonej układem nierówności:
Zadanie 6.
W ostrosłup prawidłowy czworokątny wpisany jest walec — jedna podstawa
walca jest zawarta w podstawie ostrosłupa, druga podstawa ma jeden punkt
wspólny z każdą ścianą boczną ostrosłupa. Krawędź podstawy ostrosłupa jest
równa wysokości ściany bocznej. Przy jakim stosunku wysokości
walca do wysokości ostrosłupa objętość jest największa?
Zadanie 7.
Na rysunku przedstawiono wykres funkcji, której wzór można zapisać
w postaci:
f(x) = k(x - a)(x - b)( x- c).
Korzystając z wykresu, wyznacz wartości a, b, c i k. Podaj zbiór rozwiązań
nierówności f(x)
≤ x
2
+ 3x. Naszkicuj wykres funkcji g(x) = f(x-4) - 5 i oblicz
jej miejsca zerowe.
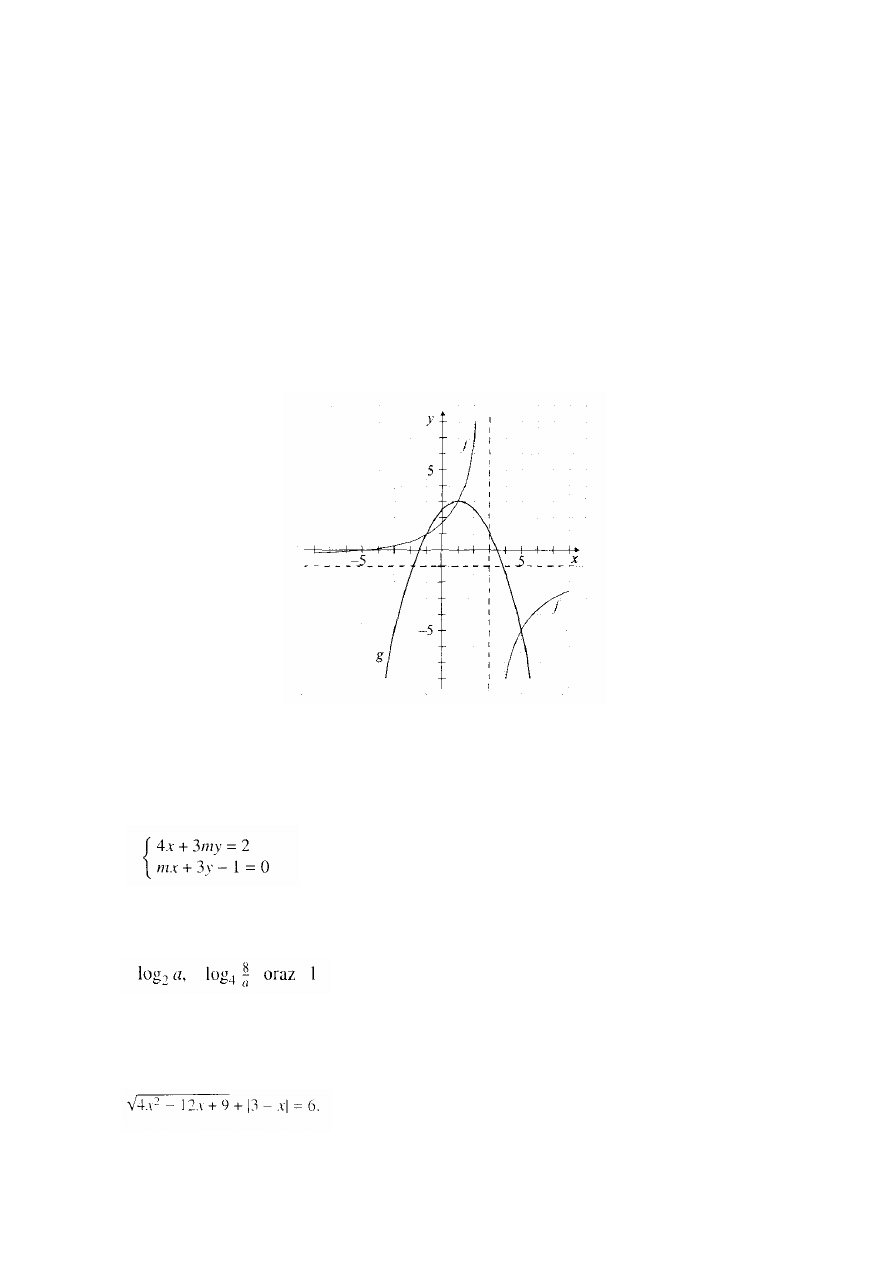
Zadanie 8.
Funkcja f określona jest następująco:
Oblicz wartości parametrów k i m tak, aby funkcja była ciągła w całej swojej
dziedzinie. Narysuj wykres funkcji f i podaj jej zbiór wartości. Wyznacz
pochodną i narysuj jej wykres.
©Irek.edu.pl
19
Zestaw 14. Poziom rozszerzony
Zadanie 13.
Na podstawie przeprowadzonych badań stwierdzono, że 20 mężczyzn na
1000 i 3 kobiety na 500 posiada wadę wymowy. Spośród 20 losowo
wybranych osób — 10 kobiet 10 mężczyzn wybrano (także losowo) jedną
osobę. Okazało się, że nie posiada ona wady wymowy. Jakie jest
prawdopodobieństwo, że był to mężczyzna?
Zadanie 14.
Na rysunku przedstawiono wykresy Funkcji f i g.
a) Odczytaj rozwiązania równania f(x) = g(x).
b) Odczytaj rozwiązanie nierówności f(x)
≥g(x).
Zadanie 15.
Określ liczbę rozwiązań układu równań
Zadanie 16.
Znajdź takie wartości parametru a, dla których liczby:
są trzema kolejnymi wyrazami ciągu geometrycznego.
Zadanie 17.
Rozwiąż graficznie równanie:

©Irek.edu.pl
20
Zadanie 18.
Równanie
można rozwiązać, stosując metodę podstawiania, w następujący sposób:
Wobec tego dla x
≥-8:
Podstawiamy
8
+
x
= t. Stąd
t
2
- 6t + 5 = 0, gdzie t
≥0.
Zatem t
1
= 1 lub t
2
= 5. Wobec tego
Podnosząc obie strony tych równości do kwadratu, otrzymujemy rozwiązanie:
x = -7 lub x = 17.
Obie liczby spełniają warunek x
≥-8.
Rozwiąż podobnie równanie:
Zadanie 19.
W graniastosłupie prawidłowym trójkątnym krawędź podstawy ma długość 4.
Kąt nachylenia płaszczyzny podstawy do płaszczyzny przechodzącej przez
krawędź podstawy i środek krawędzi bocznej ma 30
0
. Oblicz kąt nachylenia
przekątnej ściany bocznej do sąsiedniej ściany bocznej.
Zadanie 20.
Dany jest punkt P = (0,4) i okrąg o równaniu:
x2 +y2 - 6x + 4 = 0.
Znajdź równania stycznych do tego okręgu przechodzących przez punkt P oraz
miarę kąta ostrego między tymi stycznymi.
Zadanie 21.
Narysuj wykresy odpowiednich funkcji, a następnie rozwiąż nierówność:
Zadanie 22.
Dana jest funkcja f(x) =
(
)
2
3
1 x
x
−
a) Zbadaj parzystość funkcji f.
b) Podaj równania asymptot wykresu.
c) Określ przedziały monotoniczności.
d) Wyznacz ekstrema.

©Irek.edu.pl
21
Zestaw 15. Poziom rozszerzony
Zadanie 11.
Dany jest trójmian kwadratowy:
Przedstaw iloczyn dwóch różnych rzeczywistych pierwiastków tego trójmianu
jako funkcję zmiennej m. Narysuj wykres tej funkcji i podaj jej zbiór wartości.
Zadanie 12.
Wyznacz liczbę rozwiązań układu równań:
w zależności od parametru a.
Zadanie 13.
Suma wyrazów nieskończonego ciągu geometrycznego zbieżnego (a
n
)
wynosi 28. Suma wyrazów ciągu utworzonego z wyrazów ciągu (a
n
) o
numerach parzystych wynosi 12. Wyznacz pierwszy wyraz i iloraz ciągu (a
n
).
Zadanie 14.
Narysuj wykres funkcji:
f(x) = log
3
x,
a następnie, wykonując odpowiednie przekształcenia geometryczne, narysuj
wykres funkcji:
Zadanie 15.
Rozwiąż równanie:
Zadanie 16.
W trójkąt równoramienny wpisano okrąg i poprowadzono styczną do tego
okręgu równoległą do podstawy trójkąta. Pole utworzonego w ten sposób
trapezu stanowi
25
16
pola trójkąta. Oblicz cosinus kąta pomiędzy ramionami
trójkąta.

©Irek.edu.pl
22
Zadanie 17.
Niech Z będzie zbiorem punktów o współrzędnych całkowitych należących do
okręgu x
2
+ (y - 4)
2
= 5. Losujemy dwa różne punkty ze zbioru Z i
prowadzimy przez nie prostą. Jakie jest prawdopodobieństwo, że
współczynnik kierunkowy tej prostej będzie równy 3?
Zadanie 18.
Podstawą graniastosłupa jest równoległobok o bokach długości 4 i 2 oraz
dłuższej przekątnej długości 2
7
. Długość krótszej przekątnej bryły wynosi
2
15
. Oblicz objętość graniastosłupa.
Zadanie 19.
Ile jest takich stycznych do wykresu funkcji
które mają współczynnik kierunkowy równy 8. Podaj równanie jednej z tych
stycznych.

©Irek.edu.pl
23
Zestaw 16. Poziom rozszerzony
Zadanie 10.
Dla jakich wartości parametru m wielomian:
ma pierwiastek potrójny? Dla najmniejszej z wyznaczonych wartości m
rozwiąż nierówność W(x)
≤0.
Zadanie 11.
Ciąg opisany jest wzorem rekurencyjnym:
Wyznacz wzór na n-ty wyraz tego ciągu. Wykaż przez indukcję, że znaleziony
wzór jest zgodny z definicją rekurencyjną tego ciągu. Oblicz granicę ciągu.
Zadanie 12.
a) Logarytm dziesiętny pewnej liczby naturalnej wynosi w przybliżeniu 7,813
Ile cyfr ma ta liczba?
b) Wiedząc, że log 3
≈ 0,477, oblicz, ile cyfr ma liczba 3
2005
Zadanie 13.
Wykaż, że jeśli w trapez równoramienny można wpisać okrąg, to pole
powierzchni tego trapezu wyraża się wzorem P = c
2
sin
α, gdzie α jest miarą
kąta ostrego trapezu, a c - długością ramienia.
Zadanie 14.
Punkty A i B są punktami przecięcia paraboli y = - 4x + 5 z prostą
2x + y - 8 = 0. Wyznacz równanie okręgu przechodzącego przez punkty
A i B, którego środek należy do prostej x + y - l = 0.
Zadanie 15.
Walczą ze sobą dwie florecistki: A i B. Zwycięża ta z nich, która pierwsza
osiągnie 15 trafień. Prawdopodobieństwo trafienia przez zawodniczkę A
wynosi
9
5
, przez zawodniczkę B -
9
4
Jakie jest prawdopodobieństwo
zwycięstwa florecistki B, jeśli prowadzi ona 13:12?

©Irek.edu.pl
24
Zadanie 16.
Mówimy, że wykresy funkcji są styczne, jeśli mają wspólną styczną
w swoim wspólnym punkcie. Narysuj parabole
y= -x
2
-8x – 7 i y =
2
1
x
2
- 2x – 1
i sprawdź, czy są one styczne.
Zadanie 17.
Wyznacz zbiór wartości funkcji
f(x) = 5 sin
2
x + 3 cos
2
x.
Zadanie 18.
Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość a;
wysokość ściany bocznej wynosi 2a. Oblicz pole przekroju ostrosłupa
płaszczyzną zawierającą krawędź podstawy i przechodzącą przez środki
przeciwległych krawędzi bocznych.

©Irek.edu.pl
25
Zestaw 17. Poziom rozszerzony
Zadanie 10.
Wykaż, że jeśli suma trzech liczb jest podzielna przez 3, to także suma ich
sześcianów jest podzielna przez 3.
Zadanie 11.
Na poniższym rysunku przedstawiony jest trójkąt równoboczny i kwadrat.
Oblicz stosunek pola trójkąta do pola kwadratu.
Zadanie 12.
Ostrosłup prawidłowy czworokątny przecięto płaszczyzną przechodzącą przez
wierzchołek ostrosłupa i środki dwóch sąsiednich krawędzi podstawy.
Przekrój jest trójkątem równobocznym.
Oblicz miarę kąta pomiędzy płaszczyznami sąsiednich ścian ostrosłupa.
Zadanie 13.
Chcemy przedstawić liczbę 28 w postaci różnicy kwadratów dwóch liczb
naturalnych dodatnich. Jeśli takie liczby istnieją, to
28 = m
2
- n
2
= (m + n)(m - n) dla m,n
∈N
Liczby m i n możemy znaleźć następująco: zauważmy, że 28 = 2
.
14. Załóżmy,
ż
e m + n = 14 i m - n = 2. Otrzymujemy więc układ równań
Po dodaniu stronami otrzymamy 2m = 16, zatem m = 8 i n = 6. Tak więc
28 = 8
2
- 6
2
.
a) Stosując analogiczną metodę, przedstaw liczbę 33 jako różnicę kwadratów
dwóch liczb naturalnych.
b) Wykaż, że nie można w ten sposób przedstawić liczby 50.
c) Podaj warunek, jaki spełniają czynniki pierwsze liczby naturalnej, którą
można przedstawić jako różnicę kwadratów dwóch liczb naturalnych.
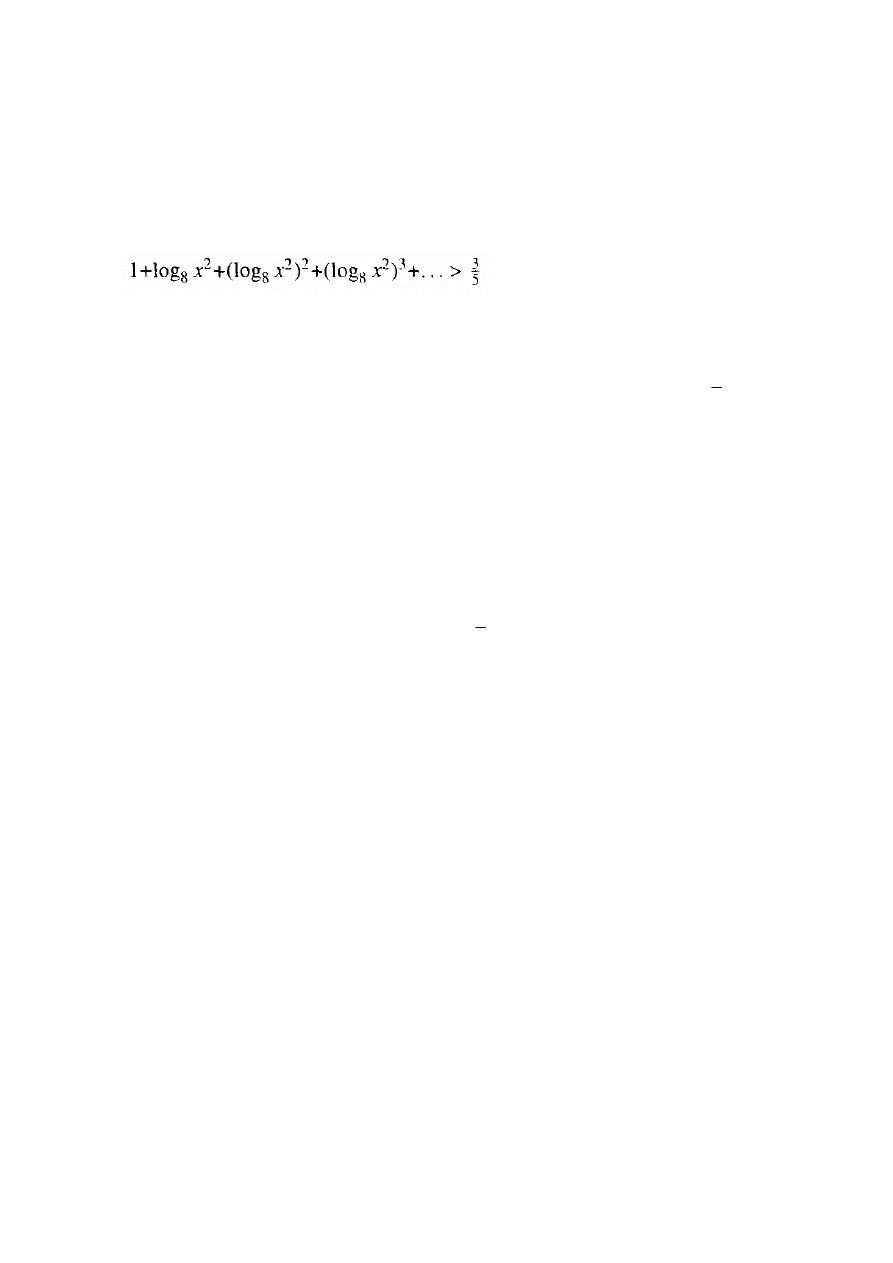
©Irek.edu.pl
26
Zadanie 14.
Udowodnij, że dla każdej liczby naturalnej parzystej n liczba 13
n
+ 6 jest
podzielna przez 7.
Zadanie 15.
Rozwiąż nierówność, której lewa strona jest sumą szeregu geometrycznego:
Zadanie 16.
W urnie są 4 kule niebieskie i pewna liczba kul czerwonych. Losujemy 2 kule.
Prawdopodobieństwo, że będą to kule w tym samym kolorze, wynosi
5
3
.
a) Ile jest czerwonych kul?
b) Wylosowano kule w tym samym kolorze. Jakie jest prawdopodobieństwo,
że są to kule niebieskie?
Zadanie 17.
Dobierz współczynniki a, b i c we wzorze funkcji f(x) = x
3
+ ax
2
+ bx + c, tak,
aby spełnione były jednocześnie dwa warunki:
• wykres funkcji f przecina się z wykresem funkcji f
`
w punkcie (-1,4),
• najmniejszą wartością funkcji f ` jest
3
1
4
−
.
Zadanie 18.
Znajdź dziesięć najmniejszych dodatnich rozwiązań równania tg 4x = sin 8x.
Uwaga do zadania 18. Znajomość wzorów na wielokrotności kąta funkcji
trygonometrycznych wykracza poza Podstawę programową, ale jest jednym z
wymagań egzaminacyjnych wymienionych w Informatorze maturalnym.
©Irek.edu.pl
27
Zestaw 18. Poziom rozszerzony
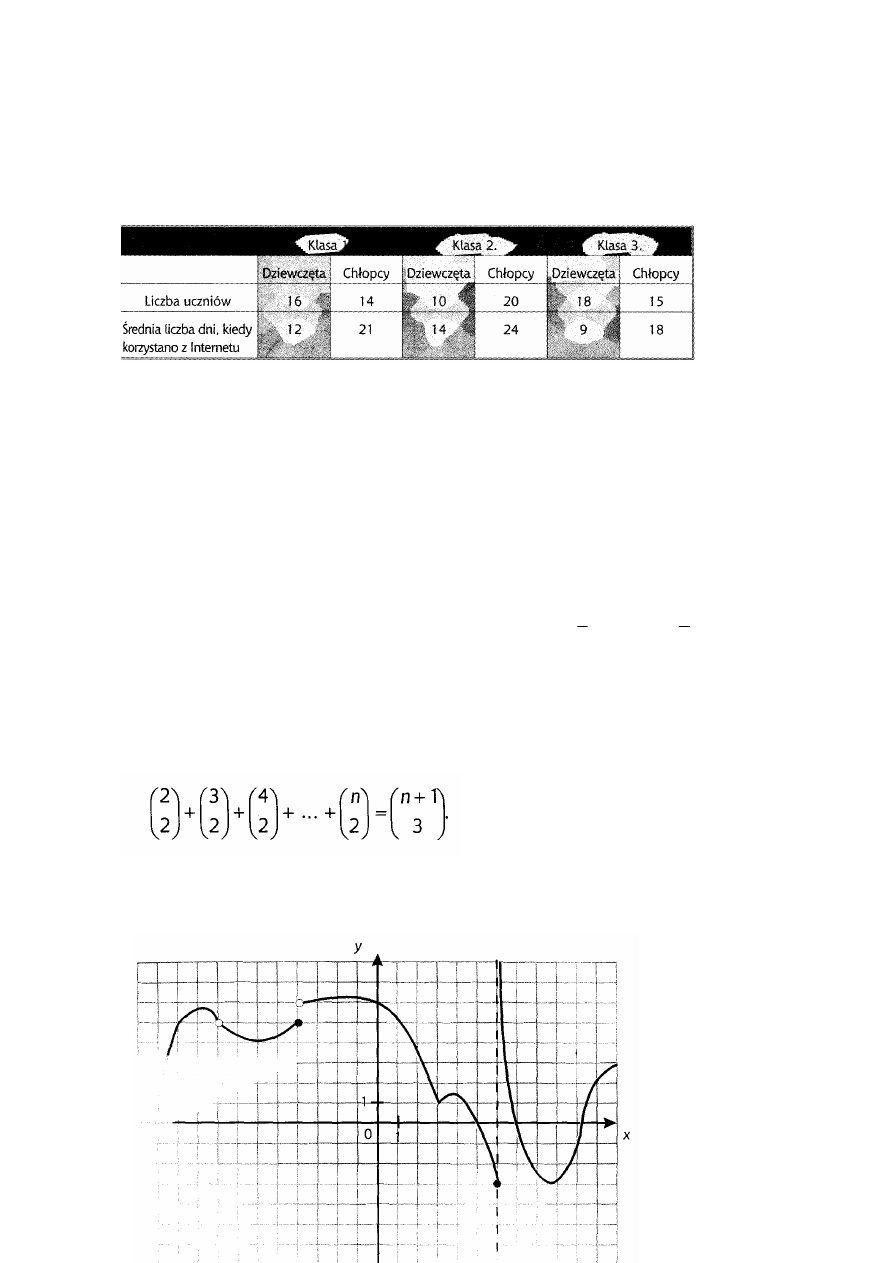
Zadanie 1.(4p.)
Młodzież pewnego liceum odpowiadała na pytanie ile razy w miesiącu
korzystasz z Internetu?”. Tabela przedstawia opracowane dane ankietowe.
Korzystając z danych w tabeli:
a) Oblicz średnią liczbę uczniów w klasach tego liceum.
b) Oblicz odchylenie standardowe liczby uczniów w poszczególnych klasach,
podając wynik z dokładnością do dwóch miejsc po przecinku.
c) Oblicz średnią liczbę dni korzystania z Internetu przez uczniów tej szkoły,
przyjmując, że każdy uczeń w opisywanych grupach dziewcząt i chłopców
danej klasy korzysta z Internetu dokładnie tyle razy ile wynosi średnia dla
danej grupy. Wynik zaokrąglij do części całkowitej.
Zadanie 2. (4p)
Zdarzenia A,B
Ω
⊂
są niezależne. Wiedząc, że P(A)=
3
1
, P(B`) =
2
1
, oblicz
P(A`
∪ B).
Zadanie 3. (6p.)
Wykaż, korzystając z zasady indukcji matematycznej, że dla każdego n
∈ℵ
+
,
n
≥ 2 prawdziwa jest równość
Zadanie 4. ( 4p)
Na rysunku przedstawiony jest wykres funkcji f.
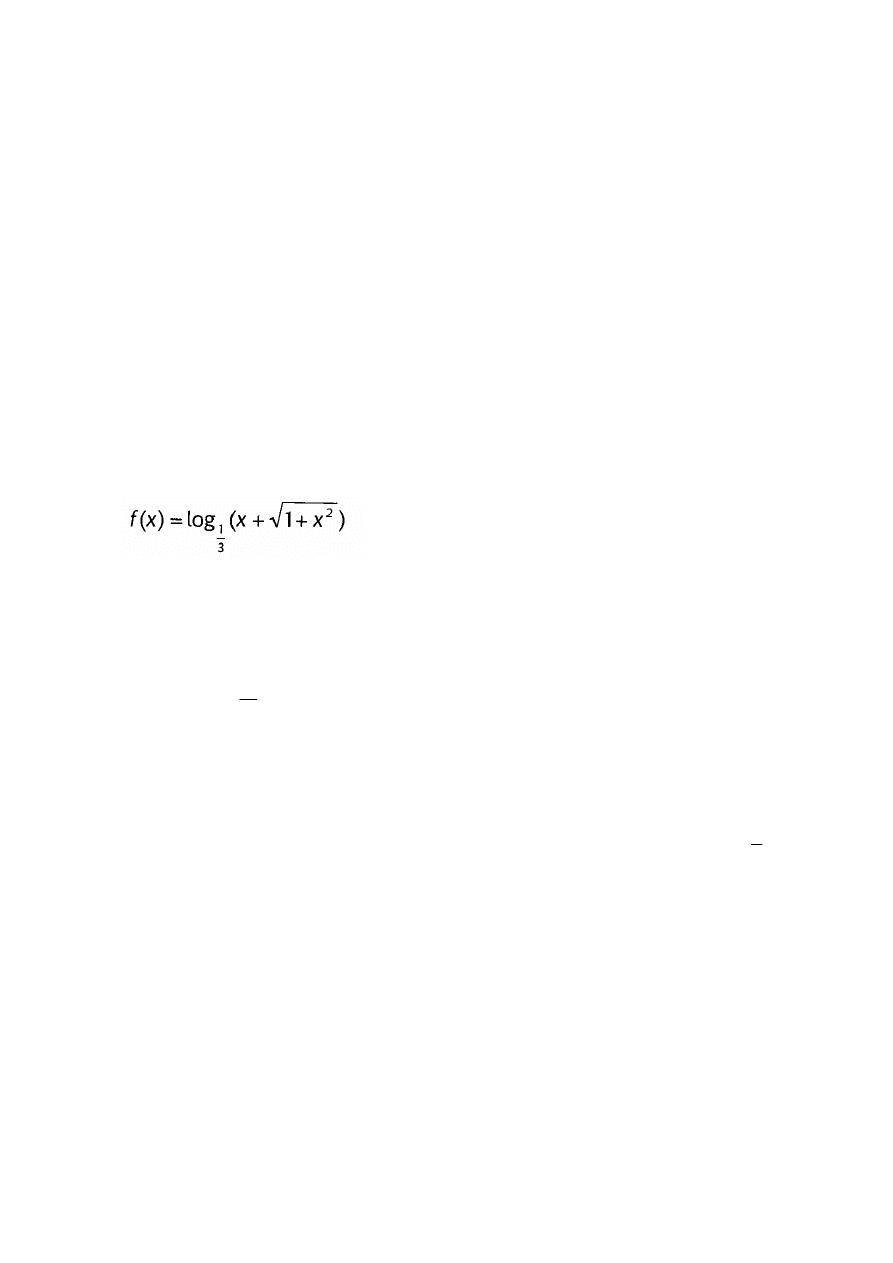
©Irek.edu.pl
28
a) Wiedząc, że prosta o równaniu y + 1 = 2(x - 1 0) jest styczną do
wykresu funkcji f, wyznacz punkt styczności.
b) Naszkicuj wykres funkcji g(x) = sgnf
`(x). która przyjmuje wartość 1 gdy
pochodna jest dodatnia, wartość -1, gdy pochodna jest ujemna oraz 0 jeśli
pochodna przyjmuje wartość 0.
Zadanie 5 (5p.)
W trójkącie ABC mamy: |AB| = 4, |AC| =6. Suma długości wysokości
opuszczonych na boki AB i AC jest równa długości wysokości opuszczonej na
bok BC. Oblicz obwód trójkąta ABC.
Zadanie 6. (5p.)
Wykaż, że funkcja f określona dla x
∈ R wzorem
jest nieparzysta.
Zadanie 7.(5 P.)
Dany jest nieskończony, malejący ciąg geometryczny (a
n
). Oblicz sumę
wszystkich jego wyrazów o numerach parzystych, jeżeli pierwszy wyraz jest
równy 2 oraz
1
1
6
13
+
−
+
=
n
n
n
a
a
a
dla n>2.
Zadanie 8. (8p.)
Wyznacz wartości parametru m
∈ R tak, aby równanie
(2m+2)x
4
—(m+4)x
2
+1=0
miało cztery pierwiastki rzeczywiste, których suma kwadratów jest równa
2
5
Zadanie 9. (4P.)
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do
płaszczyzny podstawy pod kątem o mierze 30°. Odległość spodka wysokości
ostrosłupa od krawędzi bocznej ostrosłupa jest równa 2. Oblicz objętość tego
ostrosłupa.
Zadanie 10. (5 P.)
Ze zbioru {1, 2, 3, …, 2005} losujemy kolejno bez zwracania 5 liczb. tworząc
z nich w kolejności losowania ciąg. Oblicz prawdopodobieństwo, że jest to
ciąg rosnący.

©Irek.edu.pl
29
Zestaw 19. Poziom rozszerzony
Zadanie 1. (3 P.)
Wiedząc, że
narysuj wykres funkcji f określonej wzorem f(x) = max{4 - x
2
, 2 - x}
dla x
∈<- 3;3>.
Zadanie 2. (5p)
Funkcja f określona jest wzorem:
Wyznacz wszystkie wartości parametru a
∈R, dla których funkcja f jest
ciągła w punkcie x =4.
Zadanie 3. (5p.)
Ś
rodek masy układu dwóch punktów materialnych A, B o masach
równych odpowiednio m
1
, m
2
to taki punkt S, że m
1
SA
+ m
2
SB
=
0
Korzystając z powyższej definicji, wyznacz współrzędne punktu
S — środka masy układu dwóch punktów materialnych A = (- 3. 3),
B =(7, - 2) o masach odpowiednio m
1
=3, m
2
=2.
Zadanie 4. (8 p.)
W kulę o promieniu długości 2 został wpisany stożek. Wśród wszystkich
stożków wpisanych w kulę istnieją dwa stożki o objętości 4 razy mniejszej od
objętości kuli. Oblicz, jakie długości mają wysokości tych stożków.
Zadanie 5.(4p.)
Wiadomo, że proste AD, BE i CF są równoległe oraz że |AE| = 14, |DO| = 3.
|0C| =8, |BE| =6 i |CF| = 16. Korzystając z podanych na rysunku danych, oblicz
długość odcinka AO.
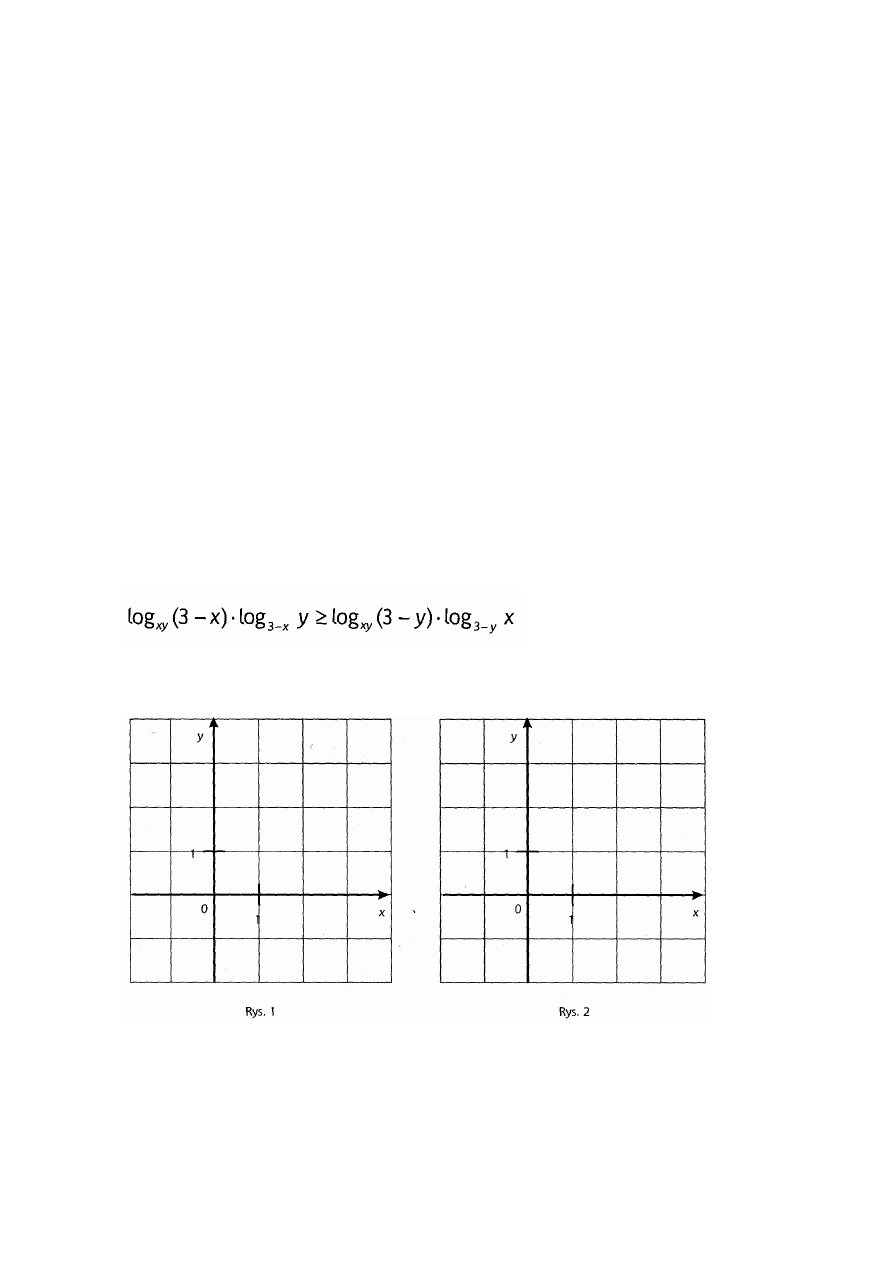
©Irek.edu.pl
30
Zadanie 7. (5 P.)
Nieskończone ciągi geometryczne (a
n
) i (b
n
) mają wszystkie wyrazy dodatnie,
ich pierwsze wyrazy są równe, iloraz ciągu (b
n
) jest 7 razy większy od ilorazu
ciągu (a
n
) i suma wszystkich wyrazów ciągu (b
n
)jest 7 razy większa od sumy
wszystkich wyrazów ciągu (a
n
). Oblicz ilorazy tych ciągów.
Zadanie 6. (6p.)
Dwa prostopadłe boki czworokąta ABCD mają równe długości i zawierają się
w dodatnich półosiach układu współrzędnych. Prosta o równaniu y = 2x jest
symetralną jednego z boków czworokąta, a punkt A = (5, 0)—jednym z jego
wierzchołków. Wyznacz współrzędne pozostałych wierzchołków czworokąta.
Sporządź rysunek w układzie współrzędnych.
Zadanie 8. (5 P.)
Punkt D należy do przeciwprostokątnej równoramiennego trójkąta
prostokątnego ABC oraz |AD|:|DB| = 1 :2. Oblicz cos|
∠ADC|. Sporządź
rysunek.
Zadanie 9. (9 P.)
Wyznacz zbiór tych wszystkich par (x, y), dla których nierówność
ma sens, i zaznacz ten zbiór na rysunku 1. Następnie rozwiąż podaną
nierówność i zbiór jej rozwiązań zaznacz na rysunku 2.

©Irek.edu.pl
31
Zestaw 20. Poziom rozszerzony
Zadanie 1(7p.)
Liczby x
1
, x
2
są pierwiastkami równania
x
2
- m
2
x- n
2
x+m•n=0. Wyznacz m i n, gdzie
Zadanie 2 (3 P.)
Aby napisać równanie prostej, do której należą punkty A = (-1, 2)
i B = (4, 6), postępujemy w następujący sposób:
o jeżeli punkt C = (x, y) należy do prostej AB, to
AB
jest równoległy do
AC
.
o istnieje t
∈ R takie, że
AB
=t
AC
⋅
.
o [5.4] =[t(x+ 1),t(y—2)],
o t=
1
5
+
x
i t=
2
4
−
y
,
o
4
2
5
1
−
=
+
y
x
o równanie prostej ma postać: 4x—5y+ 14=0.
Postępując w taki sam sposób, napisz równanie prostej, do której należą
punkty A = (0, 5) i B = (- 3, 7).
Zadanie 3 (5 P.)
Funkcja f jest określona wzorem
f(x) =2cos
2
x + cosx —l dla x
π
2
,
0
∈
.
Wyznacz najmniejszą i największą wartość tej funkcji.
Zadanie 4 (4P.)
Naszkicuj wykres funkcji f(x) = |log(x - 1)| - 2. Korzystając z wykresu tej
funkcji, ustal liczbę rozwiązań równania f(x) = m w zależności od wartości
parametru m
∈ R.
Zadanie 5. (6 p.)
Oblicz pole trójkąta ograniczonego styczną do wykresu funkcji f(x) =
x
a
(a > 0,x >0) i osiami układu współrzędnych.
Zadanie 6. (4 P.)
W graniastosłupie prawidłowym czworokątnym przekątna ściany bocznej
ma długość d. Miara kąta utworzonego przez przekątną ściany bocznej
i przekątną podstawy wychodzące z tego samego wierzchołka jest
równa
α Oblicz objętość tego graniastosłupa.
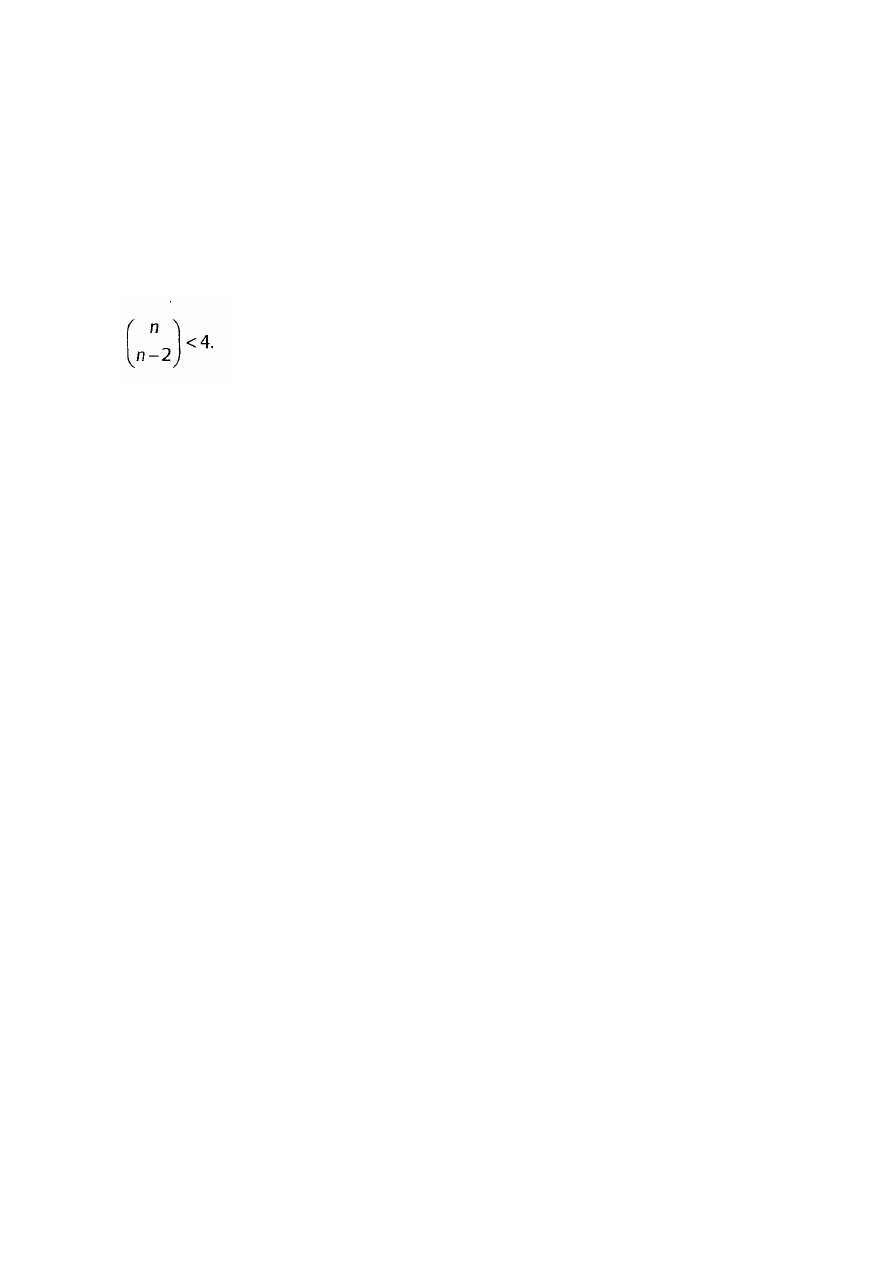
©Irek.edu.pl
32
Zadanie 7. (8p.)
Napisz równania stycznych do okręgu o równaniu x
2
+ y
2
+ 6x + = O
w punktach tego okręgu należących do osi OY. Oblicz pole czworokąta,
którego wierzchołkami są: środek okręgu, punkty wspólne okręgu i osi
OY oraz punkt przecięcia stycznych do tego okręgu.
Zadanie 8.(4P.)
Rozwiąż nierówność
Zadanie 9. (4 P.)
Zdarzenia losowe A oraz B są niezależne. Wiadomo, że P(A) = P(B) = P(B`).
Oblicz P(A`
∩B`).
Zadanie 10. (5 P.)
W trójkąt równoramienny o podstawie długości a i kącie do niej
przyległym o mierze
α wpisano prostokąt tak, że dwa jego wierzchołki
należą do podstawy trójkąta. Środek okręgu opisanego na tym trójkącie należy
do boku prostokąta przeciwległego do podstawy trójkąta. Oblicz pole
prostokąta.

©Irek.edu.pl
33
Zestaw 21. Poziom rozszerzony
Zadanie 1. (5P.)
Dane są zbiory:
Na płaszczyźnie z wprowadzonym prostokątnym układem współrzędnych
zaznacz zbiory A, B oraz A
∩B.
Zadanie 2 (6p.)
Dany jest ciąg arytmetyczny(a
n
), w którym a
1
+ a
3
= - 34 i a
2
—a
3
= - 4.
Wyznacz liczbę n tak, aby suma n początkowych kolejnych wyrazów
tego ciągu była najmniejsza.
Zadanie 3 ( 8p)
Naszkicuj wykres funkcji f określonej
f(x) = sin2x
.
|tgx|.
Z wykresu odczytaj i zapisz rozwiązania równania f(x) = 1.
Zadanie 4. (5 p.)
W stożek wpisana jest kula. Promień okręgu, który jest wspólną częścią
powierzchni kuli i powierzchni stożka, ma długość r, kąt między tworzącą
stożka i jego wysokością ma miarę
α. Oblicz objętość stożka.
Zadanie 5. (6p.)
Ze zbioru liczb {1, 2,3,.... 14} losujemy jednocześnie trzy liczby.
Opisz zbiór zdarzeń elementarnych tego doświadczenia losowego.
Oblicz prawdopodobieństwo zdarzenia A — iloczyn wylosowanych liczb
jest podzielny przez 33.
Zadanie 6. (5P.)
Zaznacz na płaszczyźnie z wprowadzonym prostokątnym układem
współrzędnych zbiór punktów (x,y). których współrzędne spełniają warunek
log(x + y) = logx + logy.
Zadanie 7. (8p.)
Wyznacz pole trójkąta o wierzchołkach A = (0, x), B = (x, 3)., C = (1, 3) jako
funkcję f zmiennej x i naszkicuj jej wykres. Wyznacz liczbę rozwiązań
równania f(x) = m w zależności od wartości parametru m
∈R.
Zadanie 8. (7p.)
W okrąg o promieniu długości 10 wpisano czworokąt ABCD w taki sposób, że
przekątna AC jest średnicą tego okręgu i tworzy z bokiem AD kąt o mierze
30
0
, a z bokiem AB kąt o mierze 45
0
. Oblicz długość przekątnej BD tego
czworokąta oraz jego pole.
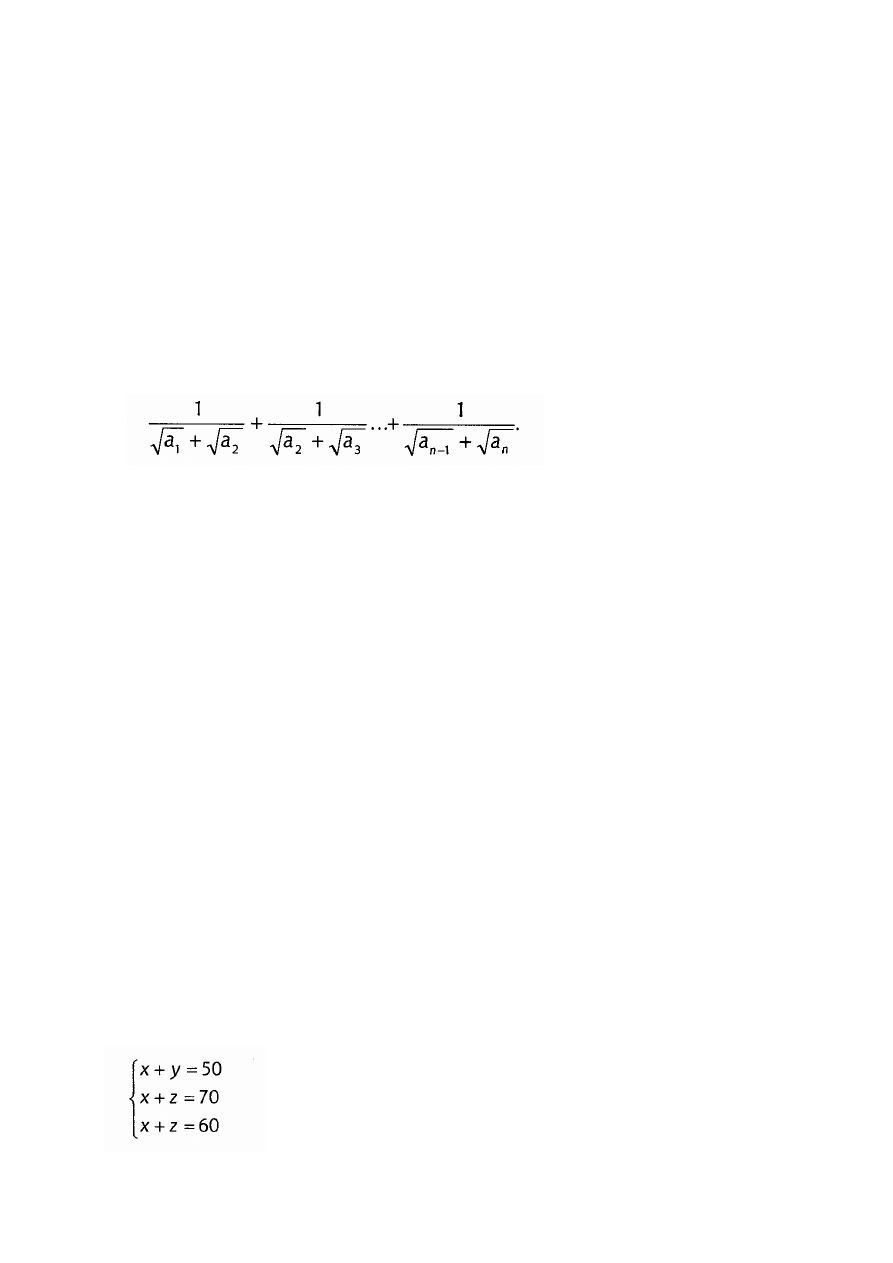
©Irek.edu.pl
34
Zestaw 22. Poziom rozszerzony
Zadanie 1. (5p.)
Funkcja f jest określona wzorem f(x) = x
3
— 3mx
2
— 3mx — 4.
Wyznacz wszystkie wartości parametru m
∈ R. dla których funkcja f jest
rosnąca w zbiorze liczb rzeczywistych.
Zadanie 2. (4p.)
Liczby a
1
, a
2
, a
3
…, a
n
są wyrazami ciągu arytmetycznego takimi, że
a
1
= a i a
n
= b. Wyraź w zależności od a, b, n sumę
Zadanie 3. (9p.)
Rozwiąż nierówność
1 + log
2
(sin2x) + log
2
2
(sin2x) + ... <0(6).
w której lewa strona jest sumą wszystkich wyrazów nieskończonego ciągu
geometrycznego i x
∈ (0; π).
Zadanie 4. (5 p.)
Udowodnij, że w dowolnym równoległoboku suma kwadratów długości
przekątnych jest równa sumie kwadratów długości wszystkich boków.
Zadanie 5. (8 p.)
Z półkuli o promieniu długości R wycinamy stożek, którego przekrój osiowy
jest trójkątem prostokątnym o przeciwprostokątnej długości 2R. Następnie
prowadzimy płaszczyznę równoległą do podstawy stożka, która przecina
powstałą bryłę. Wyznacz odległość tej płaszczyzny od płaszczyzny podstawy
stożka tak, aby pole otrzymanego przekroju było największe.
Zadanie 6 (5 P.)
Wyznacz wartość parametru a
∈ R tak, aby suma sześcianów różnych
pierwiastków równania 6x
2
+ 6(a — 1)x — 5a + 2a
2
= O była największa.
Zadanie 7(3 P.)
Aby rozwiązać układ równań

©Irek.edu.pl
35
można postąpić w następujący sposób:
•
rysujemy trójkąt ABC o bokach długości 50, 60. 70;
•
wpisujemy w ten trójkąt okrąg;
•
odległości wierzchołków A, B. C od punktów styczności z okręgiem
oznaczamy x, y, z;
•
korzystając z własności trójkąta opisanego na okręgu, otrzymujemy:
Postępując analogicznie, rozwiąż układ równań
Zadanie 8.(6 p.)
W okrąg o równaniu x
2
+ y
2
= 169 wpisano kwadrat ABCD. Wiedząc,
ż
e A = (5, 12), oblicz współrzędne pozostałych wierzchołków kwadratu.
Zadanie 9.(6 P.)
Z koszyka, w którym jest dwa razy więcej kul czarnych niż białych,
losujemy dwa razy po jednej kuli bez zwracania. Opisz zbiór zdarzeń
elementarnych tego doświadczenia losowego. Oblicz, ile jest kul
w koszyku, jeżeli prawdopodobieństwo wylosowania pary kul o różnych
kolorach jest nie mniejsze niż
22
9
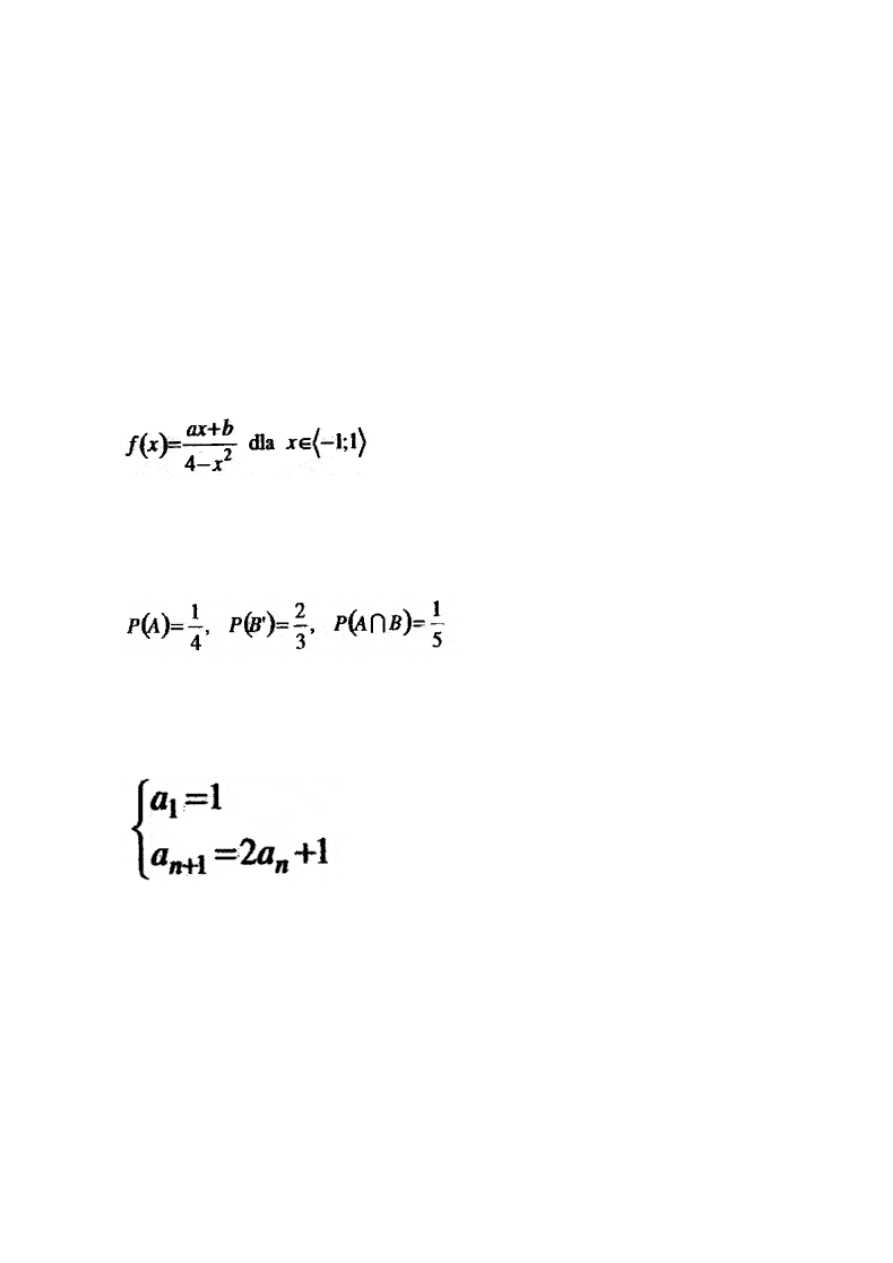
©Irek.edu.pl
36
Zestaw 23. Poziom rozszerzony
Zadanie 1. (3 punkty)
Przyjmujemy, że k jest liczbą wszystkich podzbiorów 7-elementowych zbioru
15-elementowego. Sprawdź, czy:
a) liczba 9 jest dzielnikiem liczby k;
b) liczba 12 jest dzielnikiem liczby k.
Zadanie 2. (4 punkty)
Punkty A, B, C, D są kolejnymi wierzchołkami czworokąta, gdzie A=(-6,1),
B
=(-1,2), C=(2,9), a D jest obrazem punktu B w symetrii osiowej względem
prostej wyznaczonej przez punkty A i C. Oblicz współrzędne punktu D.
Zadanie 3. (4 punkty)
Wyznacz a i b wiedząc, że funkcja f określona wzorem
przyjmuje w przedziale obustronnie domkniętym od -1 do 1 najmniejszą
wartość dla x=0 i ta najmniejsza wartość jest równa 1. Uzasadnij, że dla
wyznaczonych a i b funkcja f przyjmuje wartość najmniejszą dla x=0.
Zadanie 4. (5 punktów)
Zdarzenia losowe A zawierające się w Ω i B zawierające sie w Ω sa takie, że:
Oblicz prawdopodobieństwo P(A'*B') oraz P(A'|B), gdzie * oznacza przecięcie
zbiorów. Zbadaj, czy A' i B' są zdarzeniami niezależnymi.
Zadanie 5. (6 punktów)
Ciąg (a
n
) jest określony wzorem rekurencyjnym
a) Wyznacz wzór na n-ty wyraz tego ciągu.
b) Uzasadnij, że ciągi określone za pomocą wyznaczonego wzoru i wzoru
rekurencyjnego są równe.
c) Zbadaj monotoniczność ciągu (a
n
).
Zadanie 6. (7 punktów)
Wyznacz wszystkie wartości parametru a zawartego w zbiorze liczb
rzeczywistych, dla których układ równań
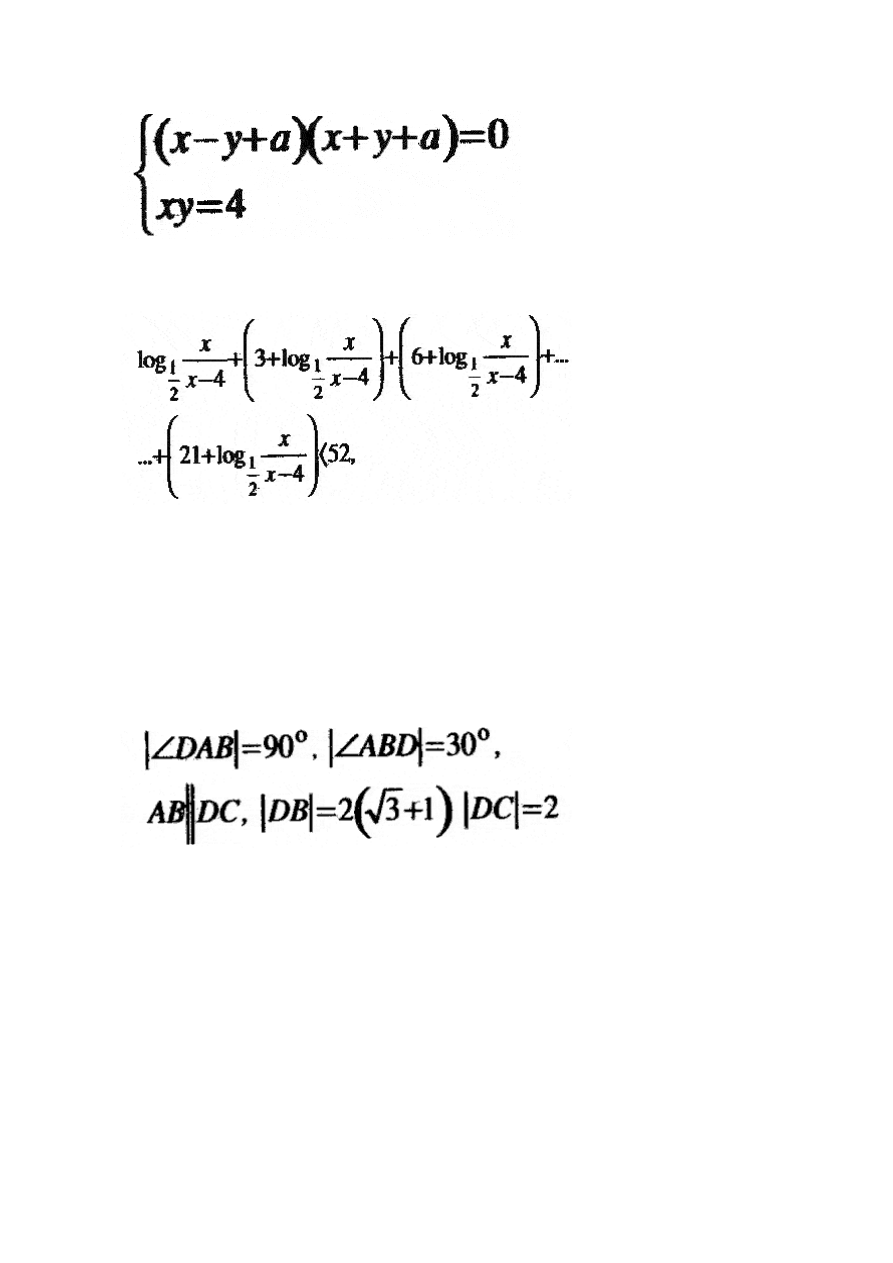
©Irek.edu.pl
37
ma co najmniej trzy różne rozwiązania.
Zadanie 7. (9 punktów)
Rozwiąż nierówność
gdzie lewa strona jest sumą kolejnych wyrazów pewnego ciągu
arytmetycznego.
Zadanie 8. (3 punkty)
W trapezie, którego podstawy mają długości a i b, suma miar kątów
wewnętrznych trapezu przy podstawie a jest równa 90
0
. Udowodnij, że
odcinek łączący środki podstaw trapezu ma długość równą a - b/ 2.
Zadanie 9. (8 punktów)
Dany jest trapez prostokątny ABCD, gdzie
Oblicz długość promienia okręgu wpisanego w trójkąt BDA.
Wyznacz sumę kwadratów sinusów kątów wewnętrznych trapezu ABCD.
Zadanie 10. (11 punktów)
Sześcian o krawędzi długości 1 przecięto płaszczyzną π przechodzącą przez
krawędź podstawy i nachyloną do płaszczyzny podstawy pod kątem o mierze
x, gdzie x zawiera się w przedziale obustronnie otwarty od ) do π / 2.
Oznaczmy przez f(x) pole przekroju sześcianu płaszczyzną π.
a) Zbadaj różniczkowalność funkcji f.
b) Wyznacz przedziały monotoniczności i ekstremum funkcji f.
c) Naszkicuj wykres funkcji f.
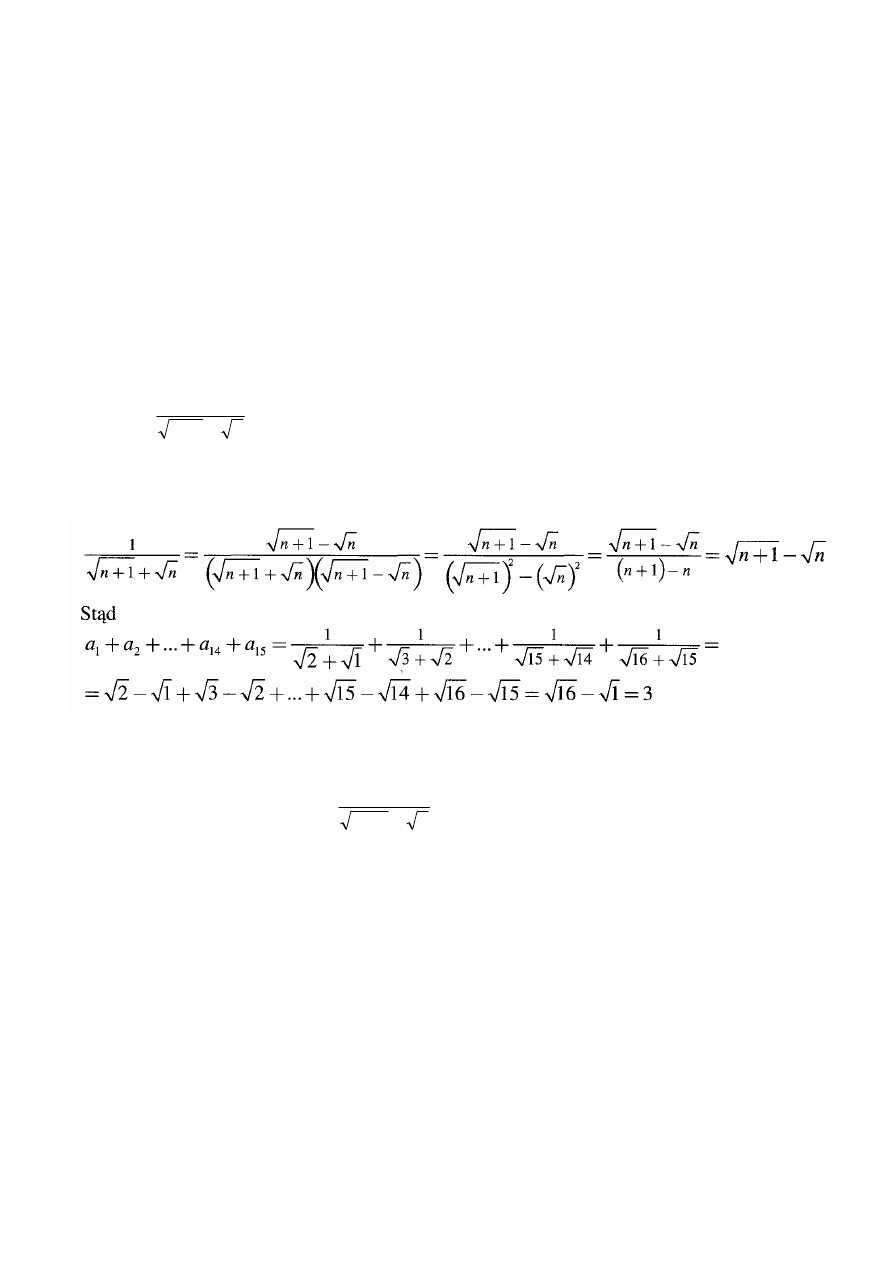
©Irek.edu.pl
38
Zestaw 24. Poziom rozszerzony
Zadanie 10 (4p)
Dane jest równanie x
2
+ (m - 3)x - 4m = 0 z parametrem m.
a. Oblicz, dla jakich wartości parametru m równanie to ma dwa różne
pierwiastki.
b. Oblicz, dla jakich wartości parametru m równanie ma dwa różne pierwiastki
o tym samym znaku.
Zadanie 11 (5p)
Sumę piętnastu początkowych wyrazów ciągu (a
n
) określonego wzorem
a
n
=
n
n
+
+1
1
można wyznaczyć w następujący sposób:
Zauważmy, że dla każdej liczby naturalnej n
≥1 zachodzi
Postępując podobnie, oblicz sumę siedmiu początkowych wyrazów ciągu (b
n
)
określonego wzorem b
n
=
n
n
+
+ 2
1
Zadanie 12 (6p)
Dany jest ośmiościan foremny o wierzchołkach A, B, C, D, E, F.
a. Naszkicuj ten ośmiościan.
b. Wskaż dowolną parę krawędzi prostopadłych, uzasadnij, że są one
prostopadłe.
c. Wypisz wszystkie pary krawędzi prostopadłych w ośmiościanie,
przyjmując, że para {a,b} jest równa parze {b,a}.
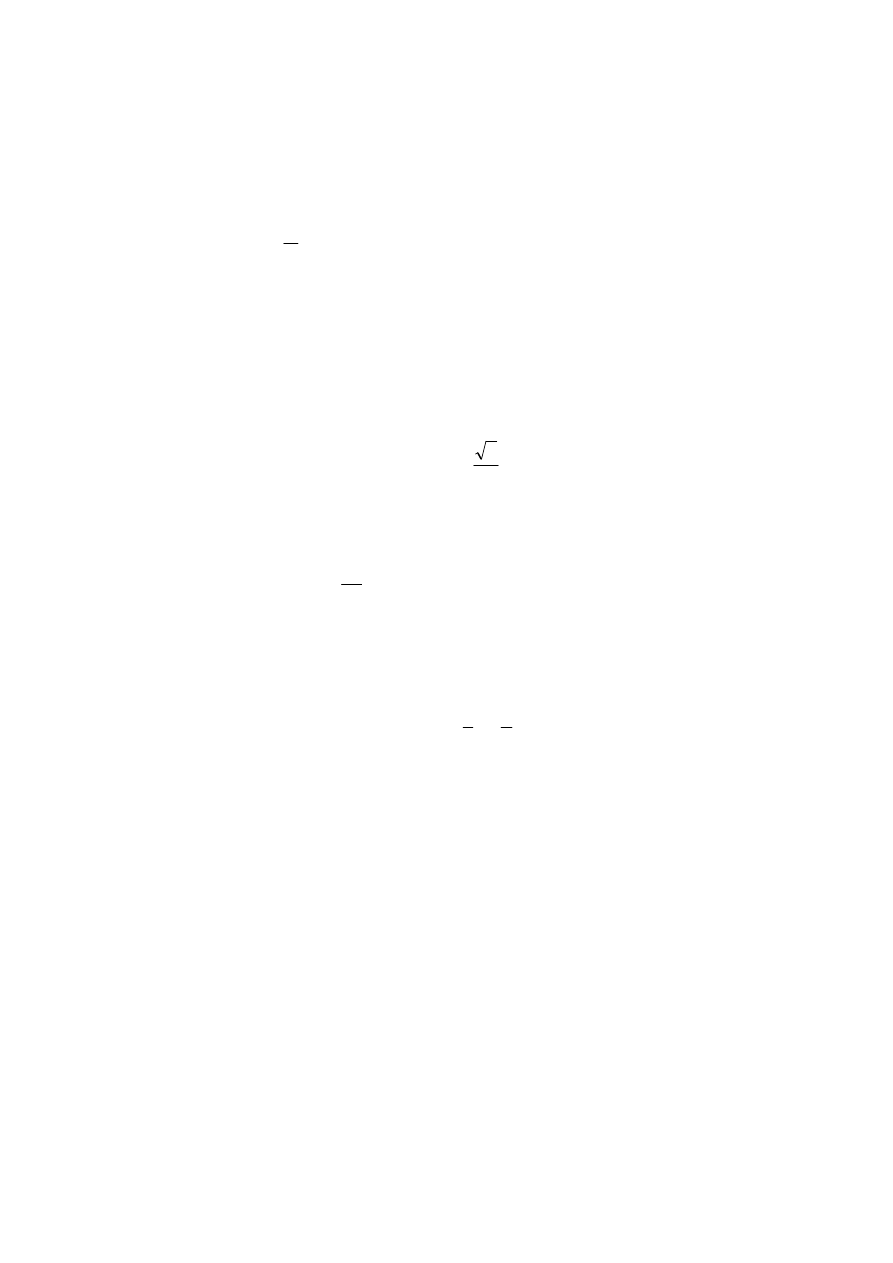
©Irek.edu.pl
39
Zadanie 13 (6p)
Farmakokinetyka to dział farmakologii badający szybkość procesów
wchłaniania, dystrybucji i wydalania leków z organizmu. Przyjmijmy, że
stężenie f(t) pewnego leku we krwi pacjenta, mierzone w mg/litr, opisane jest
wzorem
f(t)=
2
1
2
32
t
−
⋅
gdzie t to czas w godzinach, mierzony od chwili podania pacjentowi leku, przy
czym t
≥ 1.
a. Wyznacz stężenie leku we krwi pacjenta dla t = 2; wynik zaokrąglij do
liczby całkowitej.
b. Oblicz, po jakim czasie od podania leku jego stężenie spadnie do poziomu
8 mg/litr.
c. Tworzymy ciąg (a
n
) tak, że a
n
= f (n) dla n
∈N
+
udowodnij, że ciąg (a
n
) jest
ciągiem geometrycznym o ilorazie q =
2
2
Zadanie 14 (3p)
Rozwiąż nierówność
x
x
27
2
≤
Zadanie 15 (5p)
Na okręgu o promieniu r obrano dwa punkty A i B tak, że podzieliły one okrąg
na dwa łuki o długościach odpowiednio
3
1
i
3
2
obwodu okręgu. Na krótszym z
tych łuków obrano punkt C tak, że |AC| = 10, |BC|=13.
a. Wyznacz |AB|.
b. Wyznacz r.
Zadanie 16 (lp)
Dana jest parabola opisana równaniem y = (x - 3)
2
+1. Tworzymy trójkąty
ABC takie, że punkt A leży w początku układu współrzędnych, punkt B o
współrzędnych (x
b
, y
b
) leży na paraboli, punkt C ma współrzędne (x
b
, 0).
a.
Napisz wzór funkcji P, określającej pole trójkąta ABC w zależności od x
b
dla x
b
> 0.
b.
Znajdź trójkąt o największym polu dla x
b
∈ (0; 3); w odpowiedzi podaj
współrzędne punktu C.

©Irek.edu.pl
40
Zadanie 17 (3p)
Na podstawie danych z rysunku oblicz (sin
α + cosα)
2
Zadanie 18 (6p)
W poniższej grze wygrana przysługuje każdemu graczowi, który wylosuje
dwie kule zielone. Zasady gry:
gracz rzuca trzykrotnie symetryczną monetą. Jeżeli moneta upadnie
trzykrotnie na tę samą stronę, to gracz uruchamia maszynę losującą Ml; w
przeciwnym wypadku gracz uruchamia maszynę losującą M2. Każda
z maszyn losuje na raz dwie kule. W maszynie Ml jest 10 kul zielonych i 5
czarnych; w maszynie M2 są 2 kule zielone i 13 czarnych.
Oblicz prawdopodobieństwo wygranej tj. prawdopodobieństwo wylosowania
dwóch kul zielonych; wynik podaj w ułamku zwykłym.
Zadanie 19 (5p)
Dane są wyniki x
1
,x
2
,. . .,x
n
. Niech
x
oznacza ich średnią arytmetyczną, zaś s
oznacza ich standardowe odchylenie. Udowodnij twierdzenia:
a.
jeżeli od każdego z wyników x
1
,x
2
,. . .,x
n
, odejmiemy tę samą liczbę
rzeczywistą a, to średnia arytmetyczna tak uzyskanych wyników będzie
równa
x
- a,
b.
jeżeli od każdego z wyników x
1
, x
2
,.. . , x
n
,, odejmiemy tę samą liczbę
rzeczywistą a, to standardowe odchylenie nie ulegnie zmianie.

©Irek.edu.pl
41
Zestaw 25. Poziom rozszerzony
Zadanie 10 (5p)
Funkcja J dana jest wzorem f(x) = |x – 2| +|x + 3|.
a. Wyznacz przedział, w którym funkcja f jest stała.
b. Wyznacz równanie osi symetrii wykresu funkcji f
c. Sprawdź, czy funkcja f jest parzysta.
Zadanie 11 (6p)
Dany jest kwadrat K o boku a. Dwie proste prostopadłe, przecinające się w
punkcie P należącym do przekątnej kwadratu K wyznaczają w tym kwadracie
dwa mniejsze kwadraty K
1
i K
2
i dwa prostokąty. Wyznacz, przy jakim
położeniu punktu P suma pól kwadratów K
1
i K
2
jest najmniejsza.
Zadanie 12 (5p)
Figura A opisana jest układem nierówności
Narysuj w podanym układzie współrzędnych figurę A i wyznacz jej pole.
Zadanie 13 (4p)
Na rysunku naszkicowany jest wykres funkcji f (x) = a sin bx dla x
∈<O;2π>.
a. Na podstawie rysunku wyznacz wartości parametrów a i b.
b. Dla znalezionych wartości a i b ustal, ile punktów wspólnych ma wykres
funkcji g (x)= |a sinbx| + 4 z prostą o równaniu y=8 dla x
∈<O;2π>.
Zadanie 14 (5p)
Zarząd pewnej spółdzielni mieszkaniowej postanowił, że mieszkańcy
wyższych pięter w blokach wielopiętrowych będą płacić za windę więcej, niż
mieszkańcy pięter niższych. Ustalono, że mieszkańcy parteru są zwolnieni z
opłat za windę.
Do rozliczania opłat za windę dla mieszkańców pięter od pierwszego do
ostatniego wprowadzono wzór

©Irek.edu.pl
42
gdzie P (k) oznacza procentowy udział mieszkańców piętra o numerze k w
całości kosztów windy w ich bloku; n oznacza liczbę pięter w bloku (np. jeżeli
n = 10, to blok jest dziesięciopiętrowy, czyli ma parter i dziesięć pięter).
Uzasadnij, że mieszkańcy każdego z bloków ponoszą całość kosztów
utrzymania windy w ich budynku.
Zadanie 15 (6p)
Funkcja f dana jest wzorem f (x)=
1
2
+
−
x
x
m
gdzie m jest parametrem.
a. Wyznacz pochodną funkcji f.
b. Wyznacz wartość parametru m, wiedząc, że dla x = 2 funkcja osiąga
minimum.
Zadanie 16 (5p)
Dane są dwa okręgi O
1
(S
1
,1) i 0
2
(S
2
,3), przy czym S
1
S
2
= 8. Leżący na
odcinku S
1
S
2
punkt P jest środkiem jednokładności, która przekształca okrąg
0
1
na okrąg 0
2
.
a. Wykonaj rysunek.
b. Podaj skalę tej jednokładności.
c. Znajdź długość odcinka PS
1
.
Zadanie 17 (4p)
Ostrosłup prawidłowy trójkątny, w którym wysokość jest równa 6 i krawędź
podstawy jest równa 8, przecięto płaszczyzną, zawierająca krawędź boczną i
wysokość przeciwległej ściany bocznej.
a. Wykonaj rysunek.
b. Oblicz pole przekroju.
c. Podaj w zaokrągleniu do pełnych stopni kąt nachylenia ściany bocznej do
podstawy ostrosłupa.
Zadanie 18 (5p)
Oblicz, dla jakich wartości parametru p równanie kwadratowe
x
2
+ x + log
4
p = 0 ma dwa różne pierwiastki.
Zadanie 19 (5p)
Związek Ochrony Praw Konsumenta w pewnym kraju przeprowadził badania
jakości wód mineralnych podawanych w restauracjach. Badania ujawniły, że
w 10 % przebadanych restauracji zamiast wody mineralnej podaje się wodę z
kranu nasyconą dwutlenkiem węgla CO
2
. Oblicz prawdopodobieństwo, że
wśród 10 losowo wybranych restauracji w tym kraju w dokładnie jednej
podaje się wodę z kranu nasyconą dwutlenkiem węgla CO
2
zamiast wody
mineralnej. Wynik zaokrąglij do 3 miejsc po przecinku.
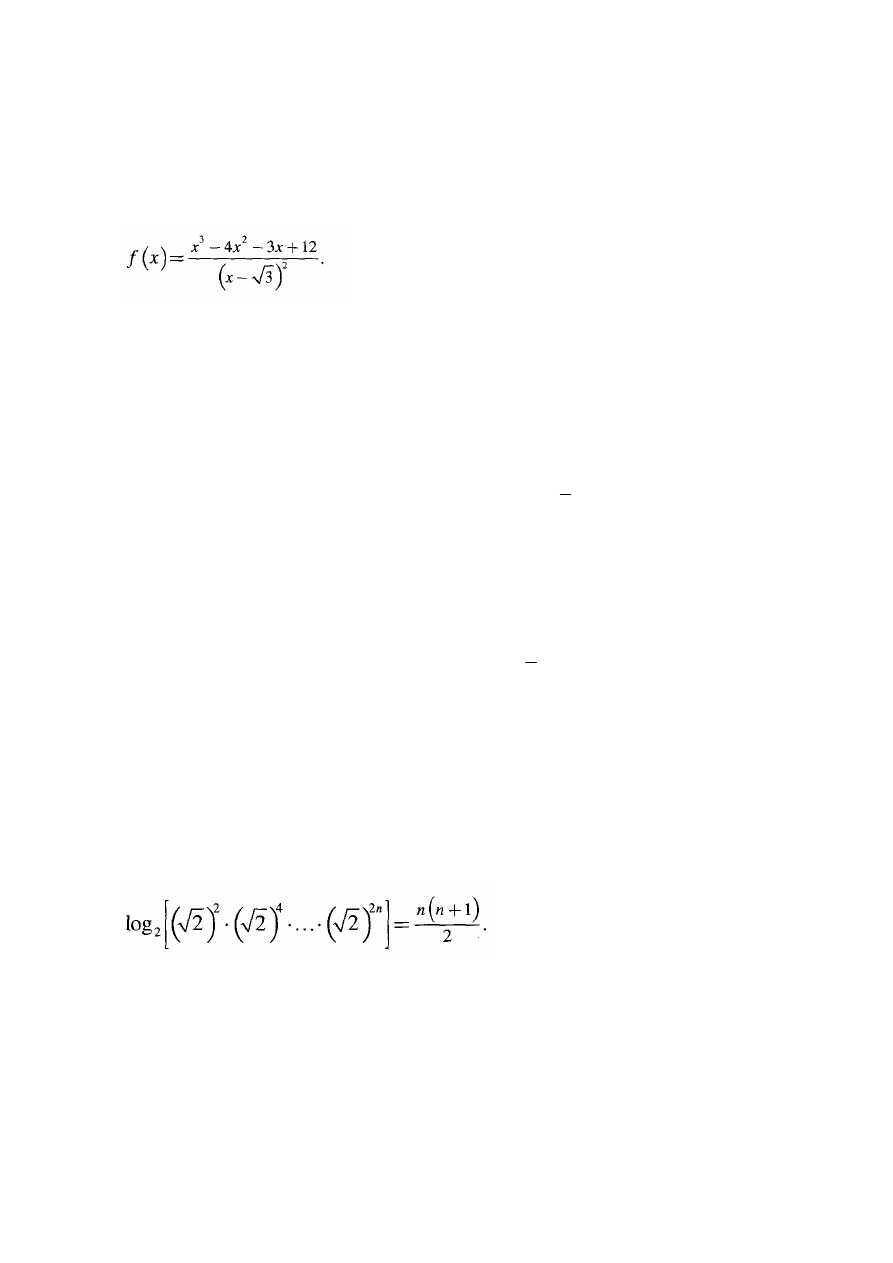
©Irek.edu.pl
43
Zestaw 26. Poziom rozszerzony
Zadanie 10 (3p)
Wyznacz dziedzinę i miejsca zerowe funkcji f danej wzorem
Zadanie 11 (6p)
Wyznacz długość łamanej, będącej częścią wspólną wykresu funkcji f danej
wzorem f (x) =|x| - 1 i kola o środku w początku układu współrzędnych i
promieniu 5.
Zadanie 12 (6p)
Funkcja f dana jest wzorem f (x)= mx
2
+ (m + 2)x -
4
1
a. Podaj, dla jakiej wartości parametru m funkcja f jest liniowa.
b. Oblicz, dla jakiej wartości parametru m funkcja f jest kwadratowa i ma
dokładnie jedno miejsce zerowe.
c.
Sprawdź, czy poniższa równoważność jest prawdziwa; odpowiedź
uzasadnij.
Funkcja f dana wzorem f (x)= mx
2
+ (m + 2)x -
4
1
ma dokładnie jedno miejsce
zerowe wtedy i tylko wtedy, gdy dla każdego x
∈
R zachodzi f (x)
≤
O.
Zadanie 13 (3p)
Rozwiąż równanie 4cos
2
x - 3 = O dla x
∈<-π,π>
Zadanie 14 (4p)
Wykaż, że dla n
∈ N
+
prawdziwa jest równość
Zadanie 15 (7p)
Dany jest nieskończony ciąg geometryczny (a
n
), w którym a
1
= 1, q = 0,2.
a. Sumę a
1
+ a
2
+ a
3
+... wszystkich wyrazów ciągu (a
n
) przybliżono sumą jego
pięciu początkowych wyrazów. Oblicz obie sumy i podaj błąd bezwzględny
przybliżenia.
b.
Ile co najmniej początkowych wyrazów należy zsumować, aby błąd
przybliżenia był mniejszy niż 10
-4
?
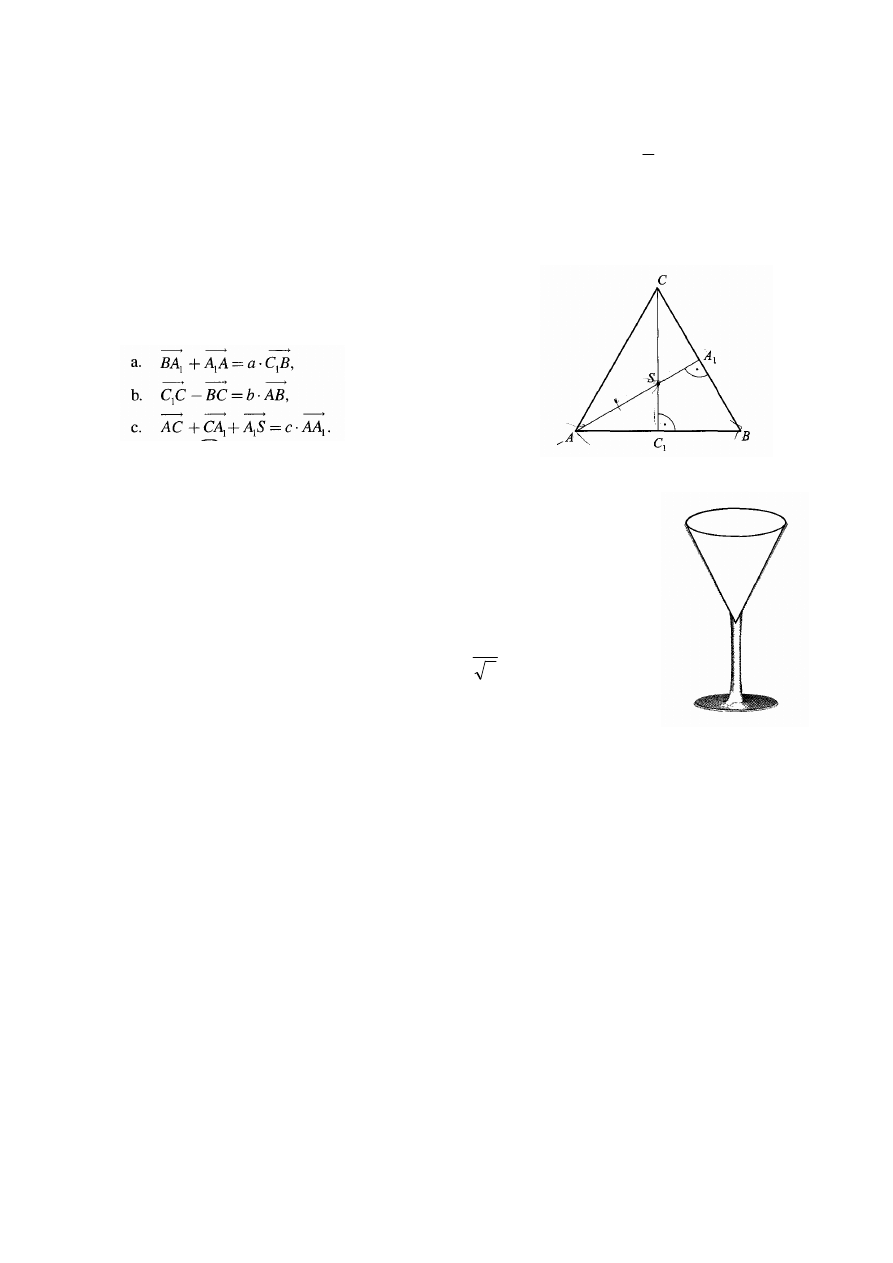
©Irek.edu.pl
44
Zadanie 16 (5p)
Wykaż, że styczne do wykresu funkcji f danej wzorem f(x) =
x
2
poprowadzone
w punktach P
1
= (1,2) i P
2
=(- 1,- 2) są równoległe.
Zadanie 17 (5p)
Trójkąt ABC (patrz rysunek) jest równoboczny.
Na podstawie rysunku wyznacz wartości a, b, c,
w poniższych równościach.
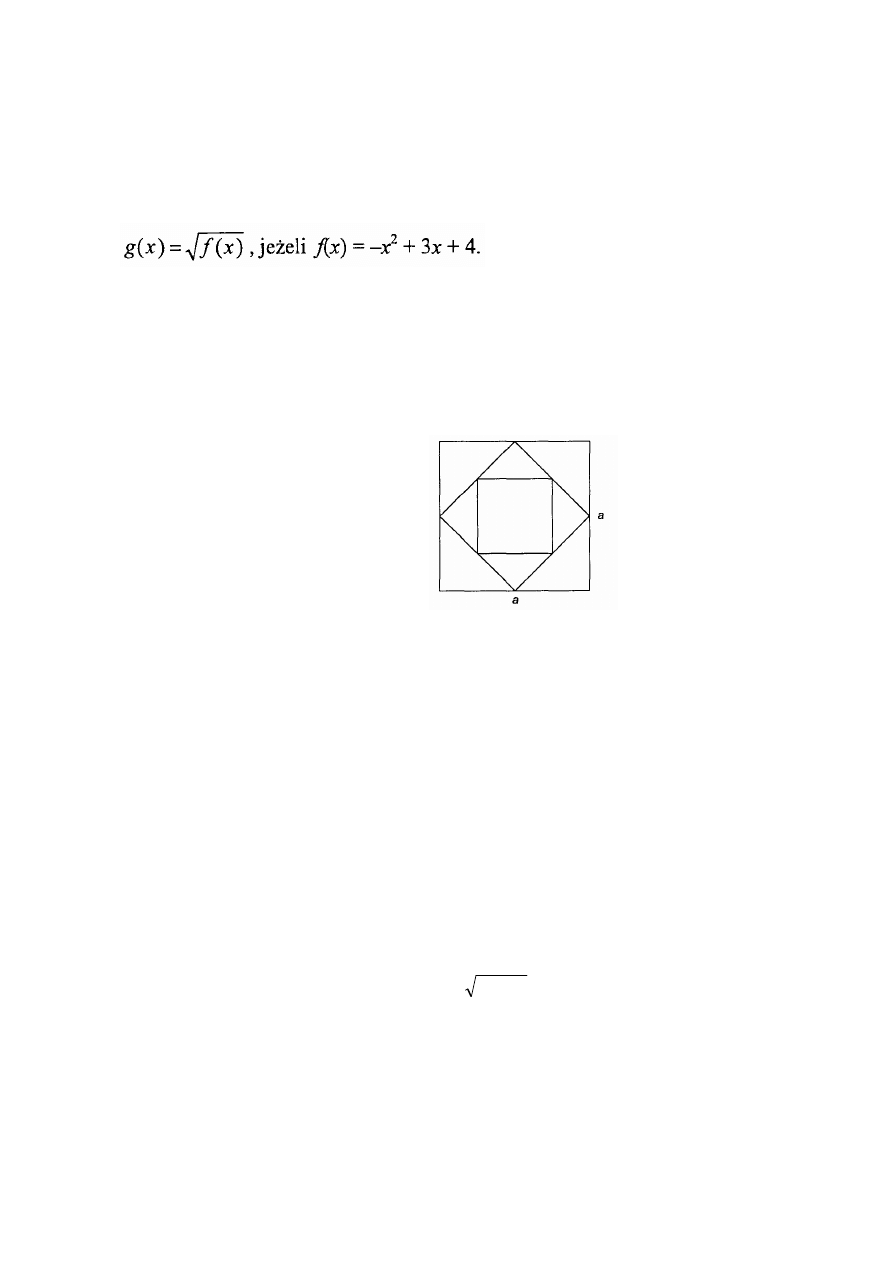
Zadanie 18 (5p)
Kieliszek ma kształt stożka, którego przekrój osiowy jest
trójkątem równobocznym.
a. Oblicz, jaką część pojemności kieliszka zajmuje wino
nalane do połowy wysokości kieliszka.
c.
Oblicz, do jakiej wysokości należy napełnić kieliszek
winem, aby objętość wina była równa połowie pojemności
kieliszka; w obliczeniach przyjmij, że
8
,
0
2
1
3
≈
Zadanie 19 (6p)
Doświadczenie polega na dwukrotnym rzucie symetryczną kostką sześcienną,
na której ściankach znajdują się cyfry 3, 4, 5, 6, 7, 8.
a. Oblicz prawdopodobieństwo zdarzenia, że suma oczek uzyskanych w
dwóch rzutach nie przekracza liczby 14.
b. Oblicz prawdopodobieństwo warunkowe, że suma oczek uzyskanych w
dwóch rzutach jest równa 10 pod warunkiem, że w każdym z rzutów
uzyskano wynik, będący liczbą nieparzystą.
©Irek.edu.pl
45
Zestaw 27. Poziom rozszerzony
Zadanie 11. (5 pkt.)
Oblicz największą wartość funkcji
Zadanie 12. (5 pkt.)
Rysunek przedstawia sposób wpisywania kolejnych kwadratów — środki
boków danego kwadratu stają się wierzchołkami następnego kwadratu. Oblicz
obwód i pole piątego kwadratu.
Zadanie 13. (7 pkt.)
Punkty A = (- 4, 3) i B = (6, 7) są symetryczne względem pewnej prostej k.
a) Wyznacz równanie prostej k.
b) Wyznacz obraz punktu P = (8, 2) w symetrii względem prostej k.
Zadanie 14. (7 pkt.)
W trójkąt równoramienny, którego ramię jest równe 5 cm, a podstawa równa
się 6 cm, wpisano prostokąt w ten sposób, że dwa jego wierzchołki leżą na
podstawie, a pozostałe leżą na ramionach trójkąta. Wyznacz obwód i pole
prostokąta jako funkcję jego wysokości.
Zadanie 15. (4 pkt.)
Dana jest funkcja określona wzorem
1
3
2
+
=
x
y
Udowodnij, że dla każdego x
∈ R funkcja ta spełnia warunek: y ∗y′ - 3x = O.
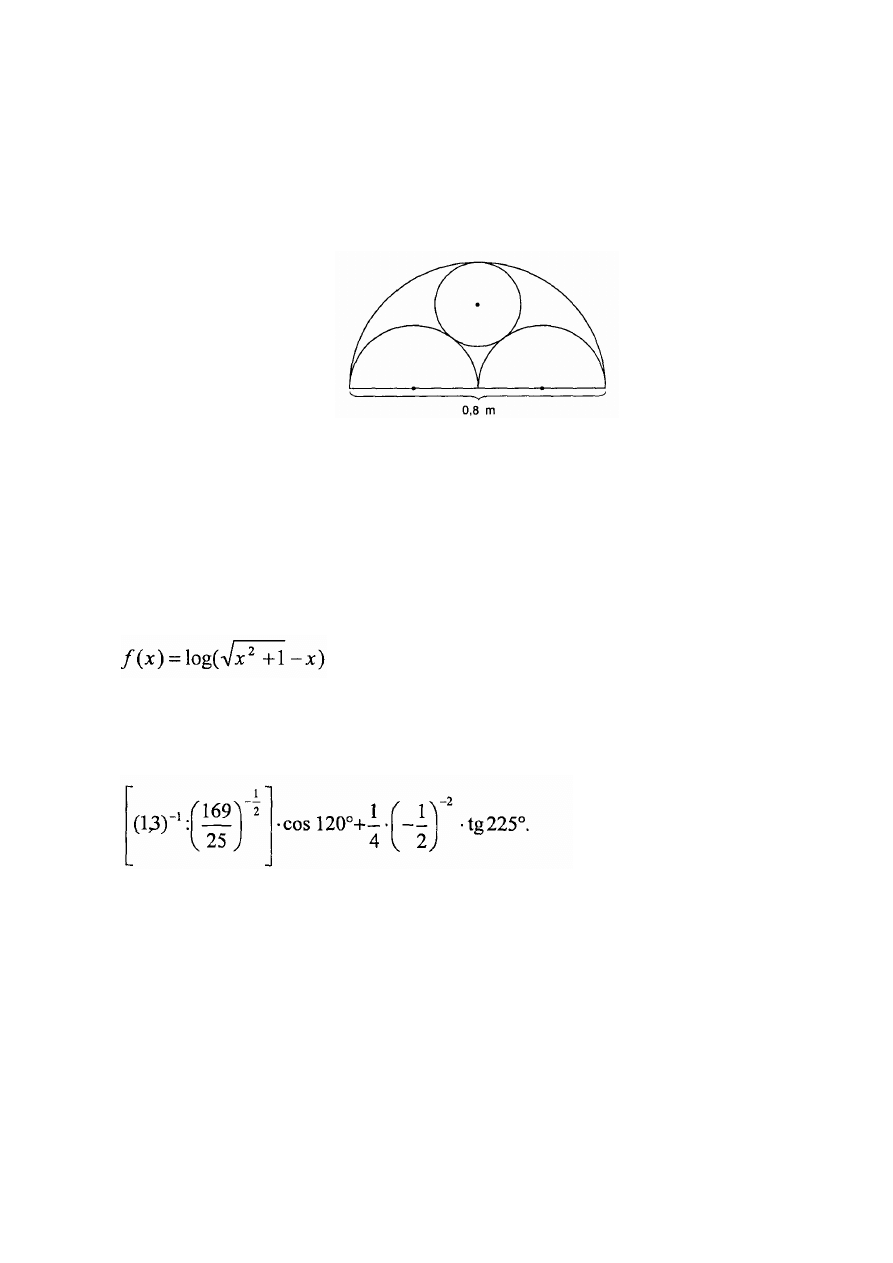
©Irek.edu.pl
46
Zadanie 16. (7 pkt.)
Okno ma kształt przedstawiony na rysunku, przy czym półkola i koło są
oszklone szkłem koloru żółtego, a pozostała część szkłem koloru błękitnego.
Oblicz pole części oszklonej szkłem koloru błękitnego, wiedząc, że średnica
wielkiego półkola ma 0,8 m.
Zadanie 17. (6 pkt.)
Soki owocowe rozlewane są do pudełek w kształcie prostopadłościanu, w
którym stosunek długości krawędzi podstawy jest równy 1 : 2, a objętość
wynosi 11. Jaka powinna być wysokość pudełka, aby zużyć jak najmniej
materiału na jego wykonanie?
Zadanie 18. (4 pkt.)
Wykaż, że funkcja f(x) jest nieparzysta.
Zadanie 19. (5 pkt.)
Oblicz wartość wyrażenia
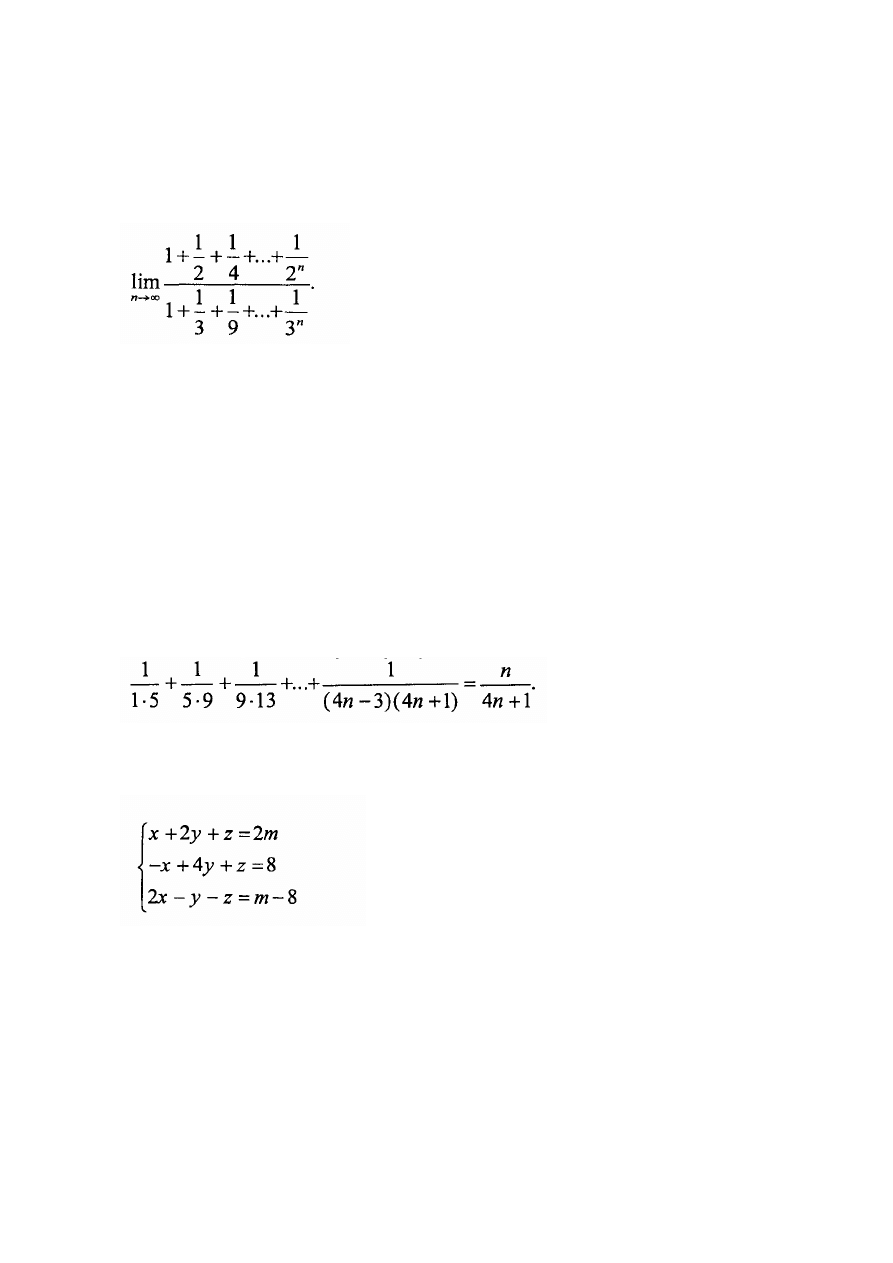
©Irek.edu.pl
47
Zestaw 28. Poziom rozszerzony
Zadanie 12. (3 pkt.)
Oblicz granicę:
Zadanie 13. (5 pkt.)
Jakie powinny być boki prostokąta o obwodzie 100 m, aby jego pole było
mniejsze od 400 m2?
Zadanie 14. (6 pkt.)
Napisz wzór funkcji, której wykres jest symetryczny do wykresu funkcji
określonej wzorem f(x) =x
2
— x —2 względem prostej y = 1.
Zadanie 15. (7 pkt.)
Stosując zasadę indukcji matematycznej, wykaż, że dla każdej liczby
naturalnej dodatniej zachodzi równość:
Zadanie 16. (6 pkt.)
Dany jest układ równań
a) Rozwiąż ten układ.
b) Dla jakich wartości parametru m rozwiązania x, y, z w podanej kolejności
tworzą ciąg arytmetyczny?
Zadanie 17. (7 pkt.)
Mając dane współrzędne punktu C = (—5, 0) kwadratu ABCD oraz
współrzędne punktu przecięcia się przekątnych S = (1, 2), wyznacz
współrzędne pozostałych wierzchołków kwadratu ABCD.
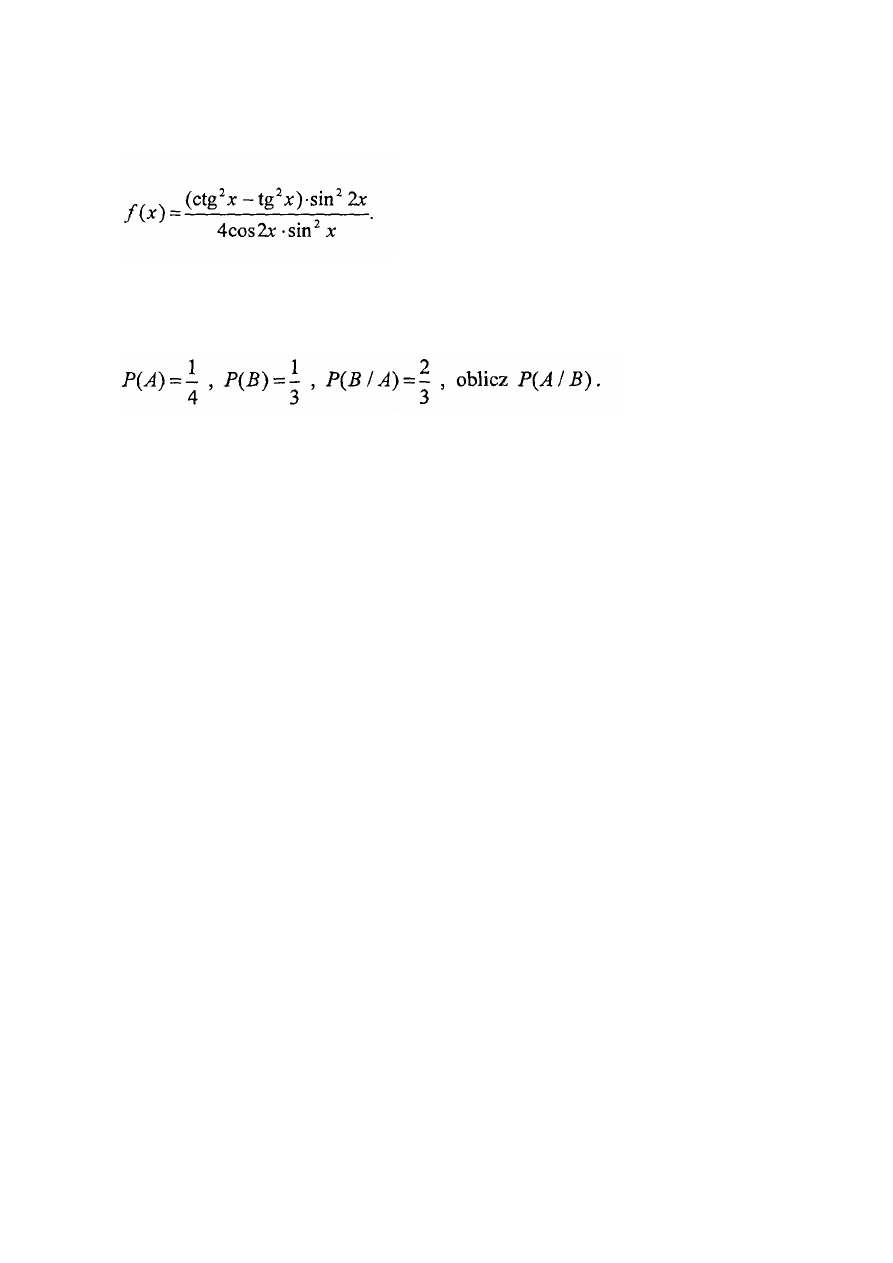
©Irek.edu.pl
48
Zadanie 18. (7 pkt.)
Wyznacz najmniejszą wartość funkcji:
Zadanie 19. (3 pkt.)
Wiedząc, że
Zadanie 20. (6 pkt.)
W pewnym szpitalu na oddziale położniczym badano wagę noworodków i
uzyskano następujące dane (w kg):
3,65 ; 4,0 ; 3,7 ; 3,9 ; 3,95 ; 3,75 ; 3,6 ; 3,7 ; 3,35 ; 3,4 ; 3,85 ; 3,15
4,25 ; 2,9 ; 2,85 ; 4,45 ; 3,7 ; 4,1.
a) Podaj najczęściej występującą wagę noworodków (dominantę).
b) Oblicz średnią wagę noworodków.
c) Oblicz, jaki procent noworodków ma wagę poniżej 3 kg.
d) Podaj rozstęp wyników (różnica między największą a najmniejszą wagą).
e) Jakie jest prawdopodobieństwo, że losowo wybrany noworodek ma wagę
powyżej 3 kg?
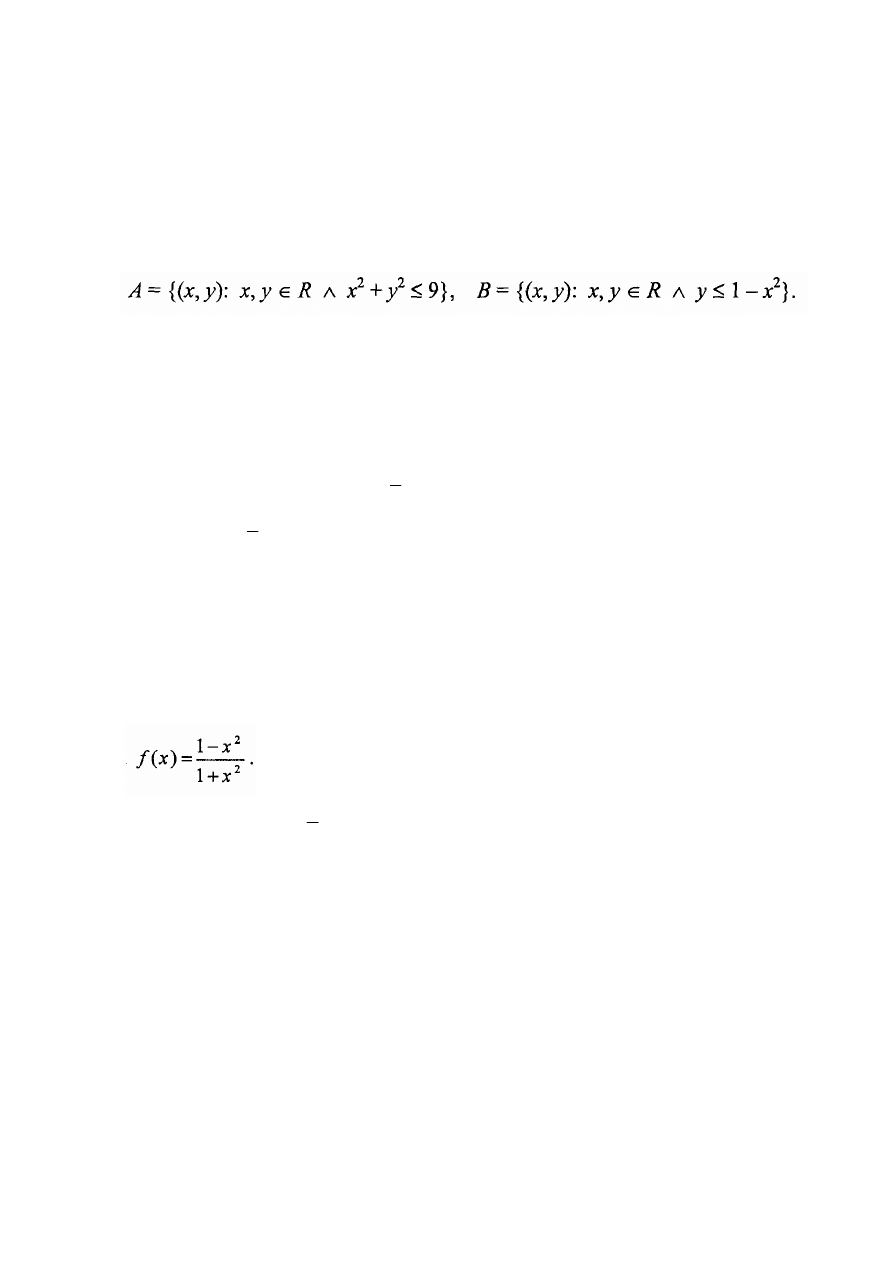
©Irek.edu.pl
49
Zestaw 29. Poziom rozszerzony
Zadanie 12. (6 pkt.)
Dane są zbiory:
Na płaszczyźnie współrzędnych zilustruj zbiory A
∩ B i A ∩ B`.
Zadanie 13. (6 pkt.)
Dana jest funkcja f określona wzorem f(x) = ax
2
+ bx - 3. Suma miejsc
zerowych funkcji f jest równa 2
2
1
, a suma odwrotności jej miejsc zerowych
jest równa —1
3
2
.
a) Wyznacz współczynniki a i b.
b) Podaj zbiór wartości funkcji f
c) Określ przedziały monotoniczności funkcji f
Zadanie 14. (4 pkt.)
Funkcja f określona jest wzorem
Rozwiąż równanie
)
(
1
x
f
x
f
=
Zadanie 15. (5 pkt.)
Oblicz siódmy wyraz ciągu (a
n
), jeżeli suma jego pierwszych n wyrazów jest
równa 5n
2
- 4n + 1.
Zadanie 16. (6 pkt.)
W kulę o promieniu długości R wpisano walec o największej objętości.
Wyznacz stosunek objętości kuli do objętości tego walca.
©Irek.edu.pl
50
Zadanie 17. (8 pkt.)
W pojemniku znajduje się 200 wybrakowanych części. 60 sztuk odrzucono z
powodu wystąpienia wady A, 40 sztuk z powodu wady B, pozostałe z powodu
wady C. Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że
wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie:
a) po jednej części z każdą wadą,
b) dwie części z wadą A,
c) dwie części z wadą B,
d) wszystkie części z tą samą jedną wadą.
Zadanie 18. (5 pkt.)
Oblicz pole i obwód trójkąta równobocznego wpisanego w okrąg o równaniu
x
2
+y
2
- 6x + l0y + 16=0.
Zadanie 19. (10 pkt.)
Korzystając z następującego zestawu danych:
oblicz:
a) średnią arytmetyczną
b) medianę i dominantę,
c) wariancję i odchylenie standardowe zestawu danych.
©Irek.edu.pl
51
Zestaw 30. Poziom rozszerzony
Zadanie 11. (7 pkt.)
Dla jakich wartości parametru m miejsca zerowe funkcji
f(x) = (2m
2
- 1)x
2
- 2mx + 1 spełniają warunek x
1
2
+x
2
2
>2?
Zadanie 12. (5 pkt.)
Oblicz wartość wyrażenia
Zadanie 13. (5 pkt.)
Basia postanowiła codziennie biegać. Pierwszego dnia biegała 20 minut, a
każdego następnego dnia o 5 minut dłużej.
a) Którego dnia Basia będzie biegać 1,5 godziny?
b) Po ilu dniach łączny czas biegania przekroczy 10 godzin?
Zadanie 14. (4 pkt.)
Półkole o promieniu długości 1 zwinięto w stożek.
Oblicz:
a) miarę kąta rozwarcia przekroju osiowego stożka,
b) pole koła wpisanego w przekrój osiowy tego stożka.
Zadanie 15 (4pkt)
Dla jakiej wartości m wykres funkcji y = x + m ma co najmniej jeden punkt
wspólny z okręgiem o promieniu r, którego środkiem jest początek układu
współrzędnych?
Zadanie 16. (8 pkt.)
Dwa wierzchołki prostokąta leżą na osi x, a pozostałe należą do paraboli o
równaniu f(x) = 4 – x
2
i znajdują się powyżej osi x.
a) Podaj wzór funkcji opisującej pole tego prostokąta w zależności od jego
podstawy.
b) Dla jakiej długości podstawy pole tego prostokąta jest równe 6?
c) Dla jakiej długości podstawy pole tego prostokąta jest największe?
©Irek.edu.pl
52
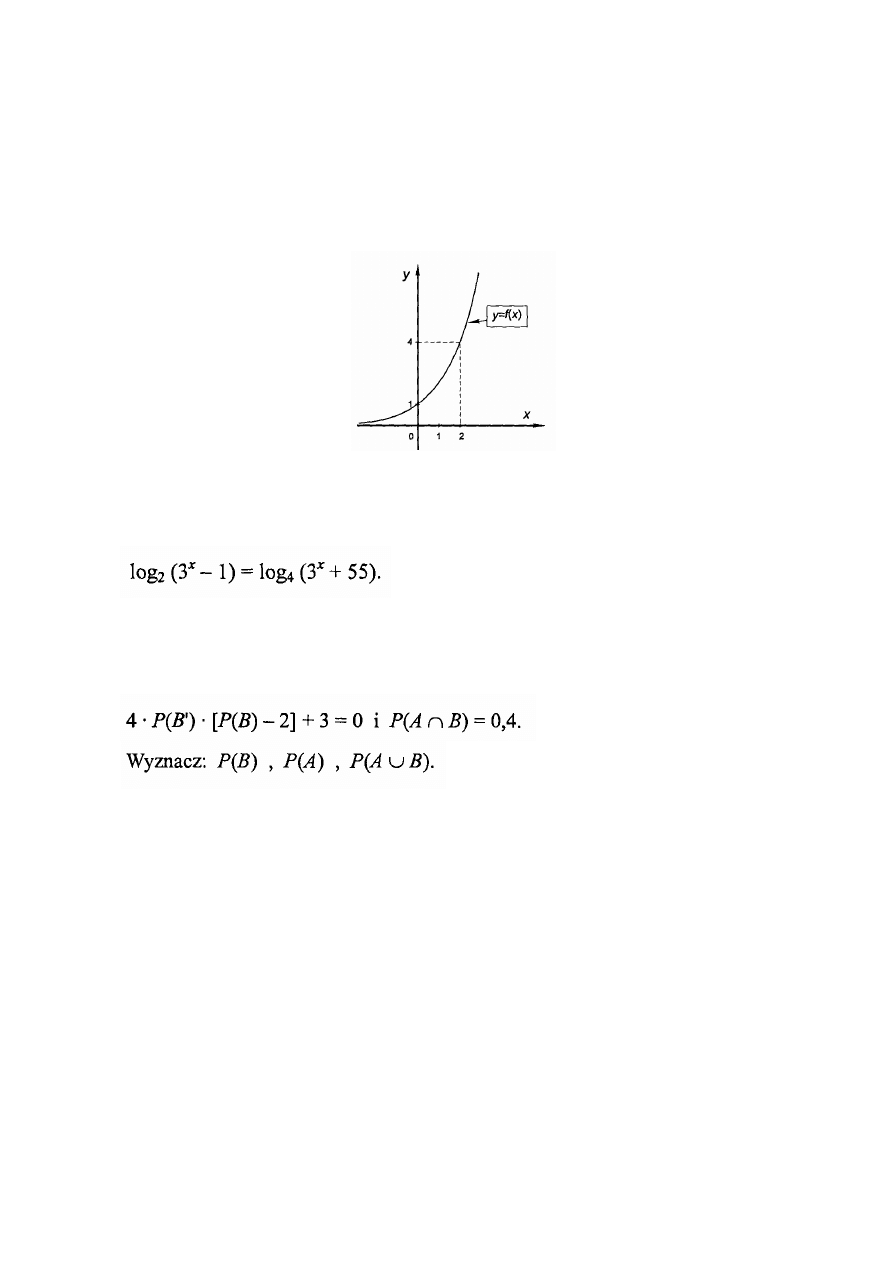
Zadanie 17. (5 pkt.)
Na rysunku przedstawiono wykres pewnej funkcji wykładniczej f
Rozwiąż nierówność:
f(x + l)+ 3 f(x— 1)— 5f(x)+ 6<0.
Zadanie 18. (6 pkt.)
Rozwiąż równanie:
Zadanie 19. (6 pkt.)
Wiadomo, że zdarzenia A i B są niezależne oraz

©Irek.edu.pl
53
Zestaw 31. Poziom rozszerzony
Zadanie 12. (8 pkt.)
Wyznacz A
∪B, A∩B, A\B, B\A zbiorów:
Zadanie 13. (6 pkt.)
Działka leśna zawierała przed 15 laty 250 000 m
3
drewna, a obecnie zawiera
350 000 m
3
. O ile procent przeciętnie wzrasta ilość drewna na tej działce w
ciągu roku (zakładamy stały przyrost procentowy)?
Zadanie 14. (5 pkt.)
Suma współczynników a, b, c równania ax
2
+ bx + c = O wynosi 24 Różnica
między tymi współczynnikami jest stała, a jednym z rozwiązań równania jest
liczba—3 Znajdź drugie rozwiązane tego równania.
Zadanie 15. (5 pkt.)
Dla jakich wartości parametru p wielomian W(x) = x
3
— 3px + 9p —27 ma
trzy różne pierwiastki rzeczywiste?
Zadanie 16. (5 pkt.)
W trójkącie ABC mamy |AB| = 6, |AC| = 12, |
∠BAC| = 120°.
Oblicz:
a) sin |
∠ABC|,
b) obwód trójkąta ABC.
Zadanie 17. (5 pkt.)
Oblicz objętość stożka wpisanego w kulę o promieniu długości R, wiedząc, że
kąt rozwarcia stożka ma miarę 2
α.
Zadanie 18. (5 pkt.)
Jaką wysokość i jaki promień powinna mieć puszka na konserwy w kształcie
walca o objętości 128
π cm
3
, aby na jej wykonanie zużyć najmniej materiału?
Zadanie 19. (5 pkt.)
Pogotowie ratunkowe dysponuje pewną liczbą karetek. Wciągu kilku miesięcy
pracy stwierdzono, że w ciągu doby dana karetka będzie na miejscu w bazie z
prawdopodobieństwem 0,4 jednakowym dla każdej karetki. Oblicz, ile karetek
musi mieć do dyspozycji pogotowie, aby w razie wypadku
prawdopodobieństwo tego, że co najmniej jedna karetka była na miejscu w
bazie, było większe od 0,9.
Zadanie 20. (6 pkt.)
Kasia w ciągu godziny zdradziła sekret Ani trzem koleżankom. Przyjmując, że
każda z koleżanek w ciągu kolejnej godziny opowie sekret Ani trzem innym
koleżankom (nie znającym go jeszcze), oblicz, po jakim czasie sekret będzie
znało ponad 360 osób (wynik podaj w pełnych godzinach).

©Irek.edu.pl
54
Zestaw 32. Poziom rozszerzony
Zadanie 12. (7 pkt.)
Suma miejsc zerowych funkcji kwadratowej f wynosi —3, a iloczyn miejsc
zerowych jest równy
4
7
−
. Do wykresu funkcji f należy punkt P (0, -7).
a) Znajdź wzór funkcji f
b) Dla jakich argumentów wartości funkcji f są ujemne?
c) Wyznacz przedziały monotoniczności funkcji f
Zadanie 13. (3 pkt.)
Wykaż, że
2
7
2
5
7
2
5
3
3
=
−
−
+
Zadanie 14. (4 pkt.)
Czy ilustracje geometryczne zbiorów:
A={(x,y): x,y
∈ℜ I x
2
+y
2
=1}, B={(x,y): x,y
∈ℜ i
2
1
x
y
−
=
},
{(x,y): x,y
∈ℜ i x
2
+y
2
=1 i y
≤ O}
są wykresami funkcji? Odpowiedź uzasadnij.
Zadanie 15. (8 pkt.)
Dana jest funkcja f(x) = (2x
2
- 1) (x + 1).
a) Rozwiąż równanie f(sin x) = O.
b) Rozwiąż nierówność f(2
x
) <2
x
+ 1.
Zadanie 16. (5 pkt.)
Za 3 książki, których ceny tworzą ciąg geometryczny, zapłacono 76 zł.
Najdroższa z tych książek kosztowała o 4 zł mniej niż dwie pozostałe razem.
Ile kosztowała każda książka?
Zadanie 17. (8 pkt.)
Dwóch równorzędnych przeciwników gra w szachy. Co jest bardziej
prawdopodobne:
a) wygranie dwóch partii z trzech, czy czterech partii z sześciu rozegranych,
b) wygranie nie mniej niż dwóch partii z trzech, czy nie mniej niż czterech
partii z sześciu rozegranych? (Remisów nie uwzględniamy).
Zadanie 18. (5 pkt.)
W prostopadłościanie przekątna d jest nachylona do płaszczyzny podstawy
pod kątem
β. Kąt pomiędzy przekątną podstawy i jej bokiem ma miarę α.
Oblicz pole powierzchni bocznej i objętość prostopadłościanu.
Zadanie 19. (6 pkt.)
Puszka na konserwy ma kształt walca. Jaką wysokość i jaki promień podstawy
powinna mieć puszka, aby przy objętości puszki 250 cm
3
zużyć jak najmniej
materiału na jej wykonanie?
Zadanie 20. (4 pkt.)
Dany jest okrąg o równaniu (x + 2)
2
+ (y — 3)
2
= 12 oraz punkt A = (-2, 0).
Napisz równanie symetralnej odcinka, którego końcami są dany punkt A i
ś
rodek S danego okręgu.

©Irek.edu.pl
55
Zestaw 33. Poziom rozszerzony
Zadanie 13. (8 pkt.)
Dla jakich wartości parametru a równanie x
2
- 2x = 2x loga + log
2
a - 1 ma dwa
różne pierwiastki dodatnie?
Zadanie 14. (8 pkt.)
Sporządź wykres funkcji
1
2
2
)
(
−
−
+
=
x
x
x
f
Zbadaj ciągłość tej funkcji w punkcie x
0
= -2.
Zadanie 15. (3 pkt.)
Rzucamy dwiema kostkami sześciennymi. Oblicz prawdopodobieństwo
wyrzucenia sumy oczek równej 4 pod warunkiem, że bezwzględna wartość
różnicy oczek wyrzuconych na poszczególnych kostkach jest równa 2.
Zadanie 16. (5 pkt.)
Liczba x jest pierwiastkiem równania 2 log x = log (4x — 4), zaś z jest
pierwiastkiem równania
81
3
1
4
3
=
−
+
z
z
.
a) Wyznacz liczbę y, tak aby liczby x, y, z były trzema kolejnymi wyrazami
ciągu geometrycznego.
b)
Znajdź sumę sześciu początkowych wyrazów powyższego ciągu
geometrycznego.
Zadanie 17. (7 pkt.)
Rozwiąż równanie: sinx +sin2x +sin3x = 4cosxcos
2
x
cos
2
3x
.
Zadanie 18. (5 pkt.)
Napisz równanie okręgu symetrycznego do okręgu o równaniu
x
2
+y
2
- 4x - 10y + 20 = 0 względem prostej o równaniu x - 2y - 2 = 0.
Zadanie 19. (8 pkt.)
Jeden z boków kwadratu ABCD jest zawarty w prostej o równaniu
2x –y -2 = 0. Wierzchołek A ma współrzędne (1, 5).
a) Znajdź współrzędne pozostałych wierzchołków tego kwadratu.
b) Oblicz pole kwadratu ABCD.
Zadanie 20. (6 pkt.)
Podstawą ostrosłupa jest trójkąt prostokątny, którego kąt ostry ma miarę
α.
Wszystkie krawędzie boczne mają długość k i są nachylone do podstawy pod
kątem o mierze
β. Oblicz objętość tego ostrosłupa.
©Irek.edu.pl
56
Zestaw 34. Poziom rozszerzony
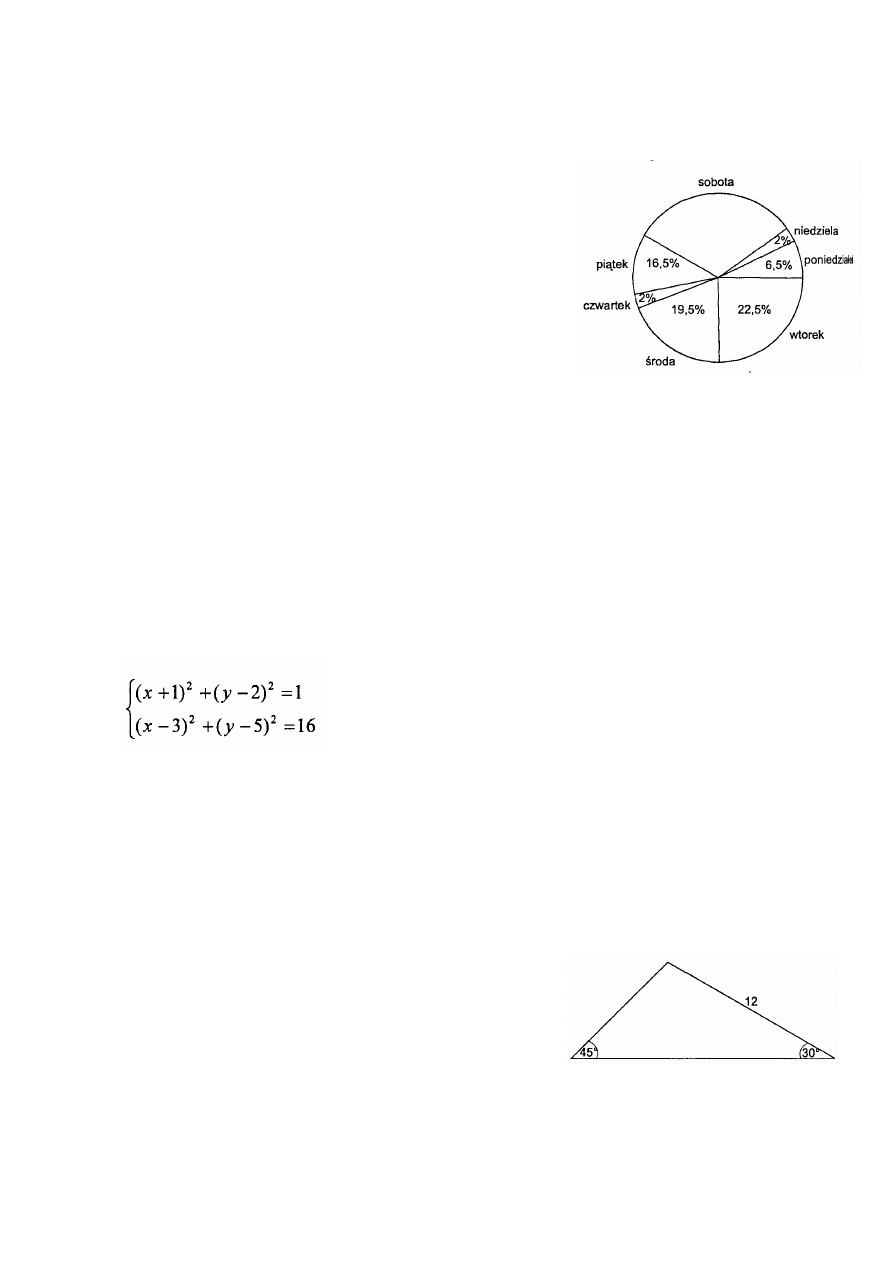
Zadanie 12. (6 pkt.)
Utarg pewnego sklepu w ciągu tygodnia wynosi
2400 zł. Procentowy rozkład utargu w poszczegól-
nych dniach przedstawiono na diagramie kołowym.
a) Przedstaw dane w postaci diagramu słupkowego.
b) Oblicz średni utarg dzienny.
c) Jaki procent tygodniowego utargu stanowi utarg
w sobotę?
Zadanie 13. (7 pkt.)
Wyznacz m i n, tak aby równanie x
2
+ 3mnx + (m
2
+ n
2
) = O miało dwa
rozwiązania; x
1
= 1 oraz x
2
= 5.
Zadanie 14. (5 pkt.)
Wykaż, że jeżeli a
≥ 0 i b ≥ 0, to prawdziwa jest nierówność:
(a
5
- 2a
4
b + a
3
b
2
+ a
4
b – 2a
3
b
2
+ a
2
b
3
)
≥0.
Zadanie 15. (4 pkt.)
Uzasadnij, że układ równań:
ma dokładnie jedno rozwiązanie.
Zadanie 16. (6 pkt.)
Oblicz sumę 1 - 4+7-10+13 -16+... „ gdy suma ta ma:
a) 2n składników,
b) 2n + 1 składników,
c) n składników.
Zadanie 17. (5 pkt.)
Wyznacz obwód i pole trójkąta przedstawionego
na rysunku.
Zadanie 18. (7 pkt.)
Rozwiąż nierówność log
m
(4- x
2
)
≥ log
m
(6x - 3) z niewiadomą x, wiedząc, że
liczba 1 należy do zbioru rozwiązań tej nierówności.
©Irek.edu.pl
57
Zadanie 19 (4pkt)
Rysunek przedstawia fragment wykresu funkcji różniczkowalnej f. Podaj
rozwiązania równania f `(x)=0 należące do przedziału < -5;7>.
Zadanie 20. (6 pkt.)
Sześcian o krawędzi długości a przecięto płaszczyzną przechodzącą przez
przekątną dolnej podstawy i środki dwóch krawędzi drugiej podstawy. Oblicz
pole i obwód otrzymanego przekroju.
©Irek.edu.pl
58
Zestaw 35. Poziom rozszerzony
Zadanie 12. (5 pkt.)
Sporządź wykres funkcji f(x) = |x + 3| - 2.
a) Wyznacz taki wektor
→
v
o jaki należy przesunąć wykres funkcji f aby
otrzymać wykres funkcji parzystej.
b) Udowodnij, że funkcja otrzymana w wyniku przesunięcia wykresu funkcji f
o wektor
→
v
jest funkcją parzystą.
Zadanie 13. (5 pkt.)
Dane jest przekształcenie P(x, y)
→ P(2y, - x + 1). Oblicz pole trójkąta
będącego obrazem trójkąta ABC o wierzchołkach A= (0, 0), B = (0,2),
C = (-2, -1) w tym przekształceniu. Sprawdź, czy przekształcenie P jest
izometrią.
Zadanie 14. (4 pkt.)
Oblicz granicę:
Zadanie 15. (6 pkt.)
a)
Sporządź wykres funkcji:
b) Na podstawie wykresu funkcji ustal liczbę pierwiastków równania f(x) = k
w zależności od parametru k.
Zadanie 16. (5 pkt.)
Wyznacz dziedzinę funkcji f(m) =
2
1
1
1
x
x
+
, gdzie x
1
, x
2
są różnymi
pierwiastkami równania x
2
- 2x + m
2
-3 =0.
Zadanie 17. (6 pkt.)
Rozwiąż równanie

©Irek.edu.pl
59
Zadanie 18. (6 pkt.)
W sześcianie o boku długości a wybieramy losowo cztery wierzchołki.
a) Oblicz prawdopodobieństwo, że wybrane punkty będą wierzchołkami
prostokąta.
b)
Oblicz sumę pól wszystkich takich prostokątów.
Zadanie 19. (5 pkt.)
Napisz równanie stycznej do krzywej f(x) =4 - x
3
, wiedząc, że jest ona
równoległa do prostej 3x +y = 5.
Zadanie 20. (8 pkt.)
Wódz indiański wysłał trzech zwiadowców na zachód, północ i wschód.
Każdy z nich oddalił się o 5 km od obozu i miał w zasięgu wzroku teren o
promieniu 5 km.
a) Jaki obszar kontrolują zwiadowcy?
b) O ile zmniejszy się kontrolowany teren, jeśli jeden ze zwiadowców zostanie
pojmany przez wrogie plemię (rozpatrz dwa przypadki)?
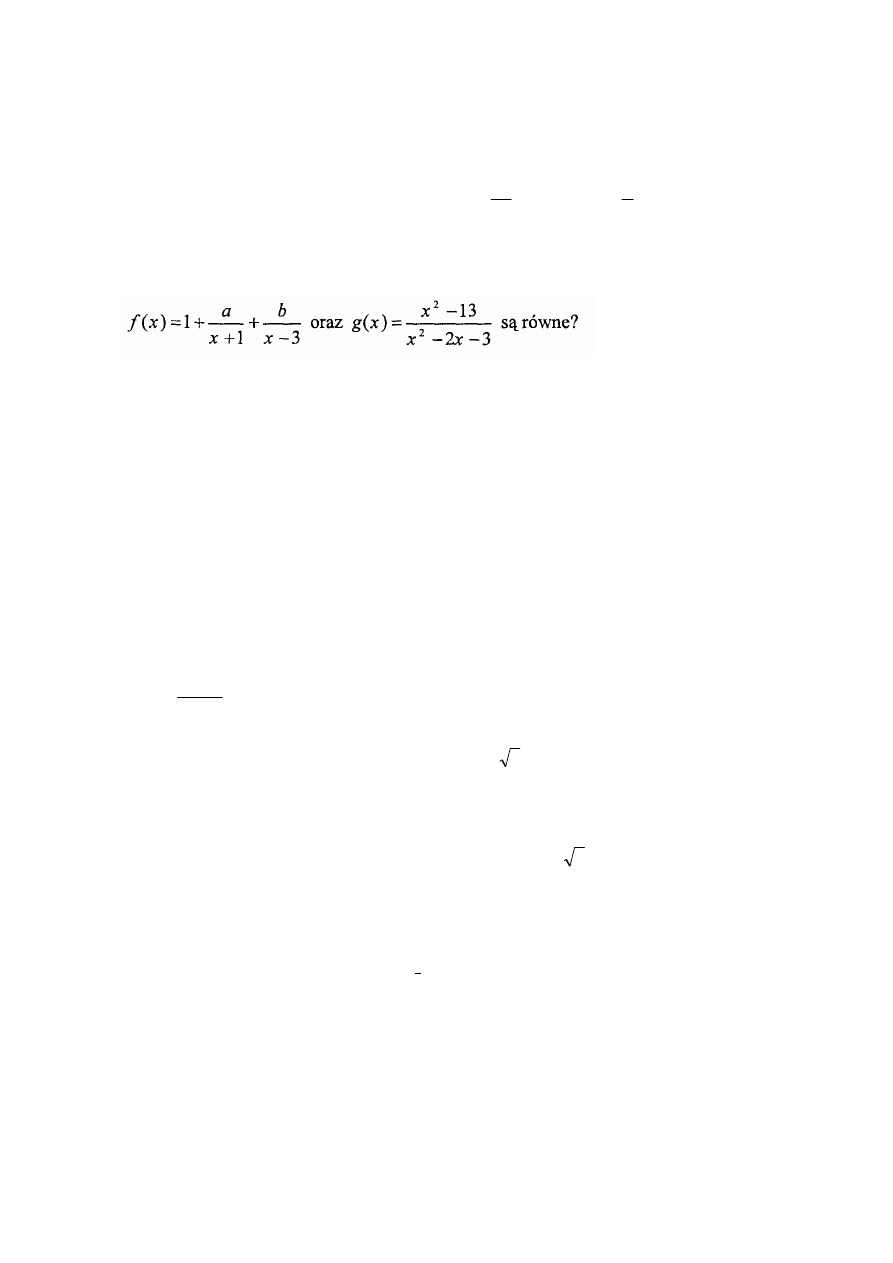
©Irek.edu.pl
60
Zestaw 36. Poziom rozszerzony
Zadanie 12. (3 pkt.)
Ś
rednia arytmetyczna liczb a i b jest równa
13
9a
. Ile wynosi
a
b
?
Zadanie 13. (5 pkt.)
Dla jakich a i b funkcje
Zadanie 14. (6 pkt.)
Dane są funkcje: f(x) = mx
2
+ 1 oraz g(x)= log
a
x.
Wiedząc, że do wykresu funkcji f należy punkt A = (-2, -3), a do wykresu
funkcji g należy punkt B = (9, 2), wyznacz:
a) wzory funkcji f i g oraz sporządź ich wykresy,
b) zbiór tych argumentów, dla których g(x) <f(x).
Zadanie 15. (6 pkt.)
Dany jest trójkąt o bokach długości 3, 6 i 7. Oblicz:
a) pole danego trójkąta,
b) długość promienia okręgu opisanego na tym trójkącie.
Zadanie 16. (6 pkt.)
Wyznacz przedziały monotoniczności oraz ekstrema lokalne funkcji
f(x) =
2
3
3
x
x
−
.
Zadanie 17. (5 pkt.)
Pole przekroju osiowego stożka jest równe 9
3
. Tworząca stożka jest
nachylona do podstawy pod kątem o mierze 30°. Oblicz objętość i pole
powierzchni bocznej tego stożka.
Zadanie 18. (6 pkt.)
a) Napisz równanie okręgu o promieniu długości r =
5
wiedząc, że do okręgu
należą punkty A=(5,l) „ B=(1,3).
c)
Napisz równanie stycznej do okręgu poprowadzonej w punkcie A.
Zadanie 19. (7 pkt.)
Dane są zbiory: A = {x: x
∈R i
(
)
0
2
8
log
2
3
1
≥
+
+ x
x
} ,
B={x: x
∈ R i 3
x+1
+3
x - 1
<30}
Wyznacz zbiory: A
∪B , A∩B „ A`∩B`.
Zadanie 20. (6 pkt.)
Dana jest funkcja określona wzorem f(x) = cos 2x - (1 - sin x).
a) Wyznacz miejsca zerowe funkcji f w przedziale <-
π; π>.
b) Rozwiąż nierówność f(x)> 0 w przedziale <-
π; π>.
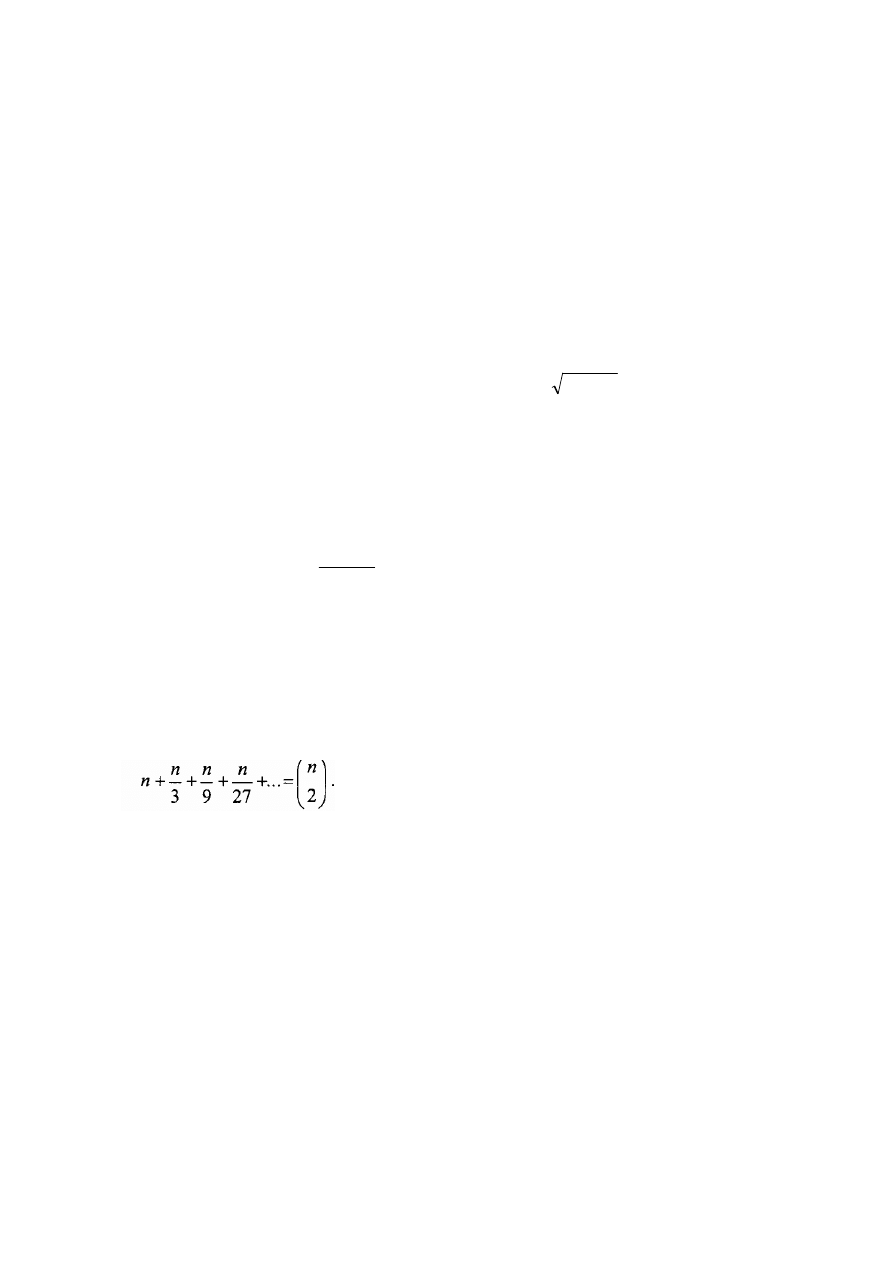
©Irek.edu.pl
61
Zestaw 37. Poziom rozszerzony
Zadanie 12. (4 pkt.)
Niech 1 oznacza iloczyn czterech kolejnych liczb naturalnych. Wykaż, że
1 + 1 jest kwadratem pewnej liczby naturalnej.
Zadanie 13. (5 pkt.)
Miejscem zerowym funkcji f(x) = ax + b jest liczba log
2
4, a współczynnik
kierunkowy jest równy granicy ciągu a
n
, gdzie a
n
=
n
n
n
−
+ 3
2
Sporządź wykresy funkcji:
a) y= - f(x),
b) y = f( - x)
Zadanie 14. (8 pkt.)
Dana jest funkcja f(x)=
(
)
2
2
2
3
x
x
x
−
−
.
a) Rozwiąż nierówność f(x)
≤ x.
b) Ustal liczbę rozwiązań równania |f(x)| = m w zależności od parametru m.
Zadanie 15. (4 pkt.)
Rozwiąż równanie, w którym lewa strona jest sumą zbieżnego szeregu
geometrycznego
Zadanie 16. (3 pkt.)
Oblicz bez użycia kalkulatora cos
4
105° - sin
4
105°.
Zadanie 17. (6 pkt.)
Robert znalazł w garażu kwadratowy arkusz blachy o długości 3 dm. Chce z
niego zbudować pojemnik w kształcie prostopadłościanu. Poprosił o pomoc
ojca. Razem zastanawiają się, jakie kwadraty należy wyciąć w narożnikach
arkusza, aby objętość pojemnika była największa. Pomóż im rozwiązać ten
problem.

©Irek.edu.pl
62
Zadanie 18. (5 pkt.)
Wyznacz współrzędne punktów wspólnych prostej o równaniu -x + y -2 = 0 i
okręgu o środku S = (-3, 2) i promieniu długości 3.
Zadanie 19. (7 pkt.)
Oblicz pole powierzchni całkowitej i objętość bryły, która powstaje w wyniku
obrotu rombu o długości a i kącie ostrym
α wokół prostej zawierającej jeden z
boków tego rombu.
Zadanie 20. (3 pkt.)
Dwaj strzelcy trafiają do celu z prawdopodobieństwem równym 0,8 i 0,7.
Strzelcy oddają po jednym strzale. Oblicz prawdopodobieństwo, że cel
zostanie trafiony:
a) dwa razy,
b) dokładnie raz,
c) co najwyżej raz.
Zadanie 21. (5 pkt.)
Rozwiąż równanie
2
1
log
log
2
4
1
−
=
⋅
x
x
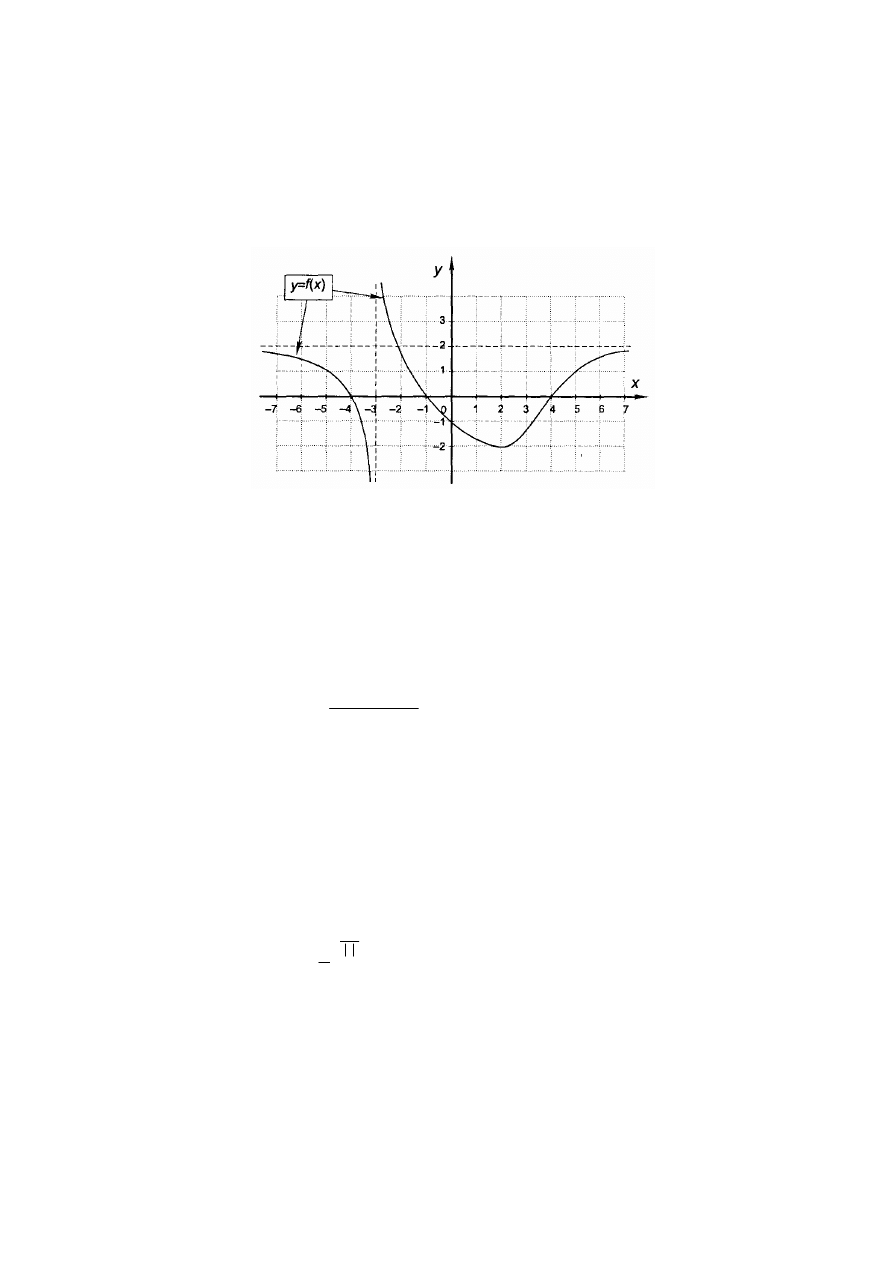
©Irek.edu.pl
63
Zestaw 38. Poziom rozszerzony
Zadanie 13. (5 pkt.)
Korzystając z wykresu funkcji y =f(x), wyznacz liczbę pierwiastków równania
f(x) = m w zależności od parametru m i sporządź wykres tej zależności.
Zadanie 14. (5 pkt.)
Budując halę sportowa, należy wykopać pod fundamenty ziemię o objętości
8000 m
3
. Przed rozpoczęciem prac skrócono termin prac o 5 dni i przez to
dzienna norma wykopu ziemi wzrosła o 80 m
3
. Ile dni trwały prace? O ile
procent podwyższono normę?
Zadanie 15. (7 pkt.)
Dana jest funkcja f(x) =
3
10
6
2
+
+
+
x
x
x
a) Wyznacz asymptoty wykresu funkcji f
b) Określ przedziały monotoniczności tej funkcji.
c) Znajdź ekstrema lokalne funkcji f
Zadanie 16. (4 pkt.)
Rozwiąż nierówność: sin
2
x < 1 - cos x dla x
∈ <0; 2π>.
Zadanie 17. (5 pkt.)
Rozwiąż nierówność:
4
2
1
4
≤
+
x
x
Zadanie 18. (6 pkt.)
Dany jest okrąg (x - 2)
2
+ (y - 1)
2
= 3,
a) Oblicz pole rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę
60
0
.
b) Oblicz długości przekątnych rombu.
c) Oblicz pole trójkąta równobocznego wpisanego w ten okrąg.
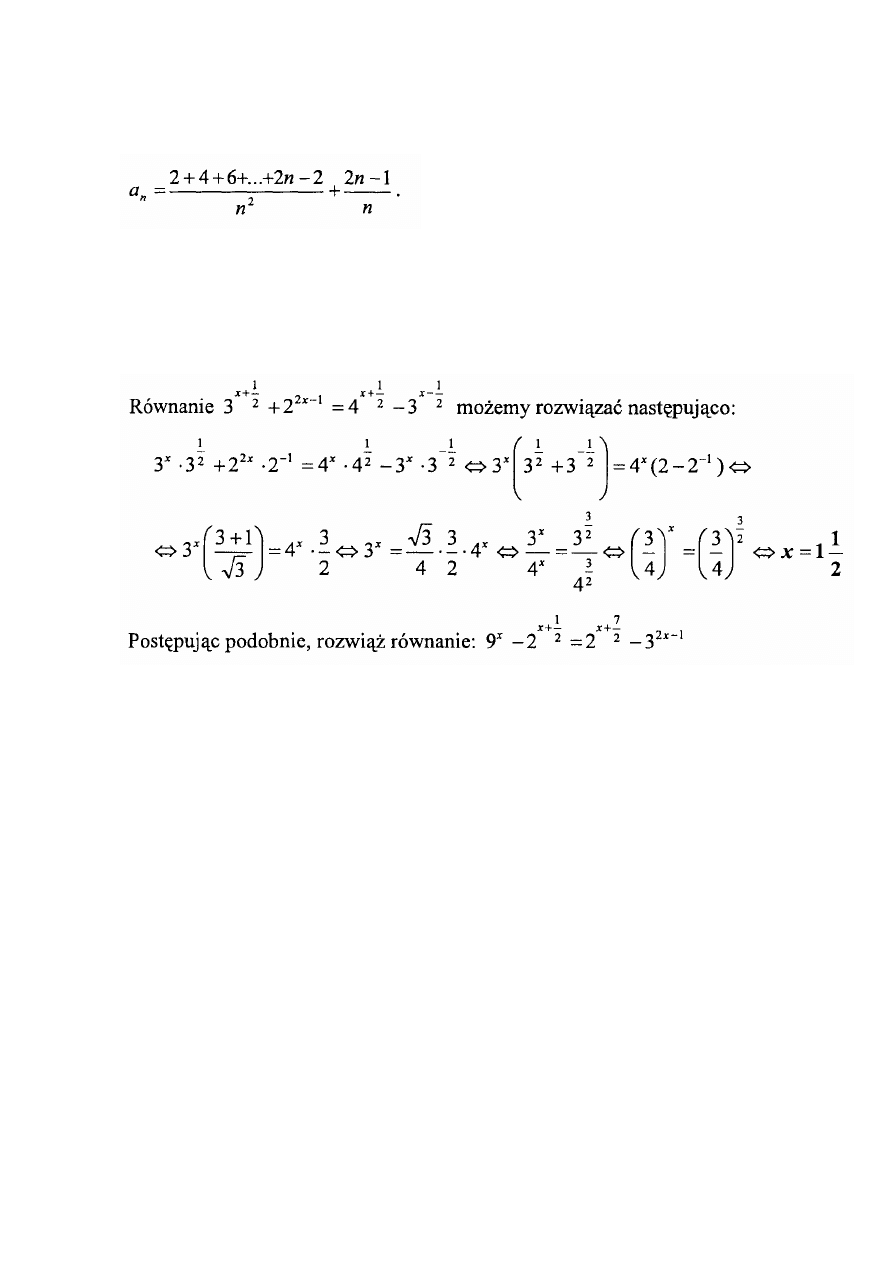
©Irek.edu.pl
64
Zadanie 19. (6 pkt.)
Zbadaj monotoniczność i oblicz granicę ciągu (a
n
), gdy
Zadanie 20. (5 pkt.)
Przekątna prostopadłościanu o długości d tworzy z odpowiednimi ścianami
bocznymi kąty o miarach
α i β. Wyznacz objętość tego prostopadłościanu.
Zadanie 21. (4 pkt.)
Zadanie 22. (3 pkt.)
Rzucamy pięć razy monetą. Jaka jest najbardziej prawdopodobna liczba
wyrzuconych orłów?

©Irek.edu.pl
65
Zestaw 39. Poziom rozszerzony
Zadanie 11. (7 pkt.)
Dany jest wielomian W(x) = -x
4
+ ax
3
+ 7x
2
+ bx - 12.
a) Wyznacz a i b, wiedząc, że wielomian W jest podzielny przez trójmian
P(x) = x
2
+ 3x + 2.
c)
Dla wyznaczonych a i b rozwiąż nierówność W(x) ≥ 0.
Zadanie 12. (7 pkt.)
Podaj ilustrację graficzną równania log
y
x + log
x
y =
3
10
Zadanie 13. (5 pkt.)
Dla jakich wartości parametru m liczby sin
α i cos α są pierwiastkami
równania x
2
+ mx -
4
1
= 0?
Zadanie 14. (5 pkt.)
Dany jest trójkąt równoboczny o boku długości a. W trójkąt ten wpisujemy
trójkąty równoboczne w ten sposób, że wierzchołkami nowego trójkąta są
ś
rodki boków poprzedniego trójkąta.
a) Oblicz pole dziesiątego trójkąta.
b) Oblicz sumę pól wszystkich utworzonych w ten sposób trójkątów.
Zadanie 15. (5 pkt.)
Napisz równanie stycznej do wykresu funkcji f(x) =
1
2
−
x
w punkcie x
0
= 5.
Zadanie 16. (6 pkt.)
Rozwiąż nierówność 2
|x-1|+1
+ 2
2|x-1|
+ 2 > 6.
Zadanie 17. (4 pkt.)
Z talii 24 kart losujemy 3 razy ze zwracaniem po jednej karcie. Oblicz
prawdopodobieństwo, że co najmniej 2 razy wylosujemy kiera.
Zadanie 18. (6 pkt)
Kąt rozwarcia stożka ma miarę
4
π
. Jaki jest kąt wycinka kołowego, który po
zwinięciu tworzy powierzchnię boczną tego stożka?
Zadanie 19. (5 pkt.)
Dane są wierzchołki A = (-6, 2) , B = (2, -2) trójkąta ABC oraz punkt
H = (1, 2), w którym przecinają się wysokości tego trójkąta. Oblicz
współrzędne trzeciego wierzchołka trójkąta.

©Irek.edu.pl
66
Zestaw 40. Poziom rozszerzony
Zadanie 12. (6 pkt.)
Dla jakiego parametru m rozwiązaniem układu równań
jest para liczb o przeciwnych znakach? Wyznacz tę parę.
Zadanie 13. (4 pkt.)
Wyznacz wzór funkcji kwadratowej, wiedząc, że jej najmniejsza wartość
wynosi - 1, a największa wartość funkcji w przedziale <2; 4> jest o 6 większa
od najmniejszej wartości w tym przedziale. Wykres funkcji kwadratowej jest
symetryczny względem osi y.
Zadanie 14. (4 pkt.)
Liczba 1 jest dwukrotnym pierwiastkiem wielomianu
W(x) = x
4
- 3x
3
- 3x
2
+ ax + b.
Znajdź resztę z dzielenia tego wielomianu przez dwumian (x — 2).
Zadanie 15. (6 pkt.)
Dane są liczby:
a) Wyznacz wyraz a
1
i różnicę r, wiedząc, że liczba a jest piątym wyrazem,
natomiast liczba b dwunastym wyrazem ciągu arytmetycznego.
b) Oblicz sumę dziesięciu początkowych wyrazów tego ciągu.
Zadanie 16. (4 pkt.)
Oblicz cos 2x, wiedząc, że cos x =
(
)
6
2
4
1
+
Zadanie 17. (6 pkt.)
Pole trójkąta prostokątnego jest równe 39 cm
2
, a wysokość poprowadzona z
wierzchołka kąta prostego tego trójkąta ma 6 cm długości. Oblicz obwód tego
trójkąta.
Zadanie 18. (4 pkt.)
Wyznacz wartości parametru a, tak aby okręgi:
(x — 3)
2
+ (y - 2)
2
= 4 i (x - a)
2
+ (y + 2)
2
= 9 były styczne zewnętrznie.

©Irek.edu.pl
67
Zadanie 19. (6 pkt.)
Rysunek przedstawia przekrój osiowy stożka. Wiedząc,
ż
e miara kąta
α jest równa
3
π
oblicz miarę kąta wycinka
kołowego, który po zwinięciu tworzy powierzchnię
boczną tego stożka.
Zadanie 20. (5 pkt.)
Udowodnij, że dla każdej liczby naturalnej 10
n
+ 4
n
- 2 jest liczbą podzielną
przez 3.
Zadanie 21. (5 pkt.)
Uzasadnij, że prosta o równaniu 3x – 4y- 1 = 0 jest styczna do wykresu funkcji
f określonej wzorem f(x)=
5
3
−
x

©Irek.edu.pl
68
Zestaw 41. Poziom rozszerzony
Zadanie 11. (5 pkt.)
Dany jest ciąg o wyrazie ogólnym
Zadanie 12. (4 pkt.)
Wiedząc, że 2,6<
7
< 2,7 ‚ oszacuj wartość wyrażenia
3
2
7
+
Zadanie rozwiązujemy następująco:
Postępując podobnie, uwolnij od niewymierności, a następnie oszacuj wartość
wyrażenia
2
7
3
7
2
−
+
Zadanie 13. (4 pkt.)
Dla jakich wartości parametru a równanie ax
2
- (a - 3)x + 1 = O ma dwa
pierwiastki różnych znaków?
Zadanie 14. (5 pkt.)
Dany jest wielomian W(x) = 6mx
3
— 1 3mx
2
+ 1 3m —6. Dla jakiej wartości
parametru m pierwiastkiem wielomianu jest parametr m?

©Irek.edu.pl
69
Zadanie 15. (7 pkt.)
Dany jest trójkąt ABC o wierzchołkach A = (2, —3), B = (4, 2) oraz wektor
AB
= [6, 8].
a) Oblicz pole trójkąta ABC.
b) Wyznacz współrzędne obrazów wierzchołków trójkąta ABC w
jednokładności o środku w punkcie O(O,O) i skali k=3.
Zadanie 16. (5 pkt.)
Dana jest funkcja f(x) = - x
3
-px
2
+ 5x- 2.
a) Znajdź taką wartość p, dla której funkcja f osiąga minimum w punkcie x =5.
b) Dla wyznaczonego p podaj przedziały monotoniczności funkcji f
Zadanie 17. (6 pkt.)
Harcerze zorganizowali biwak. Dziewczyny zabrały się do gotowania zupy.
Wspólnymi siłami przygotowały pyszną grochówkę. Zupa znajdowała się w
kotle w kształcie walca o średnicy 8 dm i wysokości 6 dm. Kocioł wypełniony
był grochówką aż po same brzegi. Chochla miała kształt półkuli o promieniu 7
cm. Harcerze i kadra dostali po dwie chochle zupy. Czy wystarczyło zupy dla
210 harcerzy i 9 osób kadry? Jeśli nie wystarczyło, to ile zabrakło chochli
zupy i dla ilu harcerzy?
Zadanie 18. (9 pkt.)
Sporządź wykresy funkcji f(x) = a
x
oraz g(x)= log
b
x, wiedząc, że a jest
rozwiązaniem równania log
5
(2a + 4) = 1, zaś b rozwiązaniem równania
(
)
2
12
3
25
,
0
2
1
+
−
=
b
b
a) Sprawdź, czy punkt P =(2,
)
4
1
należy do wykresów obu funkcji.
b) Dla jakich x spełnione są nierówności: f(x) <g(x) ; g(x) <0 ; f(x)> 2?
Zadanie 19. (5 pkt.)
W urządzeniu jest 5 lamp. Prawdopodobieństwo przepalenia się lampy w
wyniku przepięcia w sieci wynosi 0,2. Jakie jest prawdopodobieństwo, że w
następstwie przepięcia:
a) nie przepali się żadna lampa,
b) przepali się jedna lampa,
c) przepalą się trzy lampy?

©Irek.edu.pl
70
Zestaw 42 . Poziom rozszerzony
Zadanie 12. (6 pkt.)
Uporządkuj rosnąco liczby:
Zadanie 13. (5 pkt.)
Dana jest funkcja f(x)=(p—1)x
2
—4px+2p—3.
a) Dla jakich p nierówność f(x) <O jest spełniona dla każdego x
∈ℜ
b) Dla p = —1 , wyznacz największą wartość funkcji f
Zadanie 14. (4 pkt.)
Dany jest wielomian W(x)= x
4
+ 3x
3
+ 3x
2
+ 8x + 12.
a) Wykaż, że liczba —2 jest dwukrotnym pierwiastkiem wielomianu W
b) Rozwiąż nierówność W(x) < 12 + 8x —x
3
.
Zadanie 15. (6 pkt.)
Ile wyrazów ciągu arytmetycznego, w którym a
1
= —20 ,
2
log
16
log
5
5
=
r
,
należy
dodać, aby suma początkowych wyrazów tego ciągu była równa granicy ciągu
Zadanie 16. (9 pkt.)
Funkcja f określona jest wzorem f(x) =
2
−
−
x
b
ax
gdzie
a = [tg
2
3O° + ( 1— sin 45
0
)(l +sin 45
0
)
.
ctg120
0
+
18
49
,
b jest większym pierwiastkiem równania x
3
— 9x
2
—x + 9 = O.
a) Dla wyznaczonych wartości a i b sporządź wykres funkcji y =f(|x|).
b) Na podstawie sporządzonego wykresu funkcji y =f(|x|) określ liczbę
pierwiastków równania f(|x|) = m w zależności od parametru m.
Zadanie 17. (4 pkt.)
Wykaż, że w trójkącie prostokątnym suma długości obu przyprostokątnych
jest równa sumie długości średnic okręgów wpisanego i opisanego na tym
trójkącie.

©Irek.edu.pl
71
Zadanie 18. (5 pkt.)
Suma długości promienia i wysokości stożka jest równa 12.
a) Dla jakich wartości r i h objętość stożka jest największa?
b) Oblicz największą objętość tego stożka.
Zadanie 19. (7 pkt.)
Dany jest okrąg k
1
o równaniu x
2
+y
2
+6x+5=O oraz okrąg k
2
o równaniu
x
2
+y
2
—12x+8y+27=0. Oblicz współrzędne środka i skalę jednokładności, w
której obrazem okręgu k
1
jest okrąg k
2
.
Zadanie 20. (4 pkt.)
Trzy zakłady produkują towar, który pakowany jest w zestawach po 50 sztuk.
Prawdopodobieństwo wyprodukowania towaru bez wad przez te zakłady jest
odpowiednio równe: 0,98 ; 0,96 ; 0,94.
a) Oblicz prawdopodobieństwo, że losowo wzięta sztuka spośród sztuk
pochodzących z różnych zakładów jest uszkodzona.
b) O ile więcej sztuk wadliwych w jednym zestawie pochodzi z zakładu
trzeciego niż z zakładu pierwszego?
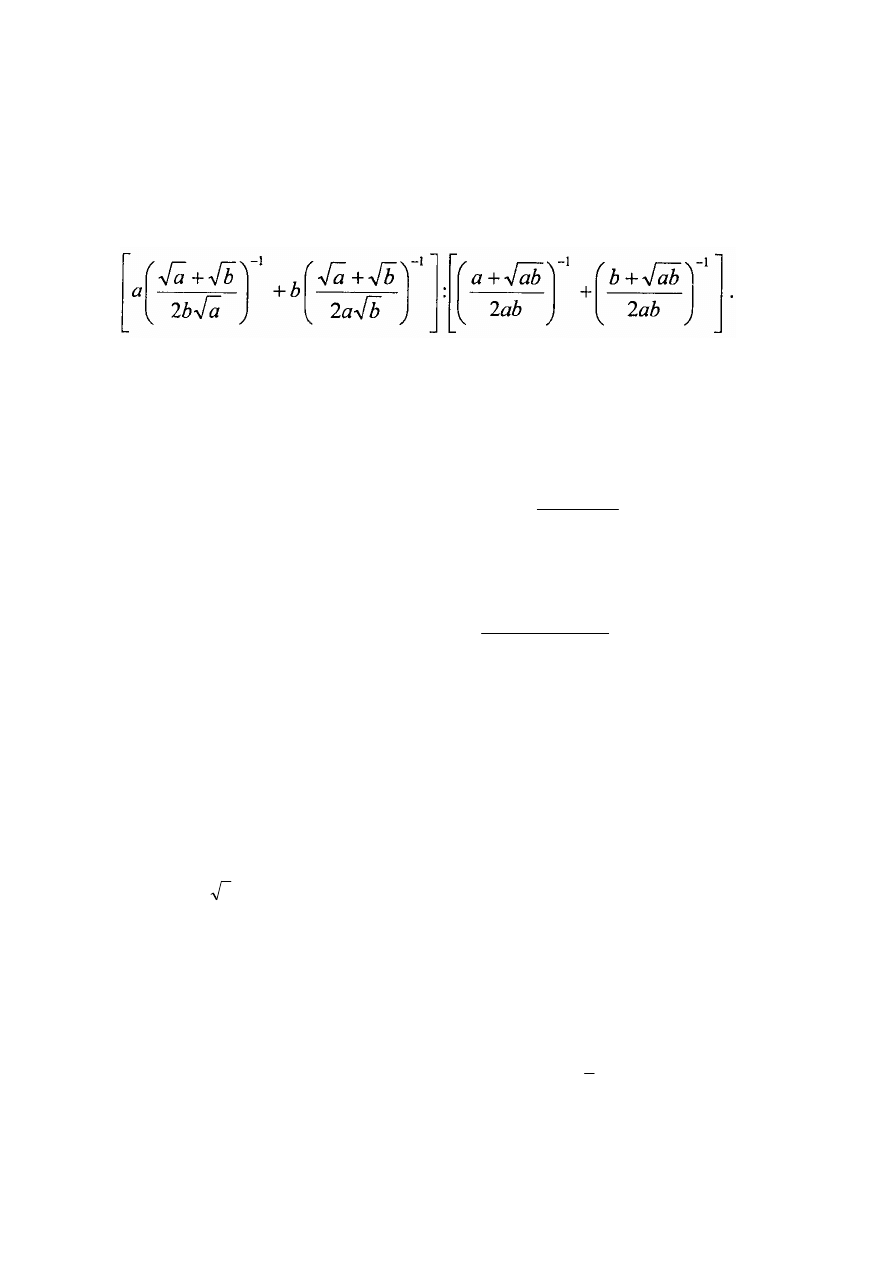
©Irek.edu.pl
72
Zestaw 43 . Poziom rozszerzony
Zadanie 12. (5 pkt.)
Wiedząc, że a> O i b> 0, sprowadź do najprostszej postaci wyrażenie:
Zadanie 13. (4 pkt.)
Znajdź argumenty, dla których funkcja f(x) = x
4
— 4x
2
+ 5 osiąga wartość
najmniejszą oraz podaj tę wartość.
Zadanie 14. (5 pkt.)
Dla jakiej wartości parametru m wartość ułamka
1
1
2
2
+
+
+
−
x
x
mx
x
jest większa od - 3
dla każdego x
∈ R?
Zadanie 15. (6 pkt.)
Ciąg liczbowy (a
n
) określony jest wzorem
(
)
(
)
4
4
1
4
3
2
2
2
+
+
−
+
+
−
n
n
k
n
n
k
gdzie k jest
parametrem.
a) Dla jakich wartości k granicą ciągu jest liczba 4?
b) Wykaż, że dla k= 1 ciąg jest malejący.
Zadanie 16. (5 pkt.)
Oblicz pole trójkąta ograniczonego osiami układu współrzędnych i styczną do
paraboli f(x) = 9—x
2
w punkcie P = (2, 5).
Zadanie 17. (5 pkt.)
Ołowiany stożek, którego przekrój jest trójkątem równobocznym o boku
długości 8
3
cm, przetopiono na kulę. Oblicz objętość i pole powierzchni tej
kuli.
Zadanie 18. (8 pkt.)
Punkty A = (5, 6) i B = (—1, 3) są końcami jednej z wysokości trójkąta
równobocznego. Napisz równania okręgów opisanego na trójkącie oraz
wpisanego w ten trójkąt, wiedząc, że punkt B nie jest jego wierzchołkiem.
Zadanie 19. (5 pkt.)
Rozwiąż równanie log
16
x + log
8
x + log
4
x + log
2
x =8
3
1
.
Zadanie 20. (7 pkt.)
Mając dane: P(A) = 0,9 , P(B/A`) = 0,75 , P(B/A) = 0,95 , oblicz P(B).
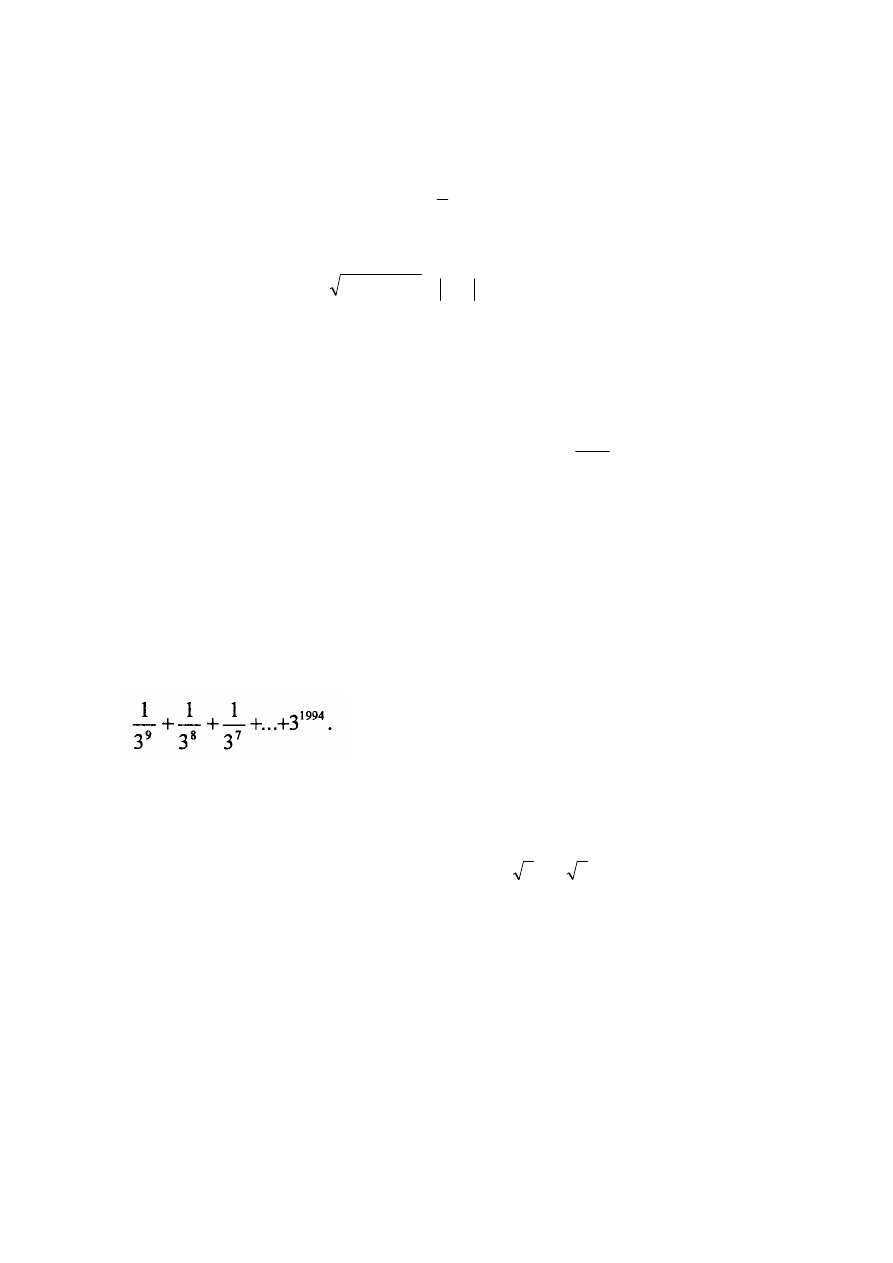
©Irek.edu.pl
73
Zestaw 44 . Poziom rozszerzony
Zadanie 12. (5 pkt.)
Dla jakiej wartości x log
x
272 jest o
4
1
1
większy od log
x
8,5?
Zadanie 13. (6 pkt.)
Dana jest funkcja
1
9
6
)
(
2
−
+
+
−
=
x
x
x
x
f
a) Sporządź wykres funkcji f
b) Sporządź wykres funkcji g(x) = - f(x)
c) Rozwiąż nierówność g(x)
≥ —4.
Zadanie 14. (8 pkt.)
Napisz równania stycznych do wykresu funkcji f(x) =
1
1
+
−
x
x
i równoległych do
prostej o równaniu y=2x+ 1.
Zadanie 15. (7 pkt.)
W zależności od parametru m wyznacz liczbę punktów wspólnych okręgu
(x — 1)
2
+ (y + 3)
2
= 3 i prostej x + y — m = O. Dla m = 1 wykonaj ilustrację
graficzną.
Zadanie 16. (3 pkt.)
Oblicz liczbę składników sumy:
Zadanie 17. (6 pkt.)
Rozwiąż równanie 4 sin
2
x + sin
2
2x = 3.
Zadanie 18. (5 pkt.)
Dany jest trójkąt ABC o bokach długości: 6, 2
5
i 4
2
.
a) Oblicz wartość kosinusa największego kąta.
b) Oblicz długość promienia okręgu opisanego na tym trójkącie.
Zadanie 19. (5 pkt.)
Szklankę o średnicy 0,3 dm napełniono pepsi—colą do wysokości 2 cm od
górnej krawędzi. Ile kulistych kostek lodu o średnicy 2 cm można wrzucić do
tej szklanki, nie powodując rozlania napoju?
Zadanie 20. (5 pkt.)
Pewna gra polega na jednoczesnym rzucie kostką sześcienną i monetą
symetryczną. Wygrywamy wtedy, gdy otrzymamy szóstkę na kostce i orła na
monecie. Jakie jest prawdopodobieństwo, że grając trzy razy, przynajmniej raz
wygramy?
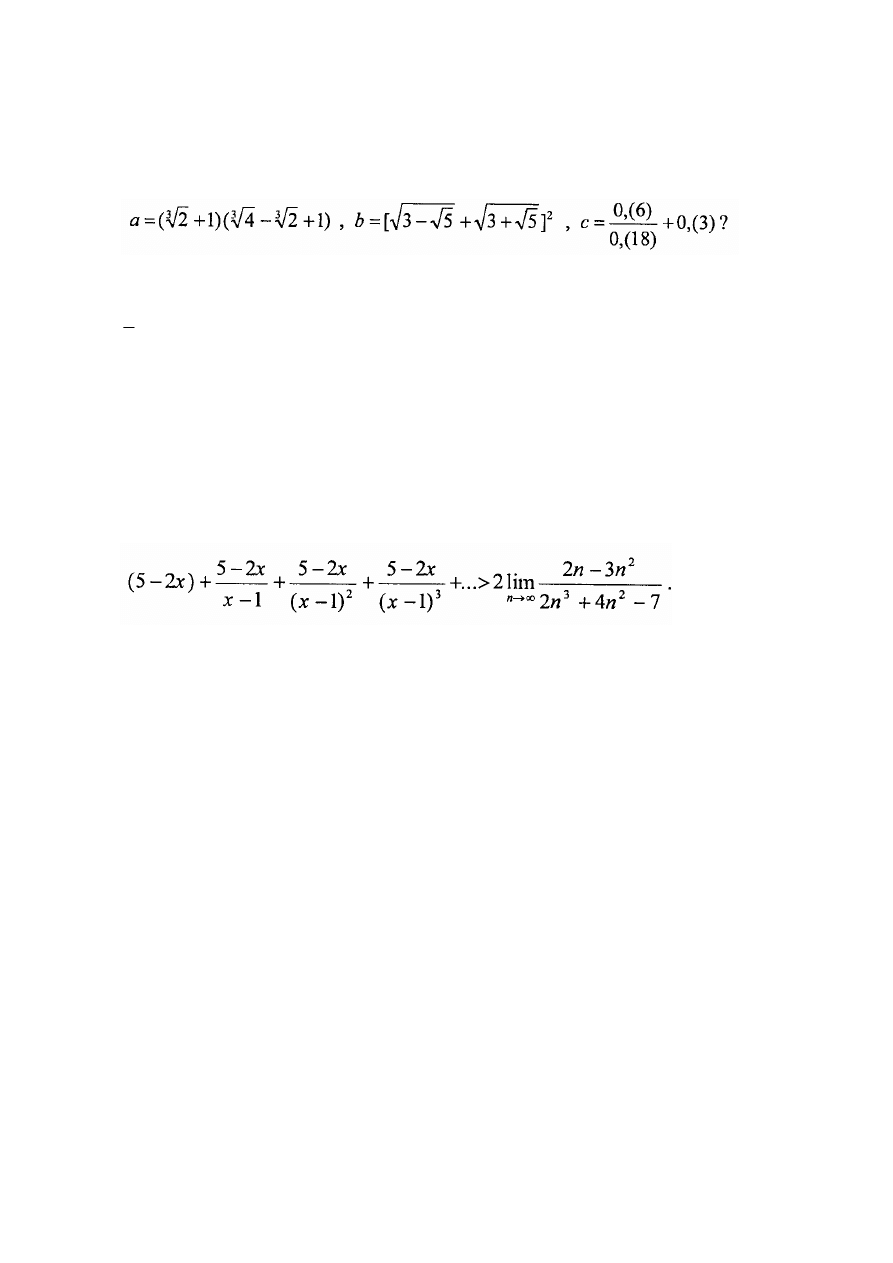
©Irek.edu.pl
74
Zestaw 45 . Poziom rozszerzony
Zadanie 11. (5 pkt.)
Która z liczb a, b, c jest liczbą parzystą:
Zadanie 12. (5 pkt.)
Wykaż, że dla dowolnego całkowitego m liczba
6
1
.
[3m(m + 3) (2m
2
+ 6m + 4) +6] jest kwadratem liczby całkowitej.
Zadanie 13. (4 pkt.)
Oblicz współczynniki a, b i c funkcji f(x) = ax
2
+ bx + c, wiedząc,
ż
e x
1
+ x
2
= 4 i x
1
.
x
2
= —3, natomiast współczynnik a funkcji f jest
mniejszym pierwiastkiem równania 2x
2
— 18x = —28.
Zadanie 14. (5 pkt.)
Rozwiąż nierówność:
Zadanie 15. (6 pkt.)
Dla jakich wartości parametru m pierwiastkami równania
(x
2
— 2mx +m
2
— 1) (x — 1) =0 są trzy kolejne liczby nieparzyste?
Zadanie 16. (7 pkt.)
Oblicz pole i obwód figury F, gdzie
F= ((x,y):x
∈ R i y∈ R i 1og
3
2
(x
2
+y
2
)—3 log
3
(x
2
+y
2
)+2
≤ 0}.
Zadanie 17. (6 pkt.)
Dane są okręgi: o
1
(S
1
, 1) i o
2
(S
2
, 1), gdzie S
1
= (3, —1) i S
2
= (k, —1).
a) Napisz równanie okręgów i 0
2
.
b) Dla jakich wartości parametru k okręgi 0
1
i 0
2
są rozłączne?
c) Przekształć okręgi 0
1
i 0
2
w symetrii względem punktu O = (0, 0) i napisz
równania obrazów okręgów 0
1
i 0
2
, przyjmując k = —1.
Zadanie 18. (6 pkt.)
Z wierzchołka kwadratu o boku długości 10 narysowano okrąg, tak że punkty
przecięcia okręgu z kwadratem oraz środek tego okręgu utworzyły trójkąt
równoboczny. Znajdź długość promienia tego okręgu.
Zadanie 19 ( 6pkt)
Jaką największą objętość ma walec wpisany w kulę o średnicy długości 12 cm.

©Irek.edu.pl
75
Zestaw 46 . Poziom rozszerzony
Zadanie 12. (6 pkt.)
Dane są zbiory:
Wyznacz zbiory: A
∪ B` , A ∩ B.
Zadanie 13. (5 pkt.)
Dla jakich liczb całkowitych a liczba
a
a
a
a
2
3
2
2
2
3
−
+
−
jest także liczbą całkowitą?
Zadanie 14. (5 pkt.)
Wykaż, że długość przekątnej kwadratu o boku długości
−
−
+
2
6
11
2
6
11
jest liczbą naturalną. Oblicz obwód i pole tego
kwadratu.
Zadanie 15. (7 pkt.)
Dane są funkcje :f(x)=x
2
—2(m+3)x—3m+1 i g(x) = x
2
+2kx+2k—3.
a) Dla jakich wartości parametrów m i k wykresy funkcji f i g są symetryczne
względem osi x?
b) Dla wyznaczonych wartości m i k napisz postać kanoniczną funkcji f i g.
Zadanie 16. (6 pkt.)
Wyznacz pole trójkąta, którego dwa boki zawierają się w asymptotach
wykresu funkcji f(x) =
2
4
3
−
−
x
x
, a trzeci bok zawiera się w stycznej do wykresu
tej funkcji w punkcie (1, 1).
Zadanie 17. (6 pkt.)
Pole przekroju osiowego stożka jest równe P, a kąt rozwarcia stożka ma
miarę
α. Oblicz objętość tego stożka oraz jego pole powierzchni bocznej.

©Irek.edu.pl
76
Zadanie 18. (5 pkt.)
W ciągu arytmetycznym różnica r jest równa liczbie
natomiast wyraz pierwszy a
1
=
(
)
2
1
2
−
a) Wyznacz wzór na wyraz ogólny tego ciągu.
b) Oblicz sumę 10 początkowych wyrazów tego ciągu.
Zadanie 19. (5 pkt.)
Rozwiąż równanie cos 2x + cos x =k
2
+ 4m + 3, wiedząc, że k jest
pierwiastkiem równania
Zadanie 20. (5 pkt.)
Rozwiąż nierówność
(
)
0
5
log
log
2
4
2
1
≥
− x
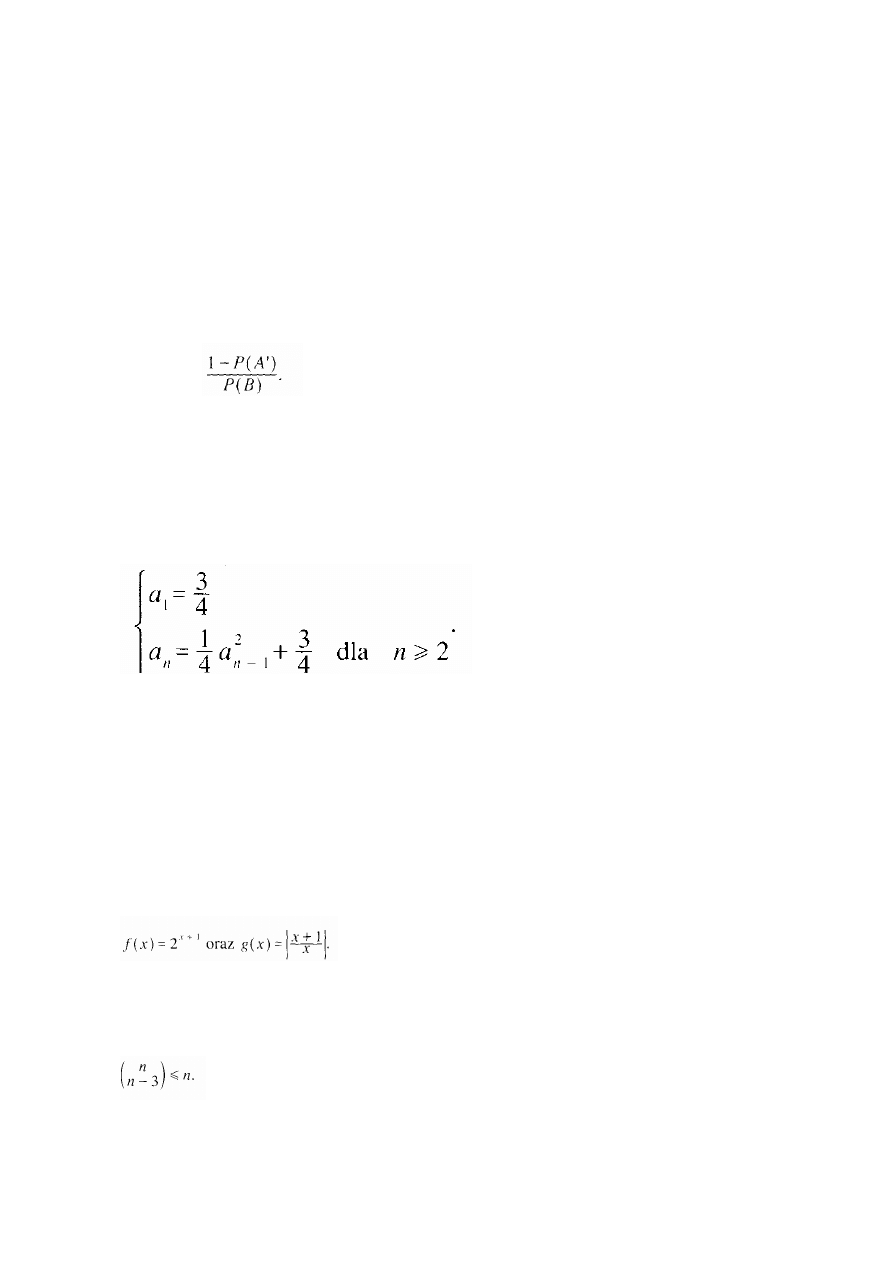
©Irek.edu.pl
77
Zestaw 47 . Poziom rozszerzony
Zadanie 12. (3 pkt)
Dane jest równanie mx
2
— 3(m + 1) x + m = 0 z niewiadomą x i parametrem
m
∈ R. Wyznacz wszystkie wartości parametru m, dla których dane równanie
nie ma rozwiązania.
Zadanie 13. (4 pkt)
A i B są zdarzeniami zbioru
Ω i P(B)>O. Sprawdź, czy P(A/B) jest mniejsze
niż
Zadanie 14. (3 pkt)
Udowodnij twierdzenie: Dla wszystkich wartości rzeczywistych zmiennej t
wyrażenie cos(sint) przyjmuje wartości dodatnie.
Zadanie 15. (5 pkt)
Ciąg (a
n
) zdefiniowany jest wzorem rekurencyjnym:
Stosując zasadę indukcji matematycznej, wykaż, że żaden wyraz tego ciągu
nie jest większy niż 1.
Zadanie 16. (4 pkt)
Objętość walca jest równa 250
π cm
3
. Przedstaw pole powierzchni całkowitej
tego walca jako funkcję długości promienia podstawy. Dla jakiej długości
promienia na wykonanie siatki walca zużyje się najmniejszą ilość materiału?
Zadanie 17. (6 pkt)
Naszkicuj w jednym układzie współrzędnych wykresy funkcji
podstawie wykonanego rysunku określ liczbę rozwiązań równania f(x) = g( x).
Zadanie 18. (4 pkt)
Rozwiąż nierówność

©Irek.edu.pl
78
Zadanie 19. (7 pkt)
Rozwiąż nierówność: + + -F ... > 2k— 0.9(9), gdzie lewa strona tej
nierówności jest sumą nieskończonego ciągu geometrycznego.
Zadanie 20. (9 pkt)
W trójkącie jeden z kątów ma miarę 120
0
, a długości boków tego trójkąta
tworzą ciąg arytmetyczny.
Obwód trójkąta jest równy 30. Wyznacz stosunek długości promienia okręgu
opisanego na tym trójkącie do długości promienia okręgu wpisanego w ten
trójkąt.
Zadanie 21. ( 5pkt)
W pudelku umieszczono 6 kul czarnych i 4 kule białe. Losujemy jedną kulę z
pudelka. Jeżeli będzie to kula biała, to wrzucamy ją z powrotem do pudelka,
jeżeli czarna, to zatrzymujemy. Następnie losujemy z pudełka jednocześnie
dwie kule. Oblicz prawdopodobieństwo zdarzenia, że obie wylosowane za
drugim razem kule są białe.

©Irek.edu.pl
79
Odpowiedzi:
Zestaw 1

©Irek.edu.pl
80
Zestaw 2

©Irek.edu.pl
81
Zestaw 3

©Irek.edu.pl
82
Zestaw 4

©Irek.edu.pl
83
Zestaw 5

©Irek.edu.pl
84
Zestaw 6

©Irek.edu.pl
85
Zestaw 7

©Irek.edu.pl
86
Zestaw 8
Zestaw 9
Zestaw 10
Zestaw 11
Zestaw 14

©Irek.edu.pl
87
Zestaw 15
Zestaw 16
Zestaw 17
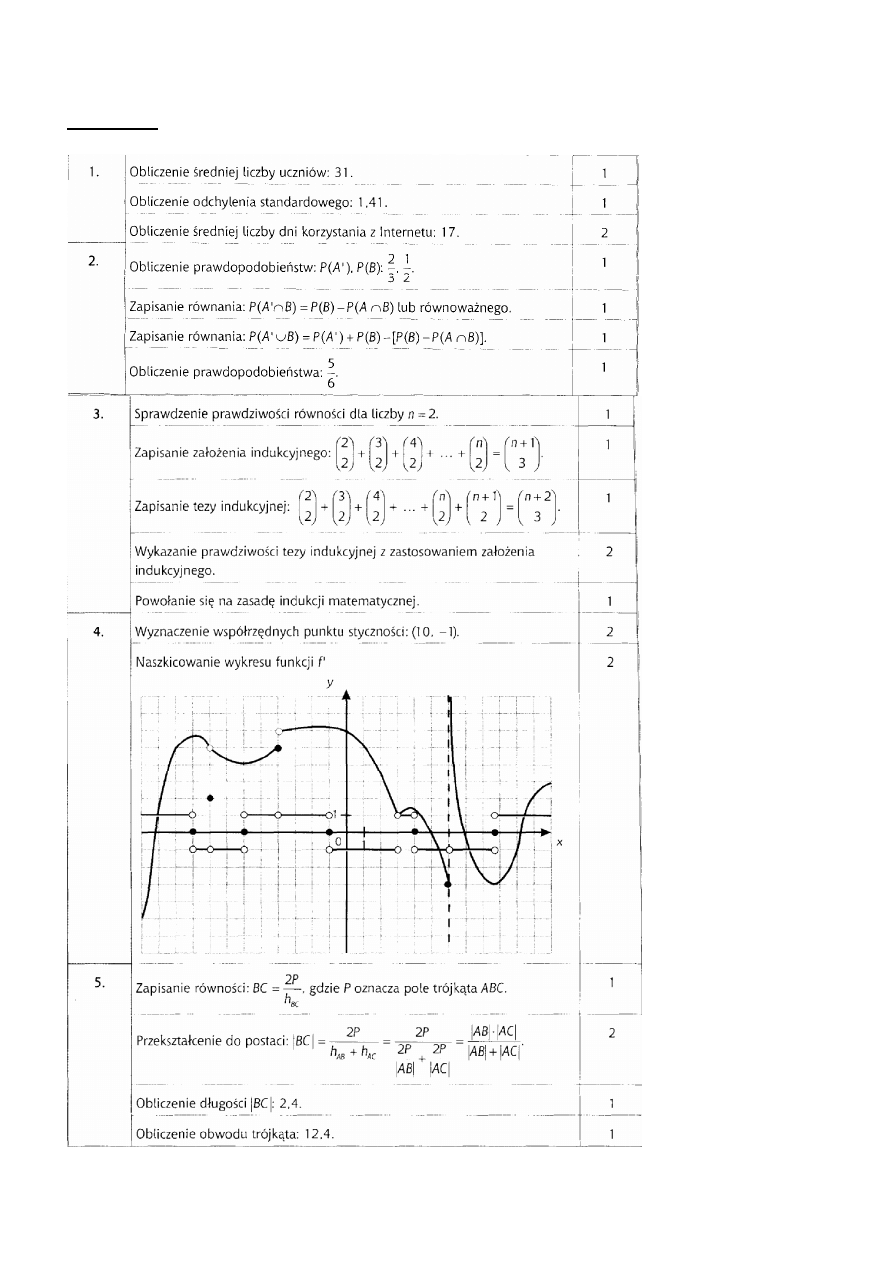
©Irek.edu.pl
88
Zestaw 18

©Irek.edu.pl
89

©Irek.edu.pl
90
Zestaw 19

©Irek.edu.pl
91

©Irek.edu.pl
92
Zestaw 20

©Irek.edu.pl
93
Zestaw 21

©Irek.edu.pl
94

©Irek.edu.pl
95
Zestaw 22

©Irek.edu.pl
96

©Irek.edu.pl
97
Zestaw 23
Zestaw 24
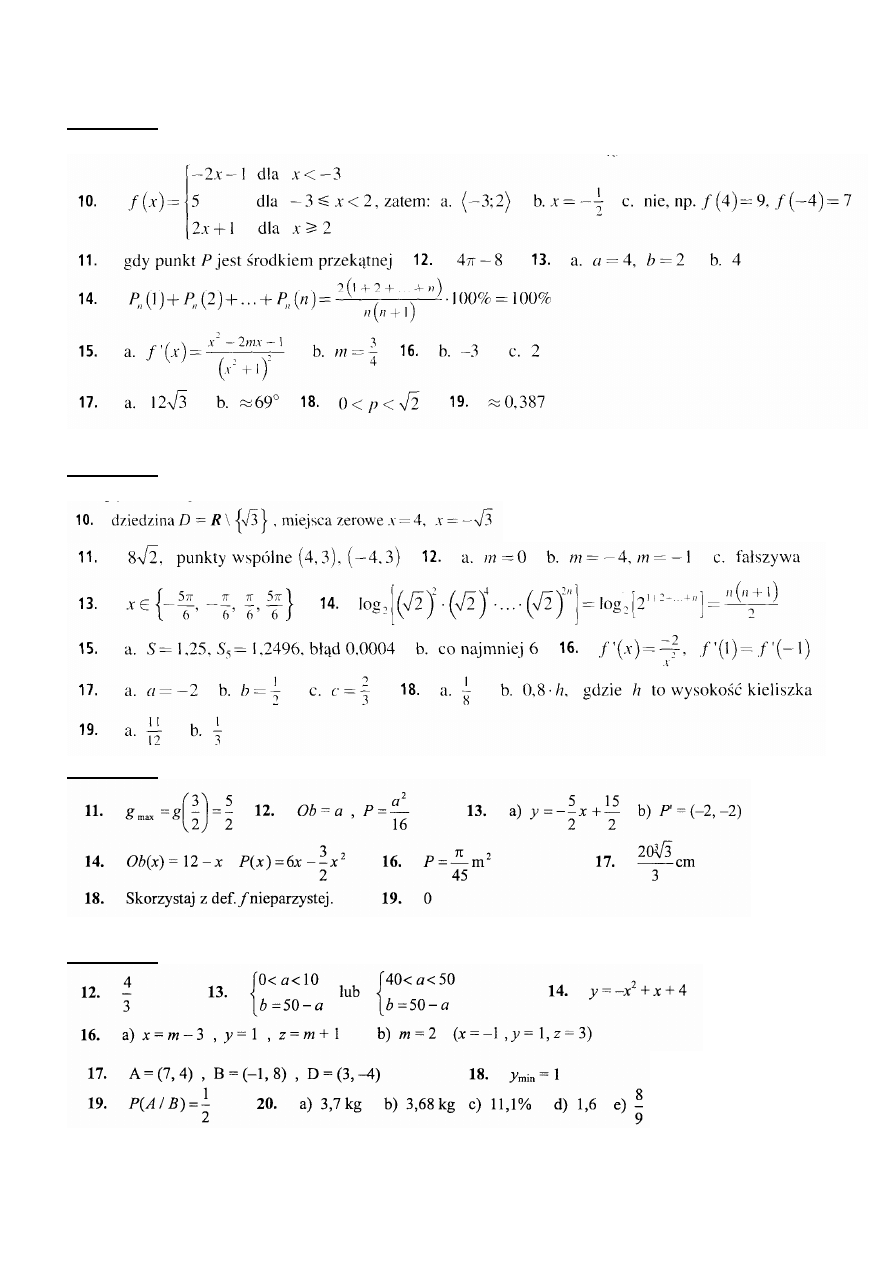
©Irek.edu.pl
98
Zestaw 25
Zestaw 26
Zestaw 27
Zestaw 28

©Irek.edu.pl
99
Zestaw 29
Zestaw 30
Zestaw 31
Zestaw 32

©Irek.edu.pl
100
Zestaw 33
Zestaw 34
Zestaw 35

©Irek.edu.pl
101
Zestaw 36
Zestaw 37
Zestaw 38

©Irek.edu.pl
102
Zestaw 39
Zestaw 40
Zestaw 41
Zestaw 42

©Irek.edu.pl
103
Zestaw 43
Zestaw 44
Zestaw 45
Zestaw 46
Wyszukiwarka
Podobne podstrony:
Matura z matematyki 2010 - przykładowe zadania na poziomie rozszerzonym, szkoła, Matura, Matura - Ma
matematyka Zadania maturalne poziom podstawowy, Matura, Matematyka
USTNY EGZAMIN MATURALNY Z MATEMATYKI, szkoła, Matura, Matura - Matematyka, Zadania maturalne
Zadania maturalne matematyka
Zadania maturalne, matura, matematyka
Matematyka zadania
Matematyka zadania egzaminacyjne Zestaw7 2002
Matematyka zadania 1
7 BUDOWA ATOMU I PROMIENIOTW ôRCZO Ü ć zadania maturalne
scenariusz matematyka, Matematyka, zadania matematyka
alkohole - zadania, Matura, Chemia, zadania z organicznej
więcej podobnych podstron