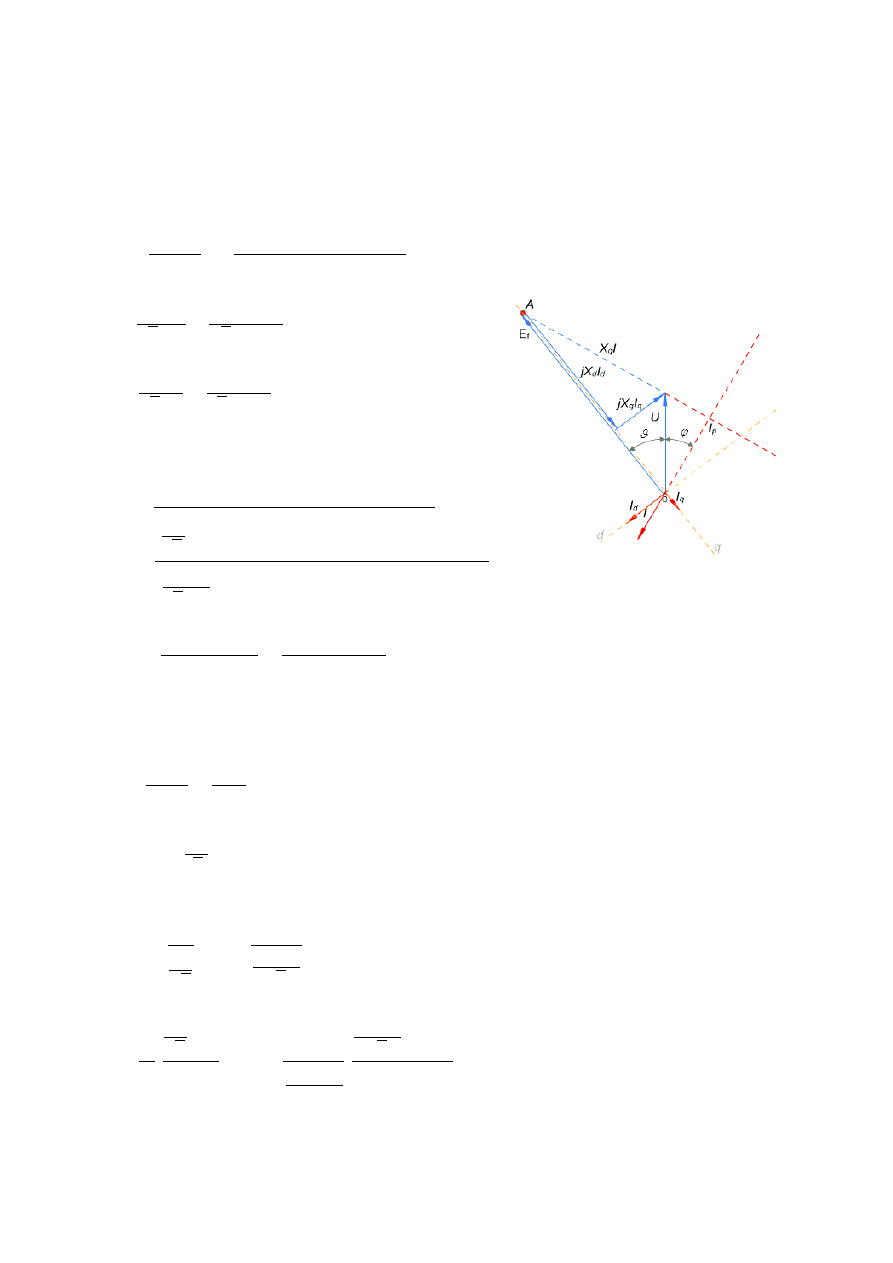
Zadanie 1

Dla turbogeneratora cylindrycznego, przewzbudzonego o danych znamionowych:
S

n

=31MVA, U

n

=10,5kV, X

dr

=1,9, cos



n

=0,8, I

f0

=160A, n

n

=3000obr/min.

Obliczyć podstawowe parametry: P

n

, Q

n

, I

n

, Z

n

, E

fn

, I

fn

, p

mn

,



n

, T

n

, T

max

P

n

= S

n

⋅cos 

n

= 31000000⋅0,8 = 24800000 W

Q

n

=



S

n

2

−P

n

2

=



31000000

2

−24800000

2

= 18600000 VAr

I

n

=

S

n



3

⋅U

n

=

31000000



3

⋅10500

= 1720 A

Z

n

=

U

n



3

⋅I

n

=

10500



3

⋅1720

= 3,5 

X

d

= X

dr

⋅Z

n

= 1,9⋅3,5 = 6,65 

E

fn

=





U

n



3

 X

q

⋅I

n

⋅sin 

2

  X

q

⋅I

n

⋅cos 

2

=

=





10500



3

 6,65⋅1720⋅0,6

2

 6,65⋅1720⋅0,8

2

= 15840

sin



n

=

X

d

⋅I

n

⋅cos

n

E

fn

=

6,65

⋅1720⋅0,8

15840

= 0,58



n

=arc sin 

n

= 35,5

o

p

mn

=

1

sin



n

=

1

0,58

= 1,73

I

f0

⇔ E

f0

=

U

n



3

I

fn

⇔ E

fn



I

fn

= I

f0

⋅

E

fn

U

n



3

= 160⋅

15840
10500



3

= 420

T

n

=

3



⋅

U

n



3

⋅E

fn

X

d

⋅sin  =

3

⋅3000

30

⋅

10500



3

⋅15840

6,65

⋅0,58 = 79980 Nm

T

max

= p

mn

⋅T

n

= 1,73⋅79980 = 138365 Nm

V

A

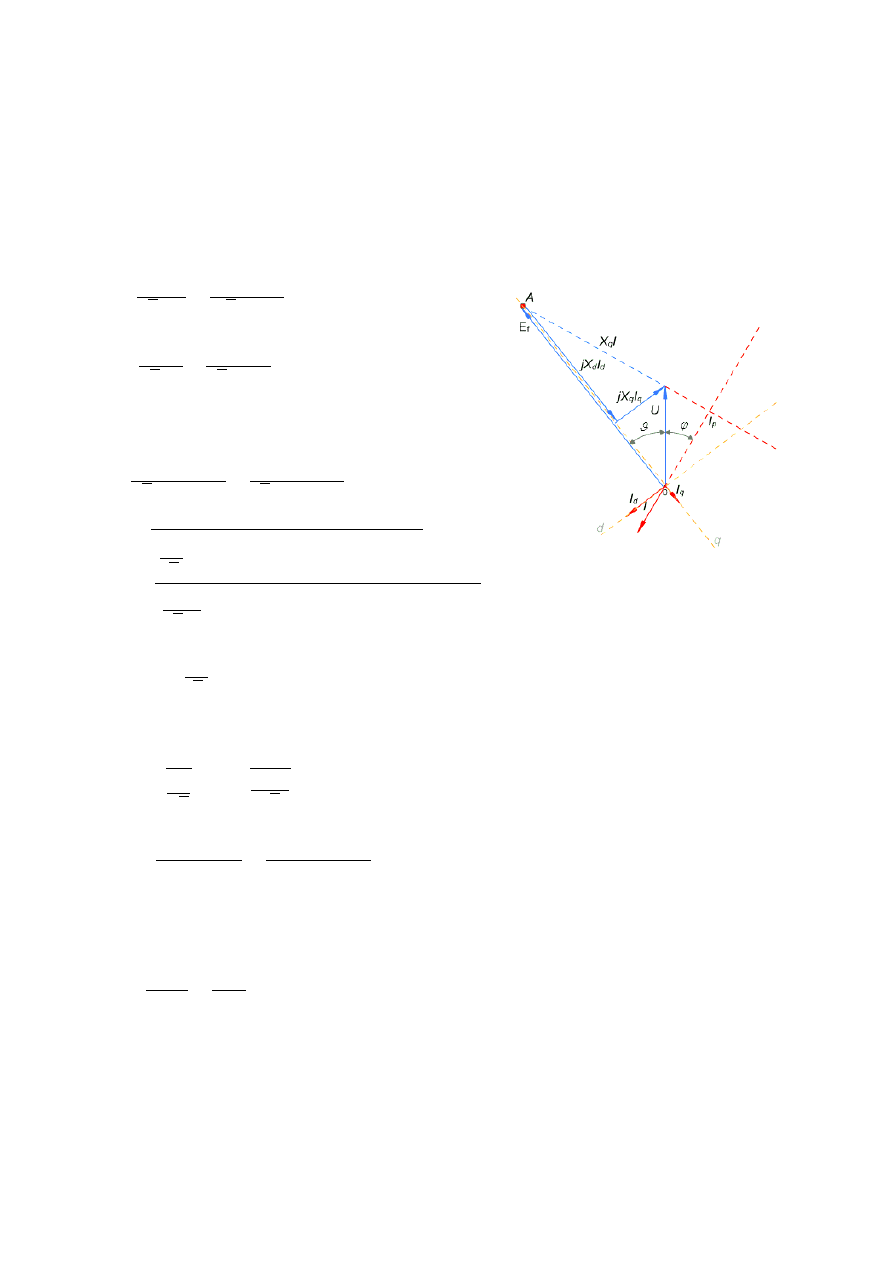
Zadanie 2

Turbogenerator cylindryczny, przewzbudzony o danych znamionowych:
S

n

=12MVA, U

n

=6,3kV(gwiazda), X

dr

=1,8, cos



n

=0,8, I

f0

=100A pracuje przy obciążeniu

mocą P=0,9P

n

i współczynniku mocy cos

=0,7.

Obliczyć prąd obciążenia i wzbudzenia oraz kąt mocy i przeciążalność.

P

n

= S

n

⋅cos 

n

= 12000000⋅0,8 = 9600000 W

I

n

=

S

n



3

⋅U

n

=

12000000



3

⋅6300

= 1100 A

Z

n

=

U

n



3

⋅I

n

=

6300



3

⋅1100

= 3,3 

X

d

= X

dr

⋅Z

n

= 1,8⋅3,3 = 5,94



I

=

0,9

⋅P

n



3

⋅U

n

⋅cos 

=

0,9

⋅9600000



3

⋅6300⋅0,7

= 1132 A

E

f

=





U

n



3

 X

q

⋅I⋅sin 

2

  X

q

⋅I⋅cos

2

=

=





6300



3

 5,94⋅1132⋅0,7

2

 5,94⋅1132⋅0,7

2

= 9580

I

f0

⇔ E

f0

=

U

n



3

I

f

⇔ E

f



I

f

= I

f0

⋅

E

fn

U

n



3

= 100⋅

9580
6300



3

= 260

sin

 =

X

d

⋅I⋅cos

E

f

=

5,94

⋅1132⋅0,7

9580

= 0,49



n

=arc sin 

n

= 29,4

o

p

mn

=

1

sin



n

=

1

0,49

= 2,035

V

A

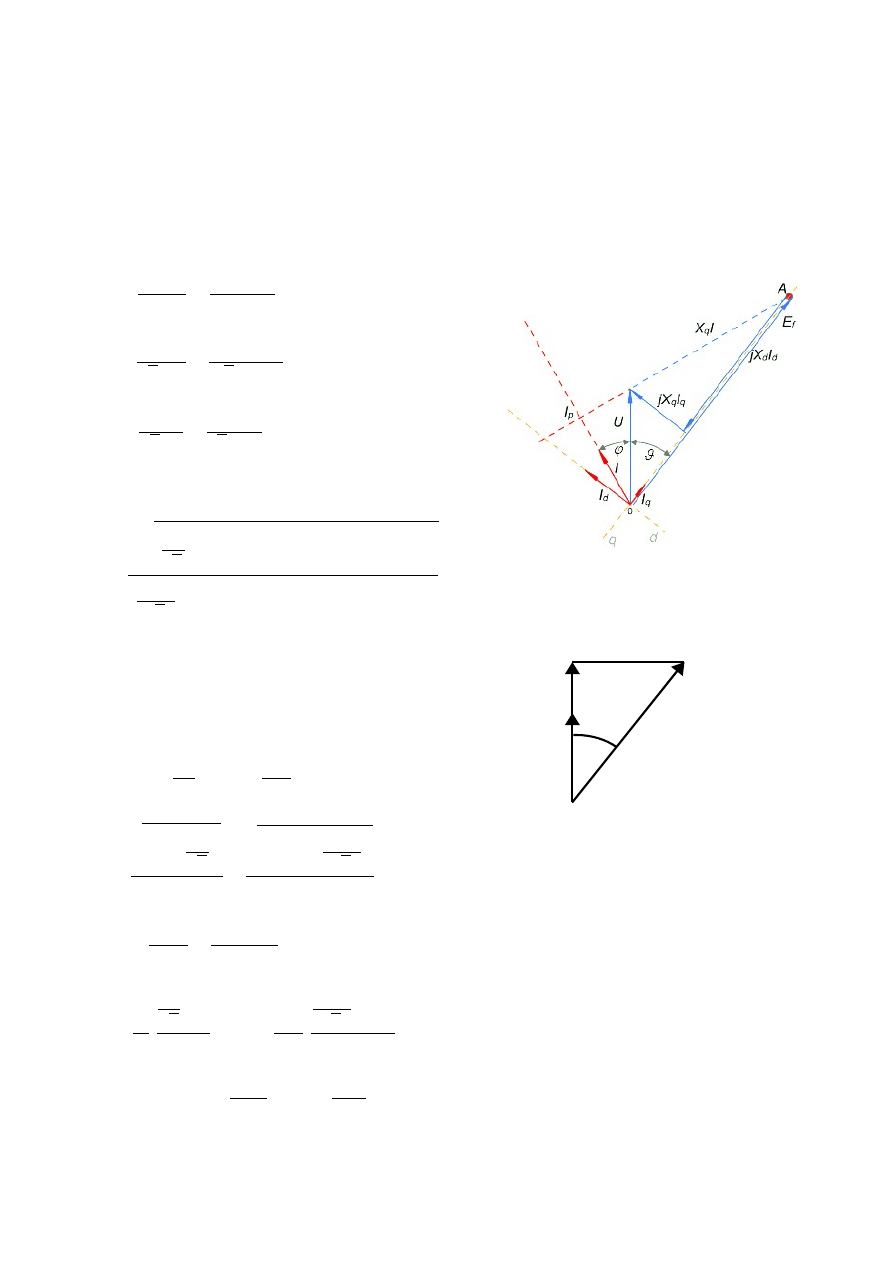
Zadanie 3

Silnik synchroniczny, cylindryczny o danych znamionowych:
P

n

=3MW, U

n

=6kV, f

n

=50Hz, n

n

=3000obr/min, cos



n

=0,9poj., X

dr

=1,5, I

fn

=350A jest zasilony

z sieci o napięciu U

s

=5800V i f

s

=50Hz, a jego prąd wzbudzenia jest równy I

f

=0,8I

fn

. Silnik

pracuje ze współczynnikiem mocy cos

=1. Obliczyć prąd i moment jakim jest obciążony

silnik. W obliczeniach pominąć straty silnika. Wyznaczyć graniczny moment, powyżej
którego silnik wypadnie z synchronizmu.

S

n

=

P

n

cos



n

=

3000000

0,9

= 3333 kVA

I

n

=

S

n



3

⋅U

n

=

33333333



3

⋅6000

= 321 A

Z

n

=

U

n



3

⋅I

n

=

6000



3

⋅321

= 10,8 

X

d

= X

dr

⋅Z

n

= 1,5⋅10,5 = 16,2 

E

fn

=





U

n



3

 I

n

⋅X

q

⋅sin 

n



2

  I

n

⋅X

q

⋅cos 

n



2

=

=





6000



3

321⋅16,2⋅0,43

2

 321⋅16,2⋅0,9

2

= 7375 V

I

f

=0,8⋅I

fn

= 0,8⋅350 = 280 A

E

f

 I

f

E

fn

 I

fn



E

f

= E

fn

⋅

I

f

I

fn

= 7375⋅

280
350

= 5900 V

I

=



E

f

2

−

U

n



3



2

X

q

=



5900

2

−

5800



3



2

16,2

= 300

sin

=

I

⋅X

q

E

f

=

300

⋅16,2

5900

= 0,82

T

=

3



⋅

U



3

⋅E

f

X

d

⋅sin  =

3

314

⋅

5800



3

⋅5900

16,2

⋅0,82 = 9555

T

max

= T⋅p

m

= T⋅

1

sin



= 9555⋅

1

0,82

= 11650 Nm

I

U

I

 X

q

E

f



Nm

A