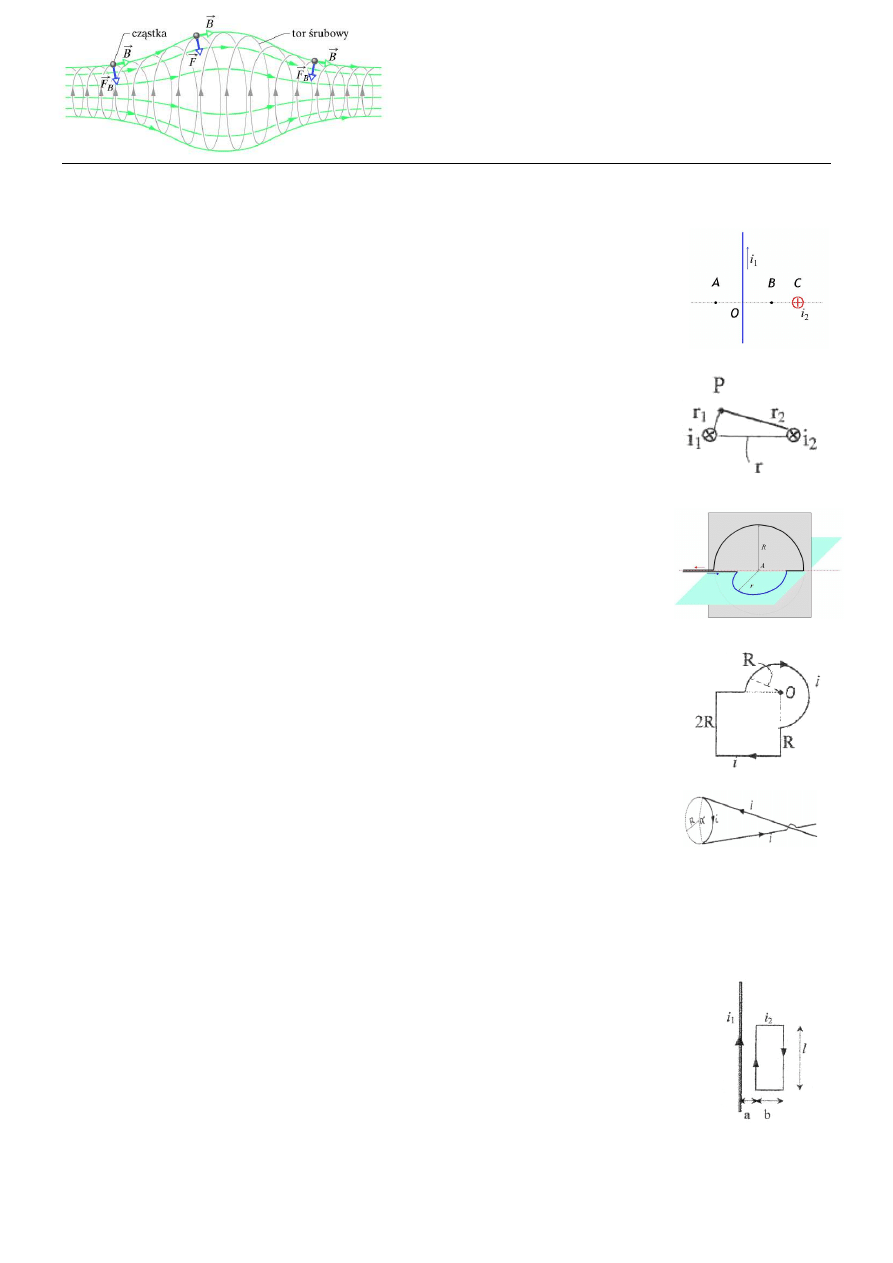
Obliczenia z fizyki II

Lista #01. Magnetyzm

1.

Elektron porusza się w jednorodnym polu magnetycznym o indukcji B = 9⋅10

-3

T, po torze spiralnym, o pro-

mieniu R = 1 cm i skoku h = 7.8 cm. Obliczyć częstotliwość (f) wykonywanych obrotów oraz prędkość (υ)
elektronu.

Odp.: 252 MHz; 2.52·10

7

m/s

2.

Dwa nieskończenie długie przewodniki prostoliniowe, w których płyną prądy
o wartości natężenia i

1

= 2 A, i

2

= 3 A, są umieszczone prostopadle względem sie-

bie i znajdują się w płaszczyznach wzajemnie prostopadłych, przy czym odległość
OA = OB = 1 cm, zaś OC = 2 cm (rysunek). Obliczyć wartość indukcji magne-
tycznej w punktach A i B.

Odp.: B

A

= 4.46⋅10

-5

T; B

B

= 1.62B

A

3.

Dwa nieskończenie długie przewodniki, w których płyną prądy o jednakowym
natężeniu, i

1

= i

2

= i = 3 A, są umieszczone równolegle, w odległości r = 13 cm od

siebie. Obliczyć wartość wektora indukcji magnetycznej B i wskazać jego kierunek
w punkcie P. Przyjąć, że r

1

= 5 cm, r

2

= 12 cm.

Odp.: 1.3·10

–5

T

4.

Przewód wygięto w dwa półkola o promieniach R = 1 m i r = 0.5 m. Półkola leżą w
płaszczyznach wzajemnie prostopadłych (rysunek). Obliczyć wartość wektora in-
dukcji magnetycznej w centrum układu (punkt A), jeżeli w przewodniku płynie
prąd i = 1/π A; kierunek prądu wskazują strzałki.

Odp.: 2.23⋅ 10

-7

T

5. Rysunek zamieszczony obok przedstawia kontur wykonany z cienkiego drutu, w

którym płynie prąd o natężeniu i = 10 A. Obliczyć wartość indukcji pola magnetycz-
nego B w punkcie O przyjmując, że wartość parametru geometrycznego konturu
R = 20 cm.

Odp.: 27.1 µT

6. Cienki drut z prądem o natężeniu i posiada płaską konfigurację. Dwa bardzo długie,

prostoliniowe fragmenty, każdy styczny do okręgu o promieniu R, łączy łuk pokry-
wający się z częścią okręgu, jak przedstawiono na rysunku. Obliczyć, dla jakiego ką-
ta α wartość indukcji pola magnetycznego B, wyznaczona w środku okręgu, jest
równa zero.

Odp.: α = 2 rad

7.

Dwa równoległe, długie przewodniki prostoliniowe są w pewnej odległości od siebie. W przewodnikach
płyną prądy o równej wartości i zgodnym kierunku. Obliczyć wartość natężenia prądu w przewodnikach, je-
żeli przy ich rozsunięciu na odległość trzykrotnie większą wykonano pracę – liczoną na jednostkę długości
przewodnika – równą 4.3·10

–5

J/m.

Odp.: 14 A

8. Na rysunku jest przedstawiony nieskończenie długi, prostoliniowy przewodnik, w

którym płynie prąd o natężeniu i

1

= 30 A. W pewnej odległości od przewodnika

znajduje się prostokątna ramka, w której płynie prąd o natężeniu i

2

= 20 A. Obliczyć

wartość i określić kierunek siły wypadkowej działającej na ramkę. Przyjąć następu-
jące parametry geometryczne: a = 10 cm, b = 15 cm, l = 45 cm.

Odp.: F

w

= 3.24·10

–4

N

Obliczenia z fizyki II

Lista #02. Prąd przemienny

1.

Maksymalne napięcie w obwodzie drgającym, składającym się z cewki o indukcyjności L = 5 µH i konden-
satora o pojemności C = 20 nF wynosi U

0

= 120 V. Obliczyć maksymalną wartość strumienia magnetyczne-

go (Φ

max

), jeżeli liczba zwojów cewki N = 30. Założyć, że opór obwodu jest do zaniedbania.

Odp.: 1.26⋅10

-6

Wb

2.

Obwód drgający tworzą: cewka o indukcyjności L = 1.2 mH i kondensator o pojemności C = 0.03 µF. Wy-
znaczyć długość fali elektromagnetycznej wytwarzanej w obwodzie. Opór omowy traktować jako znikomo
mały.

Odp.: 1.13⋅10

4

m

3.

Kondensator o pojemności C = 16 µF oraz opór omowy R = 200 Ω, są włączone szeregowo do sieci prądu
przemiennego o napięciu U = 220 V i częstotliwości f = 50 Hz. Obliczyć: zawadę (impedancję) obwodu, na-
tężenie prądu, przesunięcie fazowe między napięciem i natężeniem prądu w obwodzie oraz spadek napięcia
na kondensatorze i na oporze omowym.

Odp.: 282.1 Ω, 0.779 A, 44

o

51’, 155 V, 155.8 V

4.

Do sieci prądu przemiennego o U = 230 V i f = 50 Hz włączono szeregowo uzwojenie transformatora o in-
dukcyjności L = 5 H, opór omowy R = 100 Ω oraz kondensator, którego pojemność dobrano tak, by w ob-
wodzie wystąpił rezonans. Obliczyć pojemność kondensatora, natężenie prądu płynącego w obwodzie oraz
napięcie na okładkach kondensatora.

Odp.: 2 µF, 3.6 kV

5.

Obwód prądu przemiennego zawiera szeregowo połączone: opór R = 400 Ω, indukcyjność L = 1.3 H i po-
jemność C = 1.6 mF. Do obwodu podłączono napięcie U = 230 V, o częstotliwości f = 50 Hz. Obliczyć natę-
żenie płynącego prądu oraz moc wydzieloną w obwodzie.

Odp.: 403 mA, 65 W

6.

Cewka o oporze czynnym R = 9 Ω i indukcyjności L jest podłączona do obwodu prądu przemiennego o na-
pięciu U = 120 V i częstotliwości f = 50 Hz. Znaleźć indukcyjność cewki, jeżeli pobiera ona moc 400 W,
a przesunięcie fazowe między napięciem i natężeniem prądu wynosi 60

o

.

Odp.: ~50 mH

7.

Naładowany kondensator o pojemności C = 0.5 µF połączono z cewką o indukcyjności L = 5 mH. Obliczyć,
po jakim czasie, od momentu połączenia kondensatora z cewką, energia pola elektrycznego kondensatora
będzie równa energii pola magnetycznego w cewce. Opór omowy cewki zaniedbać.

Odp.: 39.3 µs

Obliczenia z fizyki II

Lista #03. Ruch falowy

z elementami akustyki

1.

Określić długość fal odpowiadających częstotliwościom z przedziału słyszalności ucha ludzkiego: f

1

= 16 Hz

i f

2

= 20 kHz. Prędkość dźwięku w powietrzu przyjąć równą 340 m/s.

Odp.: 21 m, 17 mm

2.

Fala dźwiękowa, biegnąca w powietrzu z prędkością 340 m/s, dociera do obserwatora znajdującego się
w odległości 800 m od źródła dźwięku opóźniona w stosunku do fali biegnącej w wodzie, przy czym różnica
czasowa wynosi 1.8 s. Obliczyć prędkość dźwięku w wodzie.

Odp.: ~1.45 km/s

3.

Prędkość rozchodzenia się dźwięku w nafcie wynosi 1.33 km/s. Obliczyć współczynnik ściśliwości nafty,
jeśli jej gęstość wynosi 0.8 g/cm

3

.

Odp.: 7.1⋅10

-10

m

2

/N

4.

Dwa pociągi jadą naprzeciw siebie, sąsiednimi torami, z prędkościami odpowiednio 72 i 54 km/h. Parowóz
pierwszego z nich daje sygnał (gwizd) o częstotliwości 600 Hz. Obliczyć częstotliwość sygnału, jaki słyszy
pasażer drugiego pociągu, gdy: a) pociągi zbliżają się, b) pociągi oddalają się od siebie. Prędkość dźwięku w
powietrzu przyjąć równą 340 m/s.

Odp.: 666 Hz, 542 Hz

5.

Zanalizować drgania powietrza znajdującego się w rurze o długości l = 0.85 cm. Przyjmując wartość prędko-
ści dźwięku w powietrzu równą 340 m/s, obliczyć tylko te drgania własne słupa powietrza, których często-
tliwości drgań f

i

są mniejsze o pewnej wartości granicznej, równej f

gr

= 650 Hz. Rozważyć dwa wypadki:

a) rura jest zamknięta z jednej strony, b) rura jest otwarta z obu końców. Przedstawić ilustrację graficzną

Odp.: a) 100, 300, 500 Hz; b) 200, 400, 600 Hz

6.

Pręt miedziany, o długości l = 50 cm, jest zamocowany w środku. Moduł Younga dla Cu wynosi
E = 1.18⋅10

11

N/m

2

, zaś gęstość Cu wynosi ρ = 8.6 g/cm

3

. Obliczyć, ile drgań własnych pręta występuje

w przedziale częstotliwości 10 ÷ 20 kHz oraz wyznaczyć wartości tych częstości.

Odp.: 11.1 kHz, 18.5 kHz

7.

W lince wytworzono falę sinusoidalną, rozchodzącą się w dodatnim kierunku osi x. Amplituda fali wynosi
15 cm, długość fali wynosi 40 cm, a częstotliwość f = 8 Hz. Dla warunków początkowych: t = 0 i x = 0, wy-
chylenie wynosi y = 15 cm. Obliczyć liczbę falową k, okres T, częstość kołową ω oraz prędkość rozchodze-
nia się fali υ

f

. Napisać równanie fali y(x, t).

Odp.: 15.7 m

-1

, 0.125 s, 50.3 rad/s, 3.2 m/s, y = 0.15sin(15x – 50.3t + π/2) [m]

8.

Sinusoidalną falę dźwiękową opisuje równanie: s(x,t) = 2 ⋅10

-6

cos(15.7x – 858t), gdzie: s jest wyrażone

w metrach, t - w sekundach.. Obliczyć długość i prędkość rozchodzącej się fali, wychylenie cząstki dla
x = 0.05 m i t = 3 ms oraz amplitudę prędkości cząstek.

Odp.: 0.4 m, 54.6 m/s, –0.433 µm, 1.716 mm/s

9.

Dwie fale biegnące w przeciwnych kierunkach tworzą falę stojącą. Równania fal są następujące:
y

1

= 4 sin(3x – 2t) oraz y

2

= 4 sin(3x + 2t), gdzie x jest wyrażone w cm, t – w sekundach. Obliczyć amplitudę

wychylenia cząstki w położeniu x = 2.3 cm, położenia węzłów oraz położenia strzałek wytworzonej fali sto-
jącej.

Odp.: 4.63 cm, węzły: x = k(π/3) [cm], k = 0, 1, 2, 3,… strzałki: x = k(π/6) [cm], k = 1, 3, 5,…

Obliczenia z fizyki II

Lista #04. Interferencja i dyfrakcja

1.

Światło monochromatyczne, o długości fali 680 nm, pada na przesłonę z dwiema szczelinami i tworzy obraz
interferencyjny na ekranie, odległym od przesłony o L = 1 m. Jasny prążek interferencyjny IV rzędu znajduje
się w odległości 28 mm od prążka centralnego. Obliczyć odległość między szczelinami.

Odp.: 97 µm

2.

W doświadczeniu Younga, na drodze jednego z interferujących promieni, o długości fali 0.6 µm, umieszczo-
no cienką płytkę szklaną (n

s

= 1.50). Wskutek tego pierwszy jasny prążek przesunął się i zajął miejsce

uprzednio zajmowane przez szósty prążek jasny. Obliczyć grubość wstawionej płytki szklanej.

Odp.: 6 µm

3.

Doświadczenie Younga przeprowadzono przy użyciu światła o długości fali 589 nm, modyfikując je przez
wstawienie w bieg jednego z promieni kuwetę o długości 2 cm, wypełnioną chlorem. Obecność chloru spo-
wodowała, że rząd widma zmienił się o 20. Obliczyć współczynnik załamania światła w gazowym chlorze,
jeśli współczynnik załamania światła w powietrzu wynosi n

p

= 1.000276.

Odp.: 1.000865

4.

Wiązka światła monochromatycznego o długości fali 0.6 µm pada pod kątem 30

o

na znajdującą się w powie-

trzu błonę mydlaną (n = 1.30). Obliczyć, przy jakiej najmniejszej grubości błony mydlanej, wskutek interfe-
rencji, promieniowanie odbite będzie a) maksymalnie wygaszone, b) maksymalnie wzmocnione.

Odp.: 0.25 µm, 0.125 µm

5.

Monochromatyczna wiązka światła pada prostopadle na cienką, jednorodna warstwę oleju pokrywającą płyt-
kę szklaną. Jeśli długość fali światła padającego zmieniać w sposób ciągły, to – wskutek interferencji – pro-
mieniowanie odbite jest całkowicie wygaszone dla dwóch długości fali: 485 nm i 679 nm (i żadnej innej
między tymi wartościami). Współczynnik załamania światła w wypadku oleju n

O

= 1.32, a w wypadku szkła

– n

s

= 1.50. Wyznaczyć grubość warstwy oleju.

Odp.: 0.643 µm

6.

Na obrazie dyfrakcyjnym pojedynczej szczeliny, obserwowanym na ekranie oddalonym o 82.3 cm, odległość
między minimami znajdującymi się po lewej i prawej stronie maksimum centralnego, wynosi 5.2 mm. Dłu-
gość falo światła padającego λ = 546 nm. Wyznaczyć szerokość szczeliny.

Odp.: 173 µm

7.

Światło, o długości fali λ = 589 nm, pada a szczelinę o szerokości 1.16 mm. Obraz dyfrakcyjny obserwowa-
ny na ekranie odległym o 2.94 m. Wyznaczyć odległość między pierwszym i drugim minimum dyfrakcyj-
nym (po tej samej stronie maksimum centralnego).

Odp.: 1.49 µm

8.

Promieniowanie lampy rtęciowej pada prostopadle na siatę dyfrakcyjną o szerokości
b = 5 cm. Siatka ma 10

4

rys. Określić kąt między fioletowym (λ

f

= 405 nm) i żółtym

(λ

ż

= 579 nm) promieniem w widmie I rzędu.

Odp.: 2.0

o

9.

W punktach A i B znajdują się spójne źródła fal świetlnych (λ = 600 nm). Obliczyć,
o ile zmieni się różnica dróg optycznych i różnica faz drgań docierających do punktu
O, jeżeli na drodze AO umieścimy cienką płytkę o grubości 1 µm z materiału o współ-
czynniku załamania n = 1.330?

Odp.: 3.3⋅10

–5

cm, 1.1π

Obliczenia z fizyki II

Lista #05. Polaryzacja światła

1.

Wąska wiązka światła monochromatycznego przechodzą c przez płytkę szklaną
o grubości d = 2 cm, ulega przesunięciu o x. Obliczyć wartość przesunięcia, jeśli
kąt padania α = 30

o

, a współczynnik załamania światła w wypadku szkła n

s

= 1.50.

Odp.: 3.9 mm


2.

Wiązka światła monochromatycznego pada prostopadle na ściankę ab szklanego
pryzmatu (n

s

= 1.520). Obliczyć: a) dla jakiej wartości kąta φ wiązka ulegnie cał-

kowitemu wewnętrznemu odbiciu, b) jaka będzie wartość kąta φ, przy którym na-
stąpi całkowite wewnętrzne odbicie po zanurzeniu pryzmatu w wodzie (n

w

=

1.333).

Odp.: 48.9

o

, 28.7

o

3.

Ciecz o współczynniku załamania n

c

= 1.33, znajduje się w szklanym naczyniu,

którego n

s

= 1.46. Pod jakim kątem powinna padać monochromatyczna wiązka

światła naturalnego, by wiązka odbita od szklanego dna była całkowicie liniowo
spolaryzowana? Kierunek padania jest podany na rysunku.

Odp.: 79.9

o

4.

Na powierzchnię oddzielającą szkło od powietrza, od strony szkła, pada wiązka światła białego, pod kątem
granicznym odpowiadającym barwie zielonej. Szkło wykazuje dyspersją normalną (λ, n). Narysować
bieg trzech promieni: fioletowego, zielonego i czerwonego.

5.

Wiązka światła naturalnego o intensywności I

0

, pada na układ trzech polaryzatorów. Pierwszy i trzeci są

skrzyżowane względem siebie, natomiast kierunek polaryzacji środkowego (drugiego) tworzy kąt 45

o

wzglę-

dem kierunków polaryzacji pierwszego i trzeciego polaryzatora. Obliczyć stosunek intensywności wiązki
opuszczającej układ do intensywności I

0

. (Rozważyć również inny kąt niż 45

o

, np. 30

o

/60

o

).

Odp.: 0.125

6.

Dwa polaryzatory zorientowane są tak, że kąt między kierunkami ich polaryzacji wynosi 34

o

. Wiązka światła

spolaryzowanego liniowo pod kątem 17

o

względem każdego polaryzatora przechodzi przez oba polaryzatory.

Obliczyć o ile procent ulegnie wiązka osłabieniu.

Odp.: 37.1 %

7.

Światło częściowo spolaryzowane składa się ze światła naturalnego (niespolaryzowanego) oraz światła o
polaryzacji liniowej. W celu określenia stosunku intensywności tych składowych, I

np

/I

p

, wiązkę skierowano

na polaryzator. Polaryzator obrócono tak, by uzyskać największą intensywność światła opuszczającego pola-
ryzator (I

1

= I

max

). Następnie polaryzator obrócono o kąt α = 60

o

względem położenia odpowiadającego I

max

,

przy czym uzyskana intensywność (I

2

) była dwukrotnie mniejsza niż I

max

. Obliczyć stosunek I

np

/I

p

. O jaki kąt

należy obrócić polaryzator od położenia odpowiadającego I

max

,

aby uzyskać minimalną intensywność

I

3

= I

min

? Obliczyć I

1

/ I

3

.

Odp.: 1; 90

o

, 3

Obliczenia z fizyki II

Lista #06. Efekty kwantowe

1.

Maksymalna zdolność emisyjna ciała doskonale czarnego (CDC) przypada na długość fali 4840 Å. Obliczyć,
jaką ilość energii promieniuje to ciało z powierzchni 1 cm

2

, w ciągu 1 minuty.

Odp.: 438.5 J

2.

Włókno żarówki promieniuje jako ciało doskonale czarne (CDC) o temperaturze równej 2400 K. Obliczyć,
ile fotonów będzie emitowanych z 1 cm

2

powierzchni włókna w ciągu 1 s, jeżeli przyjąć, że średnia energia

kwantu promieniowania wynosi 2.75 kT (k - stała Boltzmanna, k = 1.38⋅10

–23

J/K).

Odp.: 2.1⋅10

21

3.

Temperatura początkowa T

1

ciała doskonale czarnego wzrosła o 80%, przy czym długość fali, na którą przy-

pada maksimum spektralnej zdolności emisyjnej uległa przesunięciu o ∆λ = 600 nm. Obliczyć temperaturę
końcową T

2

.

Odp.: 3867 K

4.

‘Czerwona granica’ zjawiska fotoelektrycznego dla pewnego metalu wynosi λ

gr

= 275 nm. Obliczyć pracę

wyjścia elektronu z metalu ( zarówno w J, jak i w eV) oraz maksymalną prędkość elektronów wybijanych z
tego metalu przez promieniowanie o długości fali λ = 180 nm.

Odp.: 7.23⋅10

–19

J, 4.52 eV, 9.2⋅10

5

m/s

5.

Określić najmniejszą różnicę potencjałów potrzebną do zahamowania emisji z katody (Sb-K-Na), jeżeli jej
powierzchnia jest oświetlona promieniowaniem o długości fali λ = 402 nm, a czerwona granica zjawiska fo-
toelektrycznego dla tego typu katody wynosi 670 nm. Obliczyć, jaka część energii padającego fotonu jest
zużyta na pracę wyjścia.

Odp.: 1.24 V, 60%

6.

Powierzchnię pewnego metalu oświetlono promieniowaniem o długości fali 350 nm; przy określonym po-
tencjale hamującym fotoprąd jest równy zero. Przy zmianie długości fali o 50 nm potencjał hamujący należa-
ło zwiększyć o 0.59 V. Obliczyć wartość ładunku elektronu przyjmując znaną wartość stałej Plancka i war-
tość prędkości światła.

Odp.: 1.6⋅10

–19

C

7.

Przy 1.5-krotnym zwiększeniu napięcia podawanego na lampę rentgenowską długość fali ‘niebieskiej grani-
cy’ ciągłego widma rentgenowskiego przesunęła się o ∆λ = 0.26 Ǻ. Obliczyć wartość początkową napięcia
przyłożonego do lampy.

Odp.: 15.9 kV

8.

Monochromatyczna wiązka promieniowania rentgenowskiego o λ = 0.125 nm, pada
na kryształ NaCl, pod kątem 45

o

. Odległość między płaszczyznami krystalograficz-

nymi wynosi d = 0.252 nm. Obliczyć, o jaki kąt należy obrócić kryształ (obrót wokół
osi prostopadłej do rysunku), aby otrzymać wiązkę ugiętą odpowiadającą rodzinie
płaszczyzn (prawo Bragga). Zaniedbać możliwość niezerowego natężenia niektórych
wiązek.

Odp.: 30.6

o

i 15.3

o

(zgodnie z ruchem wskazówek zegara) oraz 3.1

o

i 37.8

o

(przeciwnie do

ruchu wskazówek zegara)

Obliczenia z fizyki II

Lista #07. Fale materii,

Zasada nieoznaczoności

1.

Foton promieniowania X ulega rozproszeniu Comptona zderzając się ze słabo związanym elektronem i prze-
kazuje mu 10% swojej energii. Rozproszenie następuje pod katem θ = 60

o

. Obliczyć długość fali fotonu roz-

proszonego, pęd fotonu padającego, energię elektronu odrzutu (w J i w eV), oraz kąt miedzy padającym fo-
tonem i elektronem odrzutu. Przedstawić graficznie zasadę zachowania pędu dla rozpatrywanego tu rozpro-
szenia fotonu.

Odp.: 0.121 Å, 6.13⋅10

–23

kgm/s, 1.82⋅10

–15

J (11.4 keV), 55

o

2.

Foton promieniowania rentgenowskiego o długości fali 0.708 Å jest rozproszony przez grafit pod kątem θ =
90

o

(zjawisko Comptona). Wyznaczyć kąt między padającym fotonem i elektronem odrzutu. Obliczyć, jaką

część swojej energii foton przekazał elektronowi.

Odp.: 44.0, 3,3%

3.

Obliczyć energię kinetyczną następujących cząstek, jeśli odpowiada im fala de Broglie’a równa 1 Å: elek-
tron, cząsteczkai tlenu O

2

oraz cząstka, której promień wynosi 0.1 µm, a gęstość wynosi 2 g/cm

3

.

Odp.: 151 eV, 2.6 MeV, 1.6⋅10

–11

eV

4.

Równoległa wiązka elektronów pada prostopadle na diafragmę o wąskiej, prostokątnej szczelinie, której
szerokość wynosi a = 0.1 mm. Zjawisko dyfrakcji jest obserwowane na ekranie umieszczonym w odległości
L = 0.5 m od diafragmy. Szerokość centralnego maksimum dyfrakcyjnego wynosi 8 µm. Obliczyć prędkość
padających elektronów.

Odp.: 9.1⋅10

5

m/s

5.

Z jaką dokładnością można określić położenie elektronu o energii 1.50 keV, jeżeli energia znana jest z do-
kładnością 1%?

Odp.: 1.0 nm

6.

Wzbudzony atom emituje foton w czasie 0.01 µs. Długość fali emitowanego promieniowania jest równa 600
nm. Określić dokładność, z jaką może być wyznaczona energia oraz długość fali fotonu.

Odp.: 6.6⋅10

–8

eV, 1.9⋅10

–5

nm

7.

Oko ludzkie dostrzega światło o długości fali 500 nm, jeżeli promienie niosą energię nie mniejszą niż
20.8⋅10

–18

J na sekundę. Jaka ilość kwantów światła pada wtedy, w ciągu sekundy, na siatkówkę oka?

Odp.: 53

8.

Ile fotonów znajduje się w mm

3

wiązki światła monochromatycznego o długości fali 488 nm? Moc promie-

niowania jest równa 20 W, a przekrój poprzeczny wiązki jest równy 1 cm

2

.

Odp.: 1.63⋅10

6