Rok: I WB Kierunek: Budownictwo	Marek Suchostawski	22.04.2009 r.
Nr ćw: 23	Wyznaczenie prędkości dźwięku za pomocą rury Kundta

TEORIA

Rozchodzenie się dźwięku odbywa się w postaci fali mechanicznej i może mieć miejsce tylko w ośrodku sprężystym. Falą nazywamy proces rozchodzenia się drgań w ośrodku .

Można wyróżnić fale poprzeczne (gdy kierunek drgań cząsteczek jest zgodny z kierunkiem fali) oraz fale podłużne (kierunek drgań jest prostopadły do kierunku fali). Charakter fali zależy od własności sprężystych ośrodka w którym się rozchodzi .

Podstawowymi, charakterystycznymi wielkościami występującymi w ruchu falowym są: λ - długość fali, T - okres drgań, υ - prędkość rozchodzenia się fali w danym ośrodku. Długością fali nazywamy odległość dwóch kolejnych punktów drgających w tej samej fazie, leżącym na tym samym promieniu. Inaczej mówiąc jest to droga, jaką przebędzie zaburzenie w czasie T. Pomiędzy λ, T, υ zachodzi następująca zależność:

λ = υT

Czasem analogicznie do ruchu drgającego podstawimy za
, (dzie v - częstotliwość)i można ją wówczas zapisać

Jeżeli w danym ośrodku rozchodzą się fale spójne tzn. o jednakowej częstotliwości i fazie (lub stałej różnicy faz) wówczas mamy do czynienia z interferencją tych fal. W szczególnym przypadku podczas interferencji fali biegnącej i odbitej może dojść do powstania fali stojącej (Rys.1). Fala stojąca jest to szczególny rodzaj ruchu falowego ponieważ energia nie jest przenoszona wzdłuż promienia rozchodzenia się fali, ale zmagazynowana jest trwale w cząsteczkach materii. Jeżeli fala biegnąca odbija się od ośrodka o większej gęstości niż ten w którym się rozchodzi, następuje zmiana fazy fali odbitej, a w miejscu odbicia powstaje węzeł. W przeciwnym przypadku (odbicie od ośrodka rzadszego) nie dochodzi do zmiany fazy, a na granicy ośrodków powstaje strzałka fali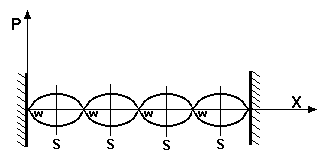
stojącej.

Rys. 1 Stojąca fala akustyczna np. w zamkniętej rurze;

X - położenie punktów w rurze, P - wartość ciśnienia

W ćwiczeniu do wyznaczania prędkości dźwięku zastosowano rurę Kundta (Rys. 2). Jest to długa, wąska, szklana rura z jednej strony zamknięta ruchomym tłoczkiem, a z drugiej prętem zakończonym krążkiem, którego średnica jest nieco mniejsza niż średnica rury. Ponieważ pręt zamocowany jest na sztywno w połowie swej długości, po wywołaniu w nim drgań (poprzez pocieranie końca skórką posypaną kalafonią) otrzymamy falę o długości λ = 2L (gdzie L - długość pręta).Drgania pręta zostaną przekazane poprzez krążek K słupowi powietrza zamkniętego w rurze. Ruchomym tłoczkiem T przesuwamy tak aby w rurze powstała fala stojąca, co uwidocznione zostanie poprzez charakterystyczne ułożenie pyłu korkowego w pewne skupiska. Najwięcej korka pozostanie tam gdzie powstaną węzły fali, natomiast miejsca wolne od pyłu korkowego to strzałki.

W obydwu ośrodkach (powietrzu i w pręcie) rozchodzi się fala o tej samej częstości (ta sama fala), dlatego też można zapisać że:

stąd: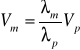

- odpowiednio prędkości fali w powietrzu w badanym materiale

- analogicznie długości fali.

Ze względu na mocowanie pręta
= 2L, natomiast
można wyznaczyć mierząc odległości między skrajnymi węzłami lub strzałkami i wtedy:

gdzie n - ilość kolejnych węzłów lub strzałek

d - odległość n węzłów lub strzałek.

Ostatecznie otrzymujemy wzór, z którego można wyznaczyć prędkość dźwięku w badanym materiale:

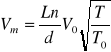
gdzie:
- prędkość dźwięku w powietrzu =331
(w temp. 273 K i przy normalnym ciśnieniu).

Prędkość rozchodzenia się fal podłużnych w ośrodku ciągłym :

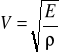
gdzie: E - jest modułem Younga ośrodka , jego gęstością .

stąd:

gdzie:

TABELA POMIARÓW

Rodzaj pręta	ρ k m^-3	Odległość d [m]	Liczba półfal n	Długość pręta L [m]	Temperatura [K]
MIEDZIANY	8,89	0,360	5	1	297
				0,365		5	1
				0,367		5	1
		ALUMINIOWY	2,7	0,350		6	1,05	297
				0,360		6	1,05
				0,355		6	1,05

OBLICZENIA

Wyznaczenie prędkości fali w pręcie:

V₀ = 331 ms^-1

T₀ = 273 K

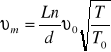
1. dla miedzianego

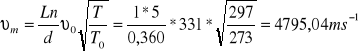
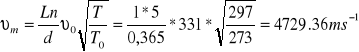
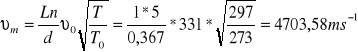
2. dla aluminiowego

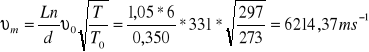
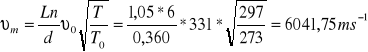
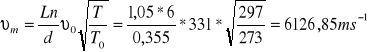
Wyznaczenie średniej arytmetycznej dla prędkości fali w pręcie:

1. dla miedzianego

Wyznaczenie modułu Younga:

E = υ² ρ

1. dla pręta miedzianego

E = (
)² * 8,89 = 20,4 * 10⁸

E = (
)² * 8,89 = 19,88 * 10⁸

E = (
)² * 8,89 = 19,67 * 10⁸

2. dla pręta aluminiowego

E = (6214,37)² * 2,7 = 10,4 * 10⁸

E = (6041,75)² * 2,7 = 9,85 * 10⁸

E = (6126,85)² * 2,7 = 10,1 * 10⁸

Wyznaczenie średniej modułu Younga:

1. dla miedzianego

2. dla aluminiowego

Wyznaczenie niepewności dla L i d:

Δ_eL = 0,01m

Δ_dL = 0,02m

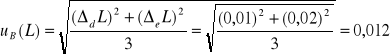
Δ_ed = 0,01m

Δ_dd = 0,03m

\

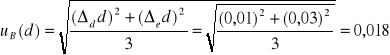
Wyznaczenie niepewności całkowitej v i E:

1. dla pręta miedzianego:

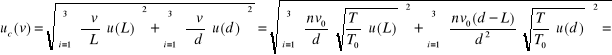
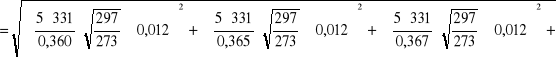
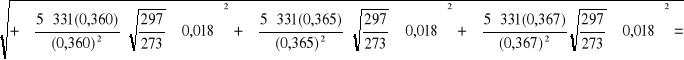
2. dla pręta aluminiowego

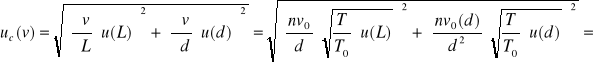
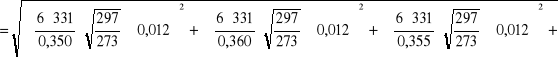
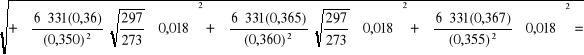
ZESTAWIENIE WYNIKÓW:

Miedź
	Wartość obliczeniowa	Wartość tablicowa
Prędkość fali w pręcie	4742,66 ms^-1+ 177,71	3560 ms^-1
Moduł Younga	*10^8N/m^2 + 0,15*10^8	10,5*10^8 N/m^2
Aluminium
Prędkość fali w pręcie	6127,66 ms^-1+220,42	5104 ms^-1
Moduł Younga	*10^8 N/m^2 + 0,73*10^8	6,8*10^8 N/m^2

WNIOSKI

Zgodnie z tabelą wartości prędkości dźwięku w różnych ośrodkach, prędkość rozchodzenia się dźwięku w aluminium przy temperaturze 293 K wynosi: V_al = 5104 [m s^-1], a dla miedzi: V_m = 3560 [m s^-1]. W wykonanym ćwiczeniu uzyskano następujące wartości dla temperatury 295 K : V_al = 6217,66 [m s^-1] ; V_m = 4742,66 [m s^-1].

Wartości otrzymane w wyniku pomiarów, są wartościami obarczonymi błędami, wynikającymi przede wszystkim z niedoskonałości przyrządów pomiarowych. Duży wpływ na wartość błędu pomiaru wartości temperatury ma fakt, że termometr i stanowisko pomiarowe znajdowały się w dwóch różnych miejscach.

Wyznaczenie niepewności całkowitej v i E:

1. dla pręta miedzianego:

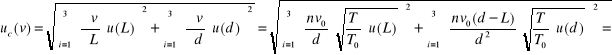
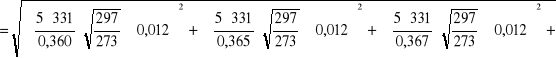
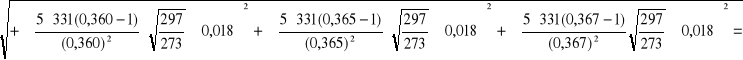
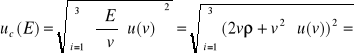
2. dla pręta aluminiowego

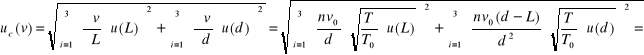
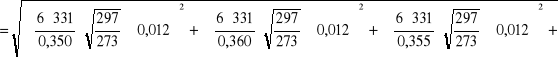
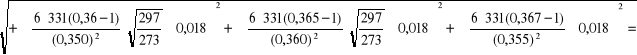
ZESTAWIENIE WYNIKÓW:

Miedź
	Wartość obliczeniowa	Wartość tablicowa
Prędkość fali w pręcie	4742,66 ms^-1+ 277,2	3560 ms^-1
Moduł Younga	*10^8N/m^2 + 0,447*10^8	10,5*10^8 N/m^2
Aluminium
Prędkość fali w pręcie	6127,66 ms^-1+352,38	5104 ms^-1
Moduł Younga	*10^8 N/m^2 + 0,743*10^8	6,8*10^8 N/m^2

WNIOSKI

Zgodnie z tabelą wartości prędkości dźwięku w różnych ośrodkach, prędkość rozchodzenia się dźwięku w aluminium przy temperaturze 293 K wynosi: V_al = 5104 [m s^-1], a dla miedzi: V_m = 3560 [m s^-1]. W wykonanym ćwiczeniu uzyskano następujące wartości dla temperatury 295 K : V_al = 6217,66 [m s^-1] ; V_m = 4742,66 [m s^-1].

Wartości otrzymane w wyniku pomiarów, są wartościami obarczonymi błędami, wynikającymi przede wszystkim z niedoskonałości przyrządów pomiarowych. Duży wpływ na wartość błędu pomiaru wartości temperatury ma fakt, że termometr i stanowisko pomiarowe znajdowały się w dwóch różnych miejscach.

---