GKIW Moduł 5 - Reprezentacja przestrzeni
trójwymiarowej na płaszczyźnie

From Studia Informatyczne

Spis treści

1 Wykład
2 Literatura

Wykład

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

1/24

Rzutowanie jest
przekształceniem
przestrzeni
trójwymiarowej na
przestrzeń
dwuwymiarową.
Rzutowanie polega
na poprowadzeniu
prostej przez dany
punkt obiektu i
znalezieniu punktu
wspólnego tej
prostej z rzutnią.
Wyznaczony punkt
nazywany jest
rzutem a prosta
promieniem
rzutującym.

Powszechna
definicja rzutu jako
przekształcenia na
płaszczyznę jest
pewnym
uproszczeniem gdyż
rozpatruje się też np.
rzuty na
powierzchnię walca
lub na wycinek
sfery. Jednak
rzeczywiście z
rzutowaniem na
płaszczyznę mamy
najczęściej do
czynienia (grafika
komputerowa,
fotografia).

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

2/24

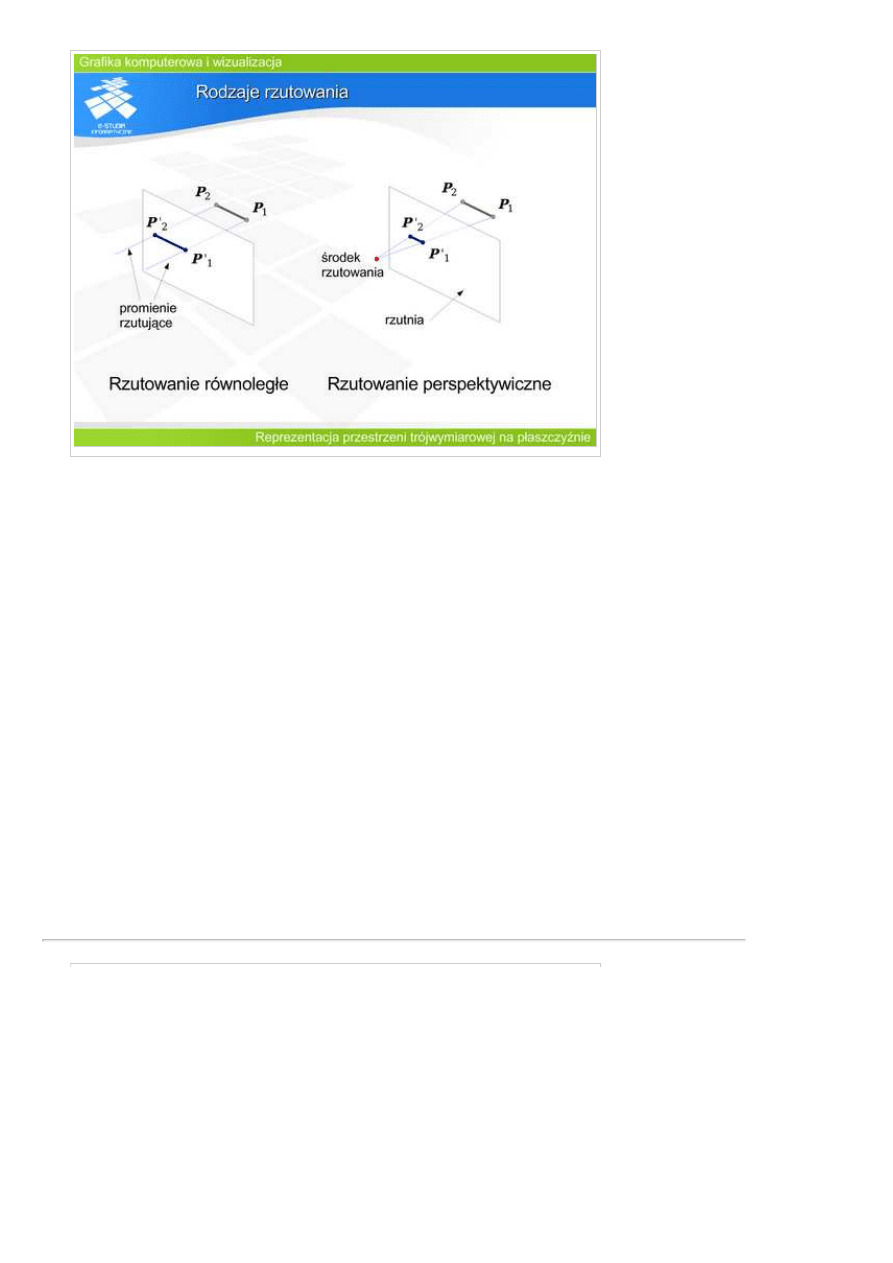
Rzutowanie
równoległe, gdy
promienie rzutujące
są prostymi
równoległymi.
Dodatkowo
mówimy o
rzutowaniu
równoległym
prostokątnym, jeśli
rzutnia jest
prostopadła do
kierunku rzutowania
oraz o rzutowaniu
równoległym
ukośnym w
każdym innym
przypadku.

Rzutowanie
perspektywiczne,
gdy promienie
rzutujące tworzą
pęk prostych.
Oczywiście,
mówienie w tym
przypadku o
prostopadłości (lub
nie) rzutni nie ma
sensu, gdyż w
rzutowaniu
perspektywicznym
dokładnie jeden
promień może być
prostopadły do
płaszczyzny rzutni, a
wszystkie pozostałe
tworzą z nią kąty
mniejsze od kąta
prostego.

Rzutowanie
perspektywiczne
jest często
nazywane
rzutowanie m
środkowym lub
centralnym.

Z rzutowaniem

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

3/24

Z rzutowaniem
równoległym mamy
najczęściej do
czynienia w różnego
typu zastosowaniach
technicznych np.
rzuty prostokątne na
3 lub 6 płaszczyzn –
tradycyjny rysunek
techniczny.
Rzutowanie
równoległe nie
pozwala
przedstawić obiektu
zgodnie z naszym
wyobrażeniem –
zgodnie z widzeniem
człowieka. Pozwala
natomiast
zdefiniować
wymiary przedmiotu
i parametry
technologiczne.

Rzutowanie
równoległe
zachowuje
równoległość
prostych oraz
proporcje długości
odcinków
równoległych

Rzutowanie
perspektywiczne
pozwala uzyskać
obraz zbliżony do
postrzeganego przez
człowieka. Trzeba
jednak pamiętać o
tym, że obraz na
siatkówce oka
powstaje w wyniku
rzutu środkowego
na wycinek sfery (w
przybliżeniu). Zatem
wszystkie promienie
rzutujące będą w
tym przypadku
prostopadle padały
na rzutnię. Oznacza
to, że rzut na
płaszczyznę będzie
tylko przybliżeniem
obrazu
powstającego na
siatkówce oka.

Oczywiście dobór
warunków
rzutowania ma
decydujący wpływ
na późniejszy, mniej
lub bardziej
realistyczny odbiór
obrazu. Jest to

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

4/24

szczególnie istotne
w przypadku
zastosowania grafiki
do generacji
efektów specjalnych
(lub całych ujęć) w
kinematografii, a
także w produkcji
gier
komputerowych,
gdzie realistyczność
odbieranego świata
decyduje często o
jakości gry.

Naturalnym i
najczęściej
stosowanym
układem
współrzędnych
związanym z
rzutowaniem i
obserwatorem jest
lewoskrętny
kartezjański układ
współrzędnych.
Kierunki osi 0X i 0Y
są zgodne ze
współrzędnymi
definiującymi
położenie na
płaszczyźnie rzutni
natomiast
współrzędna Z
określa odległość od
obserwatora.

Ponieważ położenie
przedmiotów
wyimaginowanego
świata jest
opisywane w
układzie
prawoskrętnym, to
zachodzi
konieczność nie
tylko związania
położenia
obserwatora i
kierunku rzutowania
z układem świata,
ale także
zapewnienia zmiany
skrętności układu.
Trzeba o tym
pamiętać definiując
macierze opisujące
odpowiednie
operacje. Mówimy o
układzie
współrzędnych
obiektu (sceny lub
świata) i przestrzeni
obiektu oraz
układzie
obserwatora (lub

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

5/24

rzutu) i przestrzeni
obserwatora. Takie
rozdzielenie
funkcjonalne
znacznie ułatwia
manipulację i
definiowanie
odpowiednich
parametrów.
Dodatkowo
mówimy o układzie
współrzędnych
rzutni opisującym
położenie
elementów rzutu.

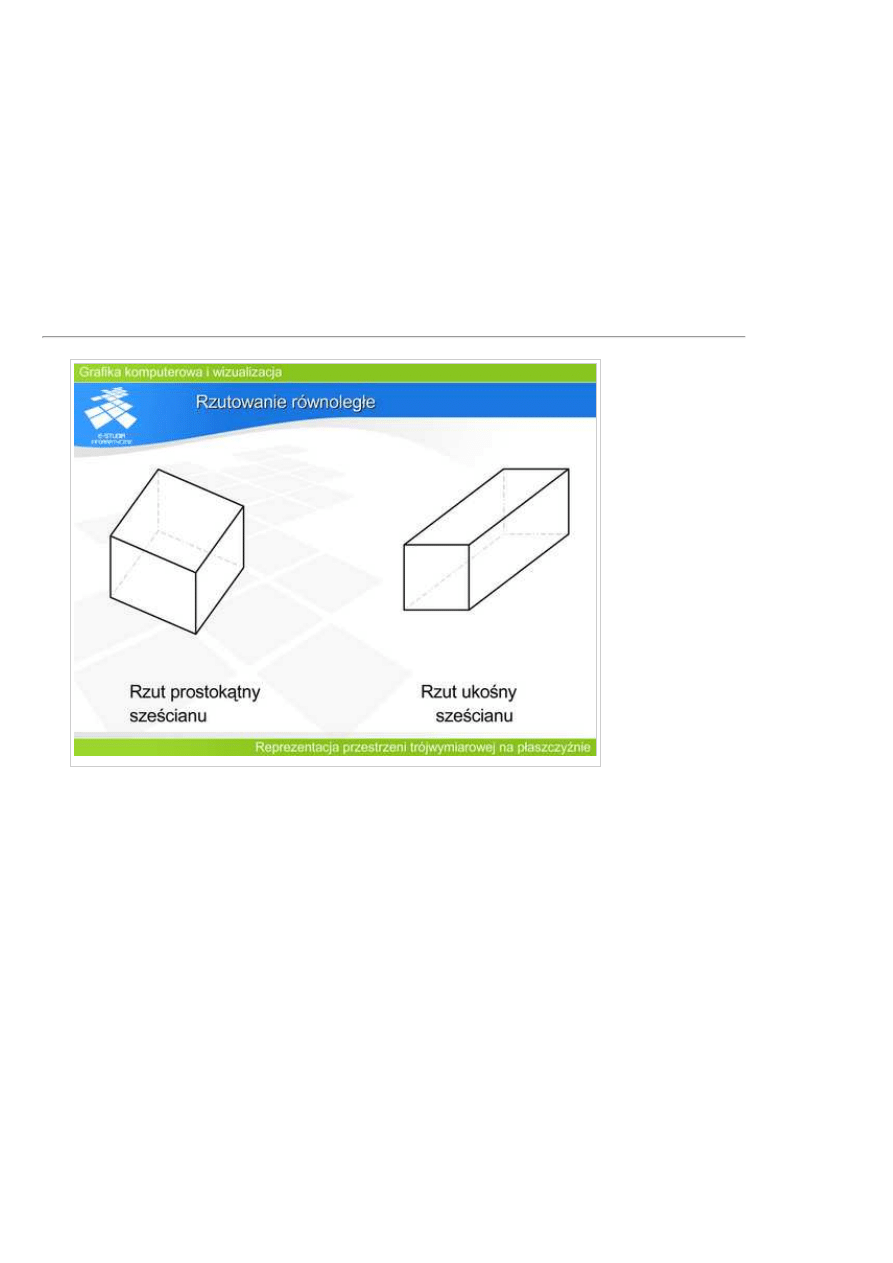
O rzutowaniu
równoległym
mówimy, że jest
prostokątne
wtedy, gdy
promienie rzutujące
są prostopadłe do
płaszczyzny rzutni.
W przeciwnym
przypadku
rzutowanie
równoległe jest
ukośne.

Rzutowanie
prostokątne jest
powszechnie
stosowane w
mechanice.
Podstawową zaletą
takiego rozwiązania
jest fakt, że
wymiary rysunku
odpowiadają
wymiarom obiektu
to znaczy długość
odcinka
równoległego do
płaszczyzny rzutni
jest równa długości
rzutu tego odcinka.
Aby na podstawie
rzutu można było
określić wymiary
przedmiotu stosuje
się zestaw trzech
rzutów danego
przedmiotu na
rzutnie, które są
wzajemnie
prostopadłe. Ze
względu na
konieczność
jednoznacznego
przedstawienia
widoków obiektu
czasami (w
przypadku bardzo

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

6/24

złożonych
elementów) stosuje
się sześć rzutów.
Tzn. są to rzuty na
trzy płaszczyzny
wzajemnie
prostopadłe, ale dla
każdej z nich
wykonuje się po
dwa rzuty dla
wzajemnie
przeciwnych
kierunków.

Można wykazać, że
rzutowanie ukośne
pozwala praktycznie
dowolnie zmieniać
proporcje wymiarów
obiektu. To znaczy
jeśli rozpatrzymy
wzajemnie
prostopadłe odcinki
o takiej samej
długości to można
uzyskać dowolne
proporcje ich rzutów
dobierając
odpowiednio
kierunek rzutowania
i położenie
płaszczyzny rzutni.
Z tego względu, w
praktycznych
zastosowaniach
rzutowania
równoległego
ukośnego w
mechanice
najczęściej definiuje
się rzut przez
podanie zmian
proporcji odległości
wzdłuż każdej z osi
układu
współrzędnych, a
nie przez podanie
położenia rzutni i
promieni
rzutujących. Na
przykład
perspektywa
kawalerska,
perspektywa
gabinetowa i
perspektywa
wojskowa są
rodzajami
rzutowania
równoległego
ukośnego
zdefiniowanymi na
tej zasadzie.

Uzyskanie dowolnej
zmiany proporcji

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

7/24

wymiarów oznacza,
że możliwe jest
uzyskanie rzutu
sześcianu jak na
rysunku. Je st to
całkowicie
poprawny rzut
równoległy
ukośny sześcianu.
Tylko że całkowicie
niezgodny z naszym
sposobem widzenia.

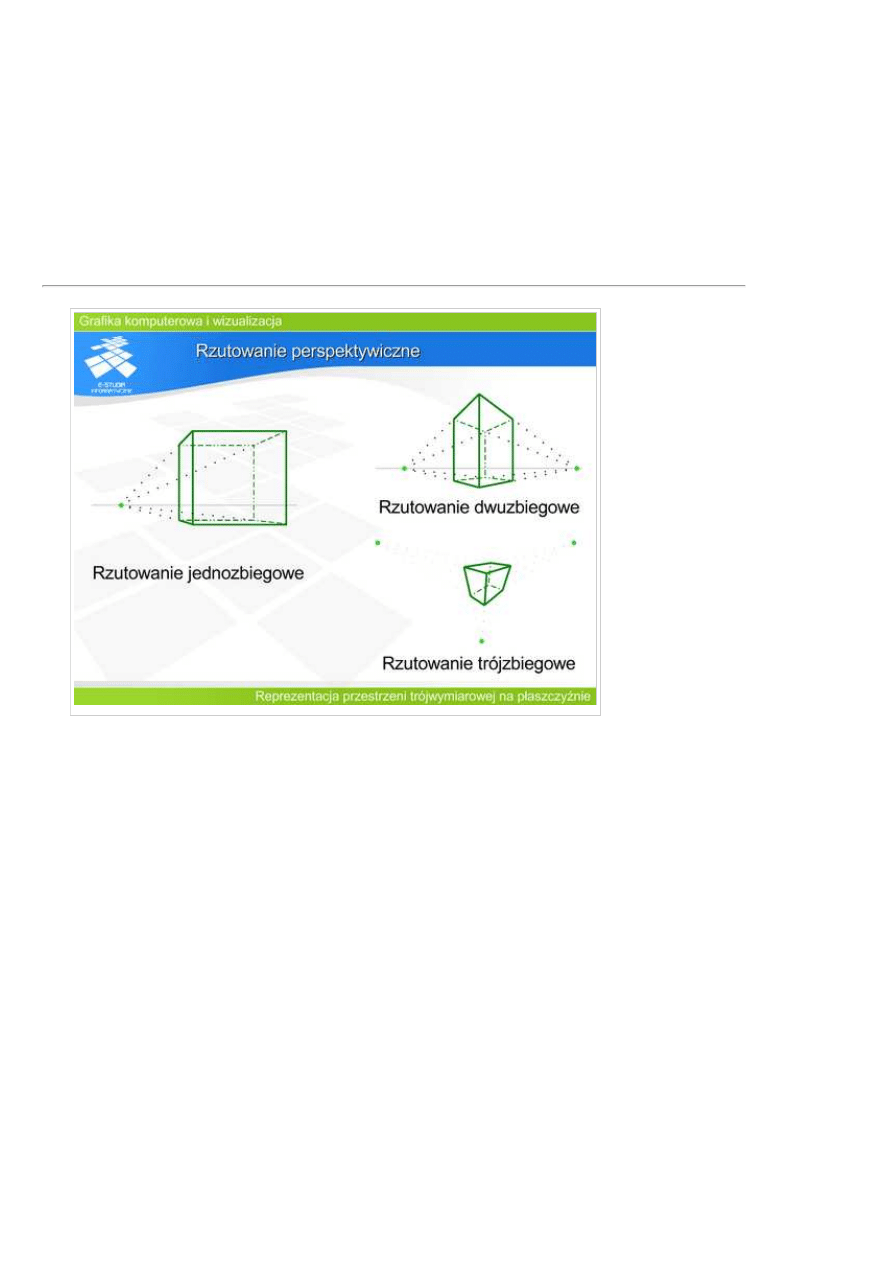
W każdym rzucie
perspektywicznym
istnieje przynajmniej
jedna rodzina
prostych
równoległych i nie
równoległych do
rzutni, taka, że rzuty
tych prostych
przecinają się w
jednym punkcie
zwanym punktem
zbiegu. W
zależności od
położenia rzutni
względem obiektu
mówimy o
rzutowaniu
perspektywicznym
jednozbiegowym,
dwuzbiegowym lub
trójzbiegowym.

Skrót
perspektywiczny
jest efektem
wizualnym
polegającym na tym,
że wielkość rzutu
perspektywicznego
jest odwrotnie
proporcjonalna do
odległości obiektu od
środka rzutowania.
Z tego względu nie
ma praktycznie
możliwości
uzyskania informacji
o wymiarach
obiektu na
podstawie jego rzutu
perspektywicznego.
Z drugiej strony
efekty wizualne
uzyskane w
rzutowaniu
perspektywicznym
są zbliżone do
wrażeń
wzrokowych oraz

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

8/24

do efektów
fotograficznych.

Rzutowanie jest
realizowane w
układzie
obserwatora
(lewoskrętnym).

Przekształcenia i
definiowanie
obiektów w układzie
sceny
(prawoskrętnym).
Jeśli przekształcenie
punktu z jednego
układu do drugiego
opiszemy
odpowiednią
macierzą takiego
przekształcenia, to
funkcjonowanie obu
układów
współrzędnych
ułatwi realizację
tworzenie obrazu.

Położenie punktów
rzutu opisuje układ
rzutni. Natomiast
dodatkowo wyróżnia
się układ urządzenia
(fizyczny) związany
bezpośrednio z
urządzeniem
wyświetlającym
(drukującym) obraz

Rzutowanie może być opisane
macierzowo, analogicznie do opisu
operacji geometrycznych
zaprezentowanych wcześniej.

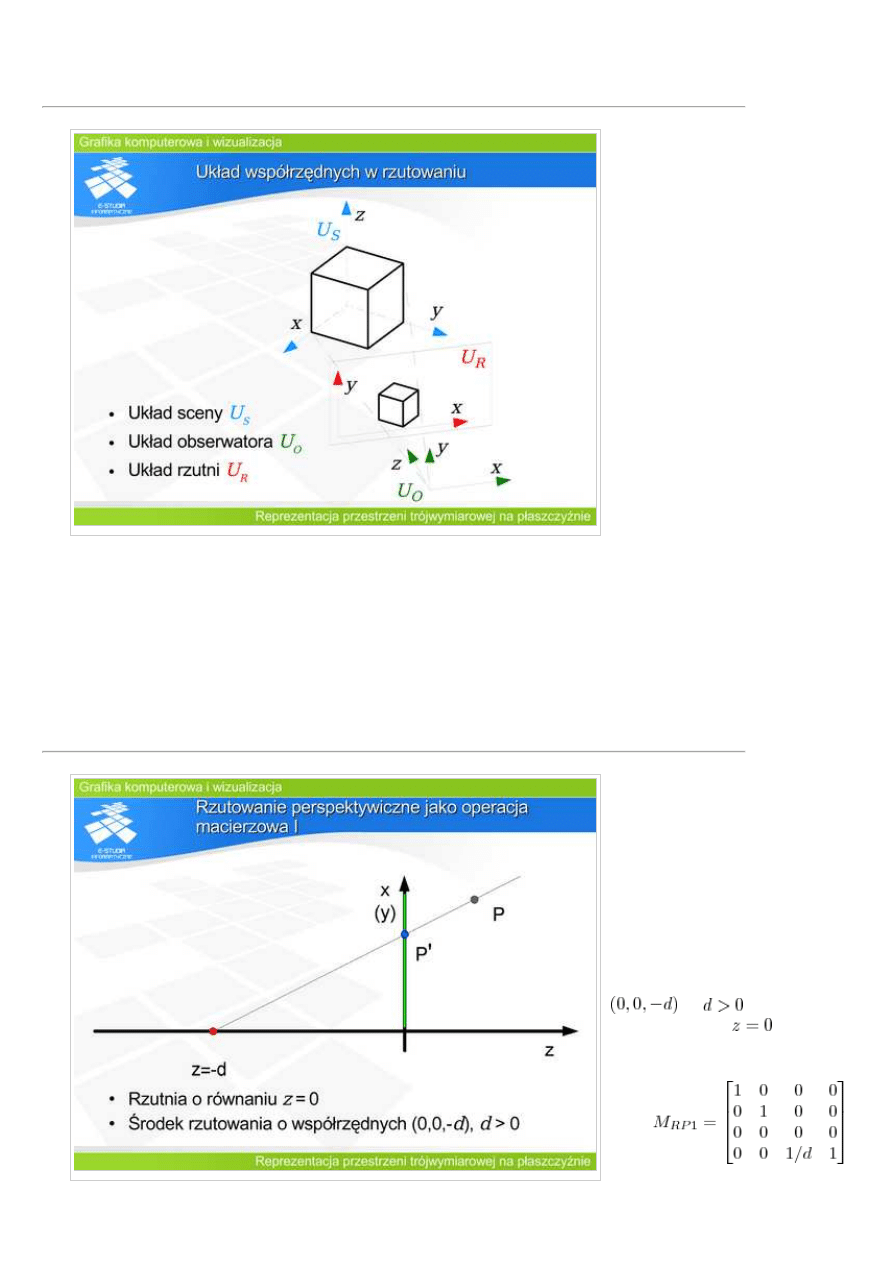
Rozpatrzmy rzutowanie
perspektywiczne w przestrzeni
obserwatora. Współrzędne opisują
położenie w lewoskrętnym układzie
współrzędnych obserwatora 0XYZ.

Niech obserwator (środek
rzutowania) znajduje się w punkcie

dla

a płaszczyzna

rzutni ma równanie

- jak na

rysunku. Macierz rzutowania będzie
wtedy miała postać:

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

9/24

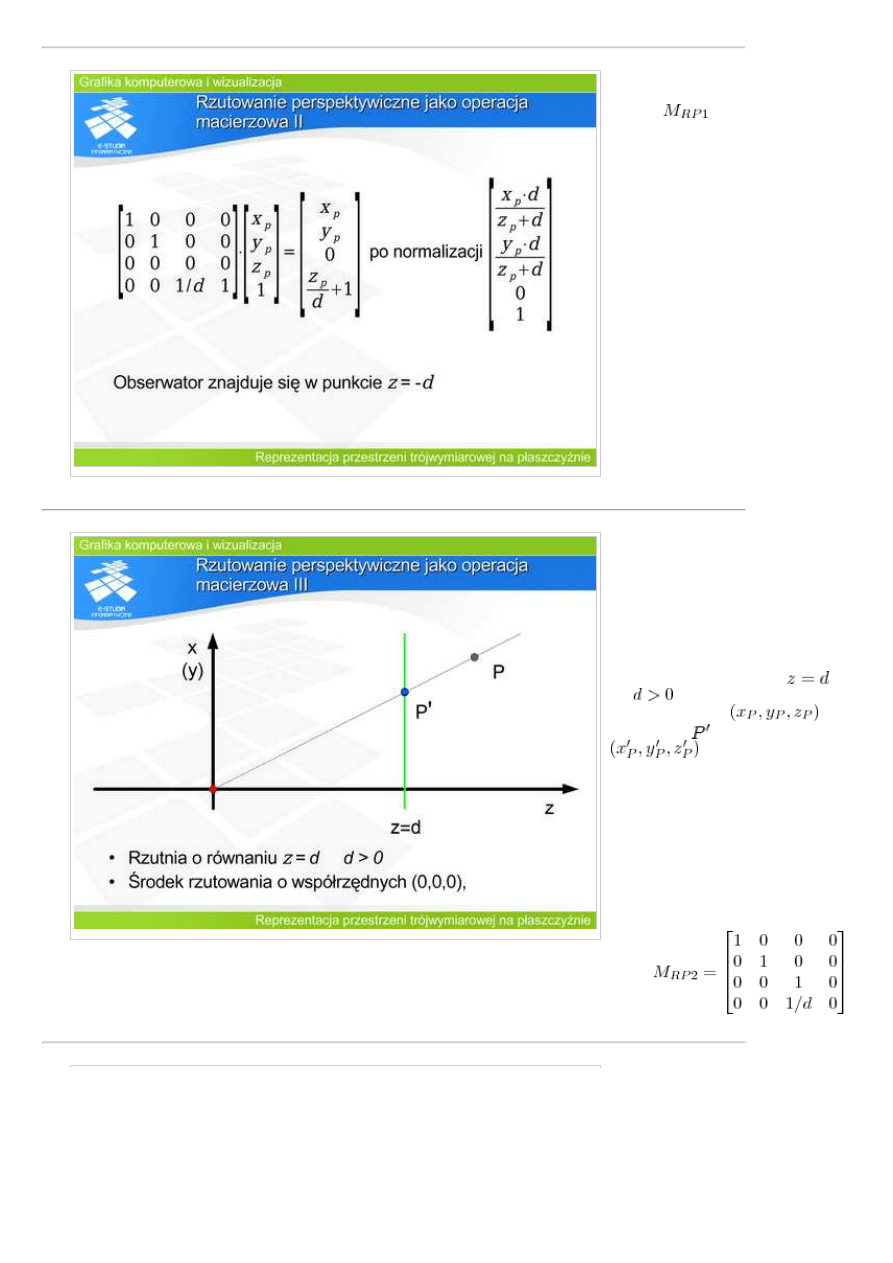
Warto zwrócić
uwagę na to, że
macierz
definiuje operację
wymagającą
normalizacji.

Rzutowanie perspektywiczne można
również prosto zdefiniować w nieco
inny sposób.

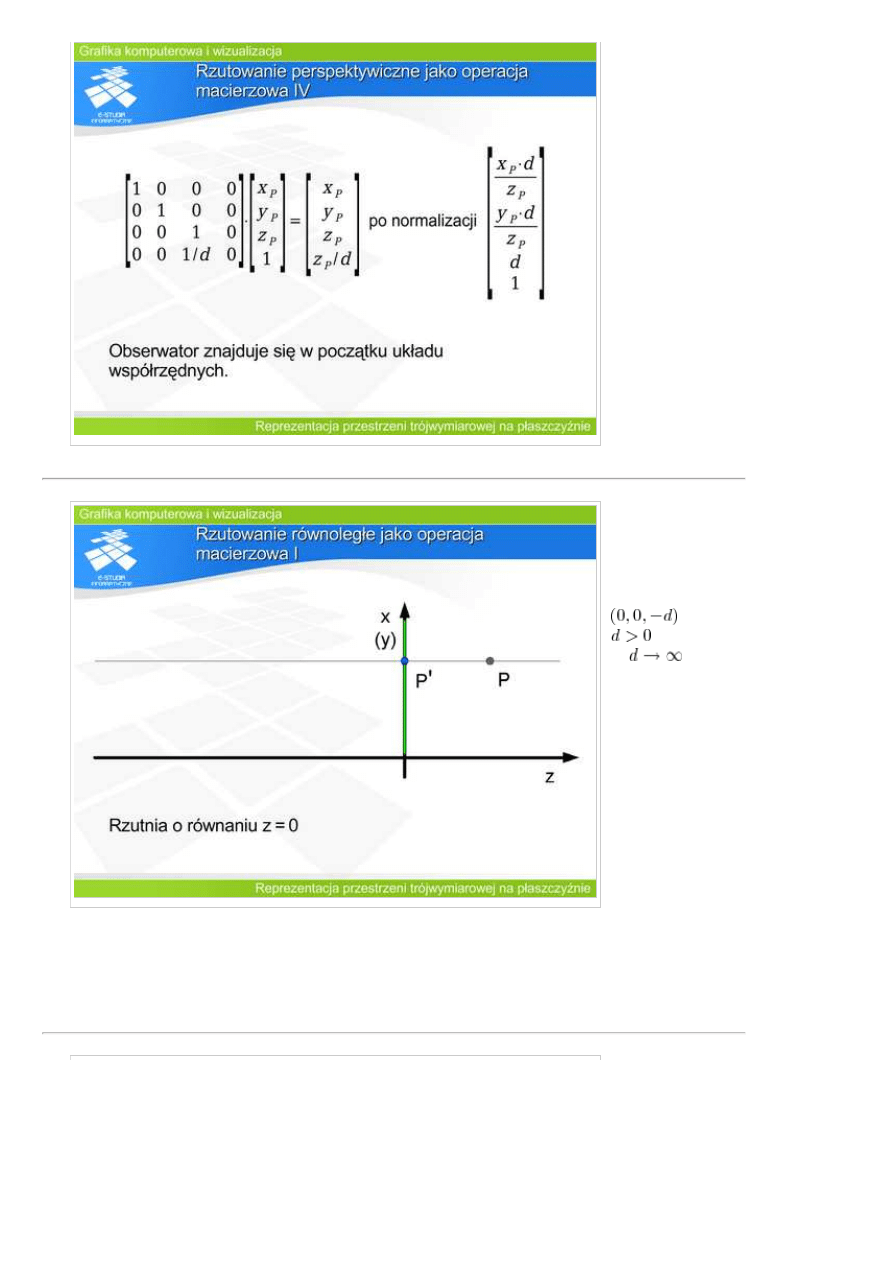
Niech w analogicznym układzie
współrzędnych obserwator (środek
rzutowania) znajduje się w początku
układu współrzędnych, a rzut jest
dokonywany na płaszczyznę
dla

(rysunek). Rzutem punktu

P o współrzędnych
będzie punkt

o współrzędnych

, który zgodnie z

definicją rzutu perspektywicznego
będzie należał do płaszczyzny rzutni i
jednocześnie do prostej przechodzącej
przez środek rzutowania i punkt .
Uwzględniając proste zależności
geometryczne można pokazać, że
macierz opisująca tak zdefiniowane
rzutowanie perspektywiczne ma
następującą postać:

W tym wariancie

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

10/24

W tym wariancie
opisu rzutowania
perspektywicznego
macierz wynikowa
również wymaga
normalizacji.

Oba warianty
definicji rzutowania
perspektywicznego
mogą być
stosowane
zamiennie zależnie
od sytuacji.

Jeżeli w pierwszym
przypadku
rzutowania
perspektywicznego
(środek rzutowania
w punkcie

dla

) przyjmiemy,

że

to

promienie rzutujące
zamiast pęku
prostych utworzą
proste równoległe i
uzyskamy
rzutowanie
równoległe
prostokątne. O
rzutowaniu
równoległym można
powiedzieć, że jest
szczególnym
przypadkiem
rzutowania
perspektywicznego,
gdy środek
rzutowania znajduje
się w
nieskończoności.

Macierz opisująca rzutowanie

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

11/24

Macierz opisująca rzutowanie
równoległe będzie miała
następującą postać:

Operacja w tym przypadku nie
wymaga normalizacji.

W
dotychczasowych
rozważaniach o
rzutowaniu nie
zwróciliśmy w ogóle
uwagi na to, które
obiekty (lub ich
fragmenty) – które
punkty przestrzeni
zostaną zrzutowane.
A przecież każdy
użytkownik aparatu
fotograficznego wie,
że tylko wybrany
przez niego
fragment przestrzeni
zostanie utrwalony
na zdjęciu. To
znaczy, że operacje
matematyczne
wynikające z
rzutowania powinny
zostać zrealizowane
tylko w odniesieniu
do określonego
zbioru punktów
(określonych
obiektów). Jeżeli
przyjmiemy, że
dokonujemy
rzutowania
perspektywicznego
na płaszczyznę i
interesuje nas
prostokąt obrazu
jako część rzutni, to
środek rzutowania i
prostokąt obrazu

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

12/24

wyznaczą pewien
fragment
przestrzeni, który
może zostać
„utrwalony”. Jeżeli
do tego dodamy
dwie płaszczyzny
równoległe do rzutni,
które ograniczą
wybrany fragment z
przodu i z tyłu, to
powstanie figura
będąca ostrosłupem
ściętym o podstawie
prostokątnej
nazywana
ostrosłupem
widzenia lub
piramidą widzenia.
Zatem po
zdefiniowaniu
położenia
obserwatora (środka
rzutowania), rzutni i
ostrosłupa widzenia,
należy wydzielić te
obiekty i punkty
przestrzeni, które
będą rzutowane.
Powstaje problem
obcinania w
przestrzeni
trójwymiarowej.
Algorytmy Cohena-
Sutherlanda i
Cyrusa-Becka
można rozszerzyć o
możliwość obcinania
trójwymiarowego.

Dla rzutowania
równoległego
odpowiednia bryła
widzenia
zdefiniowana
analogicznymi
parametrami będzie
prostopadłościanem.
Możliwe jest
przekształcenie
ostrosłupa widzenia
(ostrosłupa
ściętego !) w
odpowiadający mu
prostopadłościan.
Przekształcenie
takie nazywa się
prze kształceniem
perspektywicznym
(a nie rzutowaniem).

Patrząc na

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

13/24

Patrząc na
rzutowanie poprzez
analogię do aparatu
fotograficznego
warto zwrócić
uwagę na parametry
decydujące o
obrazie, który
powstanie. Fotograf,
wybierając temat do
zdjęcia, określa
położenie aparatu i
kierunek
fotografowania.
Określa także
ogniskową
obiektywu (funkcja
zoom) czyli kąt
„widzenia” aparatu.
Warto przy tym
pamiętać, że zdjęcie
wykonane
obiektywem
szerokokątnym z
bliskiej odległości
jest inne niż
obiektywem
wąskokątnym
(teleobiektywem) z
dużej odległości,
pomimo pozornego
podobieństwa
wybranych
fragmentów.
Dobranie
właściwego
ostrosłupa widzenia
jest szczególnie
istotne w grach
komputerowych i
zastosowaniach
filmowych grafiki
komputerowej.
Przekładając
parametry ruchu
aparatu (fotografa)
na parametry
rzutowania
definiujemy
wirtualną kame rę .
Jaki jest minimalny
zestaw operacji,
zapewniający pełną
swobodę manipulacji
taką kamerą?

Realizacja

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

14/24

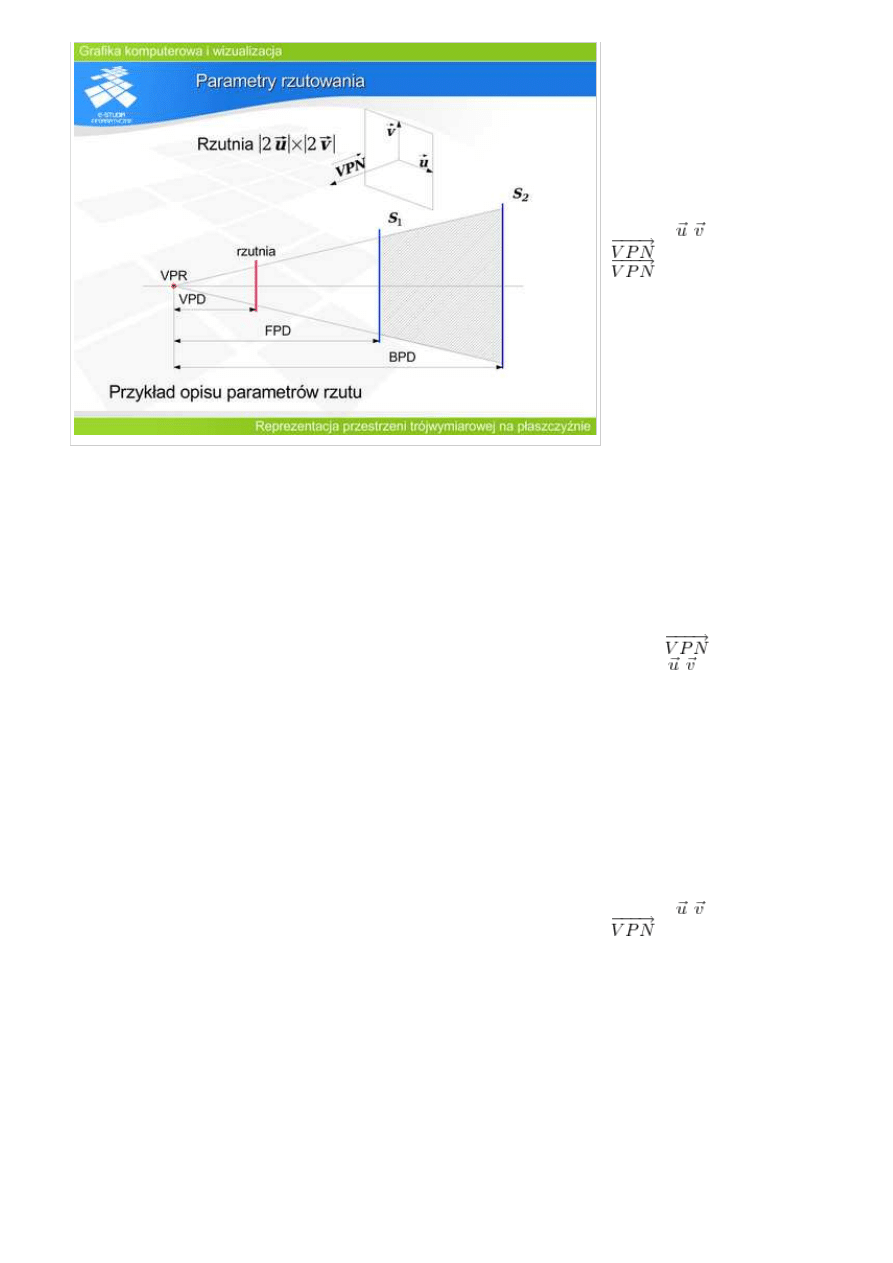
Realizacja
rzutowania
perspektywicznego
wymaga definicji
parametrów tak, aby
jednoznacznie
określić bryłę
widzenia.
Najczęściej używa
się do definicji trójki
wektorów , ,

. Wektor
definiuje oś

widzenia (kierunek
patrzenia
prostopadły do
płaszczyzny rzutni).
Jednocześnie
długość tego
wektora określa
wysokość ostrosłupa
widzenia.
Stosowane są dwa
podejścia do
określenia zwrotu
tego wektora.
Przyjęty wariant na
rysunku powoduje,
że kierunek
patrzenia wzdłuż osi
optycznej jest
przeciwny do
wektora

.

Wektory ,
definiują
płaszczyznę rzutni, a
także prostokąt
rzutni gdzie będzie
powstawał obraz
(poprzez długości
tych wektorów).
Jednocześnie
kierunki wektorów
określają obrót
rzutni wokół osi
optycznej. Zestaw
wektorów , ,

definiuje

jednoznacznie
ostrosłup
prawidłowy o
podstawie
prostokąta. Daje to
możliwość
określenia kąta
patrzenia w
rzutowaniu
perspektywicznym.
Komplet
parametrów
rzutowania wymaga
definicji: środka
rzutowania (punkt

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

15/24

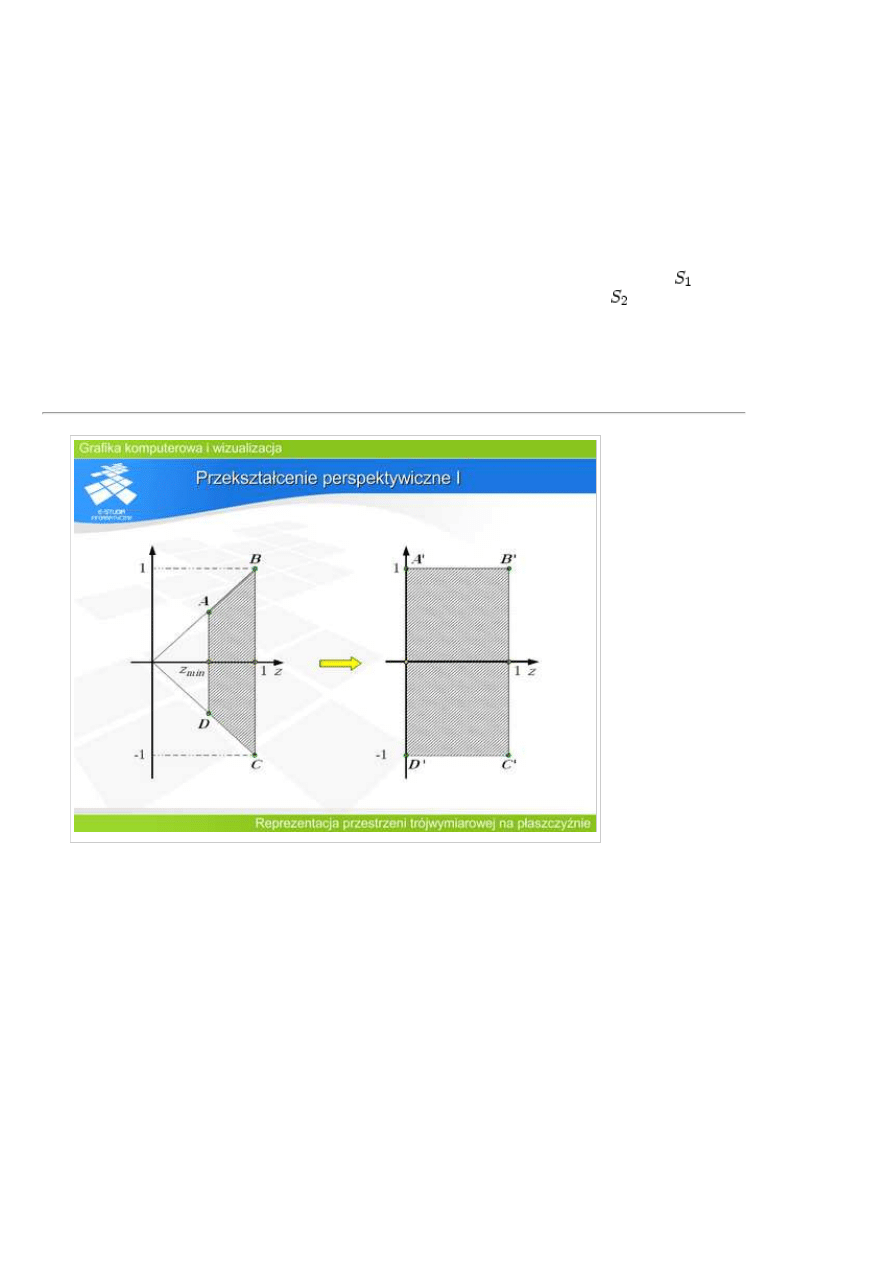
VPR) oraz trzech
odległości wzdłuż osi
optycznej względem
środka rzutowania.
Pierwszą jest
odległość do
płaszczyzny rzutni
(VPD). Dwie
pozostałe (FPD i
BPD) definiują
położenie dwóch
płaszczyzn
(przedniej

i tylnej

), które określają

ostrosłup ścięty -
wyznaczają
fragment
przestrzeni, która
będzie rzutowana.

Zaproponowane
macierze
rzutowania, zarówno
perspektywicznego
jak równoległego
mają jedną zerową
kolumnę lub wiersz.
Oznacza to że nie
jest możliwe
wyznaczenie
macierzy odwrotnej.
Czyli nie jest
możliwe
odtworzenie
trzeciego wymiaru
tylko i wyłącznie na
podstawie rzutu
obiektu. Oczywiście
jest to zgodne
definicją rzutowania:
rzutem całej prostej
rzutującej jest
dokładnie jeden
punkt. Często do
następnych operacji
(na przykład do
eliminacji
elementów
zasłoniętych)
niezbędna jest
informacja o trzecim
wymiarze
(odległości od
obserwatora -
głębokości).
Rozwiązanie tego
problemu przynosi
prze kształcenie
perspektywiczne.
Jest to operacja,
która pozwala
wyznaczyć rzut

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

16/24

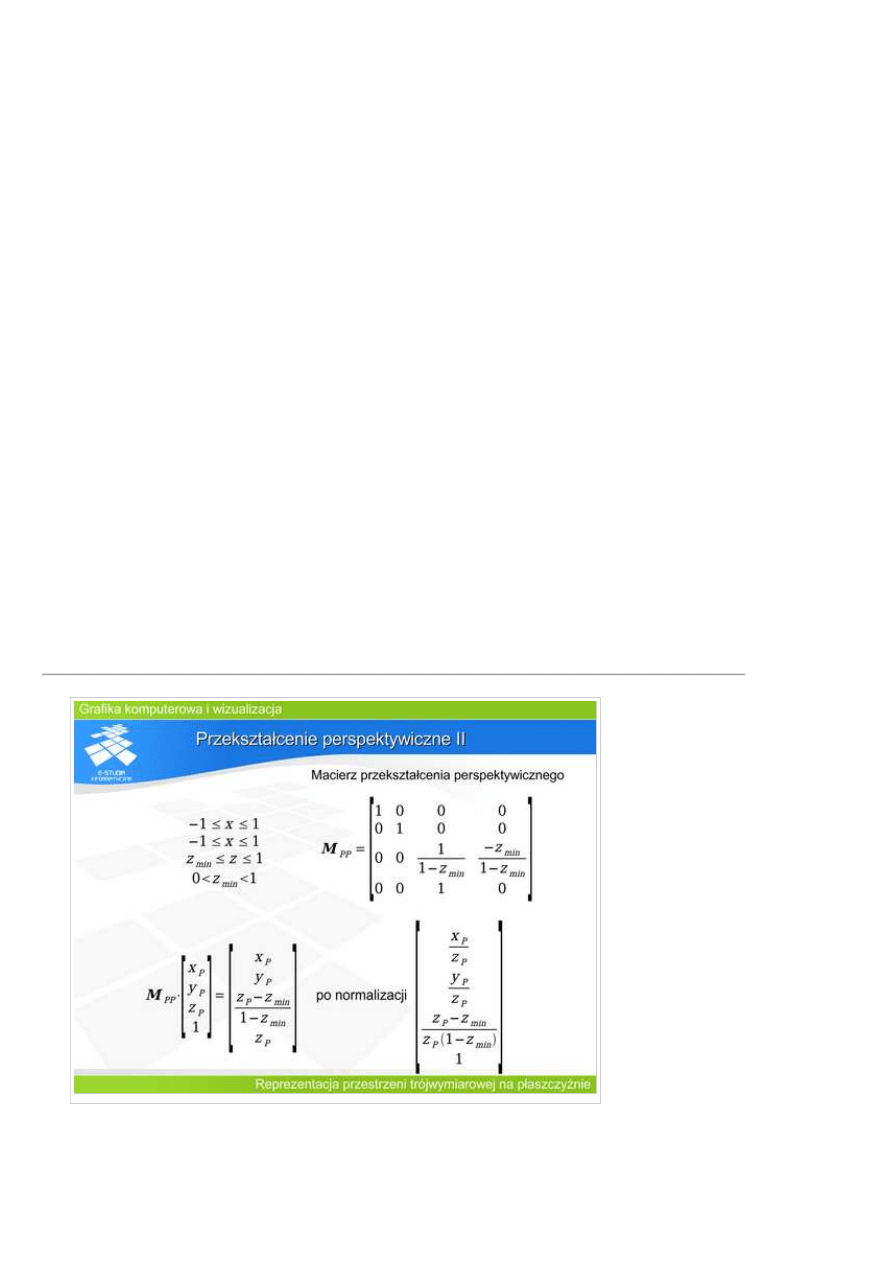
perspektywiczny i
jednocześni daje
informację o
odległości.

Jeśli rozpatrzymy
znormalizowaną
bryłę widzenia
perspektywicznego
– ostrosłup ścięty, to
promienie rzutujące
tworzą pęk prostych
w wierzchołku tego
ostrosłupa. Można
dokonać
przekształcenia,
które przekształci
ostrosłup ścięty na
prostopadłościan.
Wtedy pęk prostych
(promieni
rzutujących) stanie
się zbiorem prostych
równoległych. A to
oznacza, że po takim
zniekształceniu
przestrzeni
wszystkie punkty
leżące na prostej
rzutującej będą
miały jednakowe
współrzędne
odpowiadające
współrzędnym rzutu.

Macierz
przekształcenia
perspektywicznego
wymaga
normalizacji
operacji. Wynik na
rysunku jest podany
z uwzględnieniem
normalizacji.

Jak widać
współrzędne x i y
obrazu punktu
odpowiadają
współrzędnym rzutu
perspektywicznego
przy założeniu, że
środek rzutowania
jest w początku
układu
współrzędnych.
Jednocześnie
współrzędna z
obrazu daje
informację o
położeniu względem
osi OZ. Warto
zwrócić uwagę na
fakt, że

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

17/24

przekształcenie
wartości głębokości
jest operacją
nieliniową, ale
zachowującą
porządek na prostej,
co w zupełności
wystarcza do oceny
głębokości.

Translacja
obiektu kamery
w układzie
współrzędnych
świata,
odpowiadająca
przesuwaniu
aparatu w
dowolnym
kierunku
(przemieszczanie
się fotografa).
Obroty wokół osi
własnego układu
współrzędnych
kamery,
pozwalające
symulować
skierowanie
aparatu w
dowolnie
wybranym
kierunku.
Zmiany kątów
ostrosłupa
widzenia np.
poprzez definicję
odległości rzutni
o zadanym
prostokącie
obrazu od środka
rzutowania
(obserwatora).
Odpowiada to
zmianie
ogniskowej (kąta
„widzenia”)
obiektywu.

Związanie definicji
kształtu ostrosłupa
widzenia i obrotów z
własnym układem
współrzędnych
wirtualnej kamery
zapewnia wygodę
manipulacji oraz
zgodność symulacji z
rzeczywistością.

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

18/24

Parametrem aparatu
fotograficznego, o
którym nie było
dotychczas mowy,
jest ostrość.
Parametr ten nie daje
się w prosty sposób
przenieść na opis
rzutowania. Ostrość
zdjęcia jest wynikiem
zależności między
właściwościami
optycznymi
obiektywu, a
odległością obiektu
od obiektywu.
Rzutowanie
natomiast
odwzorowuje
wszystkie obiekty w
sposób ostry.
Niestety, nie jest to
zaletą wirtualnej
kamery, jeśli obraz
ma być zgodny z
naszym widzeniem,
gdyż akomodacja oka
powoduje powstanie
widocznych stref
ostrości. Szczególnie
jest to niekorzystne
w sytuacji
wykorzystywania
grafiki komputerowej
w kinematografii,
gdzie nieostrość
danego obiektu może
być zamierzonym
efektem reżysera.

Rzeczywisty
obiektyw aparatu
daje ostry obraz
punktu w dokładnie
określonym miejscu
– na płaszczyźnie
powstawania obrazu.
Zarówno bliżej jak i
dalej obrazem punktu
jest plamka
rozproszenia
(rozmyte koło) – stąd
nieostry obraz.
Analizę zjawiska
przeprowadził
Lommel w końcu
XIX wieku.
Zaproponował on
pewne uproszczenia
stosowane w opisie
ostrości do dzisiaj.:

Plamka
rozproszenia

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

19/24

ma średnicę
wprost
proporcjonalną
do odległości
między
płaszczyzną,
na której
powstała, a
płaszczyzną
ostrego
obrazu.
Wewnątrz
plamki
rozproszenia
jasność jest w
przybliżeniu
odwrotnie
proporcjonalna
do odległości
od środka
plamki. W
przybliżeniu,
gdyż w środku
plamki jasność
ma pewną
skończoną
wartość,
natomiast na
brzegu plami
(w skończonej
odległości
równej
promieniowi
plamki) maleje
do zera.
Zmiana
ostrości nie
powoduje
zmian jasności
całego obrazu,
tylko zmianę
rozkładu
jasności.

Stosowanym
rozwiązaniem jest
sztuczne rozmycie
symulujące
nieostrość w
wybranych
fragmentach obrazu.
Dokonuje się tego
albo stosując bufor
akumulacji albo
odpowiednie
filtrowanie. Więcej
na ten temat
zainteresowani mogą
przeczytać w pracy:
Rokita P.: Problemy
łączenia obrazów
generowanych
metodami grafiki
komputerowej z

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

20/24

obrazami
rzeczywistymi. Prace
naukowe.
Elektronika.
Politechnika
Warszawska 2001.

Umieszczenie w
wyimaginowanym
świecie wirtualnej
kamery, która daje
możliwość
manipulacji zgodnie
ze znanymi realiami
pozwala łączyć
obrazy rzeczywiste
z wirtualnymi.
Przykładem takiego
„graficznego
świata” jest
wirtualne studio,
coraz częściej
wykorzystywane
przez stacje
telewizyjne. Zamiast
budować dekoracje
do nowego
programu, tworzy
się je za pomocą
grafiki
komputerowej.
Program powstaje
w ten sposób, że
niezależnie prowadzi
się dwie rejestracje.
Rejestrację
prezenterów (lub
innych osób
występujących)
rzeczywistą kamerą
oraz „rejestrację”
wirtualnej dekoracji
wirtualną kamerą.
Oba obrazy składa
się następnie
techniką blue boxu,
tworząc to, co
potem oglądamy na
ekranie. Oczywiście
możliwe są dowolne
warianty łączenia
elementów
rzeczywistych i
wirtualnych łącznie
z dowolnym
zasłanianiem
jednych przez
drugie.

Technika ta pozwala
zaoszczędzić nie
tylko pieniądze, czas

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

21/24

i materiały przy
tworzeniu dekoracji,
pozwala też
„zaoszczędzić”
powierzchnię studia
telewizyjnego, gdzie
odbywa się
realizacja programu.
Oglądając program
wierzymy w
masywne dekoracje
rozstawione na
olbrzymiej
przestrzeni, a w
rzeczywistości
prezenter może
siedzieć w ciasnym
wnętrzu.

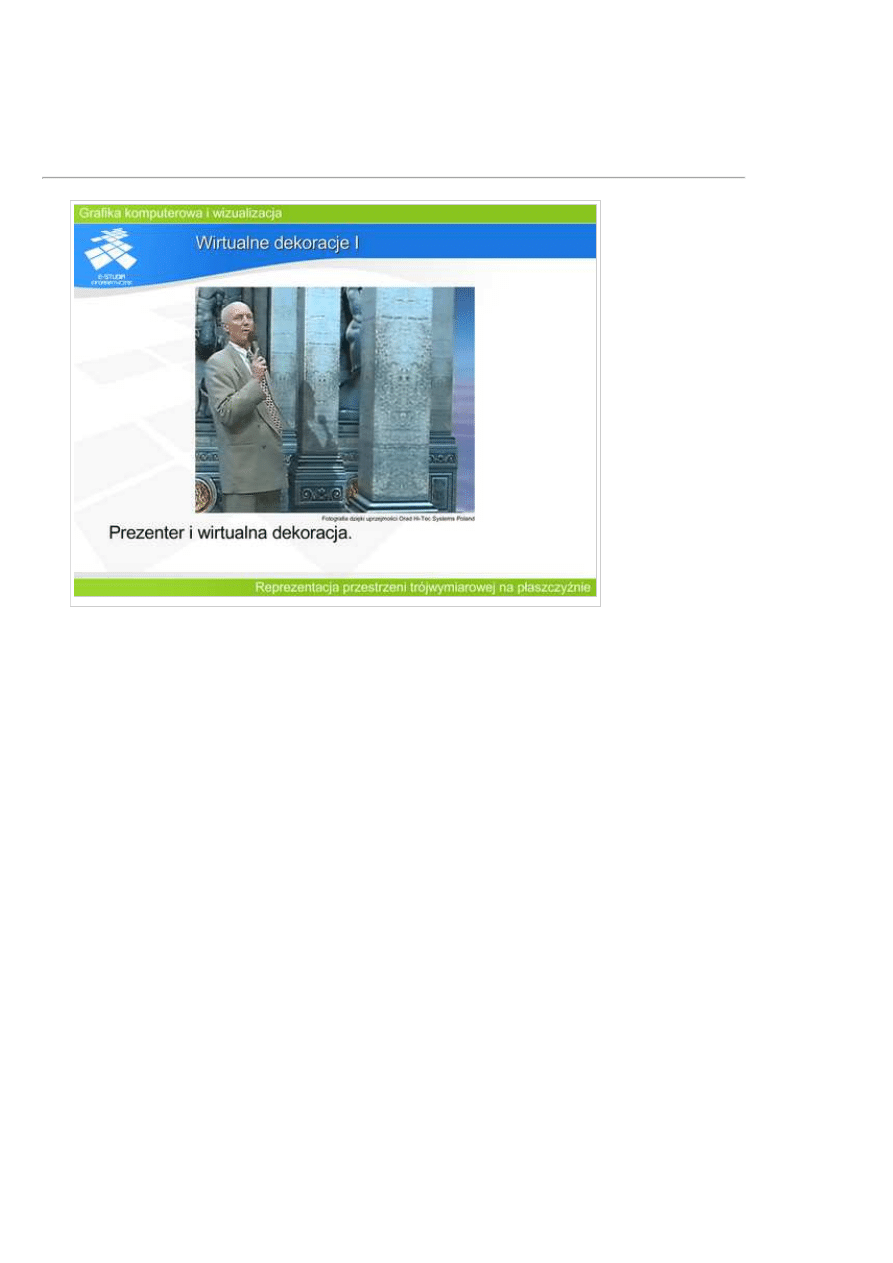
Warto zwrócić
uwagę na problem
powstawania obrazu
przy okazji
budowania
wirtualnych
dekoracji. Na
zdjęciu obok
prezenterki oraz
część obiektów są
rzeczywiste, część
obiektów jest
wirtualna. Aby
zapewnić
poprawność odbioru,
wszystkie obiekty
muszą być
rzutowane w taki
sam sposób.
Rzutowanie
obiektów
rzeczywistych
realizuje rzeczywista
kamera. Na tej
podstawie zostają
wyznaczone
parametry
definiujące rzut dla
obiektów
wirtualnych, których
obraz powstaje po
wykonaniu
odpowiednich
procedur. Zmiana
położenia kamery,
jej kąta patrzenia
(ogniskowej
obiektywu) jest
przeliczana na
parametry kamery
wirtualnej. Obie
kamery
(rzeczywista i

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

22/24

wirtualna) muszą
mieć odpowiednio
zgodne parametry
funkcjonalne oraz w
pełni
zsynchronizowane
ruchy. Brak
zgodności między
nimi byłby
natychmiast
zauważony przez
odbiorcę, mimo
wysiłków włożonych
w wygląd wirtualnej
dekoracji.

Zainteresowanych
tematem
wirtualnego studia
zachęcamy do
przeczytania pracy:
Wojdała A.,
Gruszewski M.,
Olech R.: Real-
Time Shadow
Casting in Virtual
Studio. Machine
Graphics & Vision
IPI PAN vol. 9,
nos.1/2, 2000,
ss.315-329.

Literatura

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

23/24

Źródło: "http://mediawiki.ilab.pl/index.php/GKIW_Modu%C5%82_5_-
_Reprezentacja_przestrzeni_tr%C3%B3jwymiarowej_na_p%C5%82aszczy%C5%BAnie"

Tę stronę ostatnio zmodyfikowano o 02:30, 30 lis 2007;

2009-11-07

GKIW Moduł 5 - Reprezentacja przest…

…ilab.pl/…/GKIW_Moduł_5_-_Repreze…

24/24