M
m
r
F(r)
g
F
r
G
Mm
r
r
r
®
®
®
= -
g
( )
2
Si³a grawitacji
Prawo grawitacji Newtona:
Ka¿de dwa cia³a przyci¹gaj¹ siê wzajemnie si³¹
grawitacji (ci¹¿enia) wprost proporcjonaln¹ do iloczynu ich mas i odwrotnie
proporcjonaln¹ do kwadratu odleg³oœci pomiêdzy nimi.
F
g
m
M
–F
g
r
F
G
m M
r
g
=
2
G =
×
-
6 67 10
11
,
Nm
kg
2
2
M
m
F
g
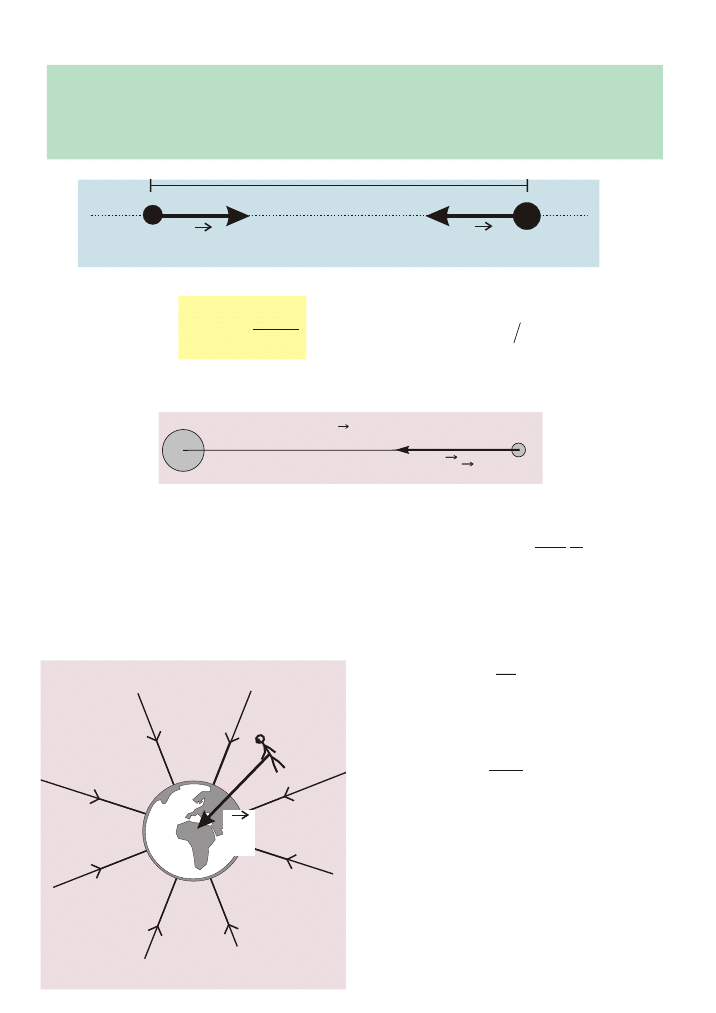
linie si³ pola wskazuj¹ w przestrzeni wokó³
Ÿród³a pola kierunek si³y grawitacji jaka zadzia³a
na cia³o o masie m umieszczone w danym polu
grawitacyjnym
g
®
®
=
F
m
g
Pole grawitacyjne
g =
G M
r
2
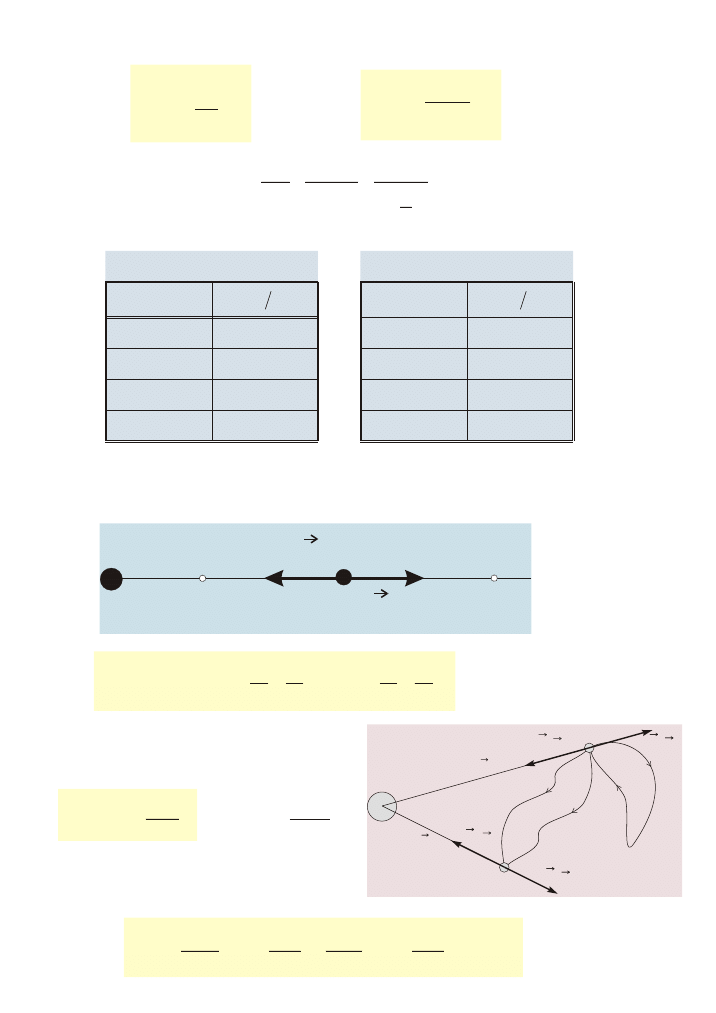
Zale¿noœæ g
g h
= ( ) dla j =
°
45
Zale¿noœæ g
g
= ( )
j dla h = 0
h [m]
g [
]
m s
2
j
g [
]
m s
2
0
9,806
0°
9,780
1 000
9,803
30°
9,793
100 000
9,600
60°
9,819
1 000 000
7,410
90°
9,832
Przyspieszenie w polu grawitacyjnym
g
F
m
g
®
®
=
g
G M
r
=
2
g
G M
r
G M
R
h
g
h
R
=
=
+
=
+
æ
è
ç
ö
ø
÷
2
2
0
2
1
(
)
Praca w polu grawitacyjnym
F
g
m
M
F
z
A
B
W
W
G M m
r
r
G M m
r
r
A
B
B
A
= -
= -
-
æ
è
ç
ç
ö
ø
÷
÷ =
-
æ
è
ç
ç
ö
ø
÷
÷
z
1
1
1
1
M
m
r
A
F (r )
g
A
r
B
A
B
F
(
r
)
B
g
s
1
s
2
s
3
F
(
r
)
A
z
F
(
r
)
B
z
E
m
G
Mm
r
m
G
Mm
r
c
A
A
B
B
v
2
v
2
const
=
+ -
æ
è
ç
ç
ö
ø
÷
÷ =
+ -
æ
è
ç
ç
ö
ø
÷
÷ =
2
2
E
G
Mm
r
p
= -
Energia potencjalna grawitacji
Zasada zachowania energii
V r
E
r
m
( )
( )
=
p
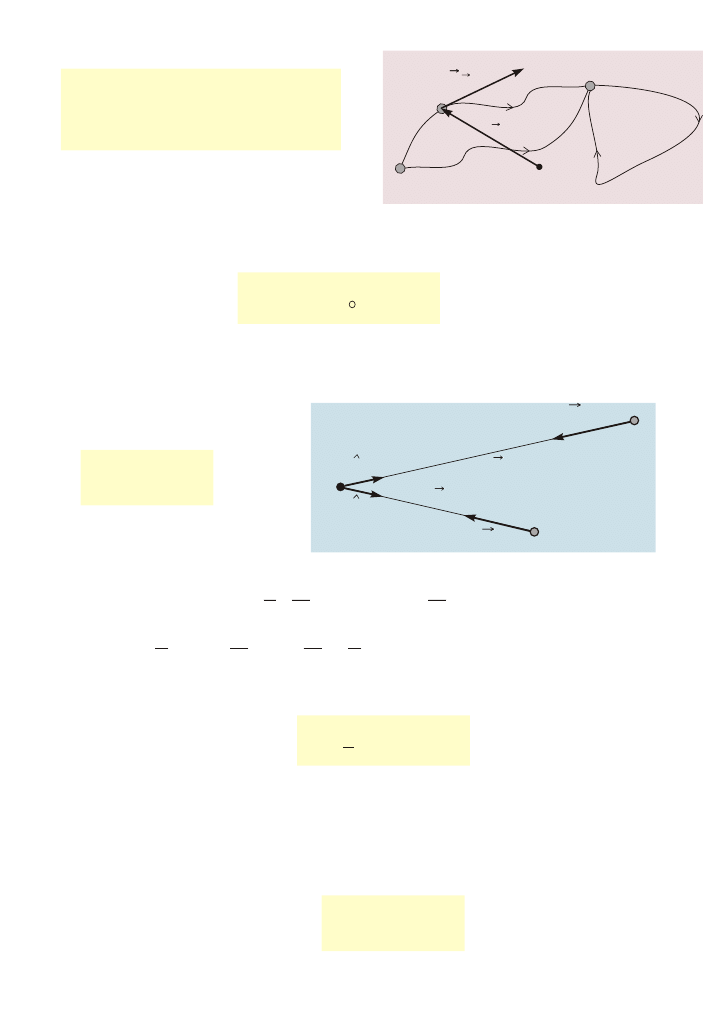
Praca po krzywej zamkniêtej
\
a
F
m
t
®
®
®
=
=
dv
d
st¹d r
t
®
®
´
=
dv
d
0 .
d
d
v
d
d
v
dv
d
t
r
r
t
r
t
®
®
®
®
®
®
´
æ
è
ç
ö
ø
÷ =
´ + ´
.
d
d
v
t
r
®
®
´
æ
è
ç
ö
ø
÷ = 0 czyli r
®
®
´
=
v
const.
Pole si³ zachowawczych (potencjalnych)
A
B
s
1
s
2
s
3
O
F(r)
r
(
)
(
)
W
W
F r
r
A
B
s
A
B
s
r
r
A
B
®
®
® ®
®
=
=
®
®
ò
1
2
( ) d
(
)
(
)
(
)
(
)
W
W
W
W
A
B
s
B
A
s
A
B
s
A
B
s
®
®
®
®
+
=
-
=
1
2
1
2
0
Pole grawitacyjne jako przyk³ad pola si³ centralnych
O
r
A
F
A
r
B
A
B
F
B
r
A
r
B
F r
f r r
® ®
=
( )
( ) $
s
®
®
®
=
´
=
1
2
(
)
r
v
const
Prêdkoœæ polowa
(
)
W
F r
B
B
s
®
® ®
=
=
ò
3
0
d
Moment pêdu w polu si³ centralnych
L
m
®
®
= 2
s.
L
r
p
®
®
®
=
´
= const
r
p
=
+
1 e
j
cos
,
p
L G M m
=
2
2
, e =
+
æ
è
ç
ç
ö
ø
÷
÷
1
2
2
2
2
2
0 5
E L
G M m
,
e = 0, E < 0 – okr¹g, r
p
= ,
0
1
< <
e
, E < 0 – elipsa, p
r
p
(
)
(
)
1
1
+
< <
-
e
e ,
e = 1, E = 0 – parabola,
e > 1 E > 0 – hiperbola.
T
GM
a
2
2
3
4
=
p
S
I
II prawo Keplera - kwadrat okresu obiegu planety dooko³a S³oñca
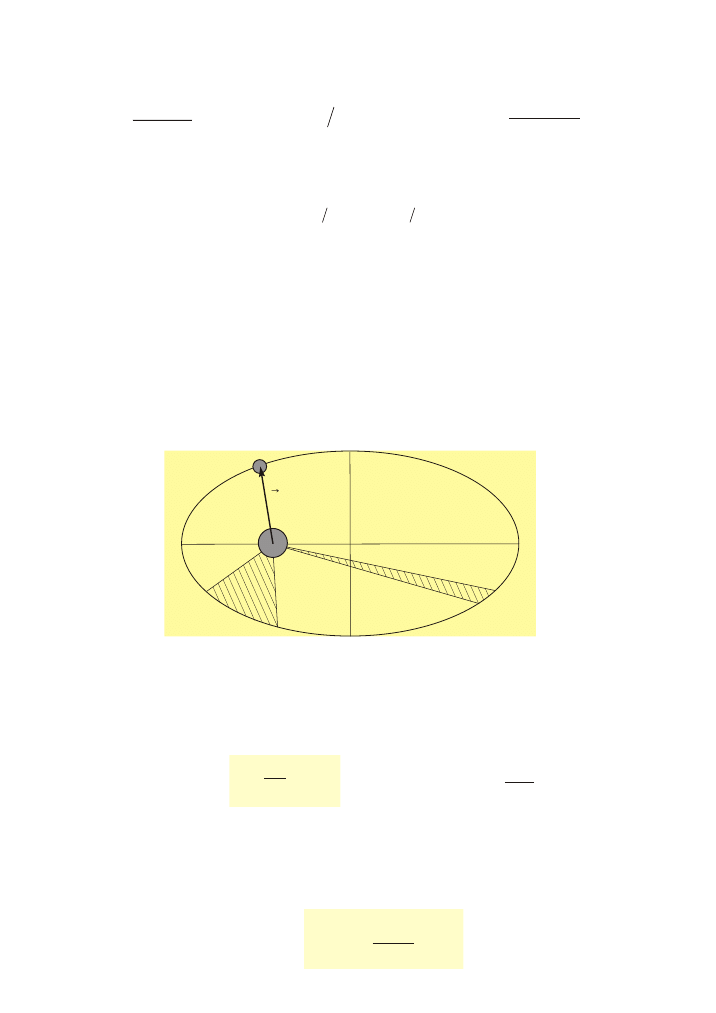
jest wprost proporcjonalny do szeœcianu wielkiej pó³osi jej orbity
Prawa Keplera
I prawo Keplera - ka¿da planeta porusza siê wokó³ S³oñca po elipsie, przy czym S³oñce
znajduje siê w jednym z ognisk tej elipsy
r
b
a
s =
=
D
D
S
t
const
s
p
=
ab
T
Ruch cia³ w polu si³y grawitacji
II prawo Keplera - pola zakreœlone przez promieñ wodz¹cy planety w takich samych
odcinkach czasu s¹ sobie równe
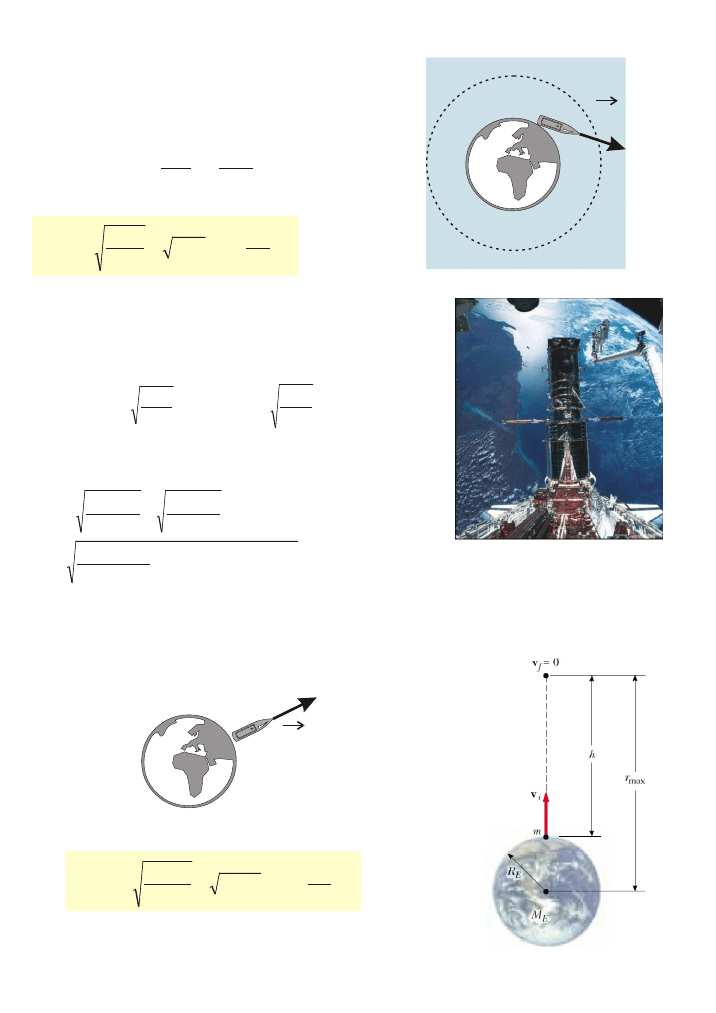
Pierwsza prêdkoœæ kosmiczna
m
R
G
mM
R
v
I
z
z
z
2
2
=
,
Satelita geostacjonarny
Druga prêdkoœæ kosmiczna - prêdkoœæ ucieczki
Prêdkoœci kosmiczne
v
km
s
II
z
z
z
=
=
=
2
2
11 2
GM
R
g R
,
v
km
s
I
z
z
z
=
=
=
GM
R
g R
7 9
,
v
I
v
II
r
T G M
T g R
=
=
=
=
×
×
×
×
-
2
2
3
2
0
2
2
3
2
2
3
4
4
3600 24
4
9 81 10
z
z
p
p
p
(
)
,
(6367 445
42 211
2
3
,
) km
km
=
v =
G M
r
T
r
G M
= 2
3
p
Wyszukiwarka
Podobne podstrony:
Na przekor grawitacji
wyk8 grawitacja
grawitacyjne zageszczanie osado Nieznany
Grawitacyjne ruchy masowe
1998 08 str 56 61 Gradientometria grawitacyjna
pole grawitacyjne teoria0001
Grawitacja 2005rok, PiwnicaGraw
4 czucie bod%c5%bac%c3%b3w akustycznych oraz grawitacji cz I
24. Pole grawitacyjne, Fizyka - Lekcje
Grawitacja - odpowiedzi, Liceum
Wyk014, Skrypty, UR - materiały ze studiów, VI, Nawodnienia grawitacyjne, Wyklady
fizyka astronomia i grawitacja sprawdzian nowa era
astronomia i grawitacja
IMIR materiały grawitacja
Wzory w dziale Grawitacja, Wzory z fizyki
19 Grawitacyjne ruchy masowe 2 (28 04 2011)
kartkowa grawitacja
Grawitacja
więcej podobnych podstron