Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

1

6.



6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

6.1. Wyznaczanie przemieszczeń z zastosowaniem równań pracy wirtualnej w układach

prętowych

W metodzie pracy wirtualnej, przy obliczaniu przemieszczeń w miejscu, w którym chcemy wyliczyć

zadane przemieszczenie przykładamy jednostkową siłę uogólnioną zgodną z kierunkiem i zwrotem szukanego
przemieszczenia.

W zależności od rodzaju szukanego przemieszczenia stosujemy różne typy obciążeń:

•

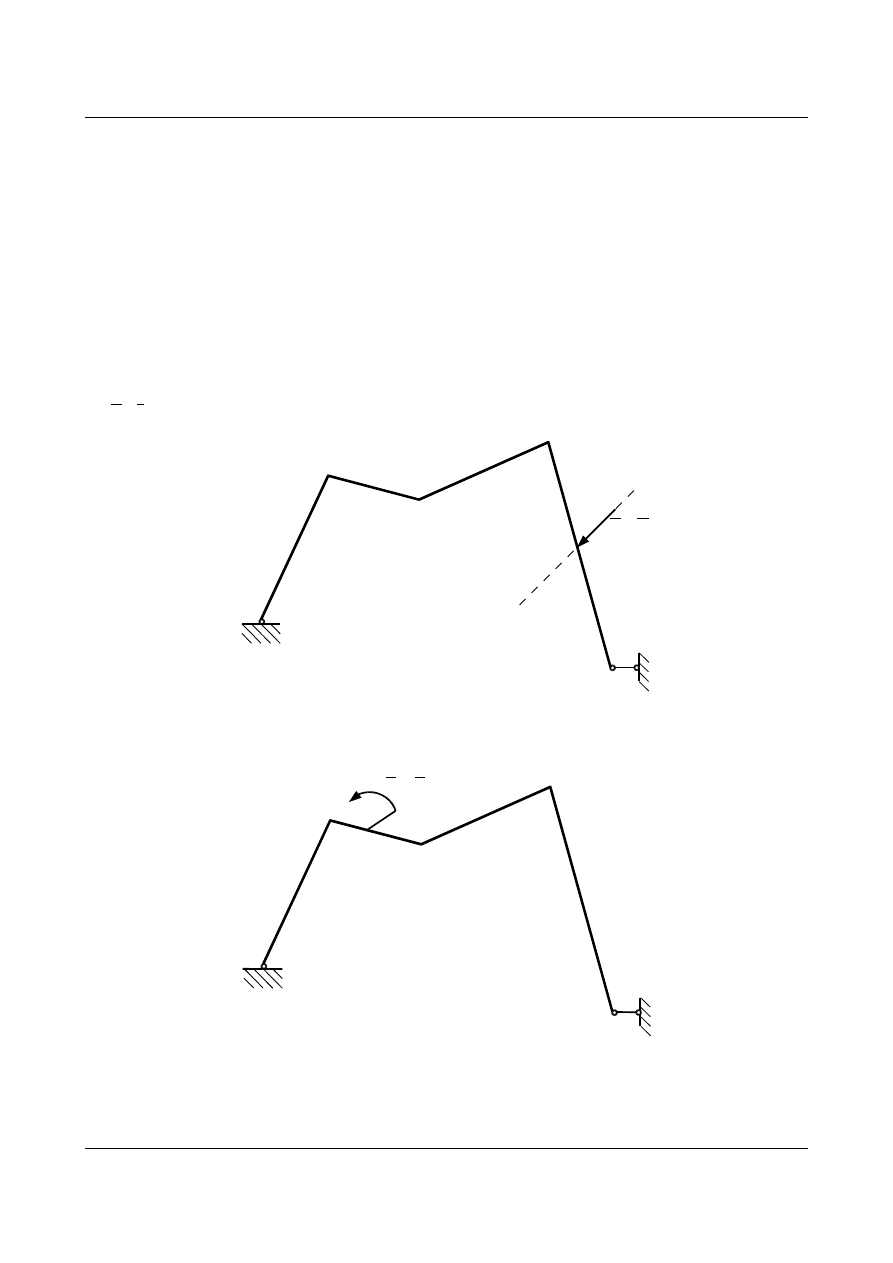
aby wyznaczyć przemieszczenie liniowe punktu

A po kierunku prostej m układ obciążamy siłą skupioną

P

=1

A

m

P = 1

•

obrót przekroju

A obliczamy przykładając skupiony moment wirtualny:

A

M = 1

•

wzajemny obrót przekrojów w punktach

A i B uzyskamy obciążając układ przeciwnie zwróconymi

momentami:

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

2

A

B

M = 1

M = 1

•

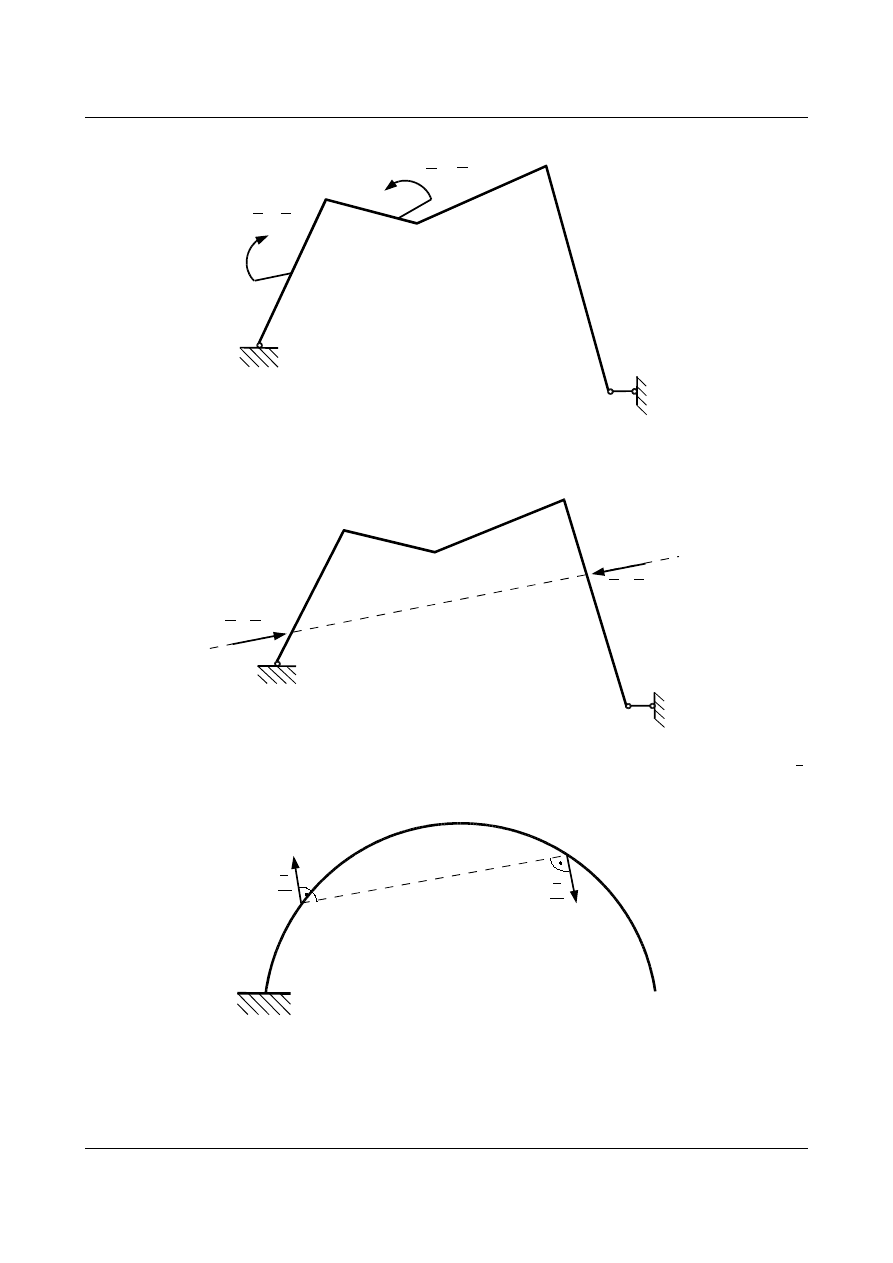
wzajemne zbliżenie punktów

A i B obliczamy przykładając siły o zgodnym kierunku, lecz przeciwnym

zwrocie:

B

A

P = 1

P = 1

•

aby wyliczyć kąt obrotu cięciwy

AB należy przyłożyć siły pod kątem prostym do tej cięciwy o wartości 1

przez odległość pomiędzy punktami

A i B (a):

A

B

a

1

a

1

a

•

zmiana kąta zawartego między stycznymi do prętów zbiegających się w przegubie

A dają dwa momenty

jednostkowe przeciwnie zwrócone:

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

3

A

M = 1

M = 1

•

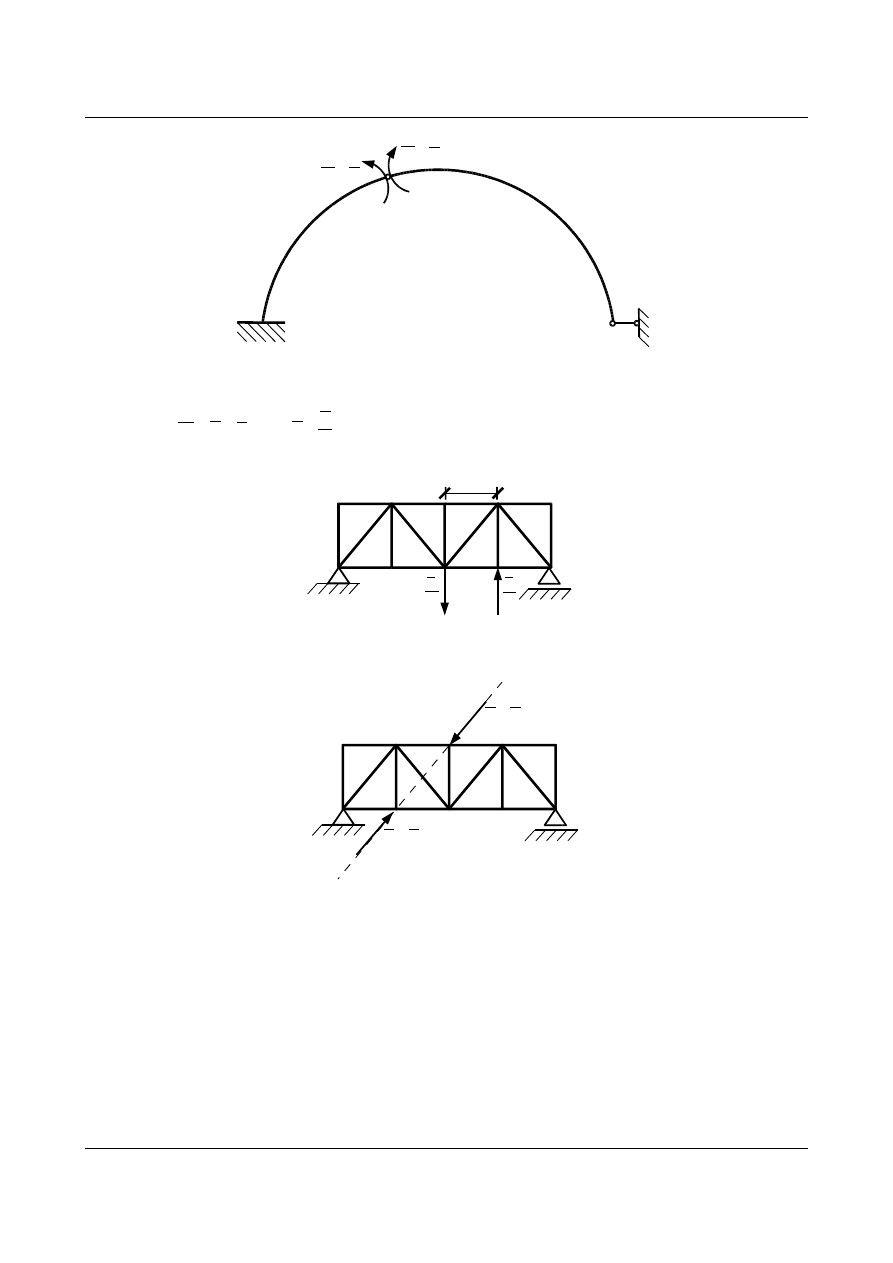
obrót pręta

D o długości a w kratownicy – w węzłach pręta przykładamy parę sił dającą jednostkowy

moment.

Ponieważ M

=1 =P⋅a to P=

1

a

.

a

D

1

a

1

a

•

wzajemne zbliżenie (względnie oddalenie) węzłów

A i B kratownicy dają dwie siły leżące na jednej prostej

A

B

P = 1

P = 1

•

zmiana kąta zawartego między prętami

S i K o długościach a i b – dwa jednostkowe momenty wyrażone

przez pary sił:

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

4

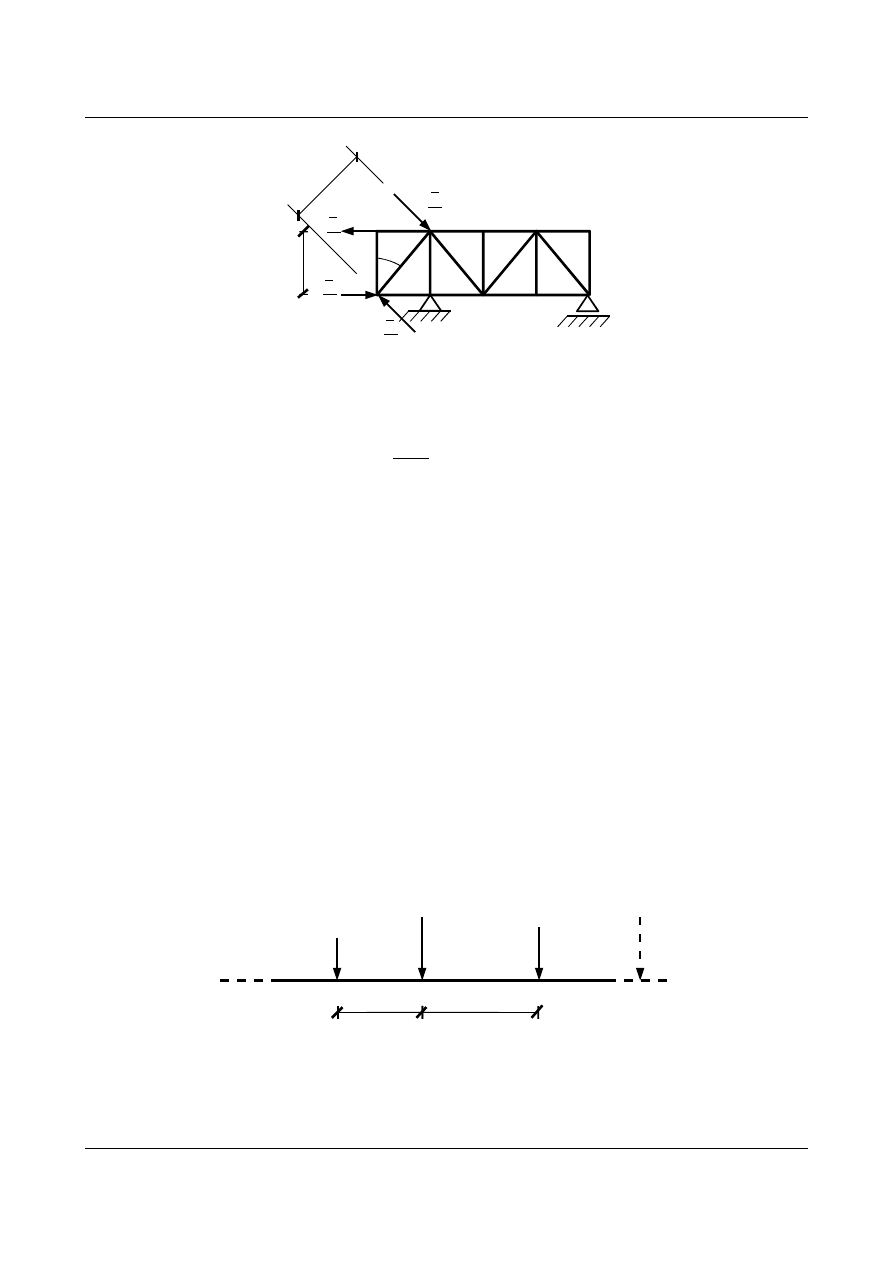
a

b

φ

K

S

1

a

1

a

1

b

1

b

Równanie pracy wirtualnej dla kratownicy ogranicza się jedynie do działania siły normalnej (podłużnej) w
prętach:

1⋅=

∑

j



N

j

⋅



N

P

 j

EA

j



t

⋅t

0

 j



⋅l

j

gdzie:

N

P

(j)

- siła normalna w

j-tym pręcie wywołana obciążeniem P,



N

j

- siła normalna a

j-tym pręcie wywołana obciążeniem wirtualnym,

t

o

(j)

- temperatura działająca na pręt j,

l

j

- długość pręta

j,

(EA)

j

- sztywność pręta j.

6.2. Metoda ciężarów sprężystych

Metoda ciężarów sprężystych jest jedną z metod obliczania linii ugięcia, stosowaną najczęściej przy

wyznaczaniu składowych przemieszczeń pewnej grupy punktów układu (np. punktów osi ramy lub łuku; pasa
górnego, dolnego lub wszystkich węzłów kratownicy równocześnie).

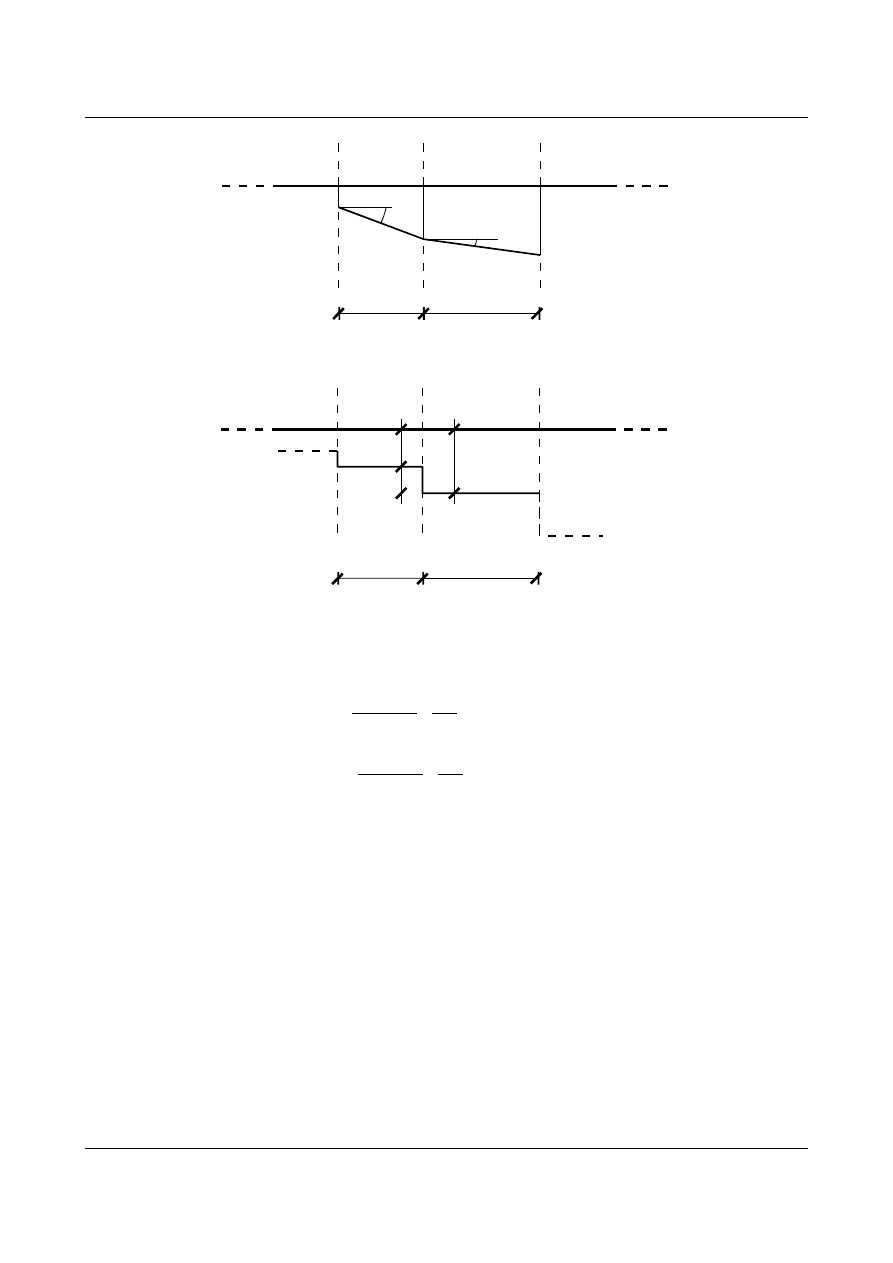
Rozpatrzmy pewien dowolny układ obciążony rzeczywistymi siłami zewnętrznymi:

i - 1

i

i + 1

P

i - 1

P

i

P

i + 1

a

i

a

i + 1

Rys. 6.1. Dowolny układ obciążony rzeczywistymi siłami zewnętrznymi

Wykresy momentów zginających i sił poprzecznych wywołanych przez siły

P

i-1

,

P

i

oraz P

i+1

, wyglądają

tak jak na rys. 6.2 i rys. 6.3:

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

5

M

i - 1

M

i

M

i + 1

i - 1

i

i + 1

φ

i

φ

i + 1

M

P

a

i

a

i + 1

Rys. 6.2. Wykres momentów zginających

i + 1

i

i - 1

T

P

a

i

a

i + 1

T

i

L

T

i

P

P

i

Rys. 6.3. Wykres sił poprzecznych

Z wykresów (rys. 6.2 i rys. 6.3) wynika, że:

tan



i

=

M

i

−M

i

−1

a

i

=

dM

dx

∣

i

 L

=T

i

L

(6.1)

tan



i

1

=

M

i

1

−M

i

a

i

1

=

dM

dx

∣

i

P

=T

i

P

(6.2)

Różnica wyrażeń (6.1) i (6.2) daje wartość siły obciążającej:

tan



i

1

−tan

i

=T

i

P

−T

i

L

=P

i

Ponieważ miary kątów są bardzo małe, możemy zapisać, że:

tan

≈

więc

P

i

=

i

1

−

i

Rozpatrzmy teraz układ belkowy obciążony fikcyjnymi siłami (rys. 6.4).

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

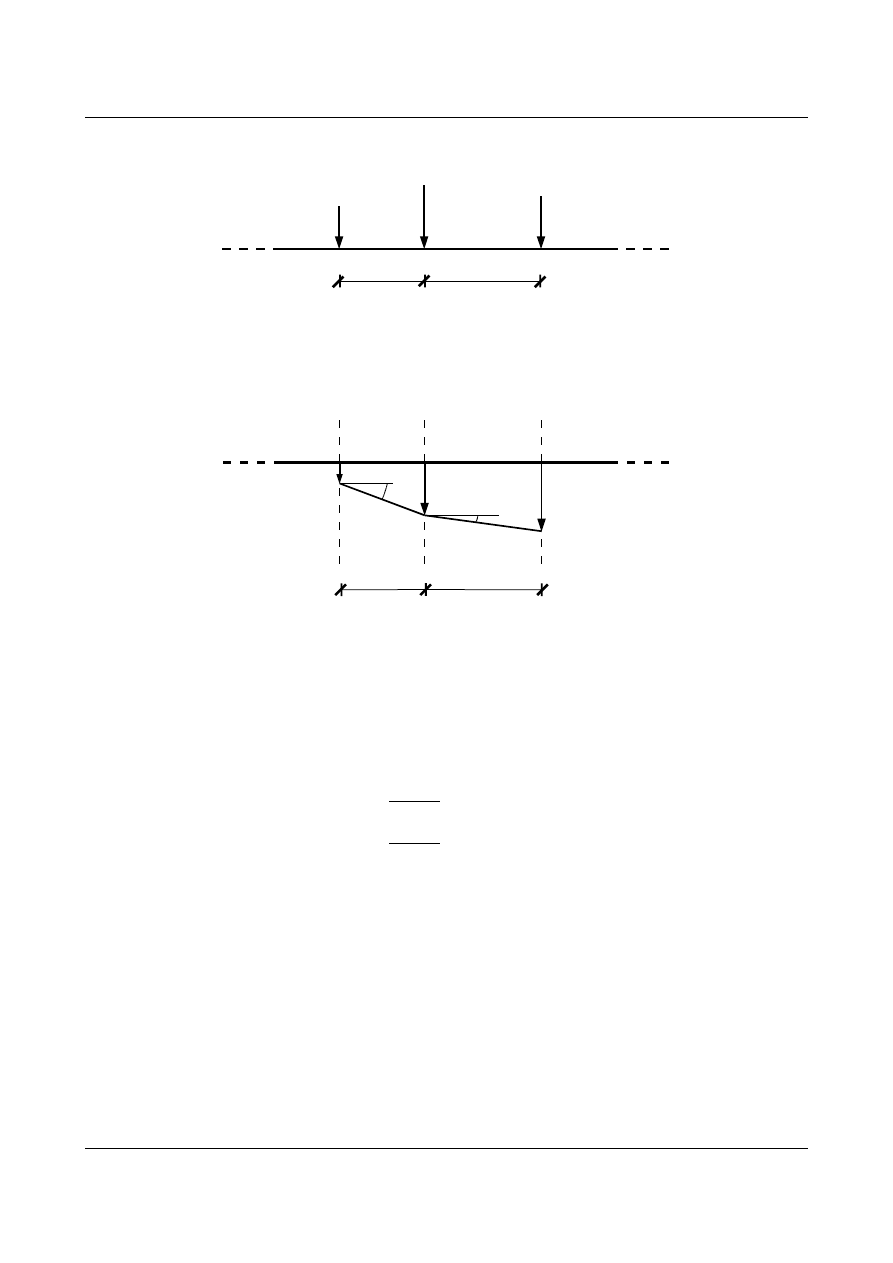
Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

6

i - 1

i

i + 1

w

i - 1

w

i

w

i + 1

a

i

a

i + 1

Rys. 6.4. Układ belkowy obciążony fikcyjnymi siłami

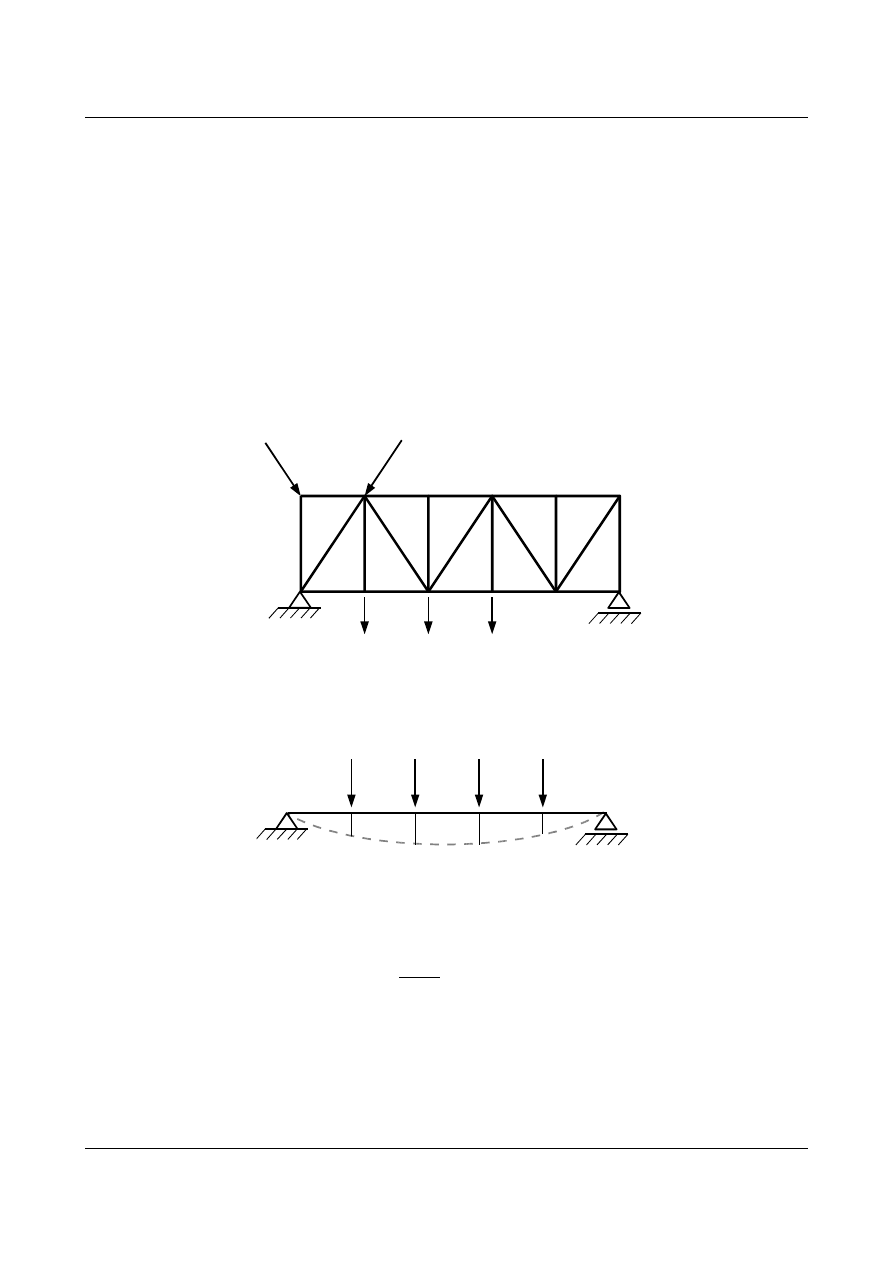
Aproksymacja linii ugięcia belki linią łamaną wygląda następująco:

i - 1

i

i + 1

a

i

a

i + 1

δ

i - 1

δ

i

δ

i + 1

φ

i + 1

φ

i

Rys. 6.5. Aproksymacja linii ugięcia belki linią łamaną

Jak wynika z porównania rys.6.2 i rys. 6.5, linia ugięcia układu prętowego jest zbieżna z wykresem

momentów zginających utworzonym dla tego układu.

Podobnie jak w przypadku obciążenia rzeczywistego, różnica kątów obrotu przekrojów z lewej i prawej

strony węzła

i jest równa sile przyłożonej w węźle i :

tan





i

=



i

−

i

−1

a

i

≈



i

tan





i

1

=



i

1

−

i

a

i

1

≈



i

1

(6.3)

(6.4)

w

i

=



i

1

−



i

Dla siły

w

i

,

nazywanej dalej ciężarem sprężystym możemy zapisać definicje:

Ciężary sprężyste

•

to różnice kątów obrotu dwóch sąsiednich odcinków pręta wywołane obciążeniem w układzie
rzeczywistym,

•

to wielkości, które po obciążeniu belki zastępczej dają wykres momentów zginających identyczny z linią
ugięcia układu rzeczywistego.

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

7

6.3. Ciężary sprężyste dla układów kratowych statycznie wyznaczalnych

Sposób obliczania ciężarów sprężystych dla układów kratowych statycznie wyznaczalnych przebiega

zawsze w dwóch etapach :

1. Obliczamy siłę będącą różnicą kątów nachylenia dwóch sąsiadujących odcinków prętowych i obciążamy

nią belkę zastępczą.

2. Rysujemy wykres momentów, który jest równy wykresowi linii ugięcia.

Należy przypomnieć, że w celu obliczenia wartości ciężarów sprężystych obciążamy układ siłami

wirtualnymi (SAME CIĘŻARY SPRĘŻYSTE TO NIE OBCIĄŻENIA WIRTUALNE!!!)

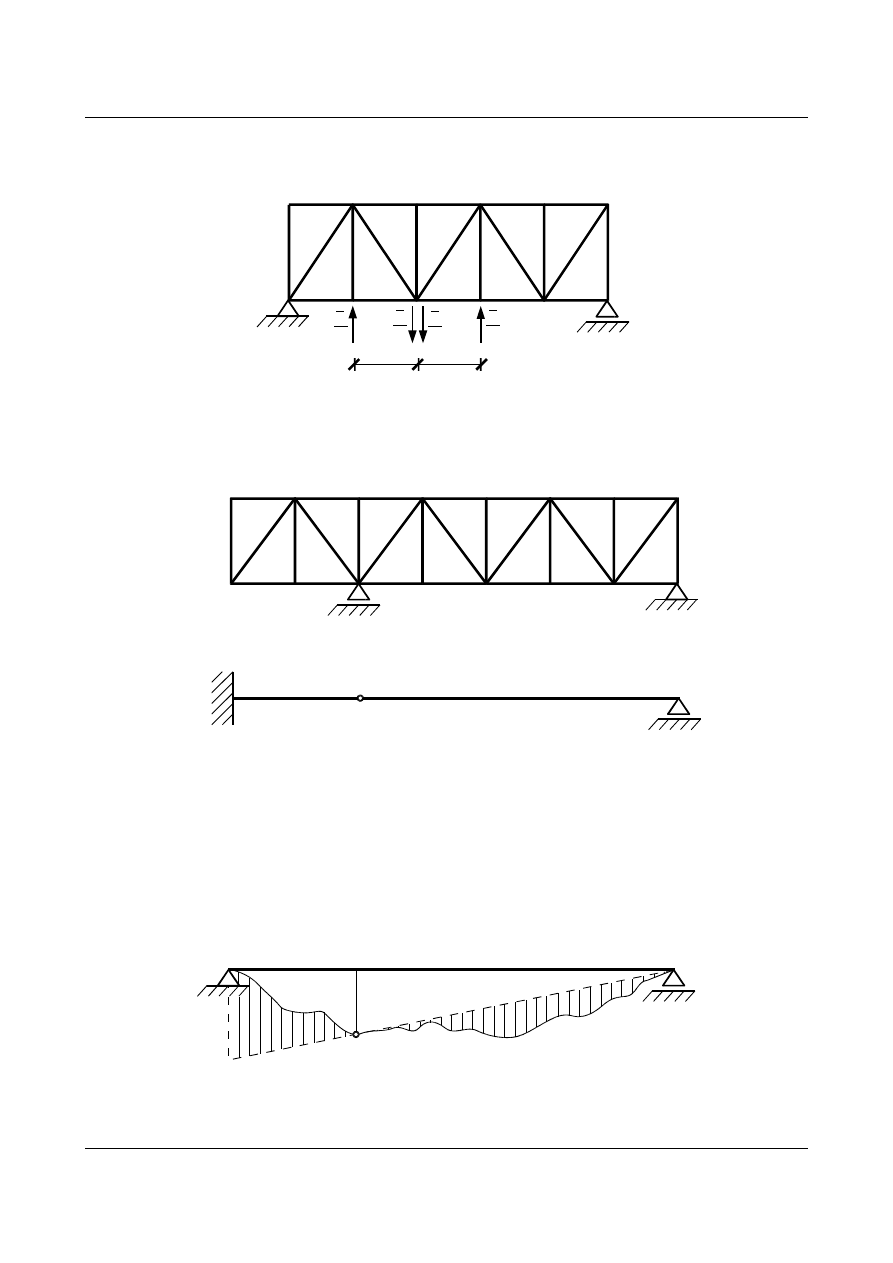
Aby wyznaczyć przemieszczenia

δ węzłów pasa dolnego kratownicy

P

2

P

1

δ

k - 1

δ

k + 1

δ

k

Rys. 6.6. Kratownica obciążona siłami P (δ – nieznane przemieszczenie)

w każdym z węzłów należy wyliczyć ciężar sprężysty w

i

i obciążyć nimi belkę zastępczą

w

k-1

w

k

w

k+1

Rys. 6.7. Belka fikcyjna (zastępcza)

ciężary sprężyste dla kratownicy możemy obliczyć ze wzoru:

w

i

=

∑

j

S

P

 j

⋅S

j

EA

j

⋅l

j

(6.5)

gdzie:

S

p

(j)

oznacza siłę w

j-tym pręcie wywołaną obciążeniem zewnętrznym,

S

j

oznacza siłę w

j-tym pręcie wywołaną obciążeniem wirtualnym.

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

8

Obciążeniem wirtualnym są jednostkowe momenty, wyrażone przez pary sił, przyłożone do prętów

dochodzących do węzła, w którym liczymy ciężar sprężysty. Na przykład dla węzła

k :

k - 1

k

k + 1

a

i

a

i + 1

1

a

i+1

1

a

i

1

a

i

1

a

i+1

Rys. 6.8. Kratownica obciążona siłami wirtualnymi

Aby przyjąć belkę zastępczą postępujemy analogiczne jak w metodzie obciążeń wtórnych kratownicę

(rys. 6.9) zamieniamy na belkę fikcyjną spełniającą warunki brzegowe układu rzeczywistego (rys. 6.10):

A

B

Rys. 6.9. Przykładowa kratownica

A

B

Rys. 6.10. Belka fikcyjna spełniająca warunki brzegowe układu rzeczywistego

Linia ugięcia pasa górnego lub dolnego kratownicy jest taka sama jak wykres momentów belki fikcyjnej.

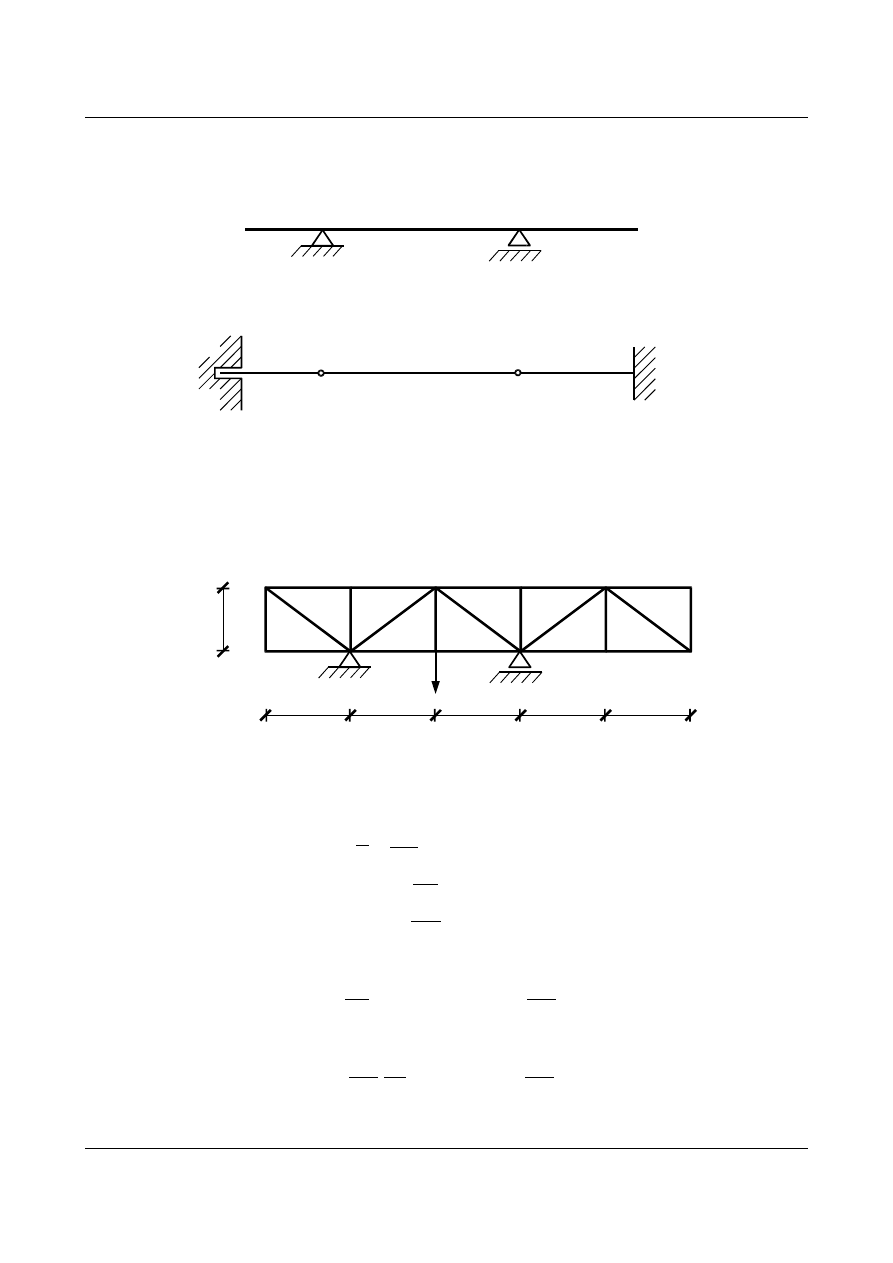
Innym sposobem tworzenia układu zastępczego jest zastosowanie belki podpartej na obu końcach. Dla

niej tworzymy wykres momentów od ciężarów sprężystych, na którym zaznaczamy rzędną punktu, gdzie
ugięcie powinno być zerowe, na rys. 6.11 są to punkty

A i B. Prowadzimy prostą zamykającą przez rzędną

wykresu w punktach

A i B. Rzędne z zakreskowanego pola między linią wykresu momentów a prostą

zamykającą, stanowią wartości ugięć kolejnych punktów układu rzeczywistego.

A

B

A'

Rys. 6.11. Schemat zastępczy dla kratownicy z rys. 6.9 - rozwiązanie drugim sposobem

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

9

Zadanie 1

Jak powinien wyglądać układ fikcyjny dla belki o podanym schemacie:

A

B

Rozwiązaniem jest belka spełniająca warunki brzegowe:

A

B

Zadanie 2

Znajdź linię ugięcia pasa dolnego kratownicy (rys. 6.12) dwoma sposobami:

a) przykładając jedynki wirtualne w kolejnych węzłach
b) stosując metodę ciężarów sprężystych

1,5

2,0

2,0

2,0

2,0

2,0

[m]

100 kN

1

2

3

4

5

6

7

8

9

10

11

12

Rys. 6.12. Zadana kratownica

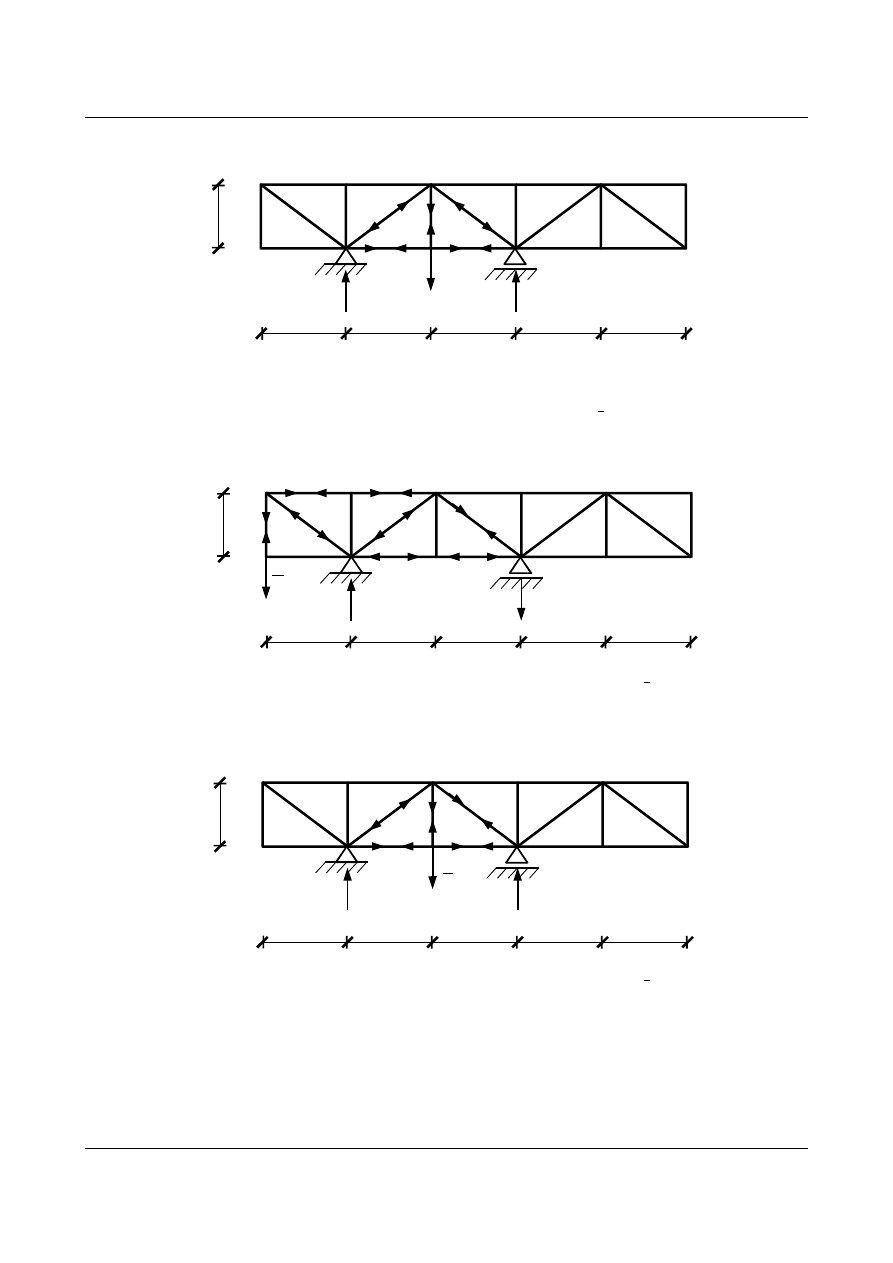
ad a) Rozwiązanie kratownicy od obciążenia zewnętrznego

c

2

=1,5

2

2

2

=2,254 =6,25



c

2

=



6,25

=∣2,5 ∣

sin

=

1,5
2,5

cos

=

2

2,5

∑

Y

2

=0 :

S

2,10

⋅sin=50

S

2,10

⋅

1,5

2,5

=50

⇒

S

2,10

=

250

3

∑

X

2

=0 ⇒

S

2,3

=S

2,10

⋅cos 

S

2,3

=

250

3

⋅

2

2,5

⇒

S

2,3

=

200

3

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

10

1,5

2,0

2,0

2,0

2,0

2,0

[m]

100

N

p

[kN]

50

50

100

83

,(3

)

66,(6)

66,(6)

83,(

3)

O

O

O

O

O

O

O

O

O

O

O

O

O

O

O

O

1

2

3

4

5

6

Rys. 6.13. Rozwiązanie kratownicy od obciążenia zewnętrznego

Siły w prętach kratownicy obciążanej w kolejnych węzłach siłą wirtualną P

=1

1,5

2,0

2,0

2,0

2,0

2,0

[m]

1,5

0,5

1

0,(6)

0,(6)

1,(3)

1,(3)

0,8

(3)

1,(6

)

0,8

(3)

O

O

O

O

O

O

O

O

O

O

O

O

O

N

1

[ - ]

1

1

2

3

4

5

6

Rys. 6.14. Kratownica obciążana w węźle nr 1 siłą wirtualną P

=1

1,5

2,0

2,0

2,0

2,0

2,0

[m]

0,5

0,5

0,(6)

0,(6)

1

0,8

(3)

0,8(

3)

O

O

O

O

O

O

O

O

O

O

O

O

O

O

O

O

N

3

[ - ]

1

1

2

3

4

5

6

Rys. 6.15. Kratownica obciążana w węźle nr 3 siłą wirtualną P

=1

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

11

1,5

2,0

2,0

2,0

2,0

2,0

[m]

N

6

[ - ]

1

2

O

O

O

O

O

O

O

O

O

O

O

1,(

6)

1,(

6)

1,(6

)

1,(6

)

2,(6)

2,(6)

1,(3)

1,(3)

1,(3)

1,(3)

1

1

2

3

4

5

6

Rys. 6.16. Kratownica obciążana w węźle nr 6 siłą wirtualną P

=1

Obliczenia przemieszczeń wykonywać będziemy na podstawie wzoru :

v

i

=

∑

N

⋅N

EA

l

Z symetrii układu wynika, że

v

1

i

v

5

są sobie równe:

v

1

=v

5

=

1

EA



5
6

⋅

250

3

⋅2,5 −

5
6

⋅

250

3

⋅2,5 −2 ⋅

200

3

⋅

2

3



=−

177,

7 

EA

Ugięcia w podporach są zerowe:

v

2

=v

4

=0

Przemieszczenia węzła 3 i 6 wynoszą:

v

3

=

1

EA



250
3

⋅

5
6

⋅2 100 ⋅1 2 ⋅

200
3

⋅

2
3



=

675

EA

v

6

=

1

EA



−

5

3

⋅

250

3

⋅2,5

5
3

⋅

250

3

⋅2,5 −2 ⋅

200

3

⋅2 ⋅

4

3



=−

355,

5

EA

Rozwiązanie przedstawiono na rys. 6.17:

2,0

2,0

2,0

2,0

2,0

[m]

177,(7)

EA

177,(7)

EA

355,(5)

EA

675,0

EA

Rys. 6.17. Linia ugięcia pasa dolnego kratownicy

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

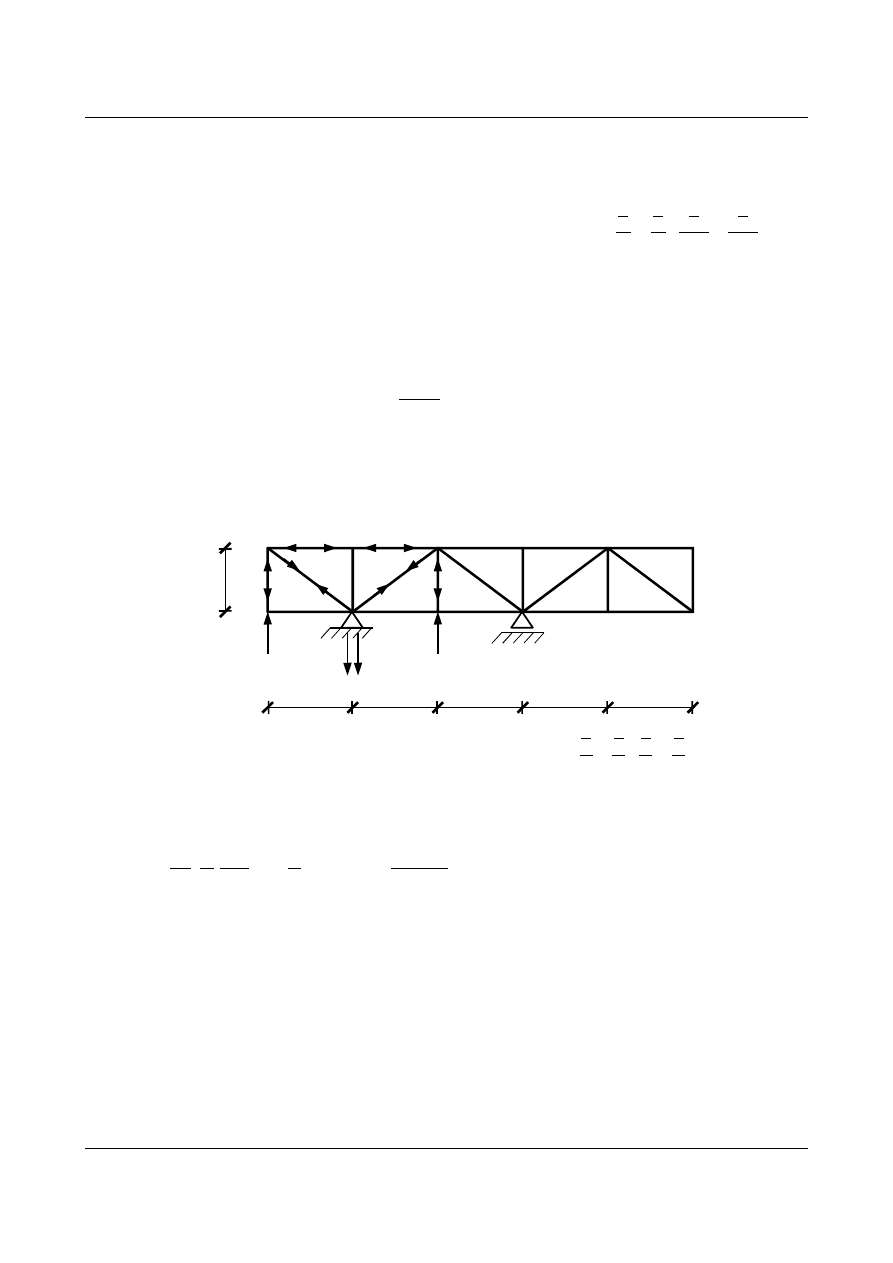
Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

12

Odcinki linii ugięcia pasa dolnego kratownicy pomiędzy wyznaczonymi w węzłach wartościami

aproksymowano liniami prostymi.

ad b) Metoda ciężarów sprężystych

W celu obliczenia ciężarów sprężystych układ obciążamy grupami sił

1

a

k

,

1

a

k



1

a

k

1

,

1

a

k

1

, które

przykładamy w sąsiadujących węzłach

k -1, k, k + 1.

W naszym przykładzie

a

k

=

a

k+1

= 2,0 m.

Ciężary sprężyste wyznaczamy na podstawie wzoru:

w

i

=

∑

j

S

P

 j

⋅S

j

EA

j

⋅l

j

(6.6)

Aby określić wartość ciężaru sprężystego w

2

wyznaczamy siły w prętach kraty (rys. 6.18) obciążonej w

węzłach 1, 2, 3.

Rys. 6.18. Kratownica obciążanej w węzłach nr 1,2,3 siłami 1

2

,

1

2



1

2

,

1

2

Obliczamy wartość ciężaru sprężystego dla węzła 2 (z symetrii układu wynika, że

w

2

=

w

4

):

w

2

=w

4

=−

1

EA



5

6

⋅

250

3

⋅2,5

1

2

⋅100 ⋅1,5



=−

248,6

1

EA

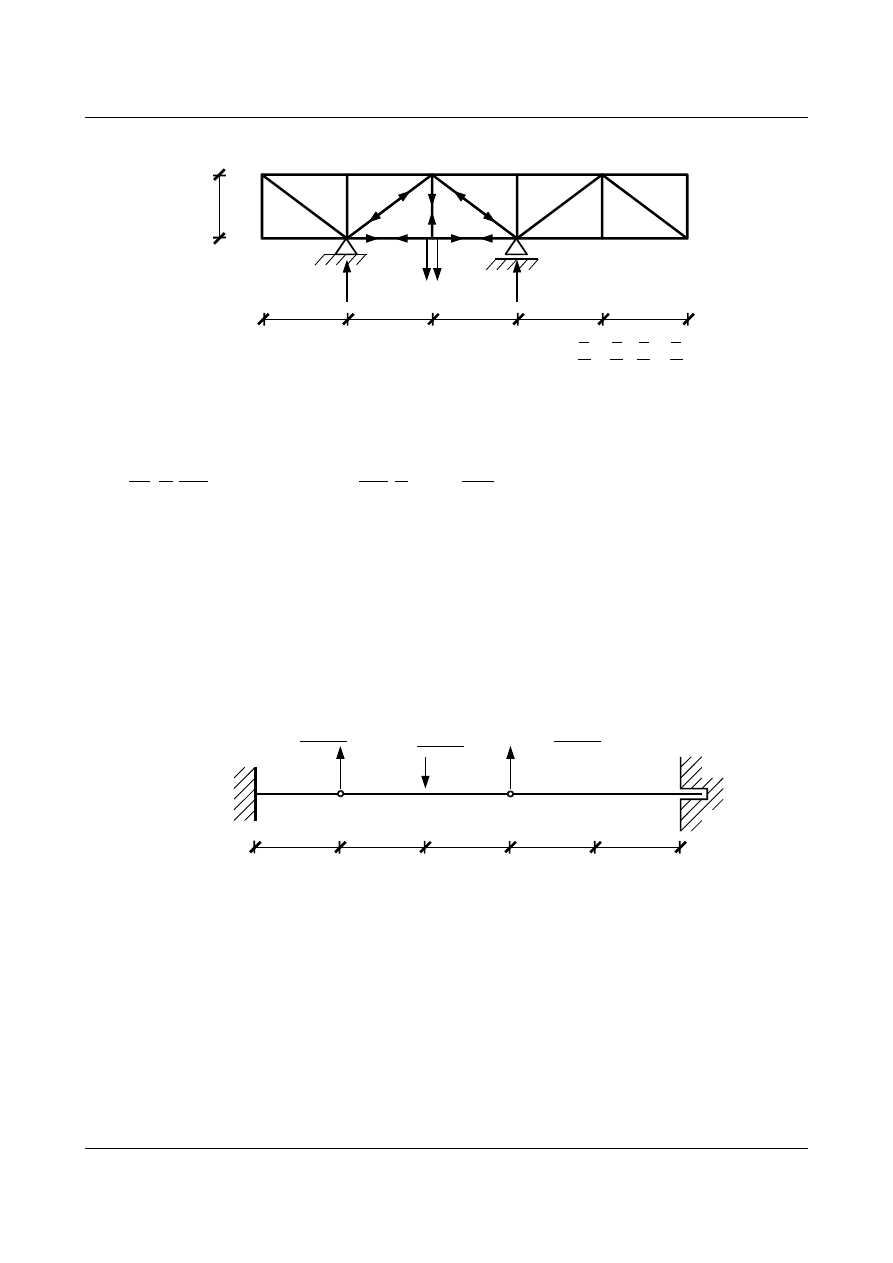
Dla ciężaru sprężystego w

3

poszukujemy sił w prętach kraty od obciążenia w węzłach 2, 3, i 4.

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

1,5

2,0

2,0

2,0

2,0

2,0

[m]

0,5

0,5

0,5

0,5

O

O

O

O

O

O

O

O

O

O

O

O

0,5

O

0,5

0,8

(3)

0,8

(3)

O

O

0,(6)

0,(6)

N

W2

[ - ]

1

2

3

4

5

6

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

13

Rys.6.19. Kratownica obciążanej w węzłach nr 2,3,4 siłami 1

2

,

1

2



1

2

,

1

2

obliczamy wartość ciężaru sprężystego:

w

3

=

1

EA



5

6

⋅

250

3

⋅2,5⋅21 ⋅100 ⋅1,5 ⋅1

200

3

⋅

2

3

⋅2 ⋅2



=

675

EA

Dla ciężaru

w

5

obciążenie wirtualne przykładamy w węzłach 4, 5 i 6. Wyznaczone w ten sposób siły

występują tylko w prętach, w których siły od obciążenia są równe zero. Wobec tego:

w

5

=0

Dobieramy układ zastępczy dla kratownicy (rys. 6.12) i obciążmy ciężarami sprężystymi:

2,0

2,0

2,0

2,0

2,0

[m]

A

B

C

D

w

2

=

248,6(1)

EA

w

3

=

675,0

EA

w

4

=

248,6(1)

EA

Rys. 6.20. Układ zastępczy dla kratownicy

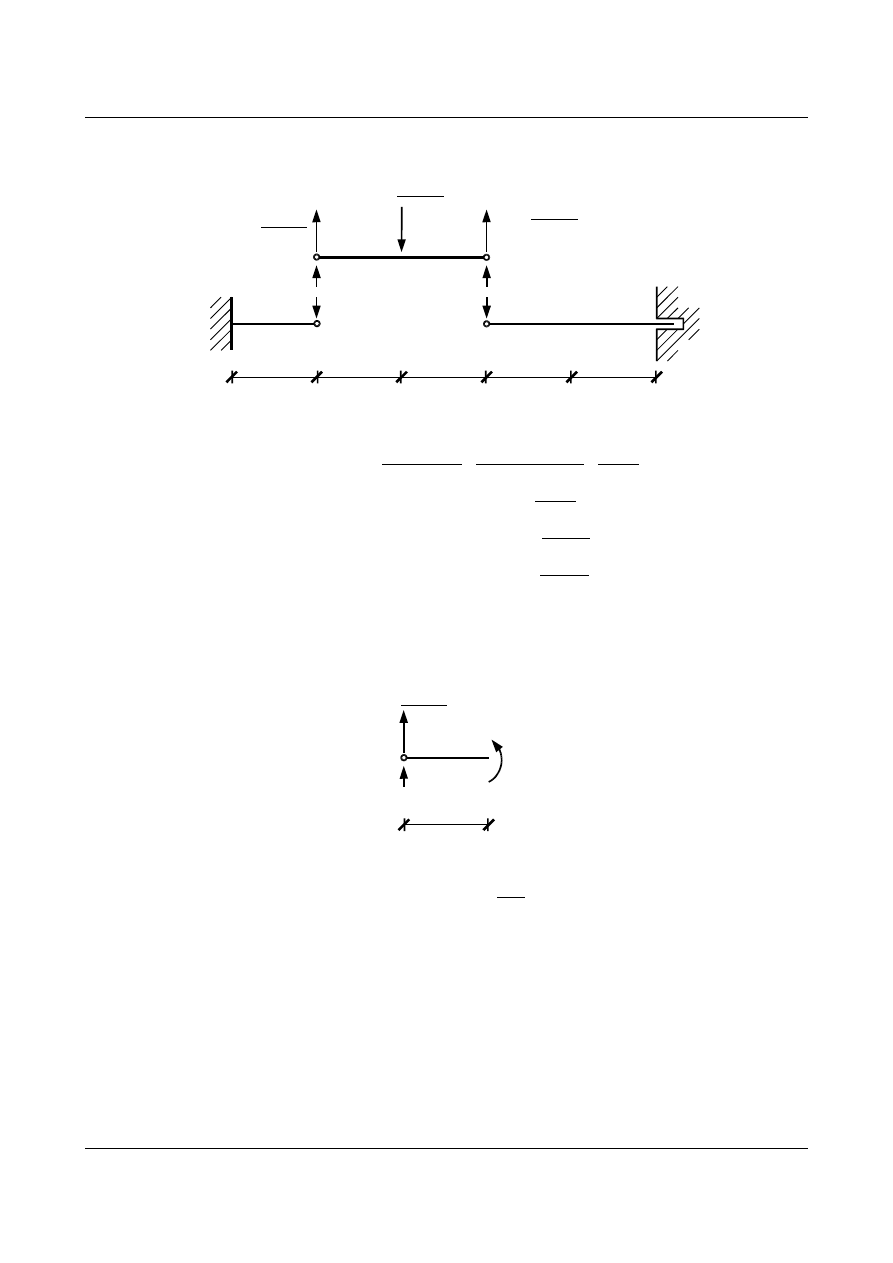
Z rys. 6.20 widać, że ciężary

w

1

i

w

6

byłyby przyłożone w podporach. Tak więc nie mają wpływu na

ugięcia.

Obliczamy reakcje podporowe:

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

1,5

2,0

2,0

2,0

2,0

2,0

[m]

0,5

0,5

0,5

0,5

N

W3

[ - ]

O

O

O

O

O

O

O

O

O

O

0,8

(3)

0,8

(3)

O

O

O

O

O

1

0,(6)

0,(6)

1

2

3

4

5

6

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

14

2,0

[m]

A

B

2,0

2,0

2,0

C

D

2,0

belka I

belka II

belka III

R

B

R

C

w

2

=

248,6(1)

EA

w

4

=

248,6(1)

EA

w

3

=

675,0

EA

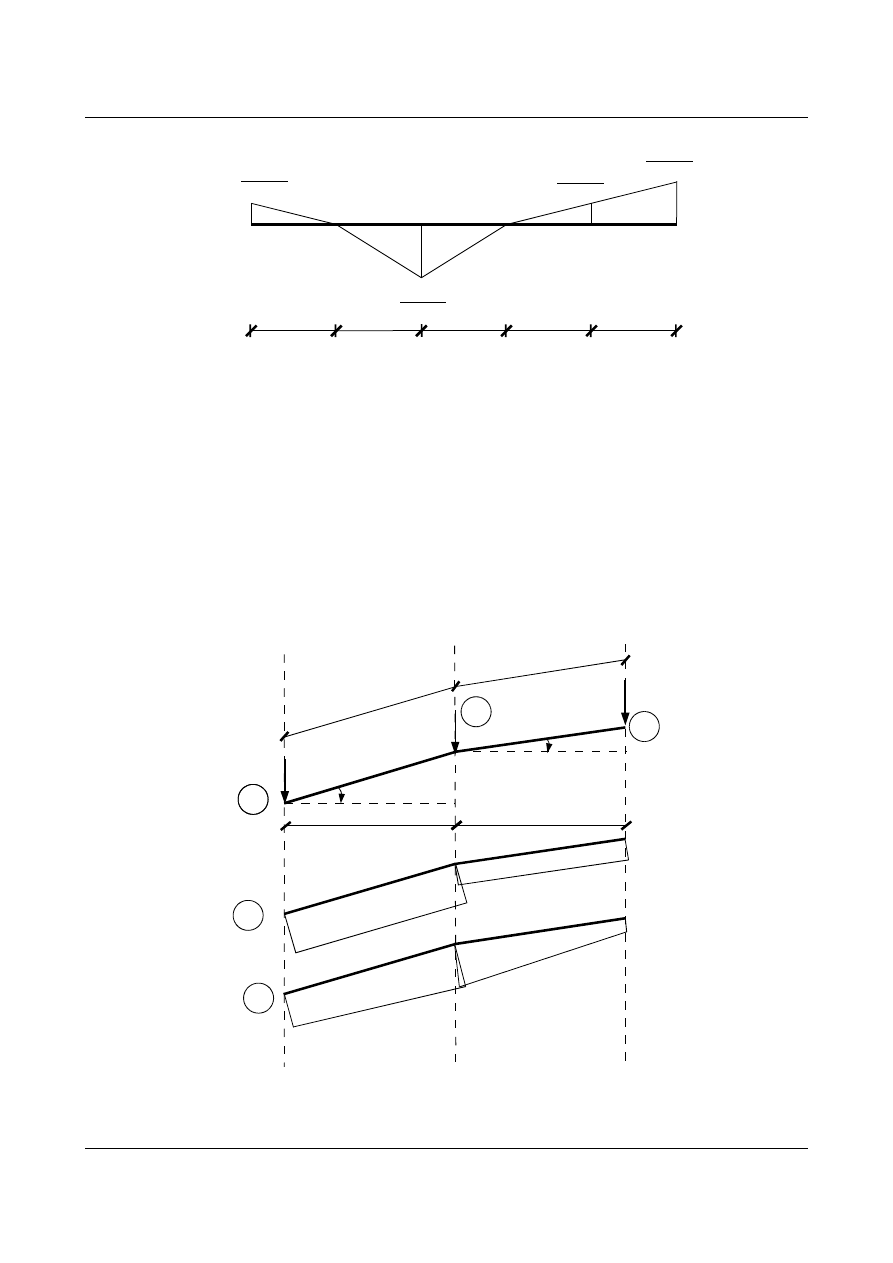
dla belki II

∑

M

C

=0 ⇒ R

B

=

w

3

⋅2 −w

2

⋅4

4

=

675

⋅2−248,6 1

EA

=

88,

8

EA

R

A

=R

B

=R

C

=R

D

=

88,

8

EA

dla belki I

∑

M

A

=0 ⇒

M

A

=R

B

⋅2 =

177,

7 

EA

dla belki II

∑

M

D

=0 ⇒

M

D

=R

C

⋅4 =

355,

5

EA

Obliczamy moment w środku rozpiętości części II :

R

B

2,0

E

M

E

w

2

=

248,6(1)

EA

∑

M

E

=0 ⇒ M

E

=R

B

w

2

⋅2=

675

EA

Wykres momentów od ciężarów sprężystych przedstawia również linię ugięcia pasa dolnego kratownicy:

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

15

2,0

2,0

2,0

2,0

2,0

[m]

177,(7)

EA

177,(7)

EA

355,(5)

EA

675,0

EA

Rys. 6.21. Wykres momentów od ciężarów sprężystych

6.4. Obliczanie ciężarów sprężystych dla układów prętowych zginanych

Rozważymy dowolny zginany układ prętowy obciążony siłami skupionymi

P

k

. Każdy z prętów układu

posiada przekrój o polu powierzchni

A

k

i momencie bezwładności

I

k

, długość pręta oznaczono

l

k

.

W celu wyznaczenia przemieszczeń

φ

k

wzdłuż kierunków działających sił P

k

należy wyznaczyć dla

każdego węzła ciężar sprężysty

w

k

.

Ciężar sprężysty jest liczony na podstawie wykresów sił wewnętrznych od obciążenia rzeczywistego i

od obciążenia wirtualnego, które stanowią pary sił (momenty jednostkowe).

k-1

k

k+1

P

k-1

P

k

P

k+1

l

k

l

k+1

a

k

a

k+1

A

k ,

J

k

A

k +1,

J

k+1

ß

k

ß

k+1

M

k-1

M

k

M

k+1

M

p

N

p

N

k

N

k

N

k+1

Rys. 6.22. Układ prętowy obciążony siłami skupionymi

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

16

+

M

1

1

tg β

k+1

a

k

a

k+1

1

N

a

k

1

a

k

1

a

k+1

1

a

k+1

l

k+1

1

tg β

k+1

l

k+1

1

tg β

k

l

k

-1

tg β

k

l

k

-1

Rys. 6.23. Układ prętowy obciążony w więzach siłami wirtualnymi

We wzorze określającym ciężar sprężysty nie uwzględniamy sił tnących i osiadań:

w

k

=

∑

{

∫

s



M



M

p

EJ





t

 t

h



ds



∫

s

N



N

p

EA



t

t

0



ds

}

(6.7)

Używając oznaczeń z wykresów sił wewnętrznych można zapisać:

w

k

=

1

E J

k

[

1
2

1 l

k



1
3

M

k

−1



2
3

M

k



]



1

E J

k

1

[

1
2

1l

k

1



1
3

M

k

1



2
3

M

k



]



1

E A

k

[

−

1

l

k

tg



k

l

k

N

k

]



1

E A

k

1

[

1

l

k

1

tg



k

1

l

k

1

N

k

1

]





t

t

h

k

1
2

1 l

k





t

 t

h

k

1

1
2

1l

k

1



t

t

0



−

1

l

k

tg



k

l

k





t

t

0



1

l

k

1

tg



k

1

l

k

1



(6.8)

Po skróceniu otrzymujemy ogólny wzór na ciężar sprężysty z uwzględnieniem momentów zginających,

sił normalnych i temperatury.

w

k

=

l

k

6 E J

k



2 M

k

M

k

−1





l

k

1

6 E J

k

1



2 M

k

M

k

1





−1tg 

k

6 E A

k

N

k



tg



k

1

6 E A

k

1

N

k

1





t

 t

2



l

k

h

k



l

k

1

h

k

1





t

t

0



−tg 

k

tg 

k

1



(6.9)

t , t

- wspólne dla obu prętów (

l

k

i

l

k + 1

).

Należy zwrócić uwagę na pewne przypadki szczególne stosowania wzoru (6.8)

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

17

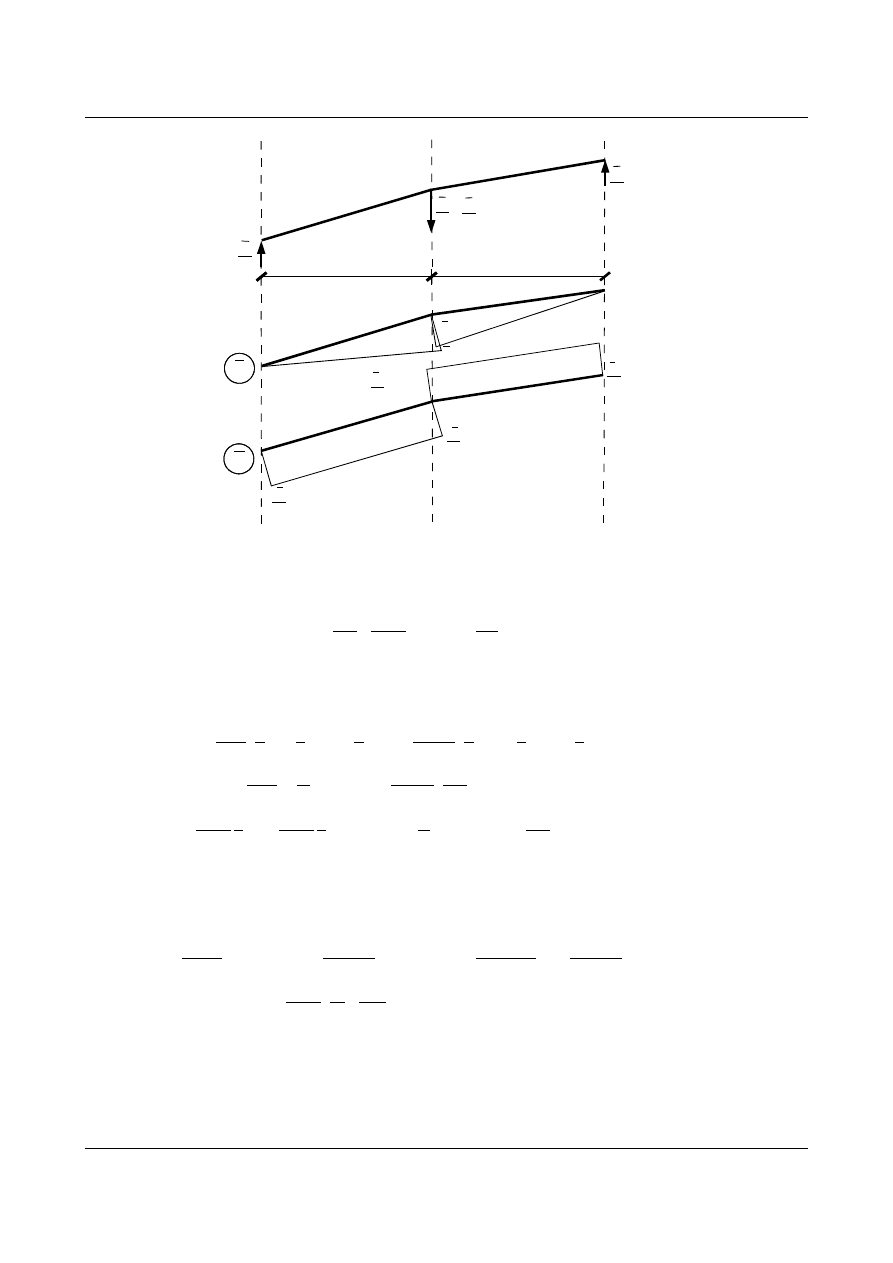
1. Dla wykresów krzywoliniowych do powyższego wzoru należy dodać poprawkę uwzględniającą parabolę

tzn. zwiększyć wartość

w

k

o część wynikającą z faktu krzywoliniowego wykresu momentów rzeczywistych.

Δw

l

k

A

k

,J

k

q

Rys. 6.24. Krzywoliniowy wykres momentów

w

k

=

1

6 E J

k

[

2 M

k

M

k

−1

]

... w

(6.10)

2. W przypadku nieciągłości wykresu, skoku o wartość momentu rzeczywistego, rozbijamy wykres na dwa

wykresy, ale całość koncepcji nie zostaje zmieniona.

Po obliczeniu ciężarów sprężystych obciążamy nimi belkę fikcyjną, tzn. taką, która spełnia warunki

brzegowe układu rzeczywistego (analogia do metody obciążeń wtórnych).

C

A

B

w

1

w

2

w

3

w

4

Rys. 6.25. Belka zastępcza (fikcyjna) obciążona ciężarami sprężystymi

Można jednak zamiast belki fikcyjnej obciążać ciężarami sprężystymi belkę spoczywającą na dwóch

podporach, wymaga to jednak pewnego zabiegu graficznego.

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

18

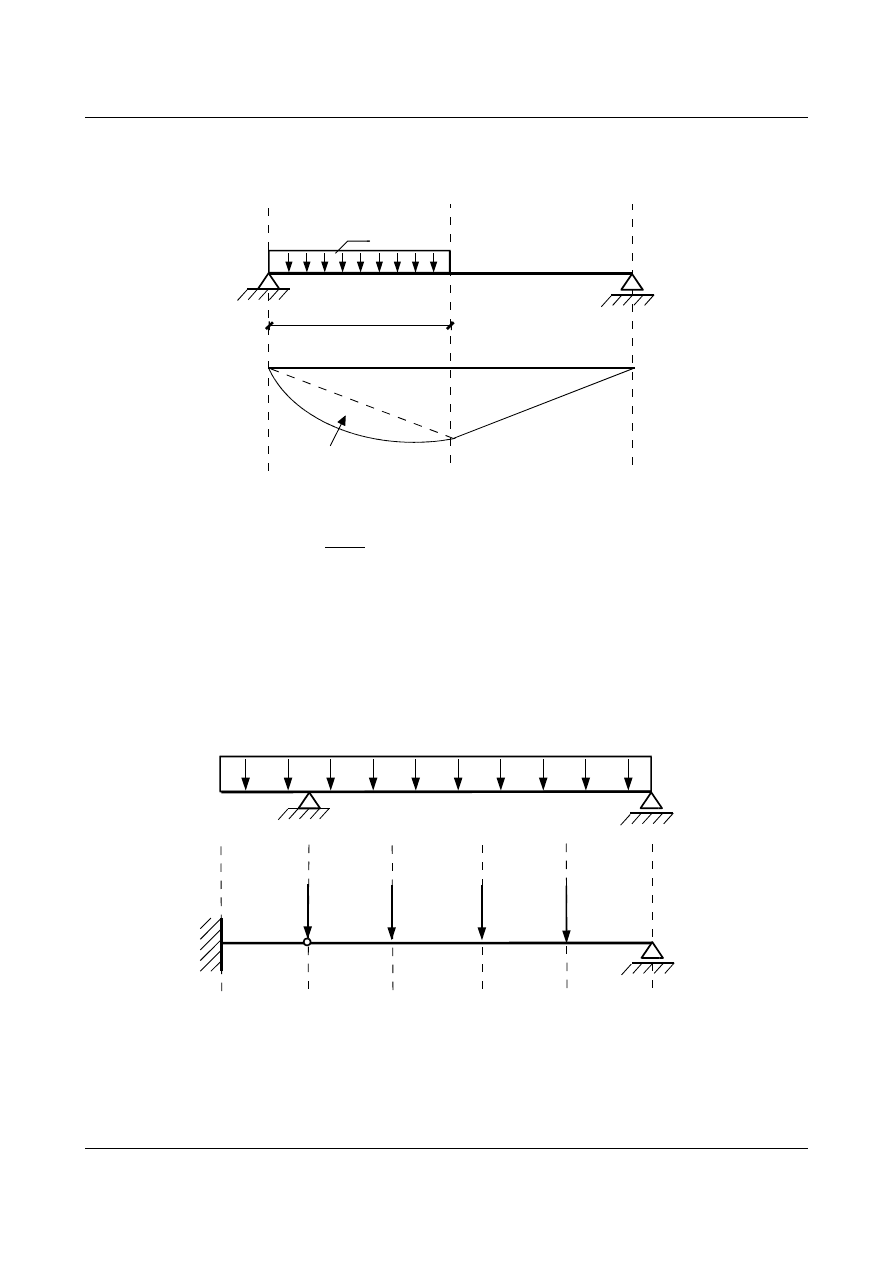
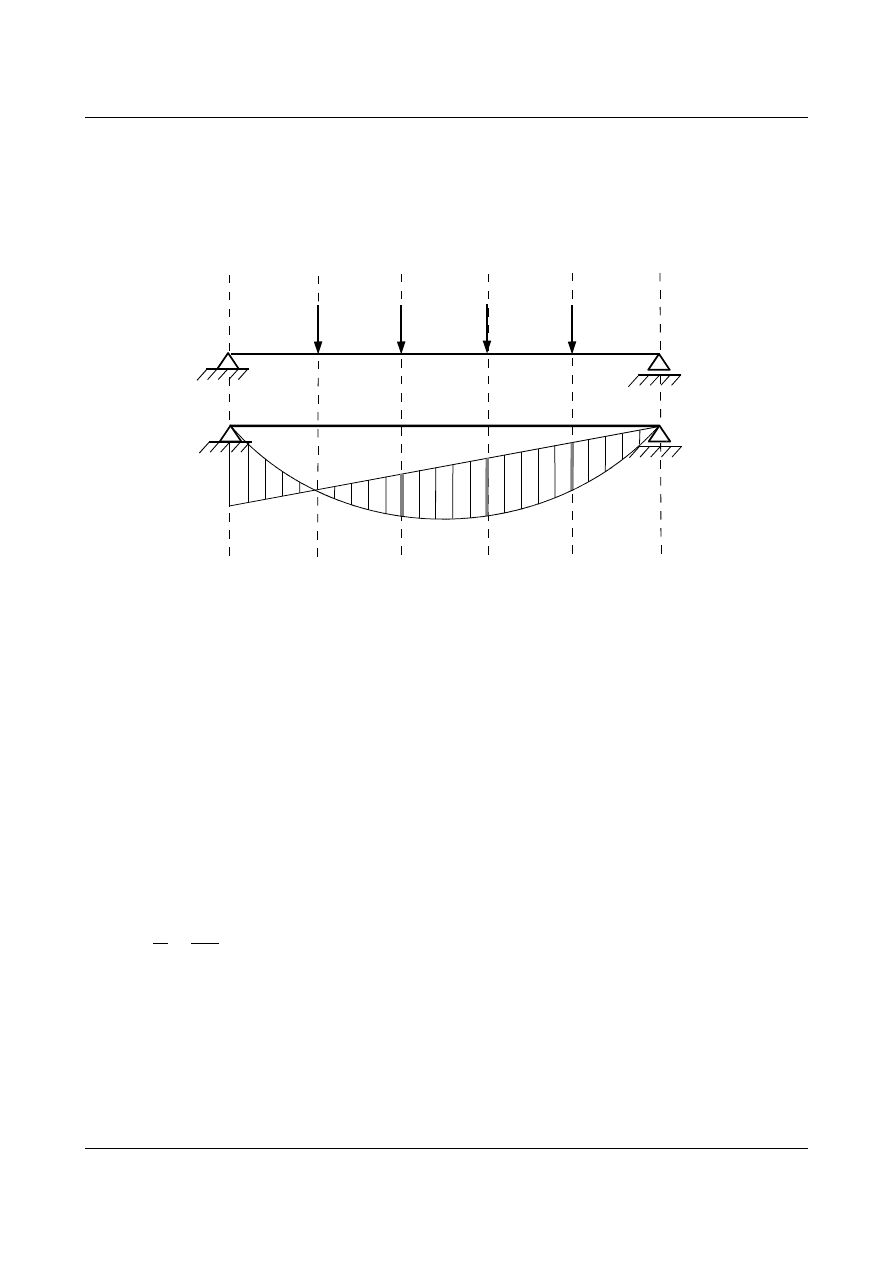
Dla belki podpartej na dwóch końcach wykres momentów powstały od obciążeń

w

k

będzie równy zeru w

punktach

A i C (rys. 6.26) (ugięcie tych punktów równe jest zeru). Jednak warunkiem brzegowym belki

rzeczywistej jest zerowe ugięcie w punktach

B i C. Należy postąpić w następujący sposób: po narysowaniu

wykresu momentów w belce podpartej na obu końcach, kreślimy prostą zamykającą tak aby przecięła rzędne
wykresu momentów dla punktów

B i C.

A

B

C

w

1

w

2

w

3

w

4

δ

3

δ

4

δ

2

B

A

C

Rys. 6.26. Belka wolnopodparta na obu końcach obciążona ciężarami sprężystymi

Rzędne zakreskowanego pola (rys. 6.26) pomiędzy linią krzywą a prostą zamykającą stanowią wartości

ugięć kolejnych punktów belki rzeczywistej (na rysunku wyróżniono ugięcia w punktach przyłożenia ciężarów
sprężystych).

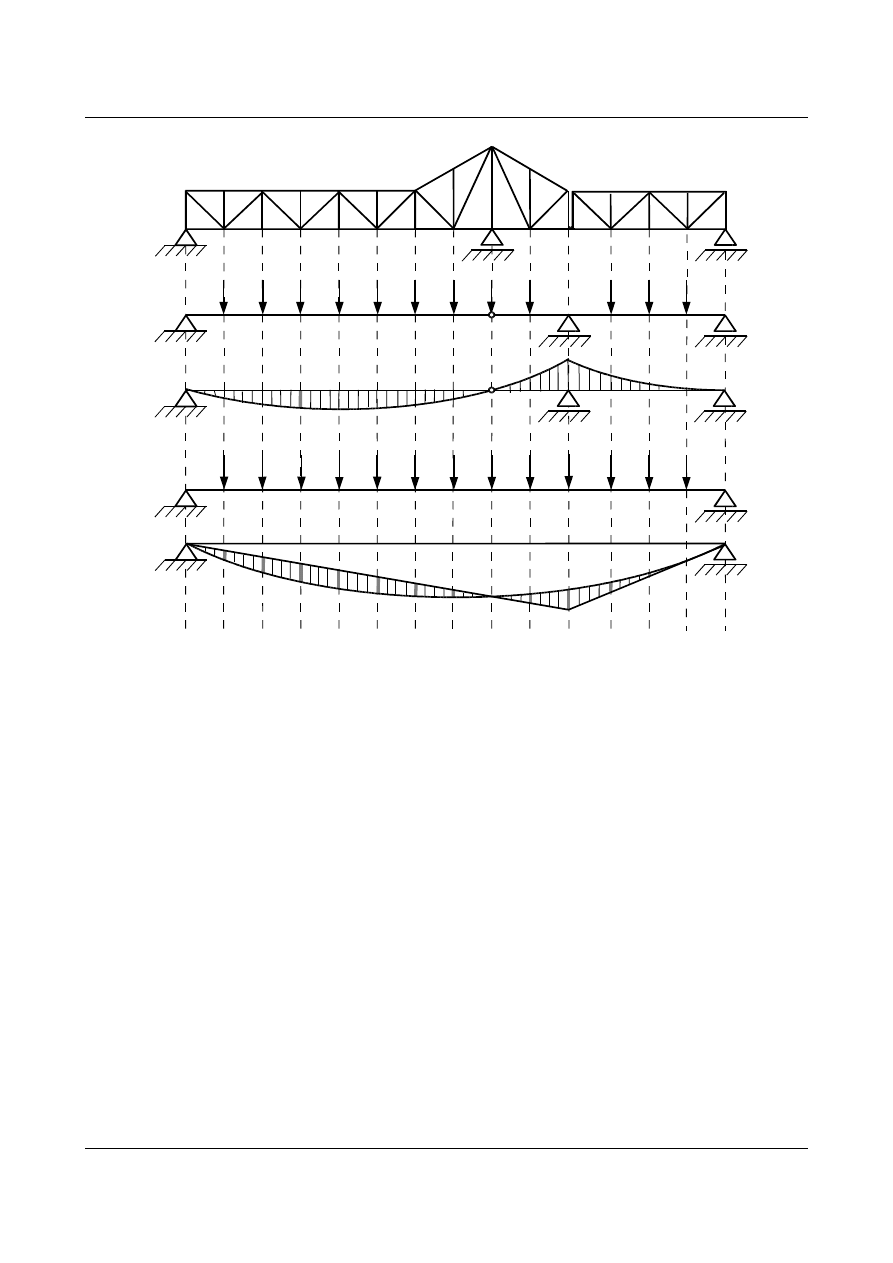
Analogicznie postępujemy w przypadku kratownic wyznaczając linię ugięcia mamy dwie możliwości:

Możemy przyjąć schemat belki zastępczej spełniającej warunki brzegowe układu rzeczywistego. W punkcie

B

(rys. 6.27a) jest podpora (przemieszczenie jest zerowe) wprowadzamy przegub aby moment od ciężarów
sprężystych był równy zero.

Drugim sposobem jest zastosowanie schematu belki wolnopodpartej (rys. 6.27c) dla której tworzymy

wykres momentów od sił

w

k

. Kreślimy prostą zamykającą przez rzędne w punktach

A i B (zerowe

przemieszczenia w kracie rzeczywistej) aż do punktu

M. Dalej łączymy prostą zamykającą punkty M i C.

Przemieszczenia to wartości pomiędzy wykresem krzywoliniowym i prostymi zamykającymi. Przypomnieć
należy, że w kratownicy możemy wyznaczyć linię ugięcia pasa dolnego lub pasa górnego w zależności od
sposobu wyznaczenia samych ciężarów sprężystych. W przypadku pasa górnego trzeba wirtualne obciążenia

(pary sił

1

a

k

i

1

a

k

1

) przykładać do węzłów górnych.

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

19

A

1

2

3

4

5

6

7

8

9

M

10

11

12

C

B

a)

b)

c)

w

1

w

2

w

3

w

4

w

5

w

6

w

7

w

9

w

10

w

11

w

12

w

8

δ

3

δ

3

w

1

w

2

w

3

w

4

w

5

w

6

w

7

w

9

w

10

w

11

w

12

w

8

w

M

Rys. 6.27. a) układ rzeczywisty, b) układ zastępczy (analogia do metody obciążeń wtórnych) - belka fikcyjna,

c) układ zastępczy (belka wolno podparta - konieczność wprowadzenia zabiegu graficznego)

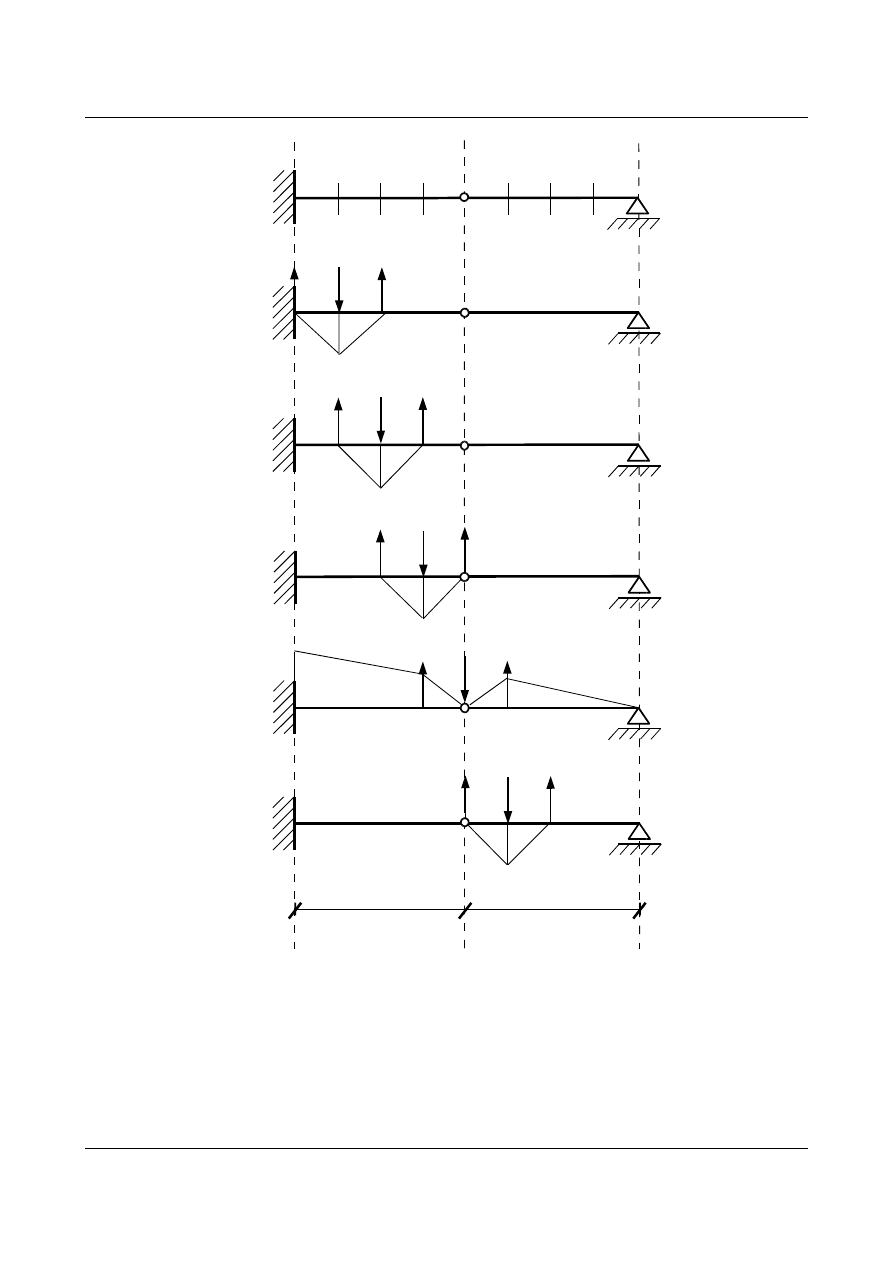
W przypadku występowania przegubu wewnętrznego ciężar sprężysty dla tego punktu należy obliczyć

indywidualnie biorąc pod uwagę fakt, że wykresy momentów wirtualnych występują w całym układzie
(rys. 6.28).

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

20

0

1

2

3

4

5

6

7

8

dla w

1

dla w

2

dla w

4

dla w

3

4

4

dla w

5

Rys. 6.28. Belka z przegubem wewnętrznym

Podobnie w układach kratowych z przegubem wewnętrznym trzeba zwrócić uwagę na ciężar sprężysty dla
przegubu.

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 1

6. WYZNACZANIE LINII UGIĘCIA W UKŁADACH PRĘTOWYCH

21

a

k

a

k+1

a

m

a

m+1

m

A

B

H

A

=0

H

B

=0

R

B

=0

R

B

=0

H

A

=

R

A

=0

R

A

=0

w

k

w

m

u

k

u

m

f

k

+

1

a

m

1

a

m+1

1

a

k

1

a

k+1

+

1

a

k

1

a

k+1

1

a

m

1

a

m+1

1

f

H

B

=

1

f

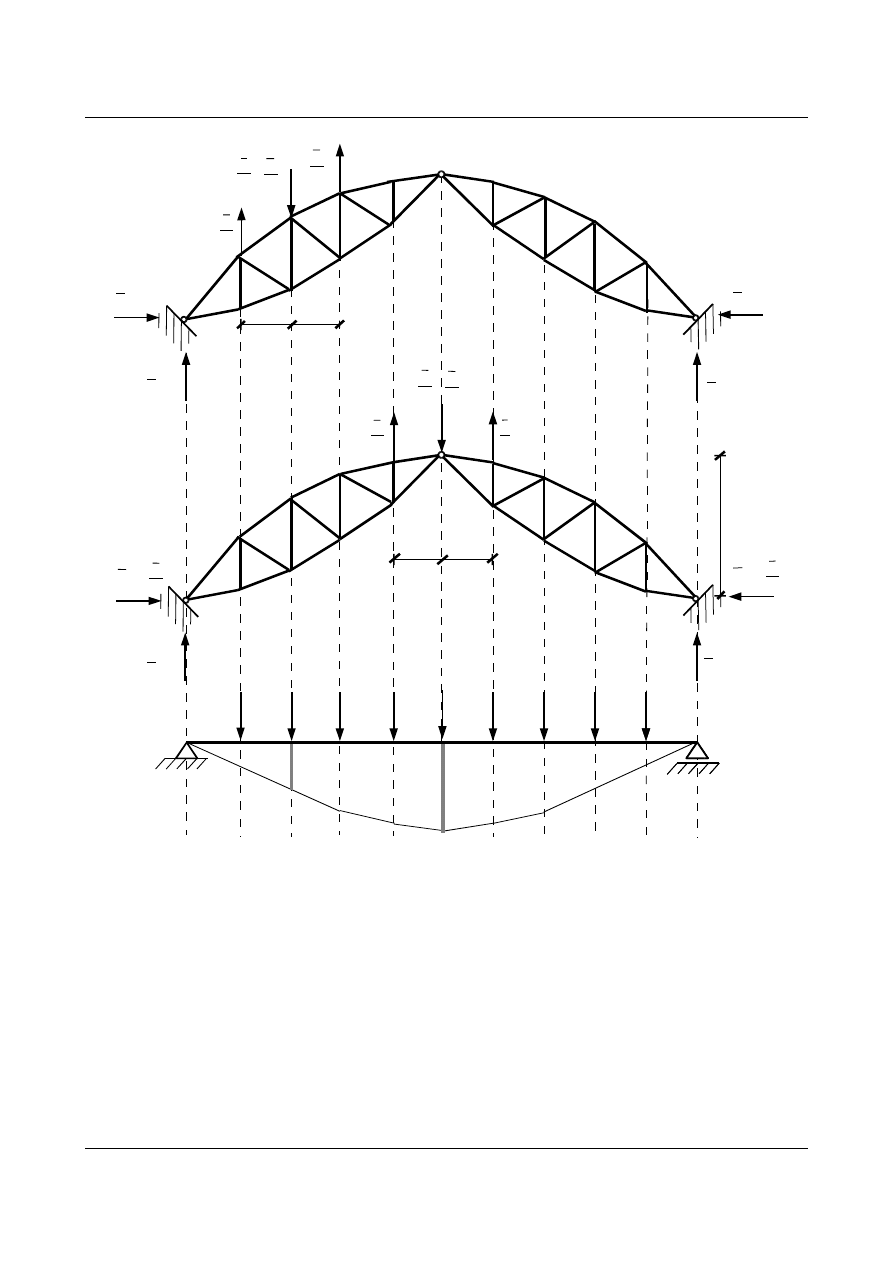
Rys. 6.29. Układ trójprzegubowy

Wszystkie wartości

w

k

obliczamy w układach samorównoważących się (siły tylko w niektórych

prętach). Natomiast wielkość

w

m

obliczamy z uwzględnieniem faktu, że obciążenie wirtualne w punkcie

m

wywołuje reakcje poziome

H. Zatem stan naprężenia występuje we wszystkich prętach kratownicy a nie jak

poprzednio tylko w otoczeniu obciążonych węzłów.

Dobra D., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater