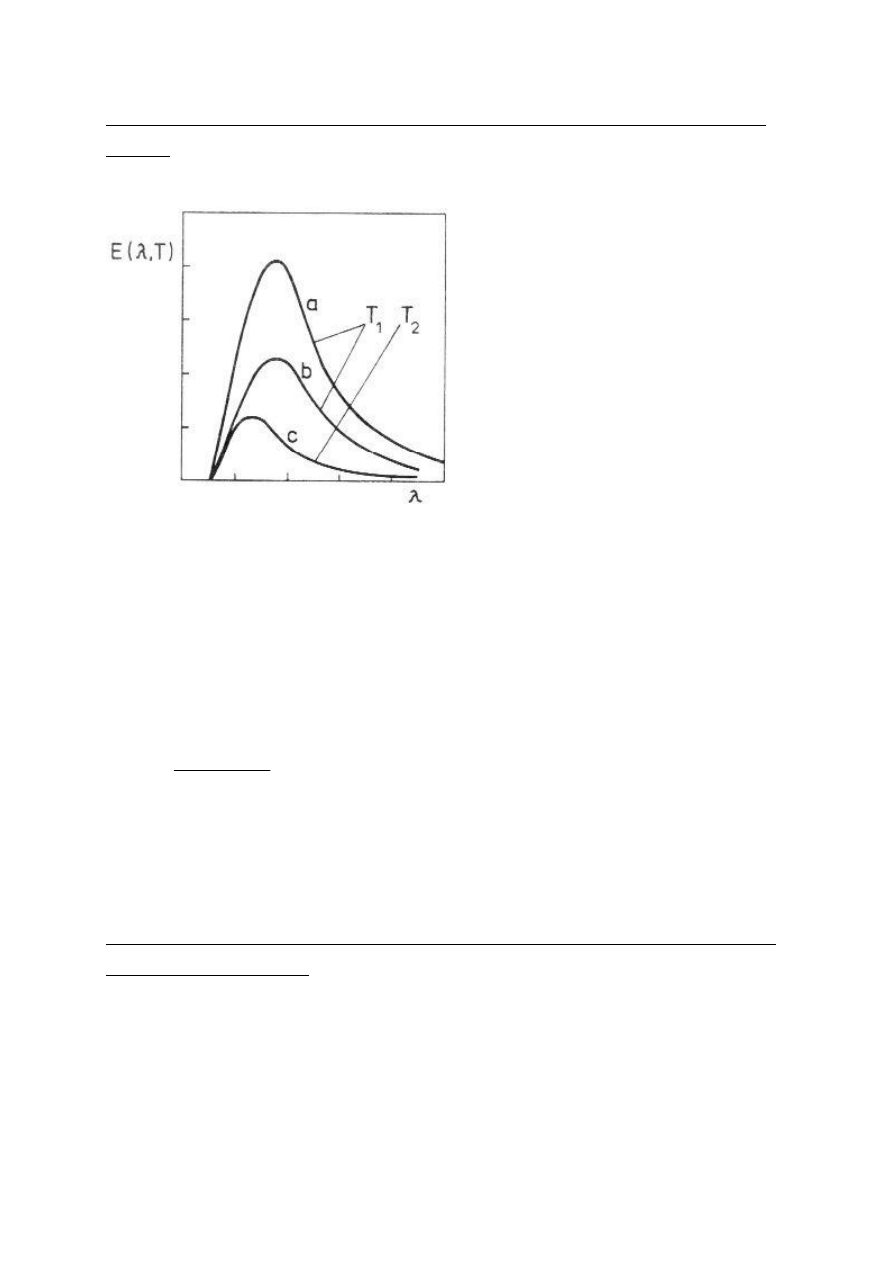
3. Rozkład widmowy natężenia promieniowania ciała doskonale czarnego, założenia i wzór 

Plancka. 

Rozkład widmowy natężenia promieniowania: 

 

Założenia teorii Plancka: 

- atomy tworzące ciało (ścianki wnęki) zachowują się jak liniowe oscylatory harmoniczne 

- energia oscylatorów może przyjmować tylko określne (skwantowane) wartości: 

 

        ;      n-liczba kwantowa, υ – częstotliwość oscylatora 

- oscylatory wypromieniowują i absorbują energię kwantami 

 

          

Wzór Plancka (opisuje 

rozkład widmowy energii emitowanej przez ciało doskonale czarne)

: 





1

e

hc

2

)

T

(

B

T

k

/

hc

5

2











 

gdzie h=6.626x10

-34

 Js,  

k=1.3806x10

-23

 J/K  - stała Boltzmana

 

 

10. Opis cząstki swobodnej jako paczki falowej, poszerzanie się paczki falowej. Interpretacja 

statystyczna funkcji falowej. 

Cząstkę swobodną można opisać jako paczkę falową rozchodzącą się w danym kierunku z 

prędkością grupową dω/dt  równej prędkości cząstki. Paczka falowa interpretuje statystycznie 

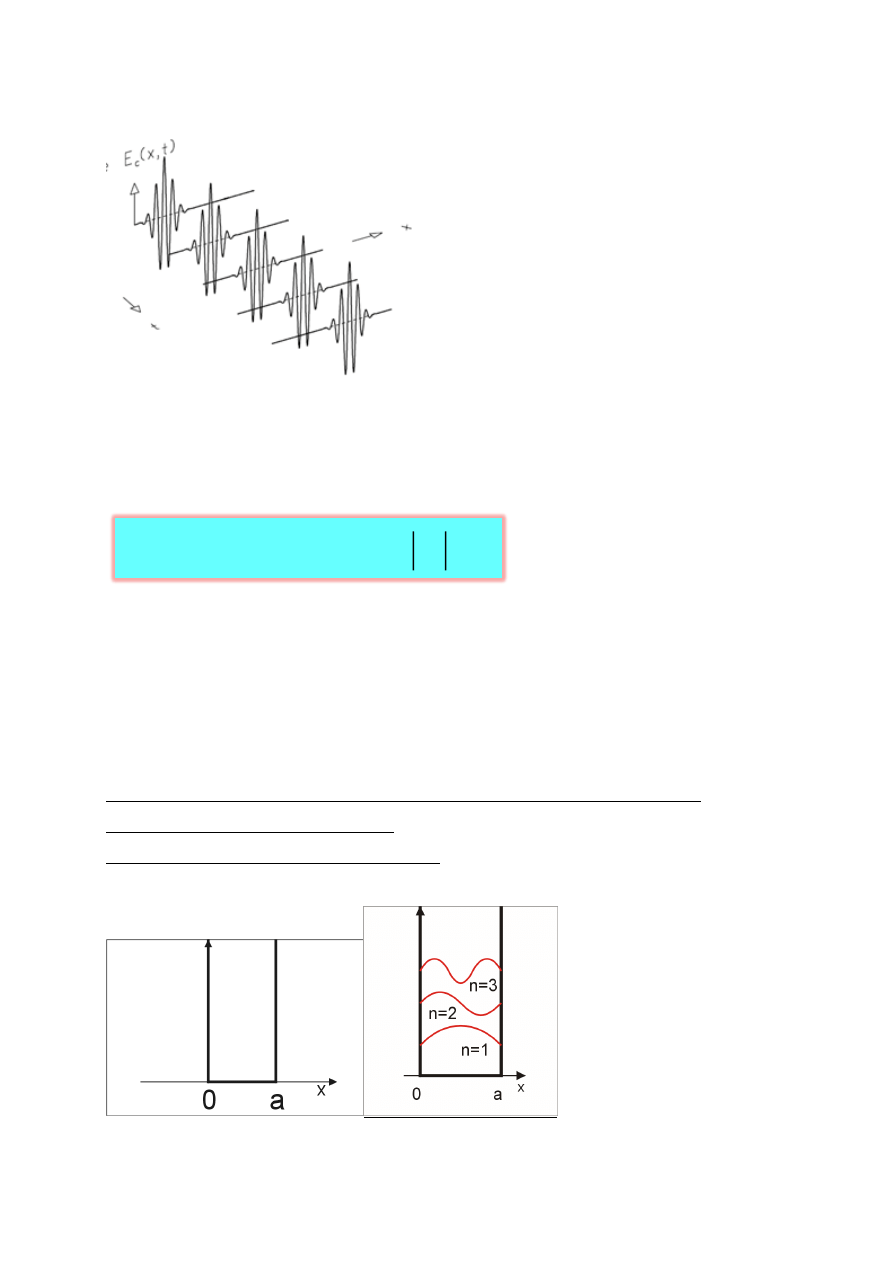
położenie poruszającej się cząstki swobodnej.  

 

Interpretacja statystyczna funkcji falowej:

 

Jeśli pomiar nastąpił w chwili t cząstka znajduje się pomiędzy x i x+dx z 

prawdopodobieństwem określonym przez kwadrat modułu zespolonej funkcji falowej: 

 

gdzie: P(x,t) – gęstość prawdopodobieństwa 

Poszerzanie się paczki falowej: 

Szerokość paczki falowej jest rozmiarem obszaru, w którym można znaleźć cząstkę. 

Paczka falowa ulega dyspersji - jej szerokość rośnie z czasem. Oznacza to, że z upływem 

czasu położenie cząstki staje się coraz bardziej nieoznaczone.  

 

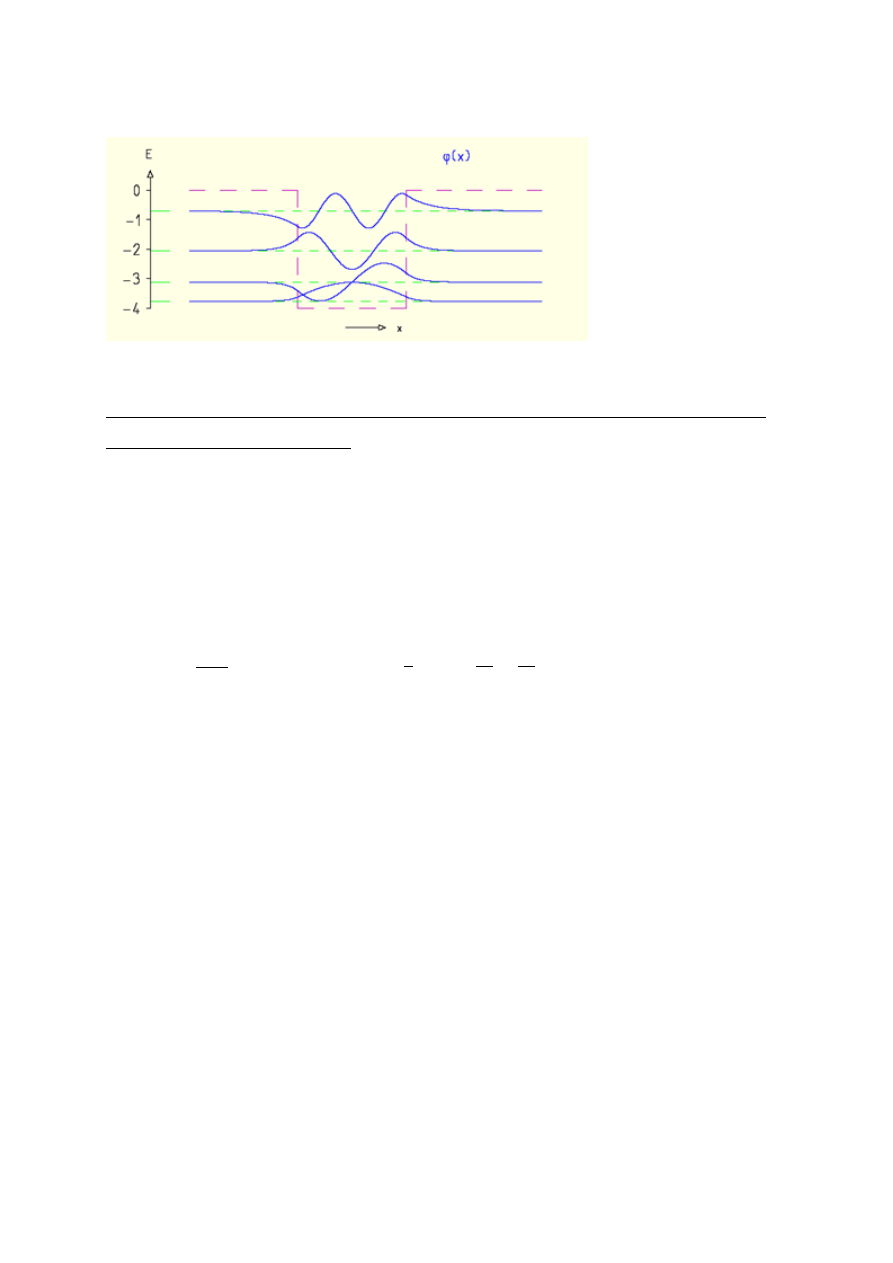
17. Studnia potencjału o skończonej głębokości, „zszywanie” rozwiązań równania 

Schrödingera, liczba poziomów energii,

 

porównanie ze studnią nieskończenie głęboką. 

 

 

dx

dx

dx

t

x

P

2

*

)

,

(











        r.S. 

           

 

 

Dla fali stojącej: 

 

 

 

Warunki zszycia funkcji – fale mają wartość 0 dla brzegów studni (o współrzędnych 

równych 0 oraz a) więc: 

- by fala biegnąca spełniała warunek 

 

 

( )        to   A= - B 

- by fala stojąca spełniała warunek 

 

 

( )     musi być w postaci  

 

 (czyli sinus jak wyżej) 

- by fala stojąca spełniała warunek 

 

 

( )      to  

  

  

 

 

Porównanie: 

W studni nieskończonej jest nieskończona liczba poziomów energii: 

W studni o skończonej głębokości liczba poziomów energii (stanów związanych) rośnie wraz 

z głębokością studni. 

W studni o skończonej głębokości  fala wnika w ściany studni potencjału, 

długość fali jest większa (a energia mniejsza) niż w studni nieskończenie głębokiej. 

 

 

24. Atomu wodoru, linie widmowe, wzór Balmera, model Bohra, energia jonizacji, poziomy 

energii, promień orbity elektronu. 

 

Widma promieniowania atomów (np. gorącego gazu) nie są ciągłe. Charakterystyczne linie 

widmowe - fale elektromagnetyczne tylko o ściśle określonej długości fali. Ich ułożenie jest 

charakterystyczne dla danego atomu. 

Jednym z charakterystycznych układów linii widmowych w atomie wodoru jest seria Balmera 

opisana wzorem: 

          

 

 

 

 

  

    

  

m    lub inaczej   

 
 

   

 

(

 

 

 

 

 

 

 

)

     n=3,4,5.. 

R

H

 = 10972000 m

-1

 – stała Rydberga 

Model Bohra – postulaty 

1.  Elektron porusza się po orbicie kołowej dookoła jądra atomowego. Energia elektronu 

jest stała (nie wypromieniowuje energii). 

2.  Dozwolone są orbity, dla których orbitalny moment pędu elektronu L jest równy 

całkowitej wielokrotności wyrażenia h/2p=ħ,  h=6,626×10

-34 

Js  

3.  Wypromieniowanie lub pochłanianie kwantu energii następuje wtedy, kiedy elektron 

przeskakuje z jednej dozwolonej orbity na drugą. Częstotliwość 



  wyemitowanego 

(pochłoniętego) promieniowania elektromagnetycznego odpowiada zmianie energii 

elektronu  

 

 

 

 

 



E = h



 

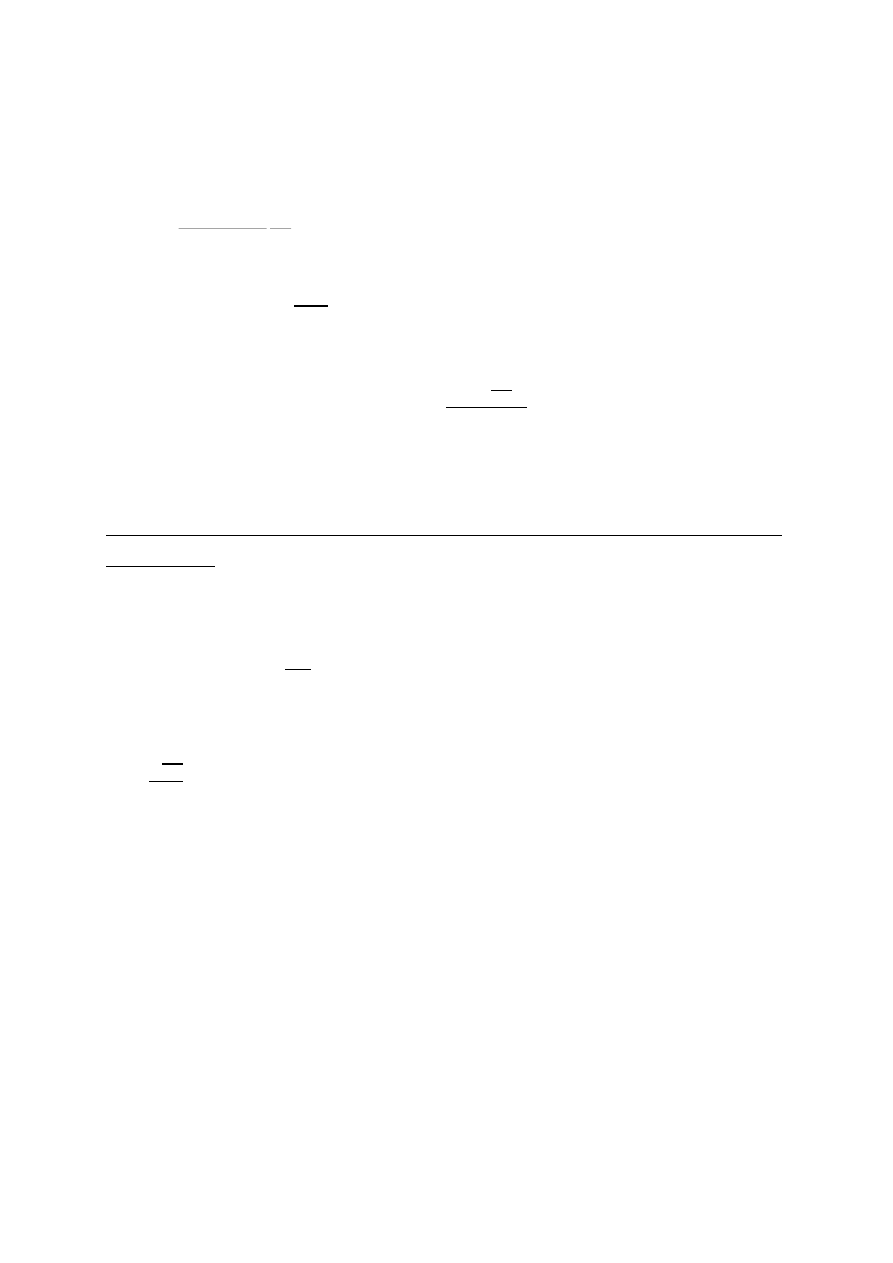
Energia jonizacji (n = inf. – oderwanie elektronu) E = 13,6 eV 

Poziomy energii: 

Jest n poziomów energii (n = 1,2,3… ; n=1 – poziom podstawowy) danych wzorem: 

 

lub inaczej 

 ( )    

    

 

 

    

Promień orbity: 

 ( )    

 

   

 

(

 

  )

 

 

 

  

 

 

gdzie Z – ładunek jądra atomowego tj. dla jądra o ładunku +2e liczba Z=2 

 

29. Związek między momentem pędu a momentem magnetycznym elektronu, magneton Bohra, 

efekt Zeemana. 

 

Związek między momentem pędu a momentem magnetycznym elektronu: 

              gdzie     

 

  

 

 

Magneton Bohra: 

 

 

 

 

 

  

  

 

           

   

  

  

 

Efekt Zeemana: 

Zjawisko fizyczne, które polega na rozszczepieniu obserwowanych linii spektralnych na 

składowe, gdy próbka emitująca promieniowanie zostaje umieszczona w polu magnetycznym. 

W zewnętrznym polu magnetycznym o indukcji B moment magnetyczny atomu będzie miał 

energię potencjalną zależną od jego położenia względem tego pola 

 

 

         . Stąd każdy 

z poziomów energii atomu ulega rozszczepieniu na kilka odrębnych składowych 

odpowiadających różnym możliwym orientacjom wektora µ względem B. Zjawisko Zeemana 

potwierdza występowanie kwantowania przestrzennego wektora µ. 





2

2

2

0

4

2

1

2

4

)

(

n

e

Z

m

n

E

e







