3. OSIĄGANIE CELU POPRZEZ

3. OSIĄGANIE CELU POPRZEZ

POSZUKIWANIA

POSZUKIWANIA

NIEINFORMOWANE

© F.A. Dul 2007

Poszukiwania nieinformowane

Poka

ż

emy w jaki sposób agent mo

ż

e

Poka

ż

emy w jaki sposób agent mo

ż

e

osi

ą

gn

ąć

zamierzony cel poprzez

osi

ą

gn

ąć

zamierzony cel poprzez

wykonanie ci

ą

gu działa

ń

.

Działania te b

ę

d

ą

wyznaczone

Działania te b

ę

d

ą

wyznaczone

poprzez poszukiwania oparte
wył

ą

cznie na definicji zadania.

wył

ą

cznie na definicji zadania.

© F.A. Dul 2007

Niniejszy rozdział po

ś

wi

ę

cony jest agentom celowym,

3.1. Wprowadzenie

Niniejszy rozdział po

ś

wi

ę

cony jest agentom celowym,

których działanie oparte jest na poszukiwaniu rozwi

ą

zania

w zbiorze rozwi

ą

za

ń

dopuszczalnych.

w zbiorze rozwi

ą

za

ń

dopuszczalnych.

Na takiej zasadzie opiera si

ę

działanie wielu agentów, np.:

• agenci - obiekty w grach komputerowych, symulatorach;

• agenci - obiekty w grach komputerowych, symulatorach;
• oprogramowanie przewodników drogi wykorzystuj

ą

cych

system GPS,

system GPS,

• agenci poszukuj

ą

cy w Internecie stron z

żą

dan

ą

zawarto

ś

ci

ą

.

Poszukiwanie nieinformowane (uninformed search) polega
na wyznaczaniu rozwi

ą

zania zadania wył

ą

cznie na podstawie

danych definiuj

ą

cych zadanie.

danych definiuj

ą

cych zadanie.

Poszukiwanie informowane (informed search) polega na
wyznaczaniu rozwi

ą

zania zadania przy wykorzystaniu innej

© F.A. Dul 2007

wyznaczaniu rozwi

ą

zania zadania przy wykorzystaniu innej

dost

ę

pnej wiedzy, specyficznej dla tego zadania.

3.1. Wprowadzenie

Plan rozdziału

• Agenci rozwi

ą

zuj

ą

cy zadania.

• Rodzaje zada

ń

.

• Sformułowania zada

ń

.

• Sformułowania zada

ń

.

• Przykłady zada

ń

.

• Podstawowe algorytmy poszukiwa

ń

.

• Podstawowe algorytmy poszukiwa

ń

.

© F.A. Dul 2007

3.2. Agent poszukuj

ą

cy rozwi

ą

zania

Agent poszukuj

ą

cy rozwi

ą

zania jest rodzajem agenta

Agent poszukuj

ą

cy rozwi

ą

zania jest rodzajem agenta

celowego.

Czetry kroki przy rozwi

ą

zywaniu problemu

• Sformułowanie celu zadania

– jaki stan systemu odpowiada osi

ą

gni

ę

ciu celu?

Czetry kroki przy rozwi

ą

zywaniu problemu

– jaki stan systemu odpowiada osi

ą

gni

ę

ciu celu?

• Sformułowanie zadania

– jakie stany i działania nale

ż

y bra

ć

pod uwag

ę

?

• Poszukiwanie

• Poszukiwanie

– okre

ś

li

ć

optymalne działania które nale

ż

y wykona

ć

aby

osi

ą

gn

ąć

cel

• Wykonanie zadania

– wyznaczy

ć

rozwi

ą

zanie

© F.A. Dul 2007

Algorytm agenta poszukuj

ą

cego rozwi

ą

zania

3.2. Agent poszukuj

ą

cy rozwi

ą

zania

function SIMPLE-PROBLEM-SOLVING-AGENT(percept) return an action

static: seq, an action sequence

state, some description of the current world state

state, some description of the current world state
goal, a goal
problem, a problem formulation

problem, a problem formulation

state

←

UPDATE-STATE(state, percept)

if seq is empty then

if seq is empty then

goal

←

FORMULATE-GOAL(state)

problem

←

FORMULATE-PROBLEM(state,goal)

problem

←

FORMULATE-PROBLEM(state,goal)

seq

←

SEARCH(problem)

action

←

FIRST(seq)

seq

←

REST(seq)

seq

←

REST(seq)

return action

© F.A. Dul 2007

3.2. Agent poszukuj

ą

cy rozwi

ą

zania

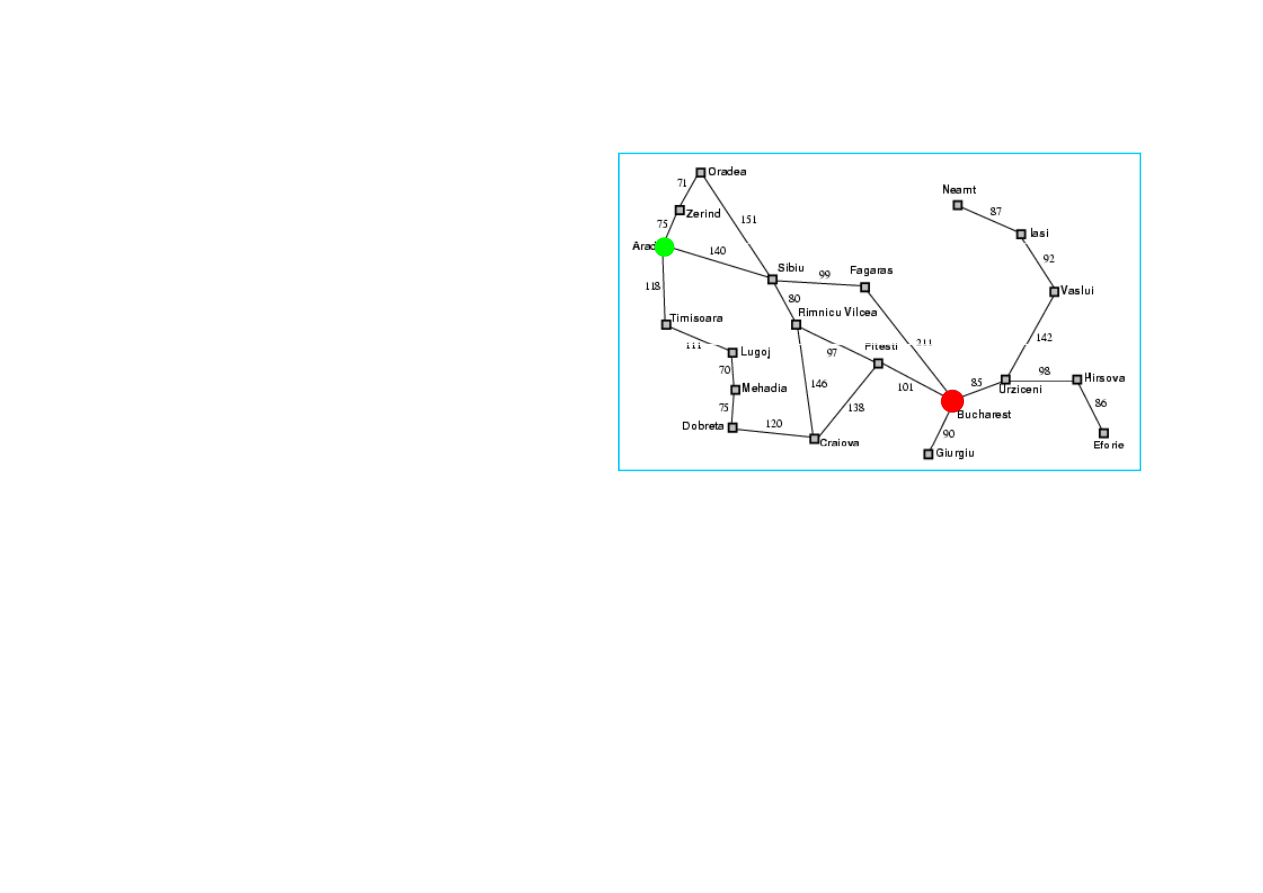
Przykład - poszukiwanie najkrótszej drogi

• Wakacje w Rumunii;

jeste

ś

my w mie

ś

cie

jeste

ś

my w mie

ś

cie

Arad.

• Jutro musimy odlecie

ć

• Sformułowanie celu

:

• Jutro musimy odlecie

ć

z Bukaresztu.

• Sformułowanie celu

:

– nale

ż

y jutro rano by

ć

w Bukareszcie.

• Sformułowanie zadania

:

• Sformułowanie zadania

:

– stan

: pobyt w jakim

ś

mie

ś

cie;

– działania

: przejazdy pomi

ę

dzy miastami.

– działania

: przejazdy pomi

ę

dzy miastami.

• Znale

źć

rozwi

ą

zanie

:

– ci

ą

g miast, { Arad , … , Bukareszt }

© F.A. Dul 2007

– ci

ą

g miast, { Arad , … , Bukareszt }

np. { Arad, Sibiu, Fagaras, Bukareszt }.

3.3. Rodzaje zada

ń

Zadanie najprostsze

• Deterministyczne, obserwowalne

⇒

⇒

⇒

⇒

zadanie jednostanowe

– agent wie w jakim jest stanie i w jakim stanie b

ę

dzie;

Zadanie najprostsze

– agent wie w jakim jest stanie i w jakim stanie b

ę

dzie;

rozwi

ą

zanie jest ci

ą

giem stanów;

Zadania znacznie trudniejsze:

• Nieobserwowalne

⇒

⇒

⇒

⇒

zadanie bez czujników (conformant

problem)

Zadania znacznie trudniejsze:

problem)

– agent nie wie, gdzie jest; rozwi

ą

zanie jest ci

ą

giem stanów;

• Niedeterministyczne lub obserwowalne cz

ęś

ciowo

• Niedeterministyczne lub obserwowalne cz

ęś

ciowo

⇒

⇒

⇒

⇒

nieprzewidywalne

(contingency problem)

– obserwacje dostarczaj

ą

nowych

informacji o stanie bie

żą

cym,

– poszukiwania cz

ę

sto

przeplataj

ą

si

ę

z działaniami.

– poszukiwania cz

ę

sto

przeplataj

ą

si

ę

z działaniami.

• Nieznana przestrze

ń

stanów

⇒

⇒

⇒

⇒

exploration problem

© F.A. Dul 2007

3.3. Rodzaje zada

ń

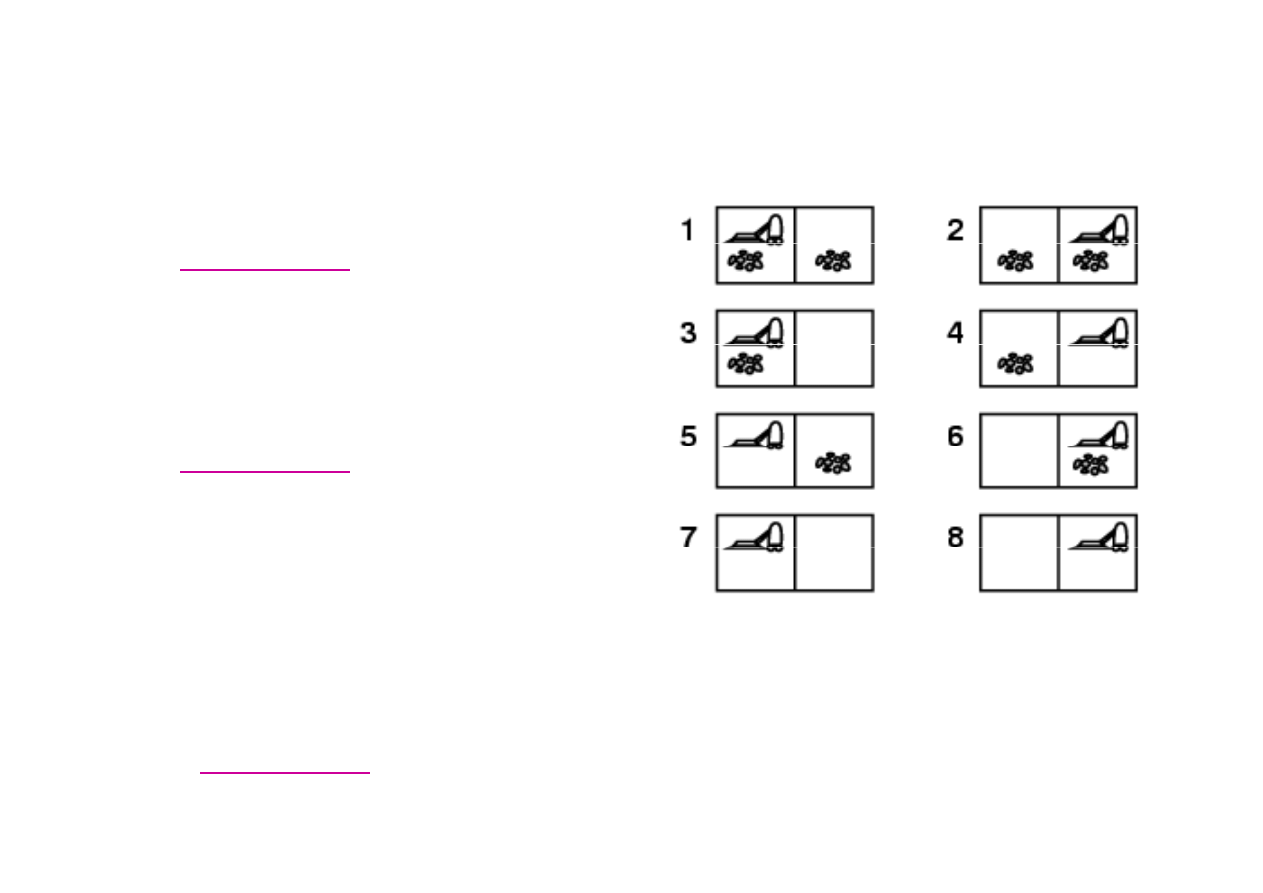
Przykład -

ś

wiat agenta-odkurzacza

•

Problem jednostanowy

, start

ze stanu {5}.

Rozwi

ą

zanie

Zbiór wszystkich stanów

Rozwi

ą

zanie

[ W PRAWO , ODKURZAJ ]

•

Bez czujników,

start z dowolnego

•

Bez czujników,

start z dowolnego

stanu spo

ś

ród {1,2,3,4,5,6,7,8}

W PRAWO {2,4,6,8}

Rozwi

ą

zanie

Rozwi

ą

zanie

[ W PRAWO , ODKURZAJ ,

W LEWO , ODKURZAJ ]

W LEWO , ODKURZAJ ]

•

Nieprzewidywalno

ść

– Niedeterministyczne: ODKURZAJ mo

ż

e za

ś

mieci

ć

czysty dywan

– Niedeterministyczne: ODKURZAJ mo

ż

e za

ś

mieci

ć

czysty dywan

– Cz

ęś

ciowa obserwowalno

ść

: poło

ż

enie,

ś

mieci w aktualnym poło

ż

eniu.

– Obserwacja: [L, CZYSTY], tj. start za stanów 5 lub 7.

Rozwi

ą

zanie

© F.A. Dul 2007

Rozwi

ą

zanie

[ W PRAWO , je

ż

eli

Ś

MIECI to ODKURZAJ ]

Zadanie jednostanowe - sformułowanie

3.3. Rodzaje zada

ń

•

stanu pocz

ą

tkowego

, np. "w Arad”,

Zadanie jednostanowe zdefiniowane jest za pomoc

ą

czterech

elementów:

•

stanu pocz

ą

tkowego

, np. "w Arad”,

•

działa

ń

lub funkcji nast

ę

pstwa

S(x) = zbiór par

〈

działanie , stan

〉

S(x) = zbiór par

〈

działanie , stan

〉

np. S(Arad) = {

〈〈〈〈

Arad

→

Zerind, Zerind

〉〉〉〉

, … }

•

testu osi

ą

gni

ę

cia celu

:

– jawny, np. x = ”w Bukareszcie”,
– niejawny, np.w szachach Mat(x);

•

kosztu drogi

(addytywnego)

•

kosztu drogi

(addytywnego)

– np. sumy odległo

ś

ci, liczby podj

ę

tych działa

ń

, etc.

– c(x,a,y) jest kosztem kroku, z zało

ż

enia c

≥

0

– c(x,a,y) jest kosztem kroku, z zało

ż

enia c

≥

0

Rozwi

ą

zaniem zadania jednostanowego jest ci

ą

g działa

ń

prowadz

ą

cych ze stanu pocz

ą

tkowego do stanu docelowego.

© F.A. Dul 2007

prowadz

ą

cych ze stanu pocz

ą

tkowego do stanu docelowego.

Rozwi

ą

zanie optymalne cechuje najmniejszy koszt.

Zadanie jednostanowe - sformułowanie

3.3. Rodzaje zada

ń

•

Ś

wiat rzeczywisty jest kra

ń

cowo skomplikowany, dlatego

przestrze

ń

stanów musi by

ć

abstrakcj

ą

stanów rzeczywistych.

Abstrakcja oznacza

pomini

ę

cie szczegółów

.

Abstrakcja oznacza

pomini

ę

cie szczegółów

.

• Stan abstrakcyjny = zbiór stanów rzeczywistych.
• Działanie abstrakcyjne = zło

ż

ona kombinacja działa

ń

• Działanie abstrakcyjne = zło

ż

ona kombinacja działa

ń

rzeczywistych,

np. "Arad

→

Zerind" reprezentuje zło

ż

ony zbiór mo

ż

liwych

np. "Arad

→

Zerind" reprezentuje zło

ż

ony zbiór mo

ż

liwych

tras, objazdy, parkingi, etc.

• Aby zapewni

ć

istnienie rozwi

ą

zania, ka

ż

dy stan rzeczywisty

(np. ”Arad“) musi prowadzi

ć

do jakiego

ś

stanu rzeczywistego

(np. ”Arad“) musi prowadzi

ć

do jakiego

ś

stanu rzeczywistego

(np. „Zerind”).

• Rozwi

ą

zanie abstrakcyjne = zbiór rzeczywistych dróg które

• Rozwi

ą

zanie abstrakcyjne = zbiór rzeczywistych dróg które

s

ą

rozwi

ą

zaniami w

ś

wiecie rzeczywistym.

• Kazde działanie abstrakcyjne powinno by

ć

łatwiejsze ni

ż

© F.A. Dul 2007

• Kazde działanie abstrakcyjne powinno by

ć

łatwiejsze ni

ż

rzeczywiste.

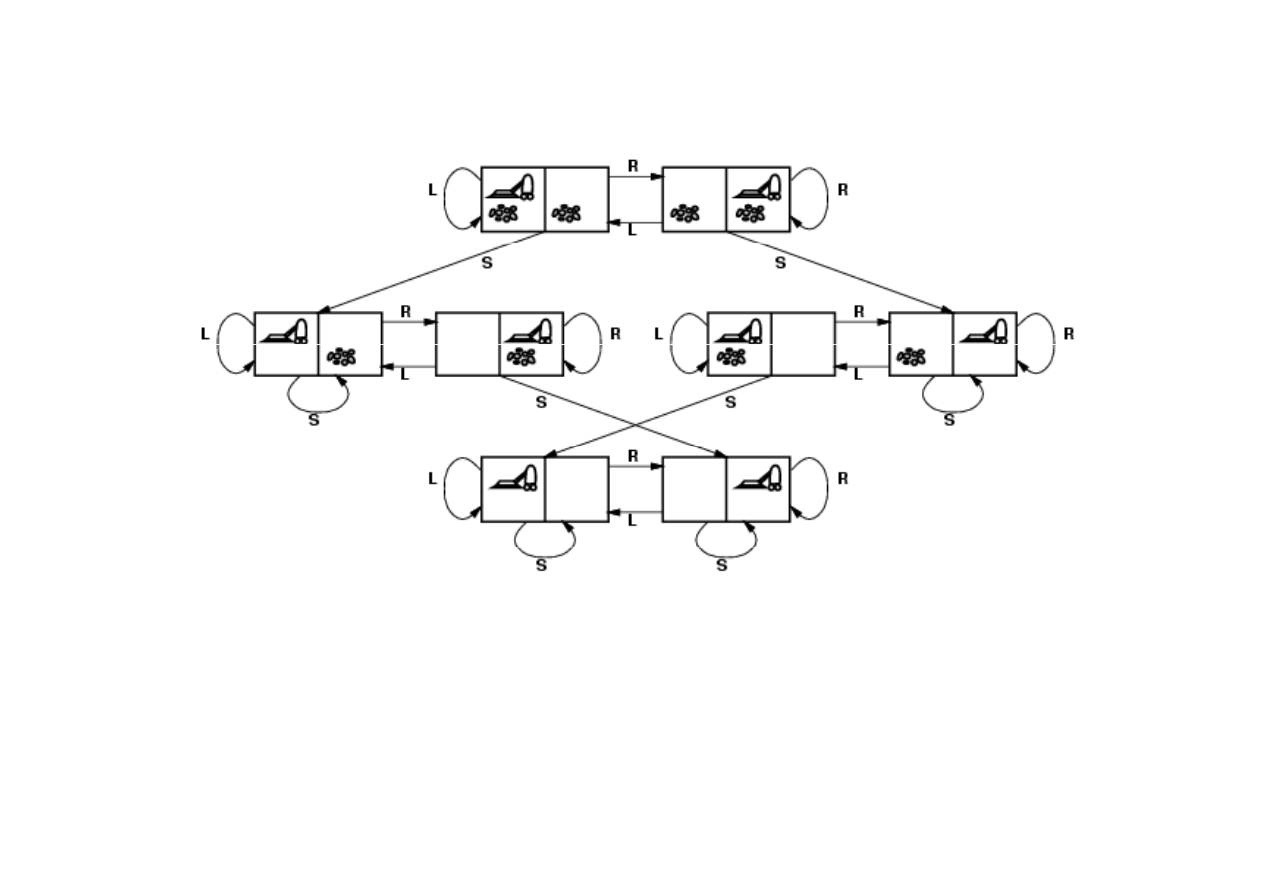
Graf przestrzeni stanów dla

ś

wiata odkurzacza

3.3. Rodzaje zada

ń

• stan:

poło

ż

enie odkurzacza oraz czysto

ść

;

• stan pocz

ą

tkowy: ka

ż

dy;

• stan pocz

ą

tkowy: ka

ż

dy;

• działania:

W LEWO, W PRAWO, ODKURZAJ;

• test celu:

czysto we wszystkich poło

ż

eniach;

© F.A. Dul 2007

• test celu:

czysto we wszystkich poło

ż

eniach;

• koszt:

1 za ka

ż

de działanie;

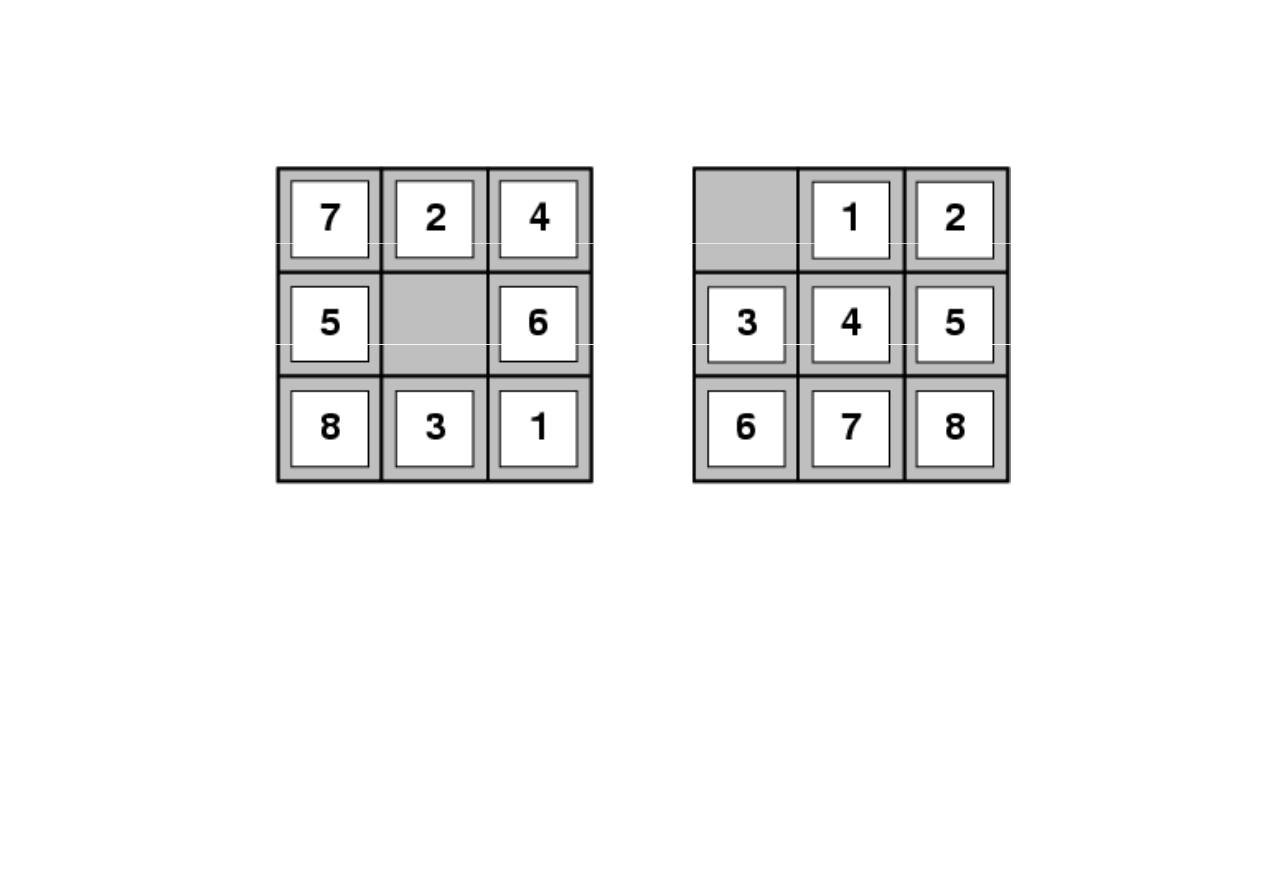
Przykład: gra w osiem puzzli

3.3. Rodzaje zada

ń

Stan pocz

ą

tkowy Stan docelowy

• stan:

poło

ż

enie puzzli 1 - 8;

• działania: ruch pola pustego: w lewo, w prawo,w gór

ę

,

w dół;

w dół;

• test celu:

osi

ą

gni

ę

cie zadanego układu puzzli;

• koszt:

1 za ka

ż

dy ruch;

© F.A. Dul 2007

• koszt:

1 za ka

ż

dy ruch;

Rozwi

ą

zanie optymalne problemu n puzzli jest zadaniem NP-hard

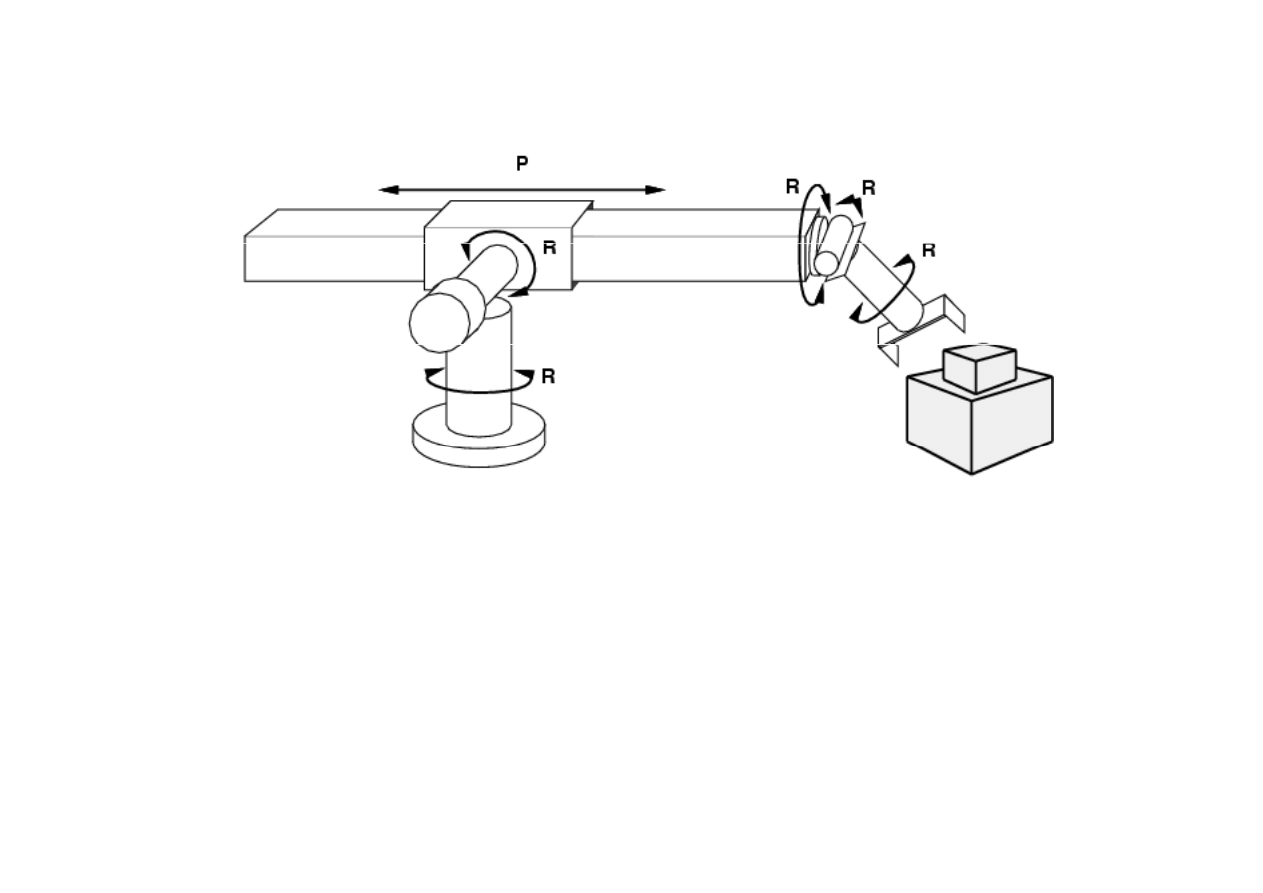
Przykład: monta

ż

przy u

ż

yciu robota

3.3. Rodzaje zada

ń

• stan:

wieloelementowa tablica poło

ż

enia

• stan:

wieloelementowa tablica poło

ż

enia

ramienia robota oraz poło

ż

enia

montowanych elementów;

• działania: ci

ą

gły ruch ramienia robota, chwytanie

• działania: ci

ą

gły ruch ramienia robota, chwytanie

i puszczanie elementów;

• test celu:

zmontowane urz

ą

dznie;

© F.A. Dul 2007

• test celu:

zmontowane urz

ą

dznie;

• koszt:

czas monta

ż

u urz

ą

dzenia;

Inne przykłady zada

ń

ze

ś

wiata rzeczywistego

3.3. Rodzaje zada

ń

• Wyznaczanie drogi: wyznaczanie trasy ł

ą

cz

ą

cej w

ę

zły:

pocz

ą

tkowy i ko

ń

cowy;

• Problem zwiedzania: wyznaczanie trasy przebiegaj

ą

cej

• Problem zwiedzania: wyznaczanie trasy przebiegaj

ą

cej

przez w

ę

zły (np. miasta) tylko jeden raz;

• Problem komiwoja

ż

era: wyznaczenie najkrótszej trasy

• Problem komiwoja

ż

era: wyznaczenie najkrótszej trasy

przebiegaj

ą

cej przez w

ę

zły tylko jeden raz;

• Planowanie obwodów VLSI: rozmieszczanie elementów

układu i wyznaczanie poł

ą

cze

ń

mi

ę

dzy nimi;

układu i wyznaczanie poł

ą

cze

ń

mi

ę

dzy nimi;

• Nawigacja robotów: ci

ą

gła wersja problemu wyznaczania

drogi;

drogi;

• Planowanie automatycznego monta

ż

u: wyznaczenie

wła

ś

ciwej kolejno

ś

ci monta

ż

u elementów;

• Synteza protein: wyznaczenie wła

ś

ciwej kolejno

ś

ci

aminokwasów białka o okre

ś

lonych własno

ś

ciach;

• Poszukiwania w Internecie: wyznaczenie trasy

© F.A. Dul 2007

• Poszukiwania w Internecie: wyznaczenie trasy

poszukiwa

ń

żą

danych informacji na stronach Internetu;

3.3. Rodzaje zada

ń

Podstawow

ą

zasad

ą

poszukiwa

ń

nieinformowanych jest korzystanie

nieinformowanych jest korzystanie
wył

ą

cznie z definicji zadania - bez

wykorzystywania dodatkowych

wykorzystywania dodatkowych
informacji.

Przypomina to prób

ę

dojechania

w mie

ś

cie samochodem na podany

w mie

ś

cie samochodem na podany

adres gdy zna si

ę

tylko ten adres oraz

adres gdy zna si

ę

tylko ten adres oraz

reguły prowadzenia samochodu.

© F.A. Dul 2007

3.4. Algorytmy przeszukiwania drzew

Idea algorytmów przeszukuj

ą

cych

Idea algorytmów przeszukuj

ą

cych

•

ś

lepe poszukiwania: analiza wszystkich mo

ż

liwych

sekwencji stanów;

sekwencji stanów;

– koszt ro

ś

nie gwałtownie ze wzrostem liczby mo

ż

liwych

stanów;

• poszukiwania poprzez budow

ę

drzewa stanów:

• poszukiwania poprzez budow

ę

drzewa stanów:

– KORZE

Ń

- stan pocz

ą

tkowy;

– w

ę

zły i gał

ę

zie generowane funkcj

ą

nast

ę

pstwa;

function TREE-SEARCH(problem,strategy) returns a solution or failure

Ogólnie: przeszukiwanie generuje graf.

function TREE-SEARCH(problem,strategy) returns a solution or failure

initialize the search tree using the initial state of problem
do

if there are no candidates to expand then return failure

if there are no candidates to expand then return failure
choose a legal node for expansion according to strategy
if the node contains a goal state then return corresponding solution

else expand the node and add the resulting nodes to the search tree

© F.A. Dul 2007

else expand the node and add the resulting nodes to the search tree

od

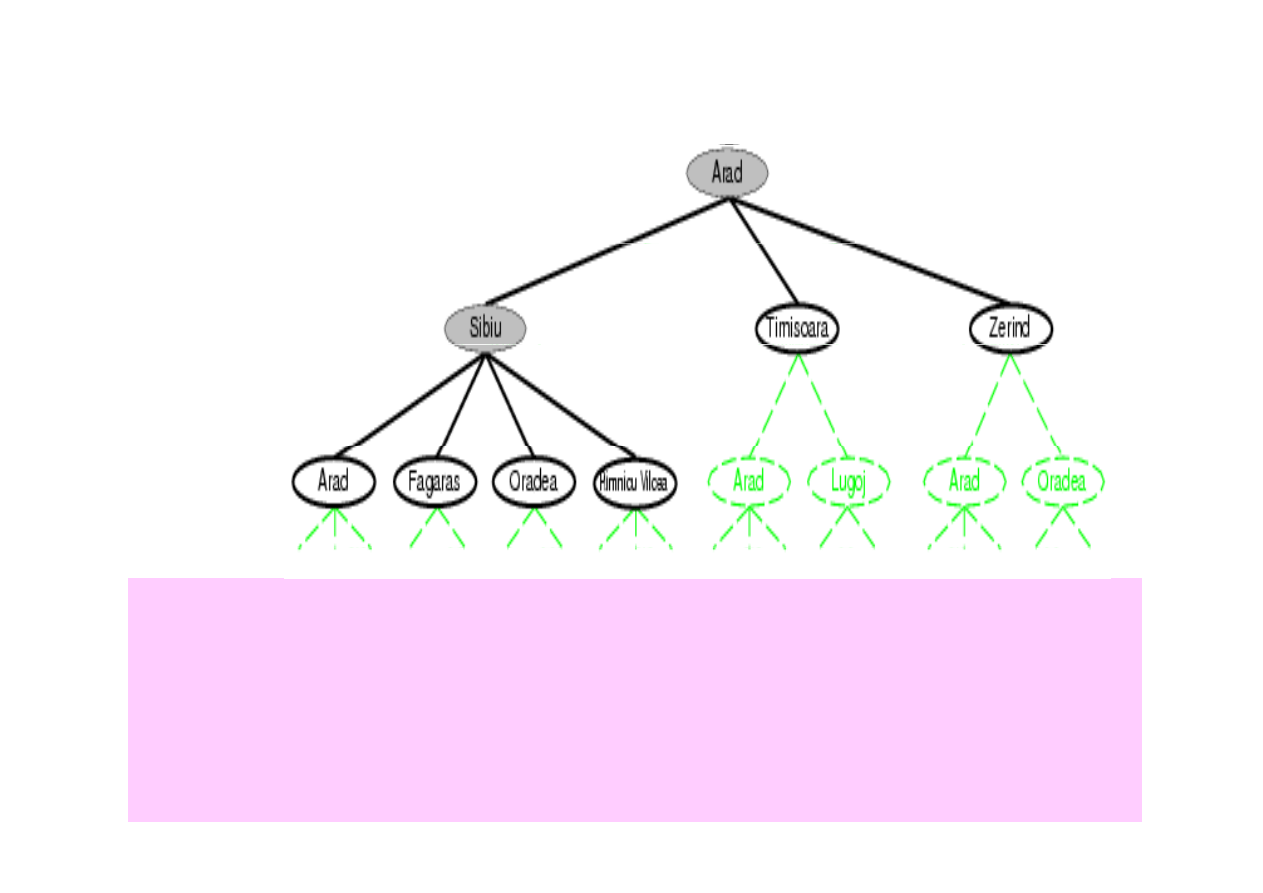
Algorytmy przeszukiwania drzewa - przykład

3.4. Algorytmy przeszukiwania drzew

Stan pocz

ą

tkowy

Poziom 1.

Poziom 2.

function TREE-SEARCH(problem,strategy) returns a solution or failure

initialize the search tree using the initial state of problem
do

function TREE-SEARCH(problem,strategy) returns a solution or failure

initialize the search tree using the initial state of problem

do

function TREE-SEARCH(problem,strategy) returns a solution or failure

initialize the search tree using the initial state of problem
do

do

if there are no candidates to expand then return failure
choose a leaf node for expansion according to strategy
if the node contains a goal state then return corresponding solution

do

if there are no candidates to expand then return failure
choose a leaf node for expansion according to strategy
if the node contains a goal state then return corresponding solution

do

if there are no candidates to expand then return failure

choose a leaf node for expansion according to strategy

if the node contains a goal state then return corresponding solution

if the node contains a goal state then return corresponding solution

else expand the node and add the resulting nodes to the search tree

od

© F.A. Dul 2007

if the node contains a goal state then return corresponding solution

else expand the node and add the resulting nodes to the search tree

od

if the node contains a goal state then return corresponding solution

else expand the node and add the resulting nodes to the search tree

od

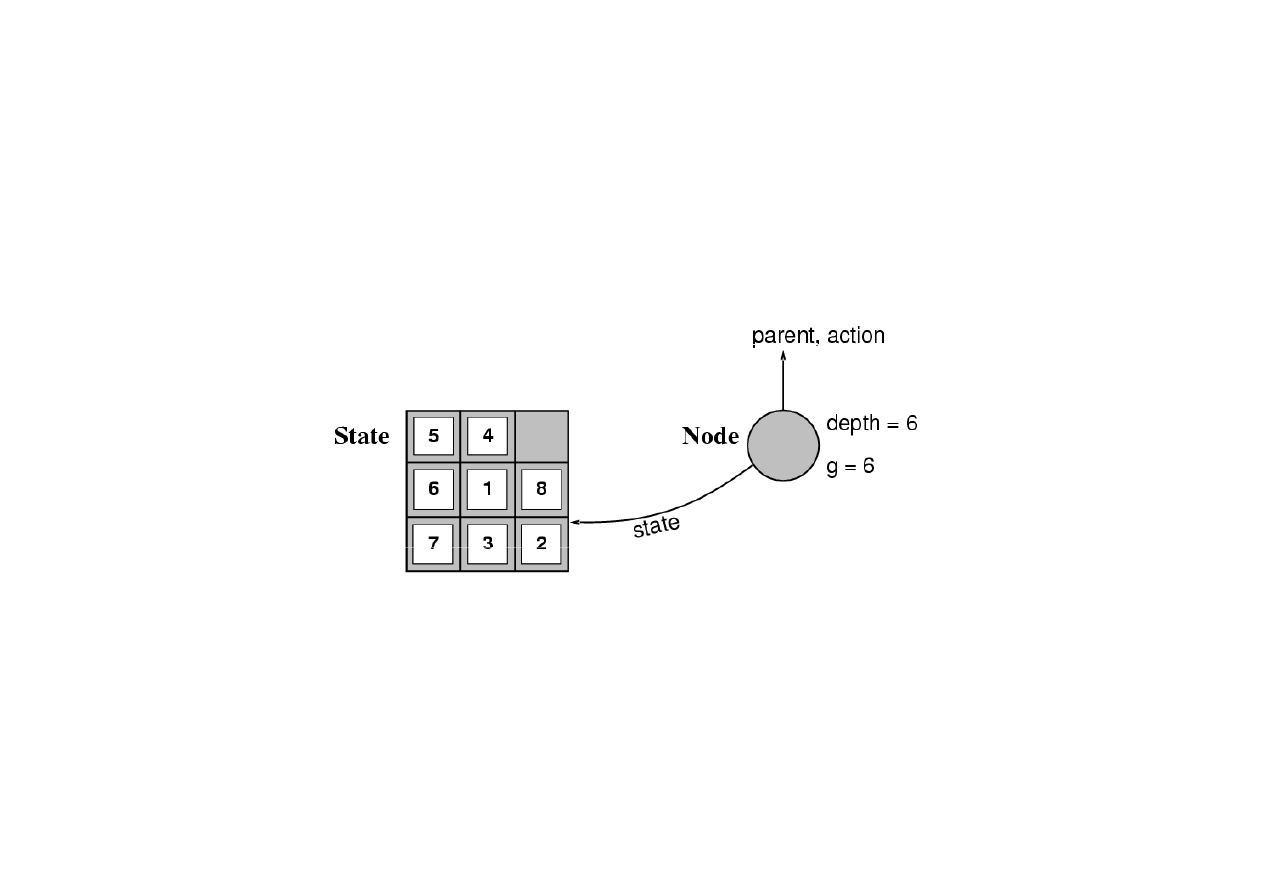
Ró

ż

nica pomi

ę

dzy stanem a w

ę

złem

3.4. Algorytmy przeszukiwania drzew

• Stan okre

ś

la konfiguracj

ę

fizyczn

ą

obiektu lub zadania;

• Stan okre

ś

la konfiguracj

ę

fizyczn

ą

obiektu lub zadania;

• W

ę

zeł jest to struktura danych okre

ś

laj

ą

ca cz

ęść

drzewa poszukiwa

ń

, obejmuj

ą

ca np.: stan, w

ę

zeł

drzewa poszukiwa

ń

, obejmuj

ą

ca np.: stan, w

ę

zeł

rodzica, w

ę

zły dzieci, koszt gał

ę

zi, aktualn

ą

gł

ę

boko

ść

,

podejmowane działanie, itp.;

w

ę

zeł =

〈〈〈〈

stan, w

ę

zeł rodzica, koszt, gł

ę

boko

ść

, działanie

〉〉〉〉

• Funkcja

Expand

tworzy nowe w

ę

zeł, wypełnia odpowiednie

• Funkcja

Expand

tworzy nowe w

ę

zeł, wypełnia odpowiednie

pola, a nast

ę

pnie przy pomocy funkcji

SuccessorFn

tworzy stan w nowym w

ęź

le.

© F.A. Dul 2007

• Brzeg (fringe) to zbiór wszystkich w

ę

złow, które nie zotały

jeszcze rozwini

ę

te.

Strategie algorytmów przeszukiwania drzew

3.4. Algorytmy przeszukiwania drzew

• Strategia poszukiwania jest okre

ś

lona

kolejno

ś

ci

ą

rozwijania w

ę

złów.

• Strategie s

ą

oceniane wg. nast

ę

puj

ą

cych kryterów:

– zupełno

ść

: mo

ż

liwo

ść

znalezienia rozwi

ą

zania, je

ż

eli

istnieje;

istnieje;

– zło

ż

ono

ść

czasowa

: liczba generowanych w

ę

złów;

– zło

ż

ono

ść

pami

ę

ciowa

: najwi

ę

ksza liczba w

ę

złów

w pami

ę

ci;

– zło

ż

ono

ść

pami

ę

ciowa

: najwi

ę

ksza liczba w

ę

złów

w pami

ę

ci;

– optymalno

ść

: mo

ż

liwo

ść

wyznaczenia najta

ń

szego

rozwi

ą

zania.

rozwi

ą

zania.

• Zło

ż

ono

ść

czasowa i pami

ę

ciowa s

ą

szacowane za pomoc

ą

nast

ę

puj

ą

cych wielko

ś

ci:

– b: maksymalny współczynnik rozgał

ę

zienia drzewa

poszukiwa

ń

,

– d: gł

ę

boko

ść

rozwi

ą

zania optymalnego,

© F.A. Dul 2007

– d: gł

ę

boko

ść

rozwi

ą

zania optymalnego,

– m: maksymalna gł

ę

boko

ść

przestrzeni stanów.

Strategie nieinformowane przeszukiwania drzew

3.4. Algorytmy przeszukiwania drzew

Strategie

nieinformowane

wykorzystuj

ą

tylko informacje

zawarte w definicji zadania.

Rodzaje strategii nieinformowanych:

Strategie nieinformowane - poszukiwania “na o

ś

lep”.

• Poszukiwanie wszerz (breadth-first search),

• Poszukiwanie w gł

ą

b (depth-first search),

• Poszukiwanie w gł

ą

b (depth-first search),

• Poszukiwanie z jednostajnym kosztem

(uniform-cost search),

• Poszukiwanie na ograniczon

ą

gł

ę

boko

ść

(depth-limited search),

• Poszukiwanie pogł

ę

biane iteracyjnie

(iterative deepening search).

• Poszukiwanie dwukierunkowe (bidrectional search).

© F.A. Dul 2007

• Poszukiwanie dwukierunkowe (bidrectional search).

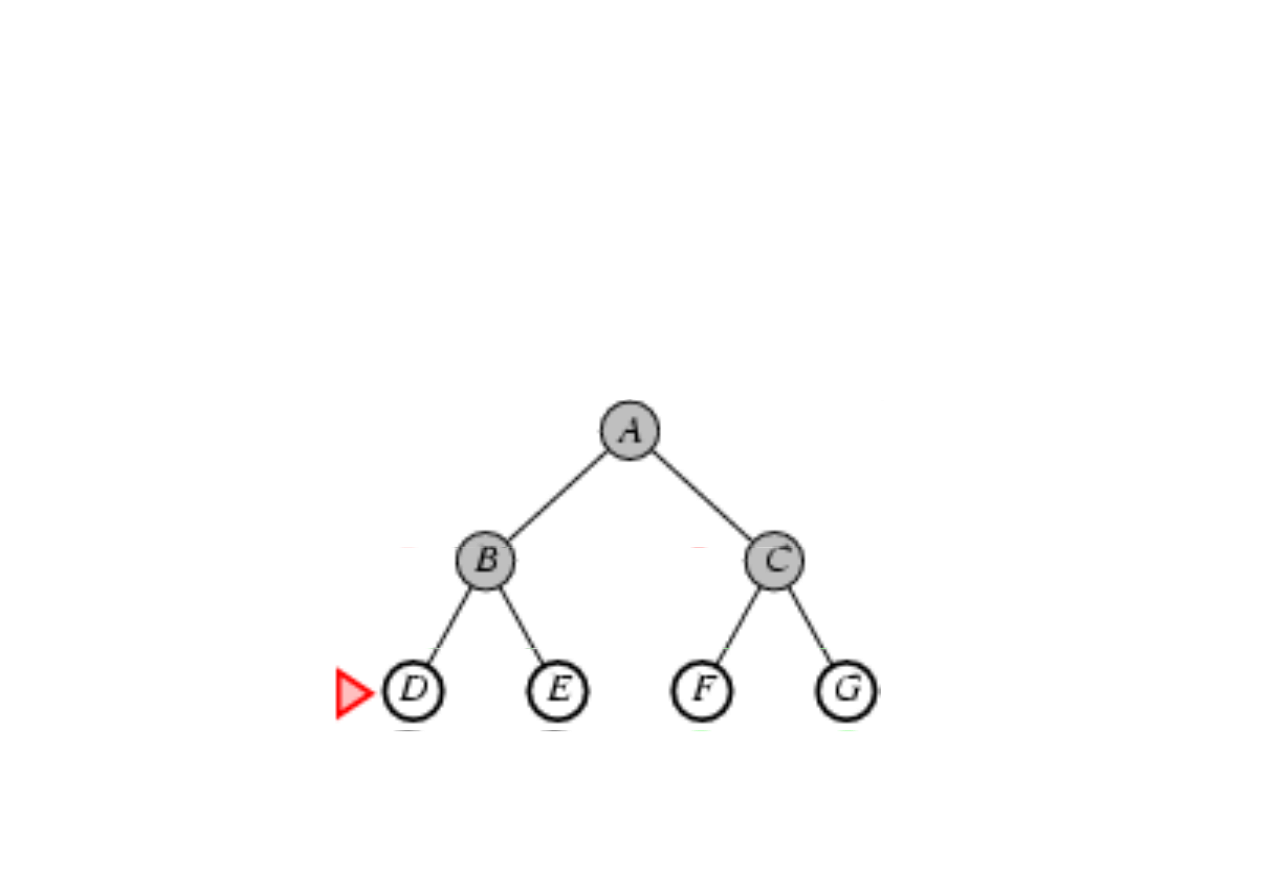
Poszukiwanie wszerz (breadth-first search)

3.4. Algorytmy przeszukiwania drzew

Zasada: rozwin

ąć

najpłytszy nierozwini

ę

ty w

ę

zeł (najpłytszy

na brzegu).

Brzeg jest kolejk

ą

FIFO, tzn. nowy w

ę

zeł wstawiany jest na

koniec kolejki.

© F.A. Dul 2007

Poszukiwanie wszerz (breadth-first search)

3.4. Algorytmy przeszukiwania drzew

Własno

ś

ci algorytmu

• Zupełno

ść

Tak, je

ż

eli b jest ograniczone

• Zupełno

ść

Tak, je

ż

eli b jest ograniczone

• Czas

1+b+b

2

+b

3

+… +b

d

+ b(b

d

-1) = O(b

d+1

)

• Pami

ęć

O(b

d+1

) (przechowywanie wszystkich

w

ę

złów w pami

ę

ci)

w

ę

złów w pami

ę

ci)

• Optymalno

ść

Tak, je

ż

eli koszt kroku jest stały

• Pami

ęć

jest najwi

ę

kszym problemem, wi

ę

kszym ni

ż

czas

poszukiwa

ń

.

poszukiwa

ń

.

© F.A. Dul 2007

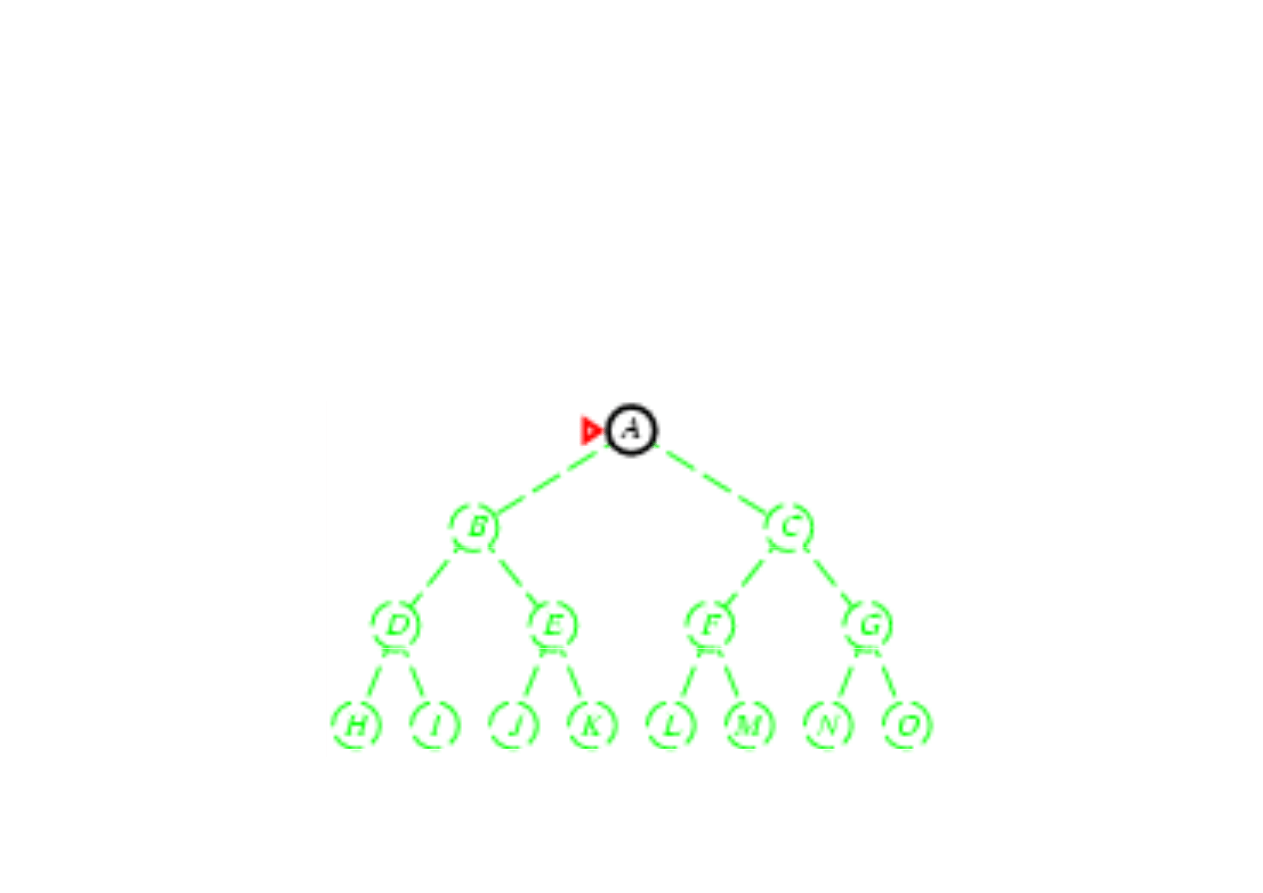
Poszukiwanie w gł

ą

b (depth-first search)

3.4. Algorytmy przeszukiwania drzew

Zasada: rozwin

ąć

najgł

ę

bszy nierozwini

ę

ty w

ę

zeł

(najgł

ę

bszy na brzegu).

Brzeg jest kolejk

ą

LIFO, tzn. nowy w

ę

zeł wstawiany jest na

pocz

ą

tek kolejki.

© F.A. Dul 2007

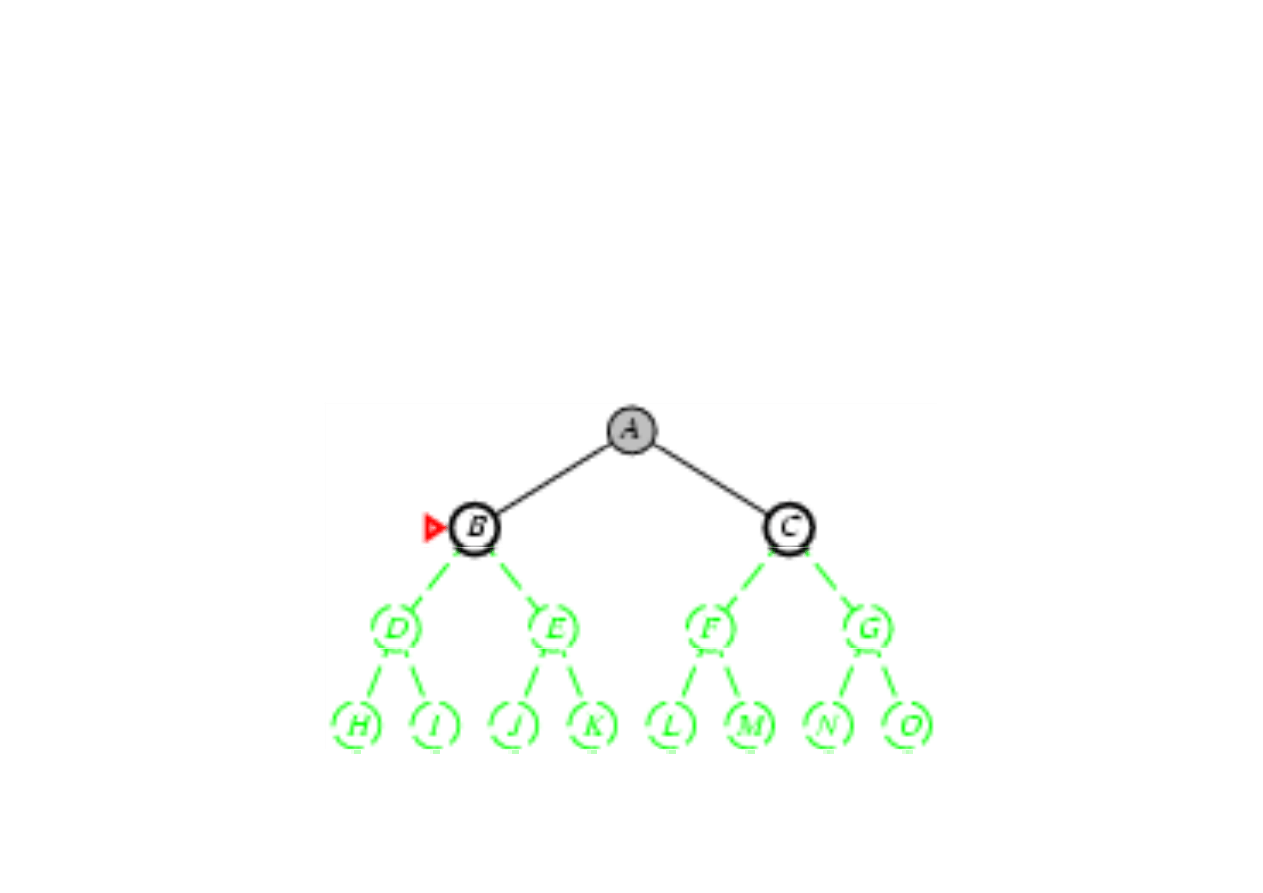
Poszukiwanie w gł

ą

b (depth-first search)

3.4. Algorytmy przeszukiwania drzew

Zasada: rozwin

ąć

najgł

ę

bszy nierozwini

ę

ty w

ę

zeł

(najgł

ę

bszy na brzegu).

Brzeg jest kolejk

ą

LIFO, tzn. nowy w

ę

zeł wstawiany jest na

pocz

ą

tek kolejki.

© F.A. Dul 2007

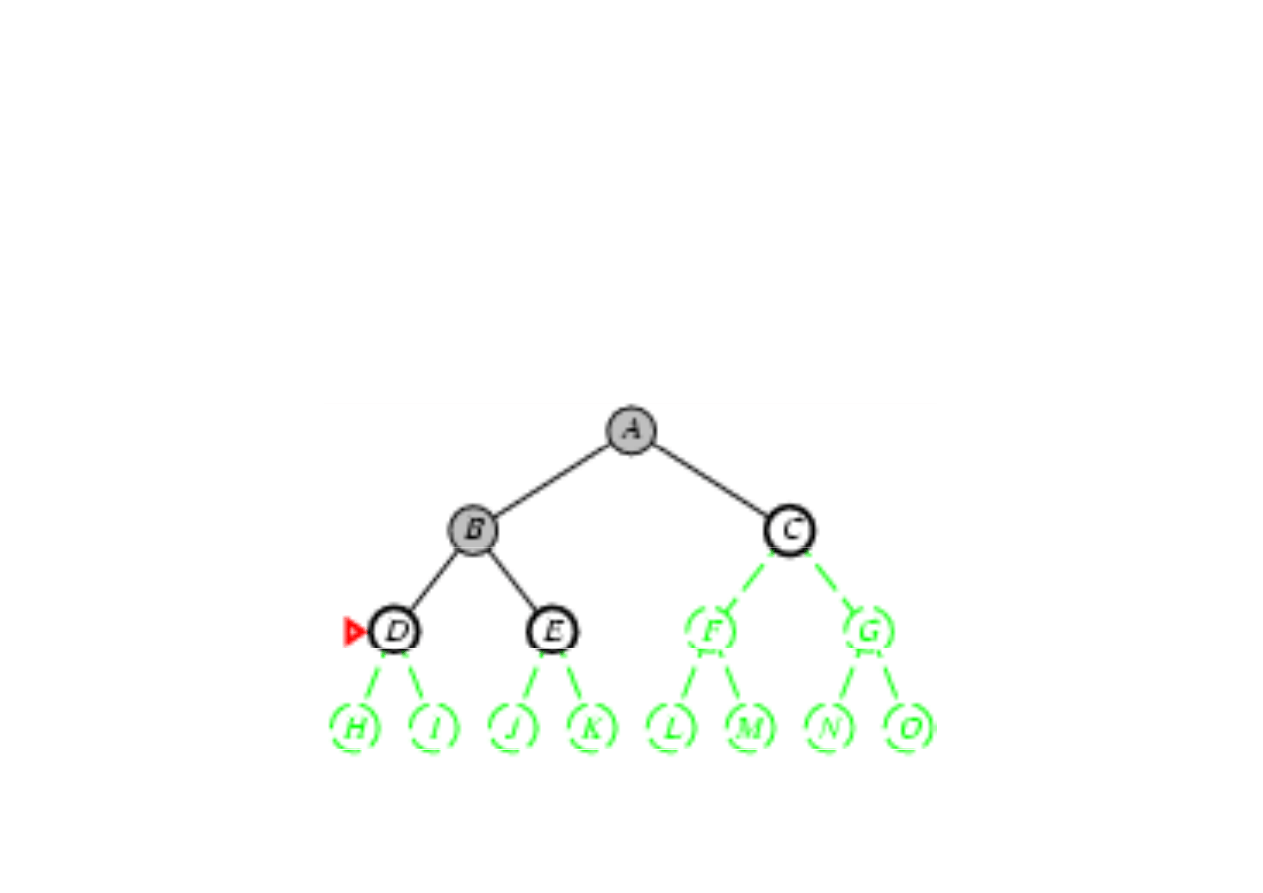
Poszukiwanie w gł

ą

b (depth-first search)

3.4. Algorytmy przeszukiwania drzew

Zasada: rozwin

ąć

najgł

ę

bszy nierozwini

ę

ty w

ę

zeł

(najgł

ę

bszy na brzegu).

Brzeg jest kolejk

ą

LIFO, tzn. nowy w

ę

zeł wstawiany jest na

pocz

ą

tek kolejki.

© F.A. Dul 2007

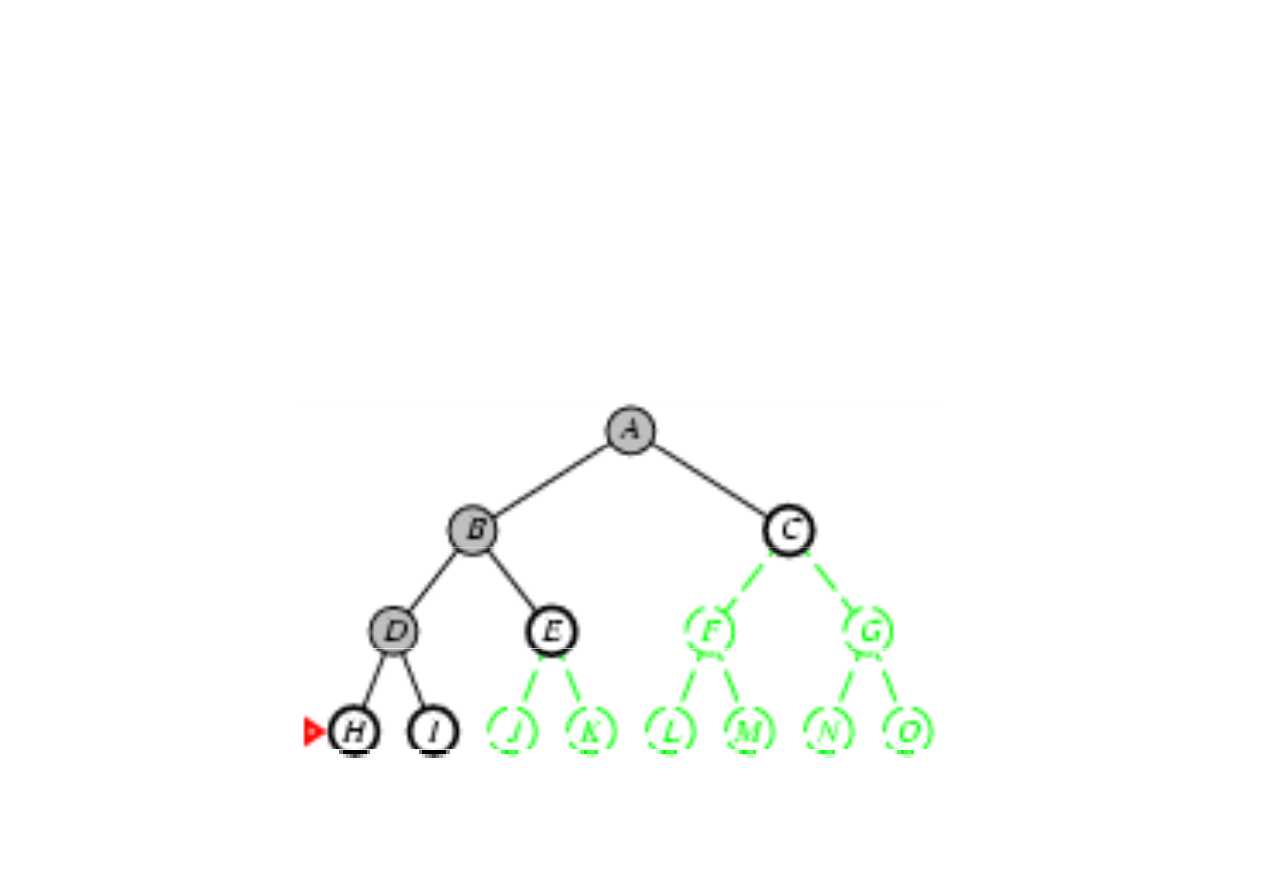
Poszukiwanie w gł

ą

b (depth-first search)

3.4. Algorytmy przeszukiwania drzew

Zasada: rozwin

ąć

najgł

ę

bszy nierozwini

ę

ty w

ę

zeł

(najgł

ę

bszy na brzegu).

Brzeg jest kolejk

ą

LIFO, tzn. nowy w

ę

zeł wstawiany jest na

pocz

ą

tek kolejki.

© F.A. Dul 2007

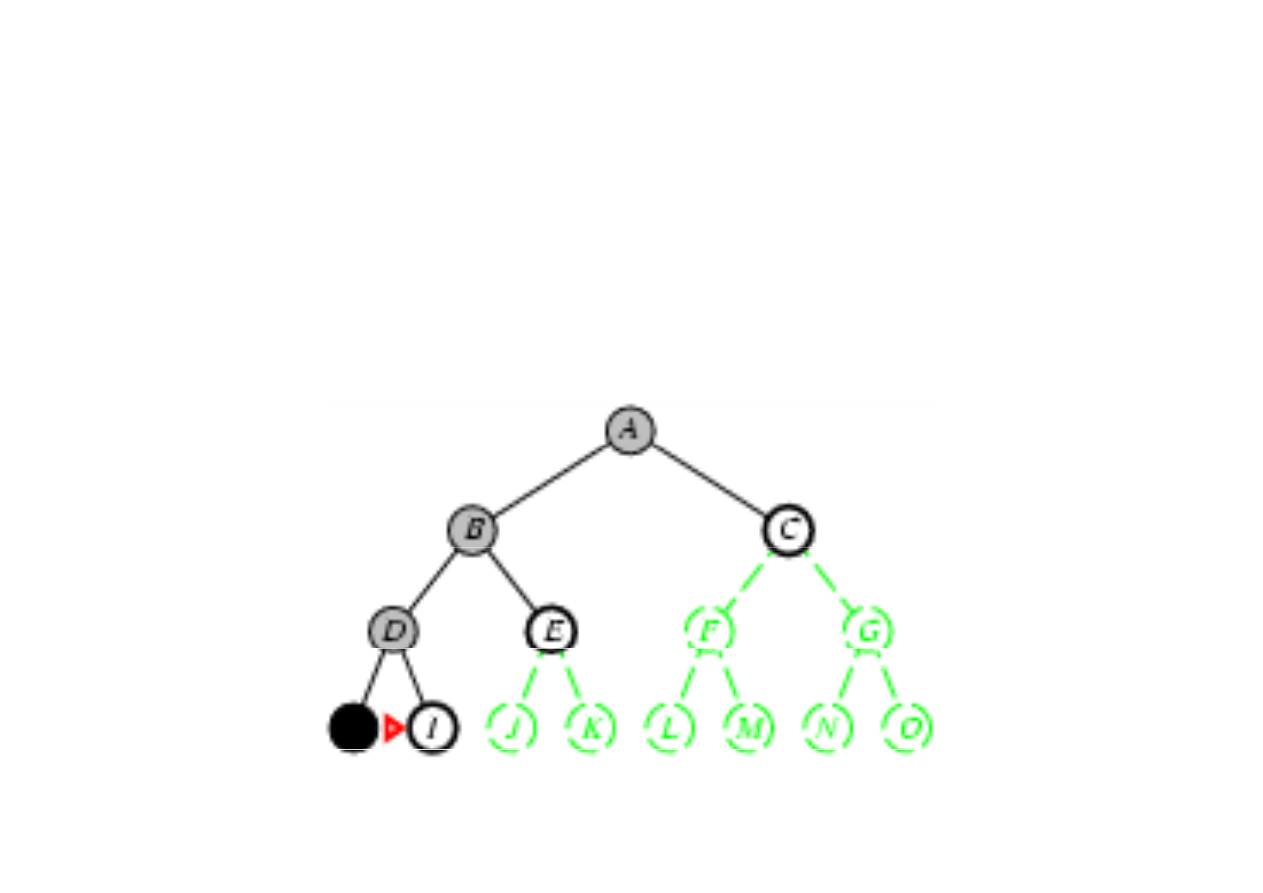
Poszukiwanie w gł

ą

b (depth-first search)

3.4. Algorytmy przeszukiwania drzew

Zasada: rozwin

ąć

najgł

ę

bszy nierozwini

ę

ty w

ę

zeł

(najgł

ę

bszy na brzegu).

Brzeg jest kolejk

ą

LIFO, tzn. nowy w

ę

zeł wstawiany jest na

pocz

ą

tek kolejki.

© F.A. Dul 2007

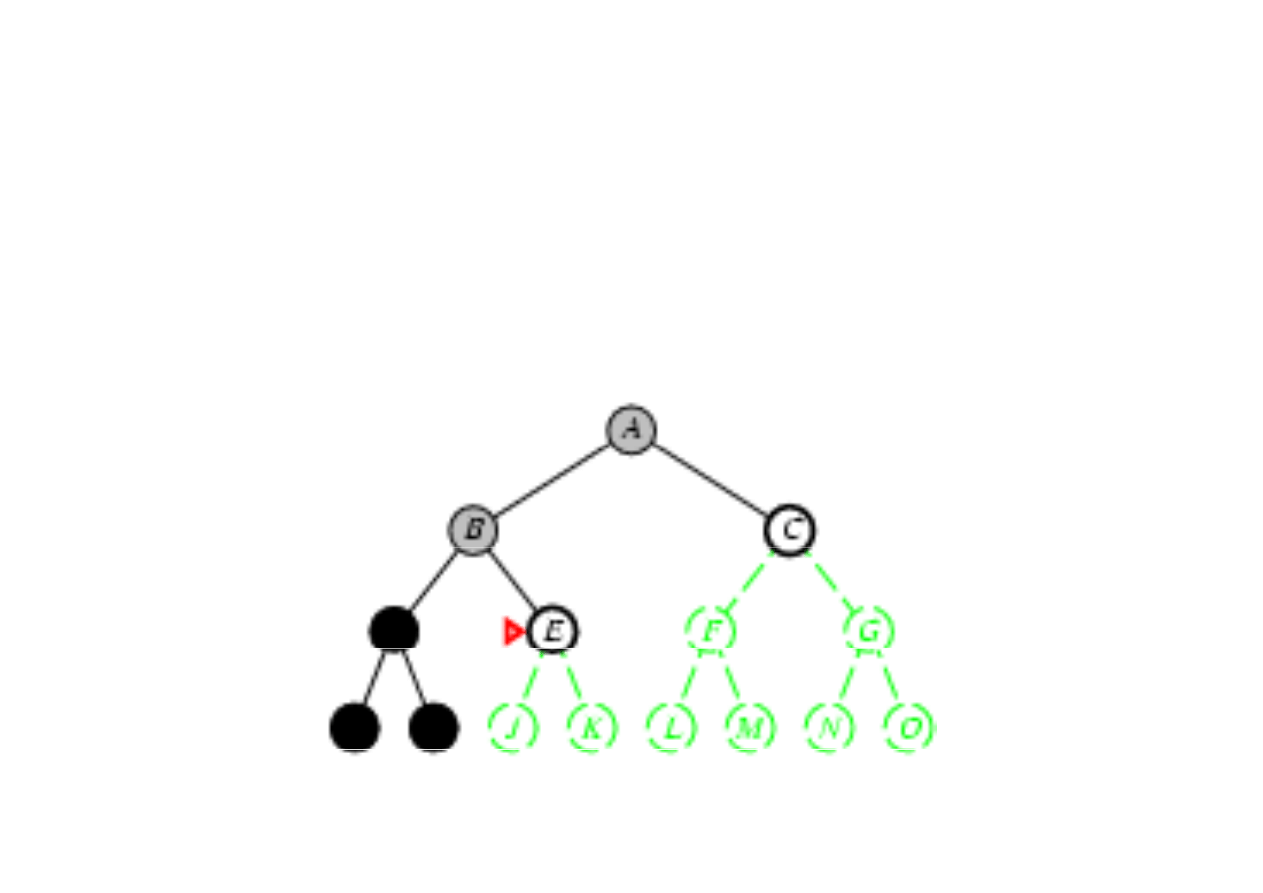
Poszukiwanie w gł

ą

b (depth-first search)

3.4. Algorytmy przeszukiwania drzew

Zasada: rozwin

ąć

najgł

ę

bszy nierozwini

ę

ty w

ę

zeł

(najgł

ę

bszy na brzegu).

Brzeg jest kolejk

ą

LIFO, tzn. nowy w

ę

zeł wstawiany jest na

pocz

ą

tek kolejki.

© F.A. Dul 2007

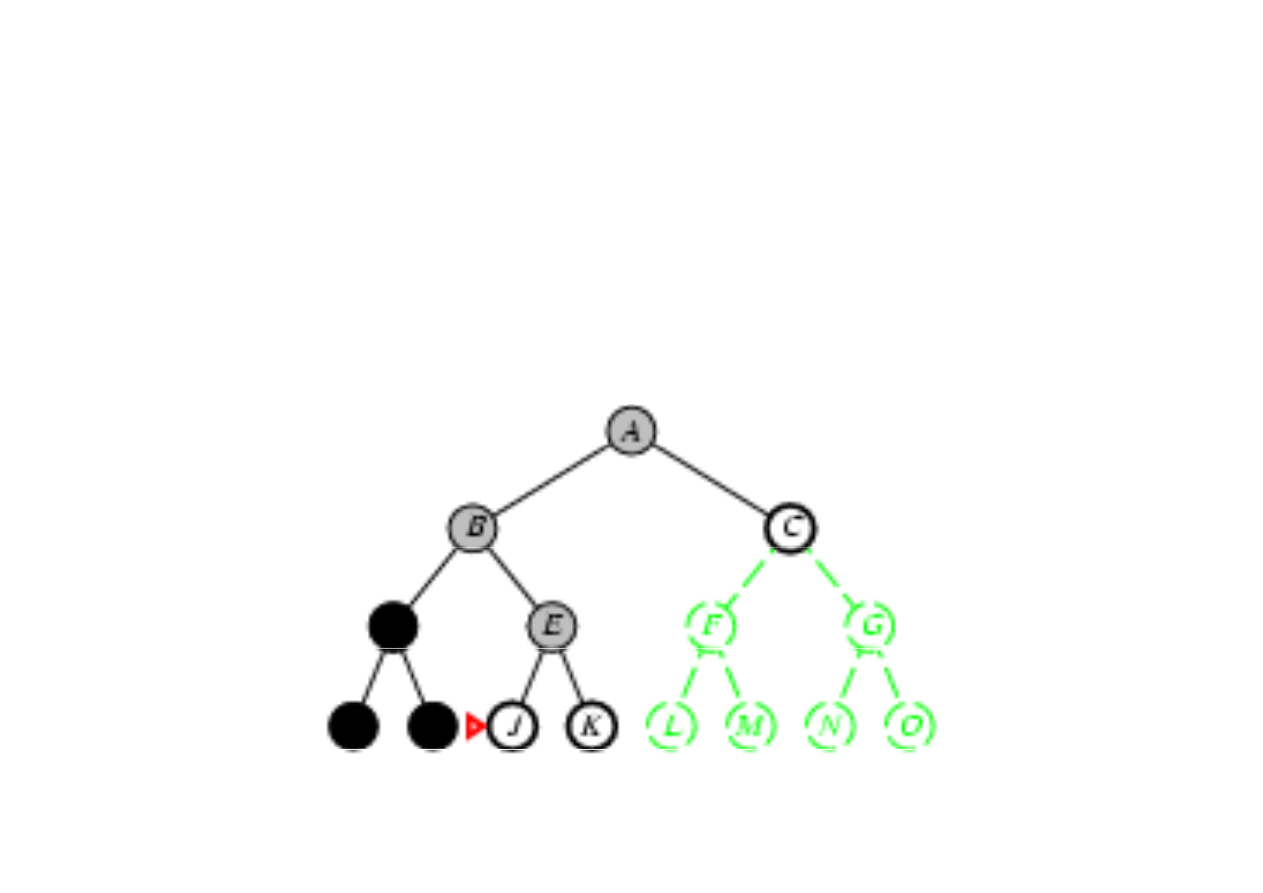
Poszukiwanie w gł

ą

b (depth-first search)

3.4. Algorytmy przeszukiwania drzew

Zasada: rozwin

ąć

najgł

ę

bszy nierozwini

ę

ty w

ę

zeł

(najgł

ę

bszy na brzegu).

Brzeg jest kolejk

ą

LIFO, tzn. nowy w

ę

zeł wstawiany jest na

pocz

ą

tek kolejki.

© F.A. Dul 2007

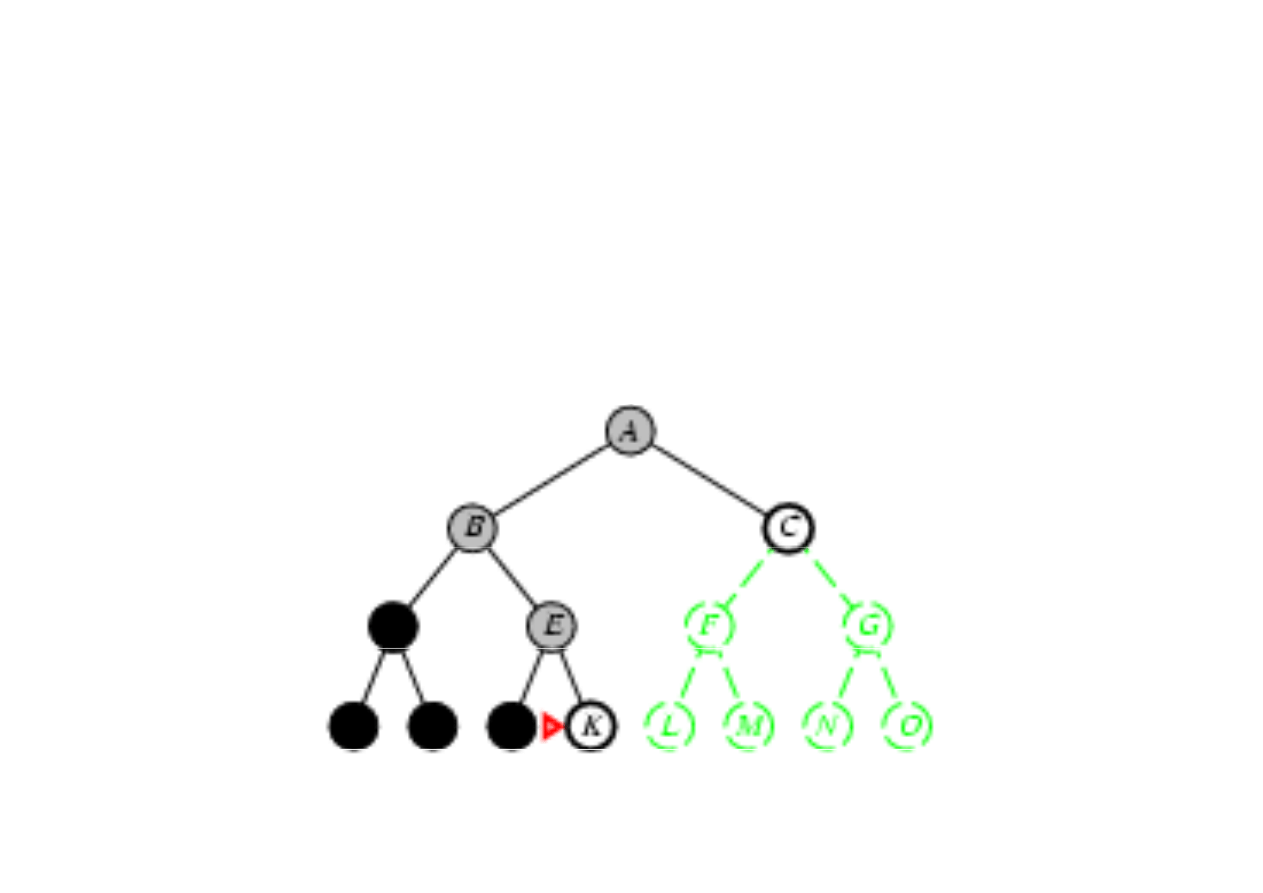
Poszukiwanie w gł

ą

b (depth-first search)

3.4. Algorytmy przeszukiwania drzew

Zasada: rozwin

ąć

najgł

ę

bszy nierozwini

ę

ty w

ę

zeł

(najgł

ę

bszy na brzegu).

Brzeg jest kolejk

ą

LIFO, tzn. nowy w

ę

zeł wstawiany jest na

pocz

ą

tek kolejki.

© F.A. Dul 2007

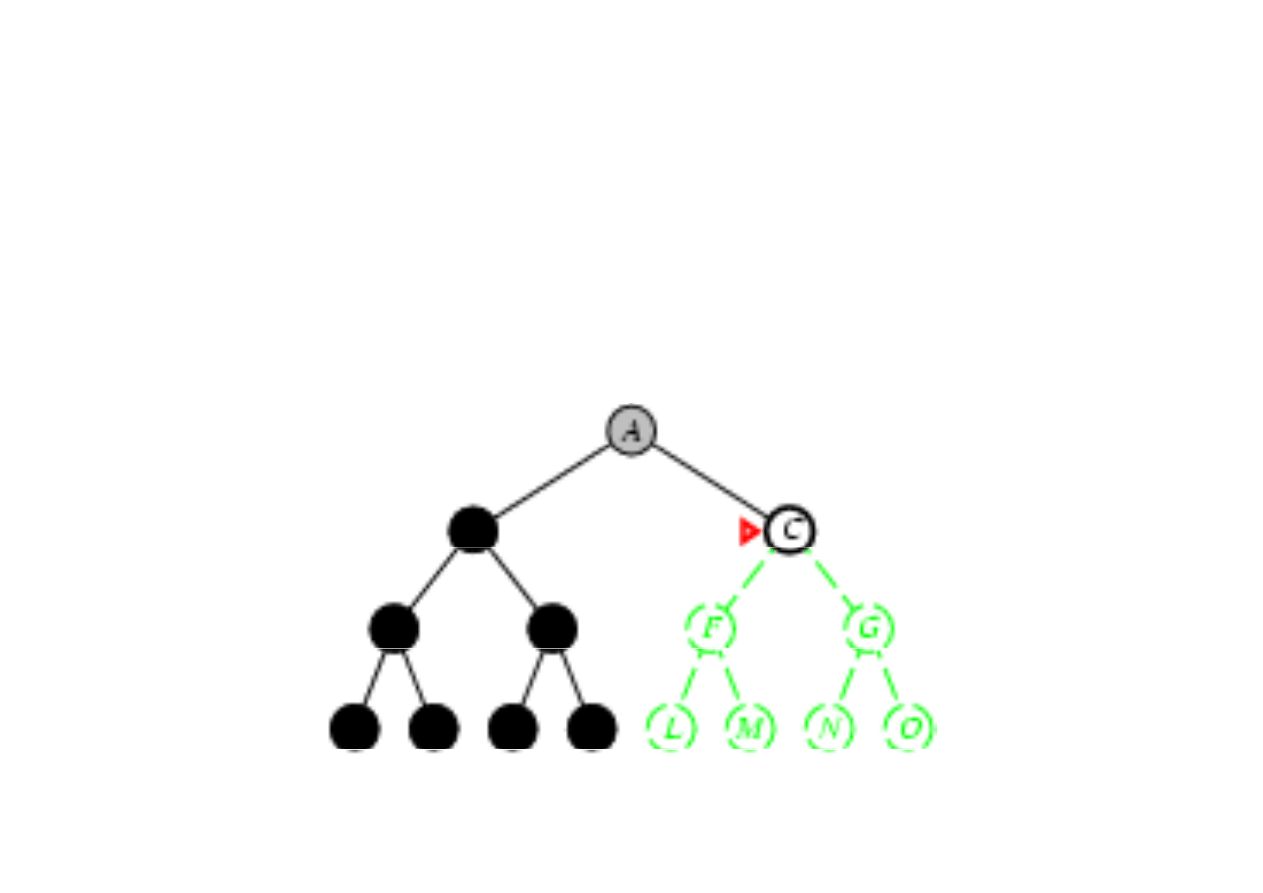
Poszukiwanie w gł

ą

b (depth-first search)

3.4. Algorytmy przeszukiwania drzew

Zasada: rozwin

ąć

najgł

ę

bszy nierozwini

ę

ty w

ę

zeł

(najgł

ę

bszy na brzegu).

Brzeg jest kolejk

ą

LIFO, tzn. nowy w

ę

zeł wstawiany jest na

pocz

ą

tek kolejki.

© F.A. Dul 2007

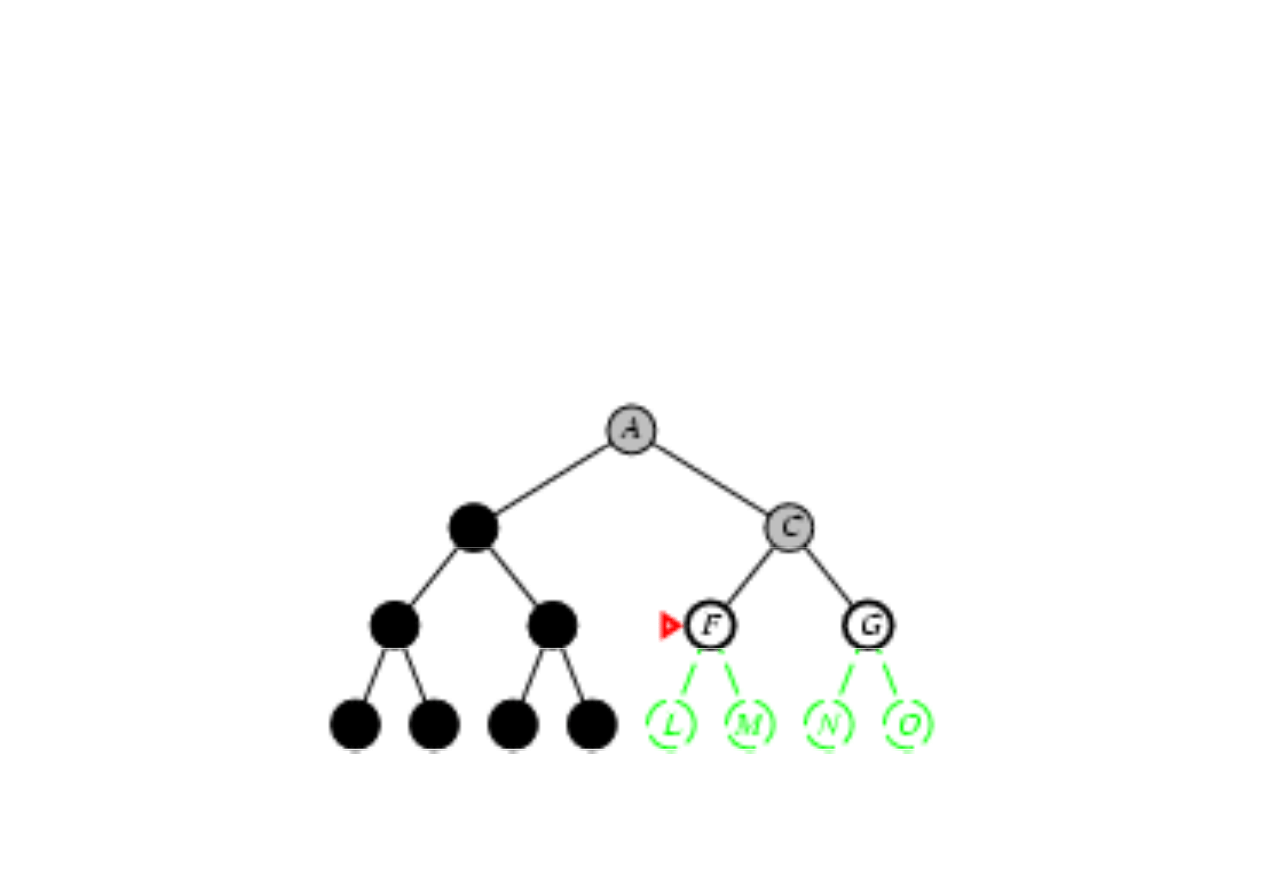
Poszukiwanie w gł

ą

b (depth-first search)

3.4. Algorytmy przeszukiwania drzew

Zasada: rozwin

ąć

najgł

ę

bszy nierozwini

ę

ty w

ę

zeł

(najgł

ę

bszy na brzegu).

Brzeg jest kolejk

ą

LIFO, tzn. nowy w

ę

zeł wstawiany jest na

pocz

ą

tek kolejki.

© F.A. Dul 2007

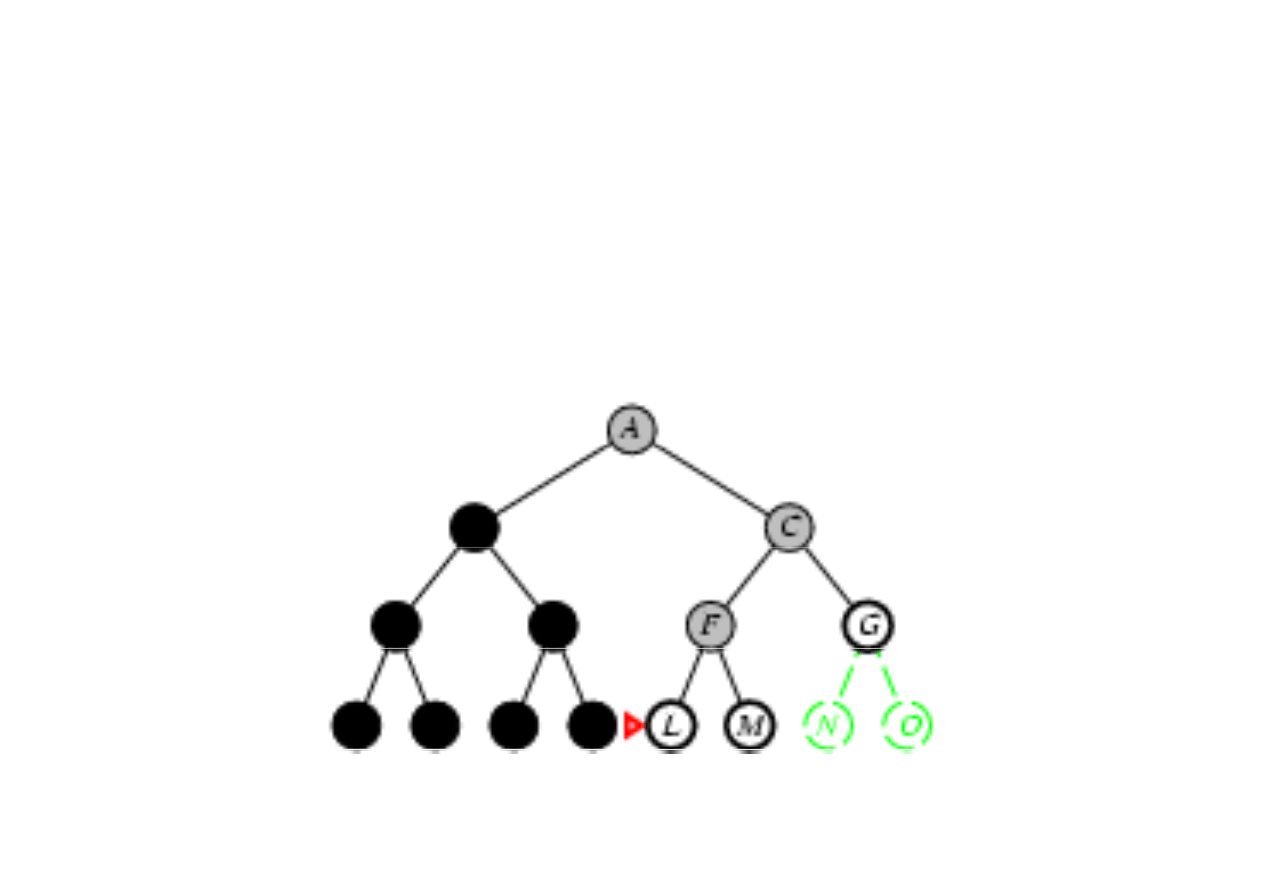
Poszukiwanie w gł

ą

b (depth-first search)

3.4. Algorytmy przeszukiwania drzew

Zasada: rozwin

ąć

najgł

ę

bszy nierozwini

ę

ty w

ę

zeł

(najgł

ę

bszy na brzegu).

Brzeg jest kolejk

ą

LIFO, tzn. nowy w

ę

zeł wstawiany jest na

pocz

ą

tek kolejki.

© F.A. Dul 2007

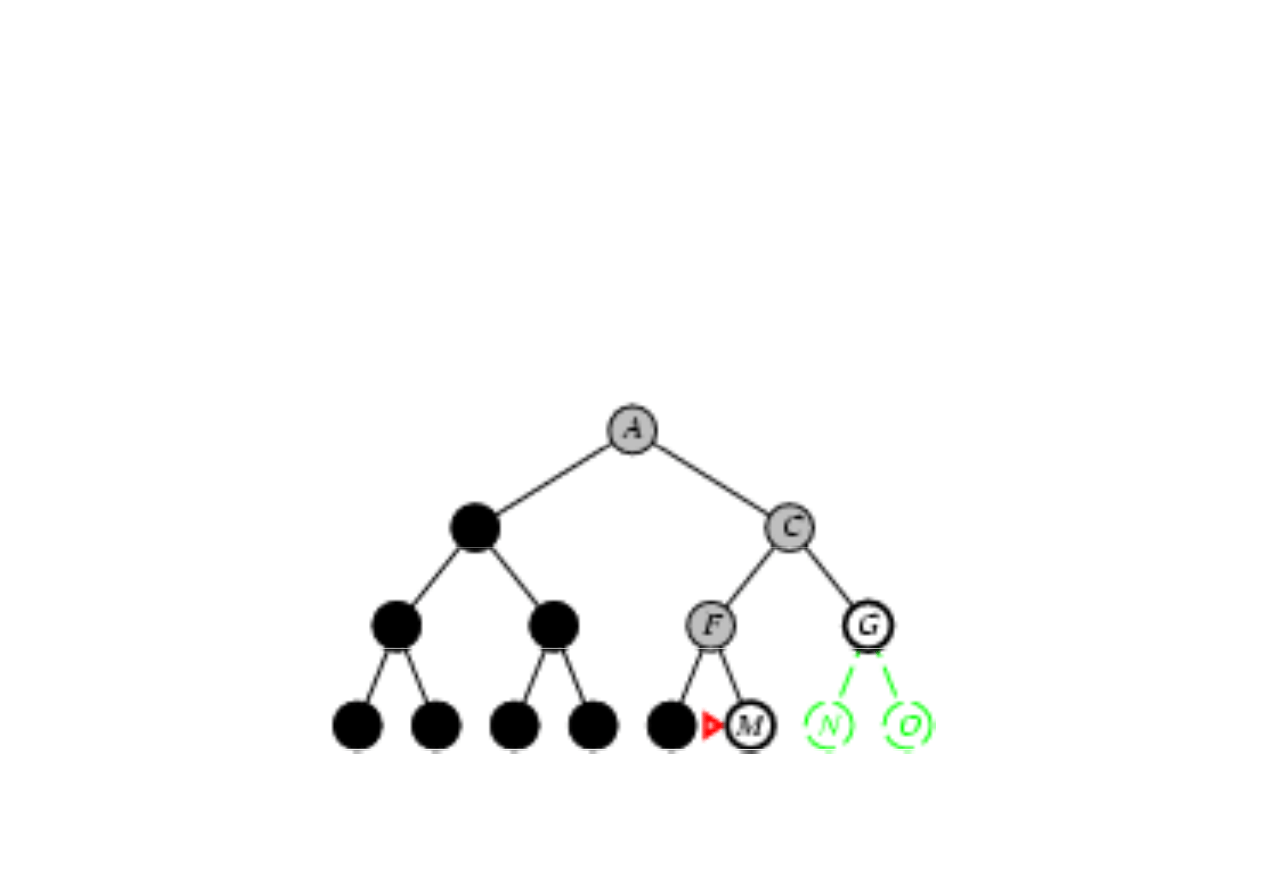
Poszukiwanie w gł

ą

b (depth-first search)

3.4. Algorytmy przeszukiwania drzew

Zasada: rozwin

ąć

najgł

ę

bszy nierozwini

ę

ty w

ę

zeł

(najgł

ę

bszy na brzegu).

Brzeg jest kolejk

ą

LIFO, tzn. nowy w

ę

zeł wstawiany jest na

pocz

ą

tek kolejki.

© F.A. Dul 2007

Poszukiwanie w gł

ą

b (depth-first search)

3.4. Algorytmy przeszukiwania drzew

Własno

ś

ci algorytmu

• Zupełno

ść

Tak w przestrzeniach sko

ń

czonych.

• Zupełno

ść

Tak w przestrzeniach sko

ń

czonych.

Nie w przestrzeniach niesko

ń

czonych,

z p

ę

tlami; (wymaga wtedy modyfikacji

w celu unikni

ę

cia powtarzaj

ą

cych si

ę

w celu unikni

ę

cia powtarzaj

ą

cych si

ę

stanów)

• Czas

O(b

m

) - ogromny je

ż

eli m >> d;

• Czas

O(b ) - ogromny je

ż

eli m >> d;

• Pami

ęć

O(bm) - liniowa wzgl

ę

dem pami

ę

ci;

• Optymalno

ść

Nie

© F.A. Dul 2007

Poszukiwanie z jednostajnym kosztem (uniform cost

3.4. Algorytmy przeszukiwania drzew

search)

Zasada: rozwin

ąć

najta

ń

szy nierozwini

ę

ty w

ę

zeł.

Własno

ś

ci algorytmu

Brzeg jest kolejk

ą

uporz

ą

dkowan

ą

według rosn

ą

cego kosztu.

• Zupełno

ść

Tak je

ż

eli koszt kroku >

ε

> 0.

• Czas

O(b

C/

ε

) - najgorszy przypadek,

C - koszt rozwi

ą

zania optymalnego;

C - koszt rozwi

ą

zania optymalnego;

• Pami

ęć

O(b

C/

ε

);

• Optymalno

ść

Tak - w

ę

zły s

ą

rozwijane według

• Optymalno

ść

Tak - w

ę

zły s

ą

rozwijane według

najwolniej rosn

ą

cego kosztu.

© F.A. Dul 2007

Poszukiwanie na ograniczon

ą

gł

ę

boko

ść

(depth

3.4. Algorytmy przeszukiwania drzew

limited search)

Zasada: jak w algorytmie poszukiwania wgł

ą

b ale z

gł

ę

boko

ś

ci

ą

ograniczon

ą

do poziomu

l

.

gł

ę

boko

ś

ci

ą

ograniczon

ą

do poziomu

l

.

Algorytm rozwi

ą

zuje problem niesko

ń

czonej

ś

cie

ż

ki.

Własno

ś

ci algorytmu

• Zupełno

ść

Tak je

ż

eli l

≥

d.

• Zupełno

ść

Tak je

ż

eli l

≥

d.

• Czas

O(b

l

);

• Pami

ęć

O(bl);

• Pami

ęć

O(bl);

• Optymalno

ść

Tak je

ż

eli l

≤

d.

© F.A. Dul 2007

Poszukiwanie pogł

ę

biane iteracyjnie (iterative deepe-

3.4. Algorytmy przeszukiwania drzew

ning search)

Zasada: wyznacz

ć

iteracyjnie najlepsz

ą

gł

ę

boko

ść

l

.

l = 0

© F.A. Dul 2007

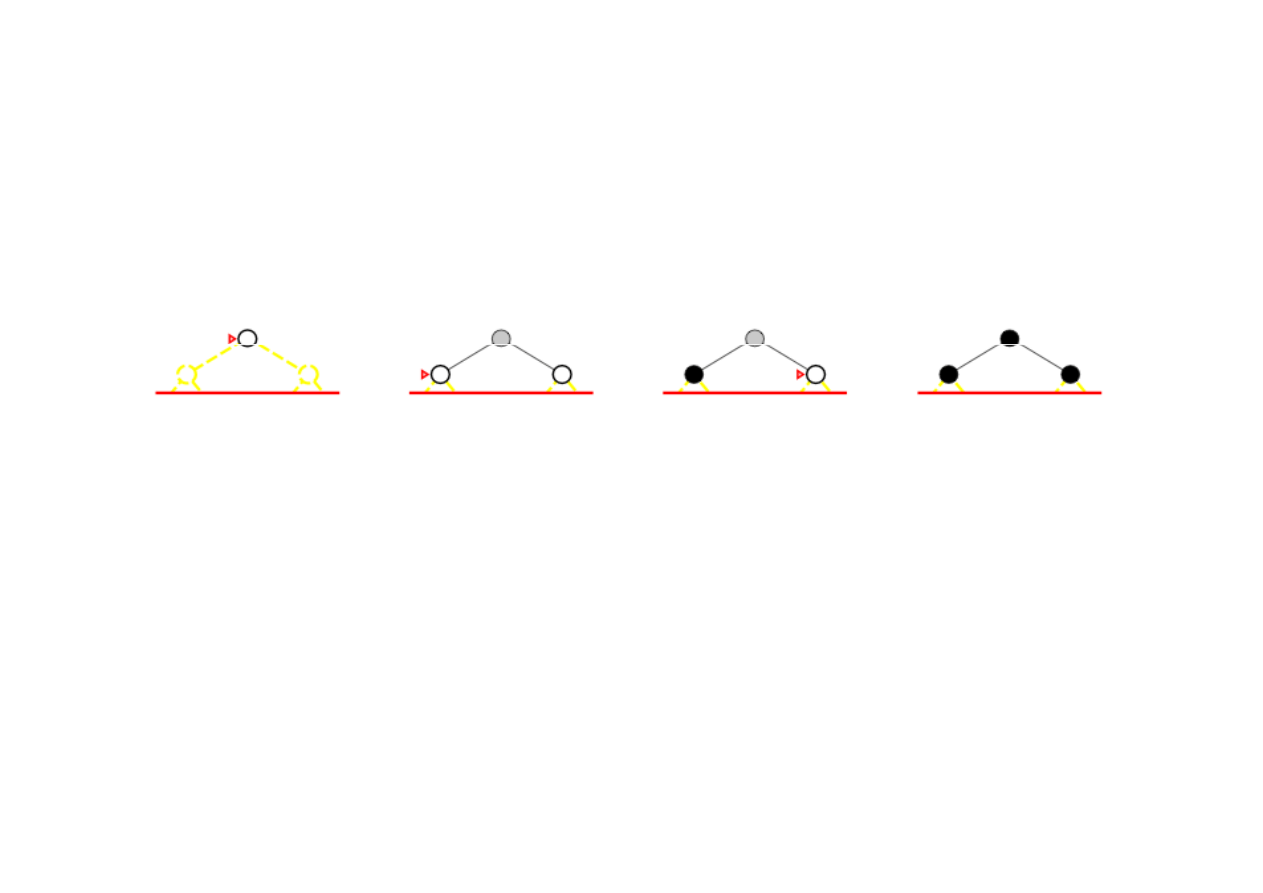
Poszukiwanie pogł

ę

biane iteracyjnie (iterative deepe-

3.4. Algorytmy przeszukiwania drzew

ning search)

Zasada: wyznacz

ć

iteracyjnie najlepsz

ą

gł

ę

boko

ść

l

.

l = 1

© F.A. Dul 2007

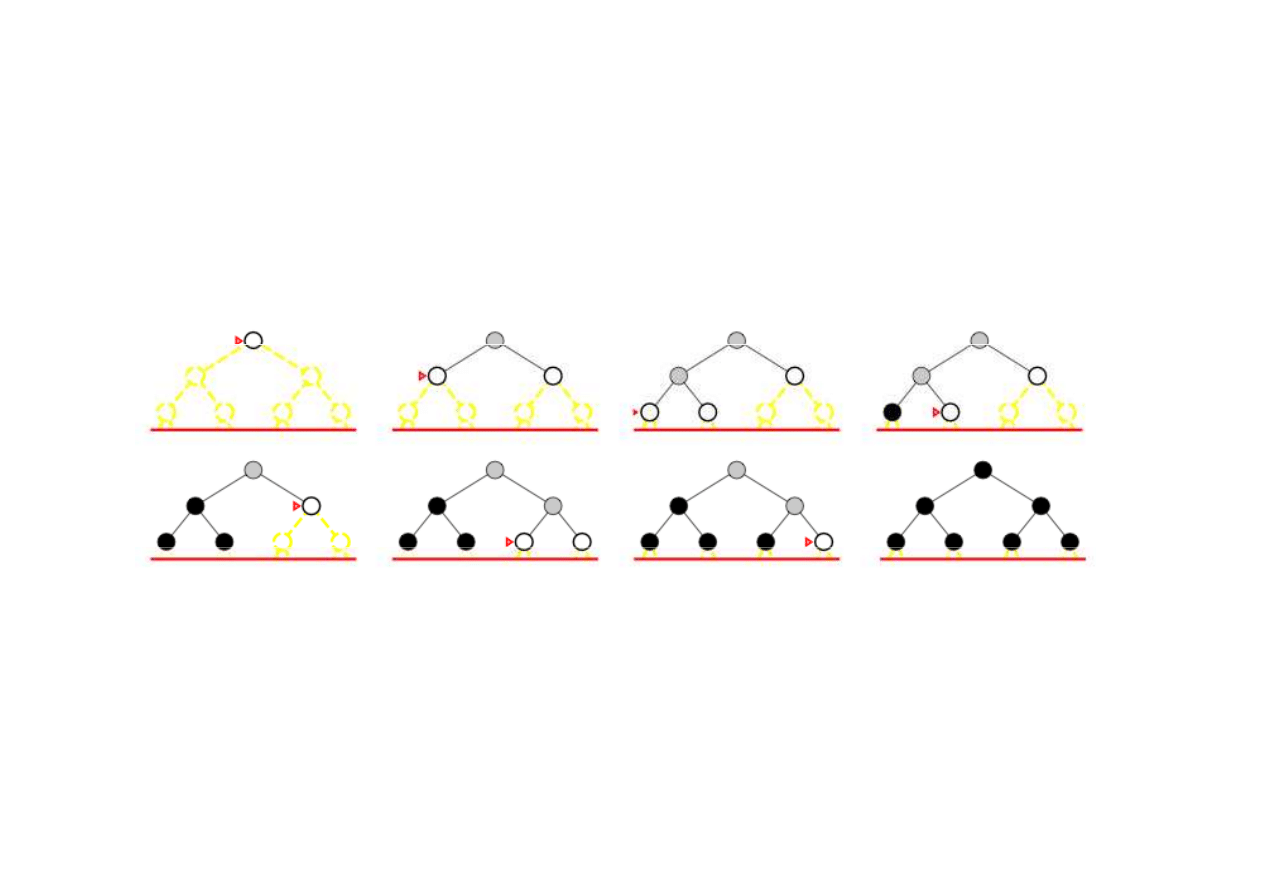
Poszukiwanie pogł

ę

biane iteracyjnie (iterative deepe-

3.4. Algorytmy przeszukiwania drzew

ning search)

Zasada: wyznacz

ć

iteracyjnie najlepsz

ą

gł

ę

boko

ść

l

.

l = 2

© F.A. Dul 2007

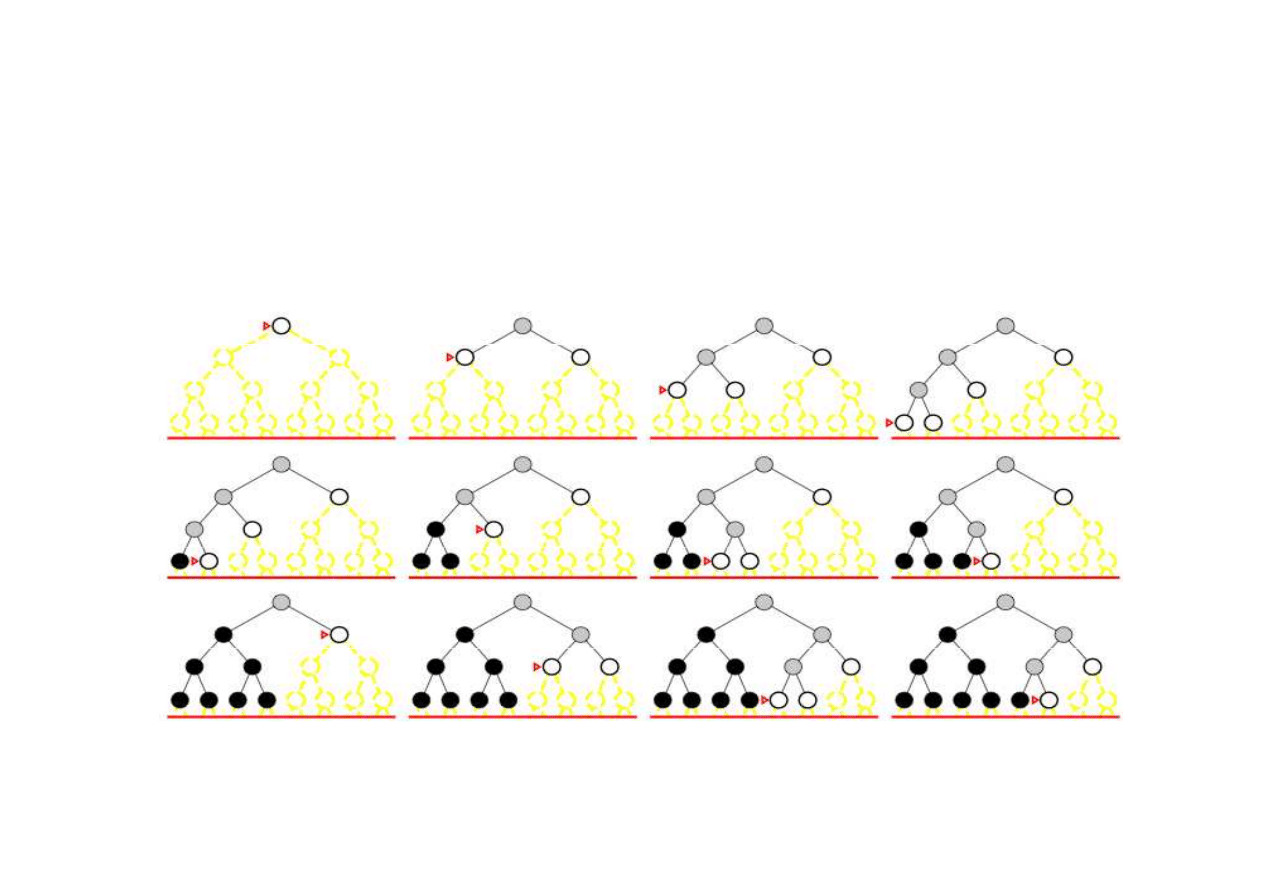
Poszukiwanie pogł

ę

biane iteracyjnie (iterative deepe-

3.4. Algorytmy przeszukiwania drzew

ning search)

Zasada: wyznacz

ć

iteracyjnie najlepsz

ą

gł

ę

boko

ść

l

.

l = 3

© F.A. Dul 2007

Poszukiwanie pogł

ę

biane iteracyjnie (iterative deepe-

3.4. Algorytmy przeszukiwania drzew

ning search)

Cel jest osi

ą

gni

ę

ty na gł

ę

boko

ś

ci d odpowiadaj

ą

cej

najpłytszemu w

ę

złowi docelowemu.

najpłytszemu w

ę

złowi docelowemu.

Algorytm ł

ą

czy zalety algorytmów poszukiwania wszerz

i w gł

ą

b.

Własno

ś

ci algorytmu

i w gł

ą

b.

• Zupełno

ść

Tak.

• Zupełno

ść

Tak.

• Czas

O(b

d

);

• Pami

ęć

O(bd);

• Pami

ęć

O(bd);

• Optymalno

ść

Tak je

ż

eli koszt kroku jest stały.

© F.A. Dul 2007

Poszukiwanie dwukierunkowe (bidrectional search)

3.4. Algorytmy przeszukiwania drzew

Zasada: jednoczesne poszukiwanie z pocz

ą

tku i ko

ń

ca;

Nale

ż

y sprawdz

ć

przed rozwini

ę

ciem czy w

ę

zły nale

żą

Nale

ż

y sprawdz

ć

przed rozwini

ę

ciem czy w

ę

zły nale

żą

do drugiego brzegu.

d

d

d

b

b

b

<

+

2

/

2

/

Własno

ś

ci algorytmu

• Zupełno

ść

Tak je

ż

eli oba poszukiwania wszerz.

• Zupełno

ść

Tak je

ż

eli oba poszukiwania wszerz.

• Czas

O(b

d/2

);

• Pami

ęć

O(b

d/2

);

© F.A. Dul 2007

• Pami

ęć

O(b

);

• Optymalno

ść

Tak je

ż

eli oba poszukiwania wszerz.

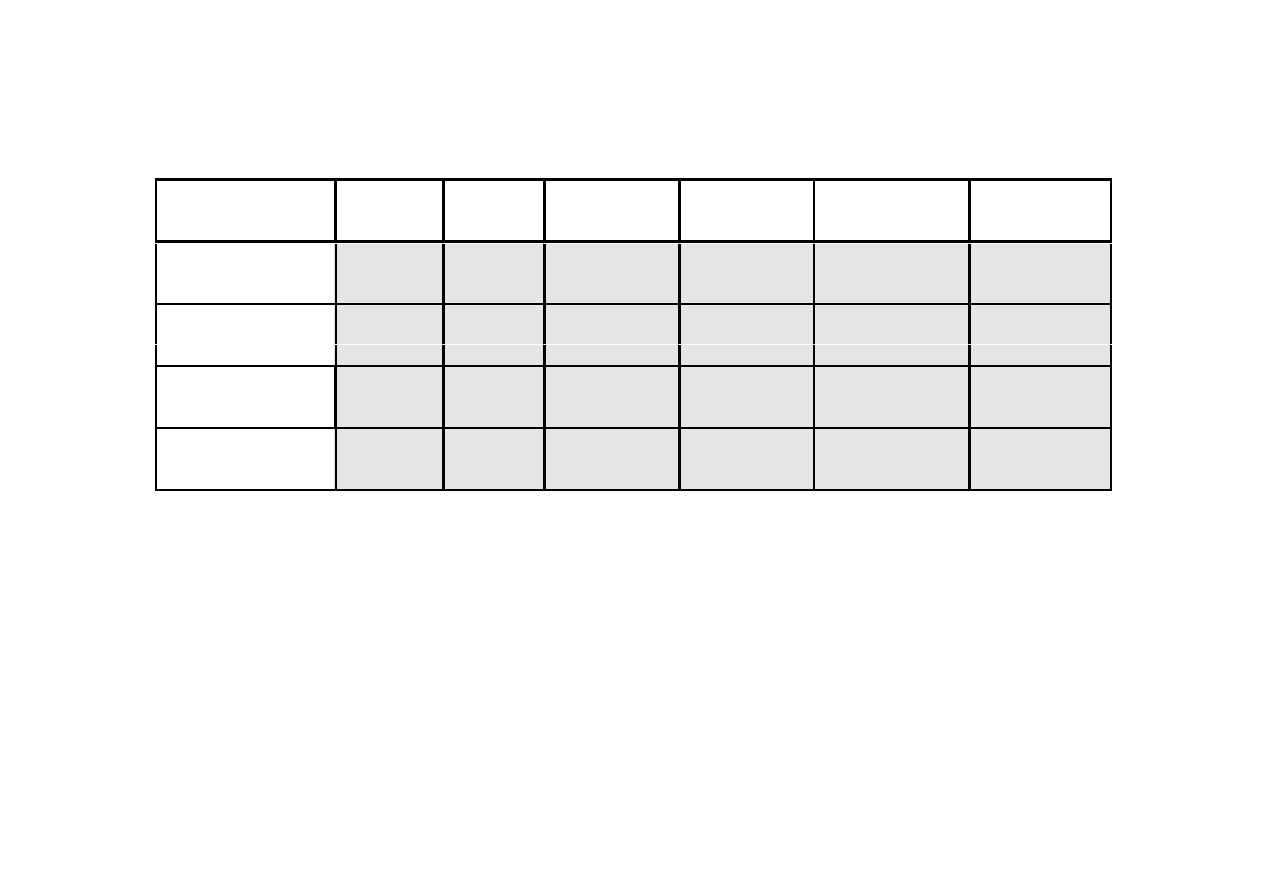
Porównanie algorytmów przeszukiwania

3.4. Algorytmy przeszukiwania drzew

Kryterium

Wszerz

W gł

ą

b

Koszt

jednordny

Stała

gł

ę

boko

ść

Pogł

ę

bianie

iteracyjne

Dwukie-

runkowe

Zupełno

ść

TAK

NIE

TAK

TAK (l

≥≥≥≥

d)

TAK

TAK

Czas

O(b

d+1

)

O(b

m

)

O(b

C/

εεεε

)

O(b

l

)

O(b

d

)

O(b

d/2

)

Czas

O(b

)

O(b )

O(b

)

O(b )

O(b )

O(b

)

Pami

ęć

O(b

d+1

)

O(bm)

O(b

C/

εεεε

)

O(bl)

O(bd)

O(b

d/2

)

Optymalno

ść

TAK

NIE

TAK

TAK (l

≤≤≤≤

d)

TAK

TAK

© F.A. Dul 2007

3.4. Algorytmy przeszukiwania drzew

Najwi

ę

ksz

ą

wad

ą

poszukiwa

ń

Najwi

ę

ksz

ą

wad

ą

poszukiwa

ń

nieinformowanych jest wykładniczy
wzrost kosztu oblicze

ń

.

wzrost kosztu oblicze

ń

.

Krytyczna jest zwłaszcza ilo

ść

Krytyczna jest zwłaszcza ilo

ść

wymaganej pami

ę

ci, gdy

ż

mo

ż

e ona

by

ć

gigantyczna nawet dla zada

ń

by

ć

gigantyczna nawet dla zada

ń

o umiarkowanych wymiarach.

o umiarkowanych wymiarach.

© F.A. Dul 2007

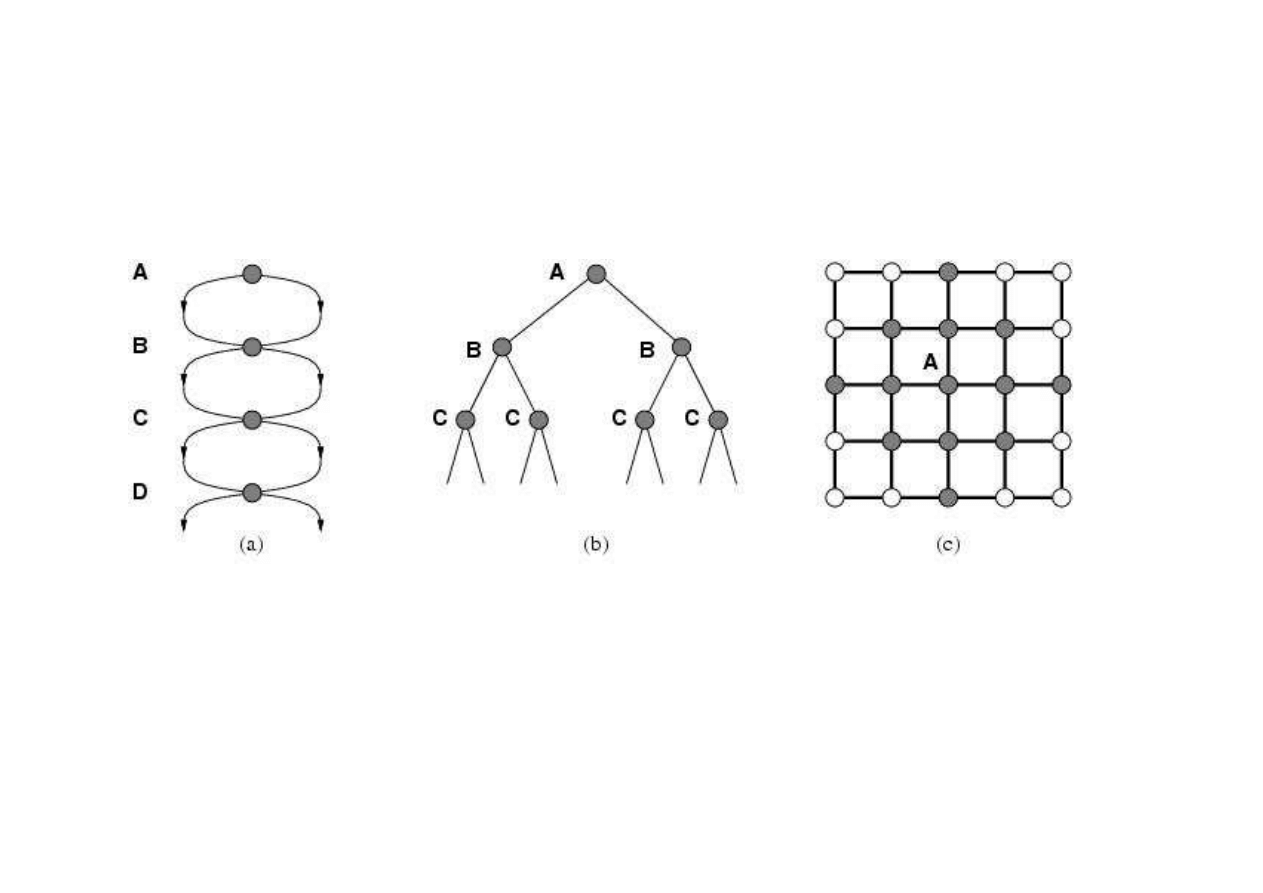
Problem powtarzaj

ą

cych si

ę

stanów

3.4. Algorytmy przeszukiwania drzew

Je

ż

eli powtarzaj

ą

ce si

ę

stany nie s

ą

wykrywane, to zadanie

rozwi

ą

zywalne mo

ż

e zmieni

ć

si

ę

w nierozwi

ą

zywalne.

(a) zbiór stanów które mog

ą

by

ć

osi

ą

gane dwiema drogami,

(b) drzewo binarne dla zbioru stanów A, B, C, D...

(b) drzewo binarne dla zbioru stanów A, B, C, D...

Ka

ż

dy stan mo

ż

e by

ć

osi

ą

gni

ę

ty kosztem liniowym,

za

ś

koszt przeszukiwania drzewa jest wykładniczy.

© F.A. Dul 2007

za

ś

koszt przeszukiwania drzewa jest wykładniczy.

(c) stan A mo

ż

e by

ć

osi

ą

gany wieloma ró

ż

nymi drogami.

3.5. Przeszukiwanie grafu (graph search)

Zasada: lista zamkni

ę

ta zawiera wszystkie rozwini

ę

te w

ę

zły.

function GRAPH-SEARCH(problem,fringe) return a solution or failure

closed

←

an empty set

closed

←

an empty set

fringe

←

INSERT(MAKE-NODE(INITIAL-STATE[problem]), fringe)

loop do

if EMPTY?(fringe) then return failure

if EMPTY?(fringe) then return failure
node

←

REMOVE-FIRST(fringe)

if GOAL-TEST[problem] applied to STATE[node] succeeds

then return SOLUTION(node)

then return SOLUTION(node)

if STATE[node] is not in closed then

add STATE[node] to closed
fringe

←

INSERT-ALL(EXPAND(node, problem), fringe)

Własno

ś

ci algorytmu

• Zupełno

ść

Tak

fringe

←

INSERT-ALL(EXPAND(node, problem), fringe)

• Zupełno

ść

Tak

• Czas

~ wymiaru przestrzeni stanu, << O(b

d

);

• Pami

ęć

~ wymiaru przestrzeni stanu, << O(b

d

)

© F.A. Dul 2007

• Pami

ęć

~ wymiaru przestrzeni stanu, << O(b )

• Optymalno

ść

Tak je

ż

eli poszukiwania wszerz.

Poszukiwanie w przypadku niepełnej informacji

3.5. Algorytmy przeszukiwania grafów

Zało

ż

enia idealne:

-

ś

rodowisko jest całkowicie obserwowalne,

-

ś

rodowisko jest deterministyczne,

-

ś

rodowisko jest deterministyczne,

- agent zna efekty swojego działania.

Co si

ę

stanie, gdy agent nie ma pełnej informacji

Co si

ę

stanie, gdy agent nie ma pełnej informacji

o stanie lub efektach działania?

• Nieobserwowalne

⇒

⇒

⇒

⇒

zadanie bez czujników (conformant

problem)

– agent nie wie, gdzie jest; rozwi

ą

zanie jest ci

ą

giem stanów;

• Niedeterministyczne lub obserwowalne cz

ęś

ciowo

⇒

⇒

⇒

⇒

nieprzewidywalne

(contingency problem)

⇒

⇒

⇒

⇒

nieprzewidywalne

(contingency problem)

– obserwacje dostarczaj

ą

nowych

informacji o stanie bie

żą

cym,

– poszukiwania cz

ę

sto

przeplataj

ą

si

ę

z działaniami.

© F.A. Dul 2007

• Nieznana przestrze

ń

stanów

⇒

⇒

⇒

⇒

exploration problem

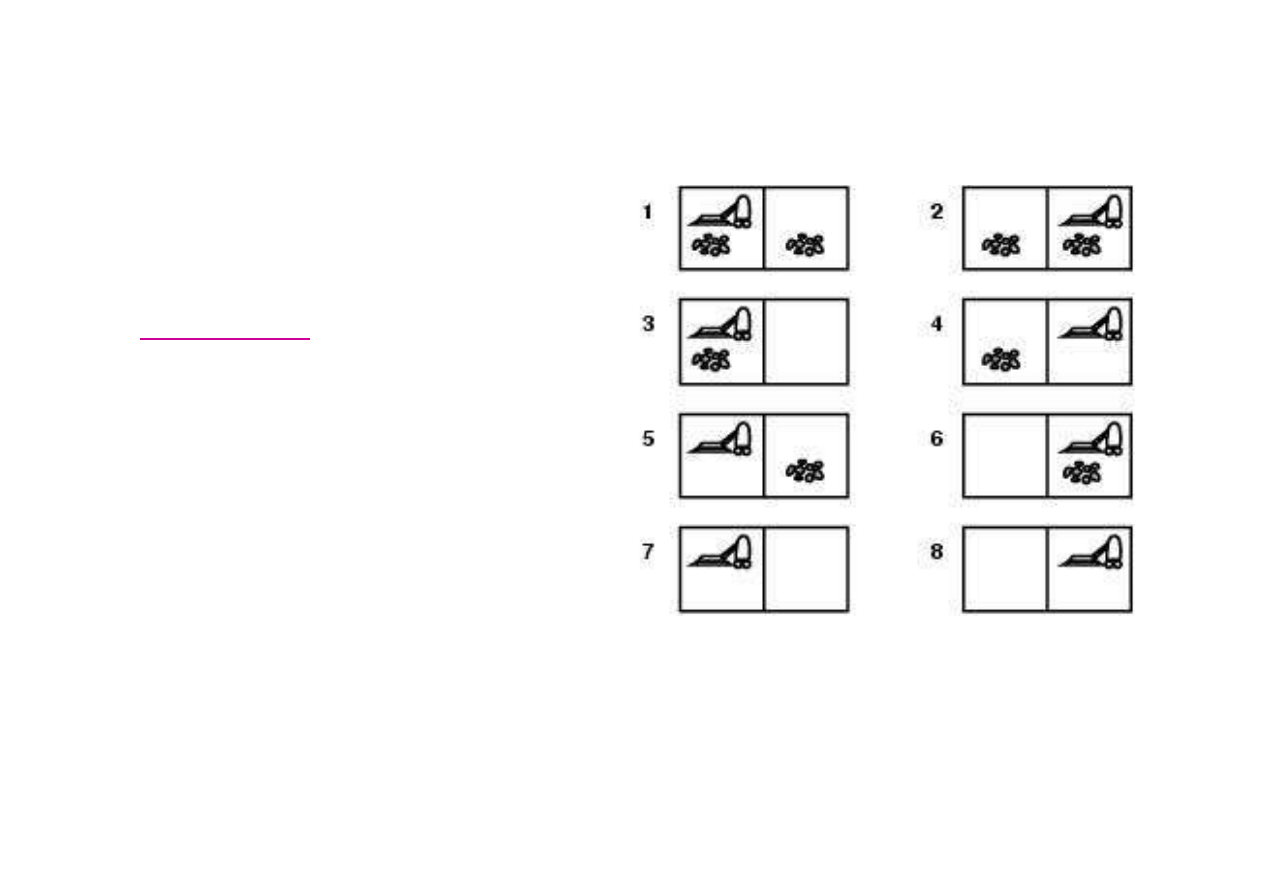
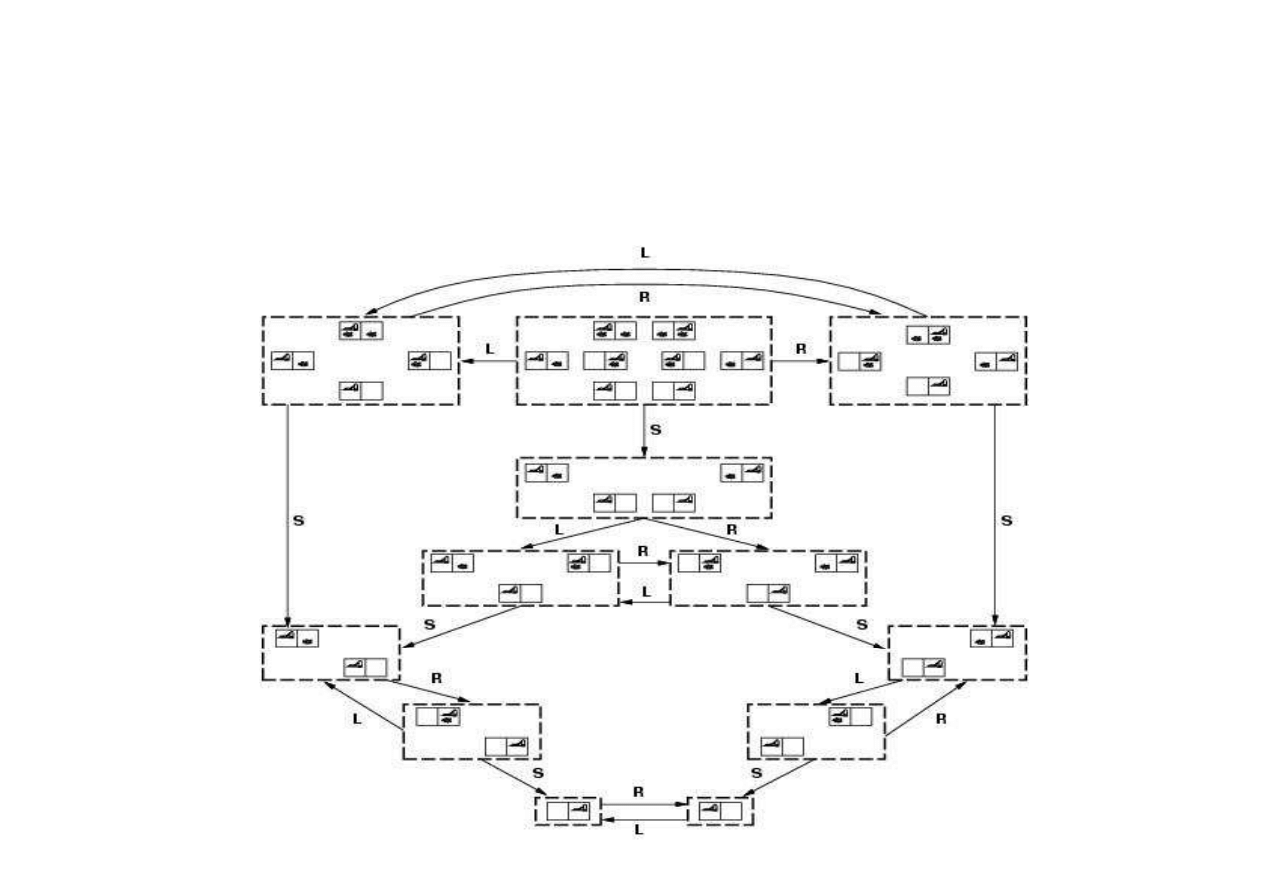
Zadanie nieobserwowalne (conformant problem)

3.5. Algorytmy przeszukiwania grafów

Start z dowolnego stanu spo

ś

ród

{1,2,3,4,5,6,7,8}

{1,2,3,4,5,6,7,8}

W PRAWO

→

{2,4,6,8}

Rozwi

ą

zanie

[ W PRAWO , ODKURZAJ ,

W LEWO , ODKURZAJ ]

Je

ż

eli

ś

wiat nie jest całkowicie obserwowalny, to stan

wiarygodny (belief state) jest zbiorem stanów, które
mog

ą

by

ć

osi

ą

gni

ę

te.

© F.A. Dul 2007

mog

ą

by

ć

osi

ą

gni

ę

te.

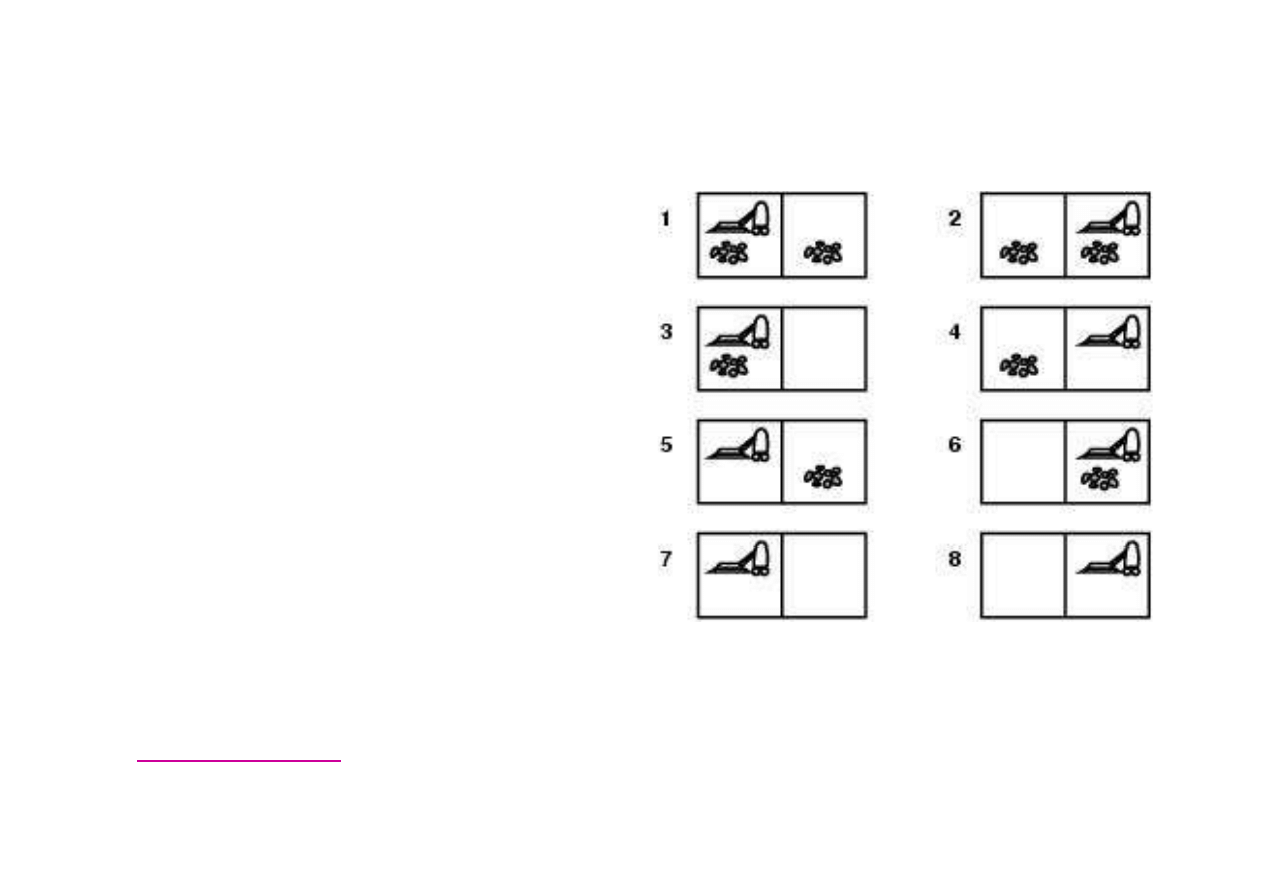
Zadanie nieobserwowalne (conformant problem)

3.5. Algorytmy przeszukiwania grafów

Rozwi

ą

zanie problemu - stan wiarygodny zawieraj

ą

cy

wszystkie mo

ż

liwe stany docelowe.

© F.A. Dul 2007

Zadanie niedeterministyczne lub obserwowalne
cz

ęś

ciowo (contingency problem)

3.5. Algorytmy przeszukiwania grafów

cz

ęś

ciowo (contingency problem)

Obserwowalno

ść

lokalna: start

z jednego ze stanów {1,3}.

z jednego ze stanów {1,3}.

Prawo Murphy’ego

:

odkurzanie czystego dywanu

mo

ż

e go zabrudzi

ć

.

mo

ż

e go zabrudzi

ć

.

Obserwacja lokalna:

zabrudzenie tylko w miejscu

pobytu agenta.

pobytu agenta.

- obserwacja: [L,

Ś

MIECI] = {1,3},

- [ODKURZAJ] = {5,7},
- [W PRAWO] = {6,8},

- [W PRAWO] = {6,8},
- [ODKURZAJ] w {6} = {8}, OK
- [ODKURZAJ] w {8} =

Ź

LE!

Rozwi

ą

zanie

Ż

aden bezwarunkowy ci

ą

g działa

ń

nie gwarantuje powodzenia.

Nale

ż

y uzale

ż

ni

ć

działania od aktualnej sytuacji.

© F.A. Dul 2007

Rozwi

ą

zanie

[ ODKURZAJ, W PRAWO, je

ż

eli

Ś

MIECI to ODKURZAJ ]

Podsumowanie

• Rozwi

ą

zywanie zada

ń

poprzez przeszukiwanie wymaga

• Rozwi

ą

zywanie zada

ń

poprzez przeszukiwanie wymaga

sformułowania zadania w postaci abstrakcyjnej.

• Je

ż

eli zadanie jest deterministyczne i obserwowalne

• Je

ż

eli zadanie jest deterministyczne i obserwowalne

(jednostanowe), to do jego rozwi

ą

zania mo

ż

na u

ż

y

ć

algorytmu poszukiwania nieinformowanego.

• Istnieje wiele algorytmów poszukiwania nieinformowanego:

• Istnieje wiele algorytmów poszukiwania nieinformowanego:

wszerz, w gł

ą

b, kosztu jednorodnego, stałej gł

ę

boko

ś

ci,

pogł

ę

biania iteracyjnego oraz poszukiwa

ń

dwukierunkowych.

• Algorytm poszukiwania poprzez pogł

ę

bianie iteracyjne jest

najlepszym algorytmem ogólnym - wymaga liniowej pami

ę

ci

a czas oblicze

ń

jest niewiele wi

ę

kszy ni

ż

w przypadku innych

a czas oblicze

ń

jest niewiele wi

ę

kszy ni

ż

w przypadku innych

algorytmów.

• Agenci działaj

ą

cy na zasadzie poszukiwania rozwi

ą

zania

s

ą

u

ż

ywani w wielu dziedzinach: wyznaczaniu drogi,

s

ą

u

ż

ywani w wielu dziedzinach: wyznaczaniu drogi,

planowaniu układów VLSI, nawigacji robotów, poszukiwa

ń

internetowych;

© F.A. Dul 2007