
MODEL ODPOWIEDZI I SCHEMAT PUNKTOWANIA
ARKUSZA EGZAMINACYJNEGO II - POZIOM ROZSZERZONY
Numer
czynnoci
Opis wykonywanej czynnoci
Liczba
punktów
Modelowy wynik etapu (czynnoci)
11.1
Sprawdzenie, ¿e dla
0
=
m
dane równanie
ma
rozwi¹zanie
1 p
11.2
Podanie uk³adu warunków (1) na to, by
równanie kwadratowe nie mia³o rozwi¹zania
1 p
(1)
<
≠
0
0
∆
m
11.3
Wyznaczenie wartoci spe³niaj¹cych
warunek
0
<
∆
1 p
−
−
∈
5
3
,
3
m
11.4
Podanie odpowiedzi.
1 p
−
−
∈
5
3
,
3
m
12.1
Wykorzystanie zale¿noci
A
B
A
⊂
∩
)
(
1 p
)
(
)
(
A
P
B
A
P
≤
∩
12.2
Zastosowanie definicji prawdopodobieñstwa
zdarzenia przeciwnego
1 p
(
)
( )
'
1
A
P
B
A
P
−
≤
∩
12.3
Wykorzystanie definicji prawdopodobieñstwa
warunkowego
1 p
)
(
1
)
(
)
/
(
A'
P
B
P
B
A
P
−
≤
⋅
12.4
Wykorzystanie zale¿noci
0
)
(
>
B
P
do
wykazania tezy
1 p
13.1
Powo³anie siê na definicjê izometrii
1 p
13.2
Wybór dwóch ró¿nych punktów A i B i
wyznaczenie wspó³rzêdnych ich obrazów A’ i
B’
1 p
13.3
Sprawdzenie, ¿e odleg³oci
AB
i
'
' B
A
s¹
równe
1 p
13.4
Wyznaczenie równania obrazu danego okrêgu
w przekszta³ceniu P
2 p
np.
0
3
4
2
2
=
+
−
+
x
y
x
14.1
Wyznaczenie dziedziny nierównoci
logarytmicznej
(
)
2
1
log
2
1
−
≥
−
x
1 p
(
) (
)
+∞
∪
−
∞
−
∈
,
1
1
,
x
14.2
Wykorzystanie monotonicznoci funkcji
logarytmicznej do rozwi¹zania nierównoci
1 p
1
4
x
− ≤
14.3
Rozwi¹zanie nierównoci
1
4
x
− ≤
z
uwzglêdnieniem jej dziedziny
1 p
5
,
1
(
)
1
,
5
∪
−
−
∈
x
14.4
Rozwi¹zanie nierównoci
0
>
y
1 p
{ }
0
\
R
y
∈
14.5
Naszkicowanie figury
F
1 p
14.6
Napisanie równañ osi symetrii figury
F
1 p
0
,
0
=
=
y
x
15.1
Wyznaczenie d³ugoci
h
wysokoci walca
w zale¿noci od d³ugoci
r
promienia
podstawy
1 p
2
250
r
h
=
15.2
Wyznaczenie pola powierzchni ca³kowitej
walca jako funkcji zmiennej
r
1 p
( )
r
r
r
P
π
π
500
2
3
+
=
15.3
Okrelenie dziedziny funkcji
( )
r
P
1 p
(
)
+∞
∈
,
0
r
15.4
Wyznaczenie
( )
r
P'
1 p
( )
2
3
500
4
'
r
r
r
P
π
π −
=
Egzamin maturalny z matematyki – maj 2002
1

15.5
Rozwi¹zanie równania
( )
0
'
=
r
P
1 p
5
=
r
15.6
Uzasadnienie, ¿e dla
5
=
r
funkcja
przyjmuje wartoæ najmniejsz¹
1 p
16.1
Naszkicowanie wykresu funkcji
x
y
2
=
1 p
16.2
Naszkicowanie wykresu funkcji
1
2
+
=
x
y
1 p
16.3
Przekszta³cenie wyra¿enia
x
x 1
+
do
postaci
x
1
1
+
1 p
16.4
Naszkicowanie wykresu funkcji
x
y
1
=
1 p
16.5
Naszkicowanie wykresu funkcji
1
1
+
=
x
y
1 p
16.6
Naszkicowanie wykresu funkcji
1
1
+
=
x
y
1 p
16.7
Podanie liczby ujemnych rozwi¹zañ
równania
( ) ( )
x
g
x
f
=
1 p 2
rozwi¹zania
17.1
Wyznaczenie dziedziny danego równania
1 p
(
) { }
π
π
\
2
,
0
∈
x
17.2
Przeksz
ta³cenie danego równania
do postaci
(1)
1p (1)
cos
4 sin cos
4 cos
sin
x
x
x
x
x
+
=
17.3
Przekszta³cenie równania z postaci
(1)
do postaci
(2)
1 p (2)
(
)
0
sin
4
1
sin
4
cos
2
=
−
+
x
x
x
17.4
Rozwi¹zanie równania
0
cos
=
x
w wyznaczonej dziedzinie
1 p
π
π
2
3
2
=
∨
=
x
x
17.5
Rozwi¹zanie równania
2
4 sin
4 sin
1
0
x
x
−
+ =
w wyznaczonej dziedzinie
1 p
π
π
6
5
6
=
∨
=
x
x
17.6
Obliczenie mocy zbioru zdarzeñ
elementarnych
1p
6
=
Ω
17.7
Obliczenie mocy zdarzenia
A
polegaj¹cego na tym, ¿e co najmniej
jedno z wylosowanych rozwi¹zañ jest
wielokrotnoci¹ liczby
2
π
1 p
5
=
A
17.8
Obliczenie prawdopodobieñstwa
zdarzenia
A
1 p
( )
6
5
=
A
P
18.1
Za
uwa¿enie, ¿e w ci¹gu, który jest lew¹
stron¹ danej nierównoci
x
q
a
2
1
1
=
=
1 p
18.2
Podanie warunku zbie¿noci i
wyznaczenie tych wartoci
x
, dla
których ci¹g, który jest lew¹ stron¹ danej
nierównoci jest zbie¿ny
1 p
0
>
x
2
Egzamin maturalny z matematyki – maj 2002
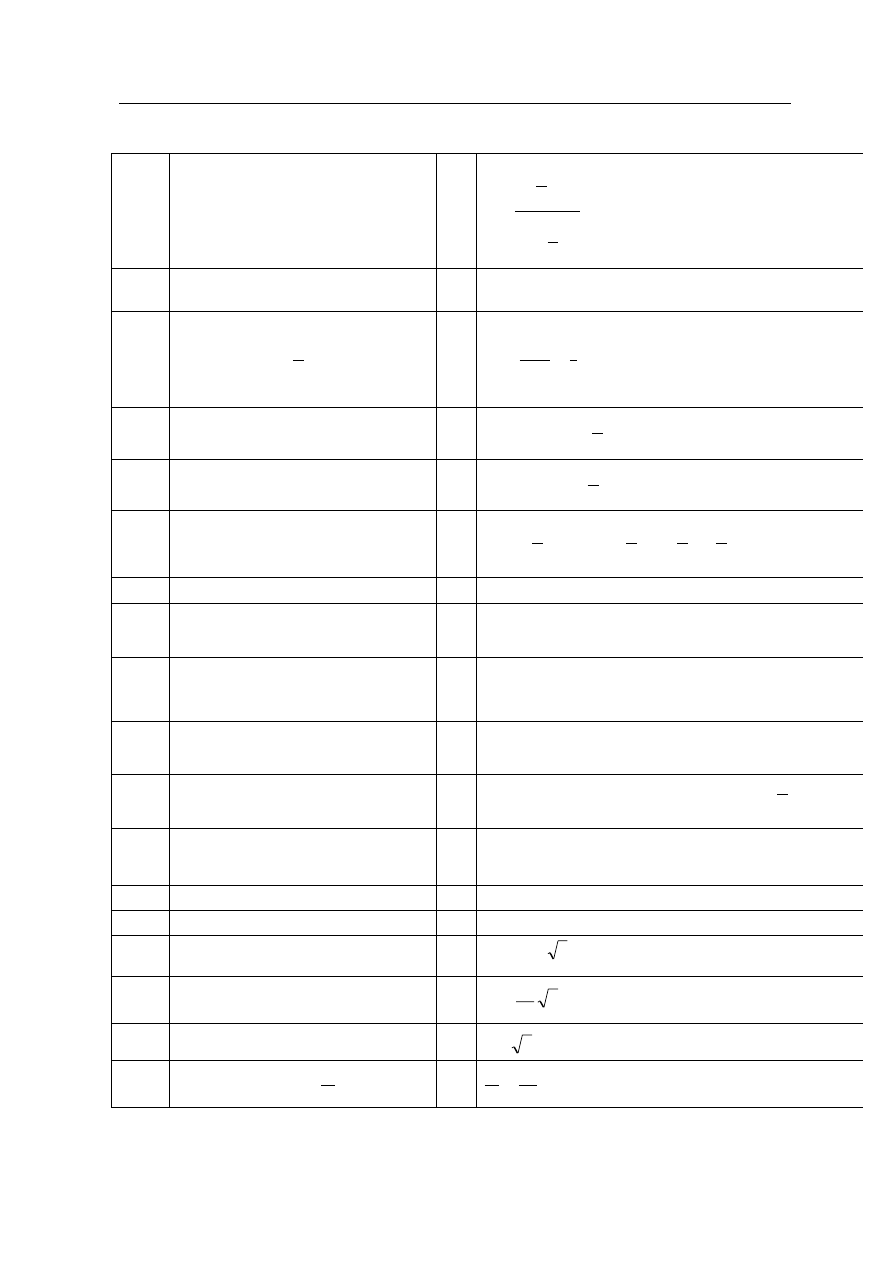
Egzamin maturalny z matematyki – maj 2002
3
18.3
Wyznaczenie sumy
S
ci¹gu, który jest
lew¹ stron¹ danej nierównoci
1 p
x
x
S
−
=
2
1
1
2
1
18.4
Zamiana u³amka okresowego
( )
9
,
0
na
zwyk³y
1 p
( )
1
9
,
0
=
18.5
Wykonanie podstawienia pomocniczej
niewiadomej
x
t
=
2
1
i zapisanie danej
nierównoci za pomoc¹ zmiennej
t
(1)
1 p (1)
1
1
1
−
>
−
t
t
t
18.6
Przekszta³cenie nierównoci
(1)
do
postaci
(2)
1 p (2)
( )
0
1
2
1
2
>
−
−
−
t
t
t
18.7
Rozwi¹zanie nierównoci
(2)
1 p
(
)
∪
∞
−
∈
1
,
2
1
0
,
t
18.8
Zapisanie warunku
(3)
1 p (3)
<
∧
>
∨
<
1
2
1
2
1
2
1
0
2
1
x
x
x
18.9
Wyznaczenie
x
z warunku
(3)
1 p
( )
1
,
0
∈
x
18.10
Sprawdzenie czy otrzymane wartoci
x
nale¿¹ do dziedziny nierównoci
i odpowied.
1 p
19.1
Wyra¿enie d³ugoci boków
c
b,
trójk¹ta
za pomoc¹
a
i
r
, gdzie
a
to d³ugoæ
najkrótszego boku i
0
>
r
1 p
r
a
c
r
a
b
2
,
+
=
+
=
19.2
Wykorzystanie informacji, ¿e suma
d³ugoci boków trójk¹ta wynosi 30 do
wyznaczenia zwi¹zku pomiêdzy
a
i
r
1 p
10
=
+
r
a
19.3
Zastosowanie twierdzenia cosinusów do
wyznaczenia drugiego zwi¹zku
pomiêdzy
a
i
r
1 p
(
)
(
)
(
)
−
⋅
+
−
+
+
=
+
2
1
2
2
2
2
2
r
a
a
r
a
a
r
a
19.4
Zapisanie uk³adu równañ
(1)
z
niewiadomymi
a
i
r
1 p (1)
2
2
10
2
3
0
a
r
a
ar
r
+ =
− −
=
19.5
Rozwi¹zanie uk³adu równañ
(1)
1 p
6
,
4
=
=
a
r
19.6
Podanie d³ugoci boków trójk¹ta
1 p
14
,
10
,
6
=
=
=
c
b
a
19.7
Obliczenie pola trójk¹ta
1 p
19.8
Obliczenie d³ugoci
R
promienia okrêgu
opisanego na trójk¹cie
1 p
3
3
14
=
R
19.9
Obliczenie d³ugoci
s
promienia okrêgu
wpisanego w trójk¹t
1 p
3
=
s
19.10
Wyznaczenie stosunku
s
R
1 p
3
14
=
s
R
3
15
=
∆
P
Wyszukiwarka
Podobne podstrony:
2002 05 rozszODP1
2002 05 rozszODP2
2002 05 10
2002 05 37
2002 05 22
2002 05 26
2002 05 23
2002 05 45
2002 05 38
2002 05 16
2002 05 36
2009 05 rozszODP
2002 05 podstODP1
2002 05 36
2002 05 28
2002 05 Osla laczka Nieznany
więcej podobnych podstron