Ć w i c z e n i e 3

WYZNACZANIE SIŁY CORIOLISA

3.1 Opis teoretyczny

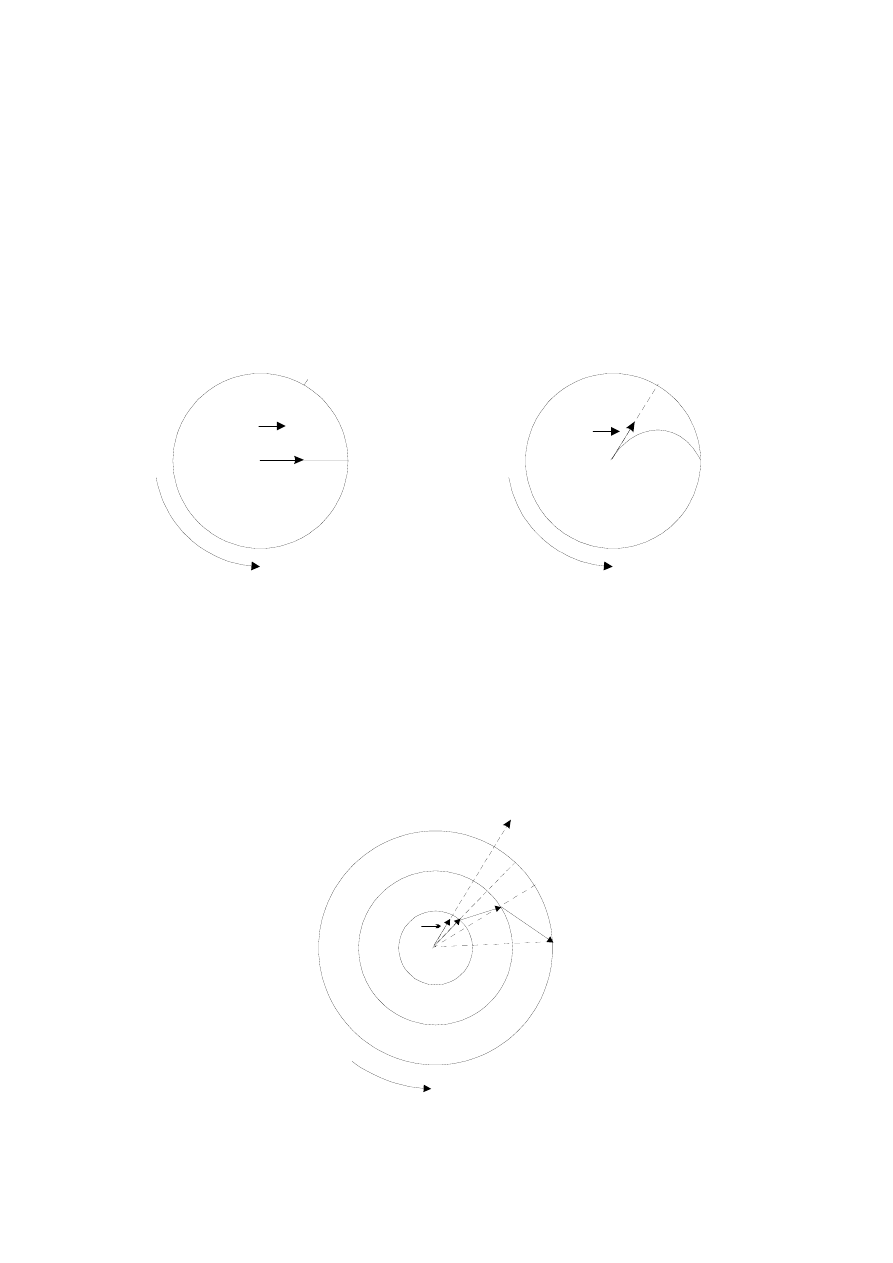
Wyobraźmy sobie obserwatora siedzącego w środku obracającej się tarczy nadającego piłce pręd-
kość początkową skierowaną wzdłuż promienia tarczy. Obserwator zewnętrzny (znajdujący się po-
za obracającym kołem) nie zobaczy w tym procesie nic szczególnego. Piłka poruszała się po prostej
ruchem jednostajnym (rys.3.1a). Natomiast obserwator siedzący na tarczy zauważył, że piłka wcale
nie poruszała się (względem jego i tarczy) po prostej OD, ale po łuku OLC (rys.3.1b).

a)

b)

Rys.3.1. Ruch piłki po wirującej tarczy: a) dla obserwatora zewnętrznego, b) dla obserwato-

ra związanego z tarczą

W

układzie wirującym dla obserwatora związanego z tym układem pojawia się pewna siła

powodująca zakrzywienie toru ruchu ciała wypadającego na zewnątrz tarczy. Siła ta odchylała się
od pierwotnego toru OD w prawo (na tarczy obracającej się niezgodnie ze wskazówkami zegara)
Działa więc ona w prawo, a zatem prostopadle do wektora prędkości

V

r

. Siłę tę od nazwiska od-

krywcy nazywamy siłą Coriolisa. Należy jeszcze raz mocno podkreślić, że nie istnieje ona w ukła-
dzie nieruchomego (zewnętrznego) obserwatora.

Rys.3.2. Odchylenie ciała od pierwotnego toru OA

3

w prawo spowodowane siłą Coriolisa.

Łuki A

1

B

1

, A

2

B

2

, A

3

B

3

są drogami przebytymi przez ciało pod wpływem tej siły odpowied-

nio po czasach

∆t, 2∆t, 3∆t.

c

c’

v

c

c’

v

L

v

O

B

1

B

2

B

3

A

3

A

2

A

1

S

Zajmijmy się teraz matematycznym opisem tego zjawiska; niech na tarczy obracającej się ruchem
jednostajnym, znajduje się w jej środku ( w punkcie O, rys.3.2.) jakieś ciało, np. kula. Udzielmy
kuli prędkości V

o

skierowanej ku punktowi A

3

. W układzie nieruchomym torem kuli będzie prosta

OA

1

A

2

A

3

, natomiast na obracającej się tarczy kula zakreśli OB

1

B

2

B

3

. Odchylony od OA

3

w kie-

runku przeciwnym w kierunku przeciwnym do kierunku ruchu tarczy. Jeśli w układzie nierucho-
mym odcinek OA

1

=

∆s

1

został przebyty przez kulę w czasie

∆t, to w tym samym czasie punkt B

1

tarczy przebył drogę B

1

A

1

. Fakt ten pozwala nam napisać dwa równania:

∆s

1

= V

∆t

i

A

1

B

1

=

∆s

1

ω ∆t

gdzie

ω oznacza prędkość kątową tarczy.

Podstawiając

∆s

1

wyrażone pierwszym równaniem do drugiego, otrzymamy

A

1

B

1 =

V

ω (∆t)

2

(3.1.)

Z zależności tej widzimy, że w układzie obserwatora związanego z tarczą drogę A

1

B

1

kula przeby-

wa ruchem jednostajnie przyśpieszonym, gdyż droga rośnie z kwadratem czasu. Żeby lepiej to zro-
zumieć, zauważmy, że odcinki OA

1

, A

1

A

2

i A

2

A

3

są sobie równe , zatem przesunięcie kuli w kie-

runku promienia, pomiędzy sąsiednimi okręgami kół, dokonuje się w równych czasach

∆t.

W tym samym czasie

∆t tarcza zakreśla kąt

ω ∆t, co na rys.3.2. powtarza się trzy razy. Kolejne dro-

gi A

1

B

1

, A

2

B

2

, A

3

B

3

pozostają do siebie w stosunku kwadratów kolejnych liczb całkowitych

(1 : 4 : 9 :...). Długość łuku AB =

α r . W tym samym czasie ∆t, gdy np. α rośnie dwa razy, to i r

rośnie dwa razy, długość łuku rośnie więc czterokrotnie. Fakt taki obserwator ruchomy może przy-
pisać tylko działaniu stałej siły. W czasie

∆t ma ona kierunek A

1

B

1, ,

a więc jest prostopadła do wek-

tora prędkości

V

r

. Wywołuje przyśpieszenie, które obliczymy ze znanego wzoru wyrażającego

przebytą drogę

A

1

B

1

=

2

)

(

2

1

t

a

C

∆

(3.2.)

Przyrównując do siebie oba ostatnie wzory otrzymujemy

C

a

= 2 V

ω

(3.3)

Jest to wzór na tzw. przyśpieszenie Coriolisa. Siła Coriolisa która działa na ciało wywołuje to przy-
śpieszenie, wyrazi się wzorem:

F

C

= 2 m V

ω

(3.4)

Wzór ten wyraża tylko wartość siły Coriolisa; brak w niej jakichkolwiek informacji o tym, że siła ta
jest prostopadła do osi obrotu i wektora prędkości

V

r

, jak też jaki ma ona zwrot. Obie te informacje

tkwić będą w samym wzorze, jeśli napiszemy go w symbolice wektorowej.
Przyśpieszenie Coriolisa jest iloczynem wektorowym, ze współczynnikiem 2, wektorów prędkości
liniowej

V

r

ciała i prędkości kątowej

ω

r układu obracającego się

ω

r

r

r

×

= V

2

C

a

(3.5)

Jeśli obie strony tego wzoru pomnożymy przez masę ciała, otrzymamy wzór na siłę Coriolisa

ω

r

r

r

×

=

V

m

2

F

C

(3.6)

Łatwo sprawdzić, że kierunek i zwrot siły Coriolisa w omówionym przez nas wypadku zgadza się z
kierunkiem i zwrotem

ω

r

r

×

V

(reguła śruby prawoskrętnej).

Obliczmy teraz odchylenie AB ciała pod wpływem siły Coriolisa. Przez analogię do wzoru (3.2)
można napisać

AB =

2

2

1

t

a

C

(3.7)

gdzie: t – czas ruchu ciała od środka tarczy wynosi

V

s

.

Podstawiając tę zależność do (3.7) i korzystając ze wzoru (3.3) otrzymujemy:

AB =

2

S

V

ω

(3.8)

W ćwiczeniu badamy tę zależność ( funkcja AB = f(s

2

) jest liniowa) oraz wyznaczamy przyśpiesze-

nie i siłę Coriolisa podczas ruchu kulki po obracającej się tarczy.

3.2. Opis układu pomiarowego

Aparatura służąca do badania siły Coriolisa składa się z tarczy wprowadzonej w ruch obrotowy za
pomocą silnika elektrycznego.
Prędkość kątową tarczy zmieniać można za pomocą autotransformatora, z którego zasilany jest sil-
nik. Kulka zostaje wprawiona w ruch po tarczy dzięki równi pochyłej obracającej się z tarczą. Może
być ona zwalniana z różnych wysokości równi pochyłej za pomocą odpowiedniego przycisku. Do
tarczy można przymocować wyprofilowaną kartkę papieru.
Kulkę przed eksperymentem macza się w tuszu, żeby podczas ruchu po tarczy pozostawiła ślad
toru.

3.3. Przeprowadzenie pomiarów

1. Przymocować okrągło wyprofilowany papier do tarczy.
2. Stosując rękawice gumowe, zamoczyć kulkę w tuszu i umocować ją na równi pochyłej przy po-

łożeniu oznaczonym cyfrą.

3. Zwolnić kulkę – zostawi ona na papierze ślad linii prostej będącej linią odniesienia (jak prosta

OC` na rys3.1b).

4. Ponownie zamoczyć kulkę w tuszu i umocować na równi pochyłej w poprzednim położeniu.
5. Włączyć silnik i autotransformator ustawić obroty tarczy na małej prędkości kątowej.
6. Po ustaleniu się obrotów zmierzyć sekundomierzem czas trwania 10 pełnych obrotów.
7. Zwolnić kulkę – zostanie ślad (odpowiadający łukowi OLC na rys.3.1b).

8. Powtórzyć 2 - 3 razy operacje 4 – 7 stosując za każdym razem coraz to większe prędkości kątowe

obrotu tarczy.

9. Zdjąć papier z tarczy.

3.4. Opracowanie wyników pomiarów

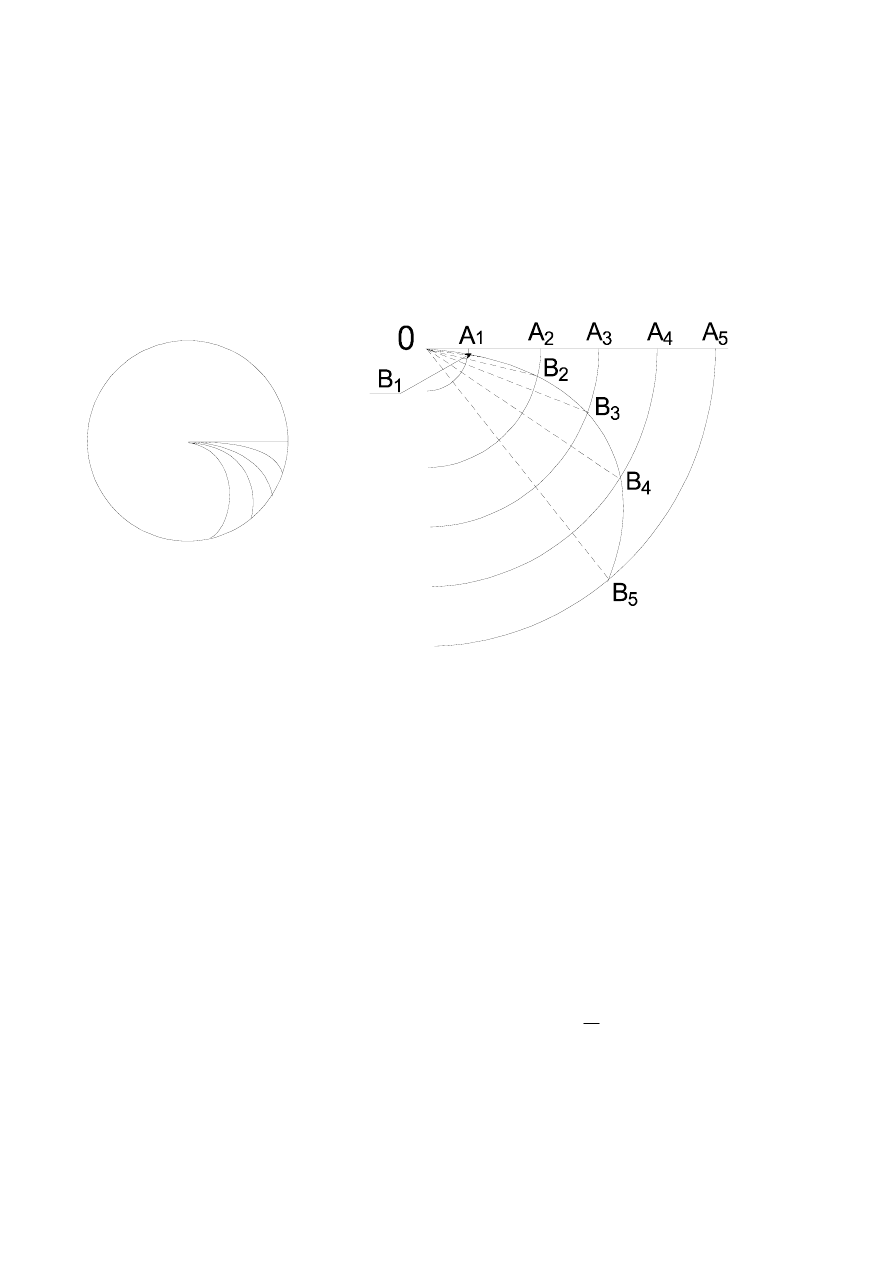
1. Na otrzymanym z doświadczenia wykresie narysować półokręgi tak, aby dzieliły one promień

tarczy na 5 – 6 równych odcinków ( patrz rys.3.3.).

Rys.3.3. Przykładowy wynik z doświadczenia (a) i sposób opracowania dla jednego łuku (b)

2. Dla każdego doświadczalnego łuku:

a) określić długość łuków A

1

B

1

, A

2

B

2

, itd. W tym celu należy wyznaczyć kąty

α

1

=

∠ A

1

OB

1

α

2

=

∠ A

2

OB

2

...................... w radianach

( np. znajdując konstrukcyjne tangensy tych kątów) oraz odcinki OA

1

OA

2,

....Wówczas

A

1

B

1

=

α

1

OA

1

A

2

B

2 =

α

2

OA

2

b) wykreślić zależność AB = f(s

2

). Zmiennej s odpowiadają odcinki OA

1

, OA

2

itd. Po punk-

tach pomiarowych przeprowadzić prostą;

c) z nachylenia prostej (wzór (3.8) wyznaczyć wartość ilorazu

V

ω

. Ponieważ z bezpośrednie-

go pomiaru znamy

ω, a więc możemy wyznaczyć prędkość kulki V;

d) obliczyć ( ze wzoru (3.5.)) przyśpieszenie Coriolisa;
e) ze wzoru (3.6) obliczyć siłę Coriolisa.

3. Zestawić wyniki otrzymane dla wszystkich doświadczalnych łuków i wyciągnąć wnioski.

0

A

1

2

3

4

3.5 Pytania kontrolne

1. Zdefiniować siłę Coriolisa.
2. Wyprowadzić wzór na przyśpieszenie Coriolisa.
3. Podać przykłady występowania siły Coriolisa.
4. Dlaczego ciała swobodnie spadające odchylają się od pionu w kierunku wschodnim?

L i t e r a t u r a

[1] Kittel C., Knight W .D., Ruderman M.A.: Mechanika, PWN, „Warszawa” 1973
[2] Szczeniowski S.: Fizyka doświadczalna, cz. I. PWN, Warszawa 1972
[3] Piekara A.: Mechanika ogólna. PWN, Warszawa 1964.