Fal Jacek

Sprawozdanie z ćwiczenia nr 2.

Pomiar siły Coriolisa

1. Zagadnienia teoretyczne.

Ruchem ciała nazywamy jego zmianę położenia w stosunku do innych ciał, które nazywamy układem odniesienia. Układ inercjalny to układ odniesienia, względem, którego każde ciało pozostaje w ruchu jednostajnym prostoliniowym lub w spoczynku, chyba, że działa na nie siła zewnętrzna. Z układem inercjalnym ściśle powiązana jest I zasada dynamiki Newtona. Z kolei układ nieinercjalny to taki układ odniesienia, który porusza się ruchem obrotowym lub postępowym względem inercjalnego układu odniesienia.

Zasada zachowania energii.

Zgodnie z tą zasadą suma energii potencjalnej i kinetycznej układu jest stała, co oznacza że jeżeli jedna z energii rośnie to druga musi równocześnie maleć.

2. Przebieg doświadczenia.

a) Ustawić koniec równi na osi obrotu tarczy.

b) Położyć na tarczy krążek papieru, tak by położona na jej wierzchołku kalka była zwrócona stroną rysującą do dołu.

c) Włączyć gramofon do sieci.

d) Puścić kulkę z górnego końca równi.

e) Zmierzyć wysokość równi h w punkcie gdzie kulka zaczyna staczać się i z zasady zachowania energii obliczyć prędkość liniową kulki na poziomie tarczy. Po zdjęciu papieru z tarczy jest na nim ślad kulki w postaci odcinka paraboli. Z punktu O wykreślamy dwa odcinki: R - styczny do toru, R₁ - łączy koniec i początek śladu. Kąt między tymi prostymi jest równy α.

f) Mierzymy czas trwania n pełnych obrotów tarczy i liczymy prędkość kątową tarczy za pomocą wzoru:

g) Następnie liczymy przyspieszenie Coriolisa za pomocą wzoru:

h) Ze wzoru:

obliczamy wartość siły Coriolisa;

1. Czynności od d do h powtarzamy dla drugiej kulki;

j) Liczymy błąd przy pomiarze przy śpieszenia Coriolisa metodą średniego błędu kwadratowego.

Obliczenia.

Kulka granitowa.

h = 0,103m

α₁=0,401rad

T_n=8,1s - czas trwania n pełnych obrotów tarczy (dla n = 5)

Wyznaczamy prędkość kątową tarczy korzystając z wzoru:

Z zależności α=ωt wyznaczamy czas w jakim tarcza obróci się o dany kąt

Następnie z zasady zachowania energii obliczamy prędkość kulki

E_p=E_k

,

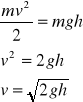
Z zależności
obliczamy promień tarczy R

R=tv

R₁=0,103·1,422=0,146m, ∆R=0,001m

Korzystając ze wzoru: a_c=2vω i podstawiając odpowiednio
i
otrzymamy;

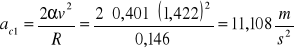
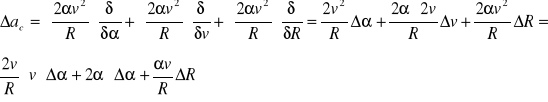
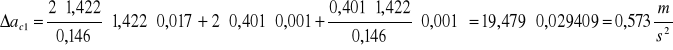
F_c=ma_c

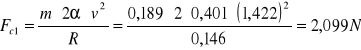
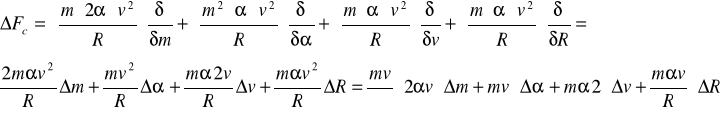
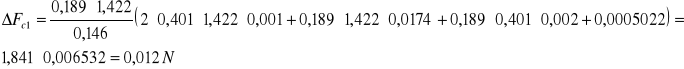
Analogicznie postępujemy w kolejnych obliczeniach:

h = 0,103m

α₂=0,366rad

T_n=8,1s

t=0,094s

R=0,134m

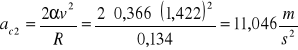
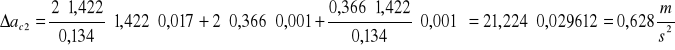
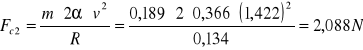
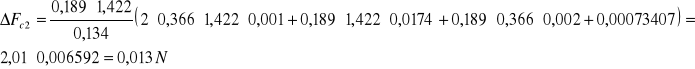
h = 0,103m

α₃=0,349rad

T_n=8,1s

t=0,09s

R=0,128m

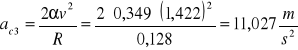
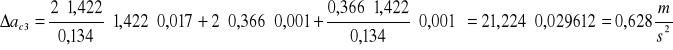
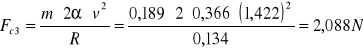
h = 0,103m

α₄=0,332rad

T_n=8,1s

t=0,086s

R=0,122m

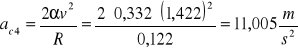
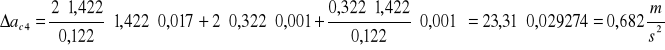
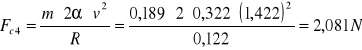
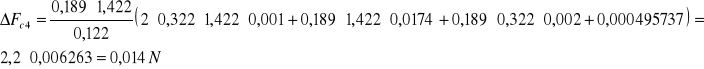
α₁=0,401rad= α₅ z tego wynika że:

R₅=R₁=0,146m

t₅=t₁=0,103s

F_c5=F_c1=2,099N

∆F_c5=∆F_c1=0,012N

Kulka metalowa

h = 0,103m

α₁=0,279rad

T_n=8,1s - czas trwania n pełnych obrotów tarczy (dla n = 5)

Wyznaczamy prędkość kątową tarczy korzystając z wzoru:

Z zależności α=ωt wyznaczamy czas w jakim tarcza obróci się o dany kąt

Następnie z zasady zachowania energii obliczamy prędkość kulki

E_p=E_k

,

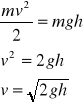
Z zależności
obliczamy promień tarczy R

R=tv

R₁=0,072·1,422=0,102m, ∆R=0,001m

Korzystając ze wzoru: a_c=2vω i podstawiając odpowiednio
i
otrzymamy;

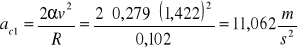
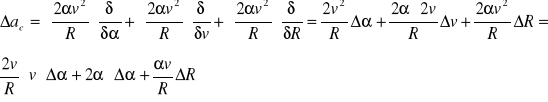
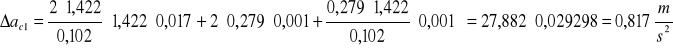
F_c=ma_c

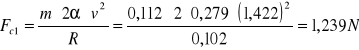
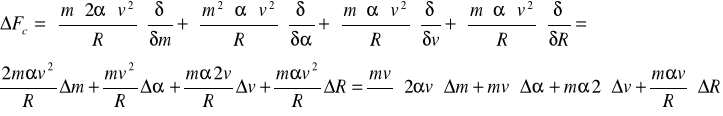
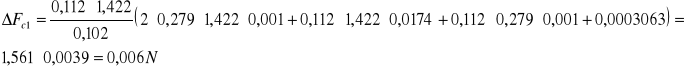
Analogicznie postępujemy w kolejnych obliczeniach:

α₂=0,279rad= α₁ z tego wynika że:

R₂=R₁=0,102m

t₂=t₁=0,072s

F_c2=F_c1=1,239N

∆F_c2=∆F_c1=0,006N

h = 0,103m

α₃=0,297rad

T_n=8,1s

t=0,076s

R=0,108m

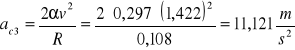
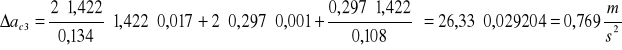
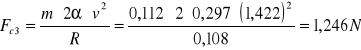
h = 0,103m

α₄=0,349rad

T_n=8,1s

t=0,09s

R=0,128m

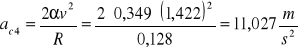
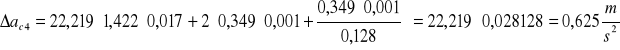
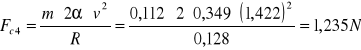
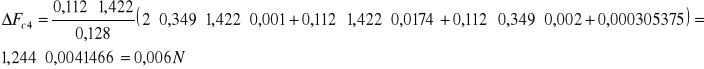
h = 0,103m

α₅=0,391rad

T_n=8,1s

t=0,1s

R=0,142m

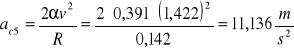
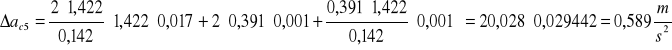
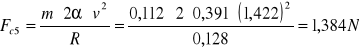
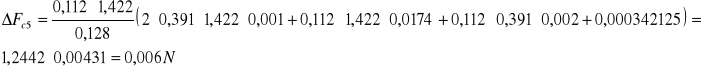
Obliczamy średni błąd kwadratowy pomiaru przyśpieszenia Coriolisa:

kulka granitowa

F_cś=(2,091±0,013)N

Kulka metalowa

F_cś=(1,269±0,029)N

Wnioski.

Na podstawie wyników z przeprowadzonego doświadczenia dochodzimy do następujących wniosków: siła Coriolisa zależy od promienia, masy i prędkości liniowej. Różnice w obliczeniach mogą być spowodowane niedokładnością przyrządów pomiarowych i możliwością popełnienia błędu przez wykonujących doświadczenie.

---