Andrzej Kądziołka 28.02.2006

1AD gr.L2

Sprawozdanie z ćwiczenia nr 21

Rozładowanie kondensatora.

1. Zagadnienia teoretyczne:

Pojemnością elektryczną odosobnionego przewodnika nazywamy wielkość fizyczna C równą stosunkowi ładunku q zgromadzonego na przewodniku do potencjału
tego przewodnika.

Odosbniony przewodnik znajduje się w tak dużej odległości od innych ciał, że wpływ ich pola elektrycznego jest pomijalny.

Kondensator to element elektryczny (elektroniczny) zbudowany z dwóch przewodników (okładzin) rozdzielonych dielektrykiem. Doprowadzenie napięcia do okładzin kondensatora powoduje zgromadzenie się na nich ładunku elektrycznego.

Kondensator charakteryzuje pojemność wyrażona w faradach. Jeden farad to bardzo duża jednostka, dlatego w praktyce spotyka się kondensatory o pojemnościach piko-, nano- i mikrofaradów.

Ogólnie, napięcie u_C i prąd i_C kondensatora w chwili t związane są zależnością:

Energię W zgromadzoną na okładkach kondensatora można policzyć korzystając z:

Wzór ten podaje pracę dW, jaka jest potrzebna na przesunięcie ładunku dq z jednej okładki kondensatora o pojemności C na drugą, przy założeniu, że jedna z okładek jest naładowana ładunkiem q, a druga - ładunkiem -q.

Całą energię zmagazynowaną w kondensatorze oblicza się przez scałkowanie powyższego wzoru, uzyskując:

przy czym Q jest ładunkiem, do którego naładowano kondensator, związanym z napięciem na okładkach za pomocą zależności:

Wiedząc o tym, że prąd elektryczny to zmiana ładunku w czasie, można również zapisać:

Dla prądu stałego (
) kondensator jest równoważny przerwie w obwodzie (i_C = 0), ale dopiero od chwili zakończenia się jego ładowania. Dla prądu przemiennego prąd płynący przez kondensator powoduje pewien spadek napięcia. Wielkość, wiążąca prąd i napięcie na kondensatorze nazywa się reaktancją, która jest tym mniejsza, im większa jest pojemność kondensatora i częstotliwość prądu. Kondensator charakteryzuje się tym, że (dla sygnałów sinusoidalnych) napięcie jest opóźnione w fazie względem prądu o kąt 90 stopni (inaczej: prąd wyprzedza napięcie o kąt 90 stopni). Z tego względu impedancja kondensatora jest wartością urojoną i opisana jest wzorem:

,

gdzie C to pojemność kondensatora w faradach, f to częstotliwość w hercach.

Kondensator jest jednym z podstawowych elementów elektronicznych, szeroko wykorzystywany we wszystkich typach układów, w szczególności razem z cewką tworzy obwód rezonansowy.

Ze względu na różną konstrukcję kondensatory można podzielić na:

• elektrolityczne (dielektrykiem jest cienka warstwa tlenku, a osadzona elektrolitycznie na okładzinie dodatniej, drugą okładziną jest elektrolit), pracują poprawnie tylko dla małych częstotliwości, ale mają duże pojemności przy małych rozmiarach

• poliestrowe (dielektrykiem jest folia poliestrowa)

• ceramiczne (dielektrykiem jest specjalna ceramika), znakomicie pracują przy wielkich częstotliwościach, bywają wykonywane też jako kondensatory o zmiennej pojemności

• powietrzne (dielektrykiem jest powietrze) - znakomicie pracują przy wysokich częstotliwościach i bardzo dużych napięciach, często wykonywane jako kondensatory zmienne.

2. Wykonanie ćwiczenia

a) połączyć obwód wg schematu,

b) naładować kondensator. Ustawić taką wartość oporu R, aby natężenie prądu było maksymalne,

c) przełączyć przełącznik K w pozycję 2 i jednocześnie włączyć sekundomierz.

Przeprowadzić pomiary natężenia prądu rozładowania kondensatora I= f(t),

d) sporządzić wykres zależności prądu rozładowania I= f(t),

e) wartość ładunku zgromadzonego na okładkach kondensatora obliczyć wyznaczając wartość

pola powierzchni zawartego między osiami współrzędnych a wykresem,

f) wyznaczyć pojemność kondensatora,

g) obliczyć stałą czasową obwodu.

3. Wyniki pomiarów

U	R	Io	t	I	Q	C	τ
[V]	[Ω]	[μA]	[s]	[μA]	[C]	[F]	[s]
4,9	33900	140	0,00	140			17,57
			1,84	130
			2,75	120
			4,62	110
			5,96	100
			8,12	90
			9,70	80
			11,94	70
			14,74	60
			18,08	50
			21,89	40
			27,10	30
			34,18	20
			46,79	10
			99,43	0

Δt=0,4s

4. Obliczenia i rachunek błędów:

Wartość ładunku zgromadzonego w kondensatorze obliczona na podstawie wykresu I= f(t):

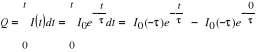
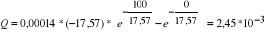
C

Pojemność kondensatora:

F

Stała czasowa obliczona z zależności
:

s

Stała czasowa obliczona korzystając z wykresu
poprzez wyznaczenie współczynnika kierunkowego tej prostej:

,

s

Błąd bezwzględny pomiaru natężenia prądu:

s

5. Wykresy

Równanie prostej obliczonej metodą najmniejszych kwadratów

(Microsoft Excel - funkcja REGLINP):

6. Wnioski:

Przeprowadzone doświadczenie miało na celu zbadanie przebiegu rozładowania kondensatora oraz wyznaczenie stałej czasowej obwodu. Przebieg narysowanych wykresów oraz obliczenia wskazują na poprawność wykonania ćwiczenia. Przeprowadzenie tego doświadczenia pozwoliło zaobserwować przebieg zmienności natężenia prądu na kondensatorze oraz wykonać zadania związane z ćwiczeniem.

---