1

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

Metoda Elementów Skończonych

LABORATORIUM METOD KOMPUTEROWYCH

ELEMENT RAMOWY

2

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

Algorytm MES

1.Dyskretyzacja
2.Obciążenie
3.Analiza elementu
4.Agregacja
5.Warunki brzegowe
6.Rozwiązanie równania MES
7.Siły wewnętrzne

► Edof
► f ,fe
► Ke
► K
► bc
► Ka=f
► M,Q,N

3

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

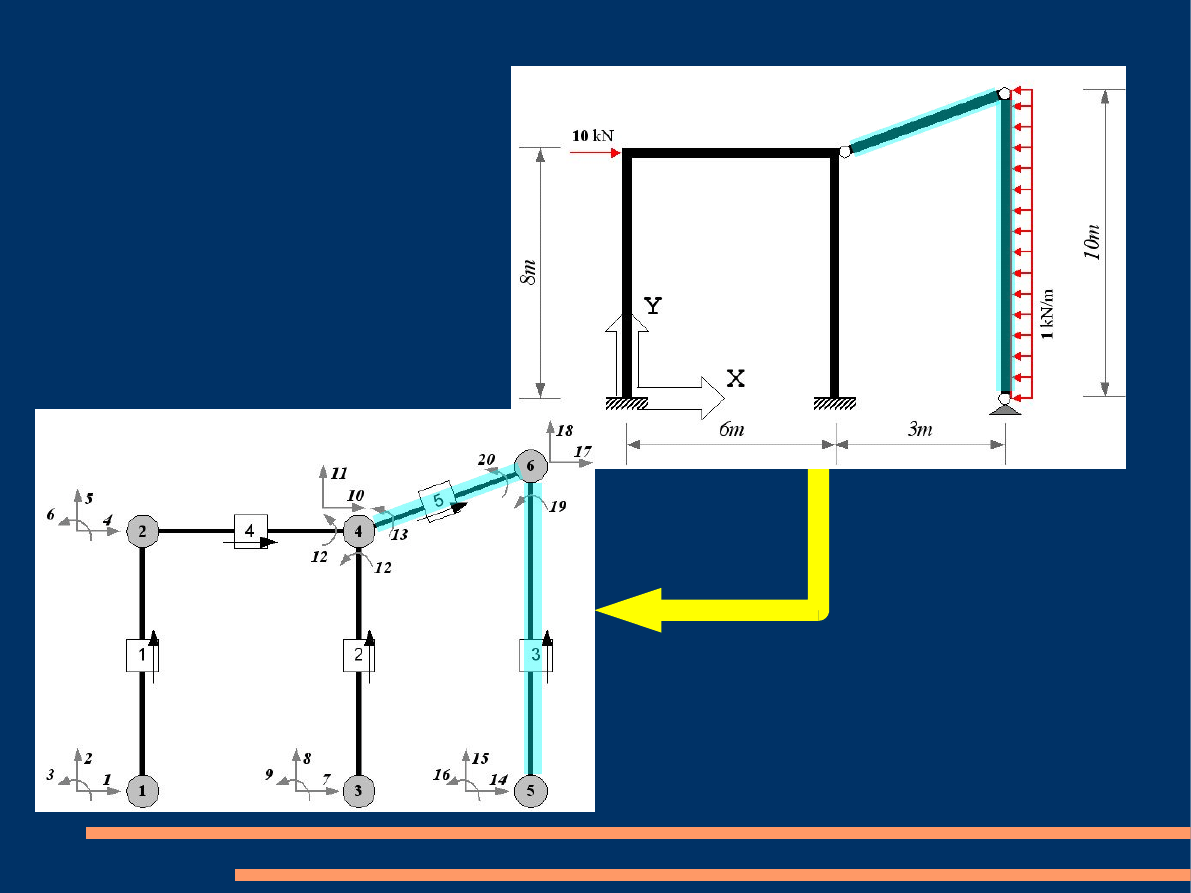
Dyskretyzacja

Schemat konstrukcji obci-

ążonej statycznie z prętów

stalowych

i żelbetowych

4

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

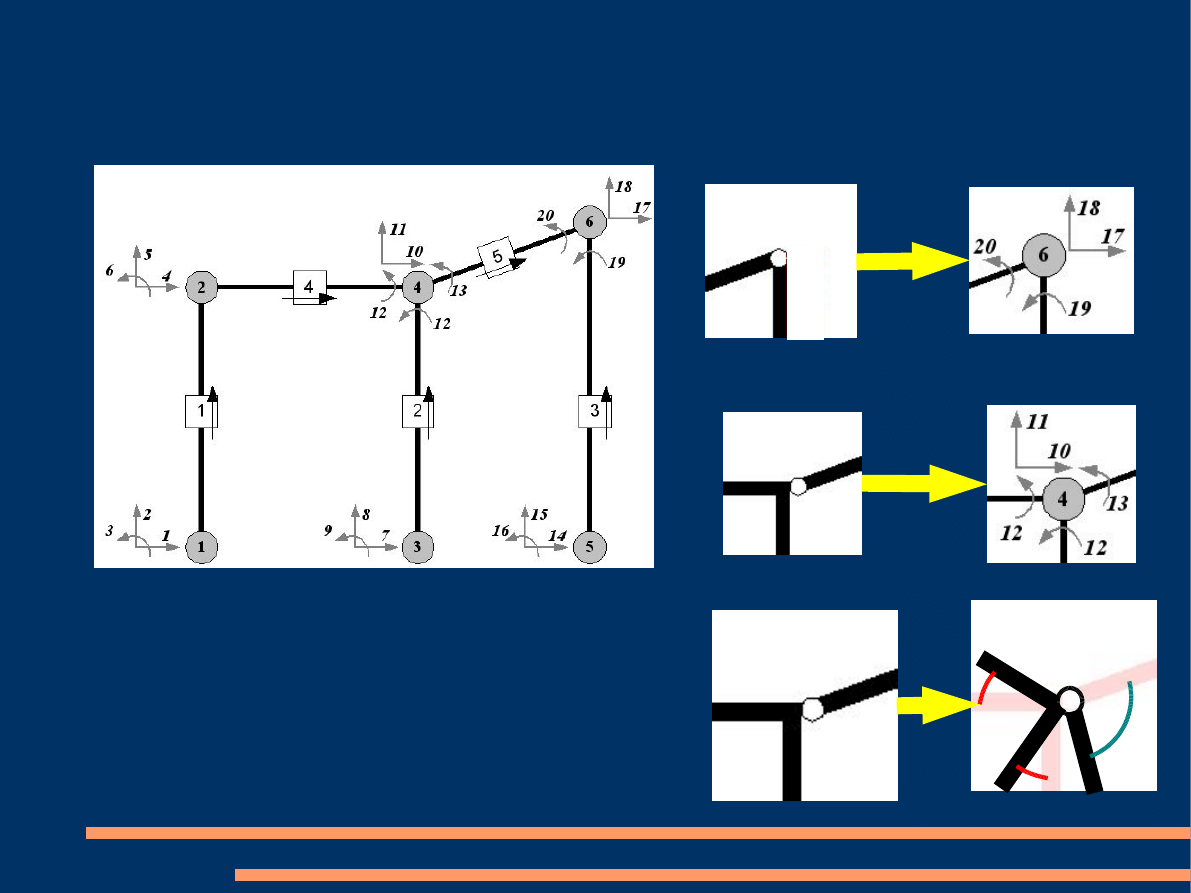
Dyskretyzacja

W miejscach wstępowania przegubów w

zależności od krotności przegubu musimy zwi-
ększyć ilość stopni swobody. Każdy element
dołączony w sposób przegubowy ma możliwo-
ść niezależnego obrotu w węźle

f1

ą

f2

5

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

Dyskretyzacja

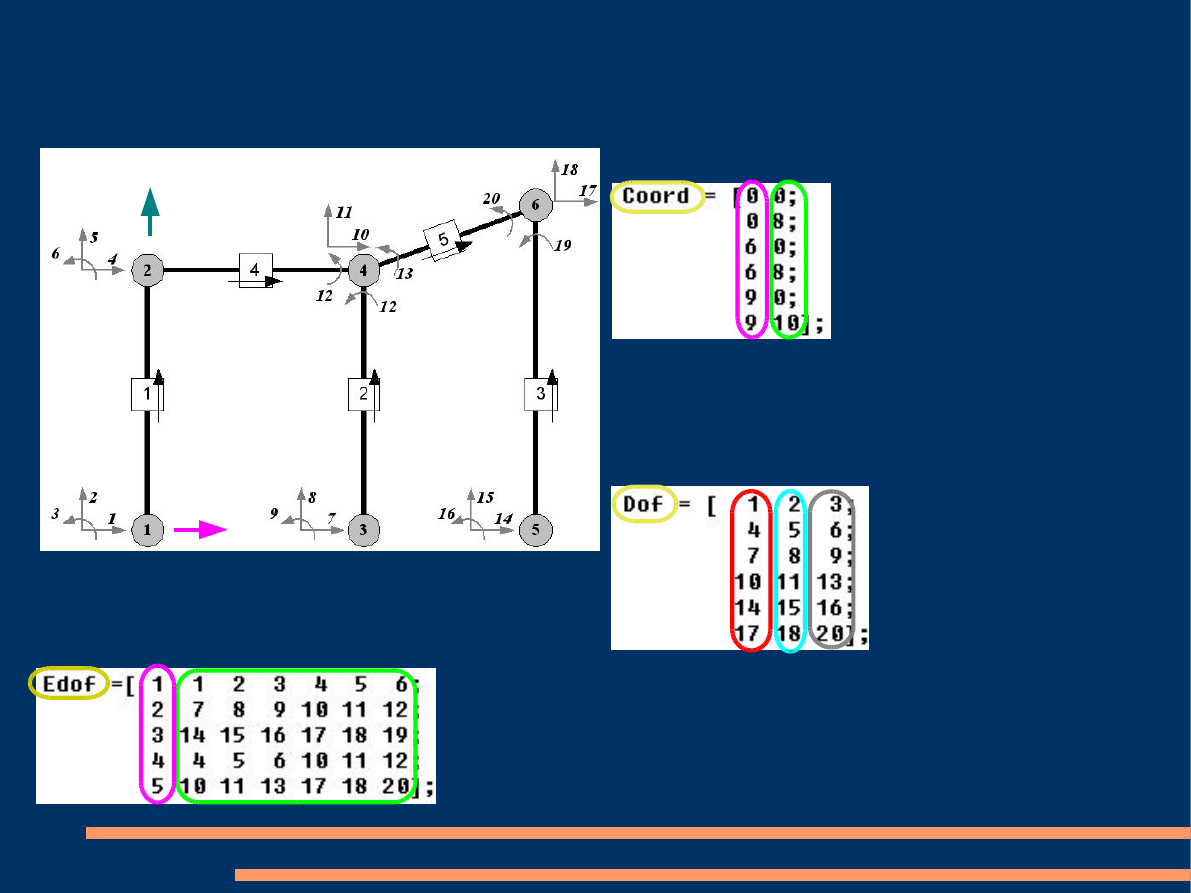
3.Macierz topologii

Edof

:

- Numery

elementów układu,

- Numery

stopni swobody wg numeracji globalnej.

Kolejność węzłów determinuje lokalne układy
współrzędnych.

1.Macierz współrzędnych

Coord

:

- odcięte

(oX)

- rzędne

(oY)

Początek układu (oXY)
w węźle nr 1 → (

0

,

0

)

2.Macierz stopni swobody

Dof

:

Dla kolejnych węzłów w wierszach po
trzy numery stopni swobody kolejno:

- poziome

(oX)

- pionowe

(oY)

- obrotowe

(XY)

``

X

Y

6

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

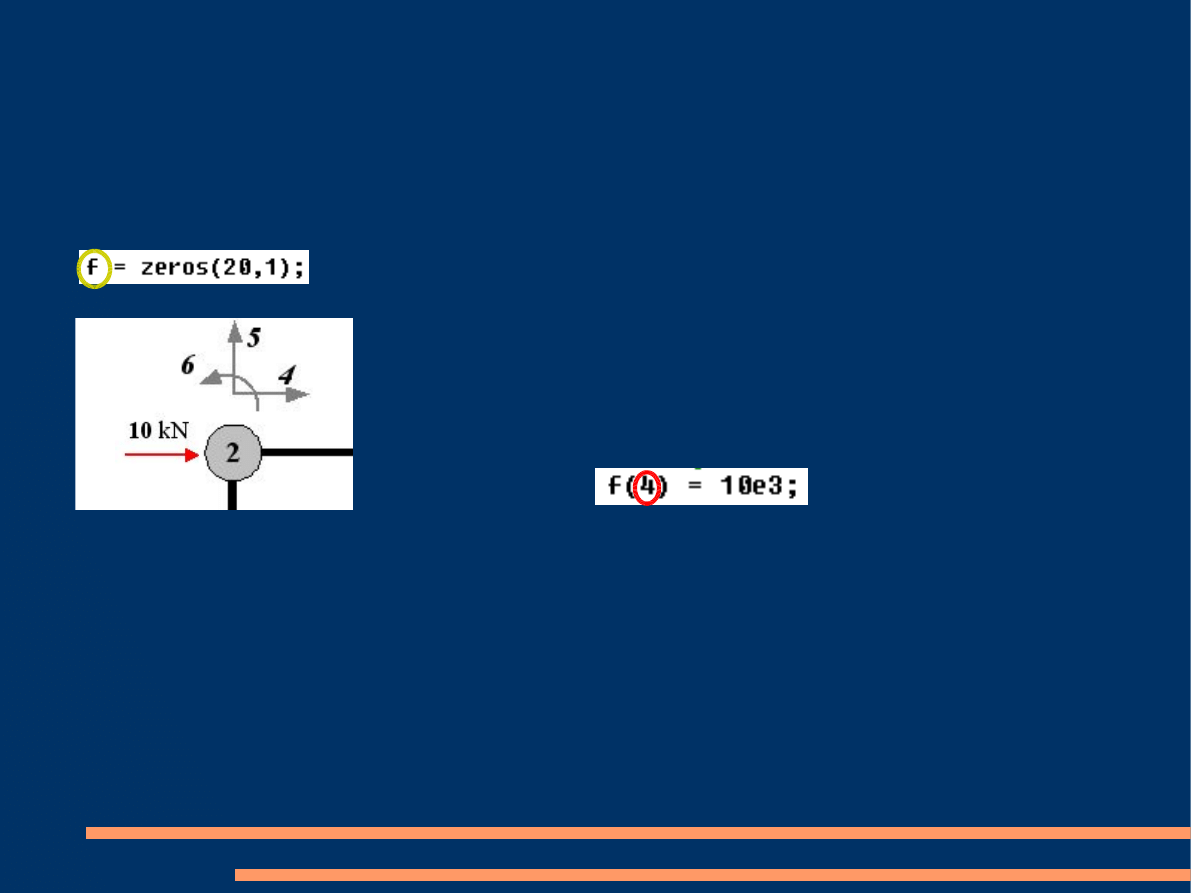
Obciążenie

Wymiar

wektora obciążenia

zależy od liczby stopni swobody układu.

Na kierunku

czwartego

stopnia swobody przyłożo-

ne jest obciążenie o wartości

N=10kN

skierowane

zgodnie z przyjętym za dodatni zwrot przemiesz-

czenia.

Metoda elementów skończonych jest metodą dyskretną dającą

rozwiązanie w skończonej liczbie punktów (węzłów). Obciążenie układu

musi być podane w sposób dyskretny tylko w węzłach. Obciążenie

ciągłe występujące na długości elementów zastępowane jest równowa-

żnym obciążeniem w węzłach. Skupianie obciążenia realizowane jest z

wykorzystaniem

funkcji kształtu.

7

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

Dyskretyzacja

Macierz

[ex,ey]

to macierz ze współrzędnymi

początku

i

końca

każdego elementu w ukła-

dzie.

Na podstawie współrzędnych obliczane są

między innymi długości elementów i kąty ich

nachylenia do poziomu.

Macierz charakterystyk fizycznych

ep

:

- moduł Young'a

,

- pole przekroju poprzecznego

- moment bezwładności przekroju

Dla każdego elementu w wierszach należy

podać stosowne wartości. Podając wartości

liczbowe należy uwzględnić przyjęty system

jednostek.

8

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

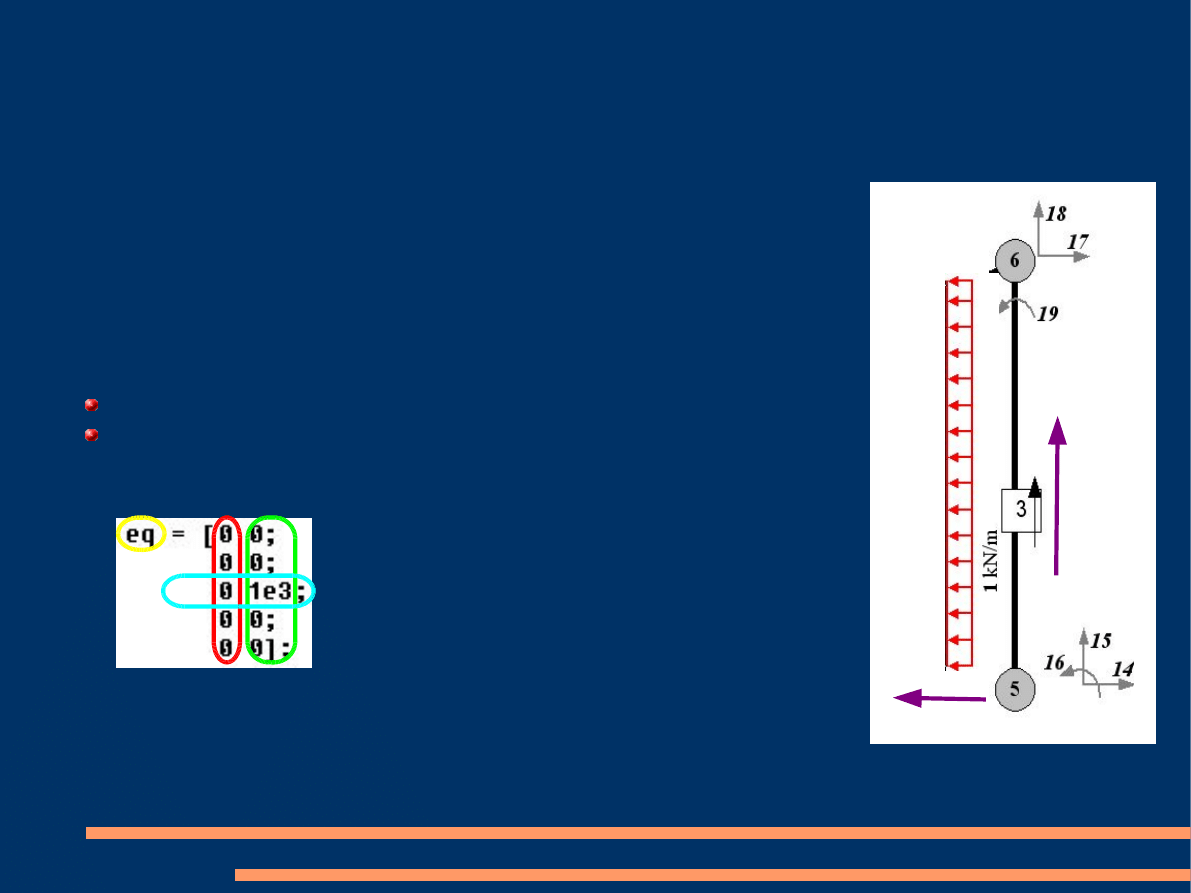
Obciążenie

q

y

q

x

Obciążenie ciągłe elementu podajemy w

macierzy obciążeń elementowych

eq

podając war-

tości obciążenia

qx

oraz

qy

zgodnie z jego

lokal-

nym

układem współrzędnym.

Zwroty osi lokalnych determinowane są przy

definicji elementu (Edof):

Oś oX ma zwrot

początek→koniec

elementu

.

Oś oY jest prostopadła do oX oraz obrócona 90° w lewo.

Element

trzeci

obciążony jest

obciążeniem o intensywności

1000 N/m.

`

9

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

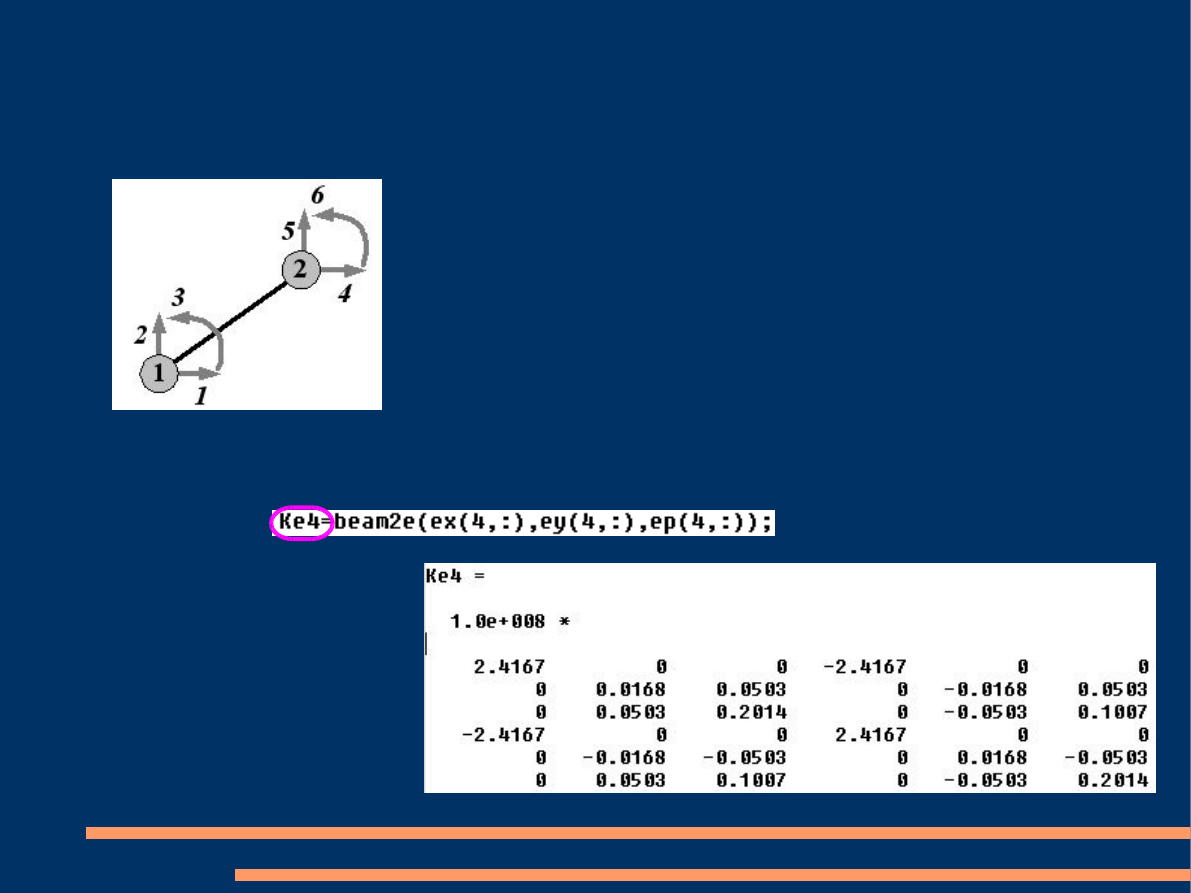
Analiza elementu

Element węzłowy jest kombinacją elementu

prętowego i belkowego. Węzły elementu ra-
mowego mają po trzy

stopnie swobody.

Wymiar

lokalnej macierzy sztywności elementu

zależy od liczby stopni swobody elementu.

►

Macierz

sztywności elementu czwartego.

10

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

Agregacja

Wymiar

globalnej macierzy sztywności układu

za-

leży od ilości stopni swobody w układzie.

Agregacja

polega na dodaniu wszystkich lokalnych macierzy

sztywności elementów

(Ke)

w jedną macierz sztywności układu

(K)

z uwzględnieniem topologii układu

(Edof).

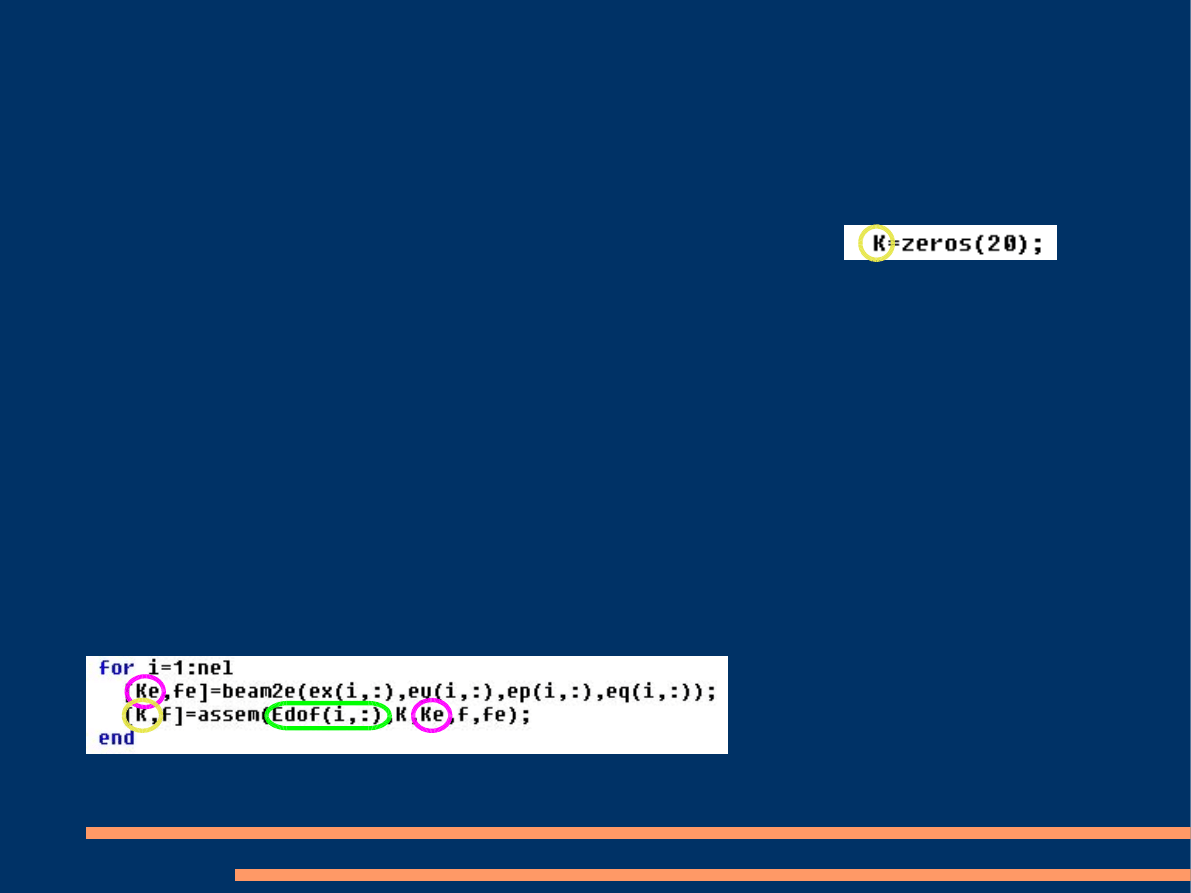
Generowanie lokalnych macierzy sztywności

(Ke)

i agregacja

odbywa się w pętli (

for

►

end

). W tej samej pętli na podstawie macierzy

obciążeń elementowych

eq

obliczane są elementy wektora obciążenia

elementowego

fe,

który następnie jest agregowany do wektora obci-

ążeń węzłowych

f

11

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

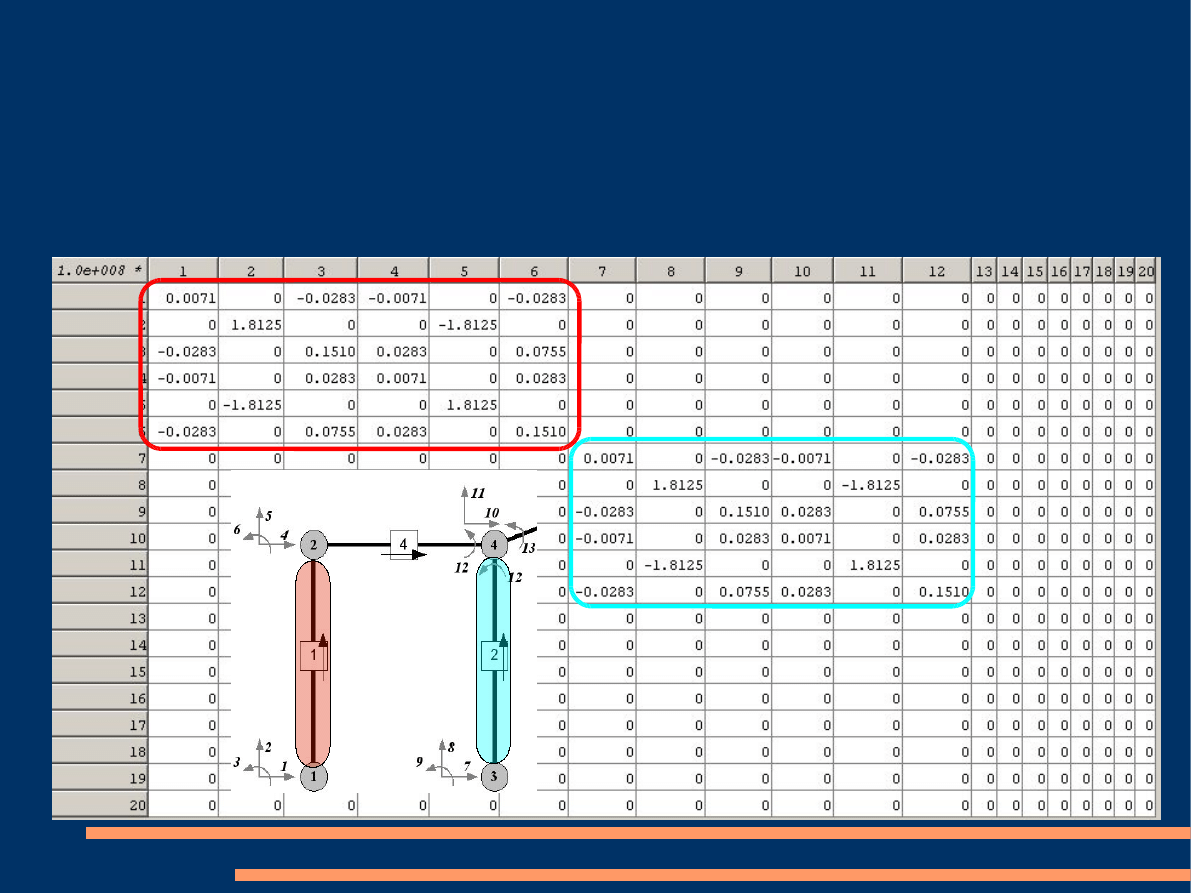
Agregacja

Na rysunku poniżej widać elementy globalnej macierzy sztywności

(K)

po dwóch krokach pętli.

12

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

Warunki brzegowe

Dla odpowiednich

stopni swobody

w układzie

globalnym podajemy

wartości

znanych prze-

mieszczeń wynikające z schematu podparcia
układu.

Uwzględnienie warunków brzegowych układu powoduje pod-

stawienie do układu równań znanych wartości niewiadomych, co przy

wartościach równych zero powoduje wykreślenie odpowiednich

wierzy i kolumn z macierzy sztywności układu.

W konsekwencji redukuje się wymiar macierzy sztywności układu i

macierz wówczas staje się macierzą nieosobliwą.

Obciążenie poza statyczne w postaci osiadania

podpór uwzględnia się w warunkach brzegowych.

13

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

Rozwiązanie równania MES

Rozwiązaniem równania MES

Ka=f

są nieznane

wartości

stopni

swobody będące przemieszczeniami węzłów układu globalnego.

Wartości

reakcji

więzów podporowych obliczane są po rozwiąza-

niu równania MES z równości

R=Ka-f

14

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

Obliczenie sił wewnętrznych

Po rozwiązaniu równania następuje rozdzielenie obliczonych

przemieszczeń

otrzymanych w układzie globalnym na przemiesz-

czenia w układach lokalnych wszystkich elementów z uwzględnieniem

topologii

układu.

Dla każdego elementu na podstawie

przemieszeń

jego węzłów,

cha-

rakterystyk przekroju

,

współrzędnych węzłów

oraz

obciążeń elemen-

towych

oblicza się wartości siły wewnętrznych w elemencie (N,Q,M) .

~`````

Funkcja kształtu

jednoznacznie określa przemieszczenia we-

wnątrz elementu na podstawie wartości przemieszczeń węzłów

elementu.

u

e

=

N

*a

e

15

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

Forma projektu

1. S

tr

ona tytułowa

2. Schemat układu

→rysunek

3. Dyskretyzacja

→rysunek

4. Macierz topologii

5. Macierz sztywności elementu piątego
6. Wektor obciążenia (elementy niezerowe)
7. Reakcje więzów podporowych (niezerowe)
8. Deformacja układu

→rysunek

9. Wykresy sił wewnętrznych z opisami wartości

w punktach charakterystycznych (N,Q,M)

→rysunek

10.Wyniki dla jednego z elementów w tabeli:

•

sztywności elementu (EA,EI)

•

przemieszczenia węzła początkowego

•

przemieszczenia węzła końcowego

16

LABORATORIUM METOD KOMPUTEROWYCH – KATEDRA MECHANIKI KONSTRUKCJI

Pytania

1.Algorytm MES z omówieniem jego etapów
2.Charakterystyka elementu ramowego

1.Stopnie swobody

3.Własności macierzy sztywności
4.Funkcja kształtu
5.Definicja obciążeń
6.Pętla

for ► end

7. Interpretacja wyników

1.Analiza zastosowanych jednostek