v

Q



const

V 

)

,

(

const

V

T

p



V

T

S

p

T

k

T

v

Q



k

S

p

S

)

,

(

const

V

S

T



Zadanie 1.26

Obliczyć wartość pracy technicznej

t

L , przyrost ilości ciepła przemiany

v

Q



oraz

przyrost zasobu entalpii

H



zasobu masy

 

kg

m

5

,

1



tlenu traktowanego jako gaz doskonały

podczas jego rozprężania w warunkach przemiany izochorycznej odwracalnej od wartości
początkowych ciśnienia





bar

p

p

5



i temperatury

 

C

t

p



 27

do wartości końcowej ciśnienia

równej

 

Tr

p

k

1500



. Zasób objętości w której zachodzi przemiana równy jest

 

3

5

,

0

m

V 

,

ciepło właściwe tlenu przy stałym ciśnieniu

















K

g

cal

c

p

22

,

0

, zaś objętościowa gęstość

zasobu masy rtęci















3

596

,

13

dm

kg

Hg



.

Dane:

Obliczyć:

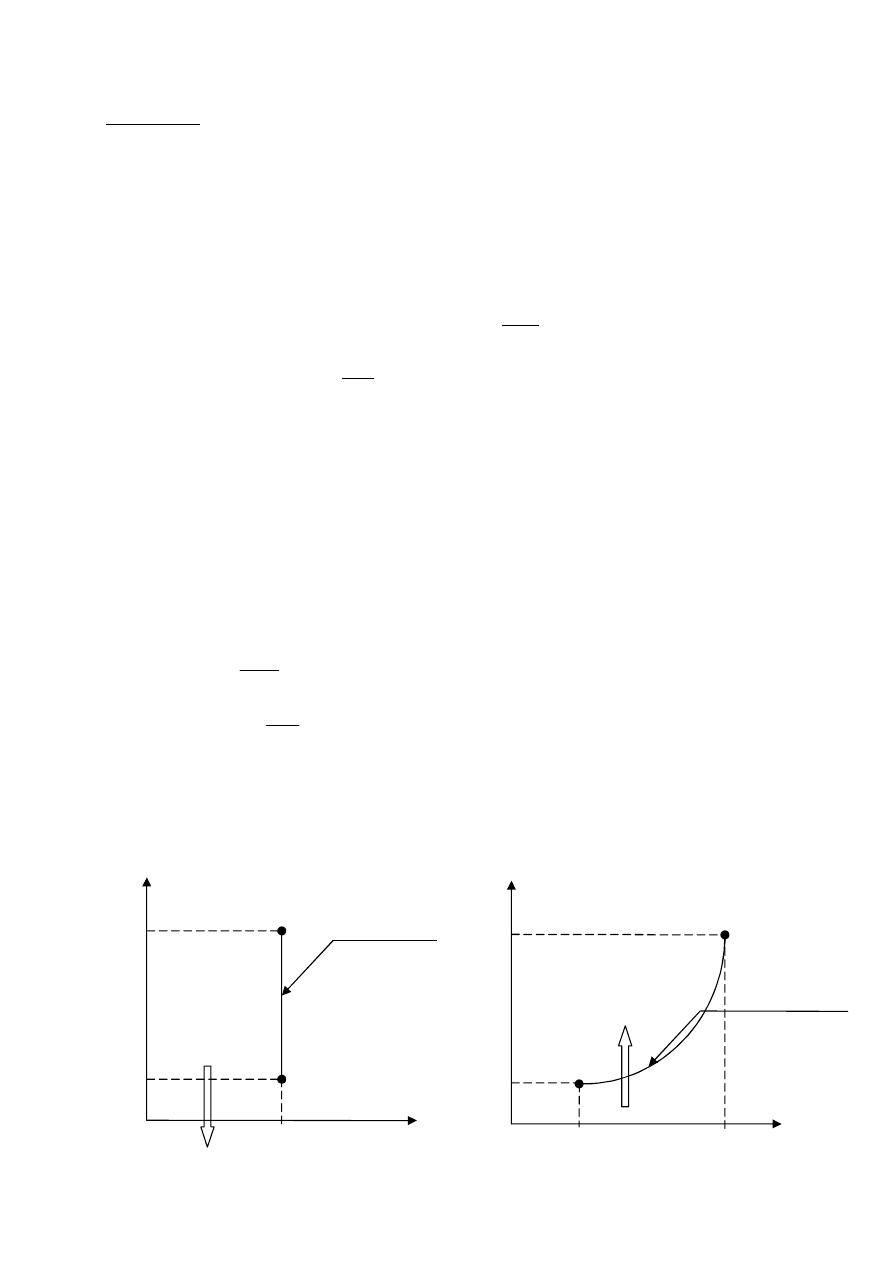
1. Rozprężanie w przemianie izochorycznej.

 





 

 

 













































3

3

596

,

13

22

,

0

5

,

0

1500

25

5

5

,

1

dm

kg

K

g

cal

c

m

V

Tr

p

C

t

bar

p

const

V

kg

m

Hg

p

k

p

p



?

?

?











H

Q

L

v

t

p

P

k

P

P

2. Bilans zasobu energii wewnętrznej i entalpii dla przemiany

odwracalnej.

- Pierwsza postać I zasady termodynamiki:

- Druga postać I zasady termodynamiki:

3. Wyznaczanie pracy technicznej przemiany izochorycznej

odwracalnej.

Praca techniczna określona jest związkiem:

Vdp

L

t







Całkując powyższe równanie w granicach:









k

p

t

p

p

L

t

dp

V

L

0



Otrzymamy:





k

p

t

p

p

V

L





Pracę techniczną rozprężania tlenu kreowaną wewnątrz układu substancjalnego o stałej
objętości:

4. Wyznaczanie temperatury końca przemiany izochorycznej.

Równanie izochory ma postać:

p

k

p

k

T

T

p

p



Temperatura końca przemiany izochorycznej jest równa:

t

L

Q

H











L

Q

E













pdV

L 



Vdp

L

t







p

p

k

k

p

T

p

T





5. Wyznaczanie przyrostu zasobu entalpii tlenu w przemianie

izochorycznej.

Zasób entalpii określany jest związkiem

T

m

c

H

p







Dla gazu doskonałego

const

c

p



Dla układu substancjalnego

const

m 

Zatem przyrost zasobu entalpii określany jest zależnością:

mdT

C

dH

p





Całkując ostatnie równanie w granicach i uwzględniając temperaturę końca przemiany
izochorycznej:









k

p

k

p

T

T

p

H

H

dT

m

C

dH

otrzymano











































1

p

k

p

p

p

k

p

p

k

p

p

T

m

C

T

T

m

C

H

H

H

6. Wyznaczanie przyrostu ilości ciepła przemiany izochorycznej,

rozprężania tlenu.

Zgodnie z drugą postacią pierwszej zasady termodynamiki mamy:

t

L

H

Q











Całkując ostatnie równanie w granicach z uwzględnieniem wyniku określającego pracę
techniczną przemiany izochorycznej:











v

t

k

p

Q

L

O

t

H

H

L

H

Q

0







Otrzymamy:





k

p

p

k

p

p

t

v

p

p

V

p

p

T

m

C

L

H

Q







































1

7. Rachunek miar dla pracy technicznej

 

t

L

 

J

s

m

kg

m

s

m

kg

m

N

m

N

m

Pa

m

L

t

























2

2

2

2

3

3

8. Rachunek miar dla przyrostu entalpii

H







J

Pa

Pa

K

kg

K

kg

J

H















9. Obliczanie wartości pracy technicznej rozprężenia tlenu w

przemianie izochorycznej.

Wyrażenie wartości ciśnienia końcowego w jednostkach SI.

 





MPa

Pa

g

h

p

Hg

k

k

19933

,

0

19930

81

,

9

13546

5

,

1



















Wyrażenie wartości ciepłą właściwego tlenu w jednostkach SI.

Mechaniczny równoważnik ciepła jest równy:















kcal

kJ

I

19

,

4

Zatem ciepło właściwe tlenu wyrażone w jednostkach SI jest równe:













































































kgK

J

kgK

J

kgK

kJ

kcal

kJ

kgK

kJ

c

p

8

,

921

10

19

,

4

22

,

0

19

,

4

22

,

0

19

,

4

22

,

0

3

Pracę techniczną wyrazimy zgodnie z zależnością:









 

 

kJ

J

p

p

V

L

k

p

t

34

,

150

10

34

,

150

10

9933

,

1

10

5

5

,

0

3

5

5





















10. Obliczanie wartości przyrostu zasobu entalpii:

Zgodnie ze związkiem określającym przyrost zasobu entalpii otrzymamy:

 

]

[

575

,

249

10

575

,

249

1

5

,

0

19933

,

0

)

16

,

273

27

(

5

,

1

8

,

921

1

3

kJ

J

p

p

T

m

C

H

p

k

p

p



























































11. Obliczanie wartości przyrostu ilości ciepła:

]

[

156

,

100

]

[

10

156

,

100

10

34

,

150

10

575

,

249

3

3

3

kJ

J

L

H

Q

t

v



























