Informatyka - Podstawy Programowania w Języku C++

prow. Sławomir Czarnecki

Zadania na laboratorium nr. 10

1. Zdefiniuj funkcję

void

point(

double

** T,

int

m,

int

n,

int

* a,

int

* b)

inicjalizującą składowe każdego wiersza

(

)

0,1,...,

1

i

i

m

=

−

T

macierzy

m n

M

×

∈

T

o

wymiarach

m n

×

całkowitymi liczbami pseudolosowymi z przedziału domkniętego

[

]

(

)

,

0,1,...,

1

i

i

a b

i

n

=

−

będącymi składowymi wektorów

,

n

∈

a b

ℝ

(

)

i

i

a

b

<

. Parametr m

oznacza żądaną liczbę punktów w przestrzeni

n

ℝ . Funkcja point(...) generuje zatem m

punktów w n wymiarowej przestrzeni Euklidesowej, których współrzędne kartezjańskie
zapisywane są do macierzy T (por. rys.1a).

2.

Zdefiniuj funkcję

double

scalar(

double

* a,

double

* b,

int

n)

która zwraca iloczyn skalarny dwóch wektorów

[

]

[

]

0

1

1

0

1

1

, ,...,

,

, ,...,

T

T

n

n

n

a a

a

b b

b

−

−

=

=

∈

a

b

ℝ .

3. Zdefiniuj funkcję

bool

separation(

double

** T,

int

m,

int

n,

bool

positive,

double

* w)

która zwraca wartość

true

jeśli odpowiednio wszystkie m punktów

(

)

0,1,...,

1

n

i

i

m

∈

=

−

T

ℝ

w przestrzeni

n

ℝ , reprezentowanych przez składowe macierzy

m n

M

×

∈

T

spełniają warunek

0

i

⋅

>

T w

(przypadek positive =

true

) lub jeśli wszystkie te punkty spełniają warunek

0

i

⋅

<

T w

(przypadek positive =

false

). W pozostałych przypadkach (positive =

true

oraz

{

}

0,1,...,

1

0

i

i

m

w

∃ ∈

−

⋅

≤

T

lub positive =

false

oraz

{

}

0,1,...,

1

0

i

i

m

w

∃ ∈

−

⋅

≥

T

)

funkcja

separation(...) zwraca wartość

false

. Zakładamy, że wektor klasyfikiujący

n

∈

w

ℝ jest różny

od zera.

4.

Zaimplementuj w postaci funkcji

void

perceptron(

double

** P,

double

** N,

int

pos,

int

neg,

int

n,

long

tmax,

long

tcon)

algorytm uczenia się perceptronu (AUP)
start: Wektor wagowy

0

n

∈

w

ℝ jest generowany losowo. Inicjalizujemy t = 0.

test:

Wektor

P

N

∈

∪

x

jest wybrany losowo,

jeśli

P

∈

x

i

0

t

⋅ >

w x

to idź do test,

jeśli

P

∈

x

i

0

t

⋅ ≤

w x

to oblicz

1

t

t

+

=

+

w

w

x

uaktualnij

1

t

t

= + , idź do test

jeśli

N

∈

x

i

0

t

⋅ <

w x

idź do test,

jeśli

N

∈

x

i

0

t

⋅ ≥

w x

to oblicz

1

t

t

+

=

−

w

w

x uaktualnij

1

t

t

= + , idź do test

Algorytm AUP dokonuje modyfikacji wektora wagowego

n

∈

w

ℝ w każdym przypadku

kiedy wybrany losowo ze zbioru

P lub N punkt

n

∈

x

ℝ nie został sklasyfikowany poprawnie.

Parametry P i N są tablicami odpowiednio

pos

n

M

×

i

neg

n

M

×

przechowującymi współrzędne

kartezjańskie

pos punktów ze zbioru

n

P ⊂ ℝ i neg punktów ze zbioru

n

N ⊂ ℝ . Zakładamy

przy tym, że zbiory te są rozłączne, tzn.

P

N

∩

= ∅ oraz, że nie zawierają punktu

n

∈

0

ℝ .

Parametr

tmax definiuje maksymalną liczbę iteracji algorytmu i zabezpiecza przed zbyt dużą

liczbą pętli. Można wykazać, że jeśli dwa zbiory

P i N są liniowo separowalne to początkowy

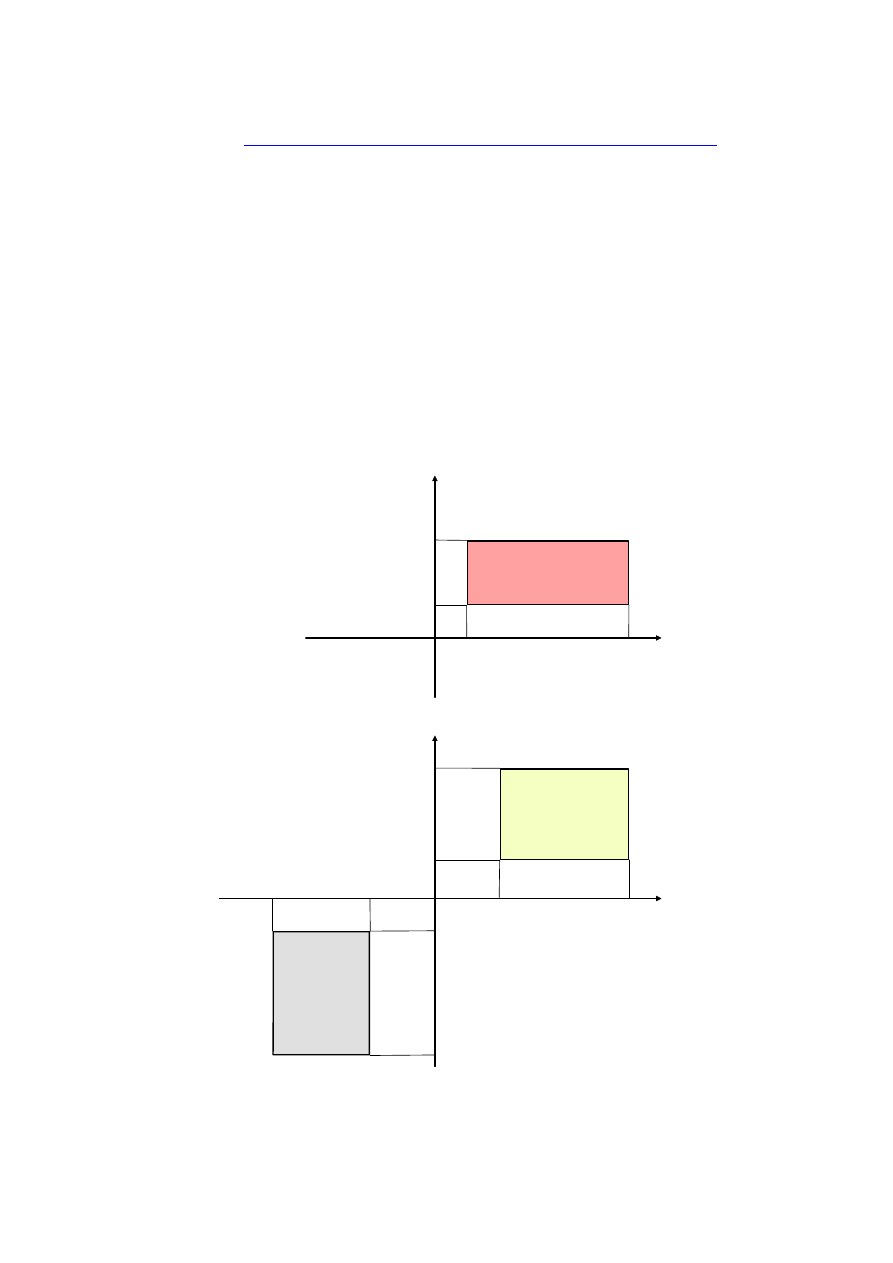
i losowo wygenerowany wektor w będzie modyfikowany w skończonej liczbie kroków (patrz
materiał na stronie

http://wektor.il.pw.edu.pl/~iap/materialy/Perceptron_Uczenie.pdf

).

Opisany powyżej algorytm AUP uzupełnić należy jeszcze, w procedurę sprawdzającą czy
wszystkie punkty zostały sklasyfikowane poprawnie, np. w oparciu o funkcję

separation(...),

której częstotliwość wywoływania definiuje parametr

tcon (funkcję separation(...) można na

przykład wywoływać wtedy kiedy

mod

0

t

tcon =

).

5.

Zdefiniuj (w ciele funkcji main()) dynamicznie dwie macierze

,

m dim

M

×

∈

P N

(m = 100,

dim

= 2) typu

double

, dwa wektory

,

dim

min

max

∈

P

P

ℝ

oraz dwa wektory

,

dim

min

max

∈

N

N

ℝ

typu

int

. Składowe wektorów

,

min

max

P

P

oraz

,

min

max

N

N

zainicjalizuj w taki sposób, aby możliwe

było wygenerowanie za pomocą wywołań:

point

(P, m, dim, Pmin, Pmax), point(N, m, dim, Nmin, Nmax)

dwóch zbiorów punktów

2

,

P N ⊂ ℝ , które będą rozłączne (tzn. P

N

∩

= ∅ ) oraz które nie

będą zawierały punktu

2

∈

0

ℝ (por. rys.1b).

x

y

0

P

N

x

y

0

T

a

0

b

0

a

1

b

1

P

min

[0]

P

max

[0]

P

min

[1]

P

max

[1]

N

min

[0]

N

max

[0]

N

min

[1]

N

max

[1]

Rys. 1a

Rys. 1b

Rys.1.

Generowanie punktów na płaszczyźnie

Wywołaj funkcję perceptron(P, N, m, m, dim, tmax) dla tmax = 1000.