2009-11-27
© Lesław ŁADNIAK
1. M
ETODA PRĄDÓW OCZKOWYCH
Metoda prądów oczkowych nazywana jest też metodą prądów
konturowych lub metodą prądów Maxwella. Ideą tej metody jest
wprowadzenie
nowych zmiennych, tak zwanych prądów
oczkowych. Prąd oczkowy jest to umowny prąd płynący przez
wszystkie gałęzie tworzące oczko.
1.1 Metoda prądów oczkowych
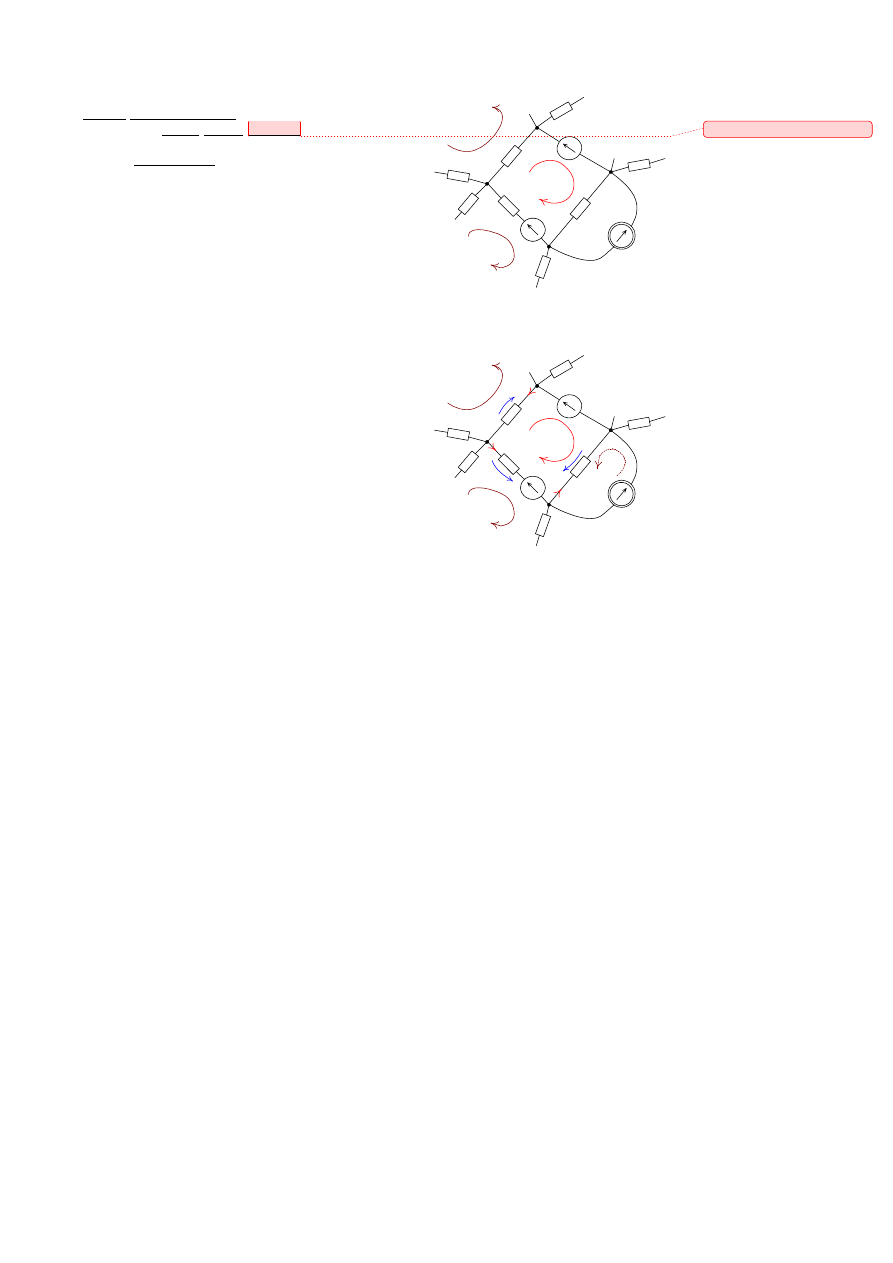
Rozpatrzmy fragment obwodu elektrycznego przedstawiony na
Rys. 1. Przyjmujmy, że znane są wartości parametrów tworzących
oczko „k” oraz wartości prądów płynących w sąsiednich oczkach.
Należy znaleźć równanie umożliwiające wyznaczenie wartości
prądu płynącego w oczku „k”.
Rozwiązanie:
1. Przyjmijmy kierunki napięć na poszczególnych pasywnych
elementach obwodu.
2. Wybierzmy niezależne oczka i przyjmijmy kierunki prądów
oczkowych w poszczególnych oczkach.
3. Napiszmy równanie wynikające z napięciowego prawa
Kirchhoffa dla oczka „k” przyjmując kierunek obiegu oczka
zgodny z kierunkiem prądu oczkowego:
u
A
- E
B
+ u
C
+ E
D
- u
D
= 0
Napięcia na poszczególnych elementach obwodu wynoszą:
u
A
= R
A
i
A
= - R
A
(i
k
+ i
m
)
u
C
= R
C
i
C
= - R
C
(i
k
+ I
ź
)
u
D
= R
D
i
D
= R
D
(i
k
- i
n
)
k
i
k
i
m
E
D
i
n
E
B
I
ź
R
D
R
C
R
A
Rys. 1. Fragment obwodu
k
i
k
i
m
E
D
i
n
E
B
I
ź
u
C
u
D
u
A
R
D
R
C
R
A
i
l
i
A
i
C
i
D
Rys. 2. Fragment obwodu z zaznaczonymi prądami
oczkowymi
Comment [LL1]:
2
© Lesław ŁADNIAK
Po podstawieniu do równania dla oczka „k” otrzymujemy:
-R
A
(i
k
+
i
m
)
-
E
B
+
-R
C
(i
k
+
I
ź
)
+
E
D
+
R
D
(i
k
-
i
n
)
=
0
- (R
A
+ R
C
+ R
D
)
i
k
- R
A
i
m
+ R
D
i
n
= E
B
- E
D
+ R
C
I
ź
(R
A
+ R
C
+ R
D
) i
k
+ R
A
i
m
- R
D
i
n
= -E
B
+ E
D
- R
C
I
ź
lub w postaci:
R
k
i
k
+ R
A
i
m
- R
D
i
n
= E
k
(*)
gdzie:
R
k
- suma rezystancji gałęzi tworzących oczko „k”,
R
A
- rezystancja wzajemna oczka „k” i oczka „m”,
R
D
- rezystancja wzajemna oczka „k” i oczka „n”,
E
k
– algebraiczna suma sił elektromotorycznych występujących
w oczku „k”.
Jak wynika z równania (*) wartość prądu płynącego w oczku
„k” zależy od sił elektromotorycznych występujących w oczku „k”,
napięć wywołanych przez prądy oczkowe płynące w oczkach
sąsiednich oraz od wartości parametrów elementów tworzących
oczko „k”.
W celu rozwiązania obwodu elektrycznego złożonego z „g”
gałęzi oraz „w” węzłów metodą prądów oczkowych, należy
napisać dla każdego oczka niezależnego równie wynikające z
napięciowego prawa Kirchhoffa.
R
1
i
1
R
12
i
2
...
R
1m
i
m
= E
1
:
R
k
i
k
R
k2
i
2
...
R
km
i
m
= E
k
:
R
m
i
m
R
m1
i
m1
...
R
mm-1
i
m-1
= E
m
Otrzymany w ten sposób układ „g - (w-1)” równań
umożliwia
wyznaczenie
wartości
wszystkich
prądów
oczkowych, a tym samym wartości prądów gałęziowych.
3
© Lesław ŁADNIAK
1.2 Metoda prądów oczkowych - algorytm
1. Przyjąć drzewo grafu dla danego schematu połączeń
elementów obwodu elektrycznego. O ile jest to możliwe, drzewo
grafu utworzyć z gałęzi pasywnych (nie zawierających źródeł).
2. Wybrać oczka niezależne i przyjąć kierunki prądów
oczkowych. Najczęściej kierunki prądów oczkowych przyjmuje
się zgodnie z kierunkiem gałęzi dopełnień drzewa lub zgodnie z
kierunkiem ruchu wskazówek zegara. Kierunek prądu oczkowego
jest kierunkiem odniesienia.
3. Dla
każdego oczka niezależnego napisać równanie
wynikające z napięciowego prawa Kirchhoffa, pamiętając, że:
napięcie na elemencie, przez który płynie tylko jeden prąd
oczkowy jest zawsze dodatnie, gdyż kierunek prądu oczkowego
jest zgodny z kierunkiem orientacji oczka,
jeżeli przez element przepływa więcej niż jeden prąd oczkowy,
to napięcie wywołane przepływem danego prądu jest dodatnie, gdy
kierunek tego prądu jest zgodny z kierunkiem prądu oczkowego,
źródło siły elektromotorycznej ma znak dodatni, jeżeli jest
zorientowane zgodnie z kierunkiem prądu oczkowego.
W celu ujednolicenia zapisu można źródła prądowe zastąpić
źródłami napięciowymi.
4. Rozwiązać
utworzony
układ
równań
(np.
metodą
wyznaczników), czyli wyznaczyć wartości wszystkich prądów
oczkowych.
Liczba
równań
jest
równa
liczbie
gałęzi
pomniejszonej o liczbę węzłów niezależnych.
W przypadku występowania w rozpatrywanym obwodzie
idealnych źródeł prądowych korzystnie jest tak wybrać oczka,
aby gałęzie z idealnymi źródłami były w gałęziami dopełniającymi
drzewo. Przy takim doborze oczek, prąd oczka zawierającego
idealne źródło prądowe jest znany, gdyż jest on równy prądowi
tego źródła. Nie ma więc potrzeby układania równań dla takiego
oczka.
k
i
k
i
m
E
D
i
n
E
B
I
ź
u
C
u
D
u
A
R
D
R
C
R
A
Rys. 3. Fragment obowdu